Kinetic Laser Absorption Spectroscopy of Vibrationally Excited Hydroxyl Radicals on Infrared Transitions ν = 3 ← 1 and ν = 4 ← 2
Abstract
1. Introduction
2. Materials and Methods
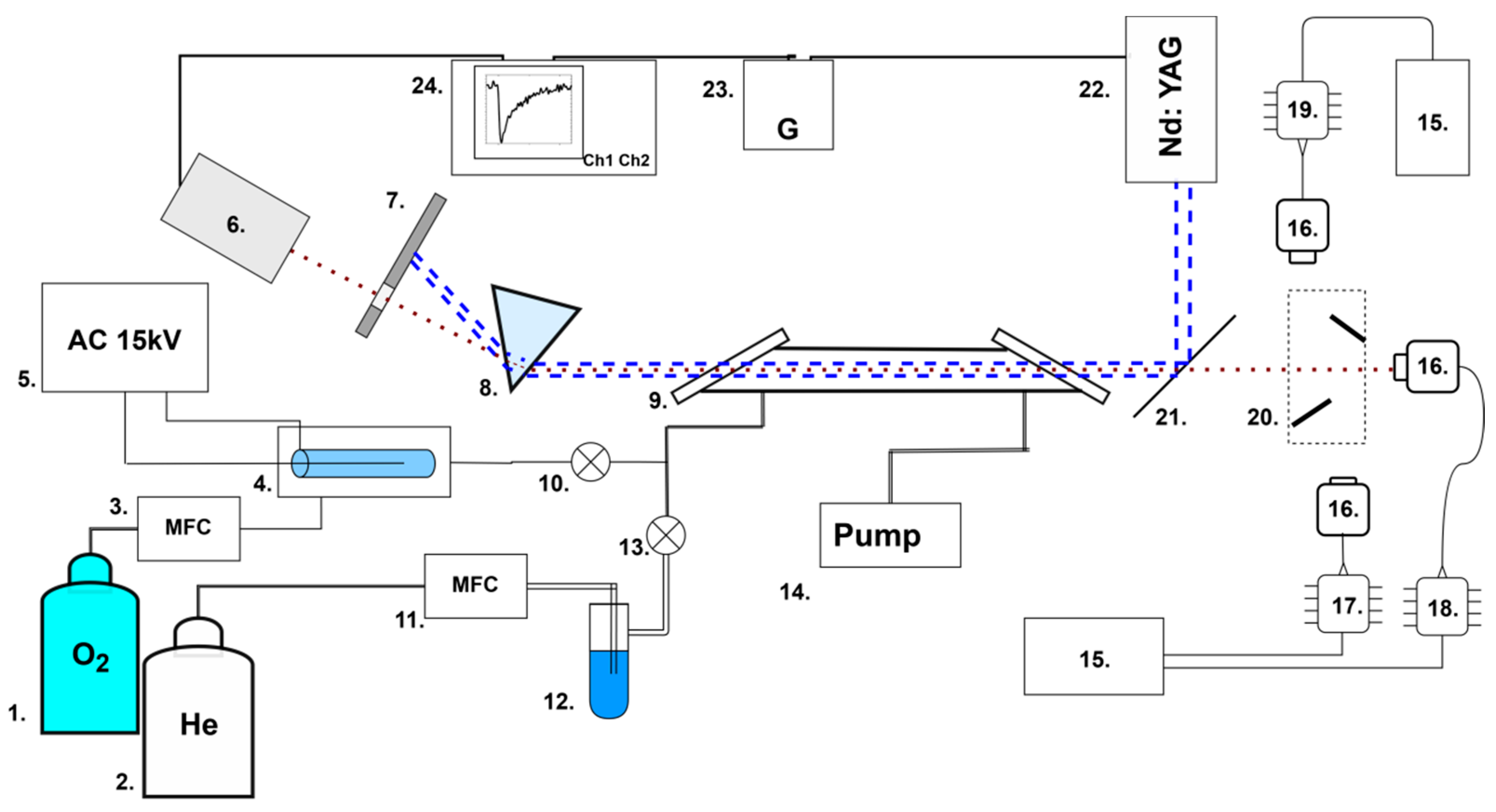
2.1. Experimental Setup
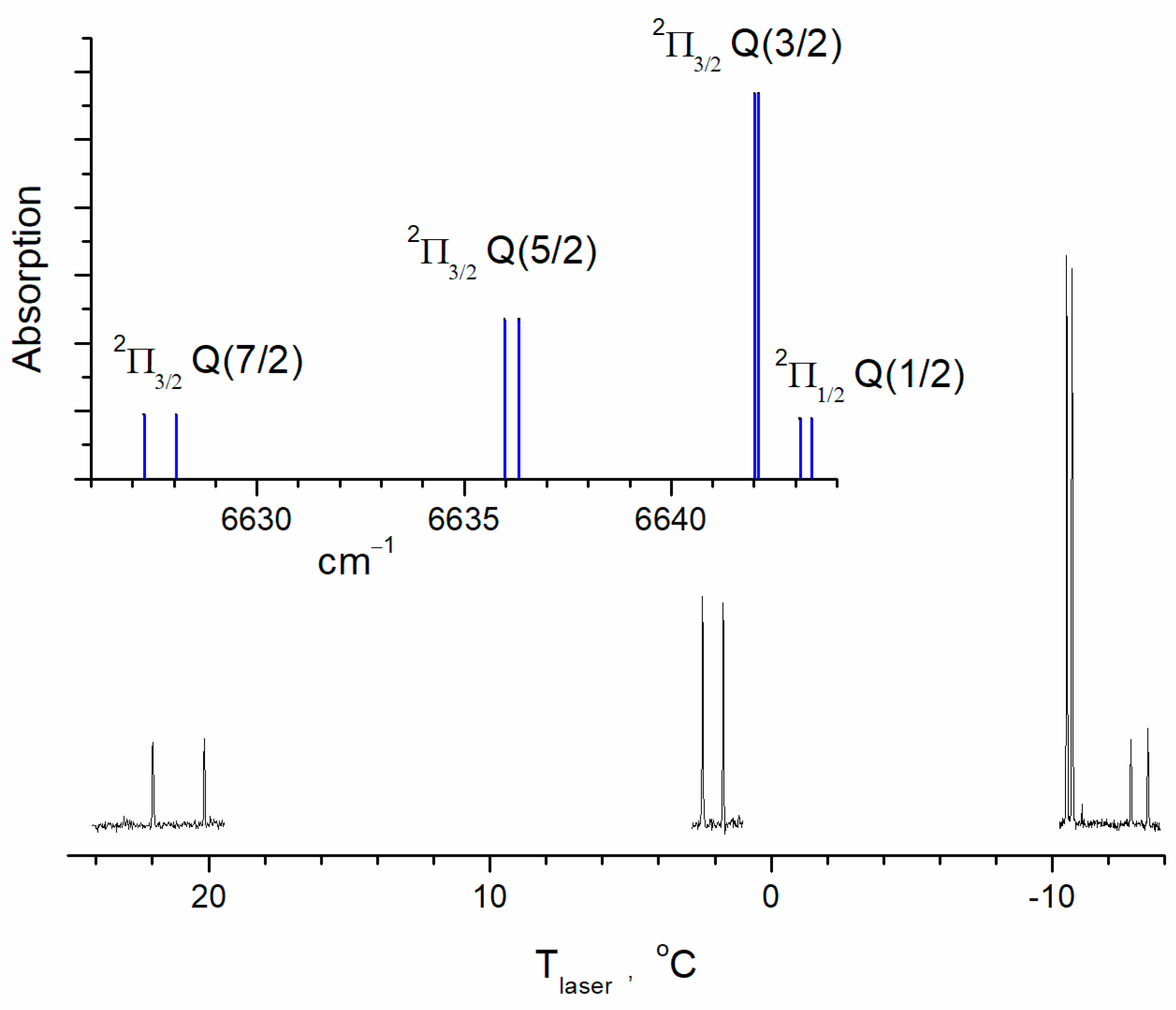
2.2. Cross-Sections of the Transitions
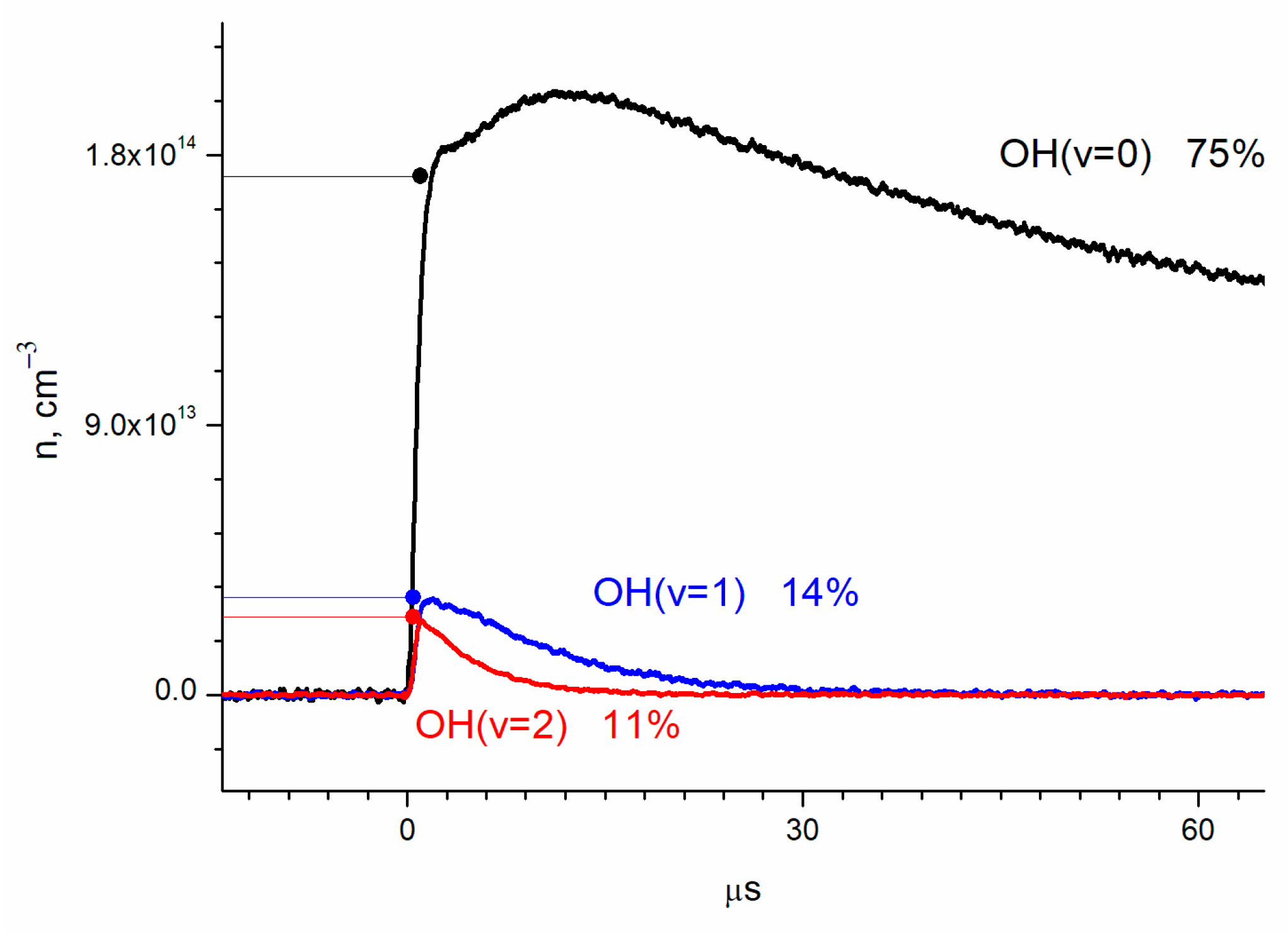
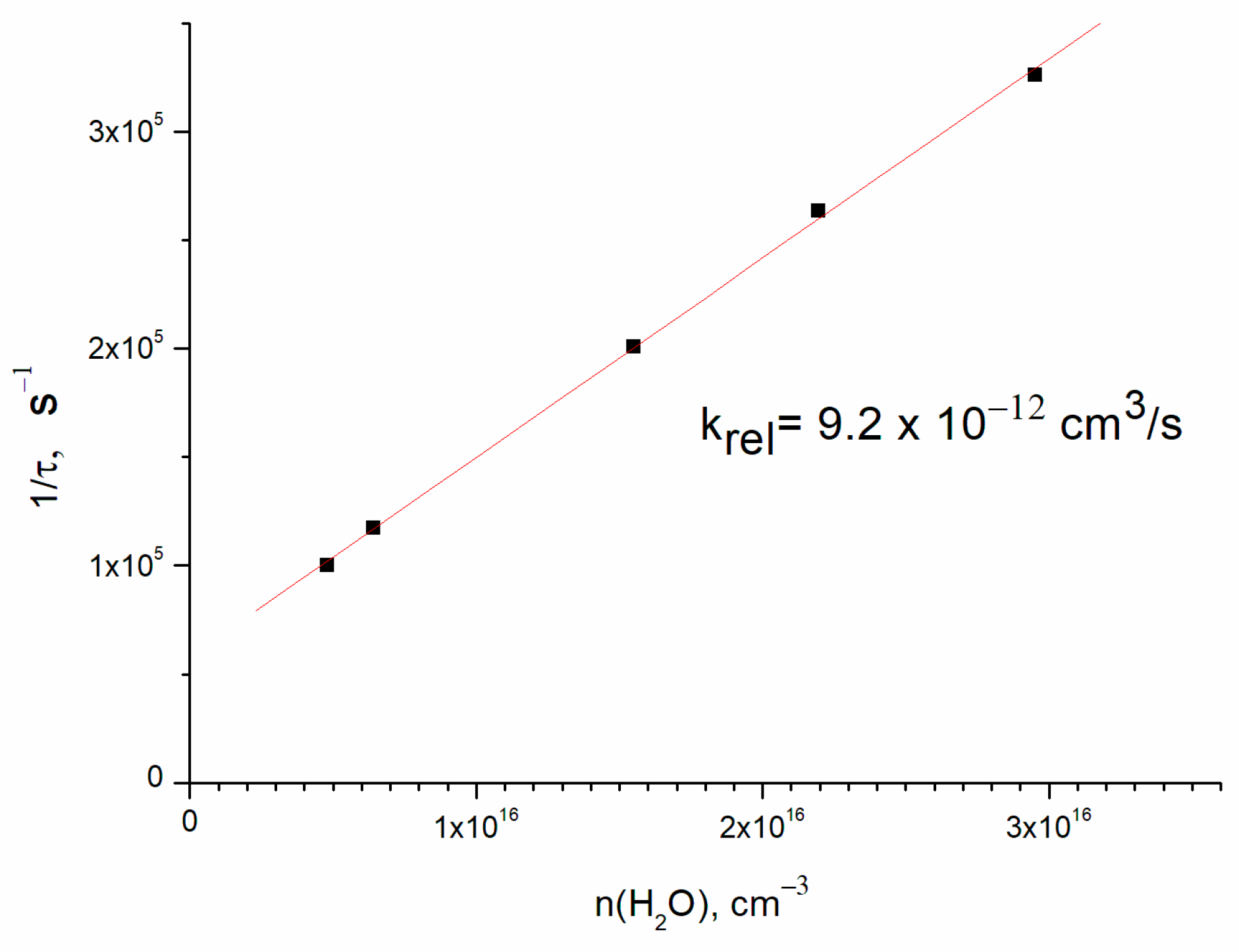
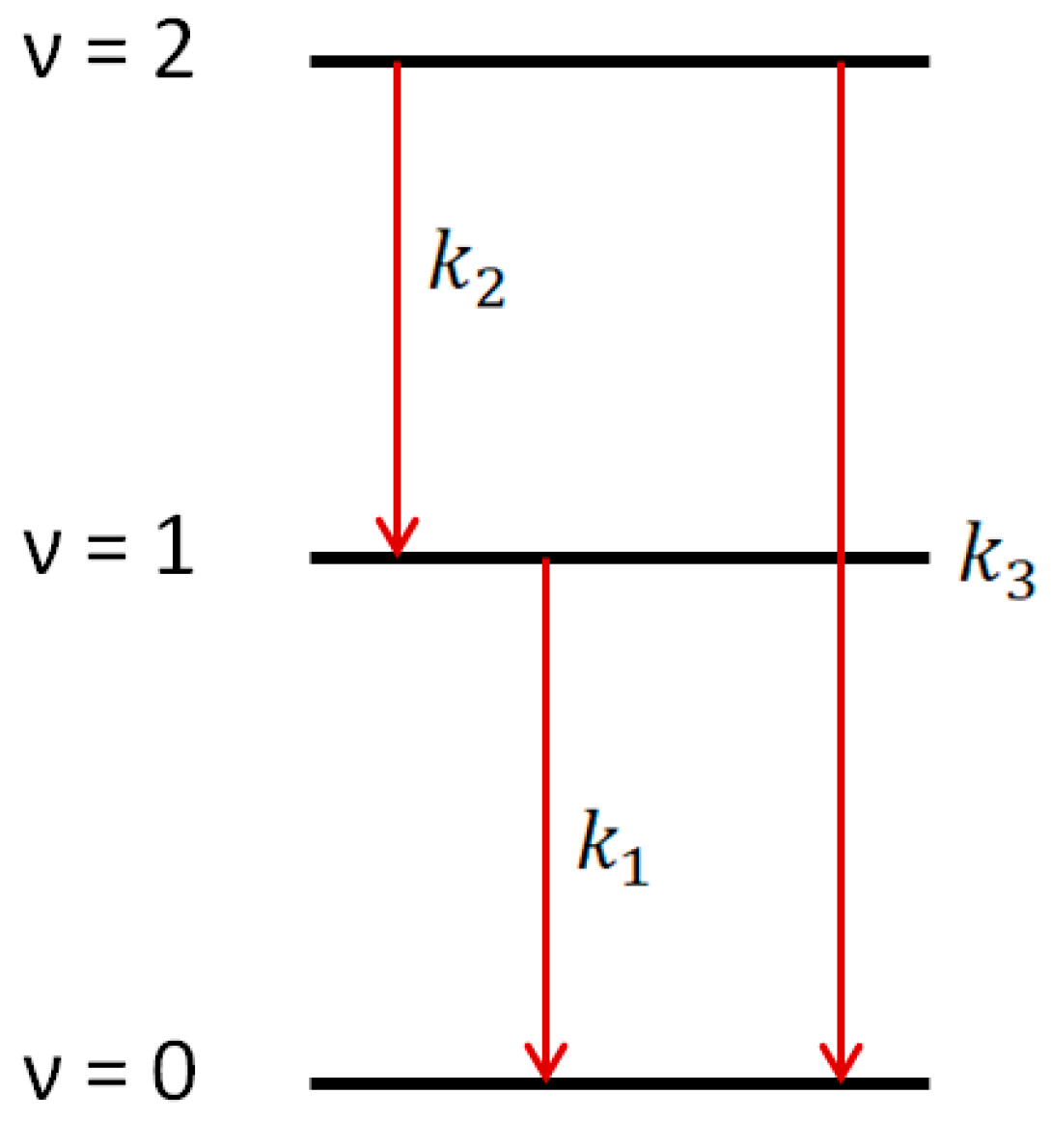
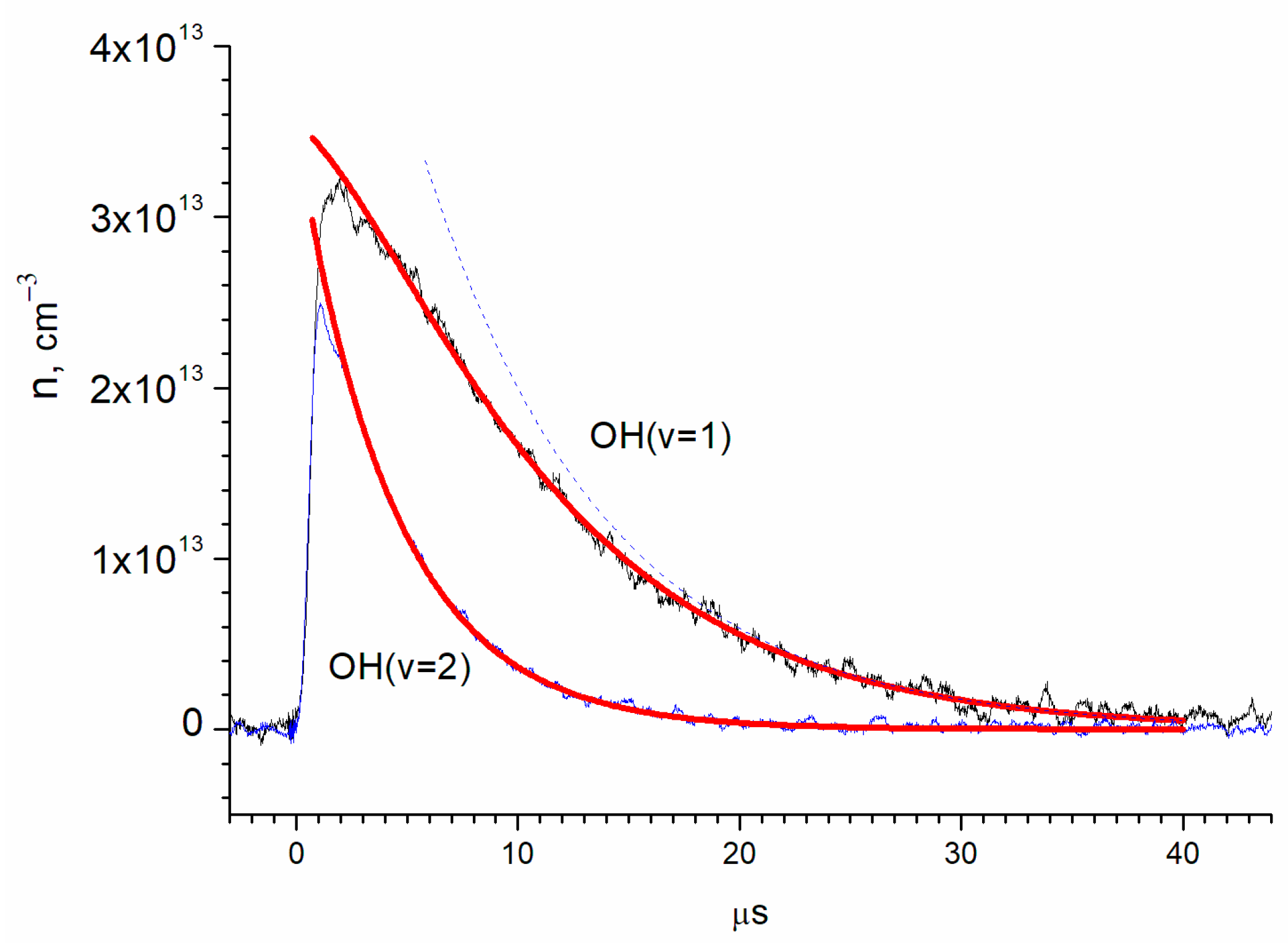
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cvetanović, R.J. Excited State Chemistry in the Stratosphere. Can. J. Chem. 1974, 52, 1452. [Google Scholar] [CrossRef]
- Gericke, K.-H.; Klee, S.; Comes, F.J.; Dixon, R.N. Dynamics of H2O2 photodissociation: OH product state and momentum distribution characterized by sub-Doppler and polarization spectroscopy. J. Chem. Phys. 1986, 85, 4463–4479. [Google Scholar] [CrossRef]
- Riffault, V.; Gierczak, T.; Burkholdera, J.B.; Ravishankara, A.R. Quantum yields for OH production in the photodissociation of HNO3. Phys. Chem. Chem. Phys. 2006, 8, 1079–1085. [Google Scholar] [CrossRef] [PubMed]
- Butler, J.E.; Talley, L.D.; Smith, G.K.; Lin, M.C. Rotational and vibrational energy distributions of 16OH(X 2Π) and 18OH(X 2Π) produced in the reaction of O(1D) with H2O and H218O. J. Chem. Phys. 1981, 74, 4501–4508. [Google Scholar] [CrossRef]
- Comes, F.J.; Gericke, K.-H.; Manz, J. Energy partitioning in the reaction 16O(1D)+H2 18O→16OH+18OH. IV. Microscopic probabilities for 16OH+18OH coincident pairs. J. Chem. Phys. 1981, 75, 2853–2863. [Google Scholar] [CrossRef]
- Gericke, K.-H.; Comes, F.J.; Levine, R.D. Energy partitioning in the reaction 16O(1D)+H2 18O→16OH+18OH. II. The distribution of 16OH and 18OH. J. Chem. Phys. 1981, 74, 6106–6112. [Google Scholar] [CrossRef]
- Cleveland, C.B.; Wiesenfeld, J.R. Nascent product population distribution in the reaction 16O(1D2)+H218O→16OH+18OH. J. Chem. Phys. 1992, 96, 248–255. [Google Scholar] [CrossRef]
- McCabe, D.C.; Rajakumar, B.; Marshall, P.; Smith, I.W.M.; Ravishankara, A.R. The relaxation of OH (v = 1) and OD (v = 1) by H2O and D2O at temperatures from 251 to 390 K. Phys. Chem. Chem. Phys. 2006, 8, 4563–4574. [Google Scholar] [CrossRef]
- Butler, J.E.; MacDonald, R.G.; Donaldson, D.J.; Sloan, J.J. Vibrational excitation of OH(X2Π) produced in the reaction of O(1D) with H2. Chem. Phys. Lett. 1983, 95, 183–188. [Google Scholar] [CrossRef]
- D’Ottone, L.; Bauer, D.; Campuzano-Jost, P.; Fardy, M.; Hynes, A.J. Kinetic and mechanistic studies of the recombination of OH with NO2: Vibrational deactivation, isotopic scrambling and product isomer branching ratios. Faraday Discuss. 2005, 130, 111–123. [Google Scholar] [CrossRef]
- McCabe, D.C.; Brown, S.S.; Gilles, M.K.; Talukdar, R.K.; Smith, I.W.M.; Ravishankara, A.R. Kinetics of the Removal of OH (v = 1) and OD (v = 1) by HNO3 and DNO3 from 253 to 383 K. J. Phys. Chem. A 2003, 107, 7762–7769. [Google Scholar] [CrossRef]
- Blitz, M.A.; Hughes, K.J.; Pilling, M.J. Determination of the High-Pressure Limiting Rate Coefficient and the Enthalpy of Reaction for OH + SO2. J. Phys. Chem. A 2003, 107, 1971–1978. [Google Scholar] [CrossRef]
- Blitz, M.A.; Salter, R.J.; Heard, D.E.; Seakins, P.W. An Experimental Study of the Kinetics of OH/OD(v = 1,2,3) + SO2: The Limiting High-Pressure Rate Coefficients as a Function of Temperature. J. Phys. Chem. A 2017, 121, 3175–3183. [Google Scholar] [CrossRef]
- Zhang, L.; Varandas, A.J.C. Dynamics of the OH(v = 1,2,4) + O3 Atmospheric Reaction. Phys. Chem. Chem. Phys. 2001, 3, 1439–1445. [Google Scholar] [CrossRef]
- Talukdar, R.K.; Gierczak, T.; McCabe, D.C.; Ravishankara, A.R. Reaction of hydroxyl radical with acetone. Products and reaction mechanism. J. Phys. Chem. A 2003, 107, 5021–5032. [Google Scholar] [CrossRef]
- Clough, P.N.; Curran, A.H.; Thrush, B.A. The E.P.R. Spectrum of Vibrationally Excited Hydroxyl Radicals. Proc. R. Soc. Lond. 1971, 323, 541–554. [Google Scholar] [CrossRef]
- Davies, P.B.; Hack, W.; Preuss, A.W.; Temps, F. Far infrared laser magnetic resonance spectra of vibrationally excited OH. Chem. Phys. Lett. 1979, 6, 94–97. [Google Scholar] [CrossRef]
- Streit, G.E.; Johnston, H.S. Reactions and quenching of vibrationally excited hydroxyl radicals. J. Chem. Phys 1976, 64, 95. [Google Scholar] [CrossRef]
- Streit, G.E.; Whitten, G.Z.; Johnston, H.S. The fate of vibrationally excited hydroxyl radicals, HO(v ≤ 9) in stratosphere. Geophys. Res. Letts. 1976, 3, 521. [Google Scholar] [CrossRef]
- Smith, G.K.; Fisher, E.R. Vibrationally excited hydroxyl in the products of the atomic hydrogen + nitrogen dioxide reaction. J. Chem. Phys 1978, 82, 2139–2140. [Google Scholar] [CrossRef]
- Plastinina, D.M.; Koshlyakov, P.V.; Chesnokov, E.N. Time-Resolved Determination of the Absolute Concentration of OH Radicals by Absorption in the Overtone Region (1434 nm). High En. Chem. 2023, 57, S455–S459. [Google Scholar] [CrossRef]
- Shengshi Optical (8–10 mw 1653.5 nm Butterfly Laser Diode for Gas Detection). Available online: http://laserdiodedevice.com/1-3-butterfly-pigtail-laser-modules.html (accessed on 9 December 2024).
- Brooke, J.S.A.; Bernath, P.F.; Western, C.M.; Sneden, C.; Afşar, M.; Li, G.; Gordon, I.E. Line strengths of rovibrational and rotational transitions in the X2Π ground state of OH. J. Quant. Spectrosc. Radiat. Transf. 2016, 168, 142–157. [Google Scholar] [CrossRef]
- Noll, S.; Winkler, H.; Goussev, O.; Proxauf, B. OH level populations and accuracies of Einstein-A coefficients from hundreds of measured lines. Atmos. Chem. Phys. 2020, 20, 5269–5292. [Google Scholar] [CrossRef]
- Mikhailenko, S.N.; Babikov, Y.L.; Golovko, V.F. Information-calculating system Spectroscopy of Atmospheric Gases. The structure and main functions. Atmos. Ocean. Opt. 2005, 18, 685–695. [Google Scholar]
- Chesnokov, E.N.; Plastinina, D.M.; Koshlyakov, P.V. Detection of vibrationally excited hydroxyl radicals by absorption of the DFB diode laser radiation at the transition (ν = 3) ← (ν = 1). Chem. Phys. Lett. 2024, 849, 141445. [Google Scholar] [CrossRef]
- Radford, H.E. Microwave Zeeman Effect of Free Hydroxyl Radicals. Phys. Rev. 1961, 122, 114. [Google Scholar] [CrossRef]
- Plastinina, D.M.; Koshlyakov, P.V.; Chesnokov, E.N. Time-resolved FRS detection of OH radical for chemical reactions rate measurement. Laser Phys. 2024, 34, 045702. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plastinina, D.M.; Chesnokov, E.N.; Koshlyakov, P.V.; Krasnoperov, L.N. Kinetic Laser Absorption Spectroscopy of Vibrationally Excited Hydroxyl Radicals on Infrared Transitions ν = 3 ← 1 and ν = 4 ← 2. Molecules 2025, 30, 540. https://doi.org/10.3390/molecules30030540
Plastinina DM, Chesnokov EN, Koshlyakov PV, Krasnoperov LN. Kinetic Laser Absorption Spectroscopy of Vibrationally Excited Hydroxyl Radicals on Infrared Transitions ν = 3 ← 1 and ν = 4 ← 2. Molecules. 2025; 30(3):540. https://doi.org/10.3390/molecules30030540
Chicago/Turabian StylePlastinina, Daria M., Evgeni N. Chesnokov, Pavel V. Koshlyakov, and Lev N. Krasnoperov. 2025. "Kinetic Laser Absorption Spectroscopy of Vibrationally Excited Hydroxyl Radicals on Infrared Transitions ν = 3 ← 1 and ν = 4 ← 2" Molecules 30, no. 3: 540. https://doi.org/10.3390/molecules30030540
APA StylePlastinina, D. M., Chesnokov, E. N., Koshlyakov, P. V., & Krasnoperov, L. N. (2025). Kinetic Laser Absorption Spectroscopy of Vibrationally Excited Hydroxyl Radicals on Infrared Transitions ν = 3 ← 1 and ν = 4 ← 2. Molecules, 30(3), 540. https://doi.org/10.3390/molecules30030540








