Uranyl(VI) Interaction with 2-Phosphonobutane-1,2,4-Tricarboxylic Acid (PBTC): A Spectroscopic and Computational Study over a Wide pH Range
Abstract
1. Introduction
2. Results and Discussion
- I.
- Investigation of complex speciation: Estimation of the number and distribution of the formed complexes using UV-Vis, Raman, TRLF, and NMR spectroscopies (Section 2.1).
- II.
- Structure elucidation: Determination of the main binding motif involved in complexation using NMR, ATR FT-IR, and DF methods (Section 2.2).
- III.
- Determination of thermodynamic data: Complex formation constants derived from UV-Vis spectra combined with species characterization (Section 2.3).
- IV.
- Consideration of additional minor U(VI)-PBTC complex species (Section 2.4).
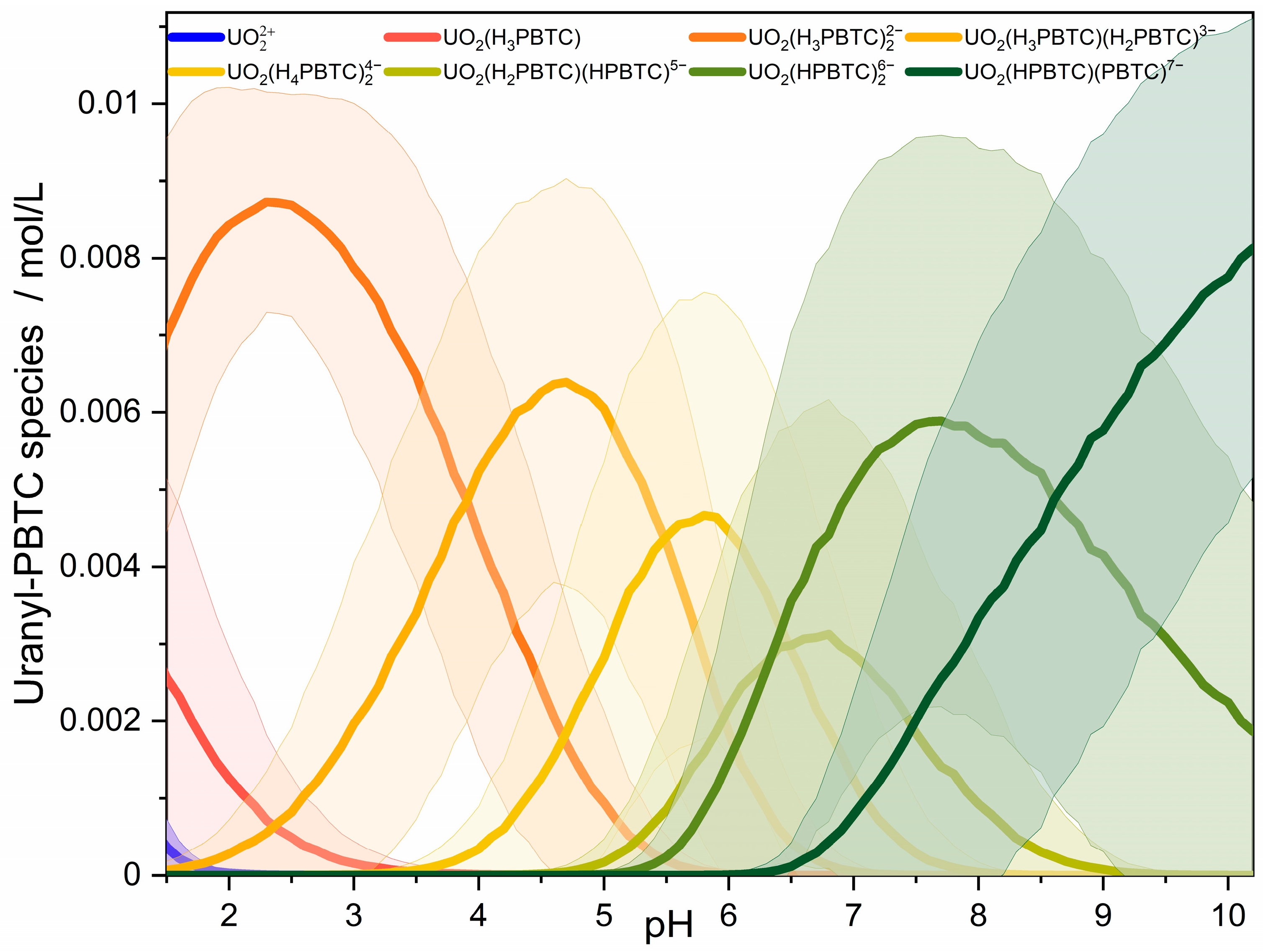
2.1. U(VI)-PBTC Complex Speciation
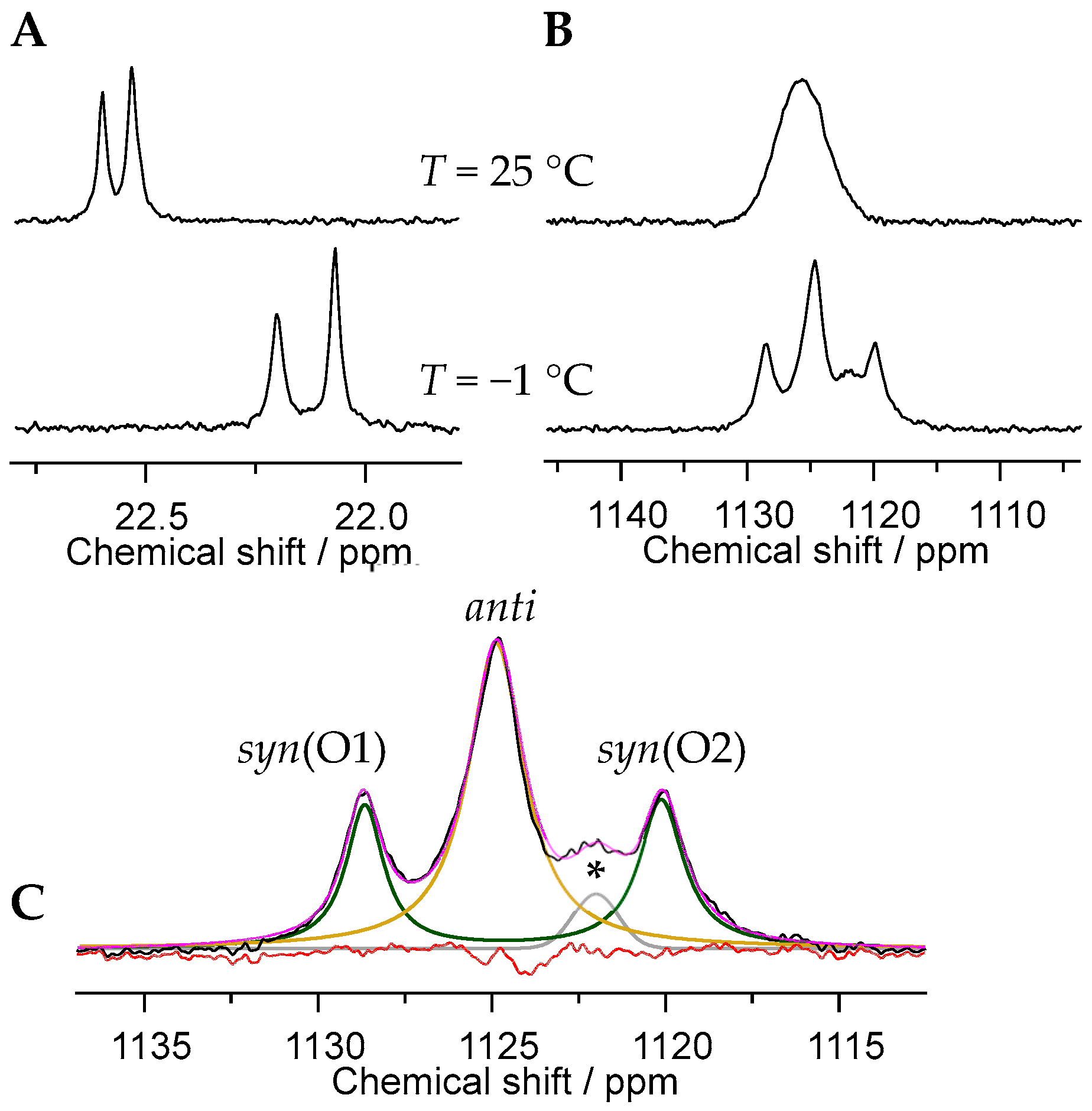
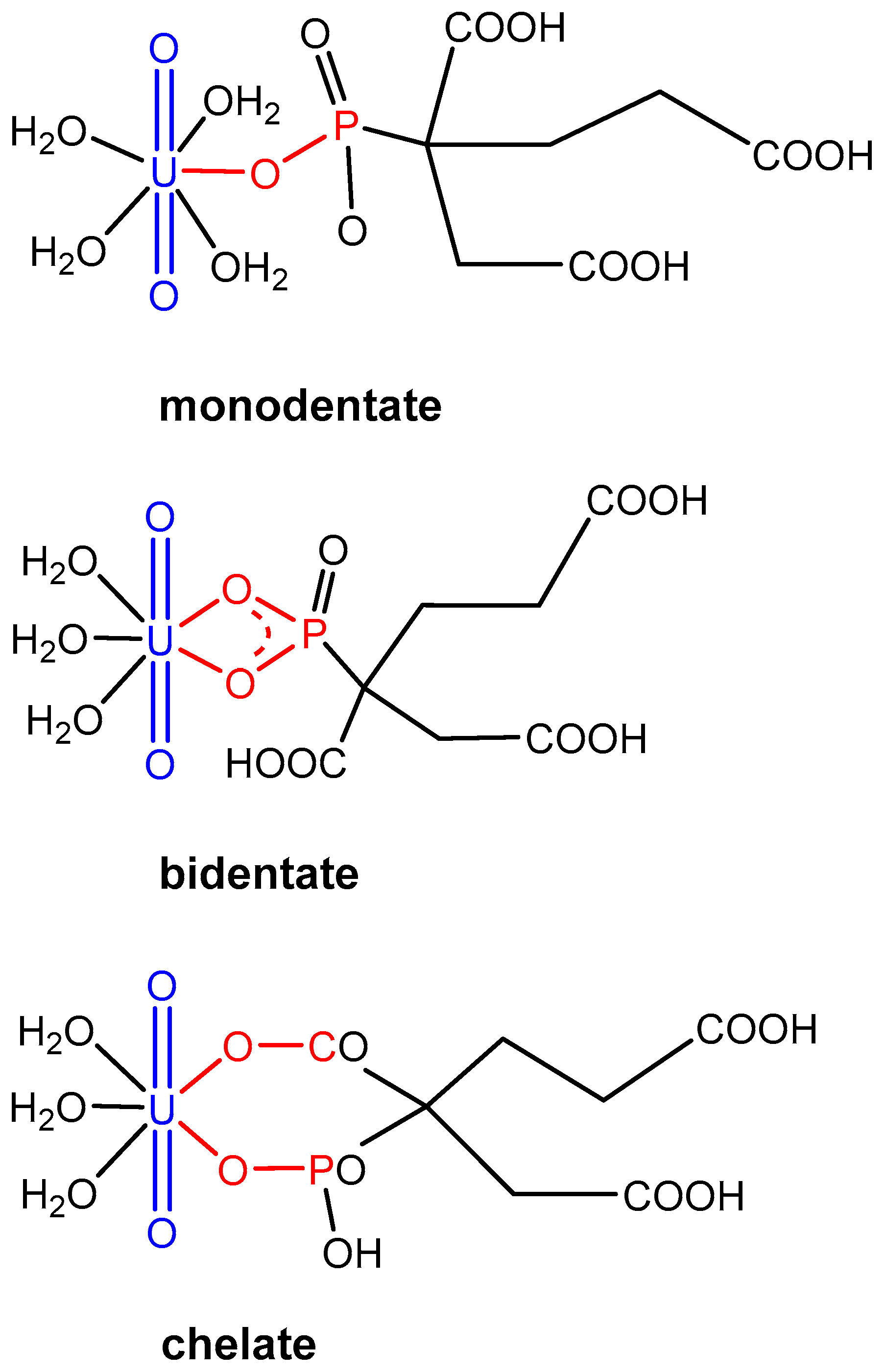
2.2. Characterization of the Principal U(VI)-PBTC Binding Motif
| Complex | U(VI)-Ligand-Proton | ΔG |
|---|---|---|
| UO2(H4PBTC)+ | 114 | −41 |
| UO2(H3PBTC)0 | 113 | −119 |
| UO2(H4PBTC)20 | 128 | −37 |
| UO2(H4PBTC)(H3PBTC)− | 127 | −106 |
| UO2(H3PBTC)22− | 126 | −180 |
| UO2(H3PBTC)(H2PBTC)3− | 125 | −216 |
| UO2(H2PBTC)24− | 124 | −278 |
| UO2(H1PBTC)26− | 122 | −294 |
| UO2(H3PBTC)34− | 139 | −129 |
2.3. Complex Stability Constant of the Main U(VI)-PBTC Complex
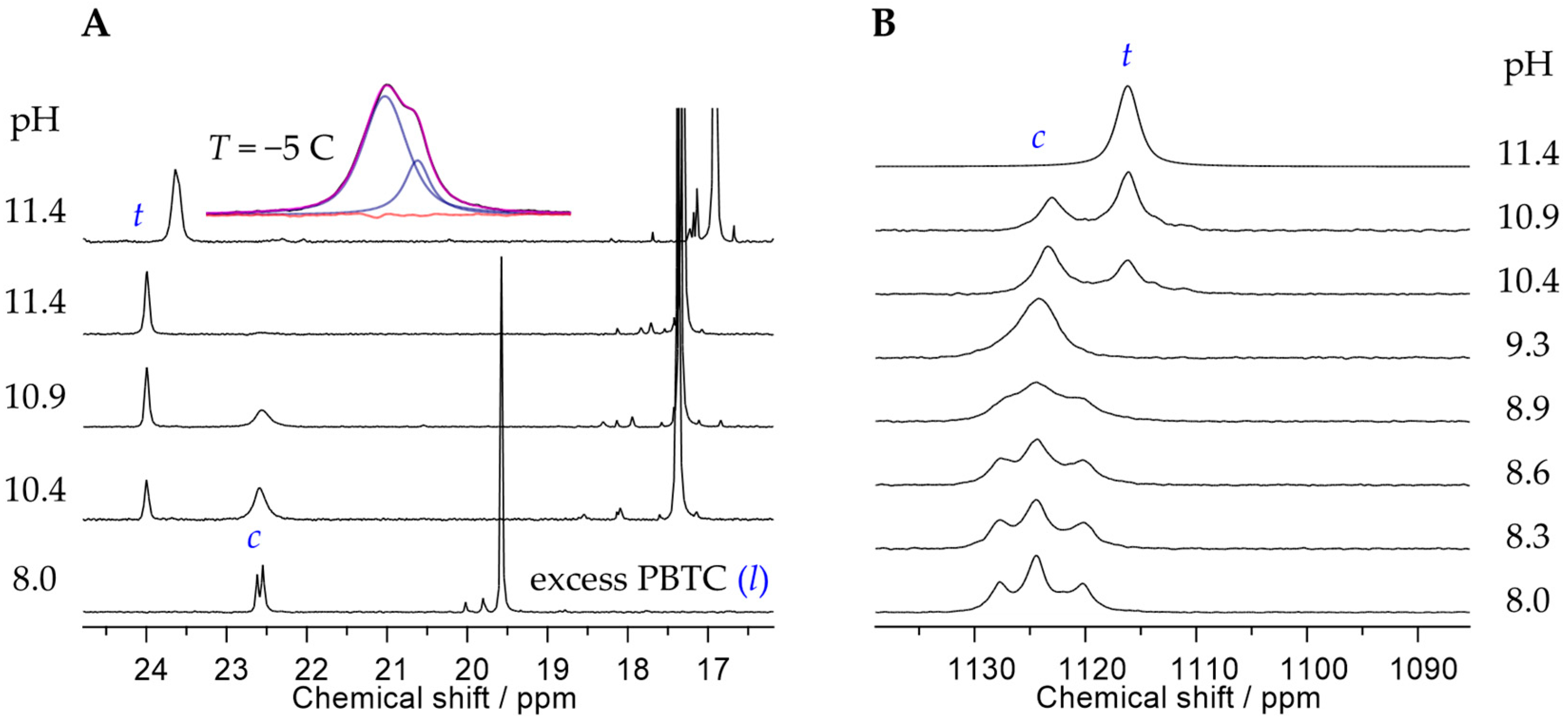
2.4. Expanded Insights into Uranyl(VI)–PBTC Speciation via Detailed 17O NMR
3. Materials and Methods
3.1. General Remarks
3.2. Preparation of Aqueous Sample Solutions
3.3. Nuclear Magnetic Resonance (NMR) Spectroscopy
3.4. Attenuated Total Reflection Fourier-Transform Infrared (ATR FT-IR) Spectroscopy
3.5. UV-Vis Spectroscopy
3.6. Raman Spectroscopy
3.7. Time-Resolved Laser-Induced Luminescence Spectroscopy (TRLFS)
3.8. Quantum Chemistry Calculations Based on the Density Functional Theory (DFT)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saedi, A.; Jamshidi-Zanjani, A.; Darban, A.K. A review of additives used in the cemented paste tailings: Environmental aspects and application. J. Environ. Manag. 2021, 289, 112501. [Google Scholar] [CrossRef]
- Chen, J.; Jia, J.; Zhu, M. A critical review of the effect of chemical organic admixtures for OPC-based materials. Mater. Chem. Phys. 2024, 322, 129591. [Google Scholar] [CrossRef]
- Demadis, K.D.; Lykoudis, P. Chemistry of Organophosphonate Scale Growth lnhibitors: 3. Physicochemical Aspects of 2-Phosphonobutane-1,2,4-tricarboxylate (PBTC) And Its Effect on CaCO3 Crystal Growth. Bioinorg. Chem. Appl. 2005, 3, 135–149. [Google Scholar] [CrossRef]
- Demadis, K.D.; Lykoudis, P.; Raptis, R.G.; Mezei, G. Phosphonopolycarboxylates as chemical additives for calcite scale dissolution and metallic corrosion inhibition based on a calcium-phosphonotricarboxylate organic−inorganic hybrid. Cryst. Growth Des. 2006, 6, 1064–1067. [Google Scholar] [CrossRef]
- Rott, E.; Happel, O.; Armbruster, D.; Minke, R. Behavior of PBTC, HEDP, and Aminophosphonates in the Process of Wastewater Treatment. Water 2020, 12, 53. [Google Scholar] [CrossRef]
- Rott, E.; Steinmetz, H.; Metzger, J.W. Organophosphonates: A review on environmental relevance, biodegradability and removal in wastewater treatment plants. Sci. Total Environ. 2018, 615, 1176–1191. [Google Scholar] [CrossRef]
- Qiao, Z.; Fan, W.; Zhang, Y.; Fu, X.; Yang, H.; Zhang, F. Enhancement of Magnesium Oxysulfate Cement by Acid Modifiers and Its Reaction Mechanism. Materials 2025, 18, 1432. [Google Scholar] [CrossRef] [PubMed]
- Heal, K.; Smith, K.; Younger, P.; McHaffie, H.; Batty, L. Phosphorus in Environmental Technology: Principles and Applications; IWA Publishing: London, UK, 2004. [Google Scholar]
- Armbruster, D.; Müller, U.; Happel, O. Characterization of phosphonate-based antiscalants used in drinking water treatment plants by anion-exchange chromatography coupled to electrospray ionization time-of-flight mass spectrometry and inductively coupled plasma mass spectrometry. J. Chromatogr. A 2019, 1601, 189–204. [Google Scholar] [CrossRef]
- Rickert, J.; Thielen, G. Influence of a long-term retarder on the hydration of clinker and cement. Cem. Concr. Aggreg. 2004, 26, 1–10. [Google Scholar] [CrossRef]
- Salvadó, V.; Escoda, M.L.s.; de la Torre, F. A study of the complex formation between trivalent ions (Al3+, Fe3+) and 2-phosphonobutane-1,2,4-tricarboxylic acid and their industrial applications. Polyhedron 1999, 18, 3275–3280. [Google Scholar] [CrossRef]
- Clearfield, A.; Demadis, K. Metal Phosphonate Chemistry: From Synthesis to Applications; Royal Society of Chemistry: London, UK, 2012. [Google Scholar]
- Huang, Y.; Zheng, H.; Li, H.; Zhao, C.; Zhao, R.; Li, S. Highly selective uranium adsorption on 2-phosphonobutane-1,2,4-tricarboxylic acid-decorated chitosan-coated magnetic silica nanoparticles. Chem. Eng. J. 2020, 388, 124349. [Google Scholar] [CrossRef]
- Spinthaki, A.; Matheis, J.; Hater, W.; Demadis, K.D. Antiscalant-driven inhibition and stabilization of “magnesium silicate” under geothermal stresses: The role of magnesium–phosphonate coordination chemistry. Energy Fuels 2018, 32, 11749–11760. [Google Scholar] [CrossRef]
- Knepper, T.P. Synthetic chelating agents and compounds exhibiting complexing properties in the aquatic environment. TrAC Trends Anal. Chem. 2003, 22, 708–724. [Google Scholar] [CrossRef]
- Srivastava, A.; Dumpala, R.M.R.; Kumar, P.; Kumar, R.; Rawat, N. Chemical and redox speciation of uranyl with three environmentally relevant bifunctional chelates: Multi-technique approach combined with theoretical estimations. Inorg. Chem. 2022, 61, 15452–15462. [Google Scholar] [CrossRef]
- Szabó, Z. Structure, equilibrium and ligand exchange dynamics in the binary and ternary dioxouranium(VI)–glyphosate–fluoride system. A multinuclear NMR study. J. Chem. Soc. Dalton Trans. 2002, 22, 4242–4247. [Google Scholar] [CrossRef]
- Nguyen Trung, C.; Begun, G.; Palmer, D.A. Aqueous uranium complexes. 2. Raman spectroscopic study of the complex formation of the dioxouranium(VI) ion with a variety of inorganic and organic ligands. Inorg. Chem. 1992, 31, 5280–5287. [Google Scholar] [CrossRef]
- Nguyen-Trung, C.; Palmer, D.; Begun, G.; Peiffert, C.; Mesmer, R. Aqueous uranyl complexes 1. Raman spectroscopic study of the hydrolysis of uranyl(VI) in solutions of trifluoromethanesulfonic acid and/or tetramethylammonium hydroxide at 25 C and 0.1 MPa. J. Solut. Chem. 2000, 29, 101–129. [Google Scholar] [CrossRef]
- Lu, G.; Forbes, T.Z.; Haes, A.J. Evaluating best practices in Raman spectral analysis for uranium speciation and relative abundance in aqueous solutions. Anal. Chem. 2016, 88, 773–780. [Google Scholar] [CrossRef]
- Tsushima, S. On the “yl” bond weakening in uranyl(VI) coordination complexes. Dalton Trans. 2011, 40, 6732–6737. [Google Scholar] [CrossRef]
- Lu, G.; Haes, A.J.; Forbes, T.Z. Detection and identification of solids, surfaces, and solutions of uranium using vibrational spectroscopy. Coord. Chem. Rev. 2018, 374, 314–344. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, Q.; Lan, Y.; Zhang, Q.; Zhu, L.; Yang, S.; Tian, G.; Cao, X.; Dolg, M. Systematic Raman Spectroscopic Study of the Complexation of Uranyl with Fluoride. Phys. Chem. Chem. Phys. 2024, 26, 18584–18591. [Google Scholar] [CrossRef]
- Kirkham, A.J.; Bryan, N.D.; May, I. Uranyl Coordination to Environmentally Relevant Polyhydroxy Carboxylate Ligands. In Recent Advances in Actinide Science; The University of Manchester: Manchester, UK, 2006; pp. 246–248. [Google Scholar]
- Birjkumar, K.H.; Bryan, N.D.; Kaltsoyannis, N. Computational investigation of the speciation of uranyl gluconate complexes in aqueous solution. Dalton Trans. 2011, 40, 11248–11257. [Google Scholar] [CrossRef] [PubMed]
- Faulques, E.; Kalashnyk, N.; Massuyeau, F.; Perry, D. Spectroscopic markers for uranium(VI) phosphates: A vibronic study. RSC Adv. 2015, 5, 71219–71227. [Google Scholar] [CrossRef]
- Drobot, B.; Bauer, A.; Steudtner, R.; Tsushima, S.; Bok, F.; Patzschke, M.; Raff, J.; Brendler, V. Speciation studies of metals in trace concentrations: The mononuclear uranyl(VI) hydroxo complexes. Anal. Chem. 2016, 88, 3548–3555. [Google Scholar] [CrossRef]
- Meinrath, G. Uranium(VI) speciation by spectroscopy. J. Radioanal. Nucl. Chem. 1997, 224, 119–126. [Google Scholar] [CrossRef]
- Rossberg, A.; Reich, T.; Bernhard, G. Complexation of uranium(VI) with protocatechuic acid—Application of iterative transformation factor analysis to EXAFS spectroscopy. Anal. Bioanal. Chem. 2003, 376, 631–638. [Google Scholar] [CrossRef]
- Malinowski, E.R.; Howery, D.G. Factor Analysis in Chemistry, 3rd ed.; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Wollenberg, A.; Tsushima, S.; Schmeide, K.; Acker, M. 2-Phosphonobutane-1,2,4,-Tricarboxylic Acid (PBTC): pH-Dependent Behavior Studied by Means of Multinuclear NMR Spectroscopy. Molecules 2022, 27, 4067. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Tsushima, S.; Lucks, C.; Jäckel, E.; Meyer, R.; Steudtner, R.; Müller, K.; Rossberg, A.; Schmeide, K.; Brendler, V. Dimeric and trimeric uranyl(VI)–citrate complexes in aqueous solution. Inorg. Chem. 2021, 60, 7998–8010. [Google Scholar] [CrossRef]
- Geipel, G. Some aspects of actinide speciation by laser-induced spectroscopy. Coord. Chem. Rev. 2006, 250, 844–854. [Google Scholar] [CrossRef]
- Kato, Y.; Meinrath, G.; Kimura, T.; Yoshida, Z. A study of U (VI) hydrolysis and carbonate complexation by time-resolved laser-induced fluorescence spectroscopy (TRLFS). Radiochim. Acta 1994, 64, 107–112. [Google Scholar] [CrossRef]
- Demnitz, M.; Hilpmann, S.; Lösch, H.; Bok, F.; Steudtner, R.; Patzschke, M.; Stumpf, T.; Huittinen, N. Temperature-dependent luminescence spectroscopic investigations of uranyl(VI) complexation with the halides F− and Cl−. Dalton Trans. 2020, 49, 7109–7122. [Google Scholar] [CrossRef]
- Shang, C.; Reiller, P.E. Determination of formation constants and specific ion interaction coefficients for CanUO2(CO3)3(4− 2n)− complexes in NaCl solution by time-resolved laser-induced luminescence spectroscopy. Dalton Trans. 2020, 49, 466–481. [Google Scholar] [CrossRef]
- Sirven, J.-B.; Szenknect, S.; Vors, E.; Anzalone, E.; Benarib, S.; Sarr, P.-M.; Reiller, P.E.; Mesbah, A.; Dacheux, N.; Vercouter, T. Time-resolved laser-induced fluorescence spectroscopy and chemometrics for fast identification of U(VI)-bearing minerals in a mining context. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 296, 122671–122683. [Google Scholar] [CrossRef] [PubMed]
- Billard, I.; Ansoborlo, E.; Apperson, K.; Arpigny, S.; Azenha, M.E.; Birch, D.; Bros, P.; Burrows, H.D.; Choppin, G.; Couston, L.; et al. Aqueous Solutions of Uranium(VI) as Studied by Time-Resolved Emission Spectroscopy: A Round-Robin Test. Appl. Spectrosc. 2003, 57, 1027–1038. [Google Scholar] [CrossRef]
- Oher, H.; Ferru, G.; Couston, L.; Berthon, L.; Guillaumont, D.; Réal, F.; Vercouter, T.; Vallet, V. Influence of the first coordination of uranyl on its luminescence properties: A study of uranyl binitrate with N, N-dialkyl amide DEHiBA and water. Inorg. Chem. 2021, 61, 890–901. [Google Scholar] [CrossRef]
- Burrows, H.; Kemp, T. The photochemistry of the uranyl ion. Chem. Soc. Rev. 1974, 3, 139–165. [Google Scholar] [CrossRef]
- Kim, Y.; Marcano, M.C.; Ellis, B.R.; Becker, U. Photocatalytic reduction of uranyl: Effects of organic ligands and UV light wavelengths. Am. J. Sci. 2018, 318, 949–968. [Google Scholar] [CrossRef]
- Wang, Z.; Zachara, J.M.; Yantasee, W.; Gassman, P.L.; Liu, C.; Joly, A.G. Cryogenic laser induced fluorescence characterization of U(VI) in Hanford vadose zone pore waters. Environ. Sci. Technol. 2004, 38, 5591–5597. [Google Scholar] [CrossRef]
- Marcantonatos, M.D.; Pawlowska, M.M. The second emission of the uranyl ion in aqueous solution. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1989, 85, 2481–2498. [Google Scholar] [CrossRef]
- Choppin, G.R.; Rao, L.F. Complexation of pentavalent and hexavalent actinides by fluoride. Radiochim. Acta 1984, 37, 143–146. [Google Scholar] [CrossRef]
- Heller, A.; Senwitz, C.; Foerstendorf, H.; Tsushima, S.; Holtmann, L.; Drobot, B.; Kretzschmar, J. Europium(III) meets etidronic acid (HEDP): A coordination study combining spectroscopic, spectrometric, and quantum chemical methods. Molecules 2023, 28, 4469. [Google Scholar] [CrossRef]
- Pasilis, S.P.; Pemberton, J.E. Speciation and coordination chemistry of uranyl (VI)− citrate complexes in aqueous solution. Inorg. Chem. 2003, 42, 6793–6800. [Google Scholar] [CrossRef]
- Zenobi, M.C.; Luengo, C.V.; Avena, M.J.; Rueda, E.H. An ATR-FTIR study of different phosphonic acids in aqueous solution. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2008, 70, 270–276. [Google Scholar] [CrossRef]
- Zou, C.J.; Tang, Q.W.; Lan, G.H.; Tian, Q.; Wang, T.Y. Enhancement inhibition efficiency of PBTCA depending on the inclusion complex with hydroxypropyl-β-cyclodextrin. J. Incl. Phenom. Macrocycl. Chem. 2012, 76, 61–68. [Google Scholar] [CrossRef]
- Barkleit, A.; Foerstendorf, H.; Li, B.; Rossberg, A.; Moll, H.; Bernhard, G. Coordination of uranium(VI) with functional groups of bacterial lipopolysaccharide studied by EXAFS and FT-IR spectroscopy. Dalton Trans. 2011, 40, 9868–9876. [Google Scholar] [CrossRef] [PubMed]
- Kakihana, M.; Nagumo, T.; Okamoto, M.; Kakihana, H. Coordination structures for uranyl carboxylate complexes in aqueous solution studied by IR and carbon-13 NMR spectra. J. Phys. Chem. 1987, 91, 6128–6136. [Google Scholar] [CrossRef]
- Deacon, G.; Phillips, R. Relationships between the carbon-oxygen stretching frequencies of carboxylato complexes and the type of carboxylate coordination. Coord. Chem. Rev. 1980, 33, 227–250. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Strobel, A.; Haubitz, T.; Drobot, B.; Steudtner, R.; Barkleit, A.; Brendler, V.; Stumpf, T. Uranium(VI) complexes of glutathione disulfide forming in aqueous solution. Inorg. Chem. 2020, 59, 4244–4254. [Google Scholar] [CrossRef]
- Müller, K.; Brendler, V.; Foerstendorf, H. Aqueous uranium(VI) hydrolysis species characterized by attenuated total reflection Fourier-transform infrared spectroscopy. Inorg. Chem. 2008, 47, 10127–10134. [Google Scholar] [CrossRef]
- Lucks, C.; Rossberg, A.; Tsushima, S.; Foerstendorf, H.; Scheinost, A.C.; Bernhard, G. Aqueous uranium(VI) complexes with acetic and succinic acid: Speciation and structure revisited. Inorg. Chem. 2012, 51, 12288–12300. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Tsushima, S.; Drobot, B.; Steudtner, R.; Schmeide, K.; Stumpf, T. Trimeric uranyl(VI)–citrate forms Na+, Ca2+, and La3+ sandwich complexes in aqueous solution. Chem. Commun. 2020, 56, 13133–13136. [Google Scholar] [CrossRef] [PubMed]
- Alsobrook, A.N.; Alekseev, E.V.; Depmeier, W.; Albrecht-Schmitt, T.E. Incorporation of Mn(II) and Fe(II) into Uranyl Carboxyphosphonates. Cryst. Growth Des. 2011, 11, 2358–2367. [Google Scholar] [CrossRef]
- Altmaier, M.; Yalçıntaş, E.; Gaona, X.; Neck, V.; Müller, R.; Schlieker, M.; Fanghänel, T. Solubility of U(VI) in chloride solutions. I. The stable oxides/hydroxides in NaCl systems, solubility products, hydrolysis constants and SIT coefficients. J. Chem. Thermodyn. 2017, 114, 2–13. [Google Scholar] [CrossRef]
- Migdisov, A.A.; Boukhalfa, H.; Timofeev, A.; Runde, W.; Roback, R.; Williams-Jones, A.E. A spectroscopic study of uranyl speciation in chloride-bearing solutions at temperatures up to 250 °C. Geochim. Cosmochim. Acta 2018, 222, 130–145. [Google Scholar] [CrossRef]
- Szabó, Z.; Glaser, J.; Grenthe, I. Kinetics of ligand exchange reactions for uranyl(2+) fluoride complexes in aqueous solution. Inorg. Chem. 1996, 35, 2036–2044. [Google Scholar] [CrossRef]
- Jung, W.-S.; Harada, M.; Tomiyasu, H.; Fukutomi, H. Oxygen-17 NMR study of the uranyl ion. V. Kinetics and mechanisms of formation and decomposition reactions of Di-. MU.-hydroxo-bis-[uranyl(VI)] ion in aqueous nitrate solutions. Bull. Chem. Soc. Jpn. 1988, 61, 3895–3900. [Google Scholar] [CrossRef]
- Moll, H.; Reich, T.; Szabo, Z. The hydrolysis of dioxouranium(VI) investigated using EXAFS and 17O-NMR. Radiochim. Acta 2000, 88, 411–416. [Google Scholar] [CrossRef]
- Banyai, I.; Glaser, J.; Micskei, K.; Toth, I.; Zekany, L. Kinetic behavior of carbonate ligands with different coordination modes: Equilibrium dynamics for uranyl(2+) carbonato complexes in aqueous solution. A 13C and 17O NMR study. Inorg. Chem. 1995, 34, 3785–3796. [Google Scholar] [CrossRef]
- Glasoe, P.K.; Long, F. Use of glass electrodes to measure acidities in deuterium oxide1,2. J. Phys. Chem. 1960, 64, 188–190. [Google Scholar] [CrossRef]
- Szabo, Z.; Grenthe, I. Reactivity of the “yl”-Bond in Uranyl (VI) Complexes. 1. Rates and Mechanisms for the Exchange between the trans-dioxo Oxygen Atoms in (UO2)2(OH)22+ and Mononuclear UO2(OH)n2-n Complexes with Solvent Water. Inorg. Chem. 2007, 46, 9372–9378. [Google Scholar] [CrossRef]
- Réal, F.; Vallet, V.; Wahlgren, U.; Grenthe, I. Ab Initio Sstudy of the Mechanism for Photoinduced Yl-Oxygen Exchange in uranyl(VI) in Acidic Aqueous Solution. J. Am. Chem. Soc. 2008, 130, 11742–11751. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, A.; Hennig, C.; Rossberg, A.; Tsushima, S.; Scheinost, A.C.; Bernhard, G. Structural determination of individual chemical species in a mixed system by iterative transformation factor analysis-based X-ray absorption spectroscopy combined with UV− Visible absorption and quantum chemical calculation. Anal. Chem. 2008, 80, 1102–1110. [Google Scholar] [CrossRef] [PubMed]
- Hennig, C.; Servaes, K.; Nockemann, P.; Van Hecke, K.; Van Meervelt, L.; Wouters, J.; Fluyt, L.; Görller-Walrand, C.; Van Deun, R. Species distribution and coordination of uranyl chloro complexes in acetonitrile. Inorg. Chem. 2008, 47, 2987–2993. [Google Scholar] [CrossRef]
- Brinkmann, H.; Patzschke, M.; Kaden, P.; Raiwa, M.; Rossberg, A.; Kloditz, R.; Heim, K.; Moll, H.; Stumpf, T. Complex formation between UO22+ and α-isosaccharinic acid: Insights on a molecular level. Dalton Trans. 2019, 48, 13440–13457. [Google Scholar] [CrossRef]
- Binstead, R.; Zuberbühler, A.; Jung, B. SPECFIT Global Analysis System; Version 3.0.37; Spectrum Software Associates: Marlborough, MA, USA, 2005. [Google Scholar]
- Gans, P.; Sabatini, A.; Vacca, A. Investigation of equilibria in solution. Determination of equilibrium constants with the HYPERQUAD suite of programs. Talanta 1996, 43, 1739–1753. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, H.; Cao, H.; Dong, X.; Wang, Z.; Chen, J.; Xu, C. Complexation of uranyl with benzoic acid in aqueous solution at variable temperatures: Potentiometry, spectrophotometry and DFT calculations. Dalton Trans. 2023, 52, 11265–11271. [Google Scholar] [CrossRef]
- Gampp, H.; Maeder, M.; Meyer, C.J.; Zuberbühler, A.D. Calculation of equilibrium constants from multiwavelength spectroscopic data—III: Model-free analysis of spectrophotometric and ESR titrations. Talanta 1985, 32, 1133–1139. [Google Scholar] [CrossRef]
- Gampp, H.; Maeder, M.; Meyer, C.J.; Zuberbühler, A.D. Calculation of equilibrium constants from multiwavelength spectroscopic data—IV: Model-free least-squares refinement by use of evolving factor analysis. Talanta 1986, 33, 943–951. [Google Scholar] [CrossRef] [PubMed]
- Gampp, H.; Maeder, M.; Meyer, C.J.; Zuberbühler, A.D. Calculation of equilibrium constants from multiwavelength spectroscopic data—I: Mathematical considerations. Talanta 1985, 32, 95–101. [Google Scholar] [CrossRef]
- Günther, A.; Geipel, G.; Bernhard, G. Complex formation of uranium(VI) with the amino acids L-glycine and L-cysteine: A fluorescence emission and UV-Vis absorption study. Polyhedron 2007, 26, 59–65. [Google Scholar] [CrossRef]
- Günther, A.; Steudtner, R.; Schmeide, K.; Bernhard, G. Luminescence properties of uranium(VI) citrate and uranium(VI) oxalate species and their application in the determination of complex formation constants. Radiochim. Acta 2011, 99, 535–542. [Google Scholar] [CrossRef]
- Lütke, L.; Moll, H.; Bernhard, G. A new uranyl benzoate species characterized by different spectroscopic techniques. Radiochim. Acta 2012, 100, 297–303. [Google Scholar] [CrossRef]
- Rutledge, D.; Barros, A. Durbin–Watson statistic as a morphological estimator of information content. Anal. Chim. Acta 2002, 454, 277–295. [Google Scholar] [CrossRef]
- Drobot, B.; Steudtner, R.; Raff, J.; Geipel, G.; Brendler, V.; Tsushima, S. Combining luminescence spectroscopy, parallel factor analysis and quantum chemistry to reveal metal speciation–a case study of uranyl(VI) hydrolysis. Chem. Sci. 2015, 6, 964–972. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic structure calculations on workstation computers: The program system turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Cao, X.; Dolg, M. Segmented contraction scheme for small-core actinide pseudopotential basis sets. J. Mol. Struct. THEOCHEM 2004, 673, 203–209. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 799–805. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
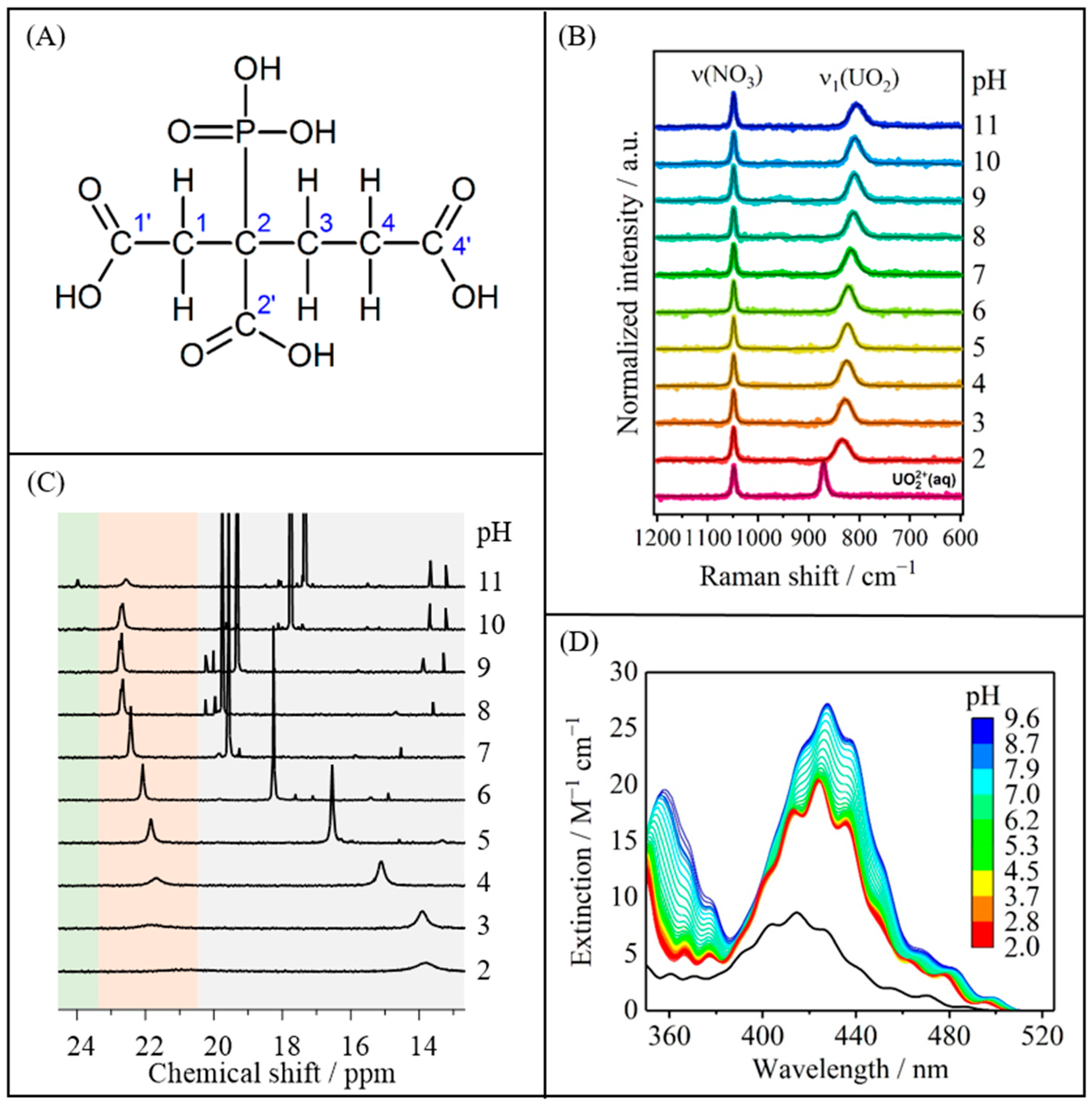
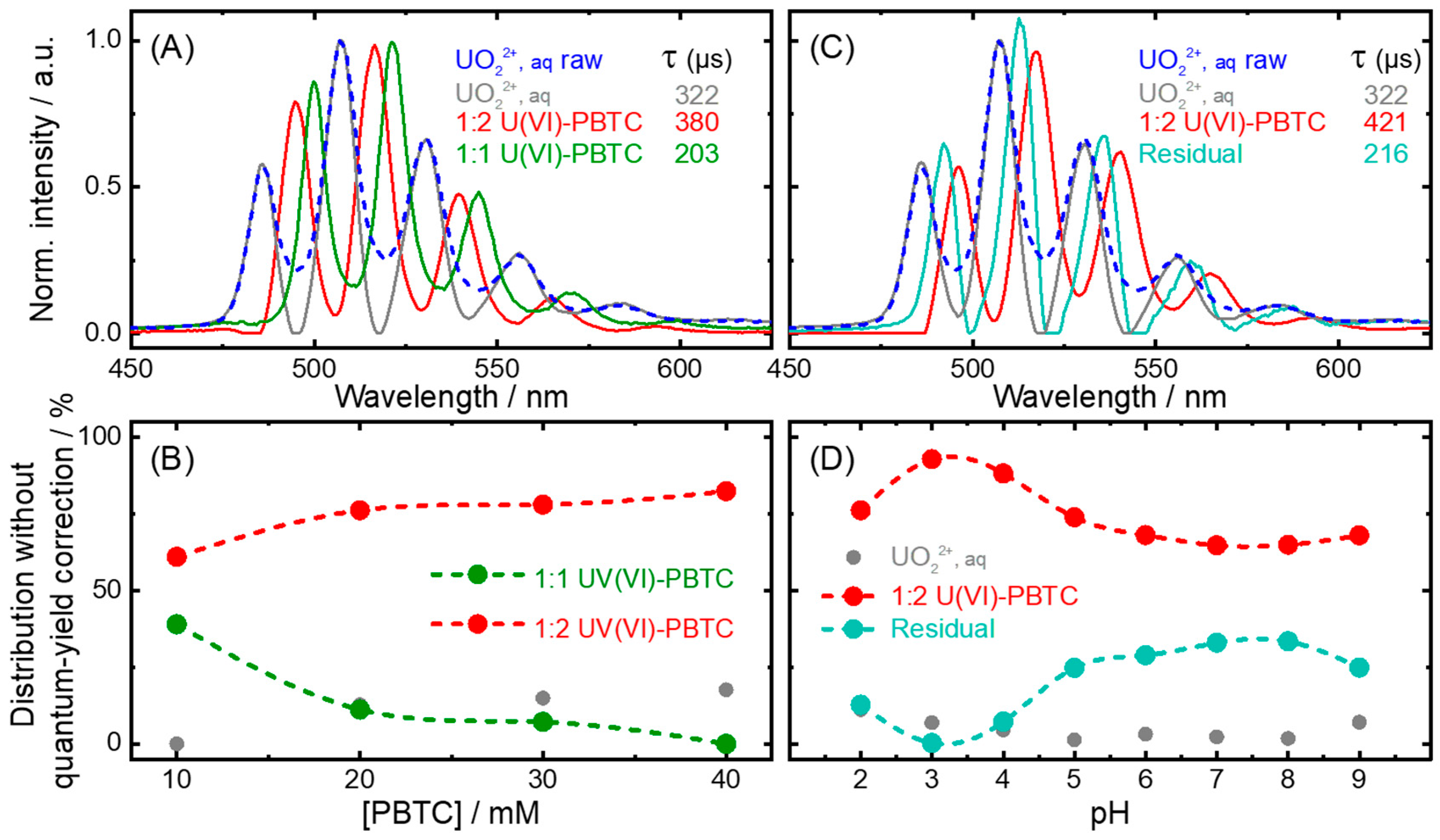

| Species | Main Peak Position/nm | ||||
|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | |
| UO22+ a | 486 | 507 | 530 | 556 | (584) |
| UO22+ from [36] | 484 | 506 | 529 | ||
| concentration series | |||||
| 1:1 U(VI)-PBTC species | 500 | 522 | 545 | 570 | (599) |
| 1:2 U(VI)-PBTC species | 495 | 516 | 540 | 564 | (593) |
| pH series | |||||
| 1:2 U(VI)-PBTC species | 496 | 517 | 540 | 565 | (593) |
| Residual spectral component | 492 | 513 | 535 | 559 | (587) |
| CM | CN | ∆Grel |
|---|---|---|
| mono | 5 | 36.9 |
| 4 | 75.6 | |
| 3 | 86.9 | |
| bi | 5 | 42.6 |
| 4 | 53.7 | |
| 3 | 92.1 | |
| chel | 5 | 0.0 |
| 4 | 2.0 | |
| 3 | 39.6 |
| Species | U(VI)-Ligand- Proton (xyz) | log K | ΔG in kJ/mol | |
|---|---|---|---|---|
| UO2(H3PBTC)0 | 113 | 25.5 ± 1.0 | 4.8 ± 0.2 | −27 |
| UO2(H3PBTC)22− | 126 | 51.0 ± 0.7 | 9.7 ± 0.1 | −55 |
| UO2(H3PBTC)(H2PBTC)3− | 125 | 47.1 ± 0.7 | 10.5 ± 0.2 | −60 |
| UO2(H2PBTC)24− | 124 | 41.6 ± 0.8 | 9.8 ± 0.2 | −56 |
| UO2(H2PBTC)(HPBTC)5− | 123 | 35.1 ± 0.9 | 9.3 ± 0.3 | −53 |
| UO2(HPBTC)26− | 122 | 28.5 ± 1.5 | 8.9 ± 0.5 | −51 |
| UO2(HPBTC)(PBTC)7− | 121 | 19.9 ± 1.5 | 10.2 ± 0.7 | −58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kretzschmar, J.; Wollenberg, A.; Chiorescu, I.; Krüger, S.; Kraft, R.; Kumke, M.U.; Tsushima, S.; Schmeide, K.; Acker, M. Uranyl(VI) Interaction with 2-Phosphonobutane-1,2,4-Tricarboxylic Acid (PBTC): A Spectroscopic and Computational Study over a Wide pH Range. Molecules 2025, 30, 4144. https://doi.org/10.3390/molecules30204144
Kretzschmar J, Wollenberg A, Chiorescu I, Krüger S, Kraft R, Kumke MU, Tsushima S, Schmeide K, Acker M. Uranyl(VI) Interaction with 2-Phosphonobutane-1,2,4-Tricarboxylic Acid (PBTC): A Spectroscopic and Computational Study over a Wide pH Range. Molecules. 2025; 30(20):4144. https://doi.org/10.3390/molecules30204144
Chicago/Turabian StyleKretzschmar, Jerome, Anne Wollenberg, Ion Chiorescu, Sven Krüger, Ronja Kraft, Michael U. Kumke, Satoru Tsushima, Katja Schmeide, and Margret Acker. 2025. "Uranyl(VI) Interaction with 2-Phosphonobutane-1,2,4-Tricarboxylic Acid (PBTC): A Spectroscopic and Computational Study over a Wide pH Range" Molecules 30, no. 20: 4144. https://doi.org/10.3390/molecules30204144
APA StyleKretzschmar, J., Wollenberg, A., Chiorescu, I., Krüger, S., Kraft, R., Kumke, M. U., Tsushima, S., Schmeide, K., & Acker, M. (2025). Uranyl(VI) Interaction with 2-Phosphonobutane-1,2,4-Tricarboxylic Acid (PBTC): A Spectroscopic and Computational Study over a Wide pH Range. Molecules, 30(20), 4144. https://doi.org/10.3390/molecules30204144







