Comparative Crystal Properties of Fluorite and Dolomite: Implications for Flotation Reagent Design
Abstract
1. Introduction
2. Results and Discussion
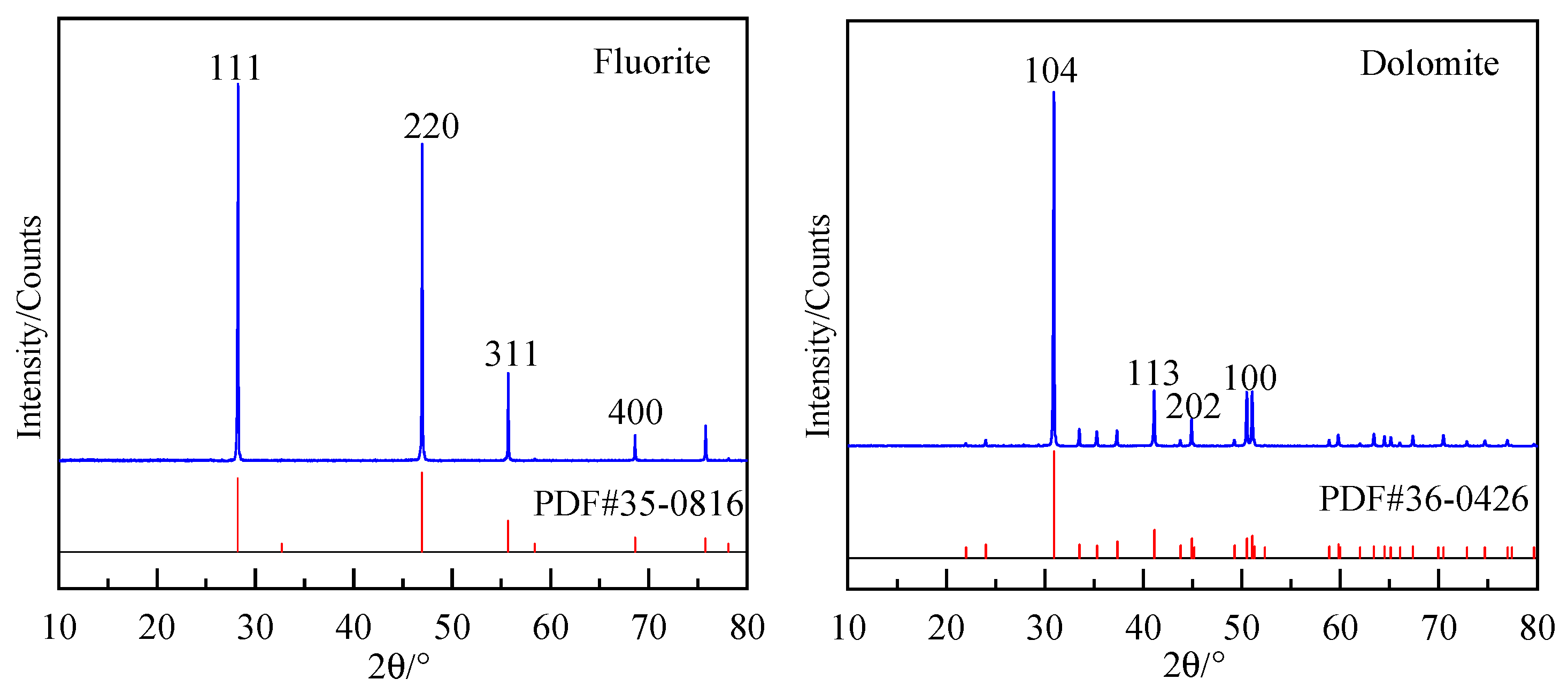
2.1. Crystal Structure Optimization
2.2. Mulliken Population of Fluorite and Dolomite
2.3. Electron Density of Fluorite and Dolomite
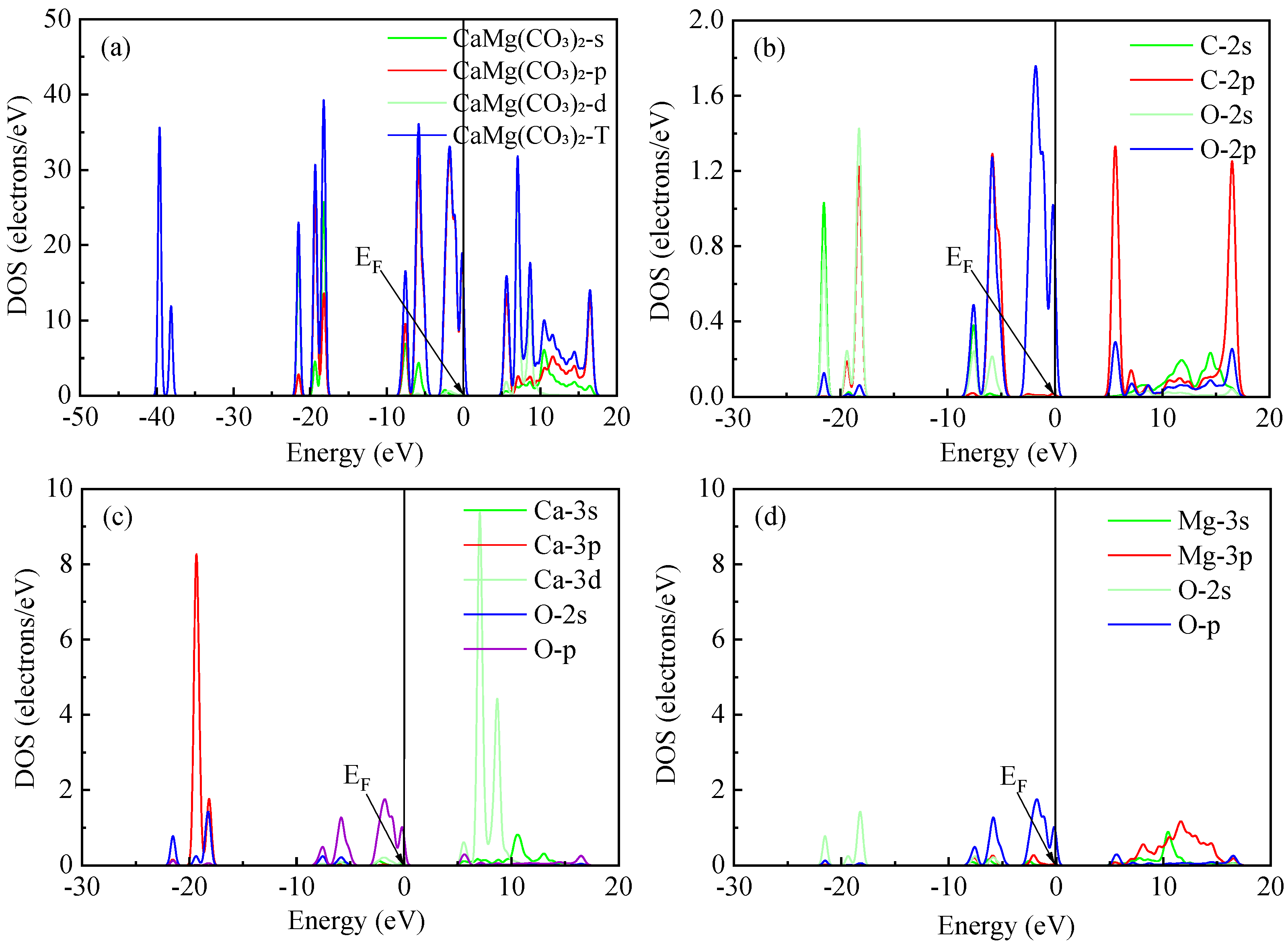
2.4. State Densities of Fluorite and Dolomite
2.5. The Cleavage Characteristics of Fluorite and Dolomite
3. Material and Methods
3.1. Materials
3.2. First-Principle Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basiev, T.T.; Doroshenko, M.E.; Konyushkin, V.A.; Osiko, V.V.; Fedorov, P.P.; Demidenko, V.A.; Dukel’sKii, K.V.; Mironov, I.A.; Smirnov, A.N. Fluoride optical nanoceramics. Russ. Chem. Bull. 2008, 57, 877–886. [Google Scholar] [CrossRef]
- Kan, W.H.; Thangadurai, V. Challenges and prospects of anodes for solid oxide fuel cells (SOFCs). Ionics 2014, 21, 301–318. [Google Scholar] [CrossRef]
- Shah, F.A. Fluoride-containing bioactive glasses: Glass design, structure, bioactivity, cellular interactions, and recent developments. Mater. Sci. Eng. C 2016, 58, 1279–1289. [Google Scholar] [CrossRef]
- Sadykov, V.A.; Simonov, M.N.; Bespalko, Y.N.; Bobrova, L.N.; Eremeev, N.F.; Arapova, M.V.; Smal’, E.A.; Mezentseva, N.V.; Pavlova, S.N. Design and Characterization of Nanocomposite Catalysts for Biofuel Conversion into Syngas and Hydrogen in Structured Reactors and Membranes. Kinet. Catal. 2019, 60, 582–605. [Google Scholar] [CrossRef]
- Shi, C.-B.; Cho, J.-W.; Zheng, D.-L.; Li, J. Fluoride evaporation and crystallization behavior of CaF2–CaO–Al2O3–(TiO2) slag for electroslag remelting of Ti-containing steels. Int. J. Miner. Met. Mater. 2016, 23, 627–636. [Google Scholar] [CrossRef]
- Zhu, H.; Qin, W.; Chen, C.; Chai, L.; Jiao, F.; Jia, W. Flotation separation of fluorite from calcite using polyaspartate as depressant. Miner. Eng. 2018, 120, 80–86. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.; Bu, X.; Long, T.; Zhang, G.; Chen, F.; Liu, R.; Jia, K.; Song, Y. Rheological investigations on the hetero-coagulation between the fine fluorite and quartz under fluorite flotation-related conditions. Powder Technol. 2019, 354, 423–431. [Google Scholar] [CrossRef]
- Cui, Y.; Jiao, F.; Wei, Q.; Wang, X.; Dong, L. Flotation separation of fluorite from calcite using sulfonated lignite as depressant. Sep. Purif. Technol. 2020, 242, 116698. [Google Scholar] [CrossRef]
- Liu, C.; Song, S.; Li, H. Selective flotation of fluorite from barite using trisodium phosphate as a depressant. Miner. Eng. 2019, 134, 390–393. [Google Scholar] [CrossRef]
- Wang, W.; Hou, S.; Li, E.; Yang, Z.; Guo, C.; Li, Q.; Jin, H.; Wang, Q. The Effect of Oleic Acid Emulsification using SPE on Fluorite and Dolomite Flotation. ChemistryOpen 2021, 10, 1227–1233. [Google Scholar] [CrossRef]
- Yu, J.X.; Liu, W.L. The Study of Pyrite Surface Properties and Effect Mechanism with Xanthate Caused by the Microscopic Crystal Structure and Defects. Adv. Mater. Res. 2012, 538-541, 363–367. [Google Scholar] [CrossRef]
- Ren, S.; Su, Z.; Liu, W.; Sun, Y.; Li, X.; Yang, J. Ti3O5 and Al2TiO5 crystals flotation characteristics from Ti-bearing blast furnace slag: A density functional theory and experimental study. Crystals 2020, 10, 838. [Google Scholar] [CrossRef]
- Hung, A.; Yarovsky, I.; Russo, S.P. Density-functional theory studies of xanthate adsorption on the pyrite FeS2(110) and (111) surfaces. J. Chem. Phys. 2003, 118, 6022–6029. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Chen, J.; Zhao, C.; Cui, W. Comparison study of crystal and electronic structures for chalcopyrite (CuFeS2) and pyrite (FeS2). Physicochem. Probl. Miner. Process. 2020, 57, 100–111. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Liu, D.; Cao, S.; Song, K.; Jing, M.; Li, K.; Wu, L.; Liu, R. Basic characteristics of hemimorphite and its transformation mechanism with Na2CO3. Minerals 2018, 8, 143. [Google Scholar] [CrossRef]
- Song, B.; Tao, D.; Li, P.; Wang, X.; Ran, J. Cleavage nature and surface appearances of wulfenite by first-principles calculations and experimental measurement. Results Phys. 2020, 16, 102849. [Google Scholar] [CrossRef]
- Nan, N.; Zhu, Y.; Han, Y.; Liu, J. Molecular Modeling of Interactions between N-(Carboxymethyl)-N-tetradecylglycine and Fluorapatite. Minerals 2019, 9, 278. [Google Scholar] [CrossRef]
- Jiao, F.; Wu, J.; Qin, W.; Wang, X.; Liu, R. Interactions of tert dodecyl mercaptan with sphalerite and effects on its flotation behavior. Colloids Surf. A Physicochem. Eng. Asp. 2016, 506, 104–113. [Google Scholar] [CrossRef]
- He, G.-C.; Xiang, H.-M.; Jiang, W.; Kang, Q.; Chen, J.-H. First-principles theory on electronic structure and floatability of spodumene. Rare Met. 2014, 33, 742–748. [Google Scholar] [CrossRef]
- Jiang, W.; Gao, Z.; Sun, W.; Gao, J.; Hu, Y. A Density Functional Theory Study on the Effect of Lattice Impurities on the Electronic Structures and Reactivity of Fluorite. Minerals 2017, 7, 160. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Chai, Y.; Zhang, Q. Crystal properties and interaction with flotation reagent of fluorapatite and dolomite. Miner. Eng. 2023, 201, 108204. [Google Scholar] [CrossRef]
- Cheetham, A.K.; Fender, B.E.F.; Cooper, M.J. Defect structure of calcium fluoride containing excess anions I. Bragg scattering. J. Phys. C Solid State Phys. 1971, 4, 3107–3121. [Google Scholar] [CrossRef]
- Rasi, N.M.; Ponnurangam, S.; Mahinpey, N. First-principles investigations into the effect of oxygen vacancies on the enhanced reactivity of NiO via Bader charge and density of states analysis. Catal. Today 2022, 407, 172–181. [Google Scholar] [CrossRef]
- Stachowicz, M.; Malinska, M.; Parafiniuk, J.; Woźniak, K. Experimental observation of charge-shift bond in fluorite CaF2. Acta Crystallogr. Sect. B Struct. Sci. 2017, 73, 643–653. [Google Scholar] [CrossRef]
- Pimentel, C.; Sainz-Díaz, C.I. New Insights into Dolomite and Dolomite-Analogue Structures from First Principles Calculations. ACS Earth Space Chem. 2022, 6, 2360–2367. [Google Scholar] [CrossRef]
- Steinfink, H.; Sans, F.J. Refinement of the crystal structure of dolomite. Am. Mineral. 1959, 44, 679–682. [Google Scholar]
- Zhang, Y.; Wang, Y.H.; Hu, Y.H.; Wen, S.M.; Wang, J.M. First-principle theory calculation of electronic structures of scheelite, fluorite and calcite. Chin. J. Rare Met. 2011, 38, 1106–1113. [Google Scholar] [CrossRef]
- Hossain, F.M.; Dlugogorski, B.Z.; Kennedy, E.M.; Belova, I.V.; Murch, G.E. Optical and bonding properties of MgCO3. Solid State Commun. 2010, 149, 1201–1203. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Yin, W.Z.; Ma, Y.Q.; Wang, C. First-principles study on flotation of magnesite, dolomite and calcite. Met. Mine 2019, 5, 62–68. [Google Scholar] [CrossRef]
- Fu, B.; Li, L.J.; Zhang, Q.; Xie, J.; Wang, X.C. Electronic structure of dolomite and molecular simulation for adsorption of sodium oleate onto dolomite (104) surface. Min. Metall. Eng. 2019, 39, 69–73. [Google Scholar] [CrossRef]
- Gu, B.L.; Wang, X.K. Solid State Physics; Tsinghua University Press: Beijing, China, 1989; p. 110. [Google Scholar]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
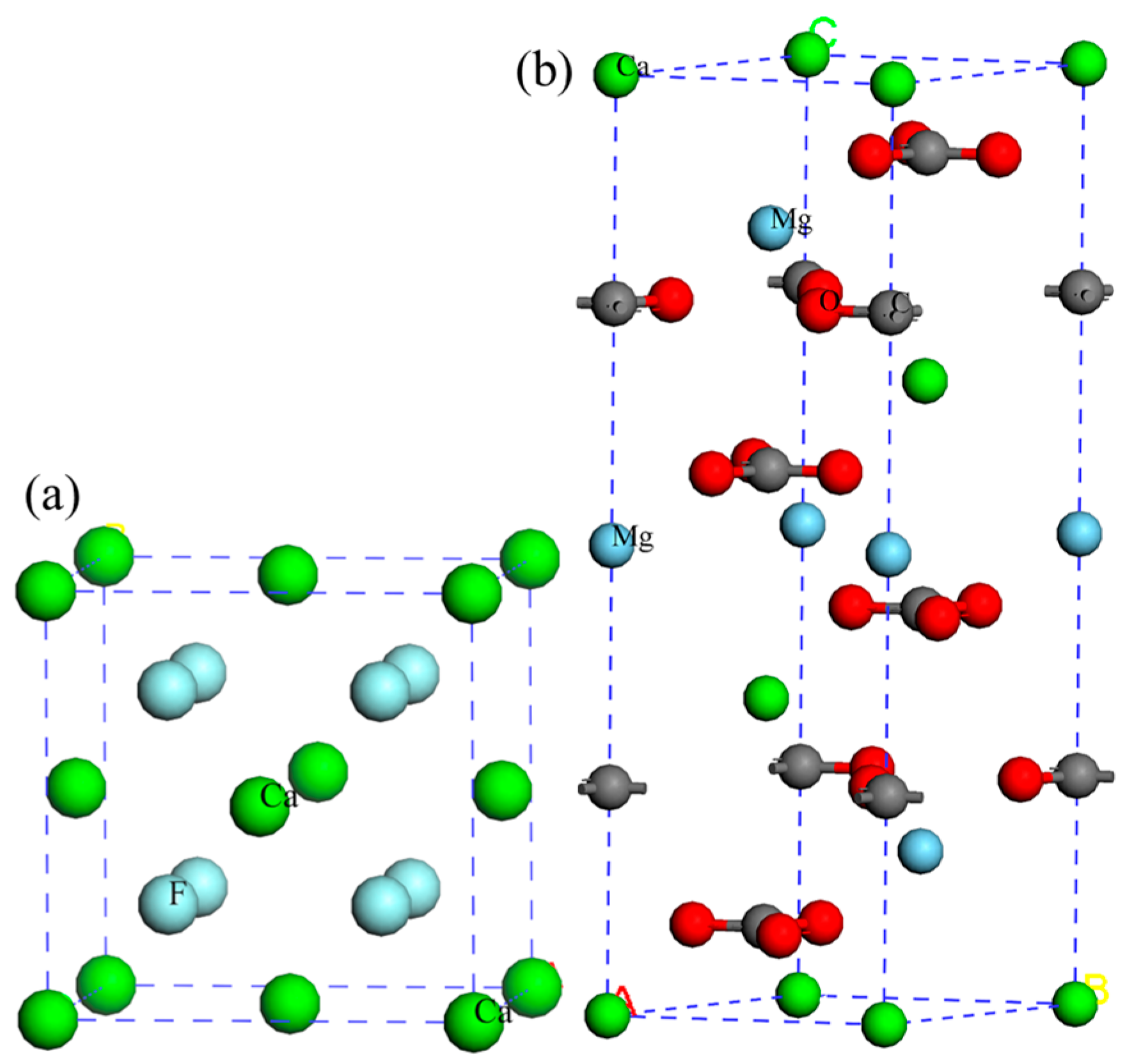





| Lattice Parameter | Theoretical Calculation Value (Å) | Experimental Value (Å) | ||
|---|---|---|---|---|
| Fluorite | Dolomite | Fluorite | Dolomite | |
| a | 5.593616 | 4.862532 | 5.56784 | 4.8069 |
| b | 5.593616 | 4.862532 | 5.56784 | 4.8069 |
| c | 5.593616 | 16.234903 | 5.56784 | 16.003 |
| Minerals | Species | s | p | d | Total/e | Charge/e |
|---|---|---|---|---|---|---|
| Fluorite | Ca | 2.15 | 6.00 | 0.46 | 8.62 | 1.38 |
| F | 1.96 | 5.73 | - | 7.69 | −0.69 | |
| Dolomite | Ca | 2.10 | 6.00 | 0.44 | 8.53 | 1.47 |
| Mg | 2.27 | 6.40 | - | 8.66 | 1.34 | |
| C | 0.87 | 2.39 | - | 3.26 | 0.74 | |
| O | 1.80 | 4.92 | - | 6.71 | −0.71 |
| Minerals | Bonds | Population | Bond Length/Å |
|---|---|---|---|
| Fluorite | Ca-F | 0.08 | 2.422 |
| F-F | −0.03 | 2.797 | |
| Dolomite | Ca-O | 0.09 | 2.408 |
| Mg-O | 0.18 | 2.116 | |
| C-O | 0.86 | 1.295 | |
| O-O | −0.22 | 2.243 |
| Minerals | Surface | Formula of Unit Area, A (nm2) | Nb | Db (nm−1) | d (nm) |
|---|---|---|---|---|---|
| Fluorite | {100} | 0.3955 × 0.3955 × sin90° = 0.1564 | 4 | 25.5754 | 0.1894 |
| {110} | 0.5594 × 0.3955 × sin90° = 0.2212 | 4 | 18.0832 | 0.2681 | |
| {111} | 0.3955 × 0.3955 × sin60° = 0.1355 | 2 | 14.7601 | 0.4713 | |
| {311} | 0.6851 × 0.3955 × sin73.22° = 0.2594 | 12 | 46.2606 | 0.1548 | |
| Dolomite | {100} | 0.4863 × 1.6235 × sin90° = 0.7895 | 16 | 20.27 | 0.1121 |
| {101} | 0.6096 × 0.4863 × sin66.50° = 0.2719 | 6 | 22.07 | 0.0865 | |
| {104} | 0.7798 × 0.4863 × sin90° = 0.3792 | 4 | 10.55 | 0.3899 | |
| {113} | 0.8422 × 0.6096 × sin76.6888 = 0.4996 | 8 | 16.01 | 0.1838 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, Z.; Wang, Z.; Hou, S.; Zhou, Z.; Guo, C.; Zhu, W. Comparative Crystal Properties of Fluorite and Dolomite: Implications for Flotation Reagent Design. Molecules 2025, 30, 3770. https://doi.org/10.3390/molecules30183770
Wang W, Li Z, Wang Z, Hou S, Zhou Z, Guo C, Zhu W. Comparative Crystal Properties of Fluorite and Dolomite: Implications for Flotation Reagent Design. Molecules. 2025; 30(18):3770. https://doi.org/10.3390/molecules30183770
Chicago/Turabian StyleWang, Weiwei, Zhengyao Li, Zhenyu Wang, Shaochun Hou, Zhengyuan Zhou, Chunlei Guo, and Weiyao Zhu. 2025. "Comparative Crystal Properties of Fluorite and Dolomite: Implications for Flotation Reagent Design" Molecules 30, no. 18: 3770. https://doi.org/10.3390/molecules30183770
APA StyleWang, W., Li, Z., Wang, Z., Hou, S., Zhou, Z., Guo, C., & Zhu, W. (2025). Comparative Crystal Properties of Fluorite and Dolomite: Implications for Flotation Reagent Design. Molecules, 30(18), 3770. https://doi.org/10.3390/molecules30183770





