Structure and Nonlinear Spectra of the Basal Face of Hexagonal Ice: A Molecular Dynamics Study
Abstract
1. Introduction
2. Results and Discussion
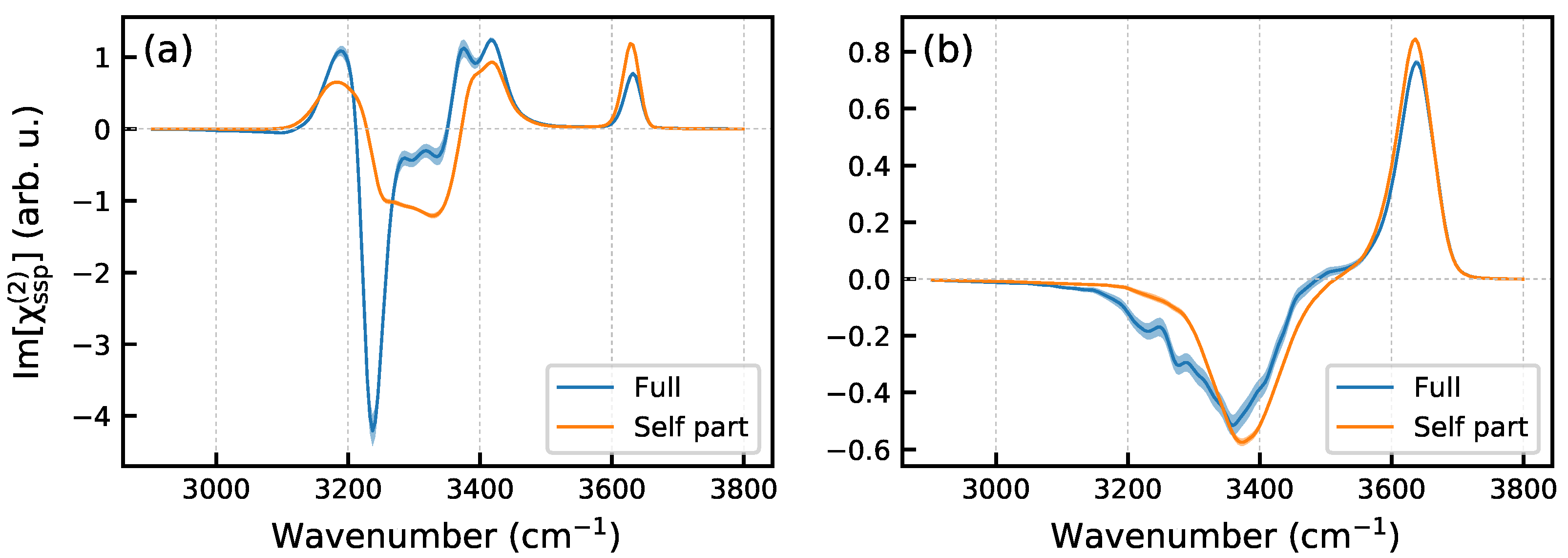
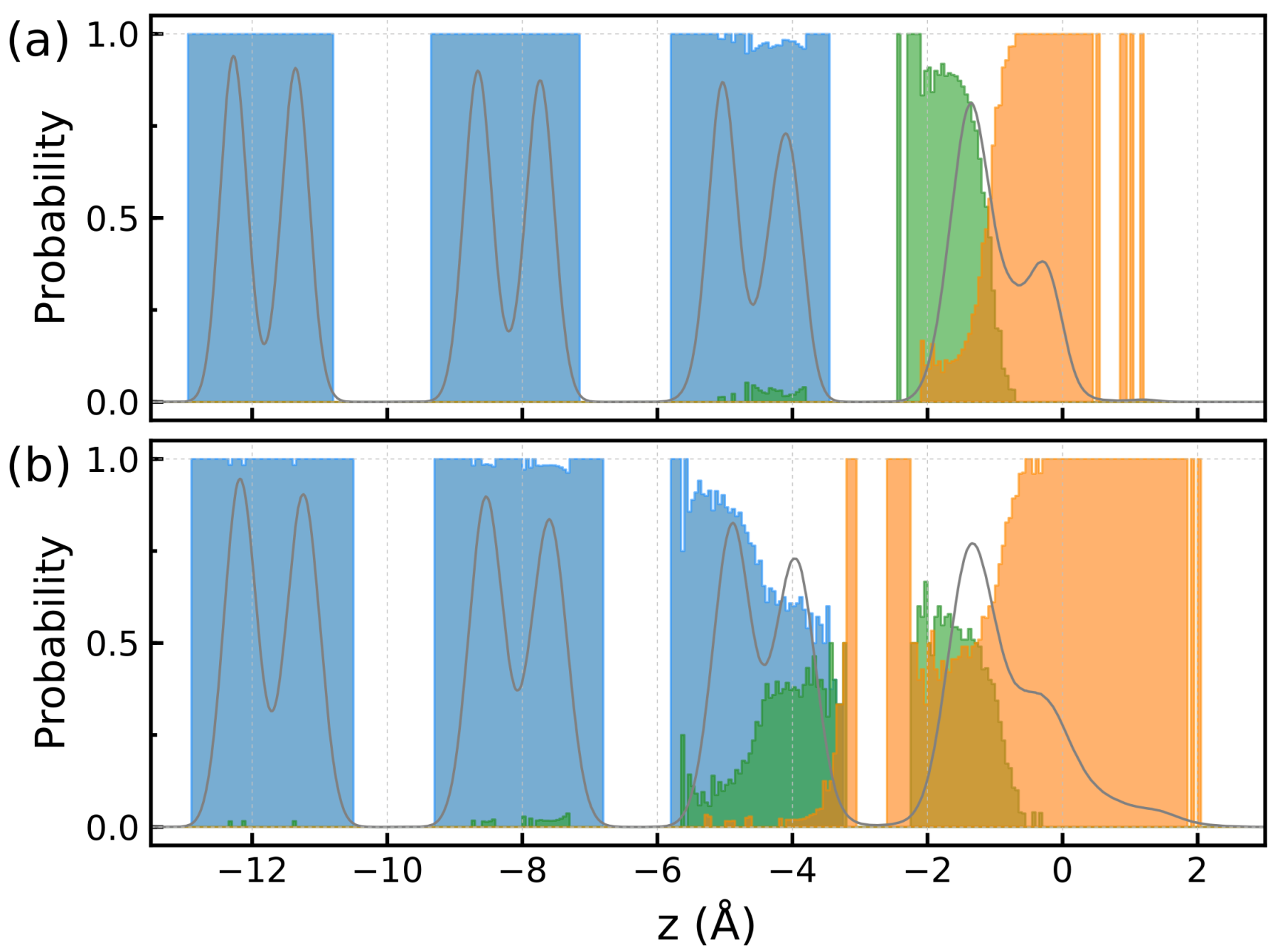
2.1. Ice/Air Interface at K
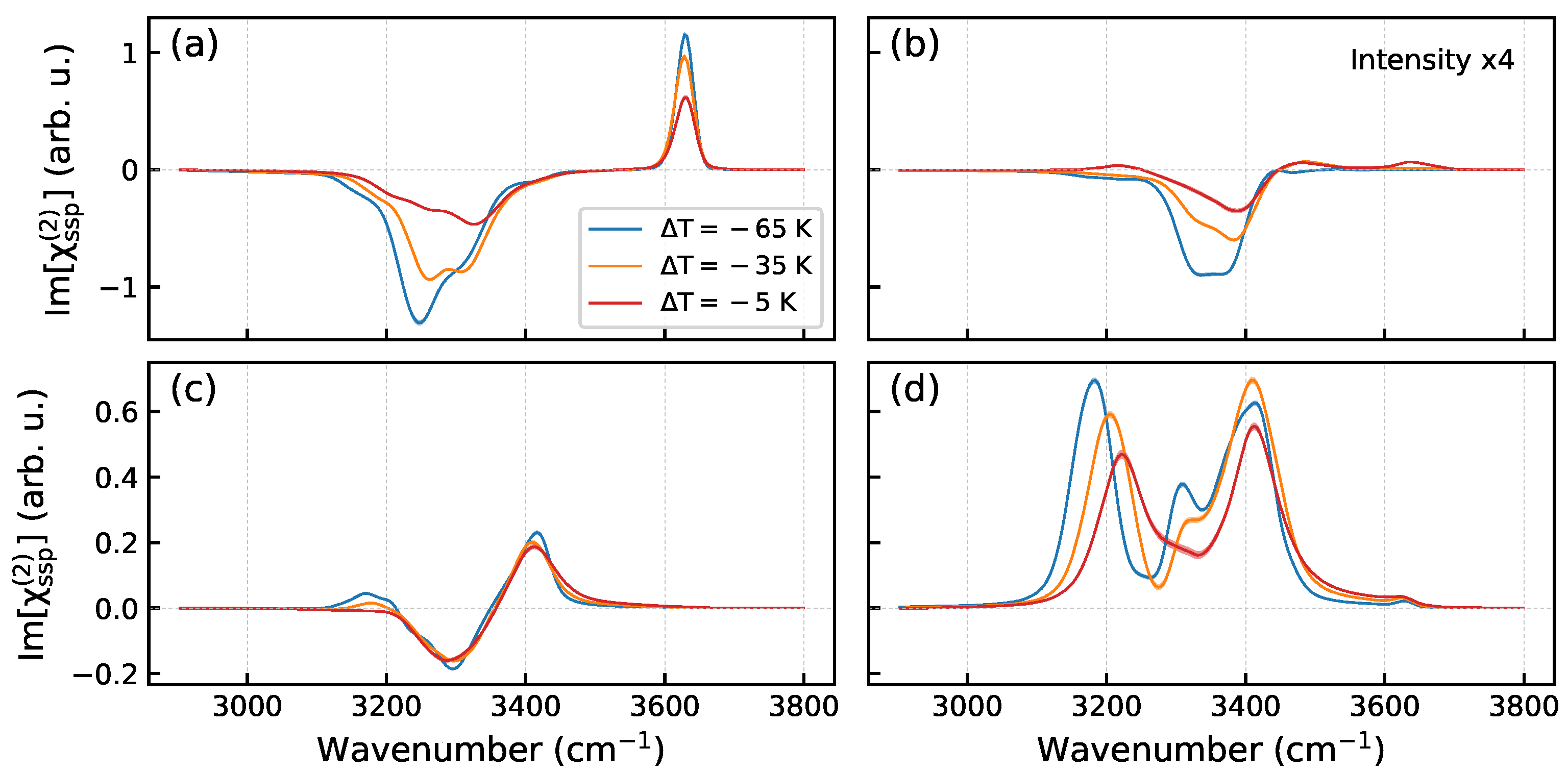
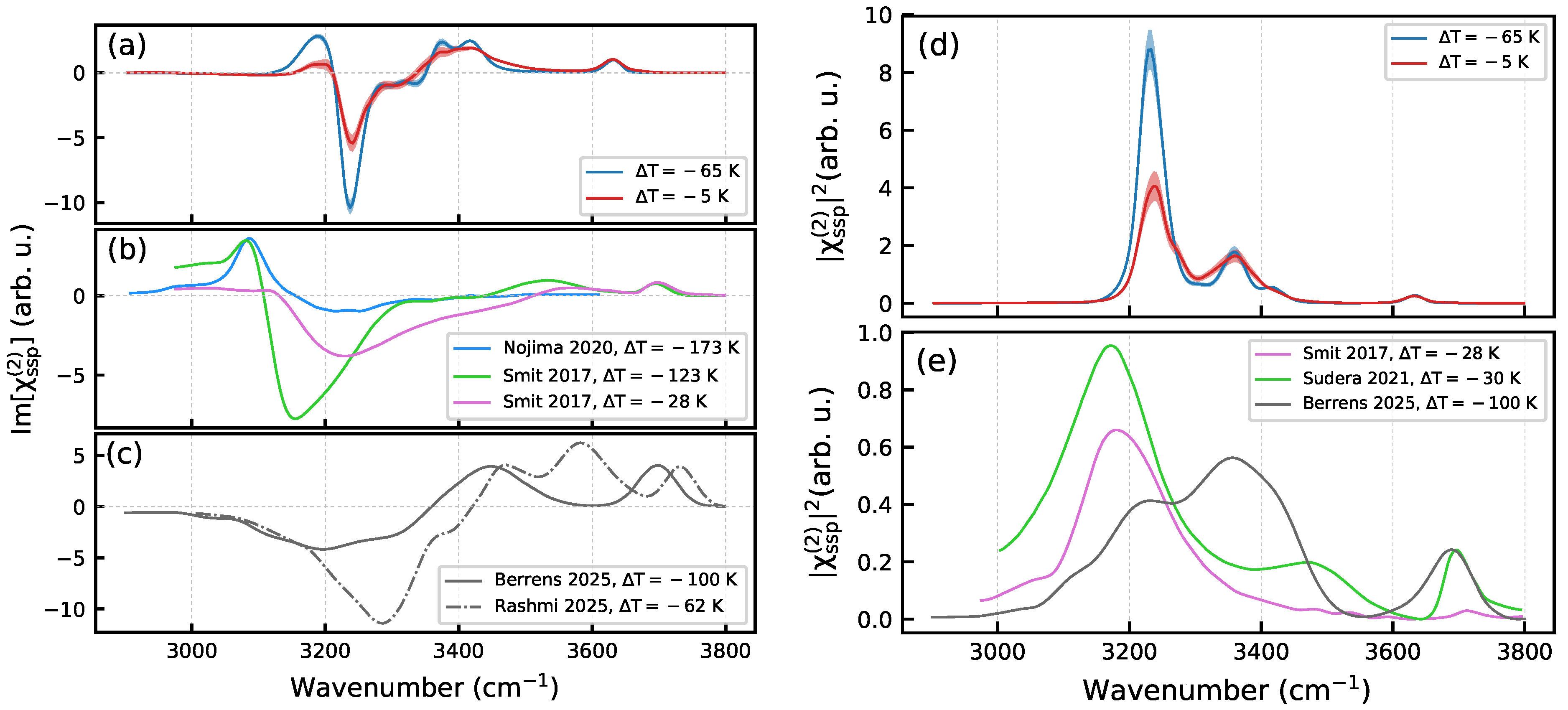
2.2. Effect of Temperature
3. Models and Computations
3.1. Simulation Setup
3.2. Interatomic Potentials
3.3. MD Simulations
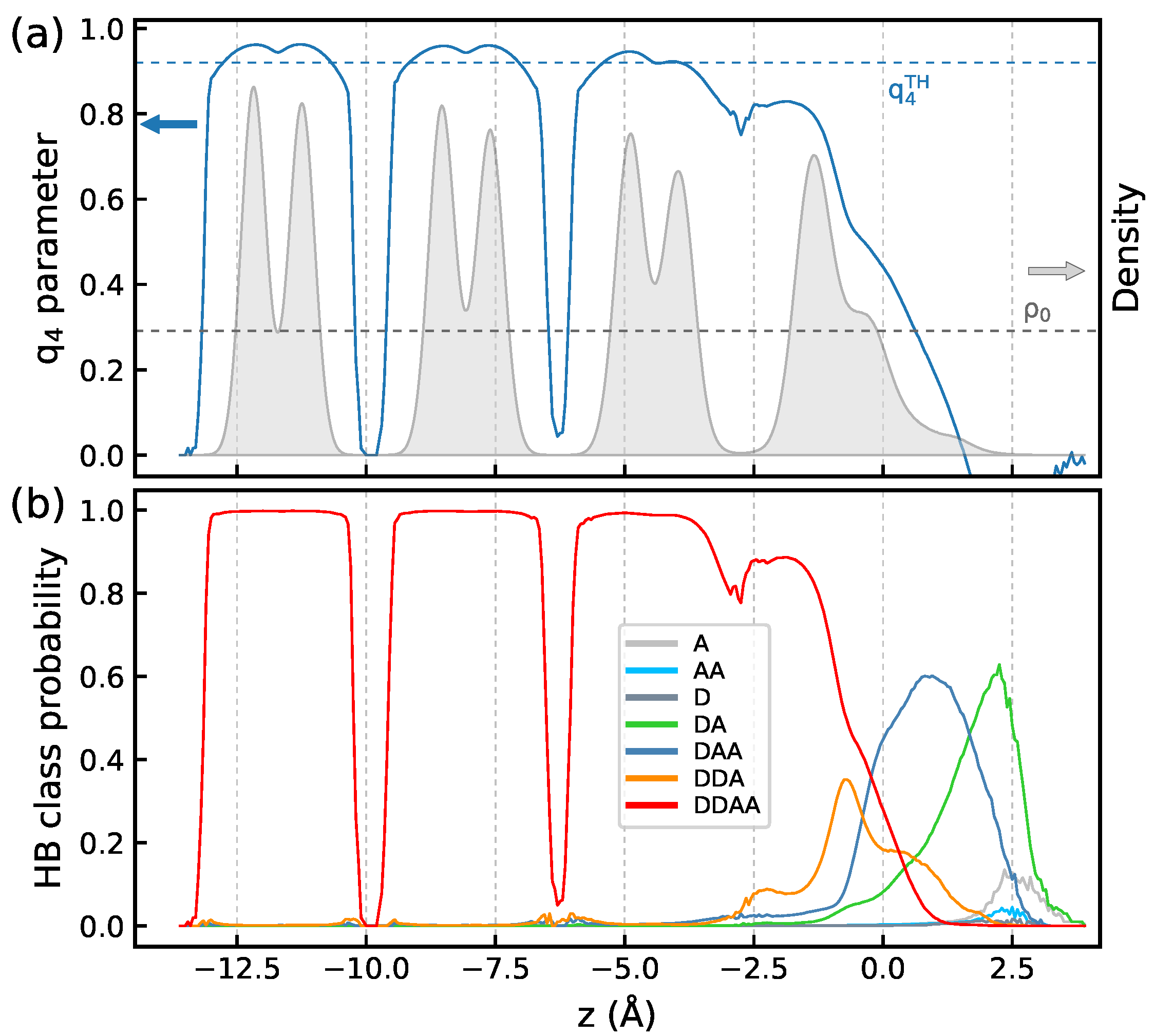
3.4. Structural Characteristics
3.5. H-Bond Analysis and H-Bonding Network
3.6. Nonlinear Spectra Computation
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Second-Order Susceptibility Calculations
Appendix B. Frequency-Dependent Scale Factor for χ(2)
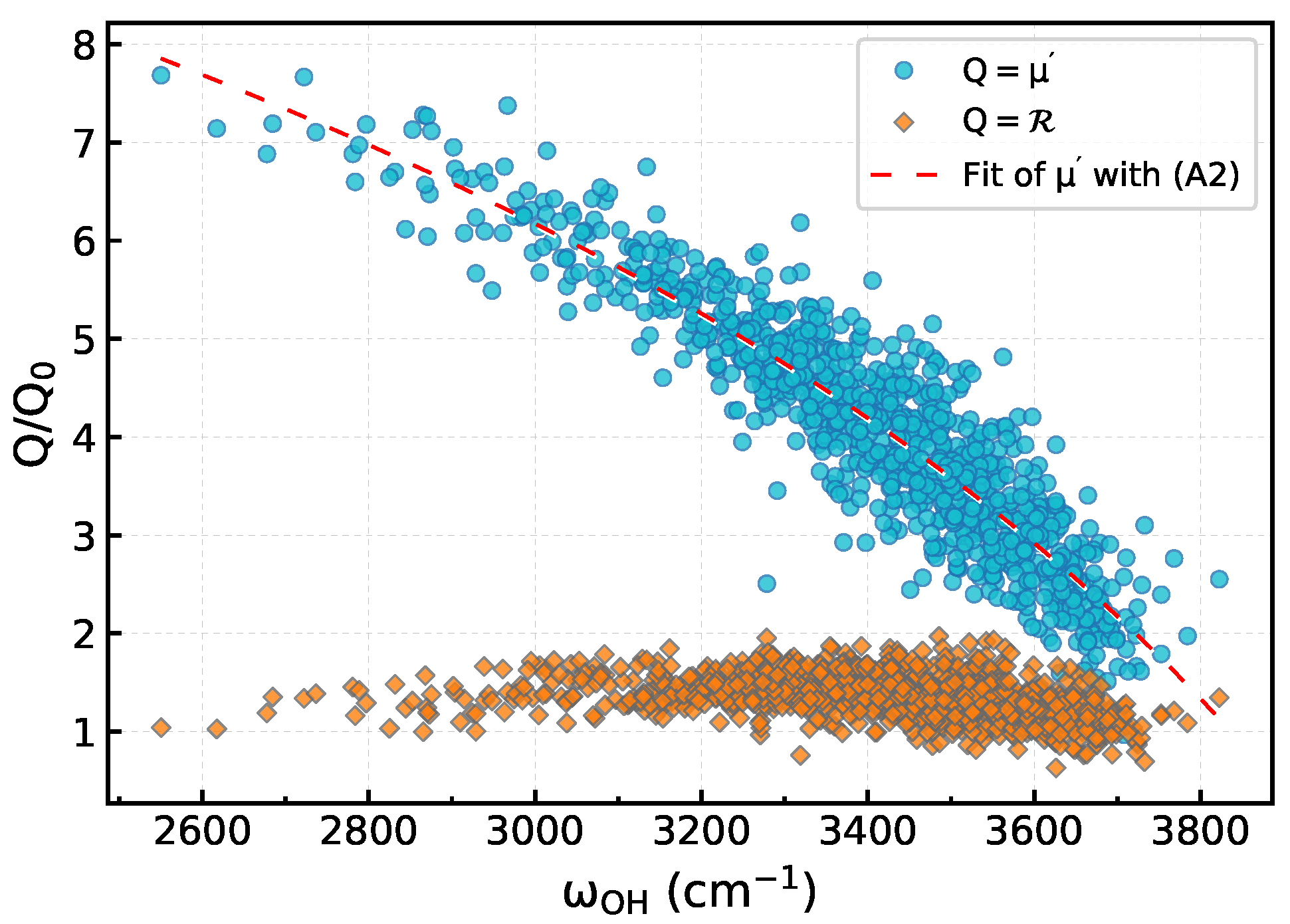
References
- Clark, R.N.; Carlson, R.; Grundy, W.; Noll, K. Observed Ices in the Solar System. In The Science of Solar System Ices; Gudipati, M.S., Castillo-Rogez, J., Eds.; Springer: New York, NY, USA, 2013; pp. 3–46. [Google Scholar] [CrossRef]
- Soare, R.; Williams, J.; Ahrens, C.; Butcher, F.; El-Maarry, M. Ices in the Solar System. In Ices in the Solar-System; Elsevier: Amsterdam, The Netherlands, 2023; pp. 1–383. [Google Scholar] [CrossRef]
- Bartels-Rausch, T.; Bergeron, V.; Cartwright, J.H.E.; Escribano, R.; Finney, J.L.; Grothe, H.; Gutiérrez, P.J.; Haapala, J.; Kuhs, W.F.; Pettersson, J.B.C.; et al. Ice structures, patterns, and processes: A view across the icefields. Rev. Mod. Phys. 2012, 84, 885–944. [Google Scholar] [CrossRef]
- Malenkov, G. Liquid water and ices: Understanding the structure and physical properties. J. Phys. Condens. Matter 2009, 21, 283101. [Google Scholar] [CrossRef] [PubMed]
- Salzmann, C.G. Advances in the experimental exploration of water’s phase diagram. J. Chem. Phys. 2019, 150, 060901. [Google Scholar] [CrossRef]
- Bartels-Rausch, T.; Montagnat, M. The physics and chemistry of ice. Philos. Trans. R. Soc. A 2019, 377, 20190138. [Google Scholar] [CrossRef]
- Zaera, F. Probing Liquid/Solid Interfaces at the Molecular Level. Chem. Rev. 2012, 112, 2920–2986. [Google Scholar] [CrossRef]
- Shen, Y.R. Fundamentals of Sum-Frequency Spectroscopy; Cambridge University Press; University Printing House: Cambridge, UK, 2016; p. 316. [Google Scholar] [CrossRef]
- Li, X.; Rupprechter, G. Sum frequency generation (SFG) spectroscopy at surfaces and interfaces: Adsorbate structure and molecular bond orientation. Surf. Sci. Rep. 2024, 79, 100645. [Google Scholar] [CrossRef]
- Yamaguchi, S.; Suzuki, Y.; Nojima, Y.; Otosu, T. Perspective on sum frequency generation spectroscopy of ice surfaces and interfaces. Chem. Phys. 2019, 522, 199–210. [Google Scholar] [CrossRef]
- Tang, F.; Ohto, T.; Sun, S.; Rouxel, J.R.; Imoto, S.; Backus, E.H.G.; Mukamel, S.; Bonn, M.; Nagata, Y. Molecular Structure and Modeling of Water-Air and Ice-Air Interfaces Monitored by Sum-Frequency Generation. Chem. Rev. 2020, 120, 3633–3667. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press, Inc.: Orlando, FL, USA, 2008. [Google Scholar]
- Morita, A. Theory of Sum Frequency Generation Spectroscopy; Springer: Singapore, 2018. [Google Scholar]
- Ishiyama, T.; Morita, A. A direct evidence of vibrationally delocalized response at ice surface. J. Chem. Phys. 2014, 141, 18C503. [Google Scholar] [CrossRef]
- Faraday, M. On certain conditions of freezing water. Athenæum 1850, 1181, 640–641. [Google Scholar] [CrossRef]
- Li, Y.; Somorjai, G.A. Surface Premelting of Ice. J. Phys. Chem. C 2007, 111, 9631–9637. [Google Scholar] [CrossRef]
- Slater, B.; Michaelides, A. Surface premelting of water ice. Nat. Rev. Chem. 2019, 3, 172–188. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K. Quasi-Liquid Layer on Ice and Its Effect on the Confined Freezing of Porous Materials. Crystals 2019, 9, 250. [Google Scholar] [CrossRef]
- Wei, X.; Miranda, P.B.; Shen, Y.R. Surface Vibrational Spectroscopic Study of Surface Melting of Ice. Phys. Rev. Lett. 2001, 86, 1554–1557. [Google Scholar] [CrossRef]
- Wei, X.; Miranda, P.B.; Zhang, C.; Shen, Y.R. Sum-frequency spectroscopic studies of ice interfaces. Phys. Rev. B 2002, 66, 085401. [Google Scholar] [CrossRef]
- Wei, X.; Shen, Y.R. Vibrational spectroscopy of ice interfaces. Appl. Phys. B 2002, 74, 617–620. [Google Scholar] [CrossRef]
- Dosch, H.; Lied, A.; Bilgram, J. Glancing-angle X-ray scattering studies of the premelting of ice surfaces. Surf. Sci. 1995, 327, 145–164. [Google Scholar] [CrossRef]
- Sánchez, M.A.; Kling, T.; Ishiyama, T.; van Zadel, M.J.; Bisson, P.J.; Mezger, M.; Jochum, M.N.; Cyran, J.D.; Smit, W.J.; Bakker, H.J.; et al. Experimental and theoretical evidence for bilayer-by-bilayer surface melting of crystalline ice. Proc. Natl. Acad. Sci. USA 2017, 114, 227–232. [Google Scholar] [CrossRef]
- Nagata, Y.; Hama, T.; Backus, E.H.G.; Mezger, M.; Bonn, D.; Bonn, M.; Sazaki, G. The Surface of Ice under Equilibrium and Nonequilibrium Conditions. Accounts Chem. Res. 2019, 52, 1006–1015. [Google Scholar] [CrossRef]
- Groenzin, H.; Li, I.; Buch, V.; Shultz, M.J. The single-crystal, basal face of ice Ih investigated with sum frequency generation. J. Chem. Phys. 2007, 127, 214502. [Google Scholar] [CrossRef] [PubMed]
- Ishiyama, T.; Takahashi, H.; Morita, A. Origin of Vibrational Spectroscopic Response at Ice Surface. J. Phys. Chem. Lett. 2012, 3, 3001–3006. [Google Scholar] [CrossRef] [PubMed]
- Groenzin, H.; Li, I.; Shultz, M.J. Sum-frequency generation: Polarization surface spectroscopy analysis of the vibrational surface modes on the basal face of ice Ih. J. Chem. Phys. 2008, 128, 214510. [Google Scholar] [CrossRef] [PubMed]
- Buch, V.; Groenzin, H.; Li, I.; Shultz, M.J.; Tosatti, E. Proton order in the ice crystal surface. Proc. Natl. Acad. Sci. USA 2008, 105, 5969–5974. [Google Scholar] [CrossRef] [PubMed]
- Smit, W.J.; Bakker, H.J. The Surface of Ice Is Like Supercooled Liquid Water. Angew. Chem.-Int. Ed. 2017, 56, 15540–15544. [Google Scholar] [CrossRef]
- Smit, W.J.; Tang, F.; Nagata, Y.; Sánchez, M.A.; Hasegawa, T.; Backus, E.H.G.; Bonn, M.; Bakker, H.J. Observation and Identification of a New OH Stretch Vibrational Band at the Surface of Ice. J. Phys. Chem. Lett. 2017, 8, 3656–3660. [Google Scholar] [CrossRef]
- Smit, W.J.; Tang, F.; Sánchez, M.A.; Backus, E.H.G.; Xu, L.; Hasegawa, T.; Bonn, M.; Bakker, H.J.; Nagata, Y. Excess Hydrogen Bond at the Ice-Vapor Interface around 200 K. Phys. Rev. Lett. 2017, 119, 133003. [Google Scholar] [CrossRef]
- Nojima, Y.; Suzuki, Y.; Takahashi, M.; Yamaguchi, S. Proton Order toward the Surface of Ice Ih Revealed by Heterodyne-Detected Sum Frequency Generation Spectroscopy. J. Phys. Chem. Lett. 2017, 8, 5031–5034. [Google Scholar] [CrossRef]
- Nojima, Y.; Shioya, Y.; Torii, H.; Yamaguchi, S. Hydrogen order at the surface of ice Ih revealed by vibrational spectroscopy. Chem. Commun. 2020, 56, 4563–4566. [Google Scholar] [CrossRef]
- Berrens, M.L.; Calegari Andrade, M.F.; Fourkas, J.T.; Pham, T.A.; Donadio, D. Molecular Fingerprints of Ice Surfaces in Sum Frequency Generation Spectra: A First-Principles Machine Learning Study. JACS Au 2025, 5, 1173–1183. [Google Scholar] [CrossRef]
- Rashmi, R.; Paesani, F. Dissecting the Molecular Structure of the Air/Ice Interface from Quantum Simulations of the Sum-Frequency Generation Spectrum. J. Am. Chem. Soc. 2025, 147, 1903–1910. [Google Scholar] [CrossRef]
- Babin, V.; Leforestier, C.; Paesani, F. Development of a “First Principles” Water Potential with Flexible Monomers: Dimer Potential Energy Surface, VRT Spectrum, and Second Virial Coefficient. J. Chem. Theory Comput. 2013, 9, 5395–5403. [Google Scholar] [CrossRef] [PubMed]
- Babin, V.; Medders, G.R.; Paesani, F. Development of a “First Principles” Water Potential with Flexible Monomers. II: Trimer Potential Energy Surface, Third Virial Coefficient, and Small Clusters. J. Chem. Theory Comput. 2014, 10, 1599–1607. [Google Scholar] [CrossRef]
- Medders, G.R.; Babin, V.; Paesani, F. Development of a “First-Principles” Water Potential with Flexible Monomers. III. Liquid Phase Properties. J. Chem. Theory Comput. 2014, 10, 2906–2910. [Google Scholar] [CrossRef]
- Zhu, X.; Riera, M.; Bull-Vulpe, E.F.; Paesani, F. MB-pol(2023): Sub-chemical Accuracy for Water Simulations from the Gas to the Liquid Phase. J. Chem. Theory Comput. 2023, 19, 3551–3566. [Google Scholar] [CrossRef]
- Zhai, Y.; Rashmi, R.; Palos, E.; Paesani, F. Many-body interactions and deep neural network potentials for water. J. Chem. Phys. 2024, 160, 144501. [Google Scholar] [CrossRef] [PubMed]
- Auer, B.M.; Skinner, J.L. Vibrational Sum-Frequency Spectroscopy of the Water Liquid/Vapor Interface. J. Phys. Chem. B 2009, 113, 4125–4130. [Google Scholar] [CrossRef]
- Ohto, T.; Usui, K.; Hasegawa, T.; Bonn, M.; Nagata, Y. Toward ab initio molecular dynamics modeling for sum-frequency generation spectra; an efficient algorithm based on surface-specific velocity-velocity correlation function. J. Chem. Phys. 2015, 143, 124702. [Google Scholar] [CrossRef]
- Nagata, Y.; Hasegawa, T.; Backus, E.H.G.; Usui, K.; Yoshimune, S.; Ohto, T.; Bonn, M. The surface roughness, but not the water molecular orientation varies with temperature at the water–air interface. Phys. Chem. Chem. Phys. 2015, 17, 23559–23564. [Google Scholar] [CrossRef]
- Schaefer, J.; Backus, E.H.G.; Nagata, Y.; Bonn, M. Both Inter- and Intramolecular Coupling of O-H Groups Determine the Vibrational Response of the Water/Air Interface. J. Phys. Chem. Lett. 2016, 7, 4591–4595. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Sharma, M.; Resta, R.; Galli, G.; Car, R. Role of dipolar correlations in the infrared spectra of water and ice. Phys. Rev. B 2008, 77, 245114. [Google Scholar] [CrossRef]
- Shi, L.; Gruenbaum, S.M.; Skinner, J.L. Interpretation of IR and Raman Line Shapes for H2O and D2O Ice Ih. J. Phys. Chem. B 2012, 116, 13821–13830. [Google Scholar] [CrossRef]
- Ojha, D.; Kaliannan, N.K.; Kühne, T.D. Time-dependent vibrational sum-frequency generation spectroscopy of the air-water interface. Commun. Chem. 2019, 2, 116. [Google Scholar] [CrossRef]
- Roudsari, G.; Veshki, F.G.; Reischl, B.; Pakarinen, O.H. Liquid Water and Interfacial, Cubic, and Hexagonal Ice Classification through Eclipsed and Staggered Conformation Template Matching. J. Phys. Chem. B 2021, 125, 3909–3917. [Google Scholar] [CrossRef] [PubMed]
- Conde, M.M.; Vega, C.; Patrykiejew, A. The thickness of a liquid layer on the free surface of ice as obtained from computer simulation. J. Chem. Phys. 2008, 129, 014702. [Google Scholar] [CrossRef]
- Bishop, C.L.; Pan, D.; Liu, L.M.; Tribello, G.A.; Michaelides, A.; Wang, E.G.; Slater, B. On thin ice: Surface order and disorder during pre-melting. Faraday Discuss. 2009, 141, 277–292. [Google Scholar] [CrossRef]
- Limmer, D.T.; Chandler, D. Premelting, fluctuations, and coarse-graining of water-ice interfaces. J. Chem. Phys. 2014, 141, 18C505. [Google Scholar] [CrossRef]
- Auer, B.; Kumar, R.; Schmidt, J.R.; Skinner, J.L. Hydrogen bonding and Raman, IR, and 2D-IR spectroscopy of dilute HOD in liquid D2O. Proc. Natl. Acad. Sci. USA 2007, 104, 14215–14220. [Google Scholar] [CrossRef]
- Sudera, P.; Cyran, J.D.; Bonn, M.; Backus, E.H.G. Interfacial Vibrational Spectroscopy of the Water Bending Mode on Ice Ih. J. Phys. Chem. C 2021, 125, 22937–22942. [Google Scholar] [CrossRef]
- Chiang, K.Y.; Hunger, J.; Bonn, M.; Nagata, Y. Experimental quantification of nuclear quantum effects on the hydrogen bond of liquid water. Sci. Adv. 2025, 11, eadv7218. [Google Scholar] [CrossRef]
- Ojha, D.; Henao, A.; Zysk, F.; Kühne, T.D. Nuclear quantum effects on the vibrational dynamics of the water–air interface. J. Chem. Phys. 2024, 160, 204114. [Google Scholar] [CrossRef] [PubMed]
- Chelli, R.; Pagliai, M.; Procacci, P.; Cardini, G.; Schettino, V. Polarization response of water and methanol investigated by a polarizable force field and density functional theory calculations: Implications for charge transfer. J. Chem. Phys. 2005, 122, 074504. [Google Scholar] [CrossRef]
- Smirnov, K.S. Assessment of split-charge equilibration model for development of polarizable force fields. Model. Simul. Mater. Sci. Eng. 2015, 23, 074006. [Google Scholar] [CrossRef]
- Matsumoto, M.; Yagasaki, T.; Tanaka, H. GenIce: Hydrogen-Disordered Ice Generator. J. Comput. Chem. 2018, 39, 61–64. [Google Scholar] [CrossRef]
- Matsumoto, M.; Yagasaki, T.; Tanaka, H. GenIce-core: Efficient algorithm for generation of hydrogen-disordered ice structures. J. Chem. Phys. 2024, 160, 094101. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Tepper, H.L.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces; Pullman, B., Ed.; Reidel: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar]
- Smirnov, K.S. Structure and sum-frequency generation spectra of water on uncharged Q4 silica surfaces: A molecular dynamics study. Phys. Chem. Chem. Phys. 2020, 22, 2033–2045. [Google Scholar] [CrossRef]
- Kroutil, O.; Pezzotti, S.; Gaigeot, M.P.; Předota, M. Phase-Sensitive Vibrational SFG Spectra from Simple Classical Force Field Molecular Dynamics Simulations. J. Phys. Chem. C 2020, 124, 15253–15263. [Google Scholar] [CrossRef]
- Smirnov, K.S. Structure and sum-frequency generation spectra of water on neutral hydroxylated silica surfaces. Phys. Chem. Chem. Phys. 2021, 23, 6929–6949. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, K.S. A molecular dynamics study of the nonlinear spectra and structure of charged (101) quartz/water interfaces. Phys. Chem. Chem. Phys. 2022, 24, 25118–25133. [Google Scholar] [CrossRef] [PubMed]
- Vega, C.; Sanz, E.; Abascal, J.L.F. The melting temperature of the most common models of water. J. Chem. Phys. 2005, 122, 114507. [Google Scholar] [CrossRef]
- Blazquez, S.; Vega, C. Melting points of water models: Current situation. J. Chem. Phys. 2022, 156, 216101. [Google Scholar] [CrossRef]
- Wolf, D.; Keblinski, P.; Phillpot, S.R.; Eggebrecht, J. Exact method for the simulation of Coulombic systems by spherically truncated, pairwise r-1 summation. J. Chem. Phys. 1999, 110, 8254–8282. [Google Scholar] [CrossRef]
- Fennell, C.J.; Gezelter, J.D. Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. J. Chem. Phys. 2006, 124, 234104. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tuckerman, M.E.; Tobias, D.J.; Klein, M.L. Explicit reversible integrators for extended systems dynamics. Mol. Phys. 1996, 87, 1117–1157. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Willard, A.P.; Chandler, D. Instantaneous Liquid Interfaces. J. Phys. Chem. B 2010, 114, 1954–1958. [Google Scholar] [CrossRef] [PubMed]
- Errington, J.R.; Debenedetti, P.G. Relationship between structural order and the anomalies of liquid water. Nature 2001, 409, 318–321. [Google Scholar] [CrossRef]
- Malaspina, D.C.; Schulz, E.P.; Alarcón, L.M.; Frechero, M.A.; Appignanesi, G.A. Structural and dynamical aspects of water in contact with a hydrophobic surface. Eur. Phys. J. E 2010, 32, 35–42. [Google Scholar] [CrossRef]
- Duboué-Dijon, E.; Laage, D. Characterization of the Local Structure in Liquid Water by Various Order Parameters. J. Phys. Chem. B 2015, 119, 8406–8418. [Google Scholar] [CrossRef] [PubMed]
- Prada-Gracia, D.; Shevchuk, R.; Rao, F. The quest for self-consistency in hydrogen bond definitions. J. Chem. Phys. 2013, 139, 084501. [Google Scholar] [CrossRef]
- Ji, N.; Ostroverkhov, V.; Tian, C.S.; Shen, Y.R. Characterization of Vibrational Resonances of Water-Vapor Interfaces by Phase-Sensitive Sum-Frequency Spectroscopy. Phys. Rev. Lett. 2008, 100, 096102. [Google Scholar] [CrossRef]
- Morita, A.; Hynes, J.T. A Theoretical Analysis of the Sum Frequency Generation Spectrum of the Water Surface. II. Time-Dependent Approach. J. Phys. Chem. B 2002, 106, 673–685. [Google Scholar] [CrossRef]
- Corcelli, S.A.; Skinner, J.L. Infrared and Raman Line Shapes of Dilute HOD in Liquid H2O and D2O from 10 to 90 °C. J. Phys. Chem. A 2005, 109, 6154–6165. [Google Scholar] [CrossRef] [PubMed]
- Auer, B.M.; Skinner, J.L. IR and Raman spectra of liquid water: Theory and interpretation. J. Chem. Phys. 2008, 128, 224511. [Google Scholar] [CrossRef] [PubMed]
- Bisson, P.J.; Shultz, M.J. Hydrogen Bonding in the Prism Face of Ice Ih via Sum Frequency Vibrational Spectroscopy. J. Phys. Chem. A 2013, 117, 6116–6125. [Google Scholar] [CrossRef]
- Ishiyama, T.; Morita, A. Intermolecular correlation effect in sum frequency generation spectroscopy of electrolyte aqueous solution. Chem. Phys. Lett. 2006, 431, 78–82. [Google Scholar] [CrossRef]
- Ishiyama, T.; Morita, A. Molecular Dynamics Study of Gas-Liquid Aqueous Sodium Halide Interfaces. II. Analysis of Vibrational Sum Frequency Generation Spectra. J. Phys. Chem. C 2007, 111, 738–748. [Google Scholar] [CrossRef]
- Nagata, Y.; Mukamel, S. Spectral Diffusion at the Water/Lipid Interface Revealed by Two-Dimensional Fourth-Order Optical Spectroscopy: A Classical Simulation Study. J. Am. Chem. Soc. 2011, 133, 3276–3279. [Google Scholar] [CrossRef][Green Version]
- Morita, A.; Hynes, J.T. A theoretical analysis of the sum frequency generation spectrum of the water surface. Chem. Phys. 2000, 258, 371–390. [Google Scholar] [CrossRef]
- Shen, Y. The Principles of Nonlinear Optics; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Ramos-Cordoba, E.; Lambrecht, D.S.; Head-Gordon, M. Charge-transfer and the hydrogen bond: Spectroscopic and structural implications from electronic structure calculations. Faraday Discuss. 2011, 150, 345–362. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Shimanouchi, T. Tables of Molecular Vibrational Frequencies. Consolidated Volume I; Number vol. 1 in National Standard Reference Data Series; National Bureau of Standards: Washington, DC, USA, 1972.
- Khatib, R.; Sulpizi, M. Sum Frequency Generation Spectra from Velocity-Velocity Correlation Functions. J. Phys. Chem. Lett. 2017, 8, 1310–1314. [Google Scholar] [CrossRef] [PubMed]




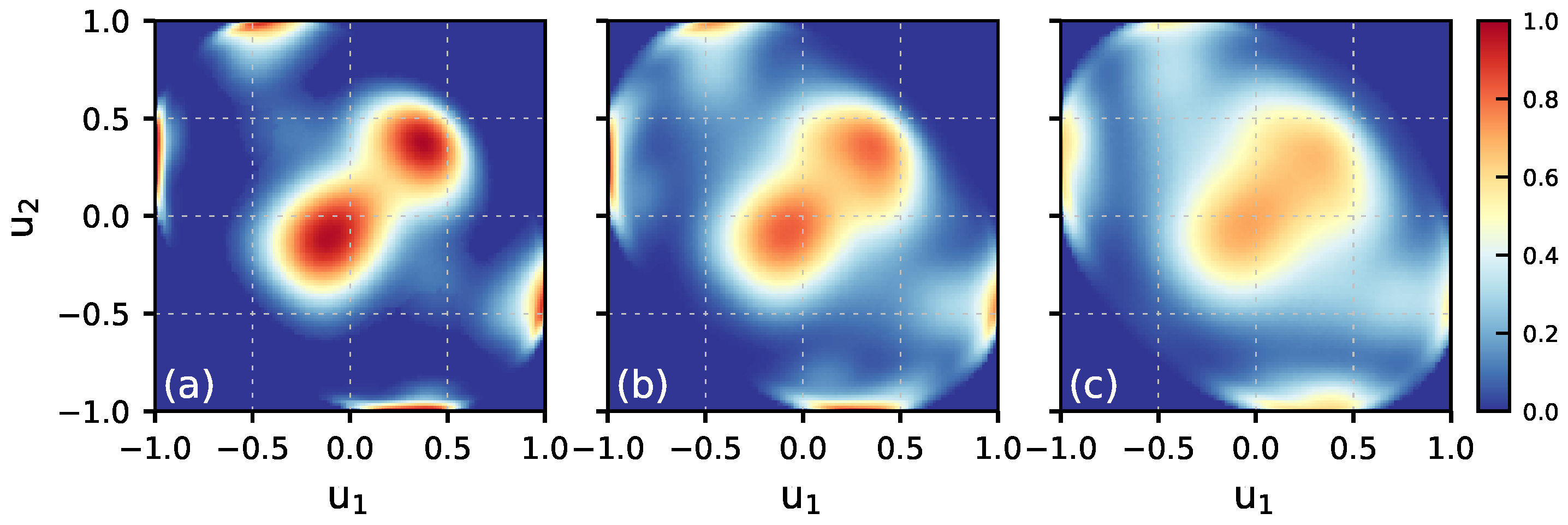

| (K) | DA | DAA | DDA | DDAA |
|---|---|---|---|---|
| 0.004 (0.002) | 0.115 (0.007) | 0.114 (0.007) | 0.766 (0.011) | |
| 0.014 (0.003) | 0.096 (0.004) | 0.100 (0.004) | 0.784 (0.005) | |
| 0.025 (0.004) | 0.085 (0.003) | 0.091 (0.004) | 0.791 (0.008) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, K.S. Structure and Nonlinear Spectra of the Basal Face of Hexagonal Ice: A Molecular Dynamics Study. Molecules 2025, 30, 3619. https://doi.org/10.3390/molecules30173619
Smirnov KS. Structure and Nonlinear Spectra of the Basal Face of Hexagonal Ice: A Molecular Dynamics Study. Molecules. 2025; 30(17):3619. https://doi.org/10.3390/molecules30173619
Chicago/Turabian StyleSmirnov, Konstantin S. 2025. "Structure and Nonlinear Spectra of the Basal Face of Hexagonal Ice: A Molecular Dynamics Study" Molecules 30, no. 17: 3619. https://doi.org/10.3390/molecules30173619
APA StyleSmirnov, K. S. (2025). Structure and Nonlinear Spectra of the Basal Face of Hexagonal Ice: A Molecular Dynamics Study. Molecules, 30(17), 3619. https://doi.org/10.3390/molecules30173619








