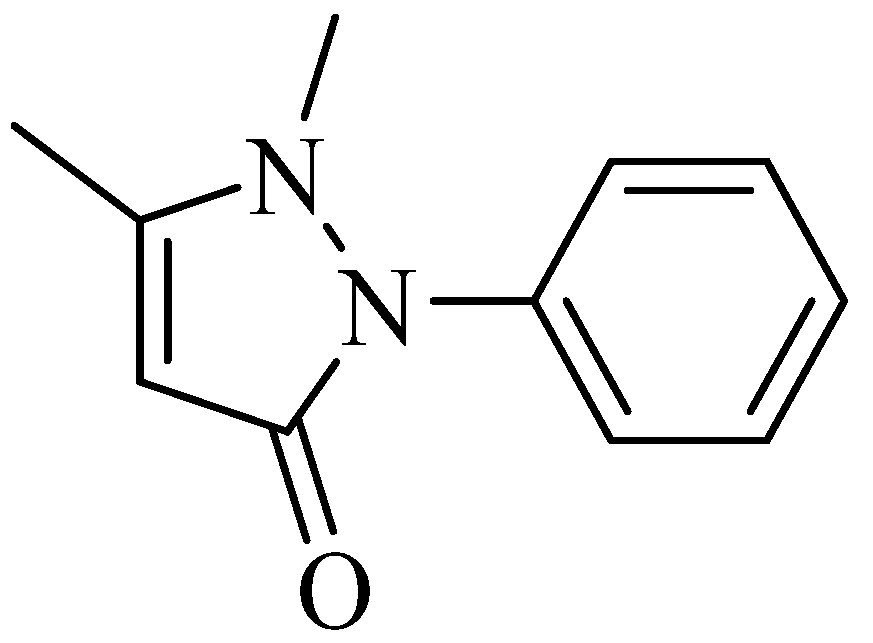
Polymorphism and Phase-Transition Thermodynamic Properties of Phenazone (Antipyrine)
Abstract
1. Introduction
2. Results
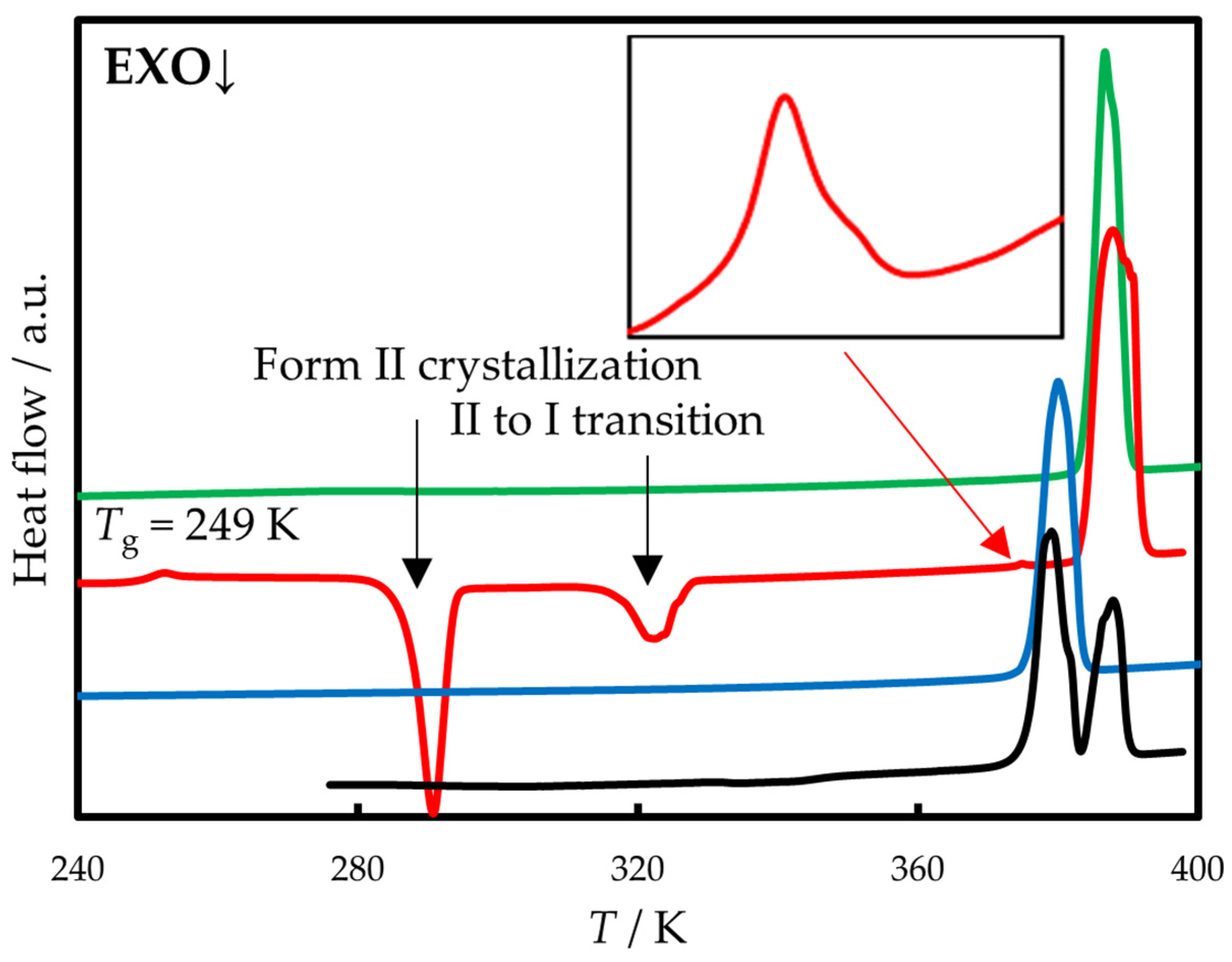
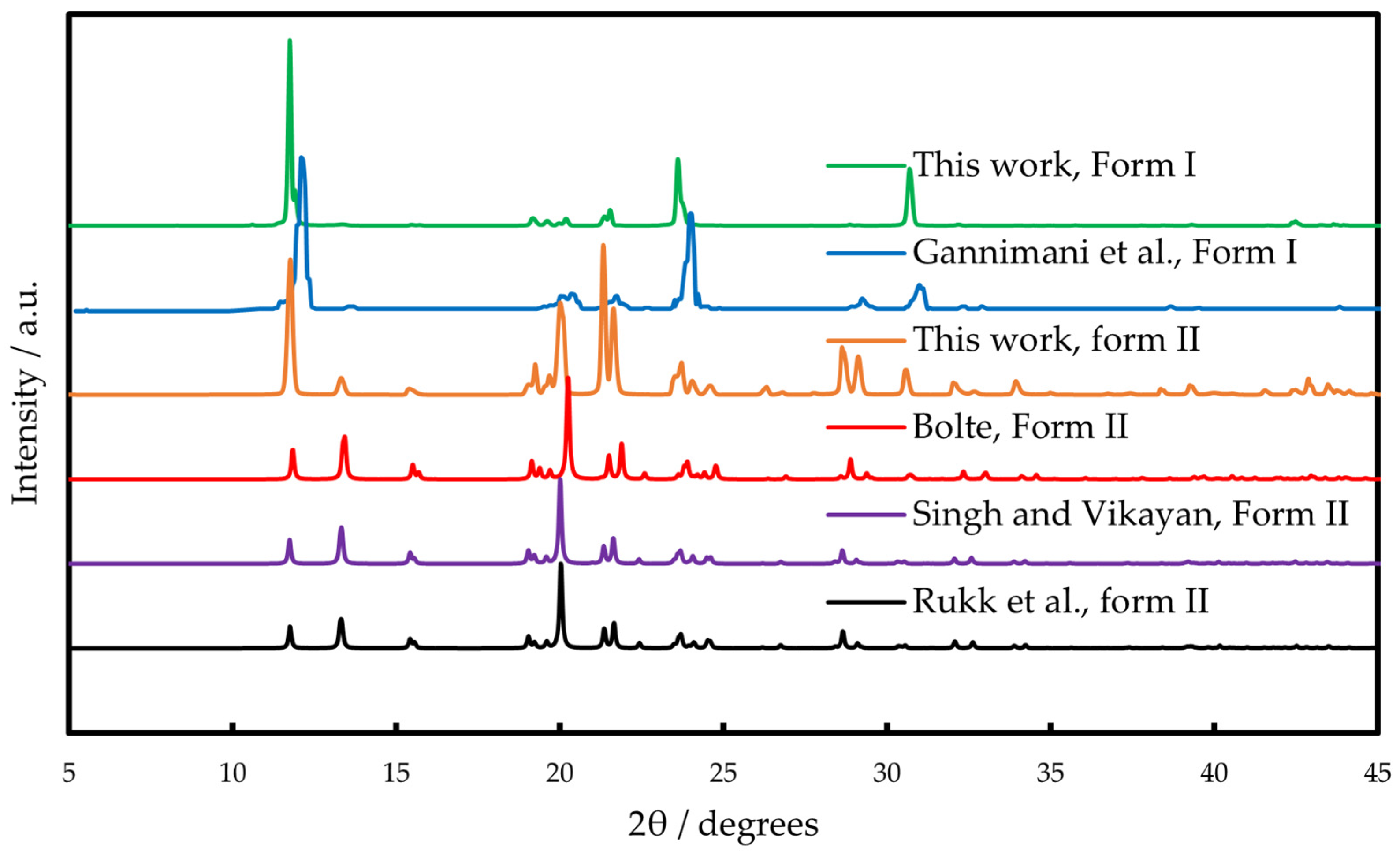
2.1. Polymorphism and Thermal Behavior
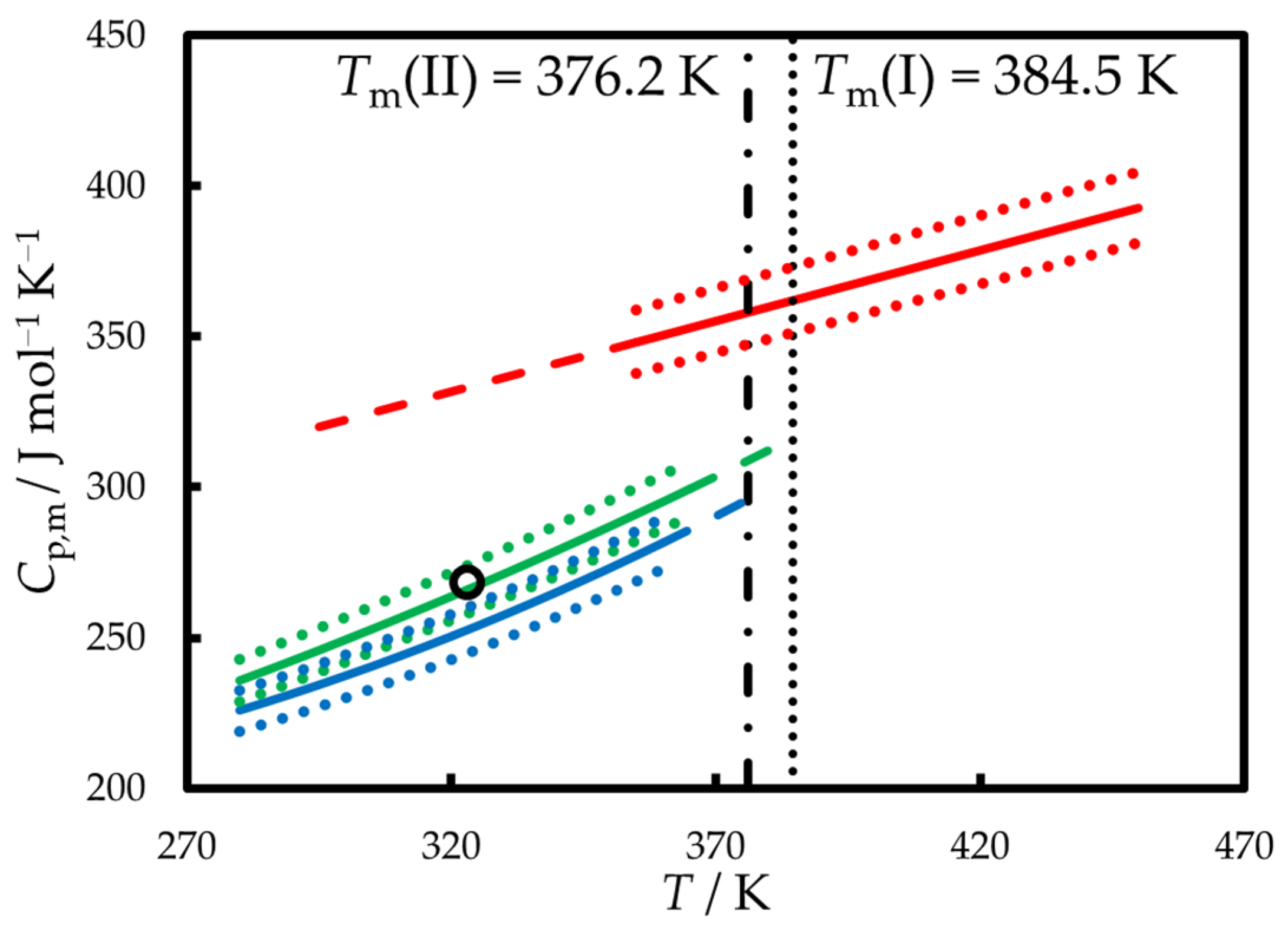
2.2. Condensed Phase Heat Capacities
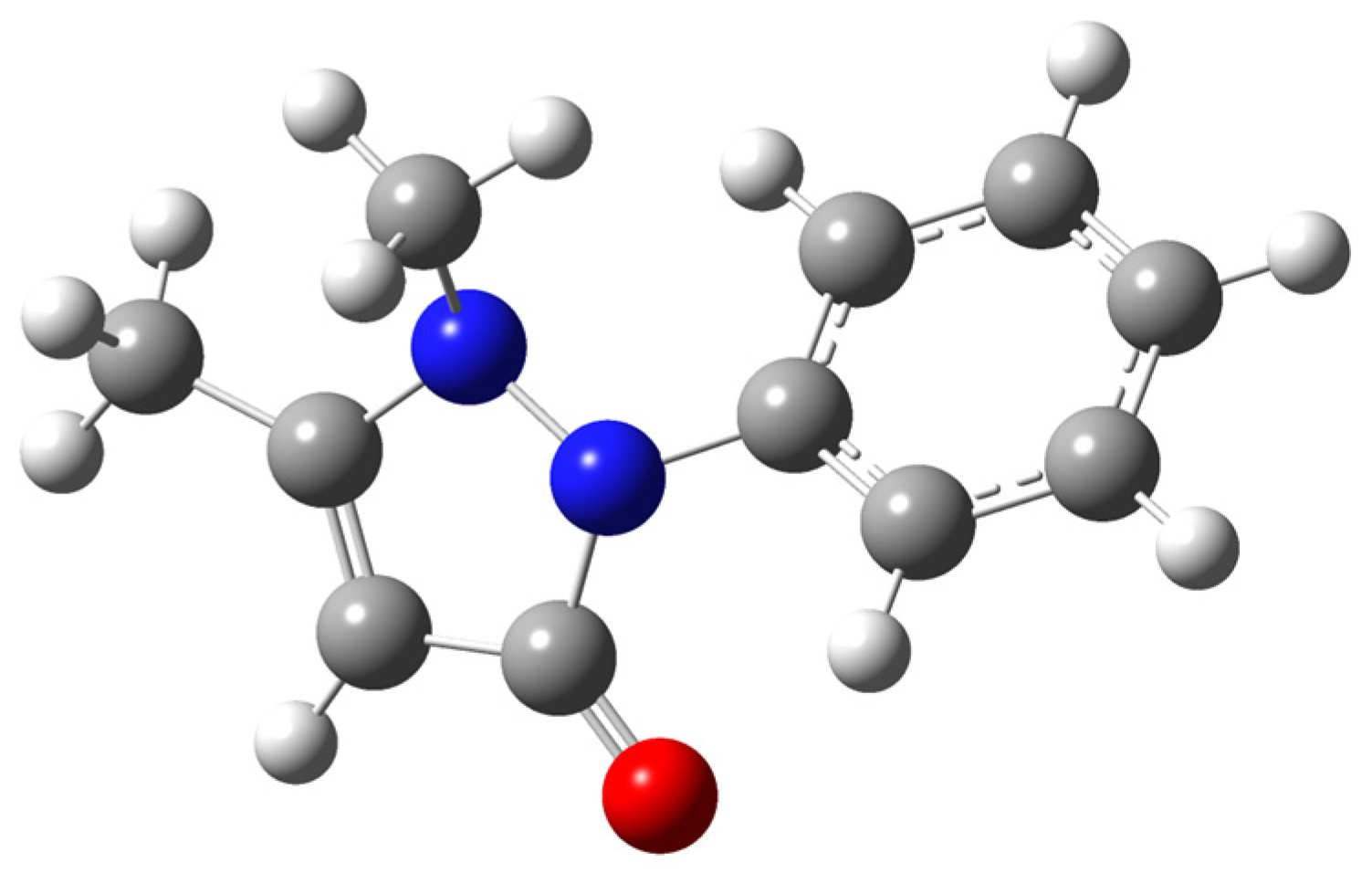
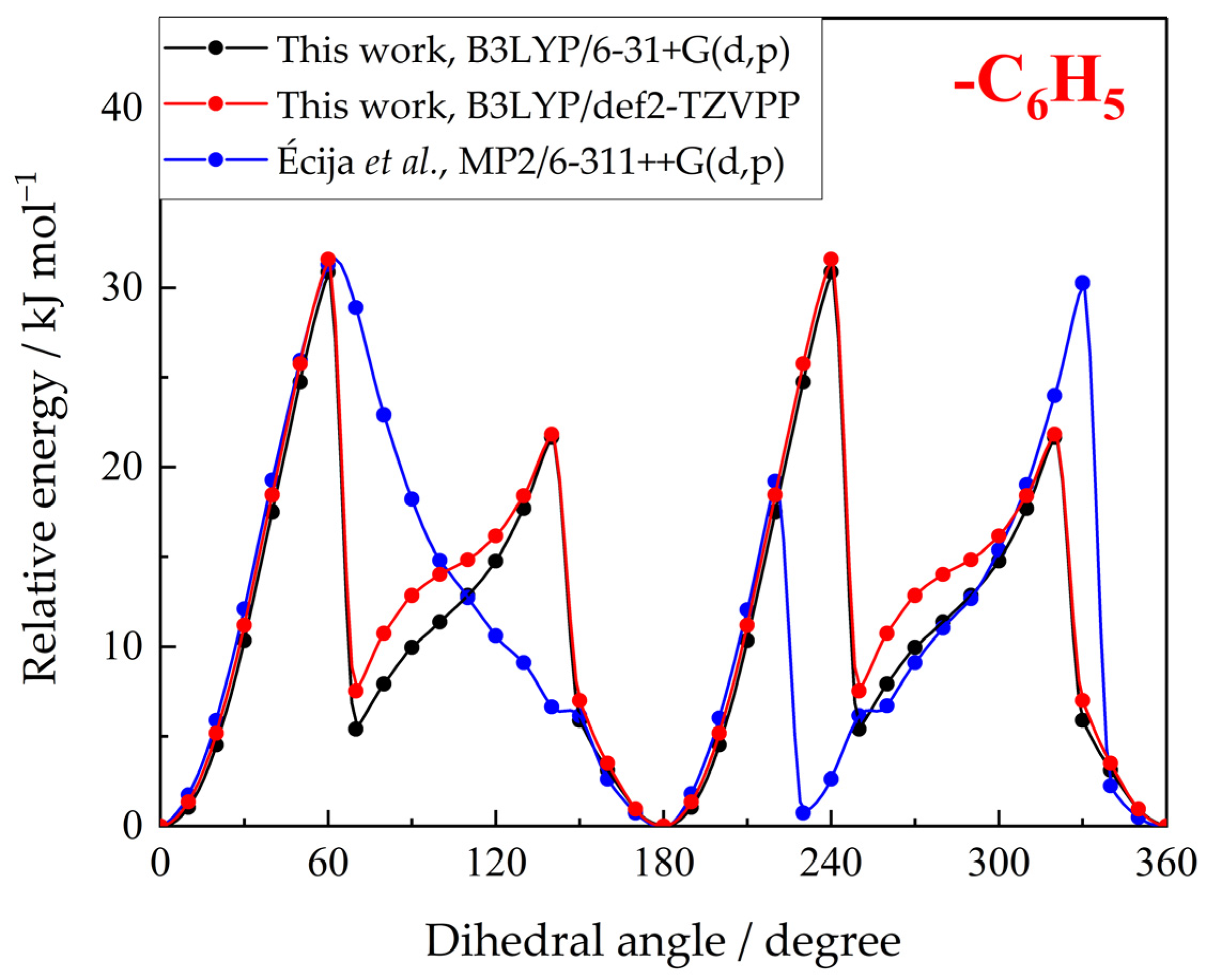
2.3. Optimized Geometry, Ideal Gas Heat Capacities and Entropies
2.4. Thermodynamics of Vaporization/Sublimation
3. Discussion
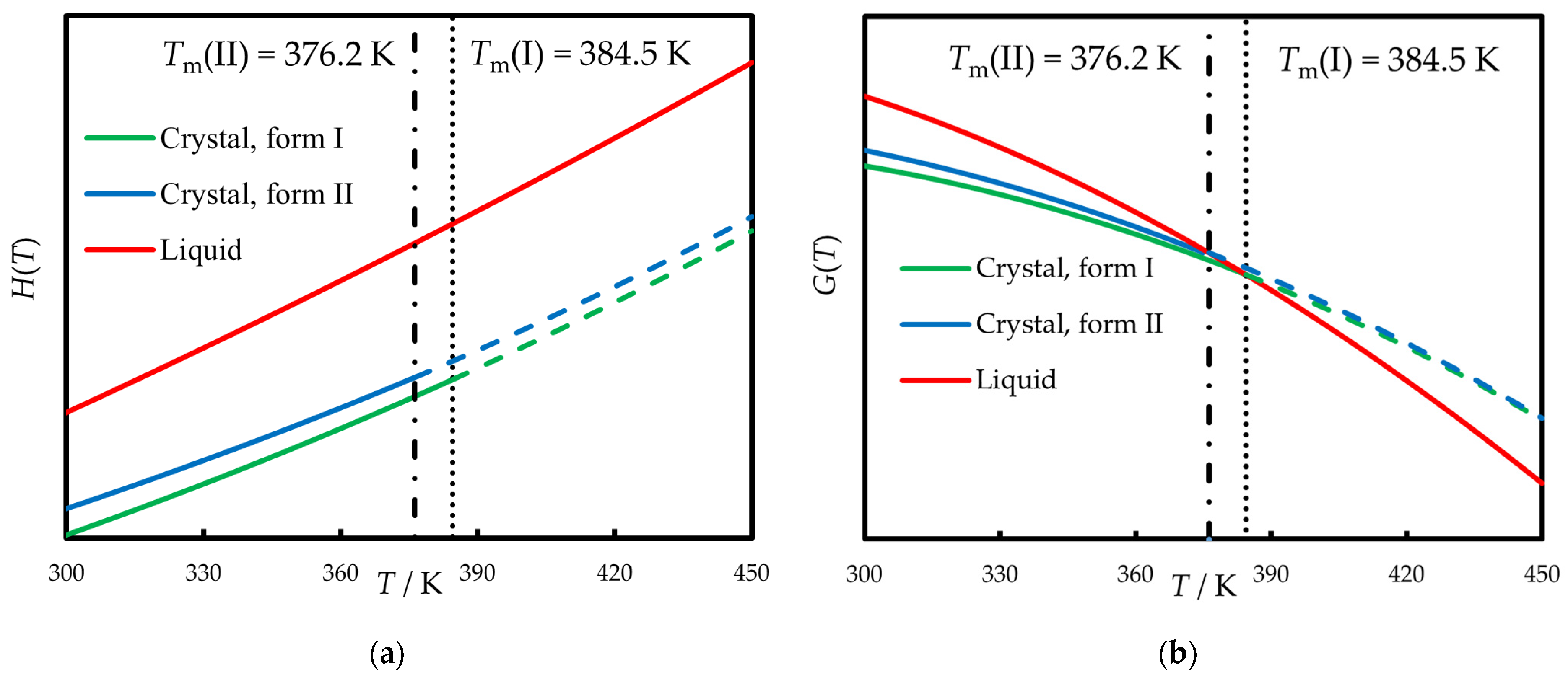
3.1. Thermodynamics of Fusion Between 298.15 K and Tm
3.2. Thermodynamics of Vaporization/Sublimation at 298.15 K
4. Materials and Methods
4.1. Materials
4.2. Differential Scanning Calorimetry
4.3. Fast Scanning Calorimetry
4.4. Solution Calorimetry
4.5. Computations
4.6. X-Ray Powder Diffraction
4.7. Temperature Dependence of the Thermodynamic Functions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DSC | Differential scanning calorimetry |
| TG-DSC | Thermogravimetry—differential scanning calorimetry |
| XRPD | X-ray powder diffraction |
| HPLC | High performance liquid chromatography |
| DMF | N,N-dimethylformamide |
References
- Barrett, P.; Smith, B.; Worlitschek, J.; Bracken, V.; O’Sullivan, B.; O’Grady, D. A review of the use of process analytical technology for the understanding and optimization of production batch crystallization processes. Org. Process Res. Dev. 2005, 9, 348–355. [Google Scholar] [CrossRef]
- Morimoto, Y.; Hori, R.; Arita, T. Solubilities of antipyrine derivatives in water and non-polar solvents. Chem. Pharm. Bull. 1974, 22, 2217–2222. [Google Scholar] [CrossRef]
- Wassvik, C.M.; Holmén, A.G.; Bergström, C.A.; Zamora, I.; Artursson, P. Contribution of solid-state properties to the aqueous solubility of drugs. Eur. J. Pharm. Sci. 2006, 29, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Ran, Y.; Yalkowsky, S.H. Prediction of drug solubility by the general solubility equation (GSE). J. Chem. Inf. Comput. Sci. 2001, 41, 354–357. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Chen, Y.-P. Measurements for the solid solubilities of antipyrine, 4-aminoantipyrine and 4-dimethylaminoantipyrine in supercritical carbon dioxide. Fluid Phase Equilibria 2009, 282, 82–87. [Google Scholar] [CrossRef]
- Yokoi, D.; Hoshina, T.-a.; Tsuji, T.; Hiaki, T.; Tomida, D.; Qiao, K.; Yokoyama, C. Measurement and correlation of solid–liquid equilibria for three binaries, ethanol–antipyrine, chloroform–antipyrine, and dimethyl ether–antipyrine. Fluid Phase Equilibria 2016, 420, 14–19. [Google Scholar] [CrossRef]
- Perlovich, G.L. Two-component molecular crystals: Evaluation of the formation thermodynamics based on melting points and sublimation data. CrystEngComm 2017, 19, 2870–2883. [Google Scholar] [CrossRef]
- Andrianov, R.; Morozova, T.A.; Snetkov, D.S.; Nizamov, I.I.; Schick, C.; Mukhametzyanov, T. Nucleation, crystal growth, nuclei stability, and polymorph selection in supercooled Tolbutamide melt. Phys. Chem. Chem. Phys. 2024, 26, 25946–25956. [Google Scholar] [CrossRef]
- Chickos, J.S.; Nichols, G.; Ruelle, P. The estimation of melting points and fusion enthalpies using experimental solubilities, estimated total phase change entropies, and mobile order and disorder theory. J. Chem. Inf. Comput. Sci. 2002, 42, 368–374. [Google Scholar] [CrossRef]
- Chickos, J.S. Enthalpies of Sublimation after a Century of Measurement A View as Seen through the Eyes of a Collector. Netsu Sokutei 2003, 30, 116–124. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E., Jr. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. Sublimation, Vaporization and Fusion Enthalpies From 1880 to 2015. Part 1. J. Phys. Chem. Ref. Data 2016, 45, 033101. [Google Scholar] [CrossRef]
- Acree, W.E., Jr.; Chickos, J.S. Phase transition enthalpy measurements of organic and organometallic compounds and ionic liquids. Sublimation, vaporization, and fusion enthalpies from 1880 to 2015. Part 2. C11–C192. J. Phys. Chem. Ref. Data 2017, 46, 013104. [Google Scholar] [CrossRef]
- Acree, W., Jr.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic Compounds. An Update of Sublimation, Vaporization, and Fusion Enthalpies from 2016 to 2021. J. Phys. Chem. Ref. Data 2022, 51, 043101. [Google Scholar] [CrossRef]
- Yu, L. Inferring thermodynamic stability relationship of polymorphs from melting data. J. Pharm. Sci. 1995, 84, 966–974. [Google Scholar] [CrossRef]
- Censi, R.; Di Martino, P. Polymorph impact on the bioavailability and stability of poorly soluble drugs. Molecules 2015, 20, 18759–18776. [Google Scholar] [CrossRef]
- Pudipeddi, M.; Serajuddin, A.T. Trends in solubility of polymorphs. J. Pharm. Sci. 2005, 94, 929–939. [Google Scholar] [CrossRef]
- Singhal, D.; Curatolo, W. Drug polymorphism and dosage form design: A practical perspective. Adv. Drug Deliv. Rev. 2004, 56, 335–347. [Google Scholar] [CrossRef]
- Almeida e Sousa, L.; Reutzel-Edens, S.M.; Stephenson, G.A.; Taylor, L.S. Assessment of the amorphous “solubility” of a group of diverse drugs using new experimental and theoretical approaches. Mol. Pharm. 2015, 12, 484–495. [Google Scholar] [CrossRef]
- Hilfiker, R.; Von Raumer, M. Polymorphism in the Pharmaceutical Industry: Solid Form and Drug Development; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Li, X.; Ou, X.; Wang, B.; Rong, H.; Wang, B.; Chang, C.; Shi, B.; Yu, L.; Lu, M. Rich polymorphism in nicotinamide revealed by melt crystallization and crystal structure prediction. Commun. Chem. 2020, 3, 152. [Google Scholar] [CrossRef]
- Price, S.L. The computational prediction of pharmaceutical crystal structures and polymorphism. Adv. Drug Deliv. Rev. 2004, 56, 301–319. [Google Scholar] [CrossRef]
- Hilfiker, R.; De Paul, S.M.; Szelagiewicz, M. Approaches to polymorphism screening. In Polymorphism: In the Pharmaceutical Industry; Wiley-VCH Verlag GmbH & Co. KGaA: Hoboken, NJ, USA, 2006; pp. 287–308. [Google Scholar]
- Tandon, R.; Tandon, N.; Gupta, N.; Gupta, R. Art of synthesis of desired polymorphs: A review. Asian J. Chem. 2018, 30, 5–14. [Google Scholar] [CrossRef]
- Brogden, R.N. Pyrazolone derivatives. Drugs 1986, 32, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhou, G.; Dong, J.; Li, Z.; Ding, L.; Wang, B. Measurement and correlation of the solubility of antipyrine in ten pure and water+ ethanol mixed solvents at temperature from (288.15 to 328.15) K. J. Mol. Liq. 2018, 268, 256–265. [Google Scholar] [CrossRef]
- Romain, P. Contribution à l’étude cristallographique de l’antipyrine. Bull. Minéralogie 1952, 75, 447–449. [Google Scholar] [CrossRef]
- Singh, T.; Vijayan, M. Structural studies of analgesics and their interactions. I. The crystal and molecular structure of antipyrene. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1973, 29, 714–720. [Google Scholar] [CrossRef]
- Bolte, M. CCDC 912076: Experimental Crystal Structure Determination; Cambridge Crystallographic Data Centre Inc.: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Écija, P.; Cocinero, E.J.; Lesarri, A.; Fernández, J.A.; Caminati, W.; Castano, F. Rotational spectroscopy of antipyretics: Conformation, structure, and internal dynamics of phenazone. J. Chem. Phys. 2013, 138, 114304. [Google Scholar] [CrossRef]
- Ohm, A.; Lippold, B. Surface tension of solid drugs and its correlation with solubility. Int. J. Pharm. Technol. Prod. Manuf. 1985, 6, 1. [Google Scholar]
- Schnitzler, E.; Lençone, K.; Kobelnik, M. Characterization of pharmaceuticals by thermal analysis. Publ. UEPG: Ciências Exatas Terra Agrárias Eng.-Atividades Encerr. 2002, 8, 91–100. [Google Scholar] [CrossRef]
- Baird, J.A.; Van Eerdenbrugh, B.; Taylor, L.S. A classification system to assess the crystallization tendency of organic molecules from undercooled melts. J. Pharm. Sci. 2010, 99, 3787–3806. [Google Scholar] [CrossRef]
- Hrynakowski, K.; Smoczkiewiczowa, A. Zastosowanie analizy termicznej do oznaczania efektów cieplnych. Roczniki Chemii 1937, 17, 165–167. [Google Scholar]
- Fasihi, Z.; Zakeri-Milani, P.; Nokhodchi, A.; Akbari, J.; Barzegar-Jalali, M.; Loebenberg, R.; Valizadeh, H. Thermodynamic approaches for the prediction of oral drug absorption. J. Therm. Anal. Calorim. 2017, 130, 1371–1382. [Google Scholar] [CrossRef]
- Yanagimoto, G.; Hayashi, T.; Hasegawa, T.; Seki, T.; JUNi, K.; Sugibayashi, K.; Morimoto, Y. Skin disposition of drugs after topical application in hairless rats. Chem. Pharm. Bull. 1999, 47, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Hatanaka, T.; Inuma, M.; Sugibayashi, K.; Morimoto, Y. Prediction of skin permeability of drugs. I. Comparison with artificial membrane. Chem. Pharm. Bull. 1990, 38, 3452–3459. [Google Scholar] [CrossRef] [PubMed]
- Satoh, S.; Sogabe, T. The heat capacities of some organic compounds containing nitrogen and the atomic heat of nitrogen 1. Sci. Pap. Inst. Phys. Chem. Res. Tokyo 1941, 38, 197–203. [Google Scholar]
- Gannimani, R.; Perumal, A.; Ramesh, M.; Pillay, K.; Soliman, M.E.; Govender, P. Antipyrine–gamma cyclodextrin inclusion complex: Molecular modeling, preparation, characterization and cytotoxicity studies. J. Mol. Struct. 2015, 1089, 38–47. [Google Scholar] [CrossRef]
- Knorr, L. Studien über Tautomerie. Justus Liebigs Ann. Chem. 1896, 293, 70–72. [Google Scholar] [CrossRef]
- Fukuoka, E.; Makita, M.; Yamamura, S. Glassy state of pharmaceuticals. III.: Thermal properties and stability of glassy pharmaceuticals and their binary glass systems. Chem. Pharm. Bull. 1989, 37, 1047–1050. [Google Scholar] [CrossRef]
- Rukk, N.S.; Shamsiev, R.S.; Albov, D.V.; Mudretsova, S.N. Structural characterization of hydrogen bonding for antipyrine derivatives: Single-crystal X-ray diffraction and theoretical studies. Fine Chem. Technol. 2021, 16, 113–137. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Nagrimanov, R.N.; Ziganshin, M.A.; Solomonov, B.N. New aspects of relationship between the enthalpies of fusion of aromatic compounds at the melting temperatures and the enthalpies of solution in benzene at 298.15 K. Part I. J. Chem. Thermodyn. 2018, 116, 152–158. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Nagrimanov, R.N.; Solomonov, B.N. New aspects in the thermochemistry of solid-liquid phase transitions of organic non-electrolytes. J. Mol. Liq. 2018, 256, 58–66. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Sokolov, A.A.; Balakhontsev, I.S.; Nizamov, I.I.; Solomonov, B.N. Thermochemistry of fusion, solution and hydrogen bonding in benzamide, N-methylbenzamide, and acetanilide. Thermochim. Acta 2023, 728, 179579. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Yagofarov, M.I.; Balakhontsev, I.S.; Nizamov, I.I.; Mukhametzyanov, T.A.; Solomonov, B.N.; Yurkshtovich, Y.N.; Stepurko, E.N. Thermodynamic Properties of 3-and 4-Ethoxyacetanilides between 80 and 480 K. Molecules 2023, 28, 7027. [Google Scholar] [CrossRef] [PubMed]
- Solomonov, B.N.; Konovalov, A.I.; Novikov, V.B.; Vedernikov, A.N.; Borisover, M.D.; Gorbachuk, V.V.; Antipin, I.S. Solvation of organic compounds. Molecular refraction, dipole moment, and enthalpy of solvation. J. Gen. Chem. USSR (Engl. Transl.) 1984, 54, 1444–1453. [Google Scholar]
- Höhne, G.W.H.; Hemminger, W.; Flammersheim, H.-J. Differential Scanning Calorimetry; Springer: Berlin, Germany, 2003; Volume 2. [Google Scholar]
- Goursot, P.; Girdhar, H.L.; Westrum, E.F., Jr. Thermodynamics of polynuclear aromatic molecules. III. Heat capacities and enthalpies of fusion of anthracene. J. Phys. Chem. 1970, 74, 2538–2541. [Google Scholar] [CrossRef]
- Grønvold, F. Heat capacity of indium from 300 to 1000 K: Enthalpy of fusion. J. Therm. Anal. Calorim. 1978, 13, 419–428. [Google Scholar] [CrossRef]
- Yagofarov, M.I.; Sokolov, A.A.; Gerasimov, A.V.; Solomonov, B.N.; Stepurko, E.N.; Yurkshtovich, Y.N. Thermodynamic Properties of Thioxanthone between 80 and 540 K. J. Chem. Eng. Data 2022, 67, 3583–3588. [Google Scholar] [CrossRef]
- Buzyurov, A.V.; Nagrimanov, R.N.; Zaitsau, D.H.; Mukhametzyanov, T.A.; Solomonov, B.N.; Abdelaziz, A.; Schick, C. Application of the Flash DSC 1 and 2+ for vapor pressure determination above solids and liquids. Thermochim. Acta 2021, 706, 179067. [Google Scholar] [CrossRef]
- Mukhametzyanov, T.A.; Notfullin, A.A.; Fatkhutdinova, A.A.; Schick, C. Organic compounds as temperature calibrants for Fast Scanning Calorimetry. Thermochim. Acta 2024, 741, 179868. [Google Scholar] [CrossRef]
- Cebe, P.; Thomas, D.; Merfeld, J.; Partlow, B.P.; Kaplan, D.L.; Alamo, R.G.; Wurm, A.; Zhuravlev, E.; Schick, C. Heat of fusion of polymer crystals by fast scanning calorimetry. Polymer 2017, 126, 240–247. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 6.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2025, 15, e70019. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Ayala, P.Y.; Schlegel, H.B. Identification and treatment of internal rotation in normal mode vibrational analysis. J. Chem. Phys. 1998, 108, 2314–2325. [Google Scholar] [CrossRef]
- Cervinka, C.; Fulem, M.; Ruzicka, K. Evaluation of accuracy of ideal-gas heat capacity and entropy calculations by density functional theory (DFT) for rigid molecules. J. Chem. Eng. Data 2012, 57, 227–232. [Google Scholar] [CrossRef]
- Kesharwani, M.K.; Brauer, B.; Martin, J.M. Frequency and zero-point vibrational energy scale factors for double-hybrid density functionals (and other selected methods): Can anharmonic force fields be avoided? J. Phys. Chem. A 2015, 119, 1701–1714. [Google Scholar] [CrossRef]
- Pfaendtner, J.; Yu, X.; Broadbelt, L.J. The 1-D hindered rotor approximation. Theor. Chem. Acc. 2007, 118, 881–898. [Google Scholar] [CrossRef]
- Kilpatrick, J.E.; Pitzer, K.S. Energy levels and thermodynamic functions for molecules with internal rotation. III. Compound rotation. J. Chem. Phys. 1949, 17, 1064–1075. [Google Scholar] [CrossRef]
- Balint-Kurti, G.G.; Dixon, R.N.; Marston, C.C. Grid methods for solving the Schrödinger equation and time dependent quantum dynamics of molecular photofragmentation and reactive scattering processes. Int. Rev. Phys. Chem. 1992, 11, 317–344. [Google Scholar] [CrossRef]
- Balint-Kurti, G.G.; Ward, C.L.; Marston, C.C. Two computer programs for solving the Schrödinger equation for bound-state eigenvalues and eigenfunctions using the Fourier grid Hamiltonian method. Comput. Phys. Commun. 1991, 67, 285–292. [Google Scholar] [CrossRef]
- Marston, C.C.; Balint-Kurti, G.G. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions. J. Chem. Phys. 1989, 91, 3571–3576. [Google Scholar] [CrossRef]
- NIST: Fourier Grid Hamiltonian (FGH) 1D Program. Available online: https://www.nist.gov/mml/csd/chemical-informatics-research-group/products-and-services/fourier-grid-hamiltonian-fgh-1d (accessed on 1 September 2024).
- Cervinka, C.; Fulem, M.; Ruzicka, K. Evaluation of uncertainty of ideal-gas entropy and heat capacity calculations by density functional theory (DFT) for molecules containing symmetrical internal rotors. J. Chem. Eng. Data 2013, 58, 1382–1390. [Google Scholar] [CrossRef]

| Space Group | a/Å | b/Å | c/Å | β/° | Ref. |
|---|---|---|---|---|---|
| C2/c a | 16.90 | 7.43 | 17.83 | 117.49 | [26] |
| C2/c b | 16.919 | 7.425 | 17.796 | 117.03 | [27] |
| C2/c c | 16.7125 | 7.3864 | 17.5905 | 116.576 | [28] |
| C2/c b | 16.8929 | 7.4293 | 17.7768 | 116.985 | [41] |
| Property | This Work, B3LYP/6-31+G(d,p) | This Work, B3LYP/def2-TZVPP | Écija et al. [29], MP2/6-311++G(d,p) |
|---|---|---|---|
| A/MHz a | 1413.1 | 1427.8 | 1416.9 |
| B/MHz a | 491.6 | 498.6 | 495.5 |
| C/MHz a | 397.6 | 400.4 | 402.5 |
| τ/degree b | 54.9 | 51.7 | 53.4 |
| V(–C6H5)/kJ mol−1 c | 30.8 | 31.6 | 30.3 |
| V(–C–CH3)/kJ mol−1 c | 6.4 | 6.6 | 7.6 |
| V(–N–CH3)/kJ mol−1 c | 10.9 | 9.6 | 10.9 |
| Ir(–C6H5)/amu Å2 d | 67.65 | 66.92 | – |
| Ir(–C–CH3)/amu Å2 d | 3.14 | 3.12 | 3.14 |
| Ir(–N–CH3)/amu Å2 d | 3.19 | 3.16 | 3.14 |
| Polymorph | Tm/K | (Tm)/kJ mol−1 | Reference |
|---|---|---|---|
| I a | 385 | 23.9 | [2] |
| I a | 385.8 | 24.52 | [30] |
| I a | 383.7 | 24.5 | [31] |
| I a | 384.0 | 25.18 | [32] |
| I b | 384 | - | [38] |
| I a | 385.1 | 22.2 | [25] |
| I a | 389.77 | 22.6 | [34] |
| I b | 383.9 ± 0.2 c | 24.0 ± 0.3 c | this work |
| I | 384.5 ± 0.8 c | 24.0 ± 1.0 d | average |
| II b | 376.2 ± 0.3 c | 20.5 ± 0.4 c | this work |
| not stated | - | 28.1 | [33] |
| T/K | p(T) a/Pa | T/K | p(T) a/Pa |
|---|---|---|---|
| 300 | 4.2∙10−4 | 350 | 0.21 |
| 310 | 1.7∙10−3 | 360 | 0.57 |
| 320 | 6.4∙10−3 | 370 | 1.5 |
| 330 | 2.2∙10−2 | 376.2 | 2.7 |
| 340 | 7.0∙10−2 |
| State | p (298.15 K) a/Pa | |
|---|---|---|
| Crystal, form I | 1.4∙10−4 | 116.3 ± 2.7 b |
| Crystal, form II | 3.2∙10−4 | 108.6 ± 2.3 c |
| Supercooled liquid | 1.4∙10−3 | 94.1 ± 2.1 b |
| Compound | CAS | Supplier | Purity |
|---|---|---|---|
| phenazone | 60-80-0 | Weifang Economic Zone Hotspot, Biotechnology Center | >0.98 a 0.9954 b |
| acetonitrile | 75-05-8 | Merck | 0.9999 a |
| N, N-dimethylformamide c | 68-12-2 | Sigma-Aldrich | 0.999 a |
| sapphire d | 1344-28-1 | Perkin Elmer | not provided |
| anthracene | 120-12-7 | Aldrich | 0.999 a |
| thioxanthone | 492-22-8 | TCI | 0.999 a |
| indium | 7440-74-6 | Perkin Elmer | 0.99999 a |
| nitrogen gas | 7727-37-9 | Nurgas | 0.99999 e |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolmatenkov, D.N.; Nizamov, I.I.; Sokolov, A.A.; Notfullin, A.A.; Solomonov, B.N.; Yagofarov, M.I. Polymorphism and Phase-Transition Thermodynamic Properties of Phenazone (Antipyrine). Molecules 2025, 30, 2814. https://doi.org/10.3390/molecules30132814
Bolmatenkov DN, Nizamov II, Sokolov AA, Notfullin AA, Solomonov BN, Yagofarov MI. Polymorphism and Phase-Transition Thermodynamic Properties of Phenazone (Antipyrine). Molecules. 2025; 30(13):2814. https://doi.org/10.3390/molecules30132814
Chicago/Turabian StyleBolmatenkov, Dmitrii N., Ilyas I. Nizamov, Andrey A. Sokolov, Airat A. Notfullin, Boris N. Solomonov, and Mikhail I. Yagofarov. 2025. "Polymorphism and Phase-Transition Thermodynamic Properties of Phenazone (Antipyrine)" Molecules 30, no. 13: 2814. https://doi.org/10.3390/molecules30132814
APA StyleBolmatenkov, D. N., Nizamov, I. I., Sokolov, A. A., Notfullin, A. A., Solomonov, B. N., & Yagofarov, M. I. (2025). Polymorphism and Phase-Transition Thermodynamic Properties of Phenazone (Antipyrine). Molecules, 30(13), 2814. https://doi.org/10.3390/molecules30132814








