Dynamics of Supramolecular Ionic Gels by Means of Nuclear Magnetic Resonance Relaxometry—The Case of [BMIM][Cl]/Propylene Carbonate Gel
Abstract
1. Introduction
2. Results
2.1. NMR Relaxation Theory
2.2. Analysis
3. Discussion
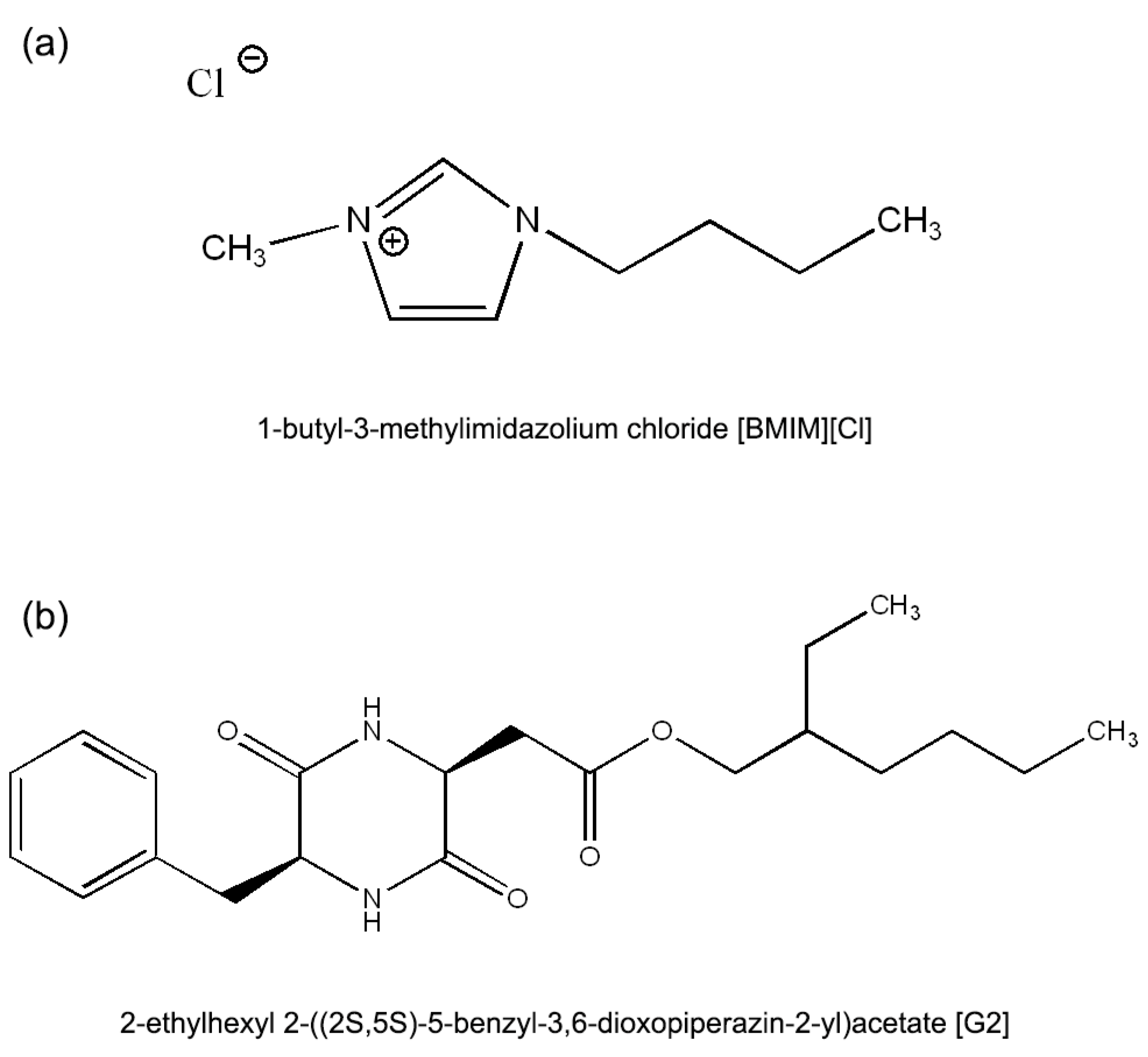
4. Materials and Methods
4.1. Gel Preparation
4.2. FFC NMR Relaxometry
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishioka, Y.; Minakuchi, N.; Mizuhata, M.; Maruyama, T. Supramolecular gelators based on benzenetricarboxamides for ionic liquids. Soft Matter 2014, 10, 965. [Google Scholar] [CrossRef] [PubMed]
- Hanabusa, K.; Fukui, H.; Suzuki, M.; Shirai, H. Specialist Gelator for Ionic Liquids. Langmuir 2005, 21, 10383. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Liu, J.; Jing, P.; Xu, C.; Wu, J.; Gao, D.; Fang, Y. Cholesterol-based low-molecular mass gelators towards smart ionogels. Soft Matter 2012, 8, 11697–11703. [Google Scholar] [CrossRef]
- Minakuchi, N.; Hoe, K.; Yamaki, D.; Ten-No, S.; Nakashima, K.; Goto, M.; Mizuhata, M.; Maruyama, T. Versatile supramolecular gelators that can harden water, organic solvents and ionic liquids. Langmuir 2012, 28, 9259–9266. [Google Scholar] [CrossRef]
- Le Bideau, J.; Viau, L.; Vioux, A. Ionogels, ionic liquid based hybrid materials. Chem. Soc. Rev. 2011, 40, 907–925. [Google Scholar] [CrossRef]
- Atsbeha, T.; Bussotti, L.; Cicchi, S.; Foggi, P.; Ghini, G.; Lascialfari, L.; Marcelli, A. Photophysical characterization of low-molecular weight organogels for energy transfer and light harvesting. J. Mol. Struct. 2011, 993, 459–463. [Google Scholar] [CrossRef]
- Gronwald, O.; Snip, E.; Shinkai, S. Gelators for organic liquids based on self-assembly: A new facet of supramolecular and combinatorial chemistry. Curr. Opin. Colloid Interface Sci. 2002, 7, 148–156. [Google Scholar] [CrossRef]
- Vintiloiu, A.; Leroux, J.C. Organogels and their use in drug delivery—A review. J. Controlled Release 2008, 125, 179–192. [Google Scholar] [CrossRef]
- Wang, Z.; Fujisawa, S.; Suzuki, M.; Hanabusa, K. Low molecular weight gelators bearing electroactive groups as cathode materials for rechargeable batteries. Macromol. Symp. 2016, 364, 38–46. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, S.; Zhang, C.; Kong, F.; Fang, X.; Guo, L.; Liu, W.; Pan, X.; Wang, K. Low molecular mass organogelator based gel electrolyte with effective charge transport property for long-term stable quasi-solid-state dye-sensitized solar cells. J. Phys. Chem. B 2008, 112, 12927–12933. [Google Scholar] [CrossRef]
- Mohmeyer, N.; Kuang, D.; Wang, P.; Schmidt, H.W.; Zakeeruddin, S.M.; Grätzel, M. An efficient organogelator for ionic liquids to prepare stable quasi-solid-state dye-sensitized solar cells. J. Mater. Chem. 2006, 16, 2978–2983. [Google Scholar] [CrossRef]
- Decoppet, J.D.; Moehl, T.; Babkair, S.S.; Alzubaydi, R.A.; Ansari, A.A.; Habib, S.S.; Zakeeruddin, S.M.; Schmidt, H.W.; Grätzel, M. Molecular gelation of ionic liquid–sulfolane mixtures, a solid electrolyte for high performance dye-sensitized solar cells. J. Mater. Chem. A 2014, 2, 15972–15977. [Google Scholar] [CrossRef]
- Mohmeyer, N.; Wang, P.; Schmidt, H.W.; Zakeeruddin, S.M.; Grätzel, M. Quasi-solid-state dye sensitized solar cells with 1, 3: 2, 4-di-O-benzylidene-D-sorbitol derivatives as low molecular weight organic gelators. J. Mater. Chem. 2004, 14, 1905–1909. [Google Scholar] [CrossRef]
- Tao, L.; Huo, Z.; Ding, Y.; Li, Y.; Dai, S.; Wang, L.; Zhu, J.; Pan, X.; Zhnag, B.; Yao, J.; et al. High-efficiency and stable quasi-solid-state dye-sensitized solar cell based on low molecular mass organogelator electrolyte. J. Mater. Chem. A 2015, 3, 2344–2352. [Google Scholar] [CrossRef]
- Bielejewski, M.; Puszkarska, A.; Tritt-Goc, J. Thermal properties, conductivity, and spin-lattice relaxation of gel electrolyte based on low molecular weight gelator and solution of high temperature ionic liquid. Electrochim. Acta 2015, 165, 122–129. [Google Scholar] [CrossRef]
- Hallett, J.P.; Welton, T. Room-temperature ionic liquids: Solvents for synthesis and catalysis. 2. Chem. Rev. 2011, 111, 3508–3576. [Google Scholar] [CrossRef]
- Bara, J.E.; Carlisle, T.K.; Gabriel, C.J.; Camper, D.; Finotello, A.; Gin, D.L.; Noble, R.D. Guide to CO2 separations in imidazolium-based room-temperature ionic liquids. Ind. Eng. Chem. Res. 2009, 48, 2739–2751. [Google Scholar] [CrossRef]
- Lei, Z.; Dai, C.; Chen, B. Gas solubility in ionic liquids. Chem. Rev. 2014, 114, 1289–1326. [Google Scholar] [CrossRef]
- Lei, Z.; Dai, C.; Zhu, J.; Chen, B. Extractive distillation with ionic liquids: A review. AIChE J. 2014, 60, 3312–3329. [Google Scholar] [CrossRef]
- Chatel, G.; Macfarlane, D.R. Ionic liquids and ultrasound in combination: Synergies and challenges. Chem. Soc. Rev. 2014, 43, 8132–8149. [Google Scholar] [CrossRef]
- Mai, N.L.; Koo, Y.M. Computer-Aided Design of Ionic Liquids for High Cellulose Dissolution ACS Sustainable Chem. ACS Sustain. Chem. Eng. 2016, 4, 541–547. [Google Scholar] [CrossRef]
- Gurkan, B.E.; de la Fuente, J.; Mindrup, E.M.; Ficke, L.E.; Goodrich, B.F.; Price, E.A.; Schneider, W.F.; Brennecke, J.F. Equimolar CO2 Absorption by Anion-Functionalized Ionic Liquids. J. Am. Chem. Soc. 2010, 132, 2116–2117. [Google Scholar] [CrossRef]
- Ruckart, K.N.; O’Brien, R.A.; Woodard, S.M.; West, K.N.; Grant, T. Glover Porous Solids Impregnated with Task-Specific Ionic Liquids as Composite Sorbents. J. Phys. Chem. C 2015, 119, 20681–20697. [Google Scholar] [CrossRef]
- Qian, W.; Texter, J.; Yan, F. Frontiers in Poly(ionic liquid)s: Syntheses and Applications. Chem. Soc. Rev. 2017, 46, 1124–1159. [Google Scholar] [CrossRef]
- Rojas, M.F.; Bernard, F.L.; Aquino, A.; Borges, J.; Dalla Vecchia, F.; Menezes, S.; Ligabue, R.; Einloft, S. Poly(ionic liquid)s as Efficient Catalyst in Transformation of CO2 to Cyclic Carbonate. J. Mol. Catal. A Chem. 2014, 392, 83–88. [Google Scholar] [CrossRef]
- Allix, F.; Curcio, P.; Pham, Q.N.; Pickaert, G.; Jamart-Gregoire, B. Evidence of Intercolumnar π−π Stacking Interactions in Amino-Acid-Based Low-Molecular-Weight Organogels. Langmuir 2010, 26, 16818. [Google Scholar] [CrossRef]
- Tritt-Goc, J.; Bielejewski, M.; Luboradzki, R.; Łapiński, A. Thermal Properties of the Gel Made by Low Molecular Weight Gelator 1,2-O-(1-ethylpropylidene)-α-d-glucofuranose with Toluene and Molecular Dynamics of Solvent. Langmuir 2008, 24, 534. [Google Scholar] [CrossRef]
- Makarević, J.; Jokić, M.; Perić, B.; Tomišić, V.; Kojić-Prodić, B.; Žinić, M. Bis (amino acid) oxalyl amides as ambidextrous gelators of water and organic solvents: Supramolecular gels with temperature dependent assembly/dissolution equilibrium. Chem.–Eur. J. 2001, 7, 3328–3341. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Dordick, J.S. Solvent effect on organogel formation by low molecular weight molecules. Chem. Mater. 2006, 18, 5988–5995. [Google Scholar] [CrossRef]
- Hanabusa, K.; Matsumoto, M.; Kimura, M.; Kakehi, A.; Shirai, H. Low molecular weight gelators for organic fluids: Gelation using a family of cyclo (dipeptide)s. J. Colloid Interface Sci. 2000, 224, 231–244. [Google Scholar] [CrossRef]
- Hirst, A.R.; Smith, D.K. Solvent effects on supramolecular gel-phase materials: Two-component dendritic gel. Langmuir 2004, 20, 10851–10857. [Google Scholar] [CrossRef] [PubMed]
- Tritt-Goc, J.; Rachocki, A.; Bielejewski, M. The solvent dynamics at pore surfaces in molecular gels studied by field-cycling magnetic resonance relaxometry. Soft Matter 2014, 10, 7810–7818. [Google Scholar] [CrossRef] [PubMed]
- Kamlet, M.J.; Abboud, J.L.M.; Abraham, M.H.; Taft, R.W. Linear solvation energy relationships. 23. A comprehensive collection of the solvatochromic parameters, π*, α, and β, and some methods for simplifying the generalized solvatochromic equation. J. Org. Chem. 1983, 48, 2877–2887. [Google Scholar] [CrossRef]
- Edwards, W.; Lagadec, C.A.; Smith, D.K. Solvent–gelator interactions—Using empirical solvent parameters to better understand the self-assembly of gel-phase materials. Soft Matter 2011, 7, 110–117. [Google Scholar] [CrossRef]
- Kaszyńska, J.; Łapiński, A.; Bielejewski, M.; Luboradzki, R.; Tritt-Goc, J. On the relation between the solvent parameters and the physical properties of methyl-4, 6-O-benzylidene-α-d-glucopyranoside organogels. Tetrahedron 2012, 68, 3803–3810. [Google Scholar] [CrossRef]
- Fries, P.H. Dipolar Nuclear Spin Relaxation in Liquids andPlane Fluids Undergoing Chemical Reactions. Mol. Phys. 1983, 48, 503–526. [Google Scholar] [CrossRef]
- Fries, P.H.; Belorizky, E. Time Correlation Functions ofIsotropic Intermolecular Site-Site Interactions in Liquids: Effects of The Site Eccentricity and of The Molecular Distribution. J. Phys. 1989, 50, 3347–3363. [Google Scholar] [CrossRef]
- Korb, J.-P. Multiscale Nuclear Magnetic Relaxation Dispersionof Complex Liquids in Bulk and Confinement. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 104, 12–55. [Google Scholar] [CrossRef]
- Janc, T.; Korb, J.-P.; Lukšič, M.; Vlachy, V.; Bryant, R.G.; Mériguet, G.; Malikova, N.; Rollet, A. Multiscale Water Dynamics on Protein Surfaces: Protein-Specific Response to Surface Ions. J. Phys. Chem. B 2021, 125, 8673–8681. [Google Scholar] [CrossRef]
- Parigi, G.; Ravera, E.; Fragai, M.; Luchinat, C. UnveilingProtein Dynamics in Solution with Field-Cycling NMR Relaxometry. Prog. Nucl. Magn. Reson. Spectrosc. 2021, 124–125, 85–98. [Google Scholar] [CrossRef]
- Kruk, D.; Wojciechowski, M.; Florek-Wojciechowska, M.; Singh, R.K. Dynamics of Ionic Liquids in Confinement by Means ofNMR Relaxometry EMIM-FSI in a Silica Matrix as an Example. Materials 2020, 13, 4351. [Google Scholar] [CrossRef]
- Kruk, D.; Kasparek, A.; Masiewicz, E.; Kolodziejski, K.; Cybulski, R.; Nowak, B. Water Dynamics in Highly Concentrated Protein Systems Insight from Nuclear Magnetic Resonance Relaxometry. Int. J. Mol. Sci. 2023, 24, 4093. [Google Scholar] [CrossRef] [PubMed]
- Stankiewicz, A.; Kasperek, A.; Masiewicz, E.; Kruk, D. Diffusion of Water Molecules on the Surface of Silica Nanoparticles—Insights from Nuclear Magnetic Resonance Relaxometry. J. Phys. Chem. B 2024, 128, 1535–1543. [Google Scholar] [CrossRef] [PubMed]
- Kubrak, A.; Pejanovic, R.; Kamau, K.; Kruk, D.; Ferrage, F.; Parigi, G. Field-dependent relaxation profiles of biomolecular systems. Phys. Chem. Chem. Phys. 2025, 27, 1756–1771. [Google Scholar] [CrossRef]
- Ravera, E.; Parigi, G.; Mainz, A.; Religa, T.L.; Reif, B.; Luchinat, C. Experimental determination of microsecond reorientation correlation times in protein solutions. J. Phys. Chem. B 2013, 117, 3548–3553. [Google Scholar] [CrossRef]
- Overbeck, V.; Golub, B.; Schroeder, H.; Appelhagen, A.; Paschek, D.; Neymeyr, K.; Ludwig, R. Probing relaxation models by means of Fast Field-Cycling relaxometry, NMR spectroscopy and molecular dynamics simulations: Detailed insight into the translational and rotational dynamics of a protic ionic liquid. J. Mol. Liq. 2020, 319, 114207. [Google Scholar] [CrossRef]
- Calucci, L. Forte C Simple expressions of the nuclear relaxation rate enhancement due to quadrupole nuclei in slowly tumbling molecules. Prog. Nucl. Magn. Reson. Spectrosc. 2009, 55, 296–323. [Google Scholar] [CrossRef]
- Bryant, R.G. Dynamics of water in and around proteins characterized by 1H-spin-lattice relaxometry Comptes Rendus. C. R. Phys. 2010, 11, 128–135. [Google Scholar] [CrossRef]
- Bormuth, A.; Hofmann, M.; Henritzi, P.; Vogel, M.; Rossler, E.A. Chain-length dependence of polymer dynamics: A comparison of results from molecular dynamics simulations and field-cycling 1H NMR. Macromolecules 2013, 46, 7805–7811. [Google Scholar] [CrossRef]
- Hofmann, M.; Kresse, B.; Privalov, A.F.; Willner, L.; Fatkulin, N.; Fujara, F.; Rossler, E.A. Field-cycling NMR relaxometry probing the microscopic dynamics in polymer melts. Macromolecules 2014, 47, 7917–7929. [Google Scholar] [CrossRef]
- Kresse, B.; Hofmann, M.; Privalov, A.F.; Fatkullin, N.; Fujara, F.; Rossler, E.A. All polymer diffusion regimes covered by combining field-cycling and field-gradient 1H NMR. Macromolecules 2015, 48, 4491–4502. [Google Scholar] [CrossRef]
- Masiewicz, E.; Ullah, F.; Mieloch, A.; Godlewski, J.; Kruk, D. Dynamical properties of solid and hydrated collagen: Insight from nuclear magnetic resonance relaxometry. J. Chem. Phys. 2024, 160, 165101. [Google Scholar] [CrossRef] [PubMed]
- Conte, P. Chapter Three—Applications of fast field cycling NMR relaxometry. In Annual Reports on NMR Spectroscopy; Graham, A.W., Ed.; Burlington House: London, UK, 2021; Volume 104, pp. 141–188. [Google Scholar] [CrossRef]
- Slichter, C.P. Principles of Magnetic Resonance, 3rd ed.; Springer: Berlin, Germany, 1990. [Google Scholar]
- Kowalewski, J.; Maler, L. Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2019. [Google Scholar]
- Hwang, L.-P.; Freed, J.H. Dynamic Effects of Pair Correlation Functions on Spin Relaxation by Translational Diffusion in Liquids. J. Chem. Phys. 1975, 63, 4017–4025. [Google Scholar] [CrossRef]
- Ayant, Y.; Belorizky, E.; Aluzon, J.; Gallice, J. Calcul desDensité s Spectrales Ré sultant D’un Mouvement Alé atoire deTranslation en Relaxation Par Interaction Dipolaire MagnétiqueDans Les Liquides. J. Phys. 1975, 36, 991–1004. [Google Scholar] [CrossRef]
- Kruk, D.; Meier, R.; Rössler, E.A. Nuclear Magnetic Resonance Relaxometry as a Method of Measuring Translational Diffusion Coefficients in Liquids. Phys. Rev. E 2012, 85, 020201. [Google Scholar] [CrossRef]
- Bryant, R.G.; Korb, J.P. Nuclear magnetic resonance and spin relaxation in biological systems. Magn. Reson. Imag. 2005, 23, 167–173. [Google Scholar] [CrossRef]
- Nusser, W.; Kimmich, R. Protein backbone fluctuations and NMR field-cycling relaxation spectroscopy. J. Phys. Chem. 1990, 94, 5637–5639. [Google Scholar] [CrossRef]
- Korb, J.P.; Van-Quynh, A.; Bryant, R.G. Proton spin relaxation induced by localized spin-dynamical coupling in proteins. Chem. Phys. Lett. 2001, 339, 77–82. [Google Scholar] [CrossRef]
- Korb, J.P.; Bryant, R.G. The physical basis for the magnetic field dependence of proton spin-lattice relaxation rates in proteins. J. Chem. Phys. 2001, 115, 10964–10974. [Google Scholar] [CrossRef]
- Korb, J.P.; Bryant, R.G. Magnetic field dependence of proton spin-lattice relaxation times. Magn. Reson. Med. 2002, 48, 21–26. [Google Scholar] [CrossRef]
- Korb, J.P.; Bryant, R.G. Magnetic field dependence of proton spin-lattice relaxation of confined proteins. C. R. Phys. 2004, 5, 349–357. [Google Scholar] [CrossRef]
- Bryant, R.G.; Mendelson, D.A.; Lester, C.C. The magnetic field dependence of proton spin relaxation in tissues. Magn. Reson. Med. 1991, 21, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Lester, C.C.; Bryant, R.G. Water–proton nuclear magnetic relaxation in heterogeneous systems: Hydrated lysozyme results. Magn. Reson. Med. 1991, 22, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Koenig, S.H. Molecular basis of magnetic relaxation of water protons of tissue. Acad. Radiol. 1996, 3, 597–606. [Google Scholar] [CrossRef] [PubMed]
- Koenig, S.H.; Brown III, R.D. Determinants of proton relaxation rates in tissue. Magn. Reson. Med. 1984, 1, 437–449. [Google Scholar] [CrossRef]
- Sum, L.; Zhuo, K.; Chen, Y.; Du, Q.; Zhang, S.; Wang, J. Ionic Liquid-Based Redox Active Electrolytes for Supercapacitors. Adv. Funct. Mater. 2022, 32, 2203611. [Google Scholar] [CrossRef]
- Tokuda, H.; Hayamizu, K.; Ishii, K.; Susan, M.A.B.H.; Watanabe, M. Physicochemical Properties and Structures of Room Temperature Ionic Liquids. 1. Variation of Anionic Species. J. Phys. Chem. B 2004, 108, 16593–16600. [Google Scholar] [CrossRef]

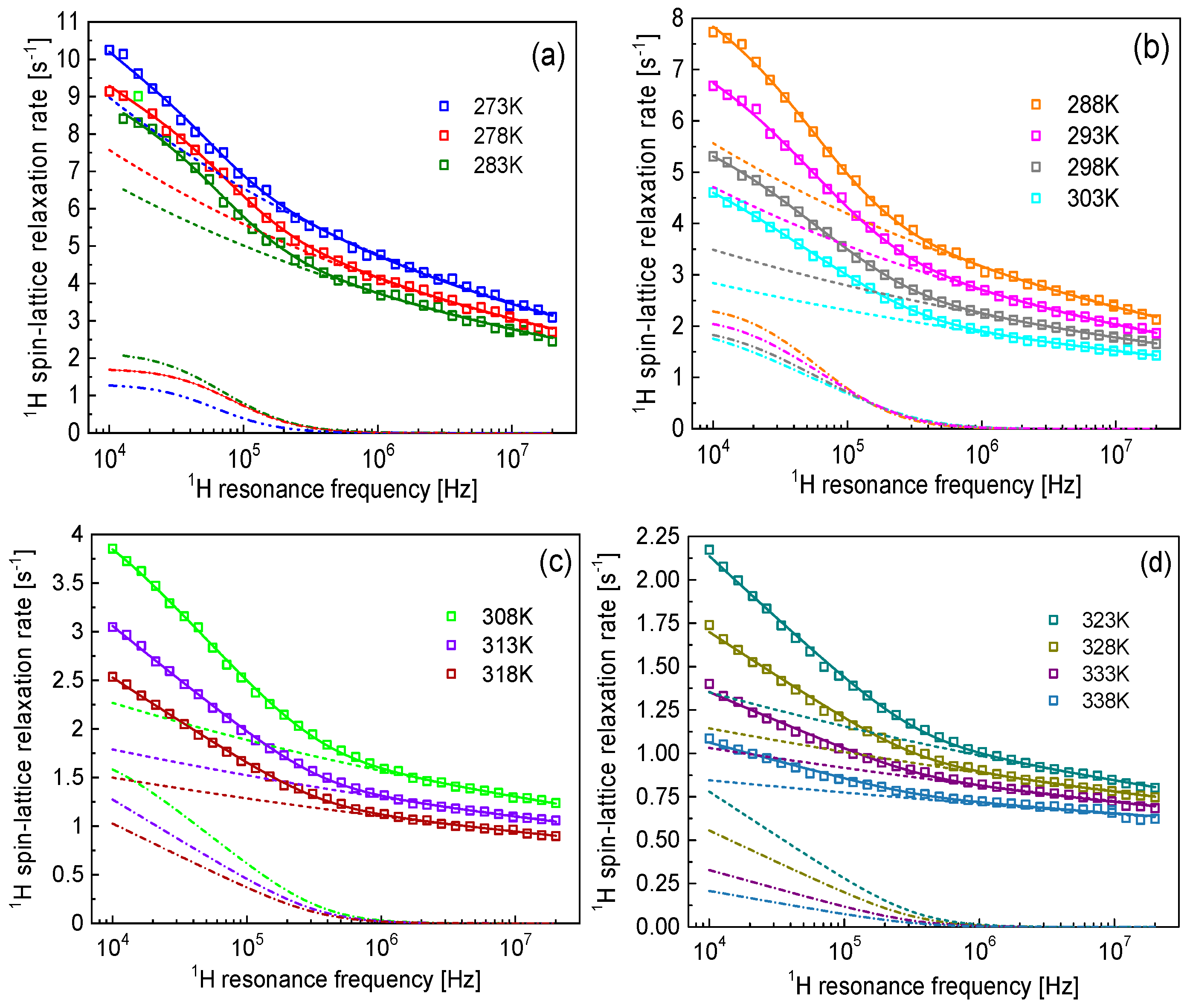

| Temp. [K] | [Hz2] | [s] | |||
|---|---|---|---|---|---|
| 273 | (2.93 ± 0.33) × 105 | (1.19 ± 0.48) × 10−6 | (1.76 ± 0.61) × 10−6 | 0.138 ± 0.038 | 31.7 ± 1.7 |
| 278 | (2.66 ± 0.18) × 105 | (6.67 ± 0.77) × 10−7 | (1.73 ± 0.34) × 10−6 | 0.132 ± 0.006 | 25.5 ± 2.3 |
| 283 | (2.46 ± 0.23) × 105 | (6.93 ± 0.65) × 10−7 | (2.54 ± 0.21) × 10−6 | 0.127 ± 0.003 | 21.6 ± 1.0 |
| 288 | (2.21 ± 0.17) × 105 | (5.40 ± 1.02) × 10−7 | (4.02 ± 0.97) × 10−6 | 0.123 ± 0.005 | 17.3 ± 1.2 |
| 293 | (2.15 ± 0.19) × 105 | (4.02 ± 0.65) × 10−7 | (5.12 ± 1.17) × 10−6 | 0.122 ± 0.005 | 14.4 ± 1.1 |
| 298 | (2.01 ± 0.23) × 105 | (3.25 ± 0.27) × 10−7 | (6.53 ± 0.89) × 10−6 | 0.097 ± 0.003 | 8.5 ± 0.4 |
| 303 | (2.02 ± 0.15) × 105 | (2.70 ± 0.22) × 10−7 | (1.05 ± 0.22) × 10−5 | 0.090 ± 0.004 | 6.5 ± 0.4 |
| 308 | (1.81 ± 0.04) × 105 | 2.70 × 10−7 | - | 0.080 ± 0.003 | 4.7 ± 0.2 |
| 313 | (1.34 ± 0.03) × 105 | 2.70 × 10−7 | - | 0.071 ± 0.002 | 3.4 ± 0.1 |
| 318 | (1.34 ± 0.08) × 105 | 2.70 × 10−7 | - | 0.067 ± 0.004 | 2.8 ± 0.1 |
| 323 | (8.20 ± 0.25) × 104 | 2.70 × 10−7 | - | 0.068 ± 0.003 | 2.6 ± 0.1 |
| 328 | (5.85 ± 0.22) × 104 | 2.70 × 10−7 | - | 0.055 ± 0.003 | 1.9 ± 0.1 |
| 333 | (3.45 ± 0.24) × 104 | 2.70 × 10−7 | - | 0.051 ± 0.003 | 1.7 ± 0.1 |
| 338 | (2.18 ± 0.19) × 104 | 2.70 × 10−7 | - | 0.038 ± 0.003 | 1.2 ± 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bielejewski, M.; Kruk, R.; Kruk, D. Dynamics of Supramolecular Ionic Gels by Means of Nuclear Magnetic Resonance Relaxometry—The Case of [BMIM][Cl]/Propylene Carbonate Gel. Molecules 2025, 30, 2598. https://doi.org/10.3390/molecules30122598
Bielejewski M, Kruk R, Kruk D. Dynamics of Supramolecular Ionic Gels by Means of Nuclear Magnetic Resonance Relaxometry—The Case of [BMIM][Cl]/Propylene Carbonate Gel. Molecules. 2025; 30(12):2598. https://doi.org/10.3390/molecules30122598
Chicago/Turabian StyleBielejewski, Michał, Robert Kruk, and Danuta Kruk. 2025. "Dynamics of Supramolecular Ionic Gels by Means of Nuclear Magnetic Resonance Relaxometry—The Case of [BMIM][Cl]/Propylene Carbonate Gel" Molecules 30, no. 12: 2598. https://doi.org/10.3390/molecules30122598
APA StyleBielejewski, M., Kruk, R., & Kruk, D. (2025). Dynamics of Supramolecular Ionic Gels by Means of Nuclear Magnetic Resonance Relaxometry—The Case of [BMIM][Cl]/Propylene Carbonate Gel. Molecules, 30(12), 2598. https://doi.org/10.3390/molecules30122598






