Counterion-Mediated Assembly of Fluorocarbon–Hydrocarbon Surfactant Mixtures at the Air–Liquid Interface: A Molecular Dynamics Study
Abstract
1. Introduction
2. Results and Discussion
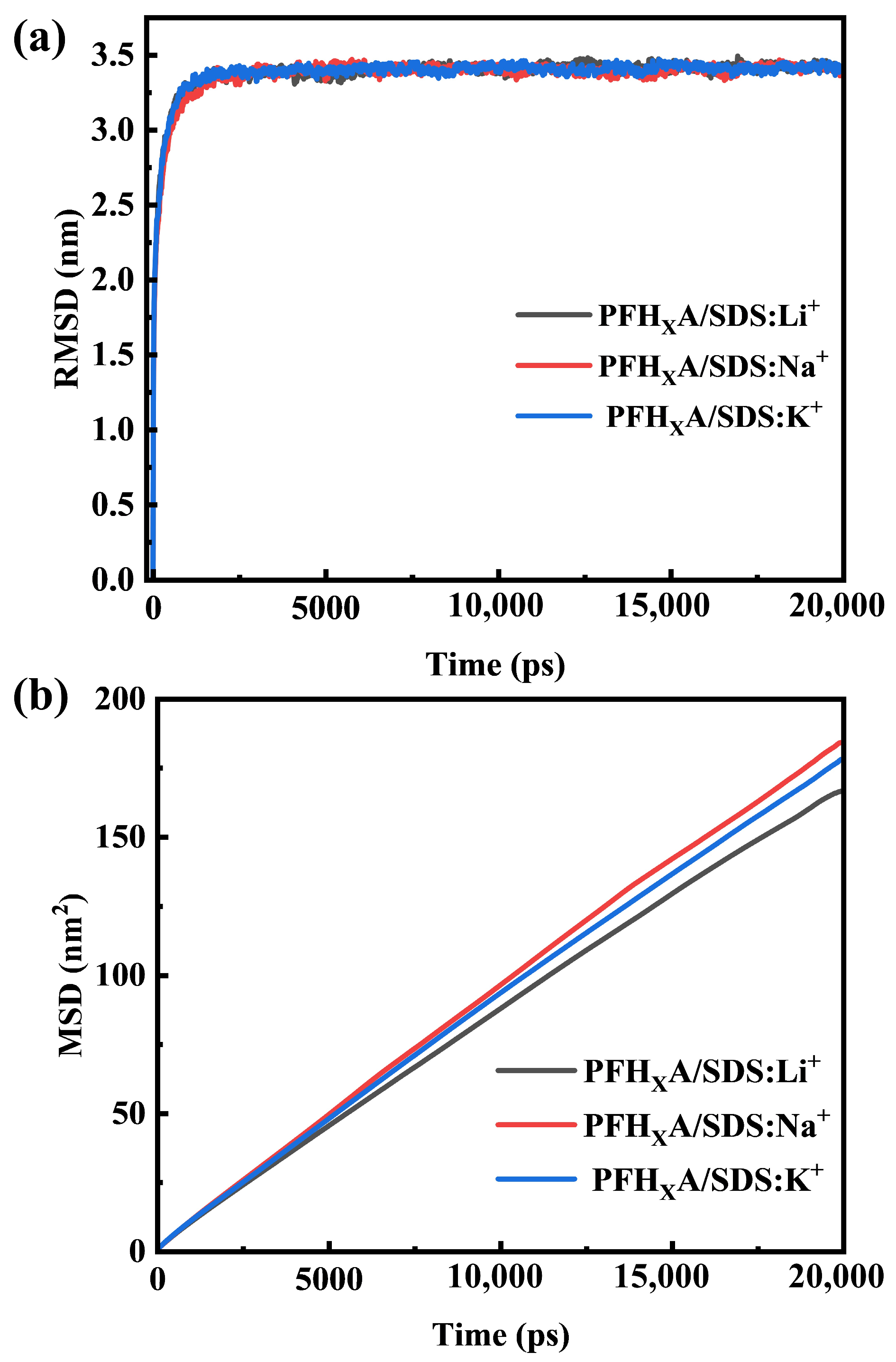
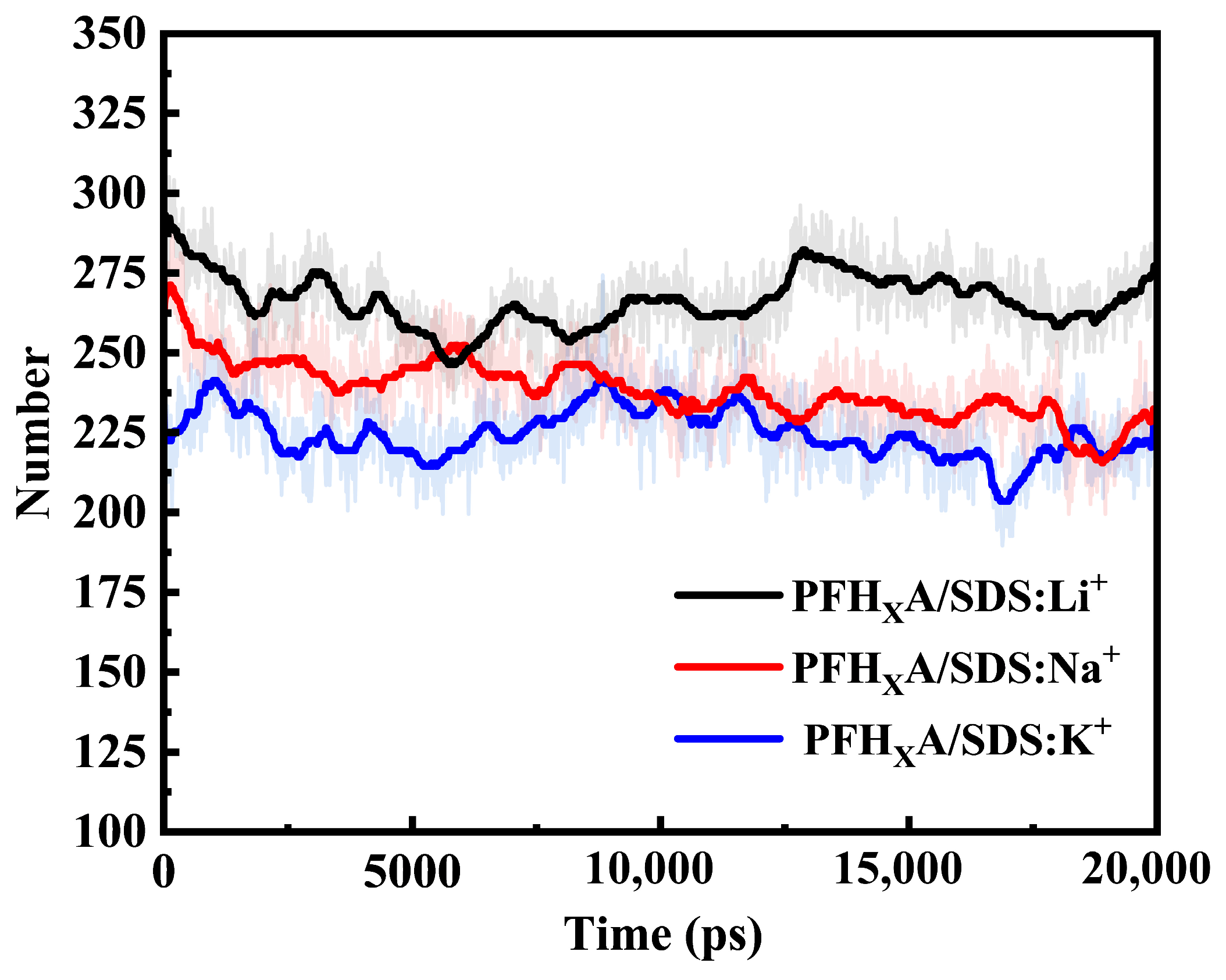
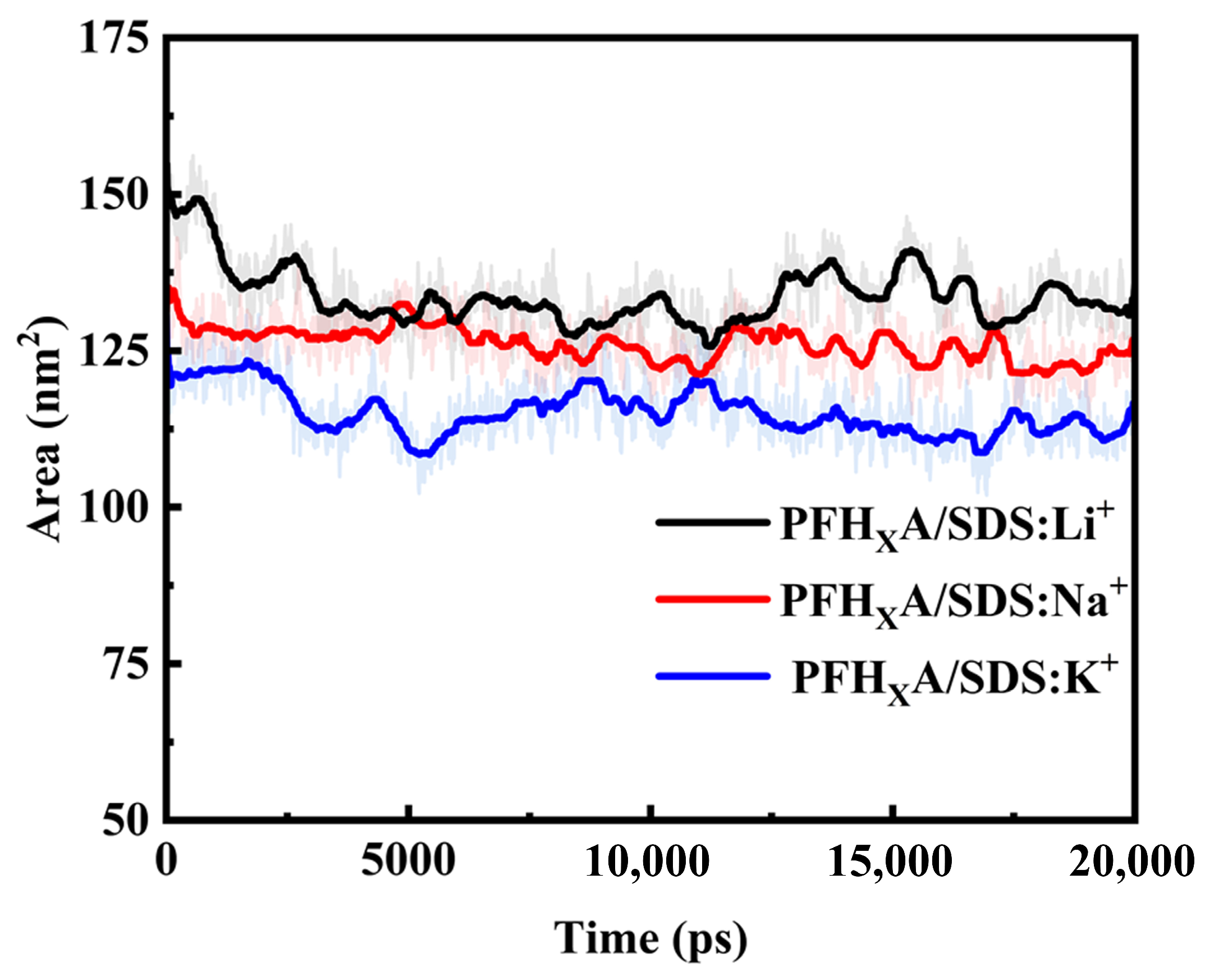
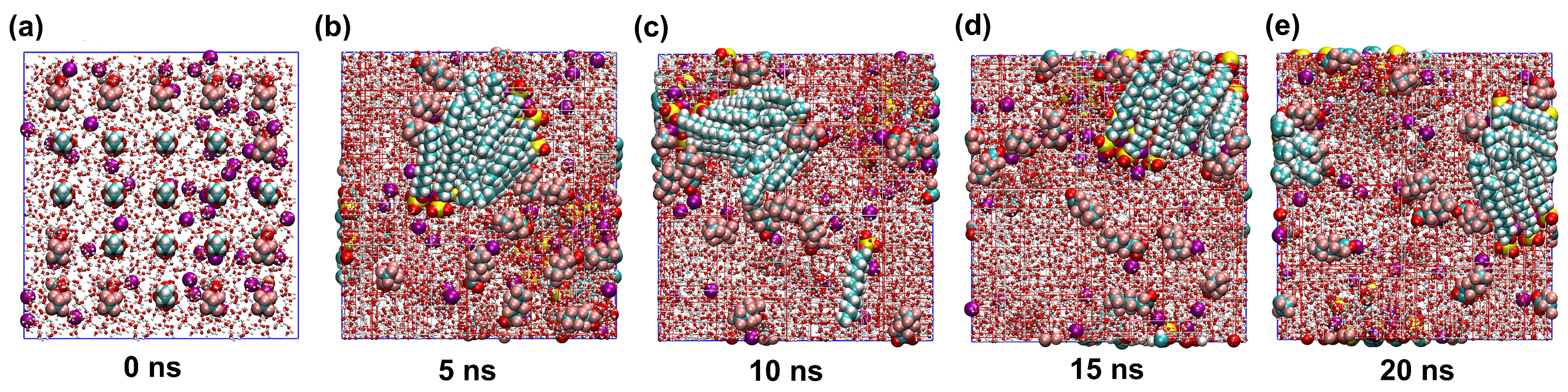
2.1. Stability of Simulated Systems
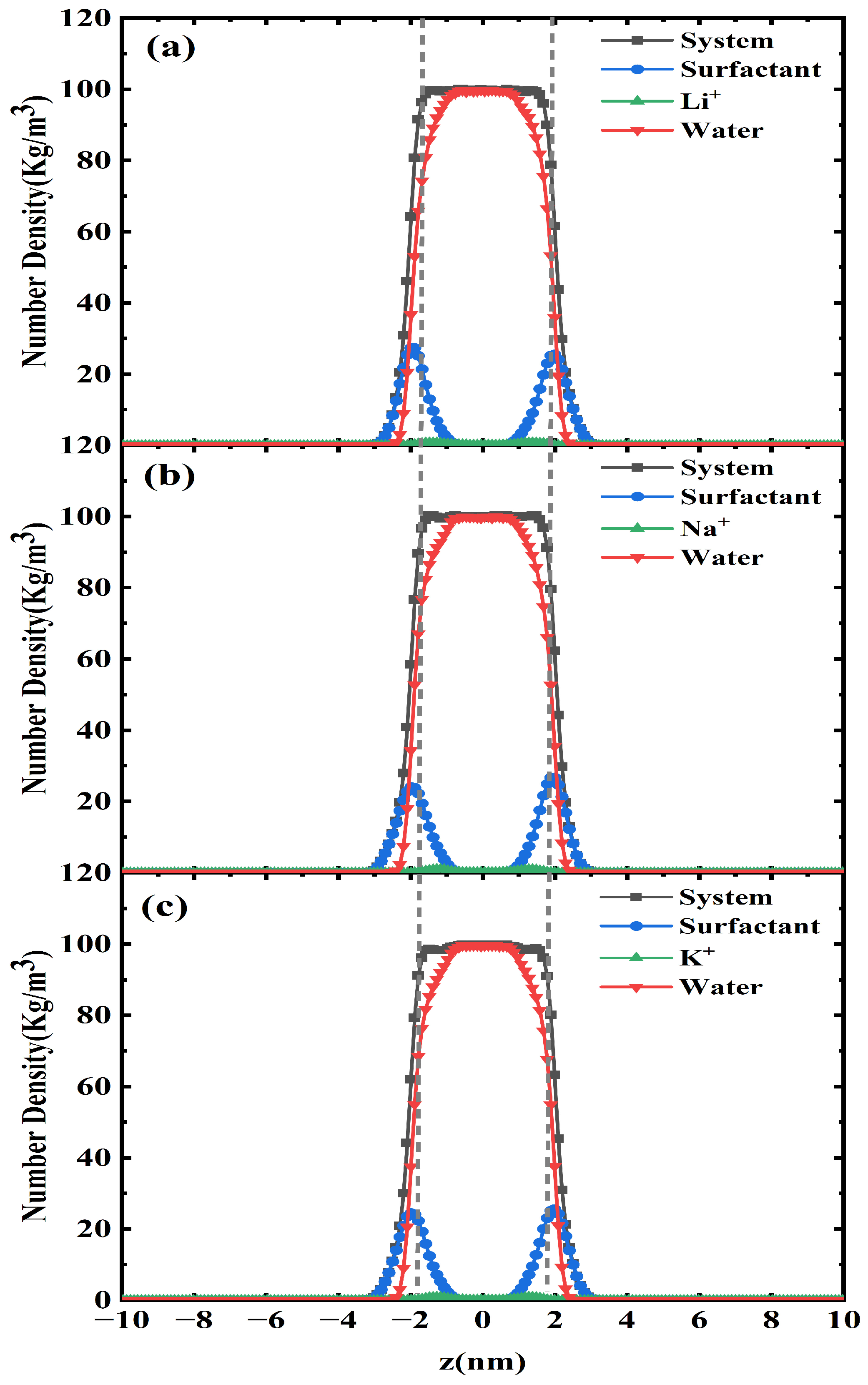
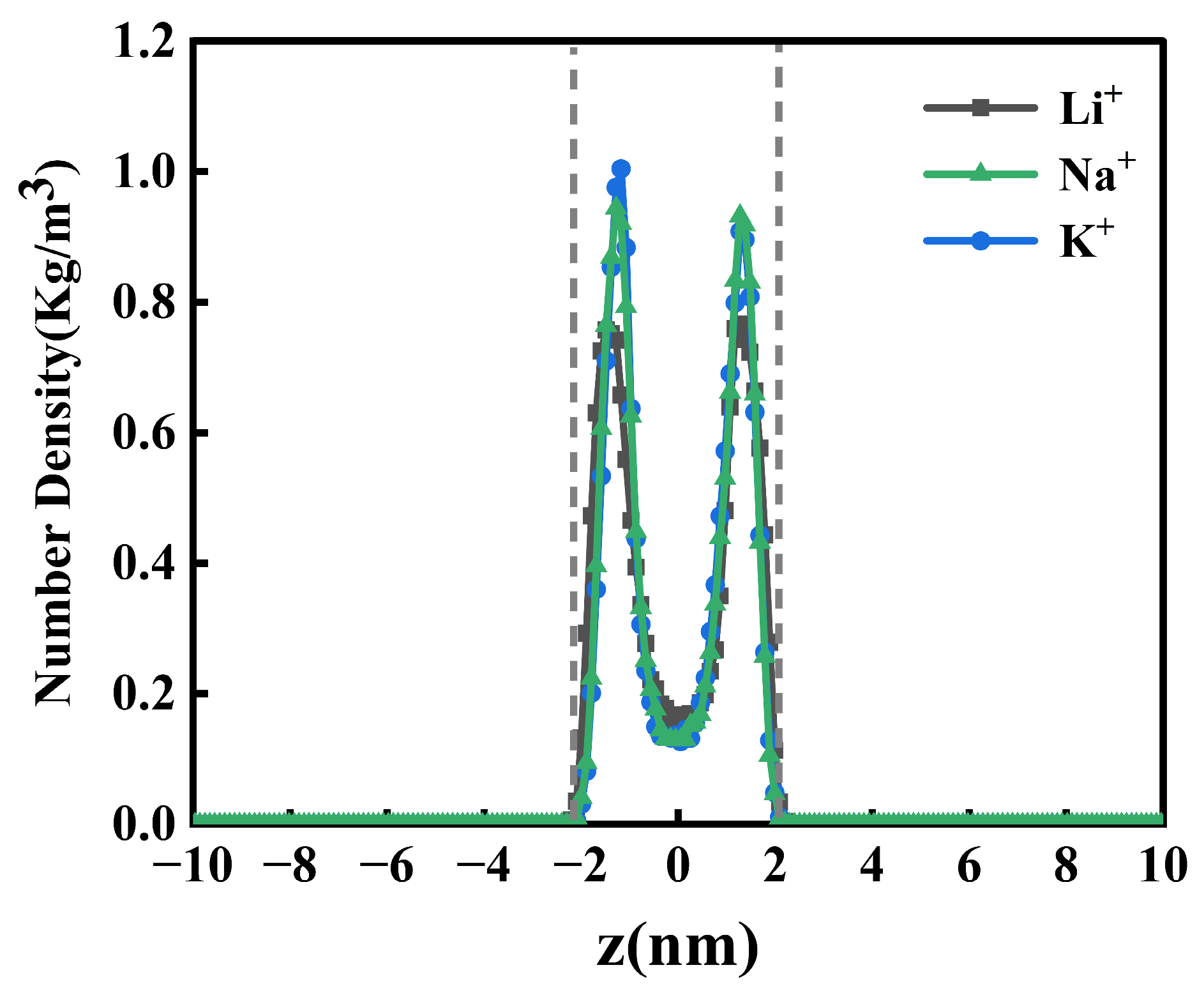
2.2. One-Dimensional -Density Distribution
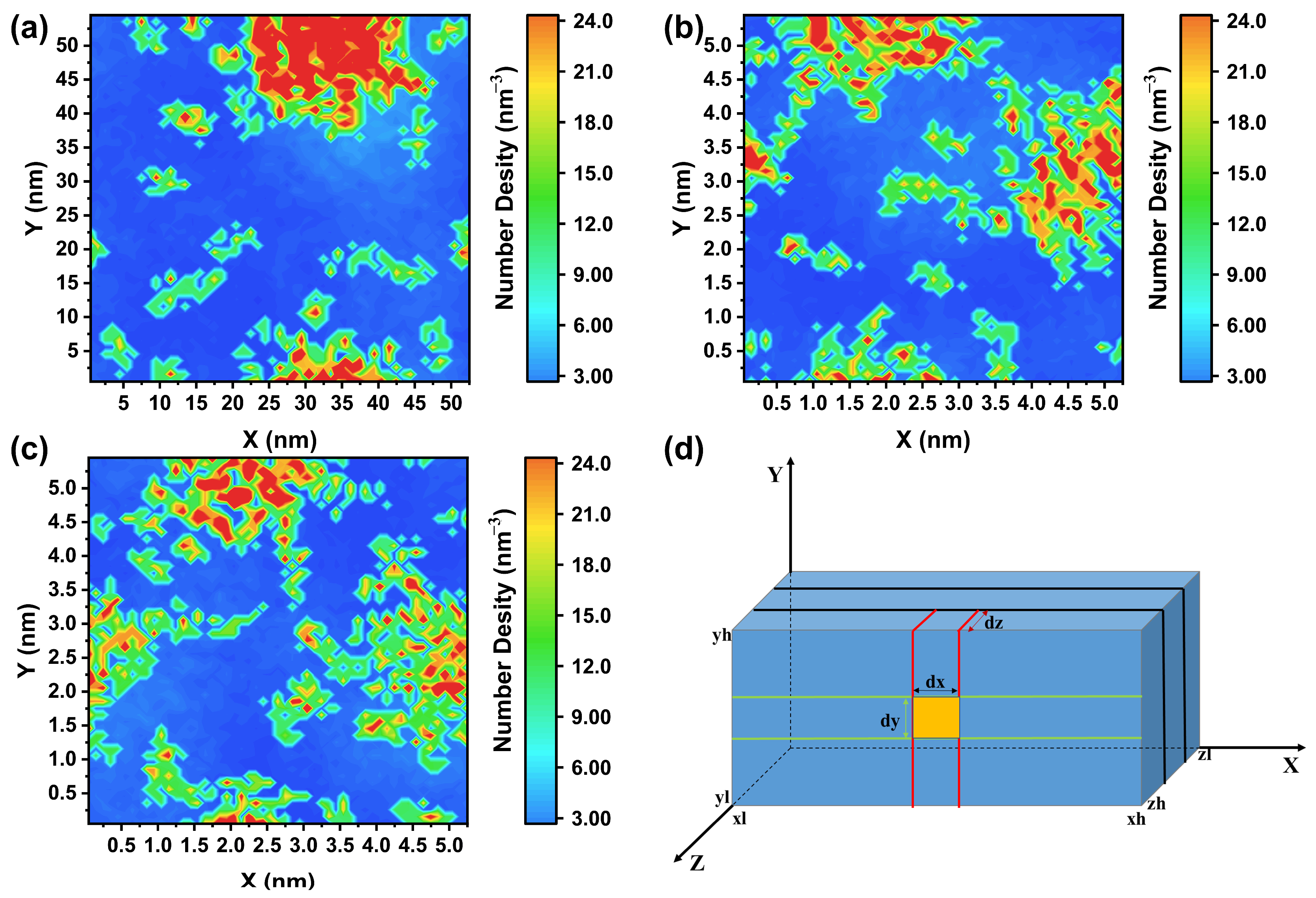
2.3. Two-Dimensional Density Distribution
2.4. Surface Tension Calculation
2.5. Radial Distribution Function
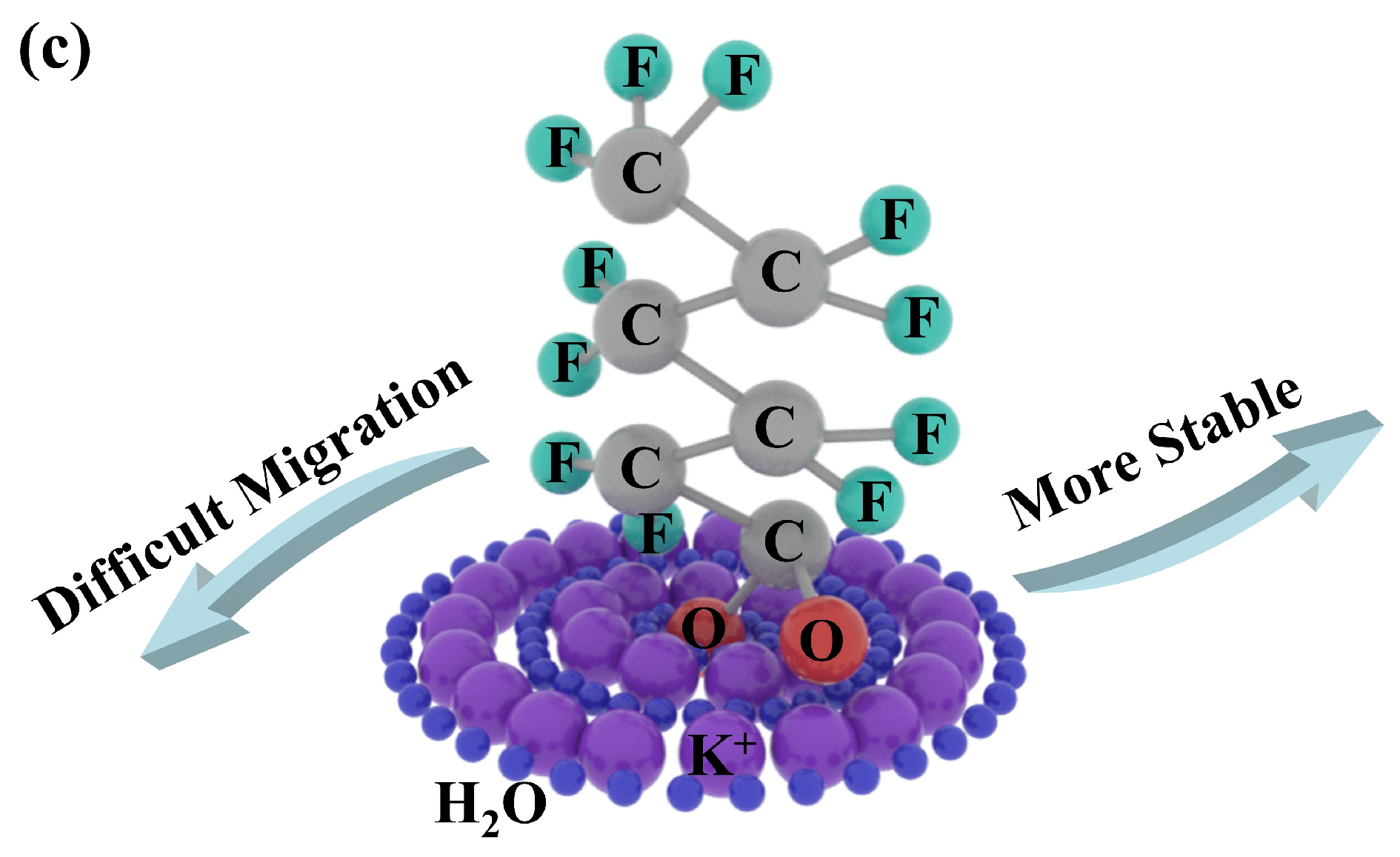
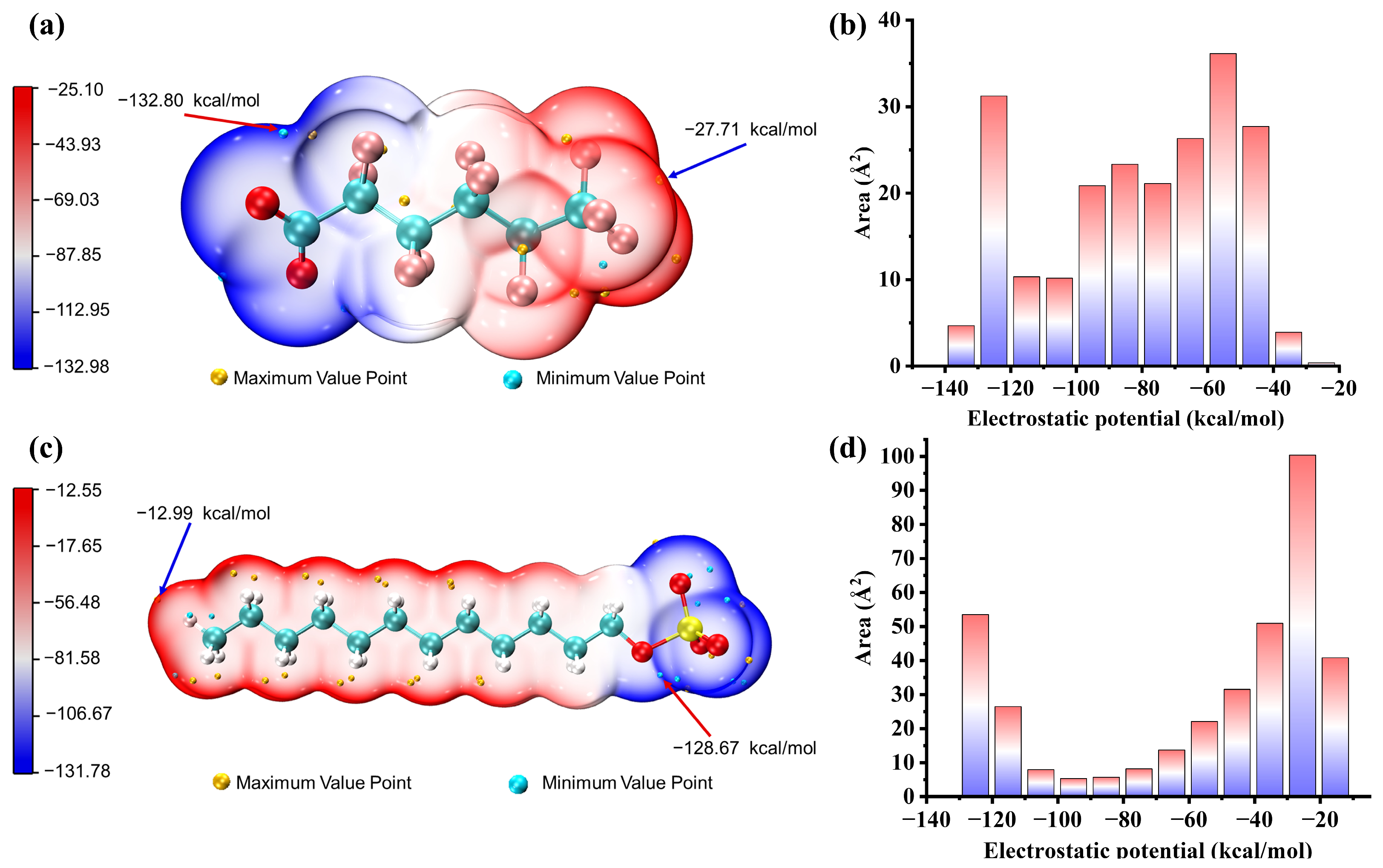
2.6. Electrostatic Potential on Van Der Waals Surfaces
2.7. Number of Hydrogen Bonds
2.8. Solvent-Accessible Surface Area
3. Modeling and Simulation Details
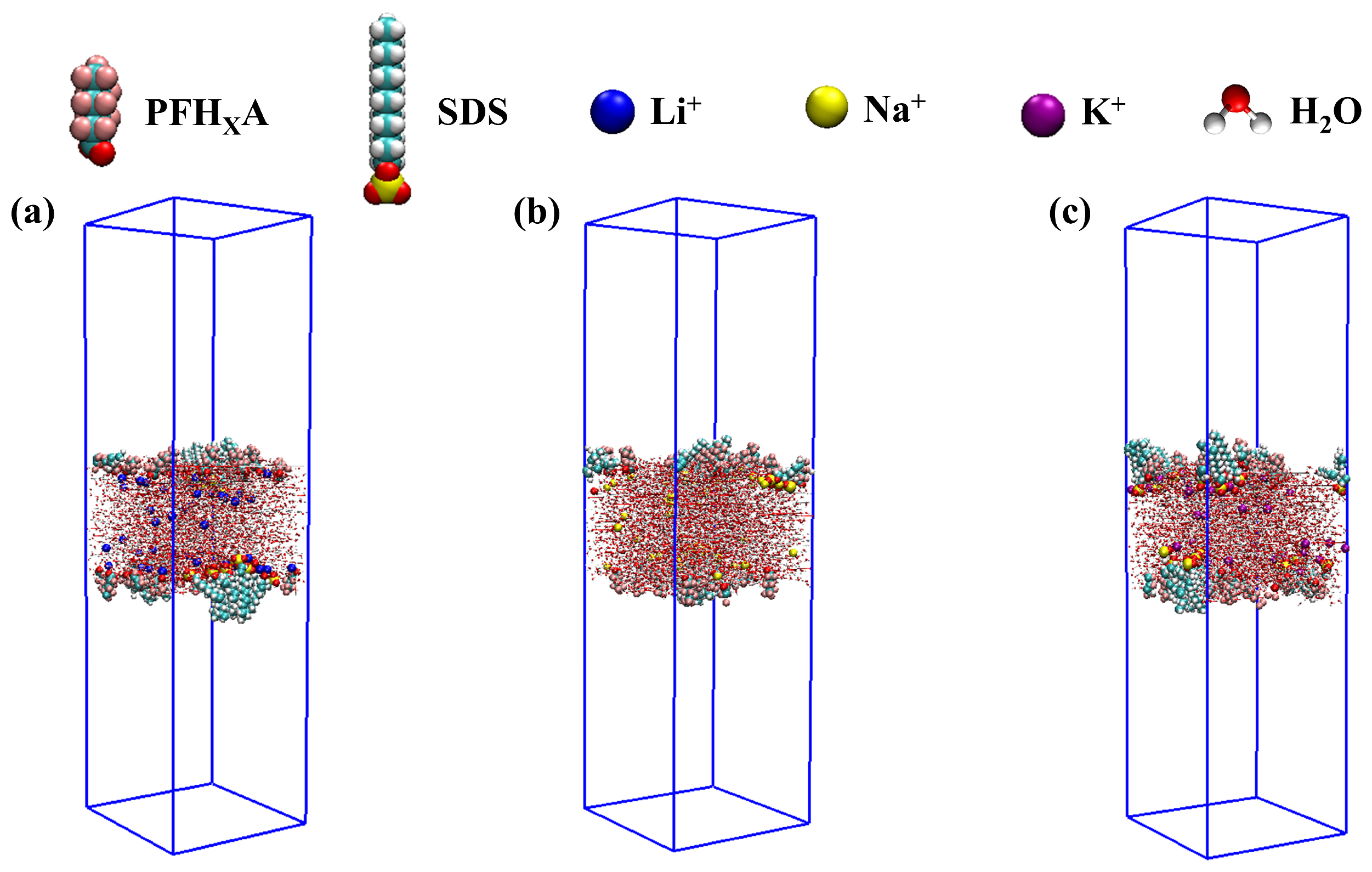
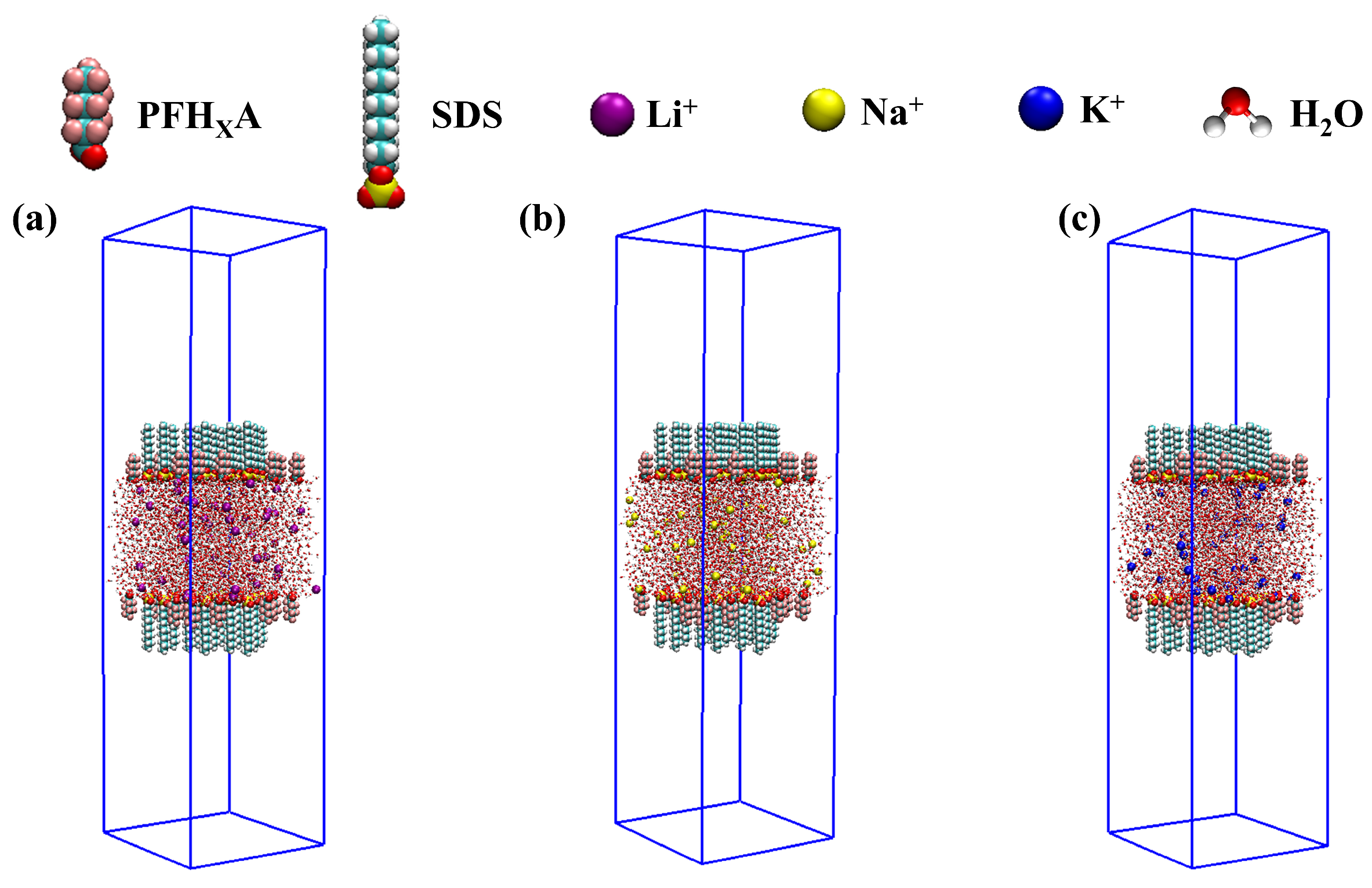
3.1. Modeling
3.2. Simulation Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, X.; Bo, H.; He, Y. Synthesis and characterization of a novel surfactant used for aqueous film-forming foam extinguishing agent. Chem. Pap. 2019, 73, 1777–1784. [Google Scholar] [CrossRef]
- Sheng, Y.; Xue, M.; Ma, L.; Zhao, Y.; Wang, Q.; Liu, X. Environmentally Friendly Firefighting Foams Used to Fight Flammable Liquid Fire. Fire Technol. 2021, 57, 2079–2096. [Google Scholar] [CrossRef]
- Valsecchi, S.; Conti, D.; Crebelli, R.; Polesello, S.; Rusconi, M.; Mazzoni, M.; Preziosi, E.; Carere, M.; Lucentini, L.; Ferretti, E.; et al. Deriving environmental quality standards for perfluorooctanoic acid (PFOA) and related short chain perfluorinated alkyl acids. J. Hazard Mater. 2017, 323 Pt A, 84–98. [Google Scholar] [CrossRef]
- Peshoria, S.; Nandini, D.; Tanwar, R.K.; Narang, R. Short-chain and long-chain fluorosurfactants in firefighting foam: A review. Environ. Chem. Lett. 2020, 18, 1277–1300. [Google Scholar] [CrossRef]
- Zhou, R.; Jin, Y.; Shen, Y.; Lai, S.; Zhou, Y.; Zhao, P. Surface activity, salt and pH tolerance, and wettability of novel nonionic fluorinated surfactants with a short fluorocarbon chain. J. Dispers. Sci. Technol. 2020, 42, 152–159. [Google Scholar] [CrossRef]
- Zhou, R.; Jin, Y.; Shen, Y.; Zhao, P.; Zhou, Y. Synthesis and application of non-bioaccumulable fluorinated surfactants: A review. J. Leather Sci. Eng. 2021, 3, 6. [Google Scholar] [CrossRef]
- Ding, X.; Wang, K.; Luo, Z.; Fu, Q.; Wang, T.; Xu, Q.; Yi, X.; Dai, R.; Jiang, H.; Xing, Z. The investigation of wetting and agglomerating mechanism of short-chain fluorocarbon surfactant suppressing coal dust from macro and molecular scales. Chem. Eng. J. 2024, 487, 150475. [Google Scholar] [CrossRef]
- Zhang, D.; Bai, Y.; Shen, J.; Wang, G. Surface activities and wetting behavior of fluorocarbon-cationic and hydrocarbon-anionic surfactant mixtures in dilute solutions. J. Mol. Liq. 2019, 286, 110947. [Google Scholar] [CrossRef]
- Hussain, S.M.S.; Adewunmi, A.A.; Mahboob, A.; Murtaza, M.; Zhou, X.; Kamal, M.S. Fluorinated surfactants: A review on recent progress on synthesis and oilfield applications. Adv. Colloid. Interface. Sci. 2022, 303, 102634. [Google Scholar] [CrossRef]
- Phan, C.M.; Haseeb, M. Relative contribution of cationic surfactant and counter-anion to a liquid film tension. J. Mol. Liq. 2020, 306, 112802. [Google Scholar] [CrossRef]
- Islam, M.S.; Shortall, S.M.; Mekhail, G.M.; Callender, S.P.; Madkhali, O.; Bharwani, Z.; Ayyash, D.; Kobernyk, K.; Wettig, S.D. Effect of counterions on the micellization and monolayer behaviour of cationic gemini surfactants. Phys. Chem. Chem. Phys. 2017, 19, 10825–10834. [Google Scholar] [CrossRef]
- McCluskey, A.R.; Grant, J.; Symington, A.R.; Snow, T.; Doutch, J.; Morgan, B.J.; Parker, S.C.; Edler, K.J. An introduction to classical molecular dynamics simulation for experimental scattering users. J. Appl. Crystallogr. 2019, 52 Pt 3, 665–668. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Loura, L.M.S. Molecular Dynamics Simulations: Advances and Applications. Molecules 2022, 27, 2105. [Google Scholar] [CrossRef]
- Gang, H.Z.; Liu, J.F.; Mu, B.Z. Molecular dynamics study of surfactin monolayer at the air/water interface. J. Phys. Chem. B 2011, 115, 12770–12777. [Google Scholar] [CrossRef] [PubMed]
- Nan, Y.; Li, W.; Jin, Z. Molecular Dynamics Studies on Effective Surface-Active Additives: Toward Hard Water-Resistant Chemical Flooding for Enhanced Oil Recovery. Langmuir 2022, 38, 4802–4811. [Google Scholar] [CrossRef]
- Jiao, J.; Li, T.; Zhang, G.; Xiong, J.; Lang, X.; Quan, X.; Cheng, Y.; Wei, Y. Molecular Dynamics Simulations of the Short-Chain Fluorocarbon Surfactant PFHXA and the Anionic Surfactant SDS at the Air/Water Interface. Molecules 2024, 29, 1606. [Google Scholar] [CrossRef] [PubMed]
- Coutsias, E.A.; Wester, M.J. RMSD and Symmetry. J. Comput. Chem. 2019, 40, 1496–1508. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Qiao, M.; Zhao, H.; Ran, Q.; Yuan, S. Effect of mixed surfactants on foam stabilization: A molecular dynamics simulation. J. Mol. Liq. 2022, 365, 120096. [Google Scholar] [CrossRef]
- Khan, J.M.; Malik, A.; Rehman, M.T.; AlAjmi, M.F.; Ahmed, M.Z.; Almutairi, G.O.; Anwer, M.K.; Khan, R.H. Cationic gemini surfactant stimulates amyloid fibril formation in bovine liver catalase at physiological pH. A biophysical study. RSC Adv. 2020, 10, 43751–43761. [Google Scholar] [CrossRef]
- Bhat, I.A.; Kausar, T.; Dar, A.A.; Nayeem, S.M.; Akram, M.; Kabir-ud-Din. Exclusive behaviour of asymmetric zwitterionic gemini surfactants towards lysozyme. J. Mol. Liq. 2021, 336, 116583. [Google Scholar] [CrossRef]
- Nightingale, E.R., Jr. Phenomenological Theory of Ion Solvation. Effective Radii of Hydrated Ions. J. Phys. Chem. 1959, 63, 1381–1387. [Google Scholar] [CrossRef]
- Wang, Y.; Kiziltas, A.; Blanchard, P.; Walsh, T.R. Calculation of 1D and 2D densities in VMD: A flexible and easy-to-use code. Comput. Phys. Commun. 2021, 266, 108032. [Google Scholar] [CrossRef]
- Tadros, T. Surface Tension. In Encyclopedia of Colloid and Interface Science; Tadros, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; p. 1052. [Google Scholar]
- An, H.; Cao, G.; Bai, Y.; Wang, D.; Meng, F. Study on the stability of emulsion based on molecular dynamics. J. Dispers. Sci. Technol. 2021, 42, 1723–1732. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, M.Y.; Wang, K.; Sun, R.; Zhao, S.; Zhang, Z.; He, Y.P.; Yu, F. Geometry transformation of ionic surfactants and adsorption behavior on water/n-decane-interface: Calculation by molecular dynamics simulation and DFT study. RSC Adv. 2021, 11, 28286–28294. [Google Scholar] [CrossRef]
- Eustaquio-Armenta, M.d.R.; González-Melchor, M. Self-diffusion and structure of monovalent ions in two dimensions: A molecular dynamics study. J. Mol. Liq. 2019, 294, 111542. [Google Scholar] [CrossRef]
- Zhang, N.; Ruan, X.; Song, Y.; Liu, Z.; He, G. Molecular dynamics simulation of the hydration structure and hydrogen bonding behavior of phenol in aqueous solution. J. Mol. Liq. 2016, 221, 942–948. [Google Scholar] [CrossRef]
- Li, Y.; Stewart, T.C.; Tang, H.L. A comparative study on electrosorptive rates of metal ions in capacitive deionization. J. Water Process. Eng. 2018, 26, 257–263. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, S.; Wang, Y.; Ullah, S.; Hu, J.; Liu, H.; Xu, B. The surface adsorption, aggregate structure and antibacterial activity of Gemini quaternary ammonium surfactants with carboxylic counterions. R. Soc. Open Sci. 2019, 6, 190378. [Google Scholar] [CrossRef]
- Manzetti, S.; Lu, T. The geometry and electronic structure of Aristolochic acid: Possible implications for a frozen resonance. J. Phys. Org. Chem. 2013, 26, 473–483. [Google Scholar] [CrossRef]
- Quan, X.; Xiong, J.; Tong, T.; Jiao, J.; Zou, J.; Wei, Y. Molecular dynamics simulation of synergistic behavior at the air–water interface: Mixed cationic–anionic fluorocarbon–hydrocarbon surfactants. Phys. Chem. Chem. Phys. 2025, 27, 6043–6055. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Hydrogen-bond kinetics in liquid water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Wang, L.; Xu, R.; Liu, R.; Ge, P.; Sun, W.; Tian, M. Self-Assembly of NaOL-DDA Mixtures in Aqueous Solution: A Molecular Dynamics Simulation Study. Molecules 2021, 26, 7117. [Google Scholar] [CrossRef] [PubMed]
- Kwiatkowski, A.L.; Molchanov, V.S.; Orekhov, A.S.; Vasiliev, A.L.; Philippova, O.E. Impact of Salt Co- and Counterions on Rheological Properties and Structure of Wormlike Micellar Solutions. J. Phys. Chem. B 2016, 120, 12547–12556. [Google Scholar] [CrossRef]
- Bain, A.; Ghosh, K.; Prisle, N.L.; Bzdek, B.R. Surface-Area-to-Volume Ratio Determines Surface Tensions in Microscopic, Surfactant-Containing Droplets. ACS Cent. Sci. 2023, 9, 2076–2083. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.; Schlegel, H.B.; Scuseria, G.E.; Robb; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09W; Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Lindahl, E.; Hess, B.; van der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. Mol. Model. Annu. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, L.; Jiang, Y.; Huang, Z.; Liu, G.; Wei, Y.; Xia, Q. Molecular Dynamics Simulations on the Adsorbed Monolayers of N-Dodecyl Betaine at the Air–Water Interface. Molecules 2023, 28, 5580. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Li, J.; Amador, C.; Wilson, M.R. Computational predictions of interfacial tension, surface tension, and surfactant adsorption isotherms. Phys. Chem. Chem. Phys. 2024, 26, 12107–12120. [Google Scholar] [CrossRef]
- Pastor, R.W.; Mackerell, A.D., Jr. Development of the CHARMM Force Field for Lipids. J. Phys. Chem. Lett. 2011, 2, 1526–1532. [Google Scholar] [CrossRef] [PubMed]
- Meyer, N.; Piquet, V.; Wax, J.-F.; Xu, H.; Millot, C. Rotational and translational dynamics of the SPC/E water model. J. Mol. Liq. 2019, 275, 895–908. [Google Scholar] [CrossRef]
- Lu, T. Sobtop Version: 1.0(dev3.1). Available online: http://sobereva.com/soft/Sobtop/ (accessed on 18 June 2024).
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Yan, G.; Chen, X.; Li, J. Adsorption Characteristics of Ionic Surfactants on Anthracite Surface: A Combined Experimental and Modeling Study. Molecules 2022, 27, 5314. [Google Scholar] [CrossRef]
- Wang, H.; Gao, X.; Fang, J. Multiple Staggered Mesh Ewald: Boosting the Accuracy of the Smooth Particle Mesh Ewald Method. J. Chem. Theory Comput. 2016, 12, 5596–5608. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Xue, C.; Zhao, H.; Wang, Q.; Zhang, K.; Li, Y. Interfacial molecular array behaviors of mixed surfactant systems based on sodium laurylglutamate and the effect on the foam properties. J. Dispers. Sci. Technol. 2017, 39, 1427–1434. [Google Scholar] [CrossRef]
- Domínguez, H. Computer Studies on the Effects of Long Chain Alcohols on Sodium Dodecyl Sulfate (SDS) Molecules in SDS/Dodecanol and SDS/Hexadecanol Monolayers at the Air/Water Interface. J. Phys. Chem. B 2006, 110, 13151–13157. [Google Scholar] [CrossRef]
- Wang, C.; Ou, L. Molecular dynamics investigation of the liquid-gas interface behavior: Simulations of the sodium oleate/sodium abietate/water system. Colloids Surf. A Physicochem. Eng. Asp. 2022, 635, 128086. [Google Scholar] [CrossRef]
- Hao, L.-S.; Yang, N.; Xu, G.-Y.; Jia, Y.-F.; Liu, Q.; Nan, Y.-Q. Specific ion effects on the micellization of aqueous mixed cationic/anionic surfactant systems with various counterions. Colloids Surf. A Physicochem. Eng. Asp. 2016, 504, 161–173. [Google Scholar] [CrossRef]
- Srivastava, A.; Uchiyama, H.; Imano, H.; Satone, H.; Iimura, K.; Kadota, K.; Tozuka, Y. Enhanced micellization of Gemini surfactants using diphenhydramine hydrochloride as an organic counterion. J. Mol. Liq. 2020, 300, 112288. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Hou, J.; Liu, F. Electric-Field-Induced Interface Behavior of Dodecyl Sulfate with Large Organic Counterions: A Molecular Dynamics Study. J. Phys. Chem. B 2020, 124, 5498–5506. [Google Scholar] [CrossRef] [PubMed]
- Peng, M.; Duignan, T.T.; Nguyen, A.V. Quantifying the Counterion-Specific Effect on Surfactant Adsorption Using Modeling, Simulation, and Experiments. Langmuir 2020, 36, 13012–13022. [Google Scholar] [CrossRef] [PubMed]


| System | Surface Tension (mN/m) | Stand Deviations | ||
|---|---|---|---|---|
| PFHXA/SDS: Li+ | 25.8 | 25.4 | 25.3 | 0.2646 |
| PFHXA/SDS: Na+ | 21.4 | 21.9 | 22.3 | 0.4848 |
| PFHXA/SDS: K+ | 20.9 | 20.1 | 20.4 | 0.4041 |
| System | Box Dimension | Counterions and Quantities | Water Molecule |
|---|---|---|---|
| PFHXA/SDS: Li+ | 5 × 5 × 20 (nm) | Li+ (50) | 3632 |
| PFHXA/SDS: Na+ | 5 × 5 × 20 (nm) | Na+ (50) | 3632 |
| PFHXA/SDS: K+ | 5 × 5 × 20 (nm) | K+ (50) | 3632 |
| PFHXA | |||||
|---|---|---|---|---|---|
| Atom | Charge | Mass | Atom | Charge | Mass |
| C1 | 0.659382 | 12.01074 | F11 | −0.20921 | 18.9984 |
| C2 | 0.208681 | 12.01074 | F12 | −0.19698 | 18.9984 |
| C3 | 0.415 | 12.01074 | F13 | −0.18355 | 18.9984 |
| C4 | 0.289425 | 12.01074 | F14 | −0.20478 | 18.9984 |
| C5 | 0.33657 | 12.01074 | F15 | −0.25376 | 18.9984 |
| F6 | −0.21045 | 18.9984 | F16 | −0.24683 | 18.9984 |
| F7 | −0.21001 | 18.9984 | C17 | 0.744484 | 12.01074 |
| F8 | −0.20967 | 18.9984 | O18 | −0.70875 | 15.99941 |
| F9 | −0.15571 | 18.9984 | O19 | −0.69536 | 15.99941 |
| F10 | −0.16849 | 18.9984 | |||
| SDS | |||||
|---|---|---|---|---|---|
| Atom | Charge | Mass | Atom | Charge | Mass |
| C1 | −0.25072 | 12.01074 | H22 | −0.00092 | 1.007941 |
| H2 | 0.058142 | 1.007941 | C23 | 0.02459 | 12.01074 |
| H3 | 0.058142 | 1.007941 | H24 | −0.00912 | 1.007941 |
| H4 | 0.058142 | 1.007941 | H25 | −0.00912 | 1.007941 |
| C5 | 0.117359 | 12.01074 | C26 | 0.072927 | 12.01074 |
| H6 | −0.01503 | 1.007941 | H27 | −0.02215 | 1.007941 |
| H7 | −0.01503 | 1.007941 | H28 | −0.02215 | 1.007941 |
| C8 | −0.00952 | 12.01074 | C29 | −0.05769 | 12.01074 |
| H9 | 0.001923 | 1.007941 | H30 | −0.00233 | 1.007941 |
| H10 | 0.001923 | 1.007941 | H31 | −0.00233 | 1.007941 |
| C11 | −0.03489 | 12.01074 | C32 | 0.002969 | 12.01074 |
| H12 | −0.00105 | 1.007941 | H33 | 0.007111 | 1.007941 |
| H13 | −0.00105 | 1.007941 | H34 | 0.007111 | 1.007941 |
| C14 | 0.058223 | 12.01074 | C35 | 0.343935 | 12.01074 |
| H15 | −0.01667 | 1.007941 | H36 | −0.02482 | 1.007941 |
| H16 | −0.01667 | 1.007941 | H37 | −0.02482 | 1.007941 |
| C17 | 0.021417 | 12.01074 | O38 | −0.54093 | 15.99941 |
| H18 | −0.00876 | 1.007941 | S39 | 1.01068 | 32.06479 |
| H19 | −0.00876 | 1.007941 | O40 | −0.58017 | 15.99941 |
| C20 | −0.02905 | 12.01074 | O41 | −0.58017 | 15.99941 |
| H21 | −0.00092 | 1.007941 | O42 | −0.55972 | 15.99941 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, X.; Tong, T.; Li, T.; Han, D.; Cui, B.; Xiong, J.; Cui, Z.; Guo, H.; Jiao, J.; Wei, Y. Counterion-Mediated Assembly of Fluorocarbon–Hydrocarbon Surfactant Mixtures at the Air–Liquid Interface: A Molecular Dynamics Study. Molecules 2025, 30, 2592. https://doi.org/10.3390/molecules30122592
Quan X, Tong T, Li T, Han D, Cui B, Xiong J, Cui Z, Guo H, Jiao J, Wei Y. Counterion-Mediated Assembly of Fluorocarbon–Hydrocarbon Surfactant Mixtures at the Air–Liquid Interface: A Molecular Dynamics Study. Molecules. 2025; 30(12):2592. https://doi.org/10.3390/molecules30122592
Chicago/Turabian StyleQuan, Xiaolong, Tong Tong, Tao Li, Dawei Han, Baolong Cui, Jing Xiong, Zekai Cui, Hao Guo, Jinqing Jiao, and Yuechang Wei. 2025. "Counterion-Mediated Assembly of Fluorocarbon–Hydrocarbon Surfactant Mixtures at the Air–Liquid Interface: A Molecular Dynamics Study" Molecules 30, no. 12: 2592. https://doi.org/10.3390/molecules30122592
APA StyleQuan, X., Tong, T., Li, T., Han, D., Cui, B., Xiong, J., Cui, Z., Guo, H., Jiao, J., & Wei, Y. (2025). Counterion-Mediated Assembly of Fluorocarbon–Hydrocarbon Surfactant Mixtures at the Air–Liquid Interface: A Molecular Dynamics Study. Molecules, 30(12), 2592. https://doi.org/10.3390/molecules30122592








