Influence of Biopolymer–Biopolymer Interactions on Selected Rheological Properties of Aqueous Ionic Hydrocolloid Solutions
Abstract
1. Introduction
| Mw, kg/mol | Mosm, kg/mol | A2 (30 °C) mol mL g−2 | Mw, kg/mol | c*, % | c**, % | c, % | Elong | Shear | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Up | Down | ||||||||||||||
| t1, ms | t2, ms | 2 | t1, ms | t2, ms | t1, ms | t2, ms | 2 | ||||||||
| KG | 990 | 1557 | −2.13 × 10−4 (a) | 1030 (1) | 0.033 | 0.072 | c*~0.05 | 1 | 50 | Newtonian viscosity 2.35 mPas | |||||
| c**~0.10 eq.4 | 2 | 50 | 10−3 | 14 | 1000 | 10 | 350 | 10−6 | |||||||
| c** < 0.20 | 2 | 50 | 10−5 | 6 | 150 | 5 | 100 | 10−6 | |||||||
| CMC | 300 | 2570 | 9.84 × 10−5 (b) | 280 (2) | 0.02 | 0.1 | c**~0.10 | 3 | 300 | 10−5 | 5 | 200 | 4 | 100 | 10−6 |
| XG | 1960 | - | −1.36 × 10−4 (b) | 2160 (3) | 0.023 | 0.07 | c** < 0.10 | 5 | 100 | 10−4 | 1 | 200 | 9 | 200 | 10−6 |
2. Results
2.1. Effect of Konjac Gum (KG) Concentration on Rheological Properties
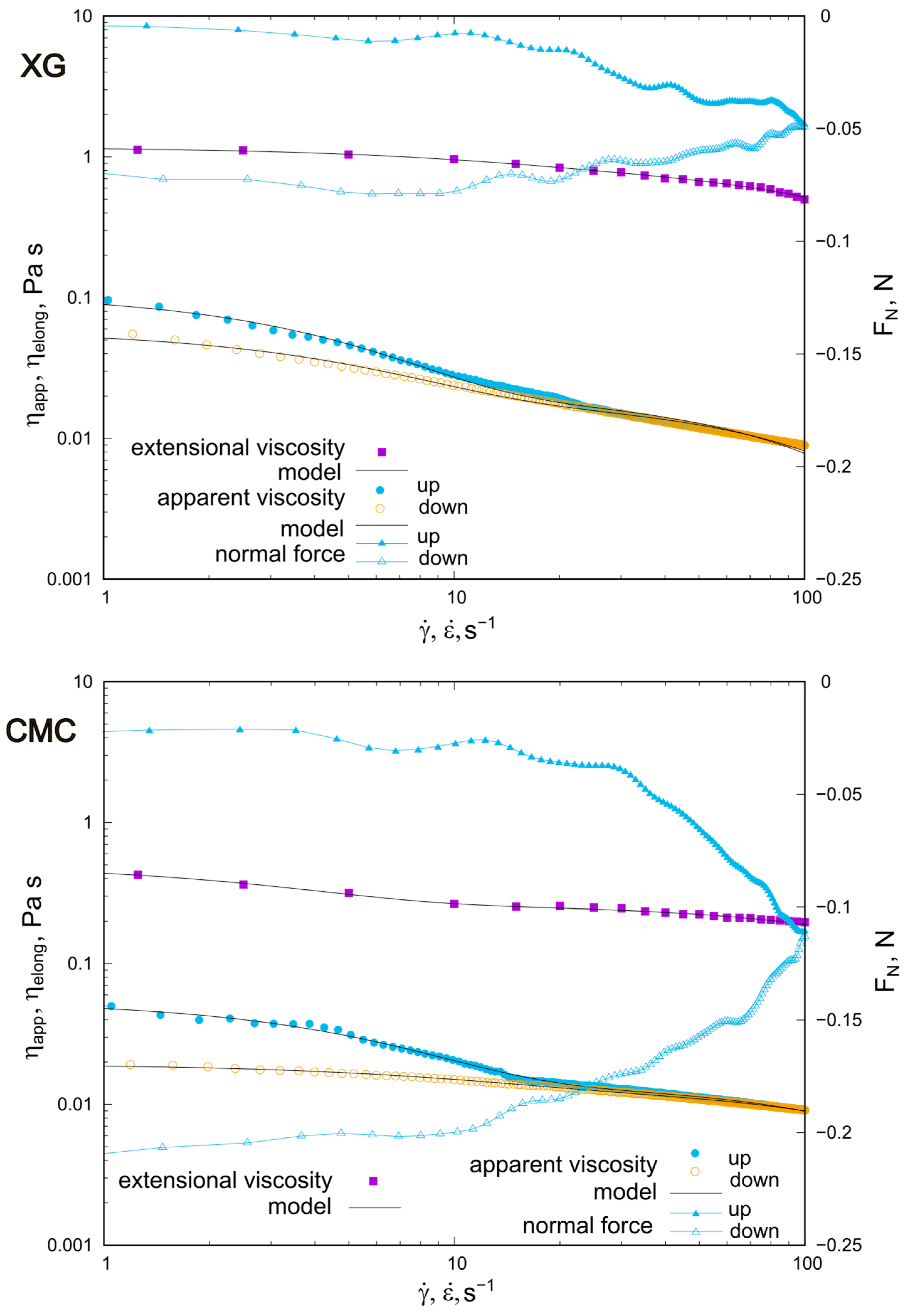
2.2. Behavior of XG and CMC Concentrated Solutions
2.3. Effect of Concentration on Characteristic Time Constants
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Methods
4.2.1. Gel Permeation Chromatography (GPC)
4.2.2. Extensional Rheology
4.2.3. Rotational Rheology
4.2.4. Modelling of Rheological Properties
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jacon, S.A.; Rao, M.A.; Cooley, H.J.; Walter, R.H. The Isolation and Characterization of a Water Extract of Konjac Flour Gum. Carbohydr. Polym. 1993, 20, 35–41. [Google Scholar] [CrossRef]
- Guo, L.; Yokoyama, W.; Chen, L.; Liu, F.; Chen, M.; Zhong, F. Characterization and Physicochemical Properties Analysis of Konjac Glucomannan: Implications for Structure-Properties Relationships. Food Hydrocoll. 2021, 120, 106818. [Google Scholar] [CrossRef]
- Castelain, C.; Doublier, J.L.; Lefebvre, J. A Study of the Viscosity of Cellulose Derivatives in Aqueous Solutions. Carbohydr. Polym. 1987, 7, 1–16. [Google Scholar] [CrossRef]
- Li, R.; Wu, M.; Guo, Y.; Zhang, H. Comprehensive Physical Visualisation of the Chain Conformation and Solution Property of Carboxymethylated Konjac Glucomannan: Comparison of Charged and Uncharged Polyelectrolytes. Food Hydrocoll. 2021, 118, 106725. [Google Scholar] [CrossRef]
- Nsengiyumva, E.M.; Alexandridis, P. Xanthan Gum in Aqueous Solutions: Fundamentals and Applications. Int. J. Biol. Macromol. 2022, 216, 583–604. [Google Scholar] [CrossRef]
- Southwick, J.G.; Jamieson, A.M.; Blackwell, J. Quasi-Elastic Light Scattering Studies of Semidilute Xanthan Solutions. Macromolecules 1981, 14, 1728–1732. [Google Scholar] [CrossRef]
- Ojima, R.; Makabe, T.; Prawitwong, P.; Takahashi, R.; Takigami, M.; Takigami, S. Rheological Property of Hydrolyzed Konjac Glucomannan. Trans. Mater. Res. Soc. Jpn. 2009, 34, 477–480. [Google Scholar] [CrossRef]
- Wu, Q.; Shangguan, Y.; Du, M.; Zhou, J.; Song, Y.; Zheng, Q. Steady and Dynamic Rheological Behaviors of Sodium Carboxymethyl Cellulose Entangled Semi-Dilute Solution with Opposite Charged Surfactant Dodecyl-Trimethylammonium Bromide. J. Colloid Interface Sci. 2009, 339, 236–242. [Google Scholar] [CrossRef]
- Evageliou, V. Shear and Extensional Rheology of Selected Polysaccharides. Int. J. Food Sci. Technol. 2020, 55, 1853–1861. [Google Scholar] [CrossRef]
- Riaz, T.; Iqbal, M.W.; Jiang, B.; Chen, J. A Review of the Enzymatic, Physical, and Chemical Modification Techniques of Xanthan Gum. Int. J. Biol. Macromol. 2021, 186, 472–489. [Google Scholar] [CrossRef]
- Cuvelier, G.; Launay, B. Concentration Regimes in Xanthan Gum Solutions Deduced from Flow and Viscoelastic Properties. Carbohydr. Polym. 1986, 6, 321–333. [Google Scholar] [CrossRef]
- Milas, M.; Rinaudo, M.; Knipper, M.; Schuppiser, J.L. Flow and Viscoelastic Properties of Xanthan Gum Solutions. Macromolecules 1990, 23, 2506–2511. [Google Scholar] [CrossRef]
- Rodd, A.B.; Dunstan, D.E.; Boger, D.V. Characterisation of Xanthan Gum Solutions Using Dynamic Light Scattering and Rheology. Carbohydr. Polym. 2000, 42, 159–174. [Google Scholar] [CrossRef]
- Wyatt, N.B.; Liberatore, M.W. Rheology and Viscosity Scaling of the Polyelectrolyte Xanthan Gum. J. Appl. Polym. Sci. 2009, 114, 4076–4084. [Google Scholar] [CrossRef]
- Li, X.; Harding, S.E.; Wolf, B.; Yakubov, G.E. Instrumental Characterization of Xanthan Gum and Scleroglucan Solutions: Comparison of Rotational Rheometry, Capillary Breakup Extensional Rheometry and Soft-Contact Tribology. Food Hydrocoll. 2022, 130, 107681. [Google Scholar] [CrossRef]
- Ng, T.S.K.; McKinley, G.H.; Ewoldt, R.H. Large Amplitude Oscillatory Shear Flow of Gluten Dough: A Model Power-Law Gel. J. Rheol. 2011, 55, 627–654. [Google Scholar] [CrossRef]
- Pelletier, L.G.; Fortier, M.S.; Vallerand, R.J.; Brì Ere, N.M. Associations Among Perceived Autonomy Support, Forms of Self-Regulation, and Persistence: A Prospective Study. Motiv. Emot. 2001, 25, 279–306. [Google Scholar] [CrossRef]
- Choi, H.; Mitchell, J.R.; Gaddipati, S.R.; Hill, S.E.; Wolf, B. Shear Rheology and Filament Stretching Behaviour of Xanthan Gum and Carboxymethyl Cellulose Solution in Presence of Saliva. Food Hydrocoll. 2014, 40, 71–75. [Google Scholar] [CrossRef]
- Funami, T.; Nakauma, M. Correlation of Human Perception in Swallowing with Extension Rheological and Tribological Characteristics in Comparison with Shear Rheology. J. Texture Stud. 2021, 53, 60–71. [Google Scholar] [CrossRef]
- Peleg-Evron, O.; Wirzeberger, D.; Davidovich-Pinhas, M.; Cometa, S.; De Giglio, E.; Bianco-Peled, H. Comparative Analysis of Classic Network vs. Nanogel Junction Network in Konjac Glucomannan/Kappa Carrageenan Hybrid Hydrogels. Int. J. Biol. Macromol. 2024, 279, 135244. [Google Scholar] [CrossRef]
- Ratcliffe, I.; Williams, P.A.; Viebke, C.; Meadows, J. Physicochemical Characterization of Konjac Glucomannan. Biomacromolecules 2005, 6, 1977–1986. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; He, P.; Lin, X. The Mechanism of Sodium Hydroxide Solution Promoting the Gelation of Konjac Glucomannan (KGM). Food Hydrocoll. 2013, 30, 92–99. [Google Scholar] [CrossRef]
- Kruk, J.; Kaczmarczyk, K.; Ptaszek, A.; Goik, U.; Ptaszek, P. The Effect of Temperature on the Colligative Properties of Food-Grade Konjac Gum in Water Solutions. Carbohydr. Polym. 2017, 174, 456–463. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Gong, T.; Lu, Y.-H.; Li, A.; Sun, L.; Guo, Y. Compatibility of Sodium Alginate and Konjac Glucomannan and Their Applications in Fabricating Low-Fat Mayonnaise-like Emulsion Gels. Carbohydr. Polym. 2020, 229, 115468. [Google Scholar] [CrossRef]
- Rashid, S.; Dutta, H. Physicochemical Characterization of Carboxymethyl Cellulose from Differently Sized Rice Husks and Application as Cake Additive. LWT 2022, 154, 112630. [Google Scholar] [CrossRef]
- Benchabane, A.; Bekkour, K. Rheological Properties of Carboxymethyl Cellulose (CMC) Solutions. Colloid Polym. Sci. 2008, 286, 1173–1180. [Google Scholar] [CrossRef]
- Lopez, C.G. Entanglement of Semiflexible Polyelectrolytes: Crossover Concentrations and Entanglement Density of Sodium Carboxymethyl Cellulose. J. Rheol. 2020, 64, 191–204. [Google Scholar] [CrossRef]
- Miehle, E.; Bader-Mittermaier, S.; Schweiggert-Weisz, U.; Hauner, H.; Eisner, P. Effect of Physicochemical Properties of Carboxymethyl Cellulose on Diffusion of Glucose. Nutrients 2021, 13, 1398. [Google Scholar] [CrossRef]
- Kokini, J.L.; Surmay, K. Steady Shear Viscosity First Normal Stress Difference and Recoverable Strain in Carboxymethyl Cellulose, Sodium Alginate and Guar Gum. Carbohydr. Polym. 1994, 23, 27–33. [Google Scholar] [CrossRef]
- Arinaitwe, E.; Pawlik, M. Dilute Solution Properties of Carboxymethyl Celluloses of Various Molecular Weights and Degrees of Substitution. Carbohydr. Polym. 2014, 99, 423–431. [Google Scholar] [CrossRef]
- Lopez, C.G.; Rogers, S.E.; Colby, R.H.; Graham, P.; Cabral, J.T. Structure of Sodium Carboxymethyl Cellulose Aqueous Solutions: A SANS and Rheology Study. J. Polym. Sci. Part B Polym. Phys. 2014, 53, 492–501. [Google Scholar] [CrossRef]
- Różańska, S.; Różański, J. Extensional Flow of Carboxymethylcellulose Sodium Salt Measured on the Opposed-Nozzle Device. Soft Mater. 2017, 15, 302–314. [Google Scholar] [CrossRef]
- Różańska, S.; Verbeke, K.; Różański, J.; Clasen, C.; Wagner, P. Capillary Breakup Extensional Rheometry of Sodium Carboxymethylcellulose Solutions in Water and Propylene Glycol/Water Mixtures. J. Polym. Sci. Part B Polym. Phys. 2019, 57, 1537–1547. [Google Scholar] [CrossRef]
- Kruk, J.; Pancerz, M.; Ptaszek, A. Osmotic Properties of Polysaccharides Solutions. In Solubility of Polysaccharides; Zhenbo, X., Ed.; InTech: Rijeka, Hrvatska, 2017. [Google Scholar]
- Goycoolea, F.M.; Morris, E.R.; Gidley, M.J. Viscosity of Galactomannans at Alkaline and Neutral PH: Evidence of ‘Hyperentanglement’ in Solution. Carbohydr. Polym. 1995, 27, 69–71. [Google Scholar] [CrossRef]
- Song, K.-W.; Kim, Y.-S.; Chang, G.-S. Rheology of Concentrated Xanthan Gum Solutions: Steady Shear Flow Behavior. Fibers Polym. 2006, 7, 129–138. [Google Scholar] [CrossRef]
- Matsuda, Y.; Biyajima, Y.; Sato, T. Thermal Denaturation, Renaturation, and Aggregation of a Double-Helical Polysaccharide Xanthan in Aqueous Solution. Polym. J. 2009, 41, 526–532. [Google Scholar] [CrossRef]
- Martín-Alfonso, J.E.; Cuadri, A.A.; Berta, M.; Stading, M. Relation between Concentration and Shear-Extensional Rheology Properties of Xanthan and Guar Gum Solutions. Carbohydr. Polym. 2018, 181, 63–70. [Google Scholar] [CrossRef]
- Lukasiewicz, M.; Bednarz, S.; Ptaszek, A. Environmental Friendly Polysaccharide Modification—Microwave-Assisted Oxidation of Starch. Starch-Stärke 2011, 63, 268–273. [Google Scholar] [CrossRef]
- Fuller, G.G.; Cathey, C.A.; Hubbard, B.; Zebrowski, B.E. Extensional Viscosity Measurements for Low-Viscosity Fluids. J. Rheol. 1987, 31, 235–249. [Google Scholar] [CrossRef]
- KÉ, D.D.E.; Turcotte, G. Viscosity of Biomaterials. Chem. Eng. Commun. 1980, 6, 273–282. [Google Scholar] [CrossRef]
- Papanastasiou, A.C.; Scriven, L.E.; Macosko, C.W. An Integral Constitutive Equation for Mixed Flows: Viscoelastic Characterization. J. Rheol. 1983, 27, 387–410. [Google Scholar] [CrossRef]
- Kaczmarczyk, K.; Kruk, J.; Ptaszek, P.; Ptaszek, A. An Investigation of Raw Aqueous Extracts. Osmotic, Hydrodynamic and Complex Rheological Characterisation. Molecules 2023, 28, 1660. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruk, J.; Kaczmarczyk, K.; Ptaszek, P.; Ptaszek, A. Influence of Biopolymer–Biopolymer Interactions on Selected Rheological Properties of Aqueous Ionic Hydrocolloid Solutions. Molecules 2025, 30, 2482. https://doi.org/10.3390/molecules30122482
Kruk J, Kaczmarczyk K, Ptaszek P, Ptaszek A. Influence of Biopolymer–Biopolymer Interactions on Selected Rheological Properties of Aqueous Ionic Hydrocolloid Solutions. Molecules. 2025; 30(12):2482. https://doi.org/10.3390/molecules30122482
Chicago/Turabian StyleKruk, Joanna, Kacper Kaczmarczyk, Paweł Ptaszek, and Anna Ptaszek. 2025. "Influence of Biopolymer–Biopolymer Interactions on Selected Rheological Properties of Aqueous Ionic Hydrocolloid Solutions" Molecules 30, no. 12: 2482. https://doi.org/10.3390/molecules30122482
APA StyleKruk, J., Kaczmarczyk, K., Ptaszek, P., & Ptaszek, A. (2025). Influence of Biopolymer–Biopolymer Interactions on Selected Rheological Properties of Aqueous Ionic Hydrocolloid Solutions. Molecules, 30(12), 2482. https://doi.org/10.3390/molecules30122482







