Evaluating Theoretical Solvent Models for Thermodynamic and Structural Descriptions of Dacarbazine–Cyclodextrin Complexes. The Theoretical and Conductometric Study
Abstract
1. Introduction
2. Results and Discussion
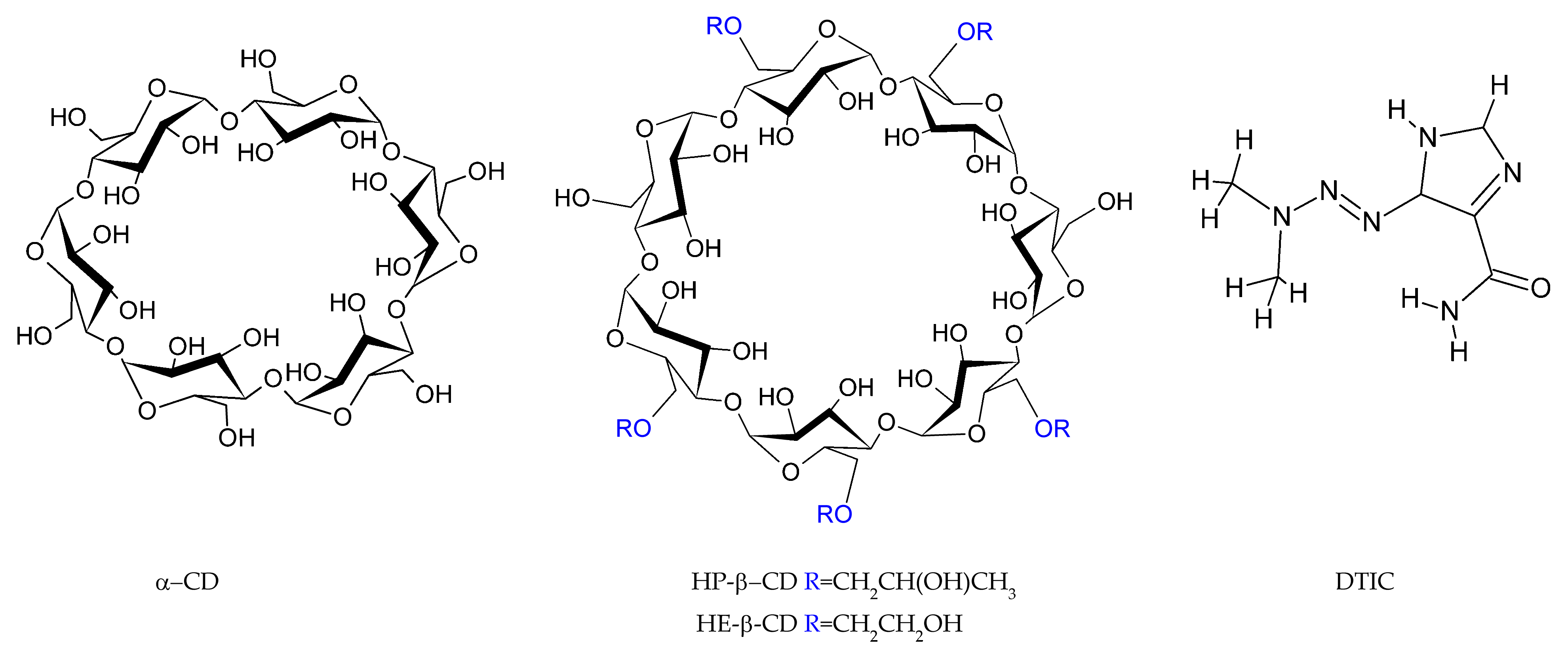
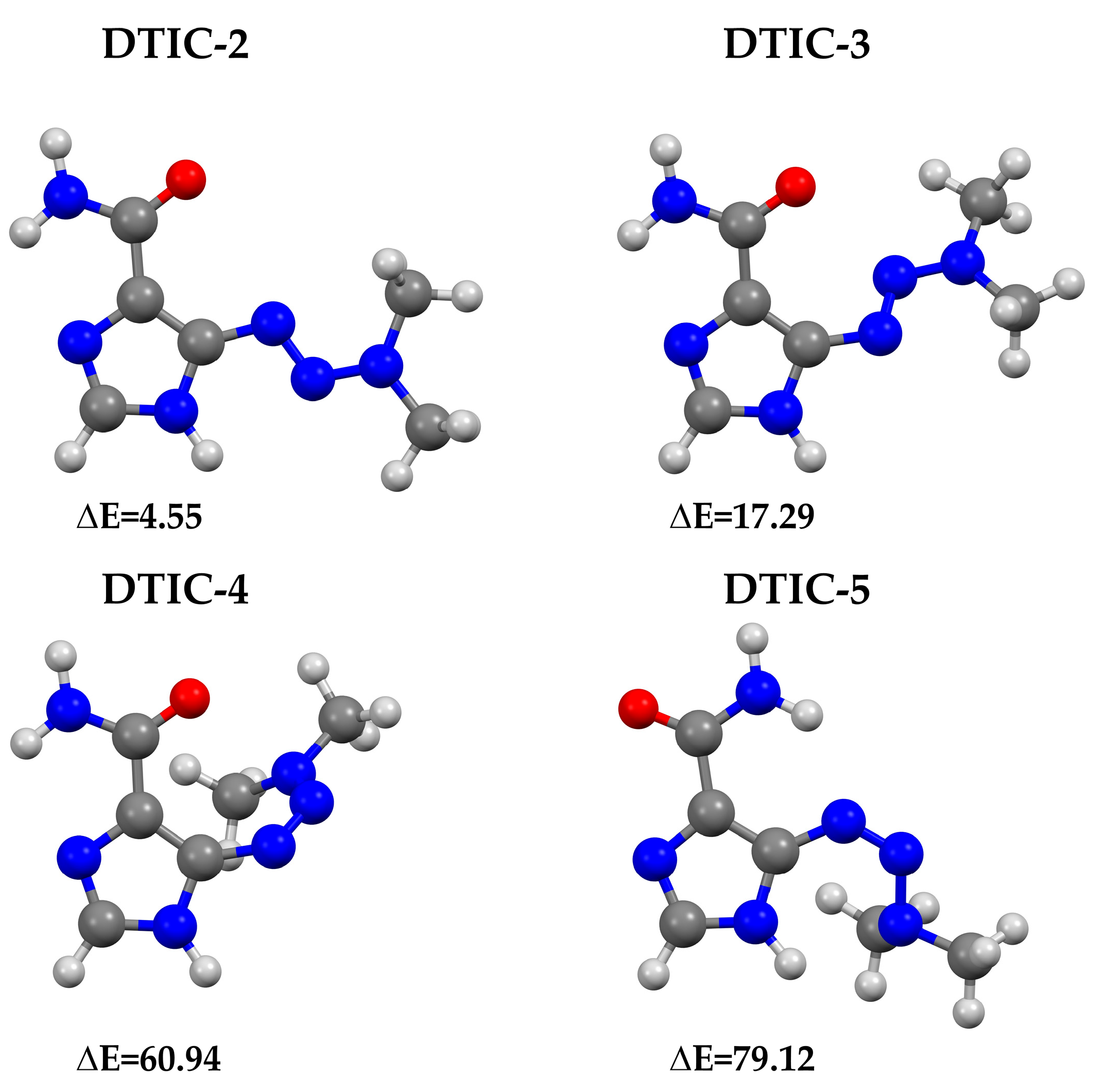
2.1. Analysis of Structural Properties of Dacarbazine-Theoretical Investigation
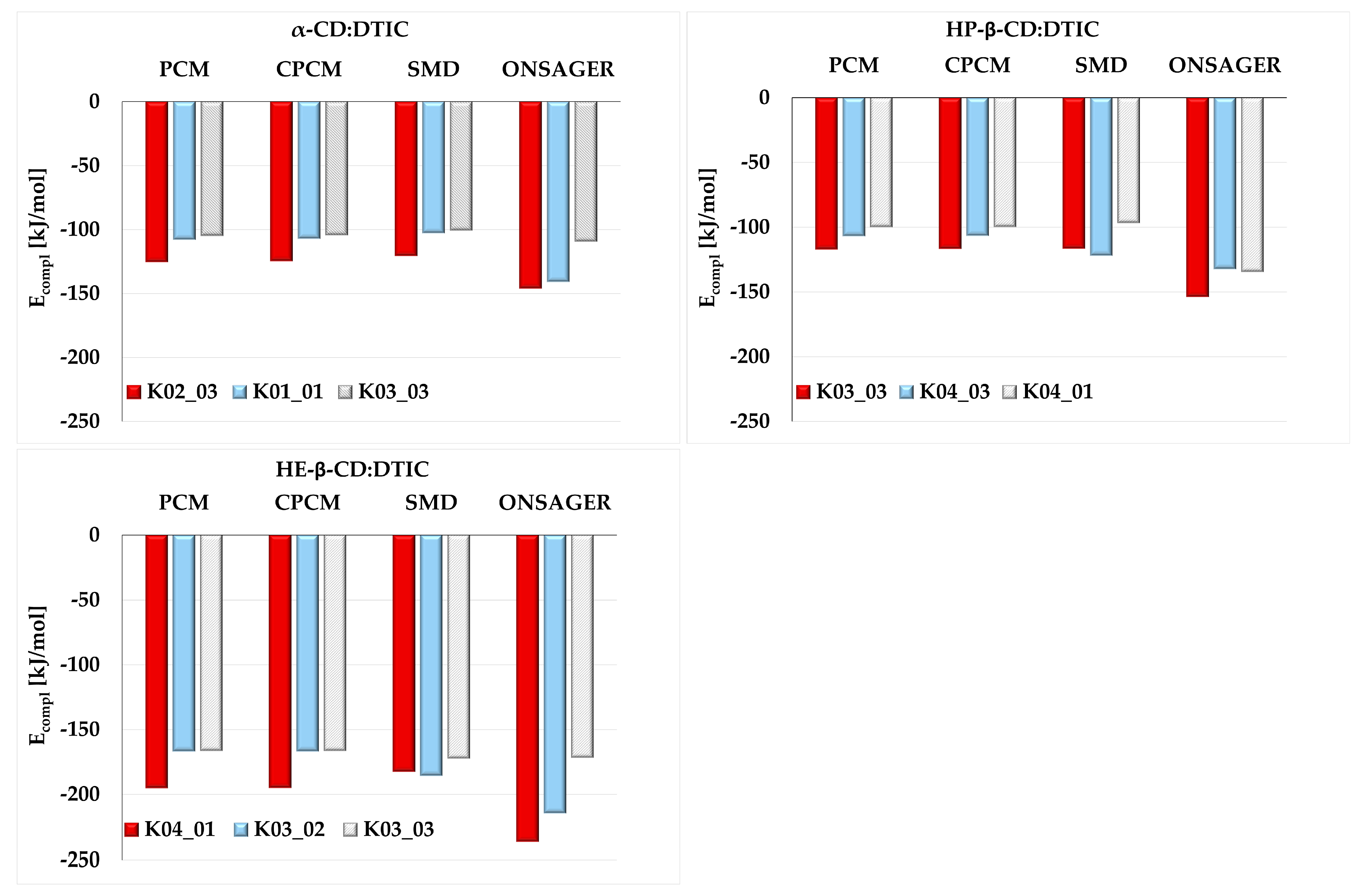
2.2. The Influence of Solvent Models on the Complexation Stability of Cyclodextrin Complexes—Theoretical Study
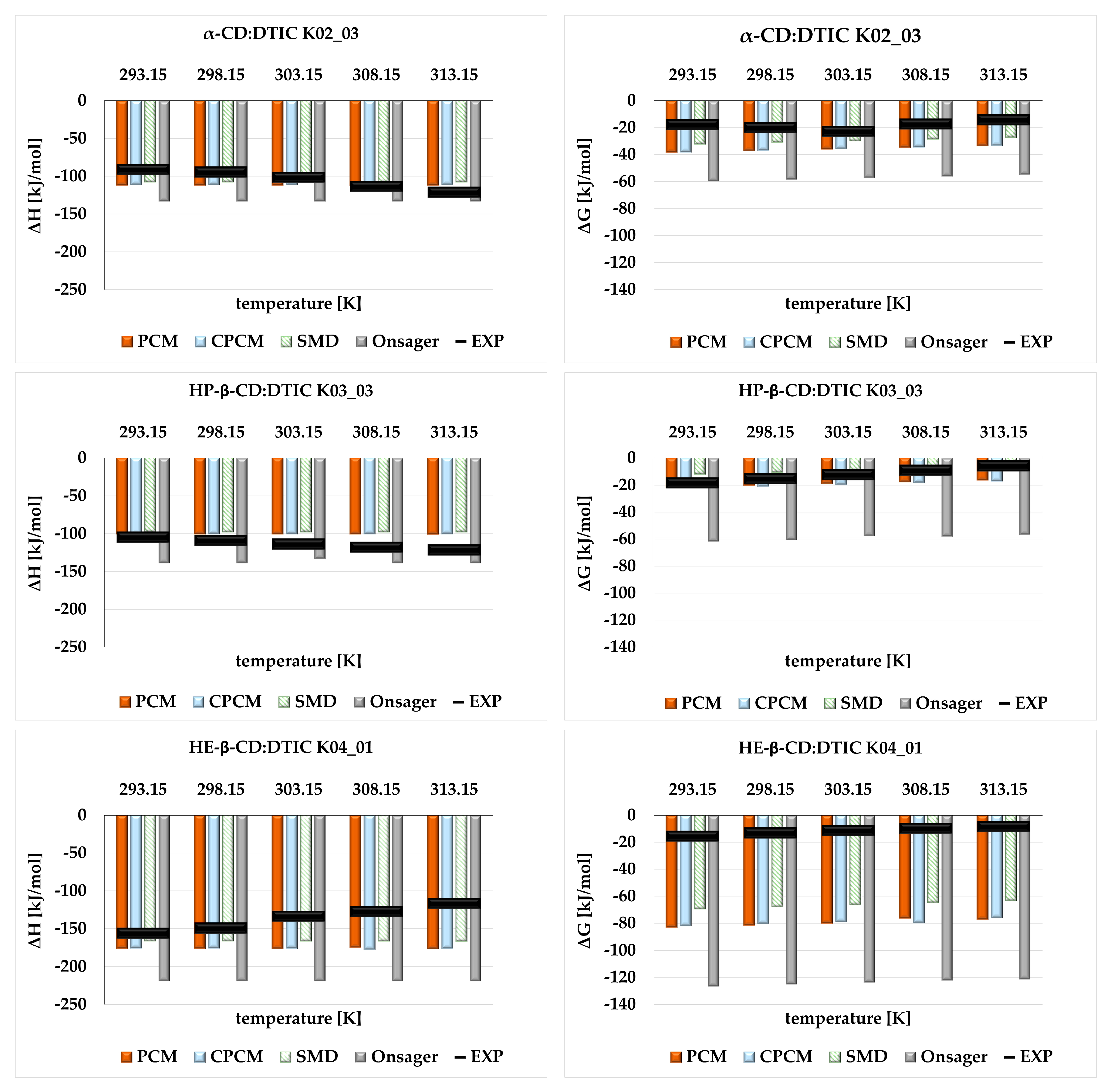
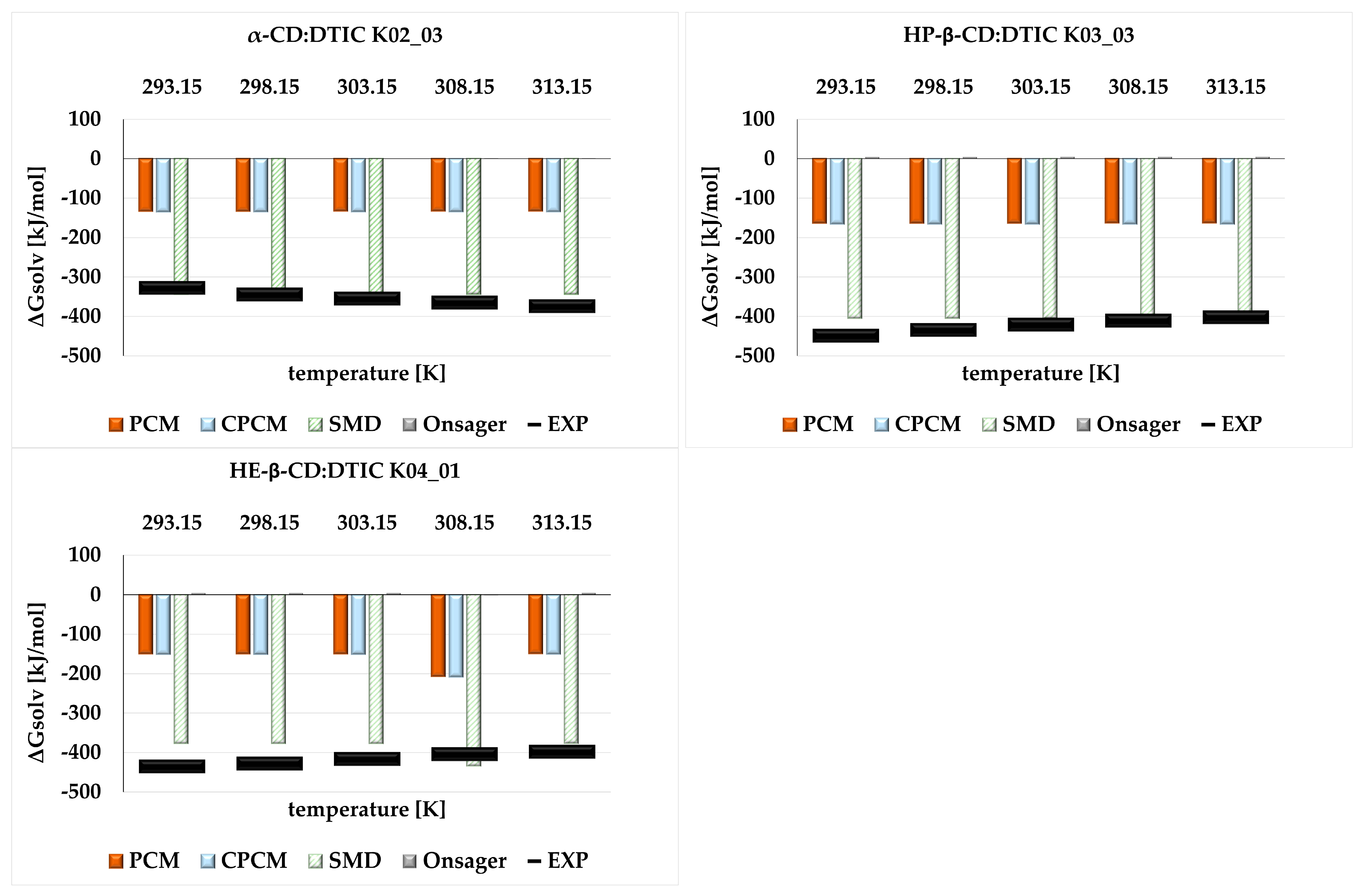
2.3. The Influnce of Solvent Models on the Thermodynamic Properties of Cyclodextrin Complexes-Comparison Between Theoretical and Experimental Study
3. Materials and Methods
3.1. Computational Analysis
3.2. Materials
3.3. Electrical Conductivity Estimation—Exploratory Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sorenson, B.A.; Hong, S.S.; Herbol, H.C.; Clancy, P. How Well Do Implicit Solvation Models Represent Intermolecular Binding Energies in Organic-Inorganic Solutions? Comput. Mater. Sci. 2019, 170, 109138. [Google Scholar] [CrossRef]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourik, T.; Mitchell, J.B.O. A Review of Methods for the Calculation of Solution Free Energies and the Modelling of Systems in Solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef]
- Guerard, J.J.; Arey, J.S. Critical Evaluation of Implicit Solvent Models for Predicting Aqueous Oxidation Potentials of Neutral Organic Compounds. J. Chem. Theory Comput. 2013, 9, 5046–5058. [Google Scholar] [CrossRef]
- Onsager, L. Electric Moments of Molecules in Liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. [Google Scholar] [CrossRef]
- Tahan, A.; Monajjemi, M. Solvent Dielectric Effect and Side Chain Mutation on the Structural Stability of Burkholderia Cepacia Lipase Active Site: A Quantum Mechanical/Molecular Mechanics Study. Acta Biotheor. 2011, 59, 291–312. [Google Scholar] [CrossRef] [PubMed]
- Wong, M.W.; Wiberg, K.B.; Frisch, M.J. Solvent Effects. 3. Tautomeric Equilibria of Formamide and 2-Pyridone in the Gas Phase and Solution: An Ab Initio SCRF Study. J. Am. Chem. Soc. 1992, 114, 1645–1652. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Mennucci, B. Polarizable Continuum Model. WIREs Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Delabie, A.; Creve, S.; Coussens, B.; Nguyen, M.T. Theoretical Study of the Solvent Effect on the Hydrogen Abstraction Reaction of the Methyl Radical with Hydrogen Peroxide. J. Chem. Soc. Perkin Trans. 2000, 2, 977–981. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Eilmes, A. Solvatochromic Probe in Molecular Solvents: Implicit versus Explicit Solvent Model. Theor. Chem. Acc. 2014, 133, 1538. [Google Scholar] [CrossRef]
- Foresman, J.B.; Keith, T.A.; Wiberg, K.B.; Snoonian, J.; Frisch, M.J. Solvent Effects. 5. Influence of Cavity Shape, Truncation of Electrostatics, and Electron Correlation on Ab Initio Reaction Field Calculations. J. Phys. Chem. 1996, 100, 16098–16104. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Han, X. Co-Delivery of Dacarbazine and All-Trans Retinoic Acid (ATRA) Using Lipid Nanoformulations for Synergistic Antitumor Efficacy Against Malignant Melanoma. Nanoscale Res. Lett. 2020, 15, 113. [Google Scholar] [CrossRef] [PubMed]
- Hersh, E.M.; Del Vecchio, M.; Brown, M.P.; Kefford, R.; Loquai, C.; Testori, A.; Bhatia, S.; Gutzmer, R.; Conry, R.; Haydon, A.; et al. A Randomized, Controlled Phase III Trial of Nab-Paclitaxel versus Dacarbazine in Chemotherapy-Naïve Patients with Metastatic Melanoma. Ann. Oncol. 2015, 26, 2267–2274. [Google Scholar] [CrossRef]
- Oh, C.S.; Sher, E.F.; Bieber, A.K. Melanoma in Pregnancy. Semin. Perinatol. 2025, 49, 152040. [Google Scholar] [CrossRef]
- Mirsalari, H.; Maleki, A.; Raissi, H.; Soltanabadi, A. Investigation of the Pristine and Functionalized Carbon Nanotubes as a Delivery System for the Anticancer Drug Dacarbazine: Drug Encapsulation. J. Pharm. Sci. 2021, 110, 2005–2016. [Google Scholar] [CrossRef]
- Hou, W.; Zou, Y.; Li, J.; Jiang, H.; Li, J.; Wu, J.; Zhu, S.; Ding, Y.; Xu, H.; Jia, F.; et al. Synergistic Therapy of Melanoma by Co-Delivery of Dacarbazine and Ferroptosis-Inducing Ursolic Acid Using Biomimetic Nanoparticles. ACS Omega 2024, 9, 41532–41543. [Google Scholar] [CrossRef]
- Rihackova, E.; Rihacek, M.; Vyskocilova, M.; Valik, D.; Elbl, L. Revisiting Treatment-Related Cardiotoxicity in Patients with Malignant Lymphoma—A Review and Prospects for the Future. Front. Cardiovasc. Med. 2023, 10, 1243531. [Google Scholar] [CrossRef]
- Zayac, A.S.; Egini, O.; Palmisiano, N.D.; Evens, A.M. Lymphoma and Leukemia Occurring during Pregnancy. Semin. Perinatol. 2025, 49, 152041. [Google Scholar] [CrossRef]
- Gao, T.; He, X.; Wang, J.; Liu, J.; Hu, X.; Bai, C.; Yin, S.; Shi, Y.; Wang, Y.; Tan, Z.; et al. Self-Assembled Patient-Derived Tumor-like Cell Clusters for Personalized Drug Testing in Diverse Sarcomas. Cell Rep. Med. 2025, 6, 101990. [Google Scholar] [CrossRef] [PubMed]
- Berclaz, L.M.; Di Gioia, D.; Jurinovic, V.; Völkl, M.; Güler, S.E.; Albertsmeier, M.; Klein, A.; Dürr, H.R.; Mansoorian, S.; Knösel, T.; et al. LDH and Hemoglobin Outperform Systemic Inflammatory Indices as Prognostic Factors in Patients with Soft Tissue Sarcoma Undergoing Neoadjuvant Treatment. BMC Cancer 2025, 25, 496. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Ma, J.; Zhou, Y.; Ying, X.; Liang, G.; Pi, G.; Li, Y.; Luo, Y.; Bi, J.; He, H.; et al. Efficacy and Safety of Ondansetron Orally Soluble Pellicle for Preventing Moderate- to High-Emetic Risk Chemotherapy-Induced Nausea and Vomiting. BMC Cancer 2025, 25, 16. [Google Scholar] [CrossRef]
- Gowda, N.; Ravichandran, M.; Indrajithu, J.; Paninathan, T.; Dubashi, B.; Kayal, S.; Ganesan, P. Addition of Thalidomide for Prevention of Chemotherapy-Induced Nausea and Vomiting in the Second Cycle after the Failure of Four-Drug Regimen in the First Cycle. Med. Oncol. 2025, 42, 121. [Google Scholar] [CrossRef] [PubMed]
- Ding, B.; Li, M.; Zhang, J.; Zhang, X.; Gao, H.; Gao, J.; Shen, C.; Zhou, Y.; Li, F.; Liu, A. Co-Delivery of Dacarbazine and MiRNA 34a Combinations to Synergistically Improve Malignant Melanoma Treatments. Drug Des. Dev. Ther. 2025, 19, 553–568. [Google Scholar] [CrossRef]
- Tiwari, P.; Shukla, R.P.; Yadav, K.; Singh, N.; Marwaha, D.; Gautam, S.; Bakshi, A.K.; Rai, N.; Kumar, A.; Sharma, D.; et al. Dacarbazine-Primed Carbon Quantum Dots Coated with Breast Cancer Cell-Derived Exosomes for Improved Breast Cancer Therapy. J. Control. Release 2024, 365, 43–59. [Google Scholar] [CrossRef]
- Shankar, R.; Radhika, R.; Thangamani, D.; Senthil Kumar, L.; Kolandaivel, P. Theoretical Studies on Interaction of Anticancer Drugs (Dacarbazine, Procarbazine and Triethylenemelamine) with Normal (AT and GC) and Mismatch (GG, CC, AA and TT) Base Pairs. Mol. Simul. 2015, 41, 633–652. [Google Scholar] [CrossRef]
- Parmar, K.; Patel, H. Dacarbazine-Loaded Lipid Polymer Hybrid Nanoparticles for Management of Skin Melanoma: Optimization and Anticancer Studies. Bionanoscience 2024, 14, 4360–4368. [Google Scholar] [CrossRef]
- Bi, Y.; Li, L.; Liu, J.; Wang, Y.; Wang, B.; Wang, Y.; Snow, C.D.; Li, J.; Kipper, M.J.; Belfiore, L.A.; et al. Smart Cancer-Targeting and Super-Sensitive Sensing of Eu3+/Tb3+-Induced Hyaluronan Characteristic Nano-Micelles with Effective Drug Loading and Release. Molecules 2024, 29, 5070. [Google Scholar] [CrossRef]
- Moyers-Montoya, E.D.; Escobedo-González, R.G.; Vargas-Requena, C.L.; Garcia-Casillas, P.E.; Martínez-Pérez, C.A. Epithelial Growth Factor-Anchored on Polycaprolactone/6-Deoxy-6-Amino-β-Cyclodextrin Nanofibers: In Vitro and In Vivo Evaluation. Polymers 2021, 13, 1303. [Google Scholar] [CrossRef]
- Escobedo-González, R.G.; Moyers-Montoya, E.D.; Martínez-Pérez, C.A.; García-Casillas, P.E.; Miranda-Ruvalcaba, R.; Nicolás-Vázquez, M.I.N. In Silico Study of Novel Cyclodextrin Inclusion Complexes of Polycaprolactone and Its Correlation with Skin Regeneration. Int. J. Mol. Sci. 2023, 24, 8932. [Google Scholar] [CrossRef] [PubMed]
- Hoelm, M.; Porwański, S.; Jóźwiak, P.; Krześlak, A. Combined Theoretical and Experimental Investigations: Design, Synthesis, Characterization, and In Vitro Cytotoxic Activity Assessment of a Complex of a Novel Ureacellobiose Drug Carrier with the Anticancer Drug Carmustine. Molecules 2024, 29, 3359. [Google Scholar] [CrossRef] [PubMed]
- Jeffrey, G.A. An Introduction to Hydrogen Bonding; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Gunasekaran, S.; Kumaresan, S.; Arunbalaji, R.; Anand, G.; Srinivasan, S. Density Functional Theory Study of Vibrational Spectra, and Assignment of Fundamental Modes of Dacarbazine. J. Chem. Sci. 2008, 120, 315–324. [Google Scholar] [CrossRef]
- Al-Otaibi, J.S.; Mary, Y.S.; Mary, Y.S.; Ullah, Z.; Yadav, R.; Gupta, N.; Churchill, D.G. Adsorption Properties of Dacarbazine with Graphene/Fullerene/Metal Nanocages—Reactivity, Spectroscopic and SERS Analysis. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2022, 268, 120677. [Google Scholar] [CrossRef]
- Świderski, G.; Łaźny, R.; Sienkiewicz, M.; Kalinowska, M.; Świsłocka, R.; Acar, A.O.; Golonko, A.; Matejczyk, M.; Lewandowski, W. Synthesis, Spectroscopic, and Theoretical Study of Copper and Cobalt Complexes with Dacarbazine. Materials 2021, 14, 3274. [Google Scholar] [CrossRef]
- Kinart, Z.; Tomaš, R. Studies of the Formation of Inclusion Complexes Derivatives of Cinnamon Acid with α-Cyclodextrin in a Wide Range of Temperatures Using Conductometric Methods. Molecules 2022, 27, 4420. [Google Scholar] [CrossRef]
- Salomon, M.; Hefter, G.T. Mobilities of Cation-Macrocyclic Ligand Complexes. Pure Appl. Chem. 1993, 65, 1533–1540. [Google Scholar] [CrossRef][Green Version]
- Salomon, M. Conductometric Study of Cationic and Anionic Complexes in Propylene Carbonate. J. Solut. Chem. 1990, 19, 1225–1236. [Google Scholar] [CrossRef]
- HyperChem(TM), Professional 8.0; Hypercube, Inc.: Gainesville, FL, USA, 2008.
- Freeman, H.C.; Hutchinson, N.D. The Crystal Structure of the Anti-Tumor Agent 5-(3,3-Dimethyl-1-Triazenyl)Imidazole-4-Carboxamide (NSC-45388). Acta Crystallogr. B 1979, 35, 2051–2054. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Case, D.A.; Singh, U.C.; Ghio, C.; Alagona, G.; Profeta, S.; Weiner, P. A New Force Field for Molecular Mechanical Simulation of Nucleic Acids and Proteins. J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Nguyen, D.T.; Case, D.A. An All Atom Force Field for Simulations of Proteins and Nucleic Acids. J. Comput. Chem. 1986, 7, 230–252. [Google Scholar] [CrossRef] [PubMed]
- Hoelm, M.; Porwański, S.; Jóźwiak, P.; Krześlak, A. Theoretical Analysis, Synthesis and Biological Activity against Normal and Cancer Cells of a Complex Formed by a Novel Sugar Cryptand and Anticancer Drug Mitomycin C. Carbohydr. Res. 2025, 551, 109425. [Google Scholar] [CrossRef]
- Hoelm, M.; Chowdhury, N.; Biswas, S.; Bagchi, A.; Małecka, M. Theoretical Investigations on Free Energy of Binding Cilostazol with Different Cyclodextrins as Complex for Selective PDE3 Inhibition. Molecules 2024, 29, 3824. [Google Scholar] [CrossRef] [PubMed]
- Pocrnić, M.; Hoelm, M.; Ignaczak, A.; Čikoš, A.; Budimir, A.; Tomišić, V.; Galić, N. Inclusion Complexes of Loratadine with β-Cyclodextrin and Its Derivatives in Solution. Integrated Spectroscopic, Thermodynamic and Computational Studies. J. Mol. Liq. 2024, 410, 125515. [Google Scholar] [CrossRef]
- Adamiak, M.; Ignaczak, A. Quantum Chemical Study of the Complexation Process of Bis-β-d-Glucopyranosyl Diazacrown Derivative with Aspirin and Paracetamol Molecules. Comput. Theor. Chem. 2019, 1167, 112591. [Google Scholar] [CrossRef]
- Řezáč, J.; Hobza, P. Advanced Corrections of Hydrogen Bonding and Dispersion for Semiempirical Quantum Mechanical Methods. J. Chem. Theory Comput. 2012, 8, 141–151. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of Parameters for Semiempirical Methods VI: More Modifications to the NDDO Approximations and Re-Optimization of Parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Stewart Computational Chemistry; MOPAC2016; MOLSIS Inc.: Colorado Springs, CO, USA, 2016; Available online: http://openmopac.net/ (accessed on 22 May 2025).
- Klamt, A.; Schüürmann, G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc., Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.02 2016; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* Basis Set for Third-row Atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. DSD-PBEP86: In Search of the Best Double-Hybrid DFT with Spin-Component Scaled MP2 and Dispersion Corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104. [Google Scholar] [CrossRef] [PubMed]
- Kozuch, S.; Martin, J.M.L. Spin-component-scaled Double Hybrids: An Extensive Search for the Best Fifth-rung Functionals Blending DFT and Perturbation Theory. J. Comput. Chem. 2013, 34, 2327–2344. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements? J. Chem. Theory Comput. 2016, 12, 4303–4325. [Google Scholar] [CrossRef]
- Luchini, G.; Alegre-Requena, J.V.; Funes-Ardoiz, I.; Paton, R.S. GoodVibes: Automated Thermochemistry for Heterogeneous Computational Chemistry Data. F1000Research 2020, 9, 291. [Google Scholar] [CrossRef]
- Klar, B.; Hingerty, B.; Saenger, W. Topography of Cyclodextrin Inclusion Complexes. XII. Hydrogen Bonding in the Crystal Structure of α-Cyclodextrin Hexahydrate: The Use of a Multicounter Detector in Neutron Diffraction. Acta Crystallogr. B 1980, 36, 1154–1165. [Google Scholar] [CrossRef]
- Steiner, T.; Koellner, G. Crystalline.Beta.-Cyclodextrin Hydrate at Various Humidities: Fast, Continuous, and Reversible Dehydration Studied by X-Ray Diffraction. J. Am. Chem. Soc. 1994, 116, 5122–5128. [Google Scholar] [CrossRef]
- Kerdpol, K.; Kicuntod, J.; Wolschann, P.; Mori, S.; Rungnim, C.; Kunaseth, M.; Okumura, H.; Kungwan, N.; Rungrotmongkol, T. Cavity Closure of 2-Hydroxypropyl-β-Cyclodextrin: Replica Exchange Molecular Dynamics Simulations. Polymers 2019, 11, 145. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Boruń, A.; Bald, A. Ionic Association and Conductance of Ionic Liquids in Dichloromethane at Temperatures from 278.15 to 303.15 K. Ionics 2016, 22, 859–867. [Google Scholar] [CrossRef]
- Kinart, Z.; Tomaš, R. Conductometric Study of Potassium Chloride in Ethylene Glycol + Water Mixtures at Different Temperatures. Int. J. Electrochem. Sci. 2020, 15, 5560–5570. [Google Scholar] [CrossRef]
- Bald, A.; Kinart, Z. Conductance Studies of NaCl, KCl, NaBr, KBr, NaI, Bu4NI, and NaBPh4 in Water + 2-Propoxyethanol Mixtures at 298.15 K. Ionics 2015, 21, 2781–2787. [Google Scholar] [CrossRef]
- Kinart, Z. Conductance Studies of Sodium Salts of Some Aliphatic Carboxylic Acids in Water at Different Temperatures. J. Mol. Liq. 2017, 248, 1059–1064. [Google Scholar] [CrossRef]
- Comminges, C.; Barhdadi, R.; Laurent, M.; Troupel, M. Determination of Viscosity, Ionic Conductivity, and Diffusion Coefficients in Some Binary Systems: Ionic Liquids + Molecular Solvents. J. Chem. Eng. Data 2006, 51, 680–685. [Google Scholar] [CrossRef]
- Barthel, J.; Feuerlein, F.; Neueder, R.; Wachter, R. Calibration of Conductance Cells at Various Temperatures. J. Solut. Chem. 1980, 9, 209–219. [Google Scholar] [CrossRef]
- Bešter-Rogač, M.; Hunger, J.; Stoppa, A.; Buchner, R. 1-Ethyl-3-Methylimidazolium Ethylsulfate in Water, Acetonitrile, and Dichloromethane: Molar Conductivities and Association Constants. J. Chem. Eng. Data 2011, 56, 1261–1267. [Google Scholar] [CrossRef]
- Bešter-Rogač, M.; Habe, D. Modern Advances in Electrical Conductivity Measurements of Solutions. Acta Chim. Slov. 2006, 53, 391–395. [Google Scholar]


| Molecule | CPCM | SMD | Onsager |
|---|---|---|---|
| α-CD:DTIC | |||
| K02_03 | 0.00236 | 0.04637 | 0.05331 |
| K01_01 | 0.00417 | 0.04407 | 0.03490 |
| K03_03 | 0.00302 | 0.01402 | 0.01769 |
| HP-β-CD:DTIC | |||
| K03_03 | 0.00433 | 0.46008 | 0.08733 |
| K04_03 | 0.00899 | 0.64110 | 0.15543 |
| K04_01 | 0.00670 | 0.33926 | 0.27704 |
| HE-β-CD:DTIC | |||
| K04_01 | 0.00674 | 0.93252 | 0.10769 |
| K03_02 | 0.00422 | 0.44491 | 0.31047 |
| K03_03 | 0.02785 | 0.60237 | 0.78544 |
| 293.15 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α-CD:DTIC | ΔH PCM | ΔH CPCM | ΔH SMD | ΔH Onsager | ΔH EXP | ΔG PCM | ΔG CPCM | ΔG SMD | ΔG Onsager | ΔG EXP |
| K01_01 | −94.38 | −93.65 | −92.68 | −127.44 | −91.32 | −18.27 | −17.98 | −15.01 | −50.49 | -17.85 |
| K03_03 | −92.22 | −91.75 | −92.41 | −96.74 | −17.17 | −16.95 | −18.46 | −22.39 | ||
| 298.15 | ||||||||||
| K01_01 | −94.41 | −93.68 | −92.68 | −127.45 | −94.72 | −17.02 | −16.74 | −13.77 | −49.23 | −20.11 |
| K03_03 | −92.21 | −91.75 | −92.38 | −96.72 | −15.95 | −15.73 | −17.26 | −21.18 | ||
| 303.15 | ||||||||||
| K01_01 | −94.44 | −83.79 | −92.68 | −127.45 | −101.52 | −15.77 | −16.57 | −12.53 | −47.99 | −22.87 |
| K03_03 | −92.20 | −91.74 | −92.34 | −96.70 | −14.72 | −14.51 | −16.07 | −19.97 | ||
| 308.15 | ||||||||||
| K01_01 | −94.42 | −93.74 | −92.67 | −127.39 | −113.65 | −14.54 | −14.26 | −11.30 | −45.66 | −17.42 |
| K03_03 | −92.16 | −91.73 | −92.30 | −96.68 | −13.51 | −13.29 | −14.88 | −18.76 | ||
| 313.15 | ||||||||||
| K01_01 | −94.49 | −95.51 | −92.67 | −127.46 | −121.23 | −13.28 | −12.28 | −10.07 | −45.49 | −14.23 |
| K03_03 | −92.13 | −91.72 | −92.27 | −96.66 | −12.88 | −12.06 | −13.69 | −17.55 | ||
| 293.15 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HP-β-CD:DTIC | ΔH PCM | ΔH CPCM | ΔH SMD | ΔH Onsager | ΔH EXP | ΔG PCM | ΔG CPCM | ΔG SMD | ΔG Onsager | ΔG EXP |
| K04_01 | −82.89 | −82.75 | −82.53 | −118.53 | −104.62 | −3.86 | −4.72 | 6.16 | −34.05 | −18.51 |
| K04_03 | −92.88 | −92.72 | −109.50 | −119.03 | −16.49 | −16.05 | −27.31 | −41.87 | ||
| 298.15 | ||||||||||
| K04_01 | −82.93 | −82.82 | −82.57 | −118.57 | −109.12 | −2.59 | −3.01 | 7.54 | −32.71 | −15.27 |
| K04_03 | −92.91 | −92.76 | −109.54 | −119.06 | −15.22 | −15.75 | −25.97 | −40.61 | ||
| 303.15 | ||||||||||
| K04_01 | −82.97 | −82.86 | −82.61 | −112.98 | −113.67 | −1.31 | −1.74 | 8.92 | −29.73 | −12.36 |
| K04_03 | −92.94 | −92.80 | −109.58 | −113.45 | −13.95 | −14.49 | −24.63 | −37.70 | ||
| 308.15 | ||||||||||
| K04_01 | −83.01 | −82.90 | −82.64 | −118.63 | −118.02 | −0.04 | −0.80 | 10.31 | −30.03 | −9.06 |
| K04_03 | −92.97 | −92.83 | −109.61 | −119.09 | −12.69 | −13.25 | −23.28 | −38.07 | ||
| 313.15 | ||||||||||
| K04_01 | −83.04 | −82.93 | −82.68 | −118.66 | −121.51 | 1.23 | 0.79 | 11.69 | −28.68 | −5.91 |
| K04_03 | −93.00 | −92.85 | −109.65 | −119.10 | −11.42 | −11.98 | −21.94 | −36.80 | ||
| 293.15 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HE-β-CD:DTIC | ΔH PCM | ΔH CPCM | ΔH SMD | ΔH Onsager | ΔH EXP | ΔG PCM | ΔG CPCM | ΔG SMD | ΔG Onsager | ΔG EXP |
| K03_02 | −149.55 | −149.66 | −169.32 | −196.69 | −156.20 | −60.99 | −60.92 | −75.34 | −105.44 | −15.49 |
| K03_03 | −149.19 | −148.66 | −156.29 | −155.99 | −61.27 | −59.47 | −62.91 | −68.11 | ||
| 298.15 | ||||||||||
| K03_02 | −149.64 | −149.75 | −169.43 | −196.78 | −149.50 | −59.56 | −59.50 | −73.84 | −103.98 | −13.25 |
| K03_03 | −149.28 | −148.76 | −156.37 | −156.06 | −59.86 | −58.05 | −61.42 | −66.70 | ||
| 303.15 | ||||||||||
| K03_02 | −149.72 | −149.83 | −169.54 | −196.86 | −133.60 | −58.13 | −58.07 | −72.35 | −102.53 | −11.43 |
| K03_03 | −149.37 | −148.86 | −156.46 | −156.13 | −58.45 | −56.62 | −59.94 | −65.30 | ||
| 308.15 | ||||||||||
| K03_02 | −148.16 | −151.56 | −169.64 | −196.94 | −127.50 | −54.43 | −58.92 | −70.85 | −101.07 | −9.79 |
| K03_03 | −147.82 | −150.59 | −156.54 | −156.19 | −54.76 | −57.47 | −58.46 | −63.89 | ||
| 313.15 | ||||||||||
| K03_02 | −149.88 | −149.99 | −169.74 | −196.20 | −116.80 | −55.28 | −55.21 | −69.36 | −100.58 | −8.45 |
| K03_03 | −149.55 | −149.03 | −156.62 | −156.25 | −55.63 | −53.76 | −56.98 | −62.27 | ||
| α-CD | HE-β-CD | |||||||
|---|---|---|---|---|---|---|---|---|
| T [K] | Kf [dm3/mol] | lnKf [dm3/mol] | ΛCD(DTIC) [S∙cm2/mol−1] | σ(Λ) | Kf [dm3/mol] | lnKf [dm3/mol] | ΛCD(DTIC) [S∙cm2/mol−1] | σ(Λ) |
| 293.15 | 1516 ± 3 | 7.3238 | 58,76 ± 0.01 | 0.01 | 575 ± 6 | 6.3547 | 61.04 ± 0.02 | 0.01 |
| 298.15 | 3337 ± 2 | 8.1127 | 65.55± 0.01 | 0.02 | 209 ± 4 | 5.3433 | 67.83 ± 0.01 | 0.02 |
| 303.15 | 8726 ± 4 | 9.0740 | 70.65 ± 0.01 | 0.01 | 93 ± 2 | 4.5345 | 72.93 ± 0.01 | 0.01 |
| 308.15 | 897 ± 5 | 6.7995 | 79.88 ± 0.02 | 0.02 | 46 ± 1 | 3.8200 | 82.16 ± 0.02 | 0.01 |
| 313.15 | 236 ± 2 | 5.4657 | 85.87 ± 0.02 | 0.02 | 26 ± 1 | 3.2456 | 88.15 ± 0.01 | 0.02 |
| HP-β-CD | ||||||||
| T [K] | Kf [dm3/mol] | lnKf [dm3/mol] | ΛCD(DTIC) [S∙cm2/mol−1] | σ(Λ) | ||||
| 293.15 | 1907 ± 7 | 7.5536 | 64.86 ± 0.02 | 0.01 | ||||
| 298.15 | 473 ± 5 | 6.1602 | 67.83 ± 0.02 | 0.01 | ||||
| 303.15 | 135 ± 4 | 4.9040 | 72.93 ± 0.01 | 0.01 | ||||
| 308.15 | 34 ± 2 | 3.5442 | 82.16 ± 0.02 | 0.02 | ||||
| 313.15 | 9.7 ± 2 | 2.2700 | 88.15 ± 0.01 | 0.01 | ||||
| Chemical Name | Chemical Formula | Source | CAS Number | Purity | Molecular Mass [g/mol] |
|---|---|---|---|---|---|
| DTIC | C6H10N6O | Merck | 4342-03-4 | ≥0.999 | 182.18 |
| α-CD | C36H60O30 | TCL | 10016-20-3 | ≥0.998 | 972.84 |
| HP-β-CD | C42H70O35·(C3H7O)n | Merck | 128446-35-5 | ≥0.998 | 1396.00 * |
| HE-β-CD | C42H70O35·(C3H7O)4 | Merck | 128446-32-2 | ≥0.998 | 1315.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinart, Z.; Hoelm, M.; Imińska, M. Evaluating Theoretical Solvent Models for Thermodynamic and Structural Descriptions of Dacarbazine–Cyclodextrin Complexes. The Theoretical and Conductometric Study. Molecules 2025, 30, 2309. https://doi.org/10.3390/molecules30112309
Kinart Z, Hoelm M, Imińska M. Evaluating Theoretical Solvent Models for Thermodynamic and Structural Descriptions of Dacarbazine–Cyclodextrin Complexes. The Theoretical and Conductometric Study. Molecules. 2025; 30(11):2309. https://doi.org/10.3390/molecules30112309
Chicago/Turabian StyleKinart, Zdzisław, Marta Hoelm, and Martyna Imińska. 2025. "Evaluating Theoretical Solvent Models for Thermodynamic and Structural Descriptions of Dacarbazine–Cyclodextrin Complexes. The Theoretical and Conductometric Study" Molecules 30, no. 11: 2309. https://doi.org/10.3390/molecules30112309
APA StyleKinart, Z., Hoelm, M., & Imińska, M. (2025). Evaluating Theoretical Solvent Models for Thermodynamic and Structural Descriptions of Dacarbazine–Cyclodextrin Complexes. The Theoretical and Conductometric Study. Molecules, 30(11), 2309. https://doi.org/10.3390/molecules30112309






