Crystal Phase Ionic Liquids for Energy Applications: Heat Capacity Prediction via a Hybrid Group Contribution Approach
Abstract
1. Introduction
2. Results
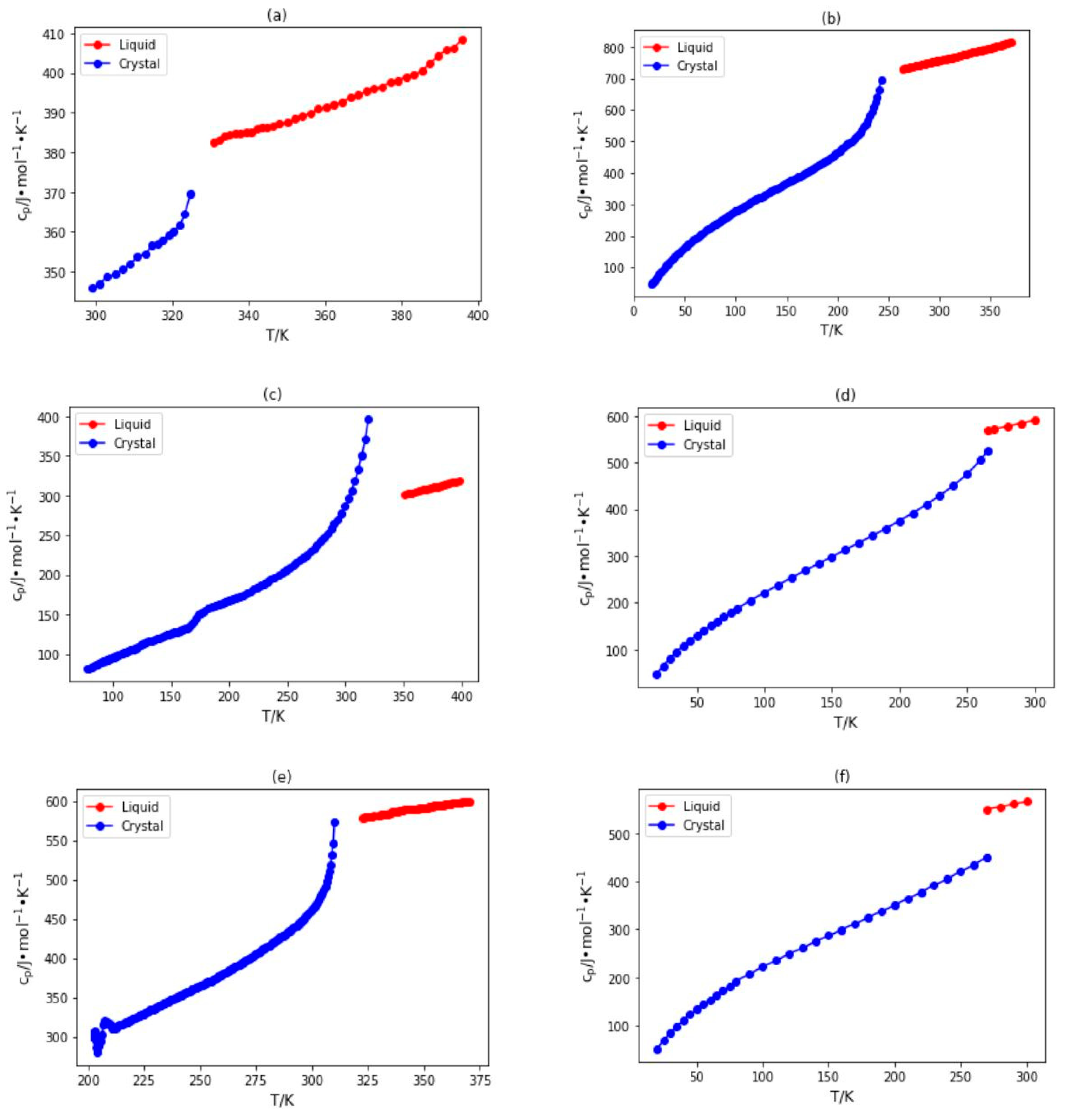
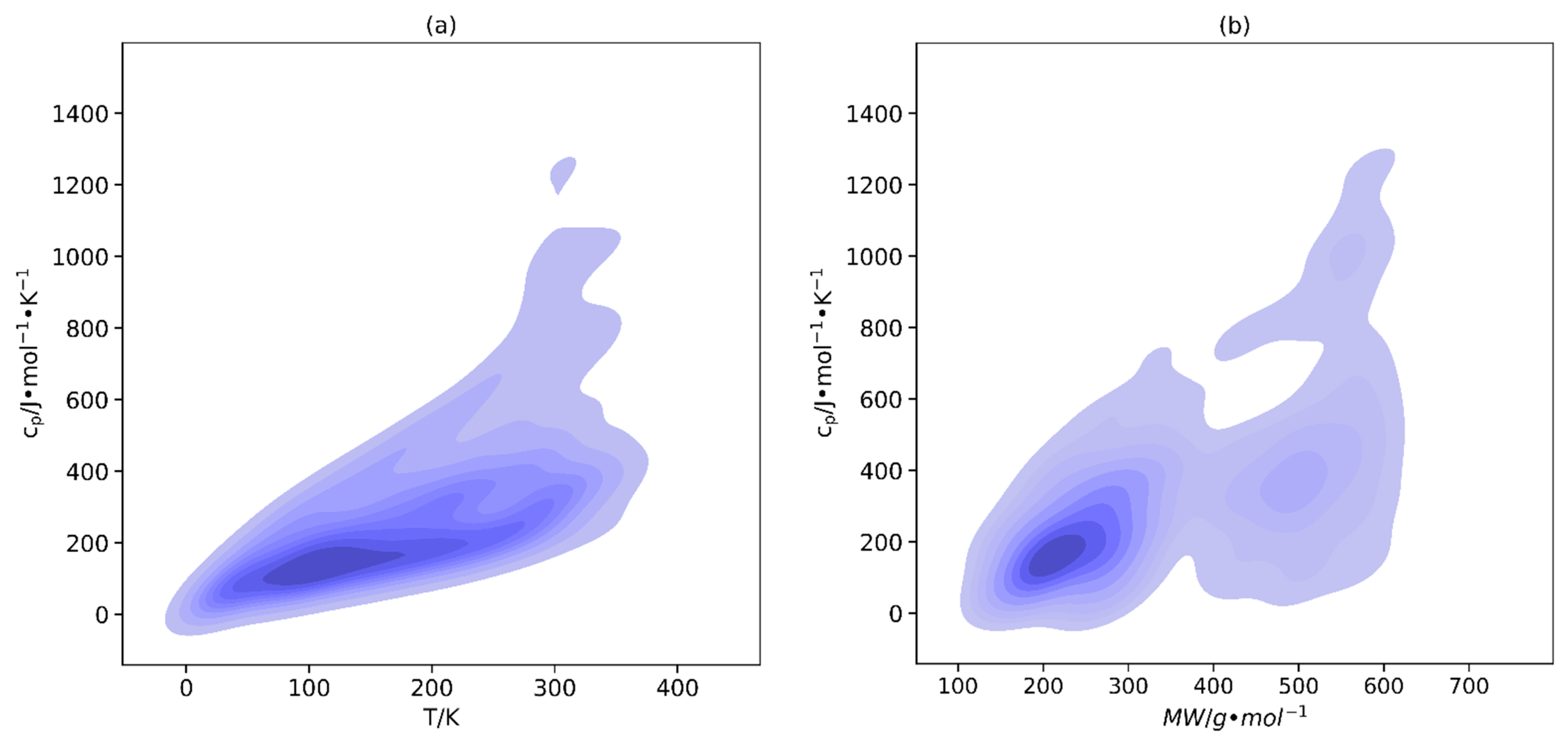
2.1. Database Development and Data Analysis
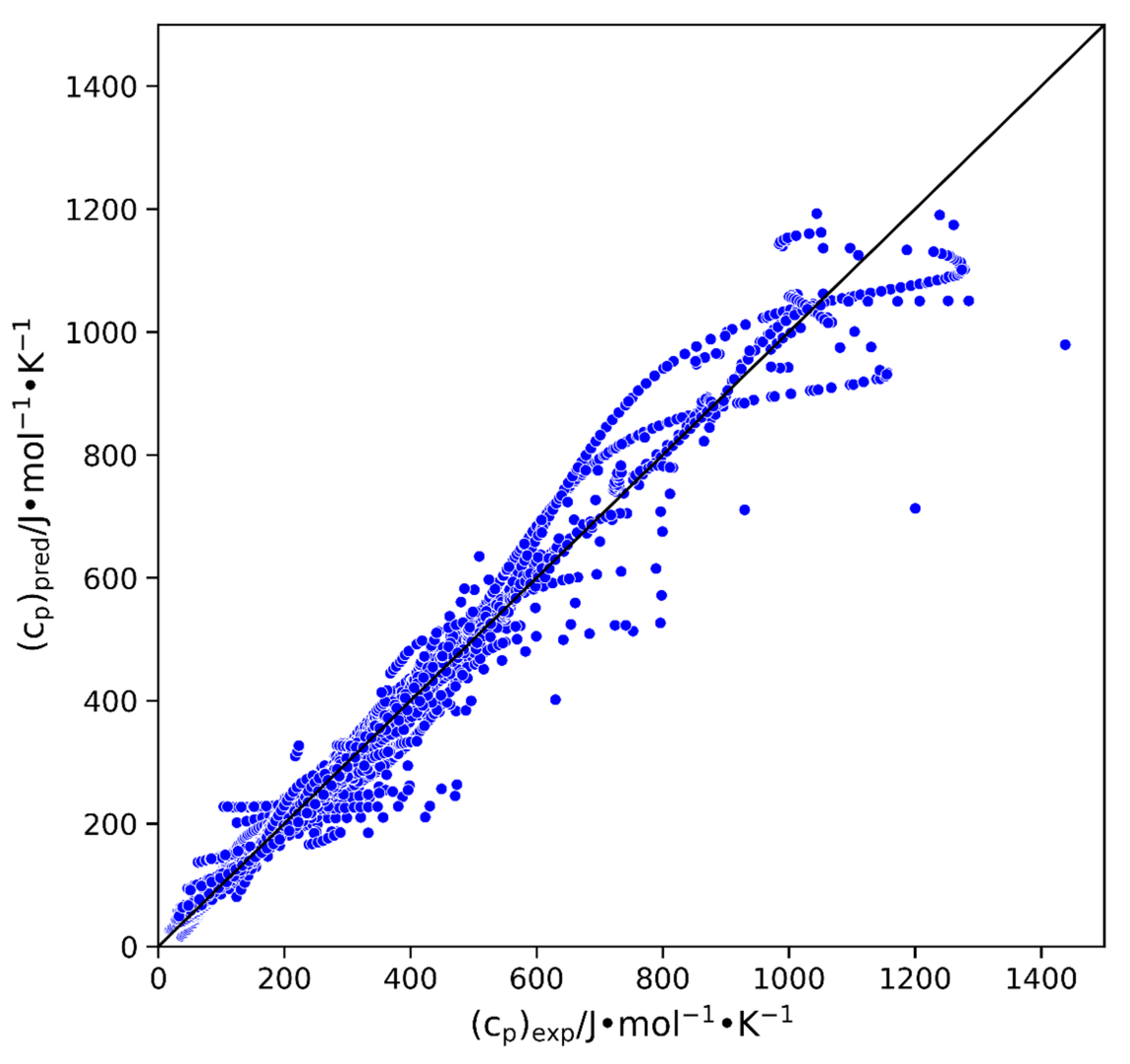
2.2. Model Development
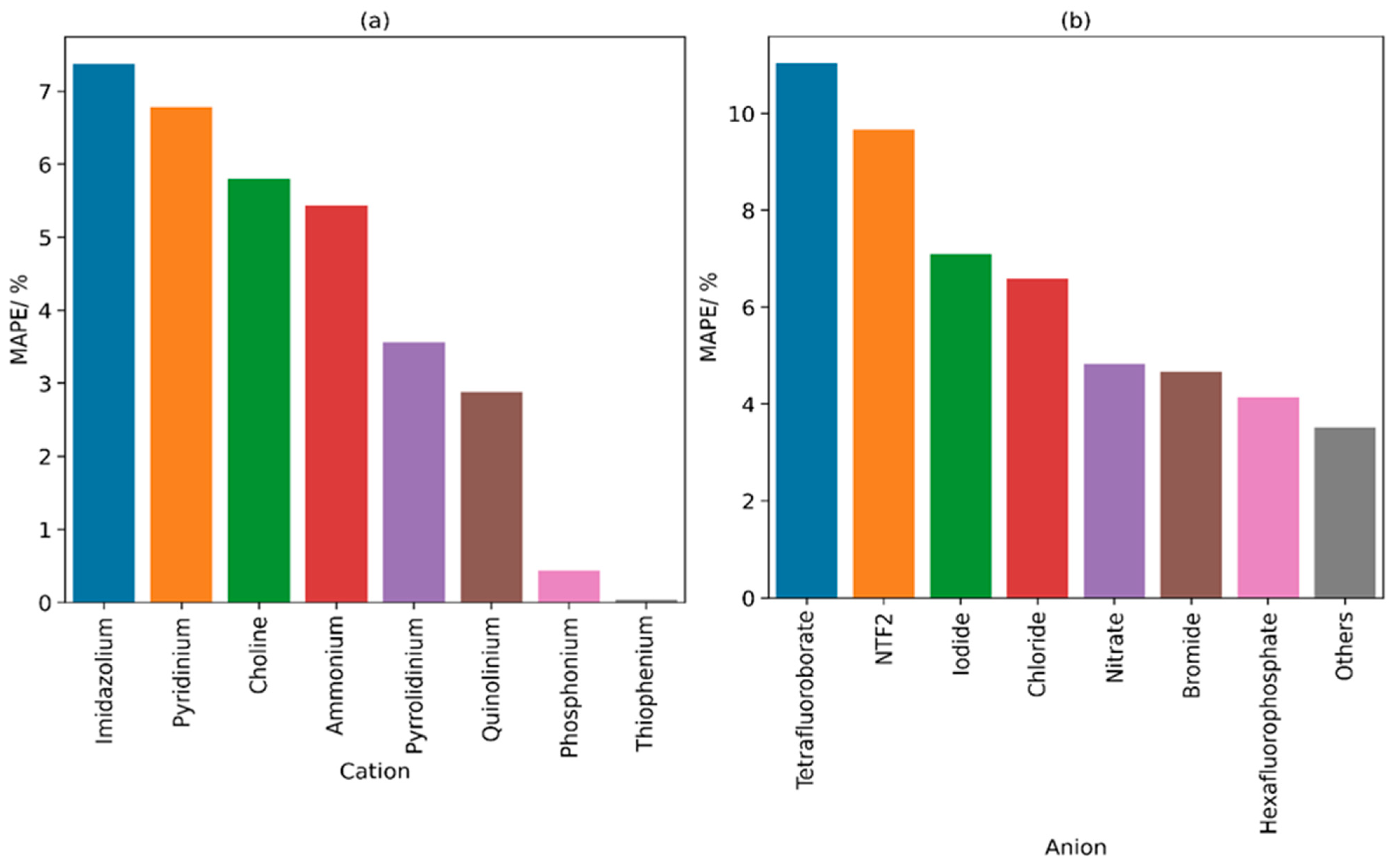
3. Discussion
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hayes, R.; Warr, G.G.; Atkin, R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [CrossRef]
- Mital, D.; Liaqat, S.; Nancarrow, P.; Ibrahim, T.; Jabbar, N.A.; Khamis, M. Thermal Conductivities of NTf2-Based Ionic Liquids: Experimental Measurement and Prediction via Group Contribution Methods. J. Chem. Eng. Data 2022, 67, 2136–2148. [Google Scholar] [CrossRef]
- Earle, M.J.; Seddon, K.R. Ionic Liquids. Green Solvents for the Future. Pure Appl. Chem. 2000, 72, 1391–1398. [Google Scholar] [CrossRef]
- Norani, N.; Mehrdad, A. Improving Performance of Mesoporous MOF AlTp Impregnated with Ionic Liquids for CO2 Adsorption. Sci. Rep. 2023, 13, 3227. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K. Solubility of Lignin and Chitin in Ionic Liquids and Their Biomedical Applications. Int. J. Biol. Macromol. 2019, 132, 265–277. [Google Scholar] [CrossRef] [PubMed]
- Ghandi, K.; Ghandi, K. A Review of Ionic Liquids, Their Limits and Applications. Green Sustain. Chem. 2014, 4, 44–53. [Google Scholar] [CrossRef]
- Kaur, G.; Kumar, H.; Singla, M. Diverse Applications of Ionic Liquids: A Comprehensive Review. J. Mol. Liq. 2022, 351, 118556. [Google Scholar] [CrossRef]
- Mohammed, H.; Al-Othman, A.; Nancarrow, P.; Elsayed, Y.; Tawalbeh, M. Enhanced Proton Conduction in Zirconium Phosphate/Ionic Liquids Materials for High-Temperature Fuel Cells. Int. J. Hydrog. Energy 2021, 46, 4857–4869. [Google Scholar] [CrossRef]
- Nancarrow, P.; Al-Othman, A.; Mital, D.K.; Döpking, S. Comprehensive Analysis and Correlation of Ionic Liquid Conductivity Data for Energy Applications. Energy 2021, 220, 119761. [Google Scholar] [CrossRef]
- Greer, A.J.; Jacquemin, J.; Hardacre, C. Industrial Applications of Ionic Liquids. Molecules 2020, 25, 5207. [Google Scholar] [CrossRef]
- Toledo Hijo, A.A.C.; Maximo, G.J.; Costa, M.C.; Batista, E.A.C.; Meirelles, A.J.A. Applications of Ionic Liquids in the Food and Bioproducts Industries. ACS Sustain. Chem. Eng. 2016, 4, 5347–5369. [Google Scholar] [CrossRef]
- Gutowski, K.E. Industrial Uses and Applications of Ionic Liquids. Phys. Sci. Rev. 2018, 3, 191–201. [Google Scholar] [CrossRef]
- Wishart, J.F. Energy Applications of Ionic Liquids. Energy Environ. Sci. 2009, 2, 956–961. [Google Scholar] [CrossRef]
- Fumino, K.; Peppel, T.; Geppert-Rybczyńska, M.; Zaitsau, D.H.; Lehmann, J.K.; Verevkin, S.P.; Köckerling, M.; Ludwig, R. The Influence of Hydrogen Bonding on the Physical Properties of Ionic Liquids. Phys. Chem. Chem. Phys. 2011, 13, 14064–14075. [Google Scholar] [CrossRef] [PubMed]
- Letcher, T.; Wilhelm, E.; Hakin, A.; Stohner, J.; Tremaine, P.; Hansen, L.D.; Raal, D.; Grolier, J.P.; Henni, A.; Wormald, C.; et al. Heat Capacities: Liquids, Solutions and Vapours. Chem. Int. 2010, 33, 480. [Google Scholar]
- Dong, K.; Zhang, S. Hydrogen Bonds: A Structural Insight into Ionic Liquids. Chem. Eur. J. 2012, 18, 2748–2761. [Google Scholar] [CrossRef] [PubMed]
- Gardas, R.L.; Coutinho, J.A.P. A Group Contribution Method for Heat Capacity Estimation of Ionic Liquids. Ind. Eng. Chem. Res. 2008, 47, 5751–5757. [Google Scholar] [CrossRef]
- Farahani, N.; Gharagheizi, F.; Mirkhani, S.A.; Tumba, K. A Simple Correlation for Prediction of Heat Capacities of Ionic Liquids. Fluid. Phase Equilib. 2013, 337, 73–82. [Google Scholar] [CrossRef]
- Rogers, R.D. Reflections on Ionic Liquids. Nature 2007, 447, 917–918. [Google Scholar] [CrossRef]
- Niedermeyer, H.; Hallett, J.P.; Villar-Garcia, I.J.; Hunt, P.A.; Welton, T. Mixtures of Ionic Liquids. Chem. Soc. Rev. 2012, 41, 7780–7802. [Google Scholar] [CrossRef]
- Holbrey, J.D.; Seddon, K.R. Ionic Liquids; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1. [Google Scholar]
- Chatel, G.; Pereira, J.F.B.; Debbeti, V.; Wang, H.; Rogers, R.D. Mixing Ionic Liquids—“Simple Mixtures” or “Double Salts”? Green Chem. 2014, 16, 2051–2083. [Google Scholar] [CrossRef]
- Sharma, R.; Mahajan, R.K. Influence of Various Additives on the Physicochemical Properties of Imidazolium Based Ionic Liquids: A Comprehensive Review. RSC Adv. 2013, 4, 748–774. [Google Scholar] [CrossRef]
- Lui, M.Y.; Crowhurst, L.; Hallett, J.P.; Hunt, P.A.; Niedermeyer, H.; Welton, T. Salts Dissolved in Salts: Ionic Liquid Mixtures. Chem. Sci. 2011, 2, 1491–1496. [Google Scholar] [CrossRef]
- Rostami, A.; Hemmati-Sarapardeh, A.; Karkevandi-Talkhooncheh, A.; Husein, M.M.; Shamshirband, S.; Rabczuk, T. Modeling Heat Capacity of Ionic Liquids Using Group Method of Data Handling: A Hybrid and Structure-Based Approach. Int. J. Heat Mass Transf. 2019, 129, 7–17. [Google Scholar] [CrossRef]
- Gani, R. Group Contribution-Based Property Estimation Methods: Advances and Perspectives. Curr. Opin. Chem. Eng. 2019, 23, 184–196. [Google Scholar] [CrossRef]
- Mital, D.K.; Nancarrow, P.; Zeinab, S.; Jabbar, N.A.; Ibrahim, T.H.; Khamis, M.I.; Taha, A. Group Contribution Estimation of Ionic Liquid Melting Points: Critical Evaluation and Refinement of Existing Models. Molecules 2021, 26, 2454. [Google Scholar] [CrossRef]
- Weis, D.C.; MacFarlane, D.R. Computer-Aided Molecular Design of Ionic Liquids: An Overview. Aust. J. Chem. 2012, 65, 1478–1486. [Google Scholar] [CrossRef]
- Gardas, R.L.; Coutinho, J.A.P. Group Contribution Methods for the Prediction of Thermophysical and Transport Properties of Ionic Liquids. AIChE J. 2009, 55, 1274–1290. [Google Scholar] [CrossRef]
- Mital, D.K.; Nancarrow, P.; Ibrahim, T.H.; Abdel Jabbar, N.; Khamis, M.I. Ionic Liquid Melting Points: Structure-Property Analysis and New Hybrid Group Contribution Model. Ind. Eng. Chem. Res. 2022, 61, 4683–4706. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Toro, A.; Rojas, R.E. Prediction of the Heat Capacity of Ionic Liquids Using the Mass Connectivity Index and a Group Contribution Method. J. Chem. Thermodyn. 2011, 43, 1068–1073. [Google Scholar] [CrossRef]
- Ge, R.; Hardacre, C.; Jacquemin, J.; Nancarrow, P.; Rooney, D.W. Heat Capacities of Ionic Liquids as a Function of Temperature at 0.1 MPa. Measurement and Prediction. J. Chem. Eng. Data 2008, 53, 2148–2153. [Google Scholar] [CrossRef]
- Soriano, A.N.; Agapito, A.M.; Lagumbay, L.J.L.I.; Caparanga, A.R.; Li, M.H. A Simple Approach to Predict Molar Heat Capacity of Ionic Liquids Using Group-Additivity Method. J. Taiwan. Inst. Chem. Eng. 2010, 41, 307–314. [Google Scholar] [CrossRef]
- Azadfar, R.; Shaabanzadeh, M.; Hashemi-Moghaddam, H.; Mohammadi Nafchi, A. A New Simple Model to Calculate the Heat Capacity of Pure Ionic Liquids. Phys. Chem. Res. 2020, 8, 139–154. [Google Scholar] [CrossRef]
- Ahmadi, A.; Haghbakhsh, R.; Raeissi, S.; Hemmati, V. A Simple Group Contribution Correlation for the Prediction of Ionic Liquid Heat Capacities at Different Temperatures. Fluid Phase Equilib. 2015, 403, 95–103. [Google Scholar] [CrossRef]
- Nancarrow, P.; Lewis, M.; Abouchacra, L. Group Contribution Methods for Estimation of Ionic Liquid Heat Capacities: Critical Evaluation and Extension. Chem. Eng. Technol. 2015, 38, 632–644. [Google Scholar] [CrossRef]
- Waliszewski, D.; Stȩpniak, I.; Piekarski, H.; Lewandowski, A. Heat Capacities of Ionic Liquids and Their Heats of Solution in Molecular Liquids. Thermochim. Acta 2005, 433, 149–152. [Google Scholar] [CrossRef]
- Müller, K.; Albert, J. Contribution of the Individual Ions to the Heat Capacity of Ionic Liquids. Ind. Eng. Chem. Res. 2014, 53, 10343–10346. [Google Scholar] [CrossRef]
- Sattari, M.; Gharagheizi, F.; Ilani-Kashkouli, P.; Mohammadi, A.H.; Ramjugernath, D. Development of a Group Contribution Method for the Estimation of Heat Capacities of Ionic Liquids. J. Therm. Anal. Calorim. 2014, 115, 1863–1882. [Google Scholar] [CrossRef]
- He, W.; Yan, F.; Jia, Q.; Xia, S.; Wang, Q. Prediction of Ionic Liquids Heat Capacity at Variable Temperatures Based on the Norm Indexes. Fluid Phase Equilib. 2019, 500, 112260. [Google Scholar] [CrossRef]
- Barati-Harooni, A.; Najafi-Marghmaleki, A.; Mohammadi, A.H. Prediction of Heat Capacities of Ionic Liquids Using Chemical Structure Based Networks. J. Mol. Liq. 2017, 227, 324–332. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Martinez, G.; Faúndez, C.A. Heat Capacity of Ionic Liquids Using Artificial Neural Networks and the Concept of Mass Connectivity. Int. J. Thermophys. 2011, 32, 942–956. [Google Scholar] [CrossRef]
- Dai, Z.; Chen, Y.; Liu, C.; Lu, X.; Liu, Y.; Ji, X. Prediction and Verification of Heat Capacities for Pure Ionic Liquids. Chin. J. Chem. Eng. 2021, 31, 169–176. [Google Scholar] [CrossRef]
- Liaqat, S.; Shahin, M.B.; Nancarrow, P.; Zeinab, S.; Ibrahim, T.; Abdel Jabbar, N.; Khamis, M.; McCormack, S. Prediction of Liquid Phase Heat Capacity of Ionic Liquids: Comparison of Existing Methods and Development of New Hybrid Group Contribution Models. Ind. Eng. Chem. Res. 2023, 62, 16093–16112. [Google Scholar] [CrossRef]
- Lazzús, J.A. A Group Contribution Method to Predict the Melting Point of Ionic Liquids. Fluid Phase Equilib. 2012, 313, 1–6. [Google Scholar] [CrossRef]
- Dong, Q.; Muzny, C.D.; Kazakov, A.; Diky, V.; Magee, J.W.; Widegren, J.A.; Chirico, R.D.; Marsh, K.N.; Frenkel, M. ILThermo: A Free-Access Web Database for Thermodynamic Properties of Ionic Liquids. J. Chem. Eng. Data 2007, 52, 1151–1159. [Google Scholar] [CrossRef]
- Paulechka, Y.U.; Blokhin, A.V. Low-Temperature Heat Capacity and Derived Thermodynamic Properties for 1-Methyl-3-Propylimidazolium Bromide and 1-Butyl-3-Methylimidazolium Iodide. J. Chem. Thermodyn. 2014, 79, 94–99. [Google Scholar] [CrossRef]
- Paulechka, Y.U.; Kabo, G.J.; Blokhin, A.V.; Shaplov, A.S.; Lozinskaya, E.I.; Vygodskii, Y.S. Thermodynamic Properties of 1-Alkyl-3-Methylimidazolium Bromide Ionic Liquids. J. Chem. Thermodyn. 2007, 39, 158–166. [Google Scholar] [CrossRef]
- Paulechka, E.; Blokhin, A.V.; Rodrigues, A.S.M.C.; Rocha, M.A.A.; Santos, L.M.N.B.F. Thermodynamics of Long-Chain 1-Alkyl-3-Methylimidazolium Bis(Trifluoromethanesulfonyl)Imide Ionic Liquids. J. Chem. Thermodyn. 2016, 97, 331–340. [Google Scholar] [CrossRef]
- Paulechka, Y.U.; Blokhin, A.V.; Kabo, G.J. Evaluation of Thermodynamic Properties for Non-Crystallizable Ionic Liquids. Thermochim. Acta 2015, 604, 122–128. [Google Scholar] [CrossRef]
- Domańska, U.; Zawadzki, M.; Zwolińska, M. Thermophysical Properties and Phase Equilibria Study of the Binary Systems {N-Hexylquinolinium Bis(Trifluoromethylsulfonyl)Imide + Aromatic Hydrocarbons, or an Alcohol}. J. Chem. Thermodyn. 2011, 43, 775–781. [Google Scholar] [CrossRef]
- Van Oort, M.J.M.; White, M.A. Polymorphism in Dialkylammonium Chlorides. An Adiabatic Calorimetry Study. Berichte Bunsenges. Phys. Chem. 1988, 92, 168–176. [Google Scholar] [CrossRef]
- Paulechka, E.; Liavitskaya, T.; Blokhin, A.V. Calorimetric Study of Polymorphism in 1-Butyl-3-Methylimidazolium Hexafluorophosphate. J. Chem. Thermodyn. 2016, 102, 211–218. [Google Scholar] [CrossRef]
- Liu, Q.S.; Tan, Z.C.; Welz-Biermann, U.; Liu, X.X. Molar Heat Capacity and Thermodynamic Properties of N-Alklypyridinium Hexafluorophosphate Salts, [Cnpy][PF6] (n = 2, 3, 5). J. Chem. Thermodyn. 2014, 68, 82–89. [Google Scholar] [CrossRef]
- Hanaya, M.; Shibazaki, H.; Oguni, M.; Nemoto, T.; Ohashi, Y. Orientational Ordering/Disordering of Ions Accompanied by Phase Transitions in Pyridinium Tetrafluoroborate Crystal. J. Phys. Chem. Solids 2000, 61, 651–657. [Google Scholar] [CrossRef]
- Hanaya, M.; Ohta, N.; Oguni, M. Calorimetric Study of Phase Transitions in Pyridinium Iodide and Pyridinium Hexafluorophosphate Crystals. J. Phys. Chem. Solids 1993, 54, 263–269. [Google Scholar] [CrossRef]
- Tong, B.; Liu, Q.S.; Tan, Z.C.; Welz-Biermann, U. Thermochemistry of Alkyl Pyridinium Bromide Ionic Liquids: Calorimetric Measurements and Calculations. J. Phys. Chem. A 2010, 114, 3782–3787. [Google Scholar] [CrossRef] [PubMed]
- Yamamuro, O.; Minamimoto, Y.; Inamura, Y.; Hayashi, S.; Hamaguchi, H.O. Heat Capacity and Glass Transition of an Ionic Liquid 1-Butyl-3-Methylimidazolium Chloride. Chem. Phys. Lett. 2006, 423, 371–375. [Google Scholar] [CrossRef]
- Archer, D.G. Thermodynamic Properties of 1-Hexyl-3-Methylimidazolium Bis(Trifluoromethylsulfonyl)Imide; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2006.
- Shimizu, Y.; Ohte, Y.; Yamamura, Y.; Saito, K.; Atake, T. Low-Temperature Heat Capacity of Room-Temperature Ionic Liquid, 1-Hexyl-3-Methylimidazolium Bis(Trifluoromethylsulfonyl)Imide. J. Phys. Chem. B 2006, 110, 13970–13975. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.H.; Sun, L.X.; Tan, Z.C.; Xu, F.; Lv, X.C.; Zeng, J.L.; Sawada, Y. Thermodynamic Investigation of Room Temperature Ionic Liquid: Heat Capacity and Thermodynamic Functions of BPBF4. J. Therm. Anal. Calorim. 2006, 89, 289–294. [Google Scholar] [CrossRef]
- Paulechka, Y.U.; Blokhin, A.V.; Kabo, G.J.; Strechan, A.A. Thermodynamic Properties and Polymorphism of 1-Alkyl-3-Methylimidazolium Bis(Triflamides). J. Chem. Thermodyn. 2007, 39, 866–877. [Google Scholar] [CrossRef]
- Blokhin, A.V.; Paulechka, Y.U.; Kabo, G.J. Thermodynamic Properties of [C6mim][NTf2] in the Condensed State. J. Chem. Eng. Data 2006, 51, 1377–1388. [Google Scholar] [CrossRef]
- Manin, N.G.; Kustov, A.V.; Antonova, O.A. Heat Capacities of Crystalline Tetraalkylammonium Salts. Russ. J. Phys. Chem. A 2012, 86, 878–880. [Google Scholar] [CrossRef]
- Domańska, U.; Bogel-Łukasik, R. Physicochemical Properties and Solubility of Alkyl-(2-Hydroxyethyl)-Dimethylammonium Bromide. J. Phys. Chem. B 2005, 109, 12124–12132. [Google Scholar] [CrossRef] [PubMed]
- Strechan, A.A.; Paulechka, Y.U.; Blokhin, A.V.; Kabo, G.J. Low-Temperature Heat Capacity of Hydrophilic Ionic Liquids [BMIM][CF3COO] and [BMIM][CH3COO] and a Correlation Scheme for Estimation of Heat Capacity of Ionic Liquids. J. Chem. Thermodyn. 2008, 40, 632–639. [Google Scholar] [CrossRef]
- Blokhin, A.V.; Paulechka, Y.U.; Strechan, A.A.; Kabo, G.J. Physicochemical Properties, Structure, and Conformations of 1-Butyl-3-Methylimidazolium Bis(Trifluoromethanesulfonyl)Imide [C 4min]NTf2 Ionic Liquid. J. Phys. Chem. B 2008, 112, 4357–4364. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhao, L.; Ma, L.; Chu, J.; Wang, J.; Zang, Y. Hydroxyethyl Group Effect on Properties of Bis[(Trifluoromethyl)Sulfonyl]Imide-Type Ionic Liquids. J. Chem. Eng. Data 2020, 65, 4780–4789. [Google Scholar] [CrossRef]
- Strechan, A.A.; Paulechka, Y.U.; Kabo, A.G.; Blokhin, A.V.; Kabo, G.J. L-Butyl-3-Methylimidazolium Tosylate Ionic Liquid: Heat Capacity, Thermal Stability, and Phase Equilibrium of Its Binary Mixtures with Water and Caprolactam. J. Chem. Eng. Data 2007, 52, 1791–1799. [Google Scholar] [CrossRef]
- Serra, P.B.P.; Ribeiro, F.M.S.; Rocha, M.A.A.; Fulem, M.; Růžička, K.; Santos, L.M.N.B.F. Phase Behavior and Heat Capacities of the 1-Benzyl-3-Methylimidazolium Ionic Liquids. J. Chem. Thermodyn. 2016, 100, 124–130. [Google Scholar] [CrossRef]
- Paulechka, Y.U.; Kohut, S.V.; Blokhin, A.V.; Kabo, G.J. Thermodynamic Properties of 1-Butyl-3-Methylimidazolium Trifluoromethanesulfonate Ionic Liquid in the Condensed State. Thermochim. Acta 2010, 511, 119–123. [Google Scholar] [CrossRef]
- Zhu, J.; Bai, L.; Chen, B.; Fei, W. Thermodynamical Properties of Phase Change Materials Based on Ionic Liquids. Chem. Eng. J. 2009, 147, 58–62. [Google Scholar] [CrossRef]
- Lamas, A.; Brito, I.; Salazar, F.; Graber, T.A. Synthesis and Characterization of Physical, Thermal and Thermodynamic Properties of Ionic Liquids Based on [C12mim] and [N444H] Cations for Thermal Energy Storage. J. Mol. Liq. 2016, 224, 999–1007. [Google Scholar] [CrossRef]
- Parajó, J.J.; Villanueva, M.; Troncoso, J.; Salgado, J. Thermophysical Properties of Choline and Pyridinium Based Ionic Liquids as Advanced Materials for Energy Applications. J. Chem. Thermodyn. 2020, 141, 105947. [Google Scholar] [CrossRef]
- Štejfa, V.; Rohlíček, J.; Červinka, C. Phase Behaviour and Heat Capacities of Selected 1-Ethyl-3-Methylimidazolium-Based Ionic Liquids. J. Chem. Thermodyn. 2020, 142, 106020. [Google Scholar] [CrossRef]
- Serra, P.B.P.; Ribeiro, F.M.S.; Rocha, M.A.A.; Fulem, M.; Růžička, K.; Coutinho, J.A.P.; Santos, L.M.N.B.F. Solid-Liquid Equilibrium and Heat Capacity Trend in the Alkylimidazolium PF6 Series. J. Mol. Liq. 2017, 248, 678–687. [Google Scholar] [CrossRef]
- Luo, C.; Li, Y.; Chen, K.; Li, N.; Su, Q. Thermodynamic Properties and Corrosivity of a New Absorption Heat Pump Working Pair: Lithium Nitrate + 1-Butyl-3- Methylimidazolium Bromide + Water. Fluid Phase Equilib. 2017, 451, 25–39. [Google Scholar] [CrossRef]
- Monteiro, B.; Maria, L.; Cruz, A.; Carretas, J.M.; Marçalo, J.; Leal, J.P. Thermal Stability and Specific Heats of Coordinating Ionic Liquids. Thermochim. Acta 2020, 684, 178482. [Google Scholar] [CrossRef]
- Salgado, J.; Teijeira, T.; Parajó, J.J.; Fernández, J.; Troncoso, J. Isobaric Heat Capacity of Nanostructured Liquids with Potential Use as Lubricants. J. Chem. Thermodyn. 2018, 123, 107–116. [Google Scholar] [CrossRef]
- Strechan, A.A.; Kabo, A.G.; Paulechka, Y.U.; Blokhin, A.V.; Kabo, G.J.; Shaplov, A.S.; Lozinskaya, E.I. Thermochemical Properties of 1-Butyl-3-Methylimidazolium Nitrate. Thermochim. Acta 2008, 474, 25–31. [Google Scholar] [CrossRef]
- Yang, D.; Zhu, Y.; Liu, S.; Lv, H.; Luo, C. Thermodynamic Properties of a Ternary AHP Working Pair: Lithium Bromide + 1-Ethyl-3-Methylimidazolium Chloride + H2O. J. Chem. Eng. Data 2019, 64, 574–583. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Z.; Zhang, J.; Zhang, S.; Zhu, L.; Yang, J.; Zhang, X.; Deng, Y. Physicochemical Properties of Nitrile-Functionalized Ionic Liquids. J. Phys. Chem. B 2007, 111, 2864–2872. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, S.; Li, Z.; Li, J.; Chen, Z.; Wang, R.; Lu, L.; Deng, Y. Novel Cyclic Sulfonium-Based Ionic Liquids: Synthesis, Characterization, and Physicochemical Properties. Chem. Eur. J. 2009, 15, 765–778. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Ohte, Y.; Yamamura, Y.; Tsuzuki, S.; Saito, K. Comparative Study of Imidazolium- and Pyrrolidinium-Based Ionic Liquids: Thermodynamic Properties. J. Phys. Chem. B 2012, 116, 5406–5413. [Google Scholar] [CrossRef] [PubMed]
- Mckinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Waskom, M.L. Seaborn: Statistical Data Visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Xin, B.; Hao, J. Imidazolium-Based Ionic Liquids Grafted on Solid Surfaces. Chem. Soc. Rev. 2014, 43, 7171–7187. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Cao, Y.; Guo, Y.; Sun, T.; Sun, Y.; Ye, Q.; Li, J.; Peng, C. Measurement and Correlation of Density, Viscosity, and Surface Tension for Imidazolium Bromide Ionic Liquids [CnMIM]Br (n = 2, 3, 4) Aqueous Solutions. J. Chem. Eng. Data 2022, 67, 1350–1357. [Google Scholar] [CrossRef]
- Biller, H.; Strassner, T. Synthesis and Physical Properties of Tunable Aryl Alkyl Ionic Liquids (TAAILs) Comprising Imidazolium Cations Blocked with Methyl-, Propyl- and Phenyl-Groups at the C2 Position. Chem. Eur. J. 2023, 29, e202202795. [Google Scholar] [CrossRef] [PubMed]
- Crosthwaite, J.M.; Muldoon, M.J.; Dixon, J.K.; Anderson, J.L.; Brennecke, J.F. Phase Transition and Decomposition Temperatures, Heat Capacities and Viscosities of Pyridinium Ionic Liquids. J. Chem. Thermodyn. 2005, 37, 559–568. [Google Scholar] [CrossRef]
- Oster, K.; Jacquemin, J.; Hardacre, C.; Ribeiro, A.P.C.; Elsinawi, A. Further Development of the Predictive Models for Physical Properties of Pure Ionic Liquids: Thermal Conductivity and Heat Capacity. J. Chem. Thermodyn. 2018, 118, 1–15. [Google Scholar] [CrossRef]
- Fredlake, C.P.; Crosthwaite, J.M.; Hert, D.G.; Aki, S.N.V.K.; Brennecke, J.F. Thermophysical Properties of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2004, 49, 954–964. [Google Scholar] [CrossRef]
- Diedrichs, A.; Gmehling, J. Measurement of Heat Capacities of Ionic Liquids by Differential Scanning Calorimetry. Fluid Phase Equilib. 2006, 244, 68–77. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Analysis of the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) in Assessing Rounding Model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 324, 012049. [Google Scholar] [CrossRef]
- Yang, S.; Ren, J.; Li, Z. Learning of Neural Networks Based on Weighted Mean Squares Error Function. In Proceedings of the ISCID 2009—2009 International Symposium on Computational Intelligence and Design, Changsha, China, 12–14 December 2009; Volume 1, pp. 241–244. [Google Scholar] [CrossRef]
- Khair, U.; Fahmi, H.; Al Hakim, S.; Rahim, R. Forecasting Error Calculation with Mean Absolute Deviation and Mean Absolute Percentage Error. J. Phys. Conf. Ser. 2017, 930, 012002. [Google Scholar] [CrossRef]
- Piepho, H.P. A Coefficient of Determination (R2) for Generalized Linear Mixed Models. Biom. J. 2019, 61, 860–872. [Google Scholar] [CrossRef]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; Cournapeau, D.; Varoquaux, G.; Gramfort, A.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bisong, E. Building Machine Learning and Deep Learning Models on Google Cloud Platform; Apress: Berkeley, CA, USA, 2019. [Google Scholar] [CrossRef]



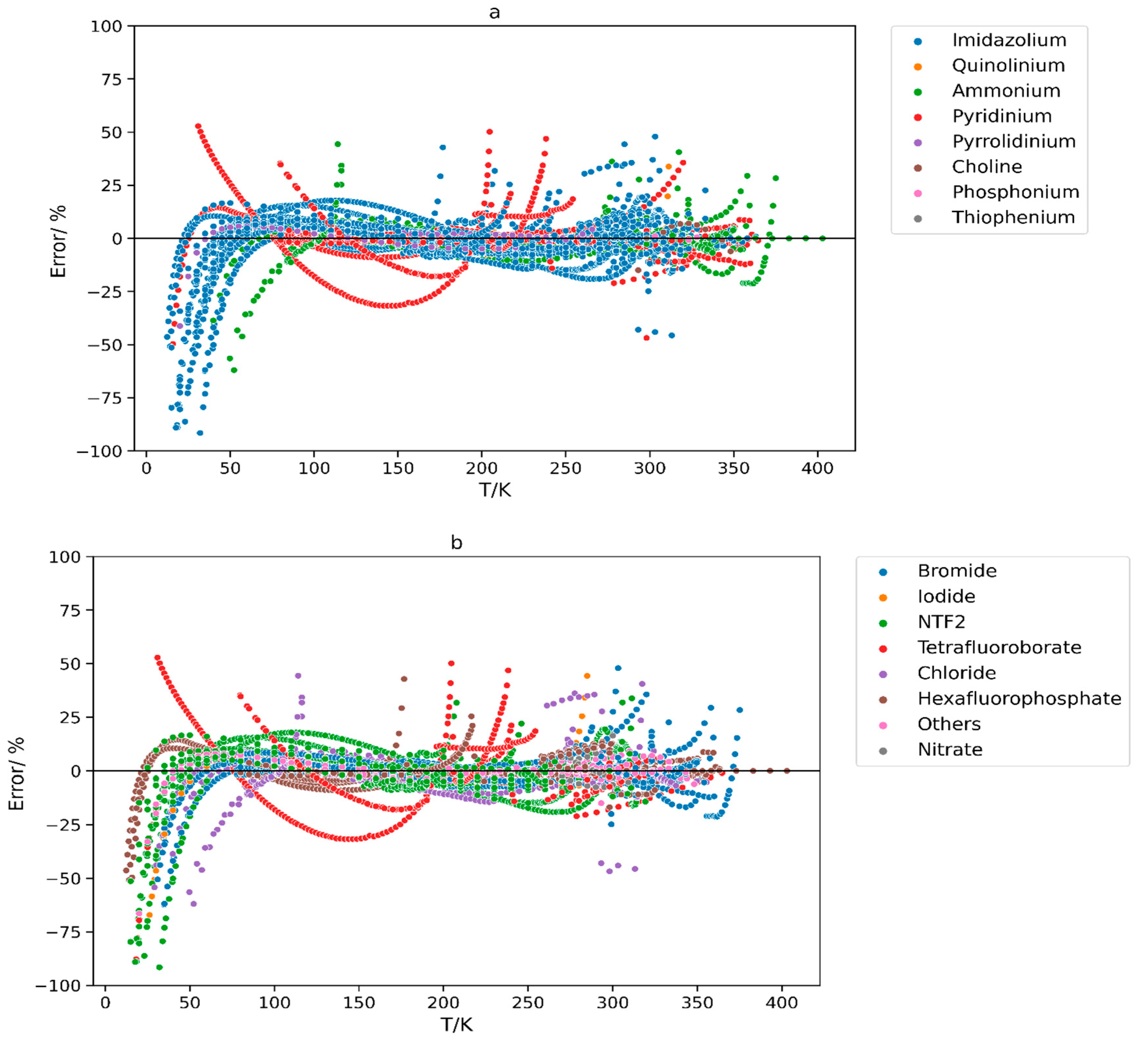

| Anion Type | Data Points | Reference |
|---|---|---|
| 1,1,2,2-tetrafluoroethanesulfonate | 20 | [70] |
| 2-methoxy-2-oxoacetate | 7 | [78] |
| 4-methylbenzenesulfonate | 18 | [74,75] |
| Dimethylphosphate | 5 | [75] |
| Tosylate | 50 | [69,74] |
| Trifluoroacetate | 30 | [66] |
| Trifluoromethanesulfonate | 38 | [71] |
| Tris(pentafluoroethyl)trifluorophosphate | 7 | [79] |
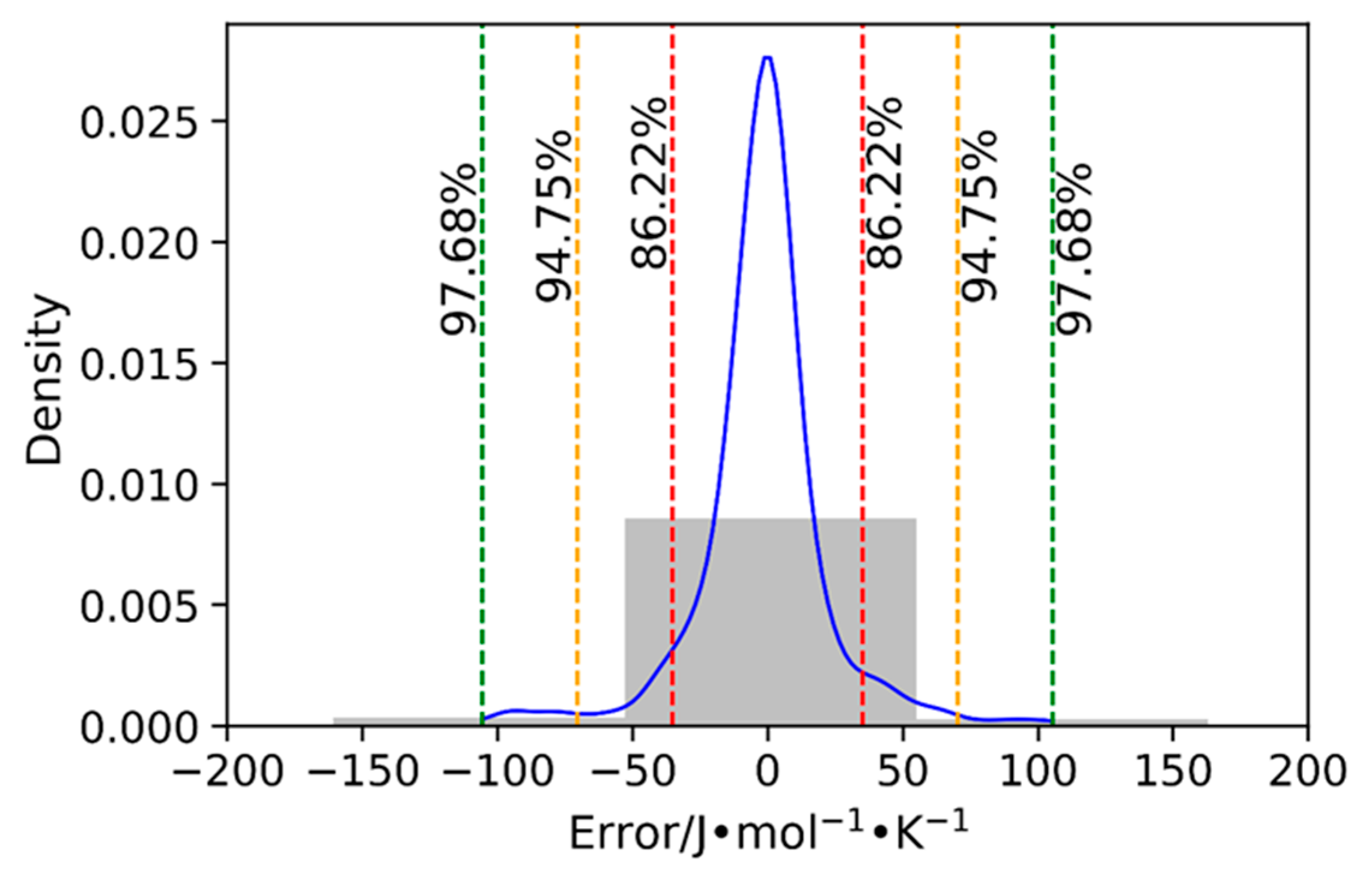
| Metric | Test Set | Overall |
|---|---|---|
| Ratio of Database (%) | 20 | 100 |
| MAPE (%) | 6.83 | 6.78 |
| R2 | 0.976 | 0.974 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahin, M.B.; Liaqat, S.; Nancarrow, P.; McCormack, S.J. Crystal Phase Ionic Liquids for Energy Applications: Heat Capacity Prediction via a Hybrid Group Contribution Approach. Molecules 2024, 29, 2130. https://doi.org/10.3390/molecules29092130
Shahin MB, Liaqat S, Nancarrow P, McCormack SJ. Crystal Phase Ionic Liquids for Energy Applications: Heat Capacity Prediction via a Hybrid Group Contribution Approach. Molecules. 2024; 29(9):2130. https://doi.org/10.3390/molecules29092130
Chicago/Turabian StyleShahin, Moh’d Basel, Shehzad Liaqat, Paul Nancarrow, and Sarah J. McCormack. 2024. "Crystal Phase Ionic Liquids for Energy Applications: Heat Capacity Prediction via a Hybrid Group Contribution Approach" Molecules 29, no. 9: 2130. https://doi.org/10.3390/molecules29092130
APA StyleShahin, M. B., Liaqat, S., Nancarrow, P., & McCormack, S. J. (2024). Crystal Phase Ionic Liquids for Energy Applications: Heat Capacity Prediction via a Hybrid Group Contribution Approach. Molecules, 29(9), 2130. https://doi.org/10.3390/molecules29092130







