Transport Properties of Protic Ionic Liquids Based on Triazolium and Imidazolium: Development of an Air-Free Conductivity Setup
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
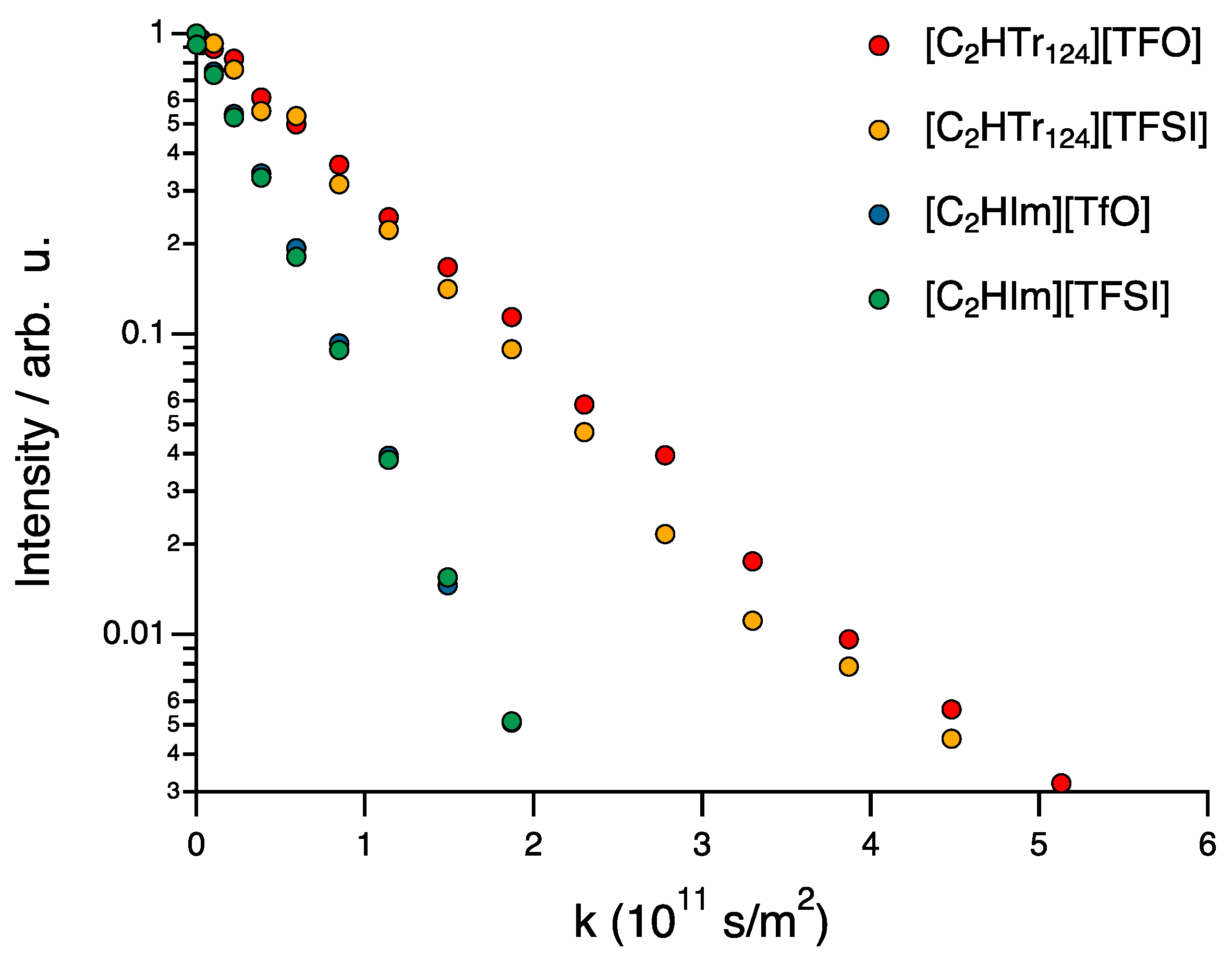
2.2. Pulsed-Field Gradient NMR Spectroscopy
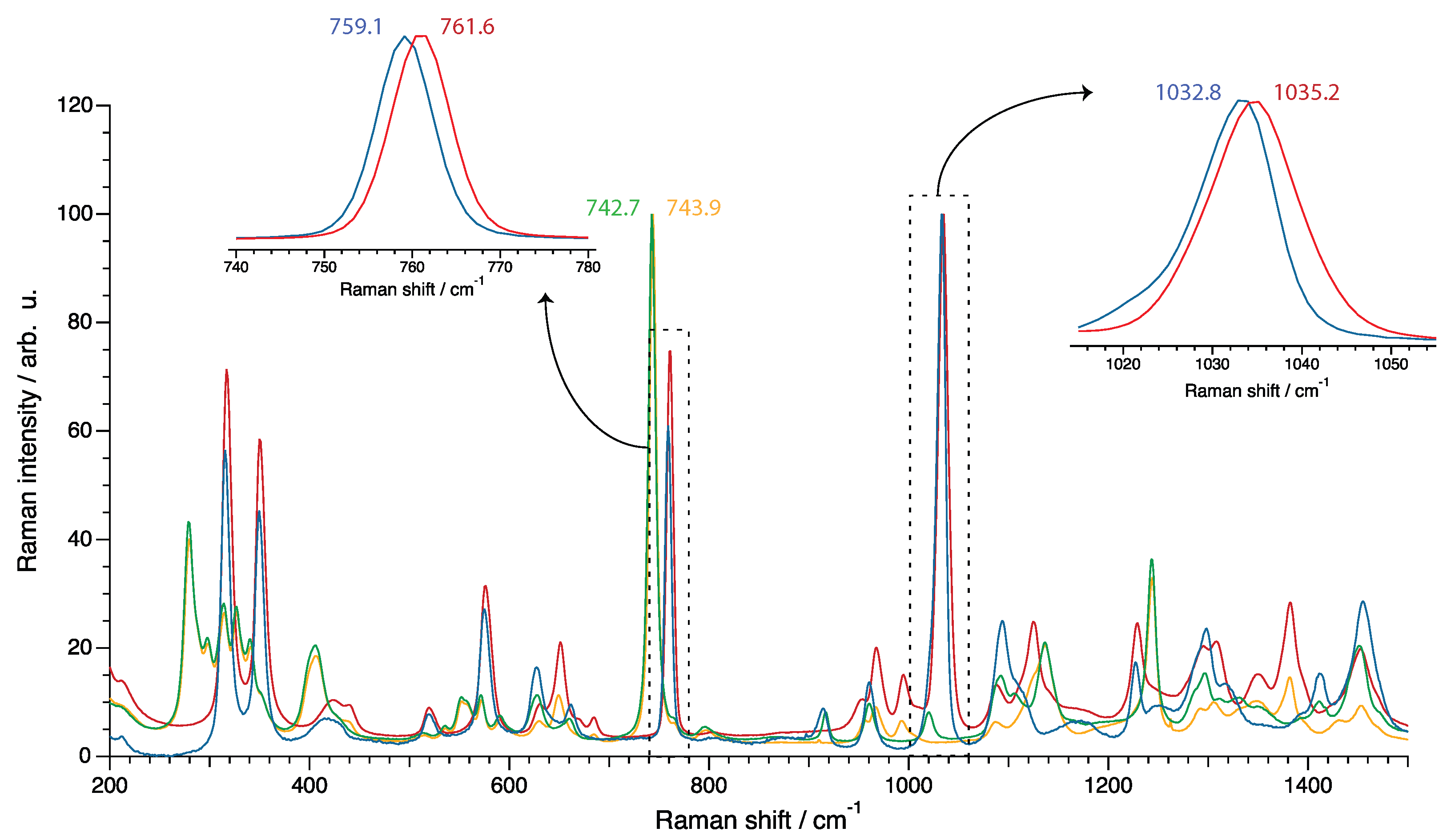
2.3. Vibrational Spectroscopy
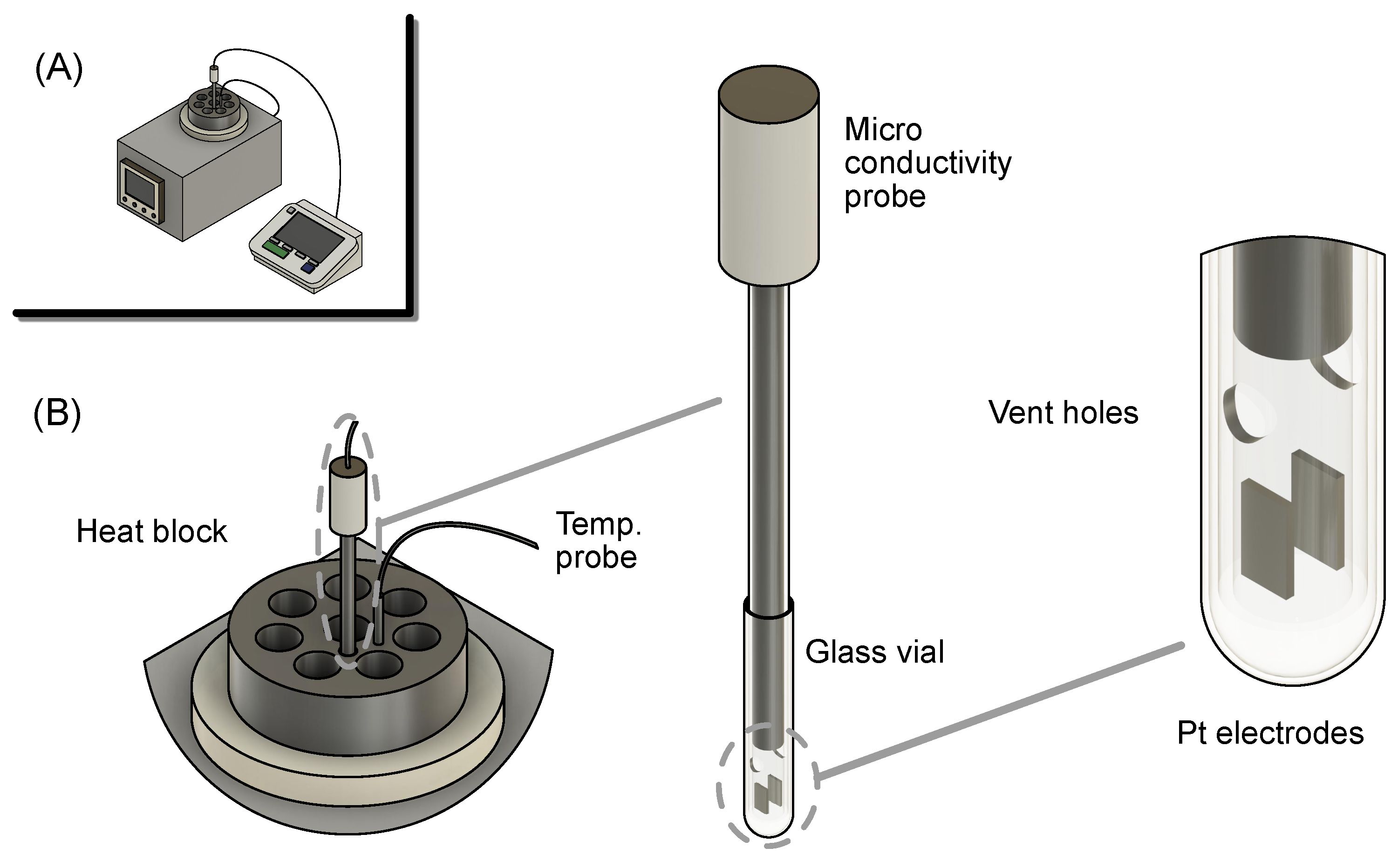
2.4. Ionic Conductivity
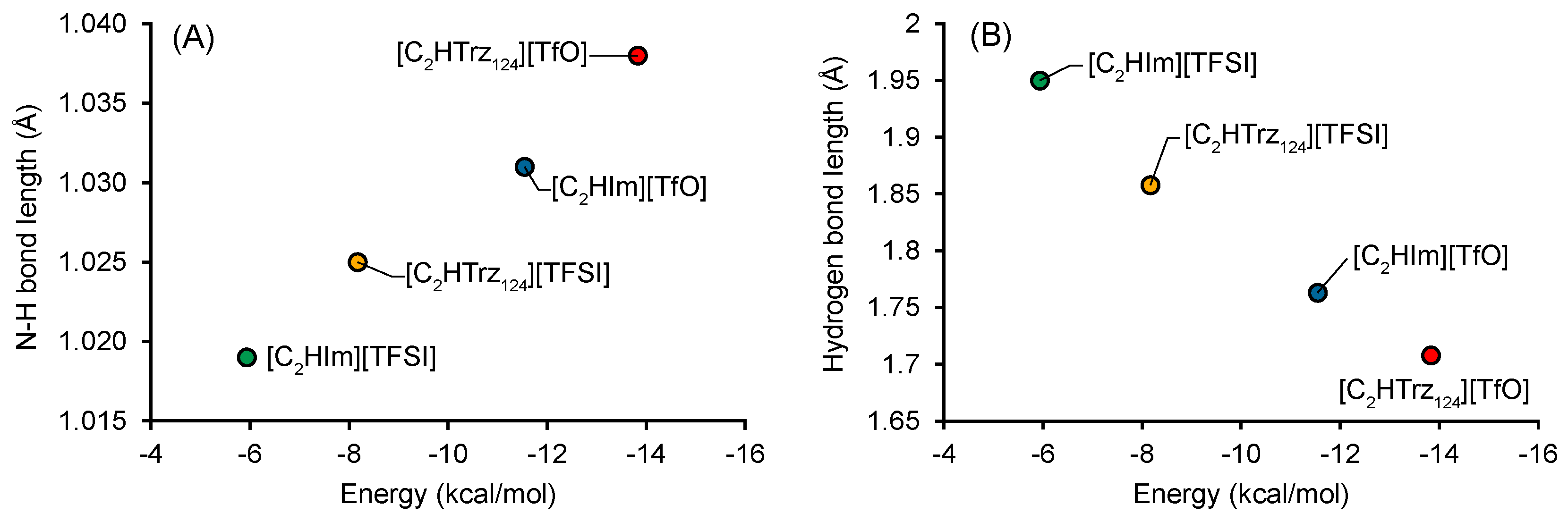
2.5. Computational Results
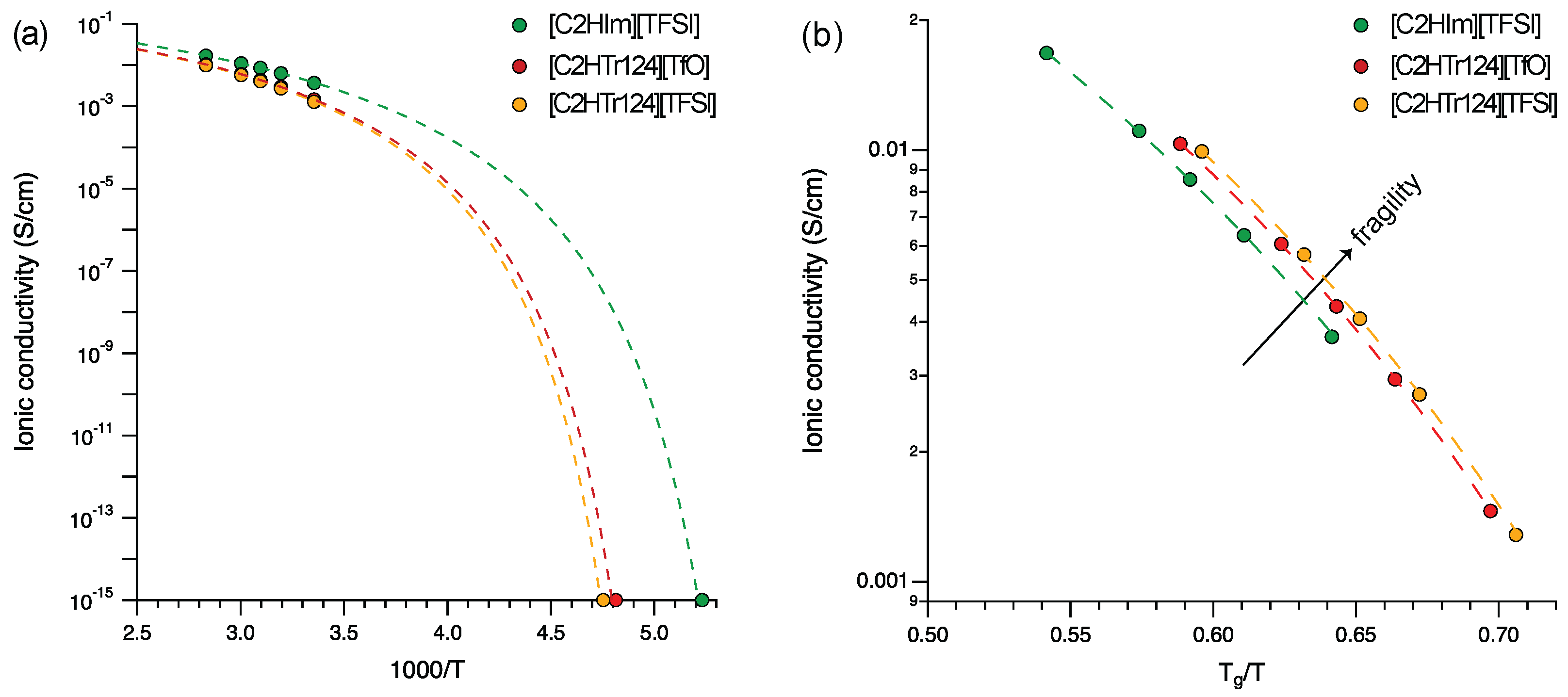
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walden, P.I. Ueber die Molekulargrosse und elektrische Leitfahigkeit einiger geschmolzenen Salze. Bull. De L’Académie Impériale Des Sci. De St.-Pétersbourg 1914, 8, 405–422. [Google Scholar]
- Armand, M.; Endres, F.; MacFarlane, D.R.; Ohno, H.; Scrosati, B. Ionic-liquid materials for the electrochemical challenges of the future. Nat. Mater. 2009, 8, 621–629. [Google Scholar] [CrossRef] [PubMed]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Noda, A.; Susan, M.A.B.H.; Kudo, K.; Mitsushima, S.; Hayamizu, K.; Watanabe, M. Brønsted Acid-Base Ionic Liquids as Proton-Conducting Nonaqueous Electrolytes. J. Phys. Chem. B 2003, 107, 4024–4033. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Ogawa, A.; Kanno, M.; Nakamoto, H.; Yasuda, T.; Watanabe, M. Nonhumidified intermediate temperature fuel cells using protic ionic liquids. J. Am. Chem. Soc. 2010, 132, 9764–9773. [Google Scholar] [CrossRef]
- Smitt, D.E.; Walsh, D.A. The nature of proton shuttling in protic ionic liquid fuel cells. Adv. Energy Mater. 2019, 9, 1900744. [Google Scholar] [CrossRef]
- East, A.L.L.; Nguyen, C.M.; Hempelmann, R. A 2023 update on the performance of ionic-liquid proton-exchange-membrane fuel cells. Front. Energy Res. 2023, 11, 1031458. [Google Scholar] [CrossRef]
- Ingenmey, J.; Gehrke, S.; Kirchner, B. How to Harvest Grotthuss Diffusion in Protic Ionic Liquid Electrolyte Systems. ChemSusChem 2018, 11, 1900. [Google Scholar] [CrossRef]
- Abdurrokhman, I.; Elamin, K.; Danyliv, O.; Hasani, M.; Swenson, J.; Martinelli, A. Protic Ionic Liquids Based on the Alkyl-Imidazolium Cation: Effect of the Alkyl Chain Length on Structure and Dynamics. J. Phys. Chem. B 2019, 123, 4044–4054. [Google Scholar] [CrossRef]
- Tsuzuki, S. Factors Controlling the Diffusion of Ions in Ionic Liquids. ChemPhysChem 2012, 13, 1664–1670. [Google Scholar] [CrossRef]
- Jannasch, P.; Rehmen, J.; Evans, D.; Karlsson, C. Charge Transport in Nonstoichiometric 2-Fluoropyridinium Triflate Protic Ionic Liquids. J. Phys. Chem. C 2019, 123, 23427–23432. [Google Scholar] [CrossRef]
- Abdurrokhman, I.; Martinelli, A. Binary Mixtures of Imidazolium-Based Protic Ionic Liquids. Extended Temperature Range of the Liquid State Keeping High Ionic Conductivities. Front. Chem. 2022, 10, 915683. [Google Scholar] [CrossRef]
- Berrod, Q.; Ferdeghini, F.; Judeinstein, P.; Genevaz, N.; Ramos, R.; Fournier, A.; Dijon, J.; Ollivier, J.; Rols, S.; Yu, D.; et al. Enhanced ionic liquid mobility induced by confinement in 1D CNT membranes. Nanoscale 2016, 8, 7845–7848. [Google Scholar] [CrossRef]
- Watanabe, H.; Arai, N.; Kameda, Y.; Buchner, R.; Umebayashi, Y. Effect of Brønsted Acidity on Ion Conduction in Fluorinated Acetic Acid and N-Methylimidazole Equimolar Mixtures as Pseudo-protic Ionic Liquids. J. Phys. Chem. B 2020, 124, 11157–11164. [Google Scholar] [CrossRef]
- Hasani, M.; Evenäs, L.; Martinelli, A. Molecular dynamics involving proton exchange of a protic ionic liquid–water mixture studied by NMR spectroscopy. Phys. Chem. Chem. Phys. 2019, 21, 22014–22021. [Google Scholar] [CrossRef]
- Yaghini, N.; Gomez-Gonzalez, V.; Varela, L.M.; Martinelli, A. Structural origin of proton mobility in a protic ionic liquid/imidazole mixture: Insights from computational and experimental results. Phys. Chem. Chem. Phys. 2016, 18, 23195–23206. [Google Scholar] [CrossRef]
- Garaga, M.N.; Dracopoulos, V.; Werner-Zwanziger, U.; Zwanziger, J.W.; Marechal, M.; Persson, M.; Nordstierna, L.; Martinelli, A. A long-chain protic ionic liquid inside silica nanopores: Enhanced proton mobility due to efficient self-assembly and decoupled proton transport. Nanoscale 2018, 10, 12337–12348. [Google Scholar] [CrossRef]
- Hoarfrost, M.L.; Tyagi, M.; Segelman, R.A.; Reimer, J.A. Proton Hopping and Long-Range Transport in the Protic Ionic Liquid [Im][TFSI], Probed by Pulsed-Field Gradient NMR and Quasi-Elastic Neutron Scattering. J. Phys. Chem. B 2012, 116, 8201–8209. [Google Scholar] [CrossRef]
- Belieres, J.-P.; Angell, C.A. Protic ionic liquids: Preparation, characterization, and proton free energy level representation. J. Phys. Chem. B 2007, 111, 4926–4937. [Google Scholar] [CrossRef]
- Morais, E.M.; Abdurrokhman, I.; Martinelli, A. Solvent-free synthesis of protic ionic liquids. Synthesis, characterization and computational studies of triazolium based ionic liquids. J. Molec. Liq. 2022, 360, 119358. [Google Scholar] [CrossRef]
- Luo, J.; Hu, J.; Saak, W.; Beckhaus, R.; Wittstock, G.; Vankelecom, I.; Agert, C.; Conrad, O. Protic ionic liquid and ionic melts prepared from methanesulfonic acid and 1H-1,2,4-triazole as high temperature PEMFC electrolytes. J. Mater. Chem. 2011, 21, 10426–10436. [Google Scholar] [CrossRef]
- Karlsson, C.; Strietzel, C.; Huang, H.; Sjödin, M.; Jannasch, P. Nonstoichiometric Triazolium Protic Ionic Liquids for All-Organic Batteries. ACS Appl. Energy Mater. 2018, 11, 6451–6462. [Google Scholar] [CrossRef]
- De La Hoz, A.; Brauer, U.; Miller, K. Physicochemical and Thermal Properties for a Series of 1-Alkyl-4-methyl-1,2,4-triazolium Bis(trifluoromethylsulfonyl)imide Ionic Liquids. J. Phys. Chem. B 2014, 118, 9944–9951. [Google Scholar] [CrossRef] [PubMed]
- Brehm, M.; Pulst, M.; Kressler, J.; Sebastiani, D. Triazolium-based ionic liquids: A novel class of cellulose solvents. J. Phys. Chem. B 2019, 123, 3994–4003. [Google Scholar] [CrossRef]
- Holz, M.; Weingartner, H. Calibration in accurate spin-echo self-diffusion measurements using 1H and less-common nuclei. Magn. Reson. 1969, 92, 115–125. [Google Scholar] [CrossRef]
- Stejskal, E.O. Use of Spin Echoes in a Pulsed Magnetic-Field Gradient to Study Anisotropic, Restricted Diffusion and Flow. J. Chem. Phys. 1965, 43, 3597–3603. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Accounts Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Huang, W.; Frech, R.; Wheeler, R.A. Molecular structures and normal vibrations of trifluoromethane sulfonate (CF3SO3-) and its lithium ion pairs and aggregates. J. Phys. Chem. 1994, 98, 100–110. [Google Scholar] [CrossRef]
- Arnaud, R.; Benrabah, D.; Sanchez, J.-Y. Theoretical Study of CF3SO3Li, (CF3SO2)2NLi, and (CF3SO2)2CHLi Ion Pairs. J. Phys. Chem. 1996, 26, 10882–10891. [Google Scholar] [CrossRef]
- Gejji, S.P.; Suresh, C.H.; Babu, K.; Gadre, S.R. Ab Initio Structure and Vibrational Frequencies of (CF3SO2)2N-Li+ Ion Pairs. J. Phys. Chem. A 1999, 103, 7474–7480. [Google Scholar] [CrossRef]
- Umebayashi, Y.; Yamaguchi, T.; Fukuda, S.; Mitsugi, T.; Takeuchi, M.; Fujii, K.; Ishiguro, S. Raman Spectroscopic Study on Alkaline Metal Ion Solvation in 1-Butyl-3-methylimidazolium Bis(trifluoromethanesulfonyl)amide Ionic Liquid. Anal. Sci. 2007, 24, 1297–1304. [Google Scholar] [CrossRef]
- Edman, L. Ion Association and Ion Solvation Effects at the Crystalline-Amorphous Phase Transition in PEO-LiTFSI. J. Phys. Chem. B 2000, 104, 7254–7258. [Google Scholar] [CrossRef]
- Castriota, M.; Caruso, T.; Agostino, R.G.; Cazzanelli, E.; Henderson, W.A.; Passerini, S. Raman Investigation of the Ionic Liquid N-Methyl-N-propylpyrrolidinium Bis(trifluoromethanesulfonyl)imide and Its Mixture with LiN(SO2CF3)2. J. Phys. Chem. A 2005, 109, 92–96. [Google Scholar] [CrossRef]
- Monteiro, M.J.; Bazito, F.F.C.; Siqueira, L.J.A.; Ribeiro, M.C.C.; Torresi, R.M. Transport Coefficients, Raman Spectroscopy, and Computer Simulation of Lithium Salt Solutions in an Ionic Liquid. J. Phys. Chem. B 2008, 112, 2102–2109. [Google Scholar] [CrossRef]
- Seo, D.M.; Borodin, O.; Han, S.-D.; Boyle, P.D.; Henderson, W.A. Electrolyte Solvation and Ionic Association II. Acetonitrile-Lithium Salt Mixtures: Highly Dissociated Salts. J. Electrochem. Soc. 2012, 159, A1489–A1500. [Google Scholar] [CrossRef]
- Mizuno, F.; Belieres, J.-P.; Kuwata, N.; Pradel, A.; Ribes, M.; Angell, C.A. Highly decoupled ionic and protonic solid electrolyte systems, in relation to other relaxing systems and their energy landscapes. J. Non-Cryst. Sol. 2006, 352, 5147–5155. [Google Scholar] [CrossRef]
- Angell, C.A. Recent developments in fast ion transport in glassy and amorphous materials. Solid State Ionics 1986, 18–19, 72–88. [Google Scholar] [CrossRef]
- Sippel, P.; Lunkenheimer, P.; Krohns, S.; Thoms, E.; Loidl, A. Importance of liquid fragility for energy applications of ionic liquids. Sci. Rep. 2015, 5, 13922. [Google Scholar] [CrossRef] [PubMed]
- Ueno, K.; Zhao, Z.; Watanabe, M.; Angell, C.A. Protic ionic liquids based on decahydroisoquinoline: Lost superfragility and ionicity-fragility correlation. J. Phys. Chem. B 2012, 116, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A. Liquid fragility and the glass transition in water and aqueous solutions. Chem. Rev. 2002, 102, 2627–2649. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Gurung, E.; Cetin, M.M.; Mayer, M.F.; Quitevis, E.L.; Simon, S.L. Fragility of ionic liquids measured by flash differential scanning calorimetry. Thermochim. Acta 2017, 654, 121–129. [Google Scholar] [CrossRef]
- Hodge, I.M. Strong and fragile liquids—A brief critique. J. Non-Cryst. Sol. 1996, 202, 164–172. [Google Scholar] [CrossRef]
- Anouti, M.; Caillon-Caravanier, M.; Le Floch, C.; Lemordant, D. Alkylammonium-Based Protic Ionic Liquids. II. Ionic Transport and Heat-Transfer Properties: Fragility and Ionicity Rule. J. Phys. Chem. B 2008, 112, 9412–9416. [Google Scholar] [CrossRef]
- Anouti, M.; Caillon-Caravanier, M.; Dridi, Y.; Galiano, H.; Lemordant, D. Synthesis and Characterization of New Pyrrolidinium Based Protic Ionic Liquids. Good and Superionic Liquids. J. Phys. Chem. B 2008, 112, 13335–13343. [Google Scholar] [CrossRef]
- Rauber, D.; Philippi, F.; Becker, J.; Zapp, J.; Morgenstern, B.; Kuttich, B.; Kraus, T.; Hempelmann, R.; Hunt, P.; Welton, T.; et al. Anion and ether group influence in protic guanidinium ionic liquids. Phys. Chem. Chem. Phys. 2023, 25, 6436–6453. [Google Scholar] [CrossRef]
- Schreiner, C.; Zugmann, S.; Hartl, R.; Gores, H.J. Temperature dependence of viscosity and specific conductivity of fluoroborate-based ionic liquids in light of the fractional Walden rule and Angell’s fragility concept. J. Phys. Eng. Data 2010, 55, 4372–4377. [Google Scholar] [CrossRef]
- Angell, C.A.; Ueno, K. Soft is strong. Nature 2009, 462, 45–46. [Google Scholar] [CrossRef]



| Property | T | D | |
|---|---|---|---|
| Units | (K) | (mS/cm) | (10 m/s) |
| Note | @ 25 °C | @ 34 °C | |
| [CHIm][TFSI] | 191 | 3.693 | 2.885 |
| [CHIm][TfO] | n.a. | 4.745 * | 2.781 |
| [CHTr][TFSI] | 211 | 1.284 | 1.313 |
| [CHTr][TfO] | 208 | 1.458 | 1.200 |
| Ionic Liquid | D | T (K) | (S/cm) | m |
|---|---|---|---|---|
| [CHIm][TFSI] | 3.4741 ± 0.0232 | 174.0 | 0.4926 ± 0.0122 | 186 |
| [CHIm][TfO] | - | - | - | - |
| [CHTr][TFSI] | 3.2471 ± 0.0106 | 192.5 | 0.4882 ± 0.0067 | 198 |
| [CHTr][TfO] | 3.3027 ± 0.0074 | 190.0 | 0.4865 ± 0.0046 | 195 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morais, E.M.; Idström, A.; Evenäs, L.; Martinelli, A. Transport Properties of Protic Ionic Liquids Based on Triazolium and Imidazolium: Development of an Air-Free Conductivity Setup. Molecules 2023, 28, 5147. https://doi.org/10.3390/molecules28135147
Morais EM, Idström A, Evenäs L, Martinelli A. Transport Properties of Protic Ionic Liquids Based on Triazolium and Imidazolium: Development of an Air-Free Conductivity Setup. Molecules. 2023; 28(13):5147. https://doi.org/10.3390/molecules28135147
Chicago/Turabian StyleMorais, Eduardo Maurina, Alexander Idström, Lars Evenäs, and Anna Martinelli. 2023. "Transport Properties of Protic Ionic Liquids Based on Triazolium and Imidazolium: Development of an Air-Free Conductivity Setup" Molecules 28, no. 13: 5147. https://doi.org/10.3390/molecules28135147
APA StyleMorais, E. M., Idström, A., Evenäs, L., & Martinelli, A. (2023). Transport Properties of Protic Ionic Liquids Based on Triazolium and Imidazolium: Development of an Air-Free Conductivity Setup. Molecules, 28(13), 5147. https://doi.org/10.3390/molecules28135147








