Molecular Dynamics Study of the Green Solvent Polyethylene Glycol with Water Impurities
Abstract
1. Introduction
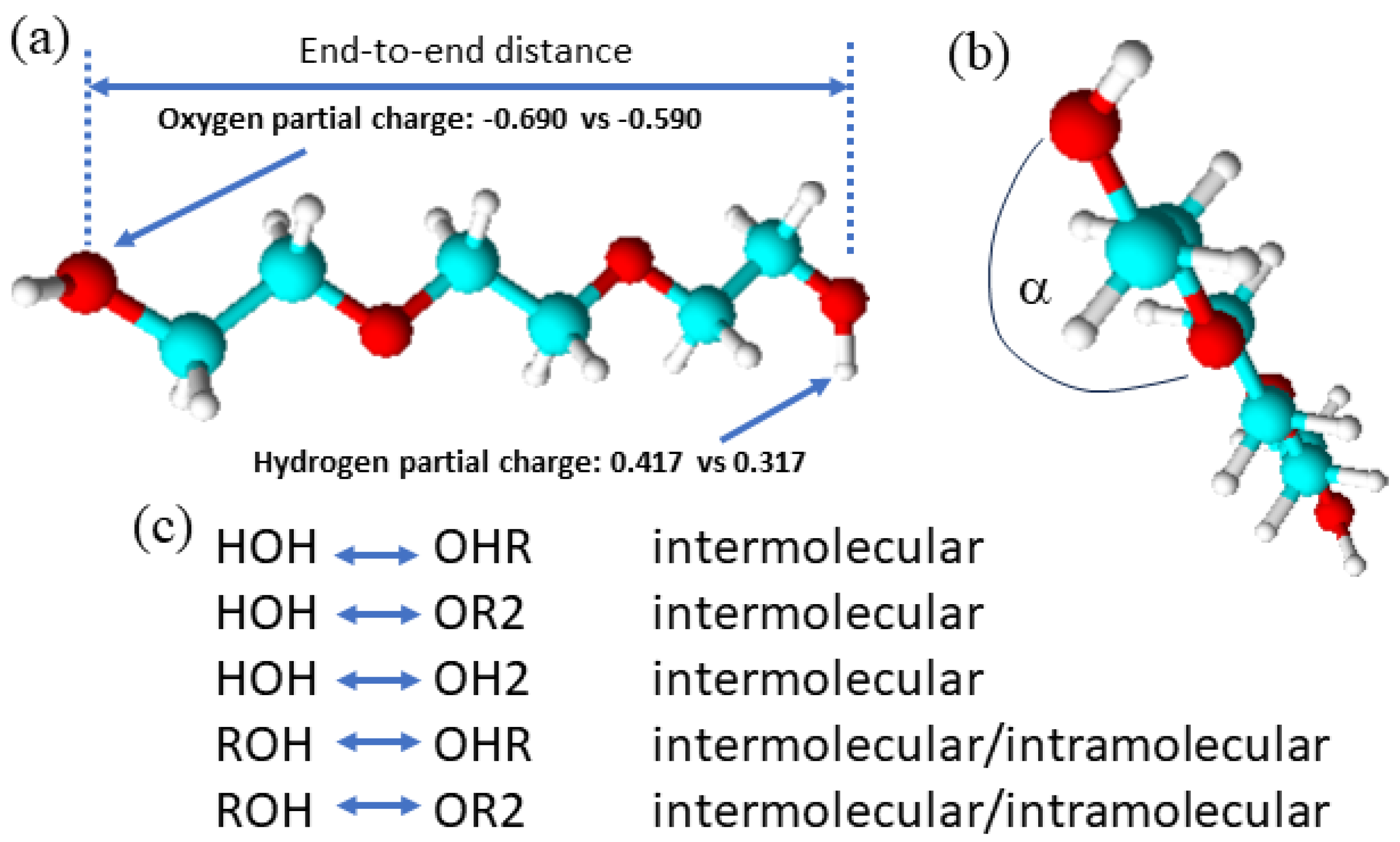
2. Results and Discussion
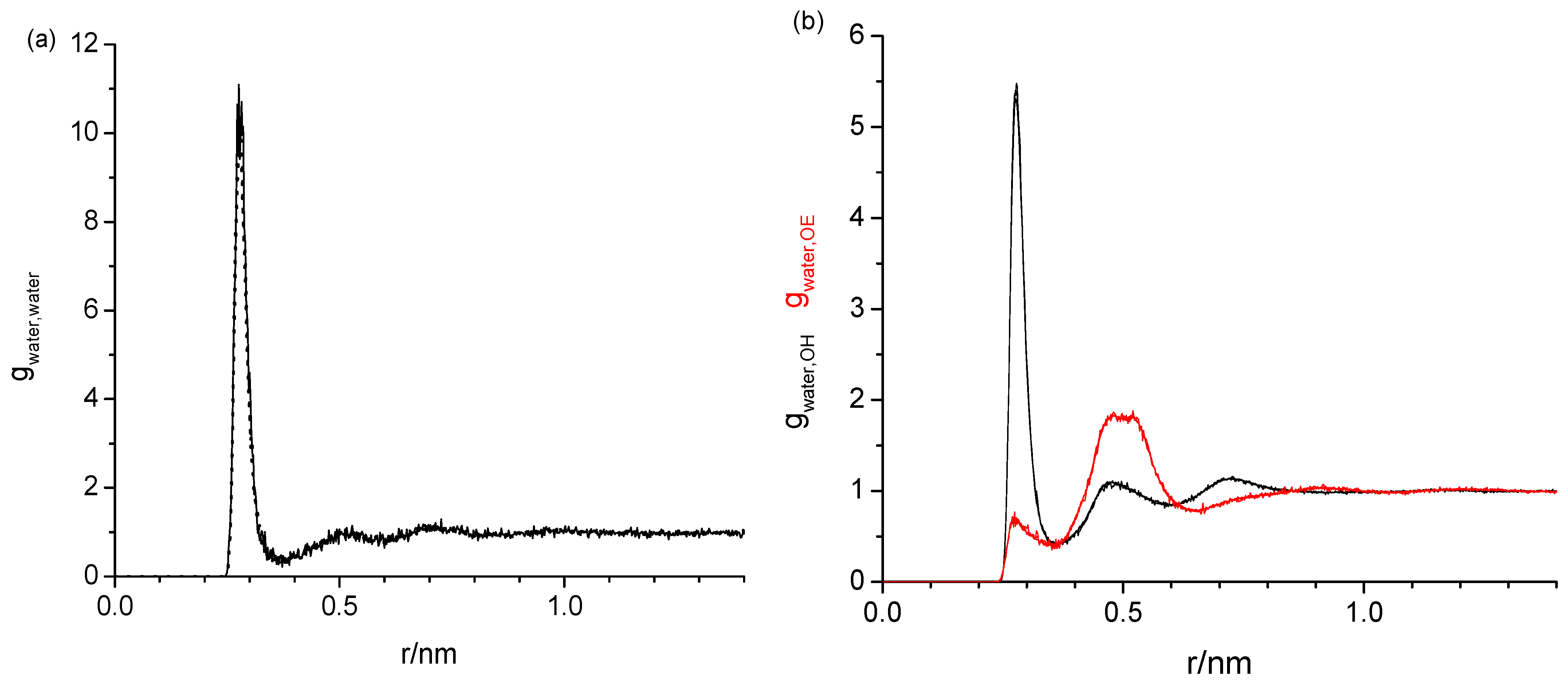
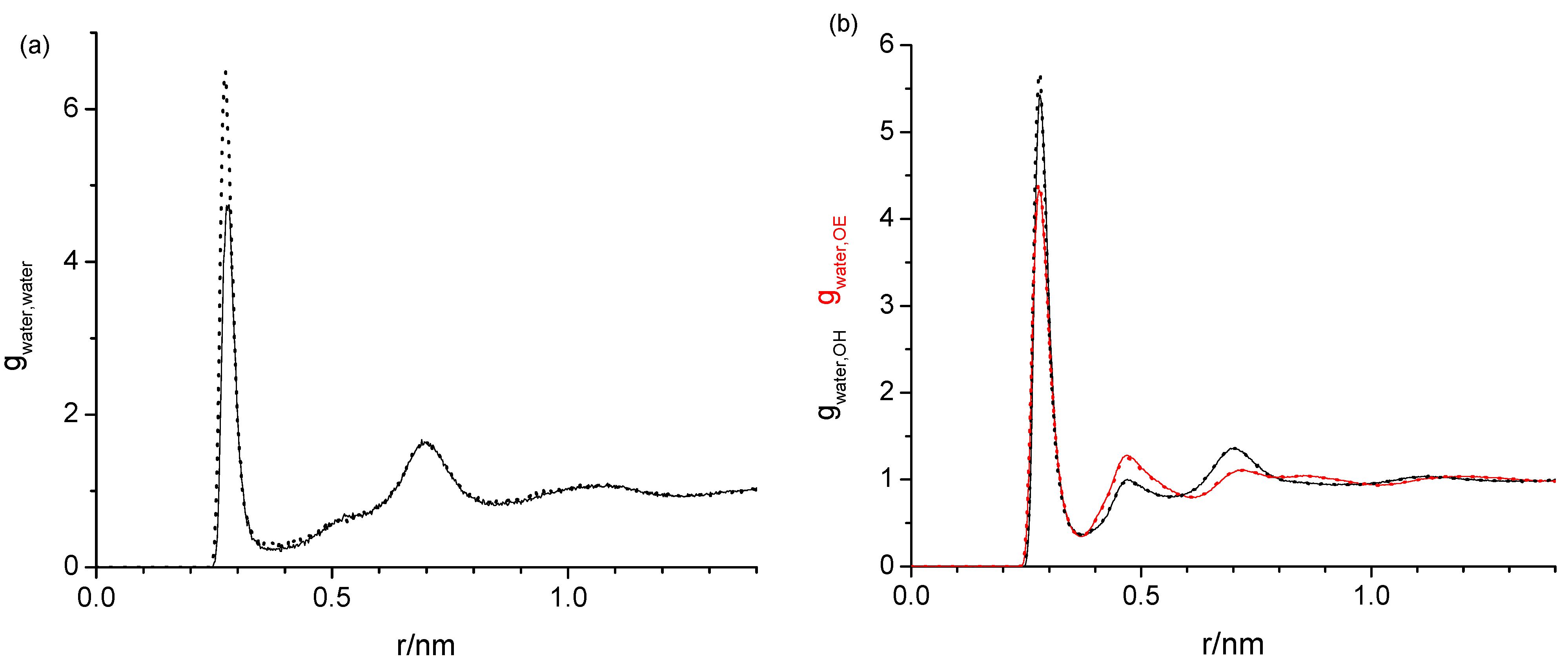
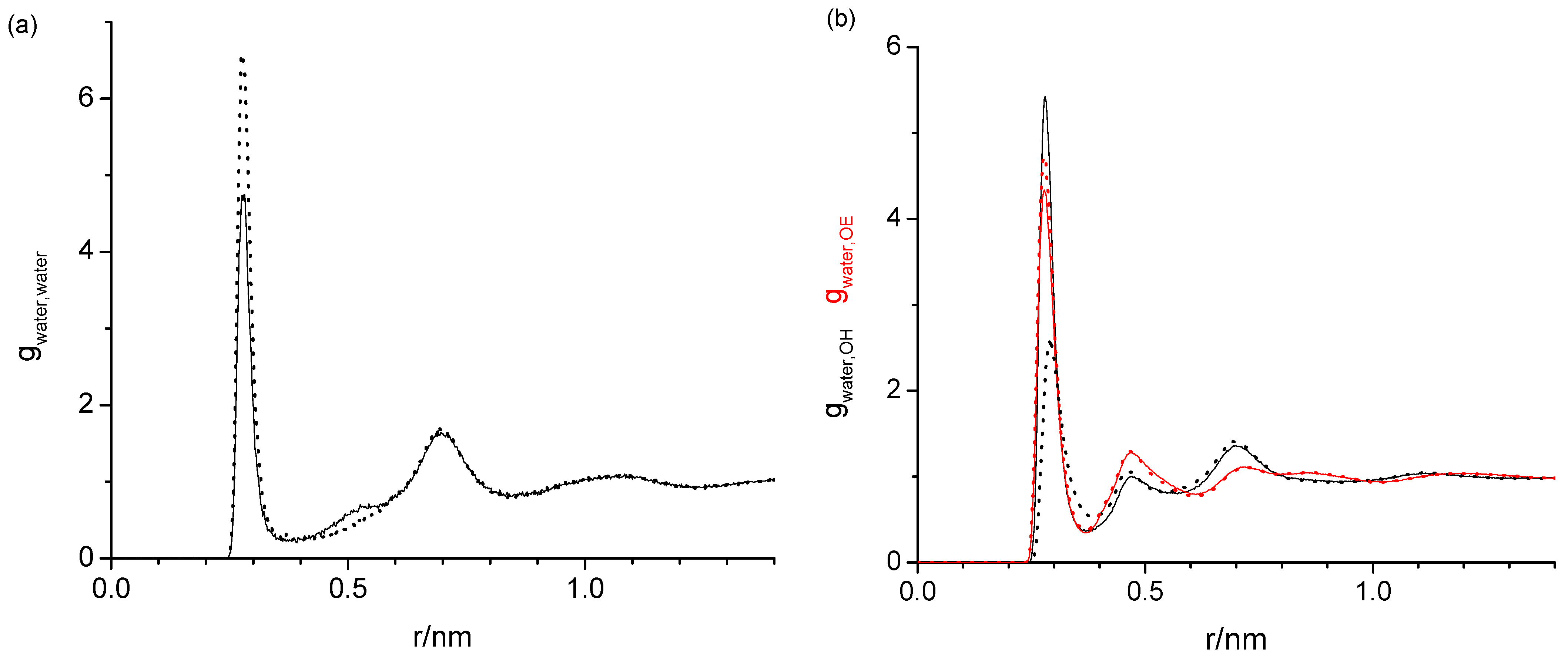
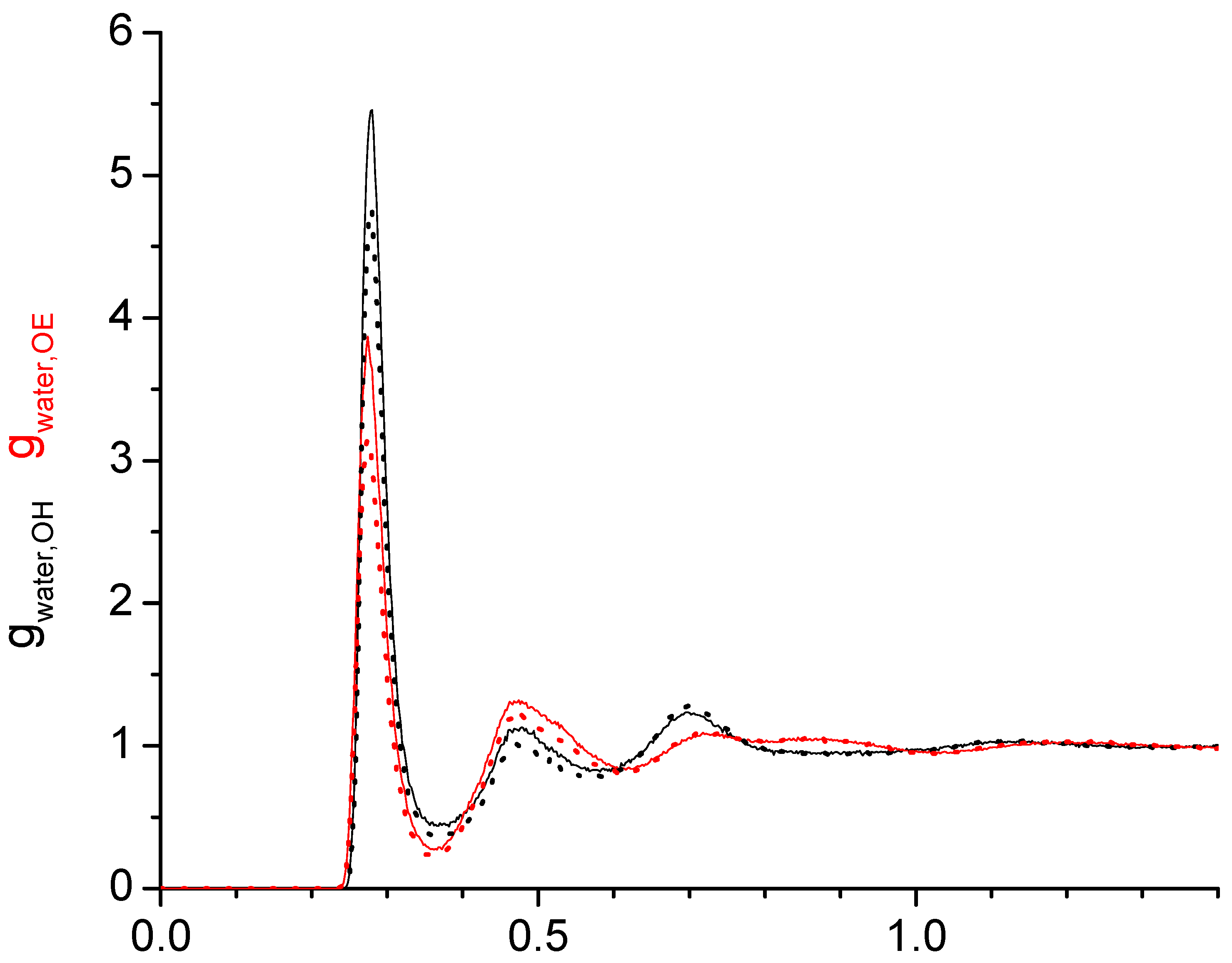
2.1. Radial Distribution Functions
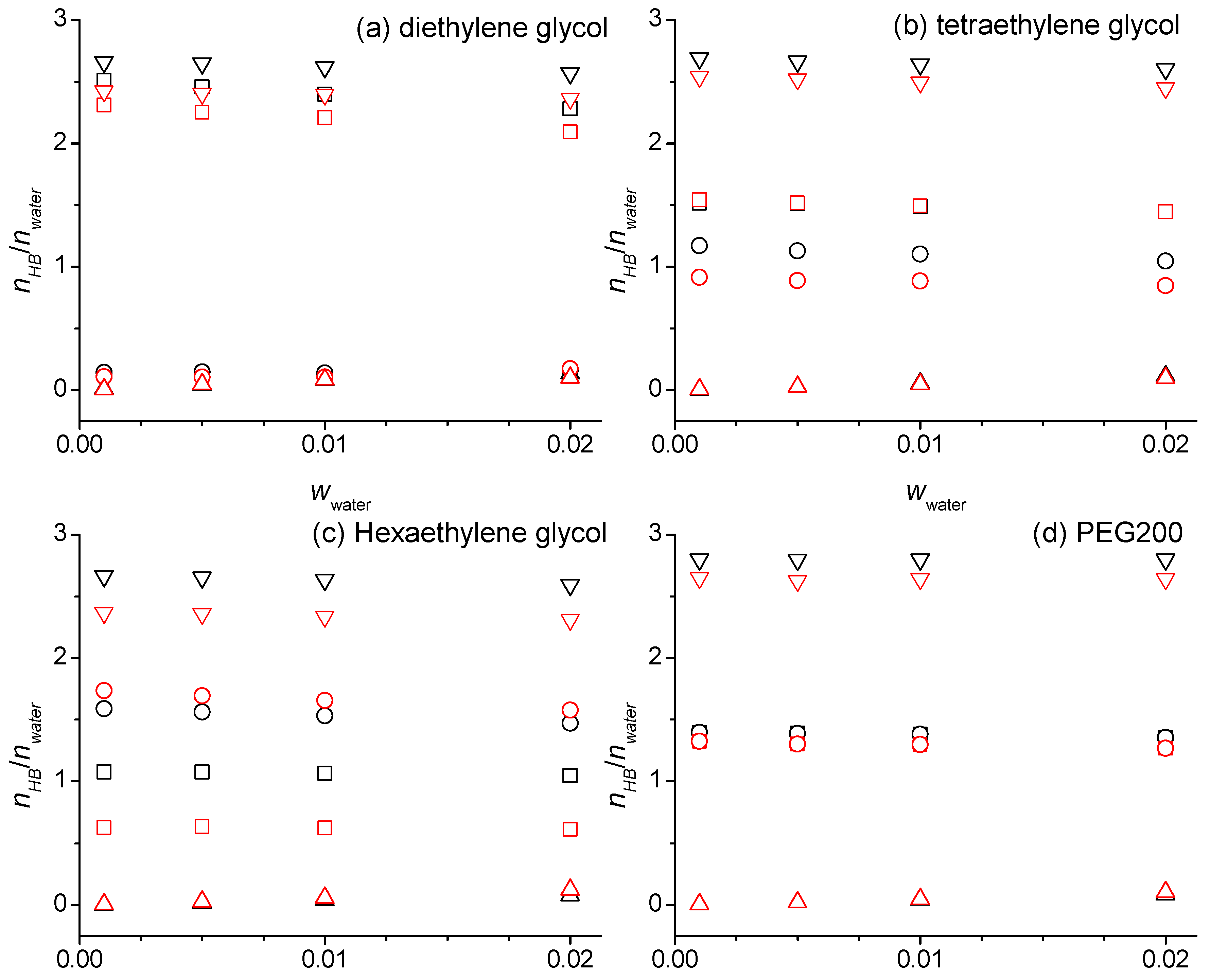
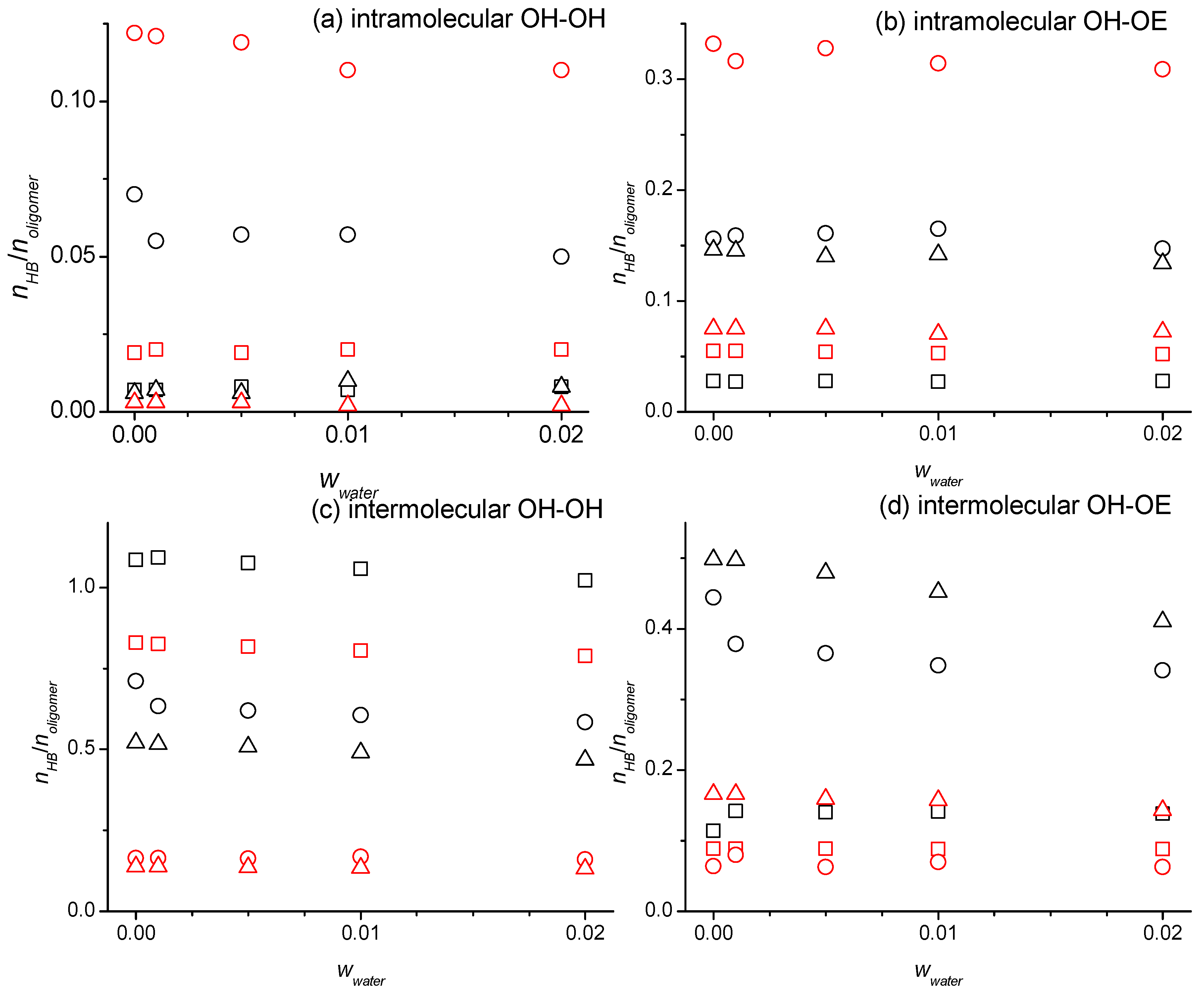
2.2. Hydrogen Bonding Numbers
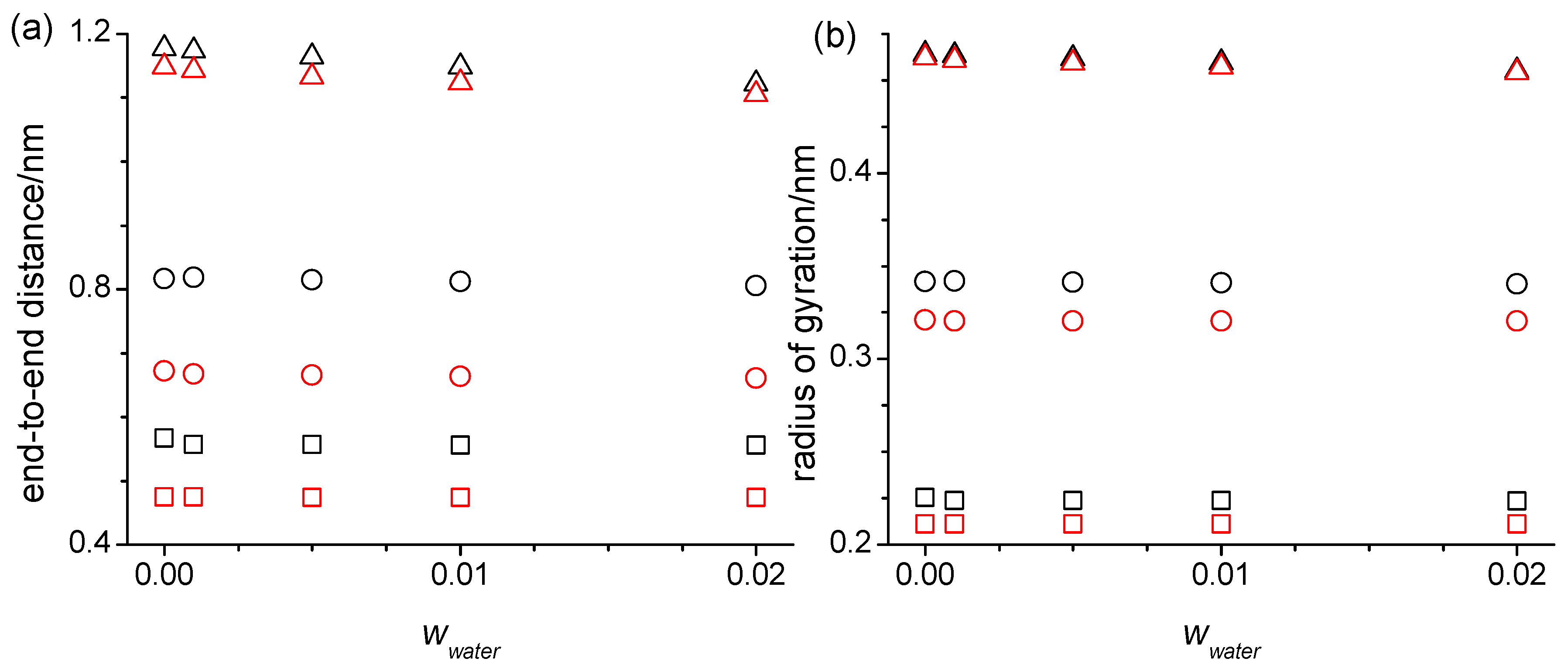
2.3. Structure, Thermodynamics, and Dynamics
3. Computational Methods
3.1. Simulation Details
3.2. Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Calvo-Flores, F.G.; Monteagudo-Arrebola, M.J.; Dobado, J.A.; Isac-Garcia, J. Green and bio-based solvents. Top. Curr. Chem. 2018, 376, 18. [Google Scholar] [CrossRef]
- Chen, J.; Spear, S.K.; Huddleston, J.G.; Rogers, R.D. Polyethylene Glycol and Solutions of Polyethylene Glycol as Green Reaction Media. Green Chem. 2005, 7, 64–82. [Google Scholar]
- Andrade, C.K.Z.; Alves, L.M. Environmentally Benign Solvents in Organic Synthesis: Current Topics. Curr. Org. Chem. 2005, 9, 195–218. [Google Scholar] [CrossRef]
- Hoffmann, M.M. Polyethylene glycol as a green chemical solvent. Curr. Opin. Colloid Interface Sci. 2022, 57, 101537. [Google Scholar] [CrossRef]
- Kardooni, R.; Kiasat, A.R. Polyethylene glycol as a green and biocompatible reaction media for the catalyst free synthesis of organic compounds. Curr. Org. Chem. 2020, 24, 1275–1314. [Google Scholar] [CrossRef]
- Campos, J.F.; Berteina-Raboin, S. Greener synthesis of nitrogen-containing heterocycles in water, PEG, and bio-based solvents. Catalysts 2020, 10, 429. [Google Scholar] [CrossRef]
- Soni, J.; Sahiba, N.; Sethiya, A.; Agarwal, S. Polyethylene glycol: A promising approach for sustainable organic synthesis. J. Mol. Liq. 2020, 315, 113766. [Google Scholar] [CrossRef]
- Visak, Z.P.; Calado, M.S.; Vuksanovic, J.M.; Ivanis, G.R.; Branco, A.S.H.; Grozdanic, N.D.; Kijevcanin, M.L.; Serbanovic, S.P. Solutions of ionic liquids with diverse aliphatic and aromatic solutes—Phase behavior and potentials for applications: A review article. Arab. J. Chem. 2019, 12, 1628–1640. [Google Scholar] [CrossRef]
- McGarvey, P.W.; Hoffmann, M.M. Solubility of some mineral salts in polyethylene glycol and related surfactants. Tens. Surf. Deterg. 2018, 55, 203–209. [Google Scholar] [CrossRef]
- Gullapalli, R.P.; Mazzitelli, C.L. Polyethylene glycols in oral and parenteral formulations—A critical review. Int. J. Pharm. 2015, 496, 219–239. [Google Scholar] [CrossRef]
- Hutanu, D. Recent applications of polyethylene glycols (PEGs) and PEG derivatives. Mod. Chem. Appl. 2014, 2, 1000132. [Google Scholar] [CrossRef]
- Kong, X.B.; Tang, Q.Y.; Chen, X.Y.; Tu, Y.; Sun, S.Z.; Sun, Z.L. Polyethylene glycol as a promising synthetic material for repair of spinal cord injury. Neural Regen. Res. 2017, 12, 1003–1008. [Google Scholar] [CrossRef] [PubMed]
- Polyethylene Glycol Market Size, Share & Trends Analysis Report by Application (Medical, Personal Care, Industrial), by Region (North America, Europe, Asia Pacific, Row), and Segment Rorecasts, 2015–2020. Available online: https://www.grandviewresearch.com/industry-analysis/polyethylene-glycol-peg-market (accessed on 7 August 2021).
- Hoffmann, M.M.; Kealy, J.D.; Gutmann, T.; Buntkowsky, G. Densities, viscosities, and self-diffusion coefficients of several polyethylene glycols. J. Chem. Eng. Data 2021, 67, 88–103. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Horowitz, R.H.; Gutmann, T.; Buntkowsky, G. Densities, viscosities, and self-Diffusion coefficients of ethylene glycol oligomers. J. Chem. Eng. Data 2021, 66, 2480–2500. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Too, M.D.; Paddock, N.A.; Horstmann, R.; Kloth, S.; Vogel, M.; Buntkowsky, G. On the Behavior of the Ethylene Glycol Components of Polydisperse Polyethylene Glycol PEG200. J. Phys. Chem. B 2023, 127, 1178–1196. [Google Scholar] [CrossRef] [PubMed]
- Seddon, K.R.; Stark, A.; Torres, M.a.-J. Influence of chloride, water, and organic solvents on the physical properties of ionic liquids. Pure Appl. Chem. 2000, 72, 2275–2287. [Google Scholar] [CrossRef]
- Seddon, K.R.; Stark, A.; Torres, M.J. Viscosity and density of 1-alkyl-3-methylimidazolium ionic liquids. In Clean Solvents—Alternative Media for Chemical Reactions and Processing; Abraham, M.A., Moens, L., Eds.; ACS Symposium Series 819; ACS: Washington DC, USA, 2002; Volume 819, pp. 34–49. [Google Scholar]
- Widegren, J.A.; Laesecke, A.; Magee, J.W. The effect of dissolved water on the viscosities of hydrophobic room-temperature ionic liquids. Chem. Commun. 2005, 2005, 1610–1612. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- McQuarrie, D.A.; Simon, J.D. Physical Chemistry a Molecular Approach; University Science Books: Sausalito, CA, USA, 1997; p. 970. [Google Scholar]
- Walrafen, G.E.; Fisher, M.R.; Hokmabadi, M.S.; Yang, W.H. Temperature dependence of the low- and high-frequency Raman scattering from liquid water. J. Chem. Phys. 1986, 85, 6970–6982. [Google Scholar] [CrossRef]
- Pabst, F.; Kraus, J.; Kloth, S.; Steinrucken, E.; Kruteva, M.; Radulescu, A.; Vogel, M.; Blochowicz, T. Evidence of supercoolable nanoscale water clusters in an amorphous ionic liquid matrix. J. Chem. Phys. 2021, 155, 174501. [Google Scholar] [CrossRef] [PubMed]
- Cassone, G.; Martelli, F. Electrofreezing of liquid water at ambient conditions. Nat. Commun. 2024, 15, 1856. [Google Scholar] [CrossRef] [PubMed]
- Caleman, C.; van Maaren, P.J.; Hong, M.; Hub, J.S.; Costa, L.T.; van der Spoel, D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J. Chem. Theory Comput. 2012, 8, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 83rd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Pokorný, V.; Serra, P.B.P.; Fulem, M.; Lima, C.F.R.A.C.; Santos, L.M.N.B.F.; Růžička, K. Heat Capacity and Phase Behavior of Selected Oligo(ethylene glycol)s. J. Chem. Eng. Data 2019, 64, 2742–2749. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Lindahl, E.; Abraham, M.J.; Hess, B.; van der Spoel, D. GROMACS 2020.4 Source Code; Zenodo: Geneva, Switzerland, 2020. [Google Scholar]
- Páll, S.; Hess, B. A flexible algorithm for calculating pair interactions on SIMD architectures. Comput. Phys. Commun. 2013, 184, 2641–2650. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. SETTLE: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Oxford Science Publications: Oxford, UK, 1987. [Google Scholar]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M.L. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Maginn, E.J.; Messerly, R.A.; Carlson, D.J.; Roe, D.R.; Elliott, J.R. Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0]. Living J. Comp. Mol. Sci. 2019, 1, 6324. [Google Scholar] [CrossRef]
- Ozkanlar, A.; Zhou, T.; Clark, A.E. Towards a unified description of the hydrogen bond network of liquid water: A dynamics based approach. J. Chem. Phys. 2014, 141, 214107. [Google Scholar] [CrossRef]
- Yeh, I.-C.; Hummer, G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. [Google Scholar] [CrossRef]
- Zhang, Y.; Otani, A.; Maginn, E.J. Reliable Viscosity Calculation from Equilibrium Molecular Dynamics Simulations: A Time Decomposition Method. J. Chem. Theory Comput. 2015, 11, 3537–3546. [Google Scholar] [CrossRef]
- Zagari, J.; Hoffmann, M.M. Polydispersity Analysis of Polyethylene Glycol by Gas and Liquid Chromatography. Chem. Educ. 2019, 24, 5. [Google Scholar]
- Edward, J.T. Molecular Volumes and the Stokes-Einstein Equation. J. Chem. Educ. 1970, 47, 261–270. [Google Scholar] [CrossRef]


| wwater | wwater | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| OPLS | Model a | 0 [16] | 0.001 | 0.005 | 0.010 | 0.020 | 0 [16] | 0.001 | 0.005 | 0.010 | 0.020 |
| Density/kg‧m−3 | Viscosity/mPa‧s | ||||||||||
| Diethylene glycol | Diethylene glycol | ||||||||||
| Exp. [15] | 1091.7 | 1091.6 | 1091.4 | 1091.2 | 1090.6 | 9.0 | 9.0 | 9.0 | 8.9 | 8.7 | |
| Unmod | SPC/E | 1077.5 | 1077.2 | 1077.2 | 1077.3 | 1077.6 | 11.2 | 11.8 | 9.8 | 10.6 | 9.9 |
| Unmod | TIP4P | 1077.5 | 1077.4 | 1077.7 | 1077.8 | 1078.0 | 11.2 | 10.5 | 10.4 | 11.2 | 11.2 |
| Mod | SPC/E | 1076.6 | 1076.2 | 1076.9 | 1076.8 | 1077.0 | 7.1 | 6.8 | 7.5 | 7.7 | 8.3 |
| Mod | TIP4P | 1076.6 | 1076.3 | 1076.5 | 1077.0 | 1077.8 | 7.1 | 7.0 | 7.3 | 7.7 | 7.8 |
| Tetraethylene glycol | Tetraethylene glycol | ||||||||||
| Exp. [15] | 1096.0 | 1096.0 | 1095.9 | 1095.9 | 1095.8 | 13.2 | 13.2 | 13.1 | 12.9 | 12.6 | |
| Unmod | SPC/E | 1103.0 | 1103.3 | 1103.7 | 1103.9 | 1104.7 | 65.1 | 88.2 | 94.1 | 86.5 | 66.6 |
| Unmod | TIP4P | 1103.0 | 1103.2 | 1103.2 | 1103.6 | 1104.6 | 65.1 | 84.2 | 71.5 | 67.8 | 84.7 |
| Mod | SPC/E | 1090.2 | 1090.4 | 1091.2 | 1091.7 | 1092.9 | 25.6 | 25.1 | 31.3 | 25.4 | 28.9 |
| Mod | TIP4P | 1090.2 | 1090.3 | 1091.0 | 1091.8 | 1093.4 | 25.6 | 23.7 | 29.1 | 31.6 | 35.2 |
| Hexaethylene glycol | Hexaethylene glycol | ||||||||||
| Exp. [15] | 1099.8 | 1099.5 | 1098.1 | 1096.4 | 1092.9 | 18.3 | 18.2 | 17.9 | 17.6 | 16.9 | |
| Unmod | SPC/E | 1113.5 | 1112.9 | 1113.9 | 1114.8 | 1115.7 | 226.0 | 187.4 | 247.7 | 211.2 | 224.2 |
| Unmod | TIP4P | 1113.5 | 1113.6 | 1114.3 | 1114.2 | 1115.8 | 226.0 | 248.5 | 238.5 | 251.9 | 258.8 |
| Mod | SPC/E | 1096.0 | 1096.7 | 1097.2 | 1097.0 | 1099.0 | 111.0 | 78.3 | 102.9 | 92.5 | 106.8 |
| Mod | TIP4P | 1096.0 | 1096.6 | 1096.9 | 1098.0 | 1099.2 | 111.0 | 107.8 | 108.1 | 83.8 | 120.0 |
| PEG200 | PEG 200 | ||||||||||
| Exp. [14] | 1097.0 | 1097.0 | 1097.0 | 1097.0 | 1097.0 | 14.7 | 14.7 | 14.6 | 14.5 | 14.3 | |
| Unmod | SPC/E | 1103.5 | 1104.2 | 1104.7 | 1106.1 | 1105.4 | 84.4 | 89.4 | 85.9 | 107.4 | 102.5 |
| Unmod | TIP4P | 1103.5 | 1104.0 | 1104.5 | 1105.5 | 1106.2 | 84.4 | 78.2 | 89.8 | 89.0 | 110.7 |
| Mod | SPC/E | 1090.3 | 1090.2 | 1091.2 | 1092.2 | 1093.8 | 32.2 | 35.8 | 35.3 | 38.1 | 37.8 |
| Mod | TIP4P | 1090.3 | 1090.3 | 1091.3 | 1091.6 | 1093.7 | 32.2 | 40.2 | 36.8 | 44.6 | 38.4 |
| Oligomer self-diffusion/10−11 m2‧s−1 | Water self-diffusion/10−11 m2‧s−1 | ||||||||||
| Diethylene glycol | Diethylene glycol | ||||||||||
| Exp. [15] | 17.4 | 17.5 | 17.6 | 17.9 | 18.3 | ||||||
| Unmod | SPC/E | 12.7 | 12.9 | 13.4 | 13.1 | 13.0 | 37.3 | 32.5 | 35.7 | 34.5 | |
| Unmod | TIP4P | 12.7 | 12.8 | 12.8 | 13.2 | 12.4 | 27.8 | 29.8 | 31.0 | 37.0 | |
| Mod | SPC/E | 19.6 | 21.8 | 18.8 | 19.1 | 19.2 | 40.9 | 48.1 | 47.2 | 43.9 | |
| Mod | TIP4P | 19.6 | 20.8 | 21.0 | 18.6 | 18.5 | 44.0 | 47.2 | 41.3 | 40.2 | |
| Tetraethylene glycol | Tetraethylene glycol | ||||||||||
| Exp. [15] | 10.1 | 10.1 | 10.2 | 10.4 | 10.6 | ||||||
| Unmod | SPC/E | 1.56 | 1.51 | 1.52 | 1.52 | 1.45 | 7.21 | 6.52 | 7.17 | 6.79 | |
| Unmod | TIP4P | 1.56 | 1.50 | 1.52 | 1.61 | 1.47 | 6.12 | 6.97 | 7.59 | 6.62 | |
| Mod | SPC/E | 4.55 | 4.37 | 4.12 | 4.35 | 3.97 | 15.60 | 18.15 | 16.71 | 16.06 | |
| Mod | TIP4P | 4.55 | 4.27 | 4.17 | 4.20 | 3.73 | 13.52 | 15.48 | 14.73 | 14.87 | |
| Hexaethylene glycol | Hexaethylene glycol | ||||||||||
| Exp. [15] | 6.6 | 6.7 | 6.7 | 6.8 | 7.0 | ||||||
| Unmod | SPC/E | 0.47 | 0.47 | 0.42 | 0.40 | 0.37 | 3.73 | 2.30 | 2.28 | 2.35 | |
| Unmod | TIP4P | 0.47 | 0.44 | 0.42 | 0.39 | 0.36 | 2.59 | 2.22 | 2.15 | 2.19 | |
| Mod | SPC/E | 1.15 | 1.17 | 1.03 | 1.15 | 0.92 | 4.41 | 4.58 | 5.61 | 4.98 | |
| Mod | TIP4P | 1.15 | 1.06 | 1.08 | 1.06 | 0.96 | 3.40 | 4.33 | 4.26 | 4.56 | |
| PEG200 | PEG200 | ||||||||||
| Exp. [14] | 8.20 | 8.24 | 8.41 | 8.62 | 9.04 | ||||||
| Unmod | SPC/E | 1.20 | 1.19 | 1.22 | 1.13 | 1.14 | 2.28 | 2.44 | 2.24 | 1.91 | |
| Unmod | TIP4P | 1.20 | 1.21 | 1.20 | 1.18 | 1.11 | 2.14 | 2.34 | 2.12 | 1.93 | |
| Mod | SPC/E | 2.95 | 3.16 | 3.28 | 2.90 | 2.84 | 5.55 | 5.90 | 4.89 | 5.10 | |
| Mod | TIP4P | 2.95 | 3.13 | 3.12 | 3.01 | 2.80 | 4.47 | 5.71 | 5.46 | 5.39 | |
| wwater | wwater | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| OPLS | Model a | 0 [16] | 0.001 | 0.005 | 0.010 | 0.020 | 0 [16] | 0.001 | 0.005 | 0.010 | 0.020 |
| Cp/J‧mol−1‧K−1 | α/1000 K−1 | ||||||||||
| Diethylene glycol | Diethylene glycol | ||||||||||
| Exp. | 256.8 [29] | 0.677 [15] | |||||||||
| Unmod | SPC/E | 493.4 | 467.6 | 472.7 | 447.1 | 425.1 | 1.080 | 0.906 | 0.986 | 0.967 | 0.934 |
| Unmod | TIP4P | 493.4 | 476.0 | 468.8 | 439.3 | 430.0 | 1.080 | 1.026 | 0.975 | 0.912 | 0.909 |
| Mod | SPC/E | 507.7 | 469.6 | 464.2 | 446.5 | 434.0 | 1.044 | 1.037 | 0.980 | 1.015 | 1.073 |
| Mod | TIP4P | 507.7 | 472.2 | 459.1 | 432.8 | 426.2 | 1.044 | 1.093 | 1.064 | 0.912 | 0.966 |
| Tetraethylene glycol | Tetraethylene glycol | ||||||||||
| Exp. | 438.6 [29] | 0.685 [15] | |||||||||
| Unmod | SPC/E | 896.7 | 854.2 | 809.1 | 794.3 | 733.1 | 0.954 | 0.828 | 0.864 | 0.919 | 0.906 |
| Unmod | TIP4P | 896.7 | 878.7 | 905.2 | 792.9 | 718.2 | 0.954 | 0.988 | 1.328 | 0.869 | 0.876 |
| Mod | SPC/E | 818.6 | 826.6 | 789.3 | 744.9 | 713.7 | 0.956 | 0.896 | 0.859 | 0.905 | 0.934 |
| Mod | TIP4P | 818.6 | 800.3 | 799.6 | 770.5 | 700.7 | 0.956 | 0.862 | 0.845 | 0.954 | 0.936 |
| Hexaethylene glycol | Hexaethylene glycol | ||||||||||
| Exp. | 625.3 [29] | 0.750 [15] | |||||||||
| Unmod | SPC/E | 1313.4 | 1255.4 | 1109.9 | 1083.8 | 925.8 | 0.961 | 0.965 | 0.747 | 0.854 | 0.771 |
| Unmod | TIP4P | 1313.4 | 1172.7 | 1074.1 | 1091.9 | 915.5 | 0.961 | 0.675 | 0.764 | 0.932 | 0.885 |
| Mod | SPC/E | 1232.3 | 1182.6 | 1156.0 | 1110.1 | 940.8 | 0.928 | 0.910 | 0.891 | 0.950 | 0.840 |
| Mod | TIP4P | 1232.3 | 1199.1 | 1075.9 | 1071.0 | 977.0 | 0.928 | 0.906 | 0.792 | 0.850 | 1.036 |
| PEG200 | PEG 200 | ||||||||||
| Exp. | 431.0 [16] | 0.727 [14] | |||||||||
| Unmod | SPC/E | 916.7 | 952.8 | 901.9 | 848.1 | 820.9 | 0.932 | 0.902 | 0.896 | 0.913 | 0.903 |
| Unmod | TIP4P | 916.7 | 861.6 | 847.5 | 864.4 | 895.3 | 0.932 | 0.696 | 0.884 | 1.035 | 1.058 |
| Mod | SPC/E | 900.9 | 889.4 | 805.0 | 835.4 | 898.2 | 0.909 | 0.868 | 0.791 | 0.916 | 0.774 |
| Mod | TIP4P | 900.9 | 867.3 | 910.2 | 899.4 | 781.7 | 0.909 | 0.918 | 0.965 | 1.027 | 0.865 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, M.M.; Too, M.D.; Paddock, N.A.; Horstmann, R.; Kloth, S.; Vogel, M.; Buntkowsky, G. Molecular Dynamics Study of the Green Solvent Polyethylene Glycol with Water Impurities. Molecules 2024, 29, 2070. https://doi.org/10.3390/molecules29092070
Hoffmann MM, Too MD, Paddock NA, Horstmann R, Kloth S, Vogel M, Buntkowsky G. Molecular Dynamics Study of the Green Solvent Polyethylene Glycol with Water Impurities. Molecules. 2024; 29(9):2070. https://doi.org/10.3390/molecules29092070
Chicago/Turabian StyleHoffmann, Markus M., Matthew D. Too, Nathaniel A. Paddock, Robin Horstmann, Sebastian Kloth, Michael Vogel, and Gerd Buntkowsky. 2024. "Molecular Dynamics Study of the Green Solvent Polyethylene Glycol with Water Impurities" Molecules 29, no. 9: 2070. https://doi.org/10.3390/molecules29092070
APA StyleHoffmann, M. M., Too, M. D., Paddock, N. A., Horstmann, R., Kloth, S., Vogel, M., & Buntkowsky, G. (2024). Molecular Dynamics Study of the Green Solvent Polyethylene Glycol with Water Impurities. Molecules, 29(9), 2070. https://doi.org/10.3390/molecules29092070