A Portrait of the Chromophore as a Young System—Quantum-Derived Force Field Unraveling Solvent Reorganization upon Optical Excitation of Cyclocurcumin Derivatives
Abstract
1. Introduction
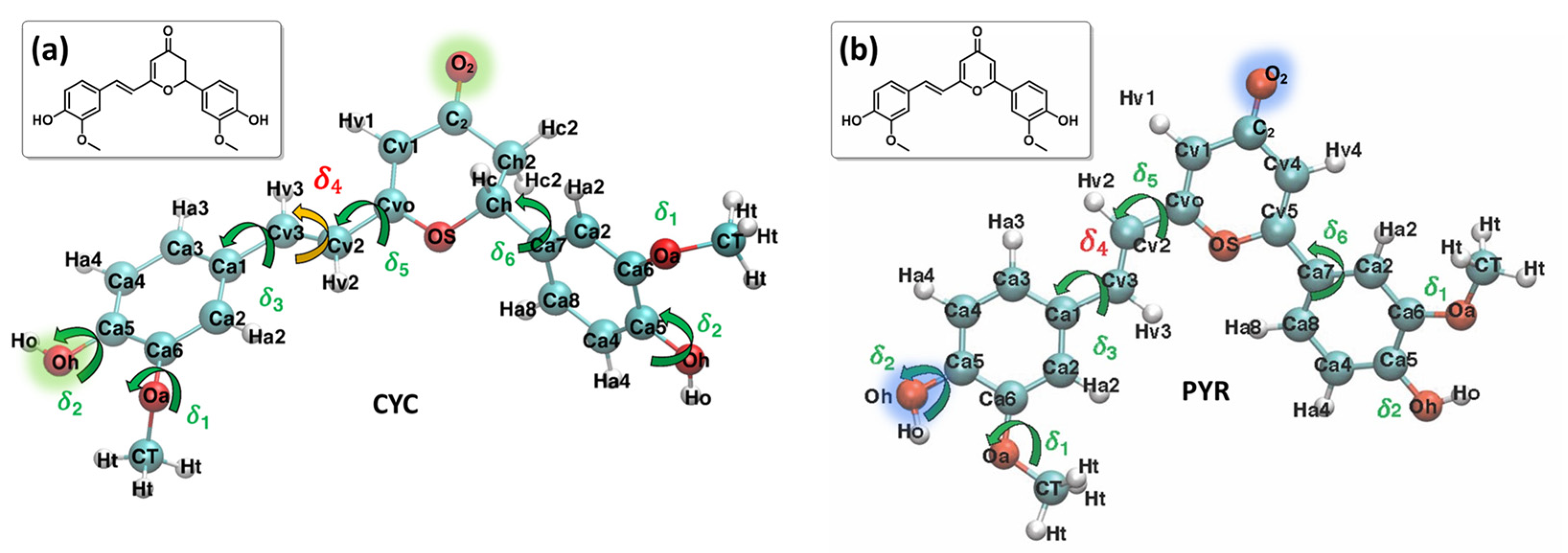
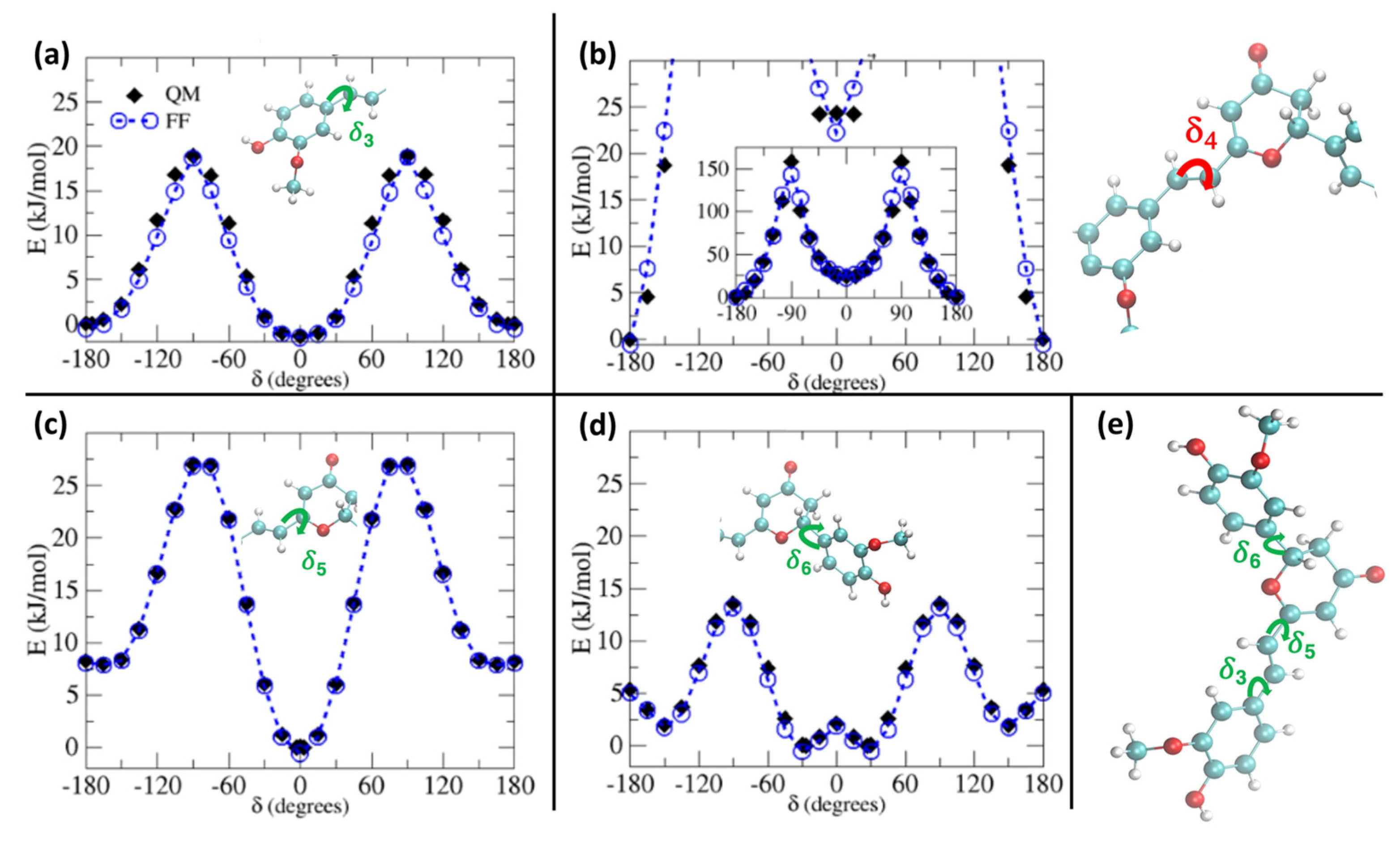
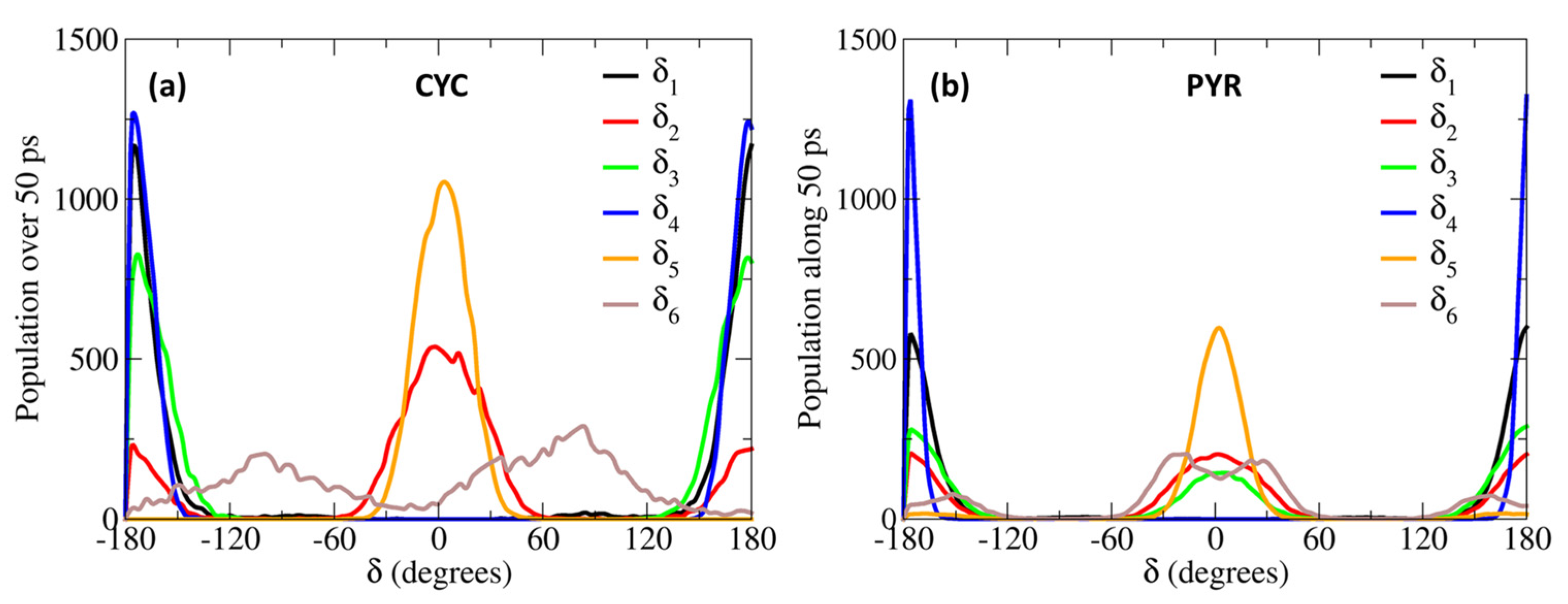
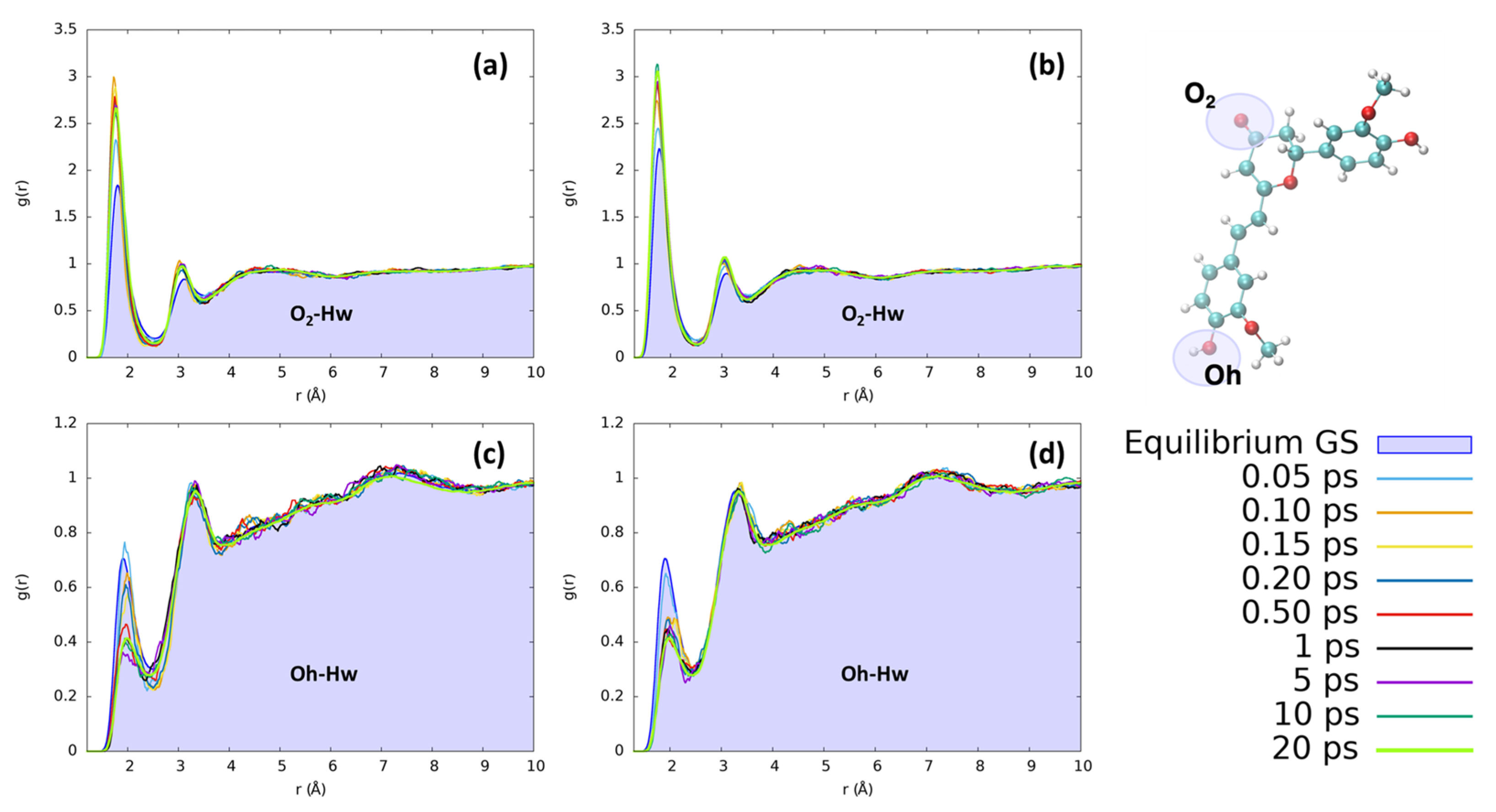
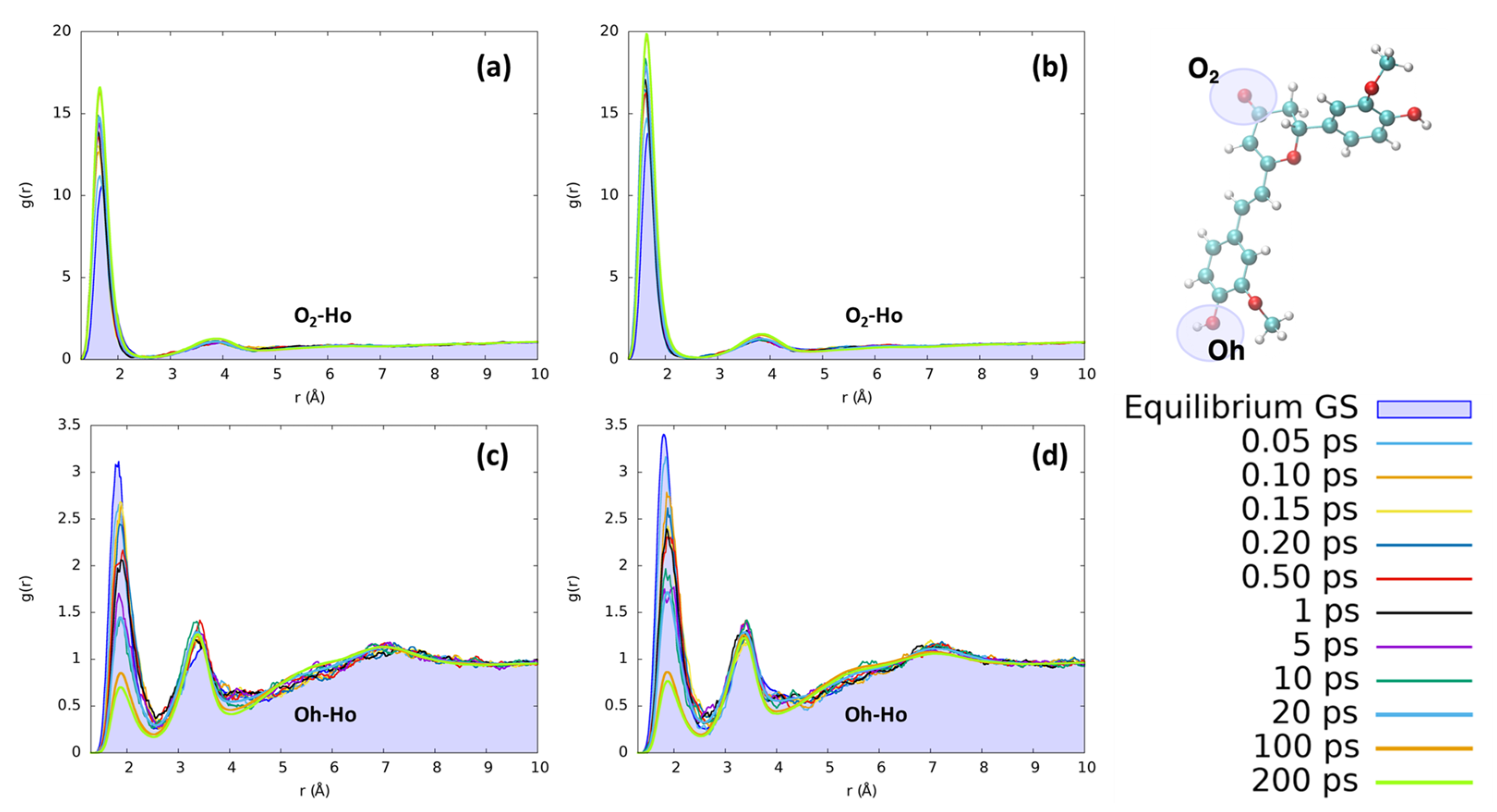
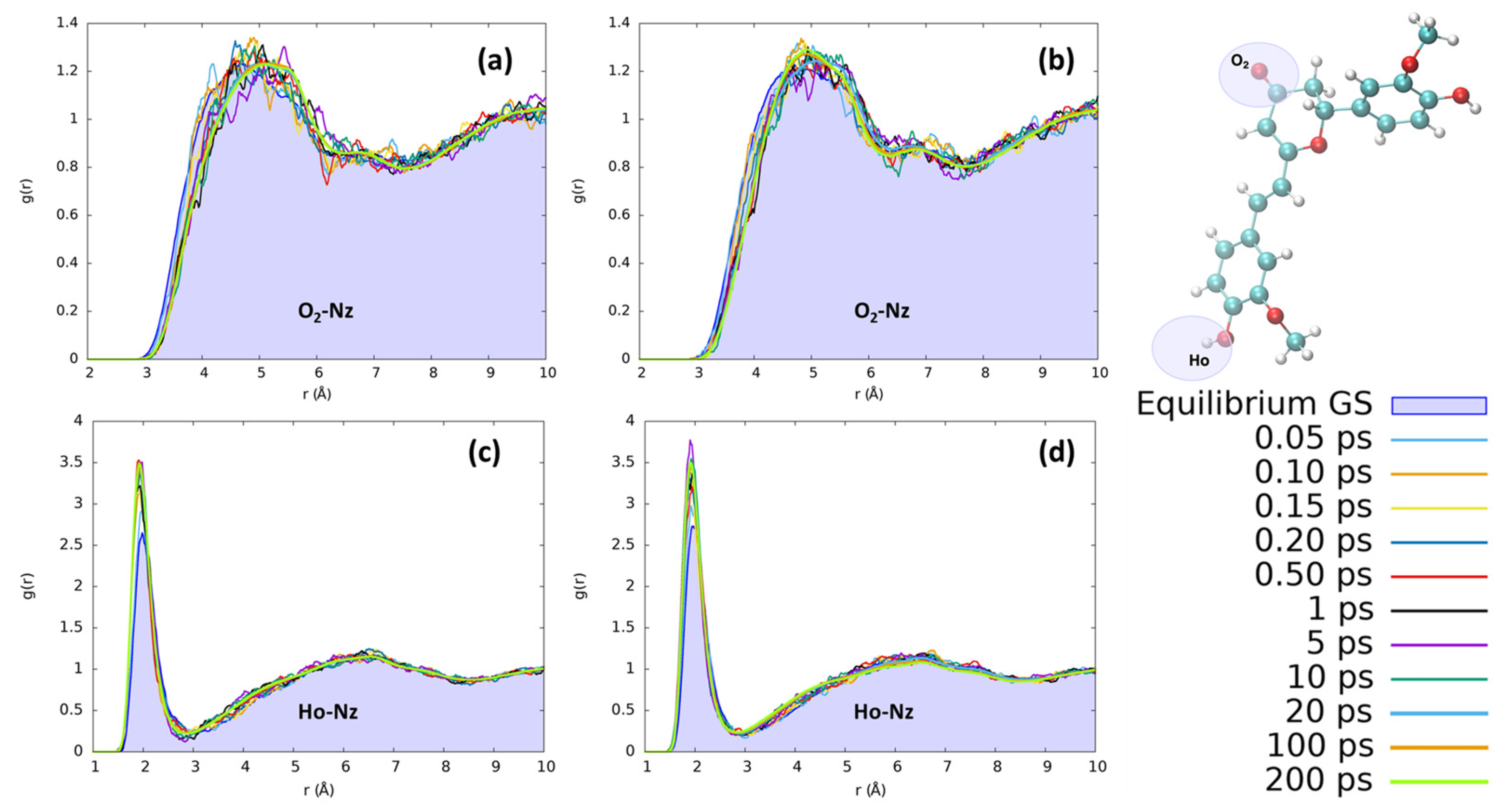
2. Results and Discussion
3. Methodology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Broichhagen, J.; Frank, J.A.; Trauner, D. A Roadmap to Success in Photopharmacology. Acc. Chem. Res. 2015, 48, 1947–1960. [Google Scholar] [CrossRef] [PubMed]
- Marazzi, M.; Garcia-Iriepa, C. Retinal Inspired Photoswitches: From the Isomerization Mechanisms toward Recent Applications. In Photoisomerization: Causes, Behavior and Effects; Sampedro, D., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2019; ISBN 978-1-53615-313-2. [Google Scholar]
- Russew, M.M.; Hecht, S. Photoswitches: From Molecules to Materials. Adv. Mater. 2010, 22, 3348–3360. [Google Scholar] [CrossRef]
- Szymański, W.; Beierle, J.M.; Kistemaker, H.A.V.; Velema, W.A.; Feringa, B.L. Reversible Photocontrol of Biological Systems by the Incorporation of Molecular Photoswitches. Chem. Rev. 2013, 113, 6114–6178. [Google Scholar] [CrossRef] [PubMed]
- Wald, G. Molecular Basis of Visual Excitation. Science 1968, 162, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Weingart, O.; Schapiro, I.; Buss, V. Photochemistry of Visual Pigment Chromophore Models by Ab Initio Molecular Dynamics. J. Phys. Chem. B 2007, 111, 3782–3788. [Google Scholar] [CrossRef]
- Wietek, J.; Wiegert, J.S.; Adeishvili, N.; Schneider, F.; Watanabe, H.; Tsunoda, S.P.; Vogt, A.; Elstner, M.; Oertner, T.G.; Hegemann, P. Conversion of Channelrhodopsin into a Light-Gated Chloride Channel. Science 2014, 344, 409–412. [Google Scholar] [CrossRef]
- Fan, W.; Huang, P.; Chen, X. Overcoming the Achilles’ Heel of Photodynamic Therapy. Chem. Soc. Rev. 2016, 45, 6488–6519. [Google Scholar] [CrossRef]
- Reessing, F.; Szymanski, W. Beyond Photodynamic Therapy: Light-Activated Cancer Chemotherapy. Curr. Med. Chem. 2017, 24, 4905–4950. [Google Scholar] [PubMed]
- Babilas, P.; Landthaler, M.; Szeimies, R.-M. Photodynamic Therapy in Dermatology. Eur. J. Dermatol. 2006, 16, 340–348. [Google Scholar]
- Ethirajan, M.; Chen, Y.; Joshi, P.; Pandey, R.K. The Role of Porphyrin Chemistry in Tumor Imaging and Photodynamic Therapy. Chem. Soc. Rev. 2011, 40, 340–362. [Google Scholar] [CrossRef]
- Yanovsky, R.L.; Bartenstein, D.W.; Rogers, G.S.; Isakoff, S.J.; Chen, S.T. Photodynamic Therapy for Solid Tumors: A Review of the Literature. Photodermatol. Photoimmunol. Photomed. 2019, 35, 295–303. [Google Scholar] [CrossRef] [PubMed]
- DeRosa, M.C.; Crutchley, R.J. Photosensitized Singlet Oxygen and Its Applications. Coord. Chem. Rev. 2002, 233–234, 351–371. [Google Scholar] [CrossRef]
- Zhang, L.; Ji, Z.; Zhang, J.; Yang, S. Photodynamic Therapy Enhances Skin Cancer Chemotherapy Effects through Autophagy Regulation. Photodiagn. Photodyn. Ther. 2019, 28, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Winkler, K.; Simon, C.; Finke, M.; Bleses, K.; Birke, M.; Szentmáry, N.; Hüttenberger, D.; Eppig, T.; Stachon, T.; Langenbucher, A.; et al. Photodynamic Inactivation of Multidrug-Resistant Staphylococcus Aureus by Chlorin E6 and Red Light (λ = 670 nm). J. Photochem. Photobiol. B 2016, 162, 340–347. [Google Scholar] [CrossRef] [PubMed]
- Penha, C.B.; Bonin, E.; da Silva, A.F.; Hioka, N.; Zanqueta, É.B.; Nakamura, T.U.; de Abreu Filho, B.A.; Campanerut-Sá, P.A.Z.; Mikcha, J.M.G. Photodynamic Inactivation of Foodborne and Food Spoilage Bacteria by Curcumin. LWT-Food Sci. Technol. 2017, 76, 198–202. [Google Scholar] [CrossRef]
- Yi, F.; Zheng, X.; Fang, F.; Zhang, J.; Zhou, B.; Chen, X. ALA-PDT Alleviates the Psoriasis by Inhibiting JAK Signalling Pathway. Exp. Dermatol. 2019, 28, 1227–1236. [Google Scholar] [CrossRef] [PubMed]
- Josefsen, L.B.; Boyle, R.W. Photodynamic Therapy and the Development of Metal-Based Photosensitisers. Met. Based Drugs 2008, 2008, 276109. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.C.; Nguyen, V.N.; Choi, Y.; Lee, S.; Yoon, J. Recent Strategies to Develop Innovative Photosensitizers for Enhanced Photodynamic Therapy. Chem. Rev. 2021, 121, 13454–13619. [Google Scholar] [CrossRef] [PubMed]
- Hamblin, M.R. Photodynamic Therapy for Cancer: What’s Past Is Prologue. Photochem. Photobiol. 2020, 96, 506–516. [Google Scholar] [CrossRef]
- Brown, J.M. Tumor Hypoxia in Cancer Therapy. Methods Enzymol. 2007, 435, 297–321. [Google Scholar] [CrossRef]
- Dunkel, P.; Ilaš, J. Targeted Cancer Therapy Using Compounds Activated by Light. Cancers 2021, 13, 3237. [Google Scholar] [CrossRef]
- Askes, S.H.C.; Reddy, G.U.; Wyrwa, R.; Bonnet, S.; Schiller, A. Red Light-Triggered CO Release from Mn2(CO)10 Using Triplet Sensitization in Polymer Nonwoven Fabrics. J. Am. Chem. Soc. 2017, 139, 15292–15295. [Google Scholar] [CrossRef] [PubMed]
- García-López, V.; Chen, F.; Nilewski, L.G.; Duret, G.; Aliyan, A.; Kolomeisky, A.B.; Robinson, J.T.; Wang, G.; Pal, R.; Tour, J.M. Molecular Machines Open Cell Membranes. Nature 2017, 548, 567–572. [Google Scholar] [CrossRef] [PubMed]
- Ayala-Orozco, C.; Galvez-Aranda, D.; Corona, A.; Seminario, J.M.; Rangel, R.; Myers, J.N.; Tour, J.M. Molecular Jackhammers Eradicate Cancer Cells by Vibronic-Driven Action. Nat. Chem. 2024, 16, 456–465. [Google Scholar] [CrossRef] [PubMed]
- Sinkger, N.K.; Gonzalez, L.; Monari, A. Molecular Photoswitches Regulating the Activity of the Human Serotonin Transporter. J. Phys. Chem. Lett. 2023, 14, 10333–10339. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Morstein, J.; Ladefoged, L.K.; Maesen, J.B.; Schiøtt, B.; Sinning, S.; Trauner, D. A Photoswitchable Inhibitor of the Human Serotonin Transporter. ACS Chem. Neurosci. 2020, 11, 1231–1237. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zheng, M.; Xie, Z. Carrier-Free Core–Shell Nanodrugs for Synergistic Two-Photon Photodynamic Therapy of Cervical Cancer. J. Colloid. Interface Sci. 2019, 535, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Kuptniratsaikul, V.; Dajpratham, P.; Taechaarpornkul, W.; Buntragulpoontawee, M.; Lukkanapichonchut, P.; Chootip, C.; Saengsuwan, J.; Tantayakom, K.; Laongpech, S. Efficacy and Safety of Curcuma Domestica Extracts Compared with Ibuprofen in Patients with Knee Osteoarthritis: A Multicenter Study. Clin. Interv. Aging 2014, 9, 451–458. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Zhuang, X.; Xiang, X.; Liu, Y.; Zhang, S.; Liu, C.; Barnes, S.; Grizzle, W.; Miller, D.; Zhang, H.G. A Novel Nanoparticle Drug Delivery System: The Anti-Inflammatory Activity of Curcumin Is Enhanced When Encapsulated in Exosomes. Mol. Ther. 2010, 18, 1606–1614. [Google Scholar] [CrossRef]
- Losantos, R.; Pasc, A.; Monari, A. Don’t Help Them to Bury the Light. The Interplay between Intersystem Crossing and Hydrogen Transfer in Photoexcited Curcumin Revealed by Surface-Hopping Dynamics. Phys. Chem. Chem. Phys. 2021, 23, 24757–24764. [Google Scholar] [CrossRef]
- Tao, R.; Zhang, F.; Tang, Q.J.; Xu, C.S.; Ni, Z.J.; Meng, X. Effects of Curcumin-Based Photodynamic Treatment on the Storage Quality of Fresh-Cut Apples. Food Chem. 2019, 274, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Adhikary, R.; Barnes, C.A.; Trampel, R.L.; Wallace, S.J.; Kee, T.W.; Petrich, J.W. Photoinduced Trans-to-Cis Isomerization of Cyclocurcumin. J. Phys. Chem. B 2011, 115, 10707–10714. [Google Scholar] [CrossRef] [PubMed]
- Marazzi, M.; Francés-Monerris, A.; Mourer, M.; Pasc, A.; Monari, A. Trans -to- Cis Photoisomerization of Cyclocurcumin in Different Environments Rationalized by Computational Photochemistry. Phys. Chem. Chem. Phys. 2020, 22, 4749–4757. [Google Scholar] [CrossRef]
- Pecourneau, J.; Losantos, R.; Monari, A.; Parant, S.; Pasc, A.; Mourer, M. Synthesis and Photoswitching Properties of Bioinspired Dissymmetric γ-Pyrone, an Analogue of Cyclocurcumin. J. Org. Chem. 2021, 86, 8112–8126. [Google Scholar] [CrossRef]
- Losantos, R.; Pecourneau, J.; Mourer, M.; Parant, S.; Pasc, A.; Monari, A. Trans-CisPhotoisomerization of a Biomimetic Cyclocurcumin Analogue Rationalized by Molecular Modelling. Phys. Chem. Chem. Phys. 2021, 23, 12842–12849. [Google Scholar] [CrossRef]
- Delova, A.; Losantos, R.; Pecourneau, J.; Mourer, M.; Pasc, A.; Monari, A. Modelling the Effects of E/Z Photoisomerization of a Cyclocurcumin Analogue on the Properties of Cellular Lipid Membranes. Phys. Chem. Chem. Phys. 2023, 25, 20567–20574. [Google Scholar] [CrossRef]
- Pecourneau, J.; Losantos, R.R.; Delova, A.; Bernhard, Y.; Parant, S.S.; Mourer, M.; Monari, A.; Pasc, A. Biomimetic Photo-Switches Softening Model Lipid Membranes. Langmuir 2022, 38, 15642–15655. [Google Scholar] [CrossRef]
- Delova, A.; Losantos, R.; Pecourneau, J.; Bernhard, Y.; Mourer, M.; Pasc, A.; Monari, A. Perturbation of Lipid Bilayers by Biomimetic Photoswitches Based on Cyclocurcumin. J. Chem. Inf. Model. 2023, 63, 299–307. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef] [PubMed]
- Mennucci, B. Polarizable Continuum Model. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Barbatti, M. Nonadiabatic Dynamics with Trajectory Surface Hopping Method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 620–633. [Google Scholar] [CrossRef]
- Crespo-Otero, R.; Barbatti, M. Recent Advances and Perspectives on Nonadiabatic Mixed Quantum-Classical Dynamics. Chem. Rev. 2018, 118, 7026–7068. [Google Scholar] [CrossRef] [PubMed]
- Mai, S.; Marquetand, P.; González, L. Nonadiabatic Dynamics: The SHARC Approach. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1370. [Google Scholar] [CrossRef] [PubMed]
- Mai, S.; Avagliano, D.; Heindl, M.; Marquetand, P.; Menger, M.F.S.J.; Oppel, M.; Plasser, F.; Polonius, S.; Ruckenbauer, M.; Shu, Y.; et al. SHARC3.0: Surface Hopping Including Arbitrary Couplings—Program Package for Non-Adiabatic Dynamics. 2023. Available online: https://sharc-md.org/ (accessed on 5 April 2024).
- Polli, D.; Altoè, P.; Weingart, O.; Spillane, K.M.; Manzoni, C.; Brida, D.; Tomasello, G.; Orlandi, G.; Kukura, P.; Mathies, R.A.; et al. Conical Intersection Dynamics of the Primary Photoisomerization Event in Vision. Nature 2010, 467, 440–443. [Google Scholar] [CrossRef] [PubMed]
- Gozem, S.; Schapiro, I.; Ferre, N.; Olivucci, M. The Molecular Mechanism of Thermal Noise in Rod Photoreceptors. Science 2012, 337, 1225–1228. [Google Scholar] [CrossRef] [PubMed]
- Avagliano, D.; Bonfanti, M.; Garavelli, M.; González, L. QM/MM Nonadiabatic Dynamics: The SHARC/COBRAMM Approach. J. Chem. Theory Comput. 2021, 17, 4639–4647. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, V.K.; Kabaciński, P.; Nogueira de Faria, B.E.; Gentile, M.; de Paula, A.M.; Borrego-Varillas, R.; Nenov, A.; Conti, I.; Cerullo, G.; Garavelli, M. Environment-Driven Coherent Population Transfer Governs the Ultrafast Photophysics of Tryptophan. J. Am. Chem. Soc. 2022, 144, 12884–12892. [Google Scholar] [CrossRef] [PubMed]
- Bondanza, M.; Demoulin, B.; Lipparini, F.; Barbatti, M.; Mennucci, B. Trajectory Surface Hopping for a Polarizable Embedding QM/MM Formulation. J. Phys. Chem. A 2022, 126, 6780–6789. [Google Scholar] [CrossRef]
- Stojanović, L.; Aziz, S.G.; Hilal, R.H.; Plasser, F.; Niehaus, T.A.; Barbatti, M. Nonadiabatic Dynamics of Cycloparaphenylenes with TD-DFTB Surface Hopping. J. Chem. Theory Comput. 2017, 13, 5846–5860. [Google Scholar] [CrossRef]
- Dral, P.O.; Barbatti, M.; Thiel, W. Nonadiabatic Excited-State Dynamics with Machine Learning. J. Phys. Chem. Lett. 2018, 9, 5660–5663. [Google Scholar] [CrossRef]
- Zobel, J.P.; Heindl, M.; Plasser, F.; Mai, S.; González, L. Surface Hopping Dynamics on Vibronic Coupling Models. Acc. Chem. Res. 2021, 54, 3760–3771. [Google Scholar] [CrossRef]
- Plasser, F.; Gómez, S.; Menger, M.F.S.J.; Mai, S.; González, L. Highly Efficient Surface Hopping Dynamics Using a Linear Vibronic Coupling Model. Phys. Chem. Chem. Phys. 2019, 21, 57–69. [Google Scholar] [CrossRef]
- Mai, S.; Menger, M.F.S.J.; Marazzi, M.; Stolba, D.L.; Monari, A.; González, L. Competing Ultrafast Photoinduced Electron Transfer and Intersystem Crossing of [Re(CO)3(Dmp)(His124)(Trp122)]+ in Pseudomonas Aeruginosa Azurin: A Nonadiabatic Dynamics Study. Theor. Chem. Acc. 2020, 139, 65. [Google Scholar] [CrossRef] [PubMed]
- Mai, S.; González, L. Unconventional Two-Step Spin Relaxation Dynamics of [Re(CO)3(Im)(Phen)]+ in Aqueous Solution. Chem. Sci. 2019, 10, 10405–10411. [Google Scholar] [CrossRef]
- Vilhena, J.G.; Greff Da Silveira, L.; Livotto, P.R.; Cacelli, I.; Prampolini, G. Automated Parameterization of Quantum Mechanically Derived Force Fields for Soft Materials and Complex Fluids: Development and Validation. J. Chem. Theory Comput. 2021, 17, 4449–4464. [Google Scholar] [CrossRef]
- Barone, V.; Cacelli, I.; De Mitri, N.; Licari, D.; Monti, S.; Prampolini, G. Joyce and Ulysses: Integrated and User-Friendly Tools for the Parameterization of Intramolecular Force Fields from Quantum Mechanical Data. Phys. Chem. Chem. Phys. 2013, 15, 3736–3751. [Google Scholar] [CrossRef]
- Segalina, A.; Aranda, D.; Green, J.A.; Cristino, V.; Caramori, S.; Prampolini, G.; Pastore, M.; Santoro, F. How the Interplay among Conformational Disorder, Solvation, Local, and Charge-Transfer Excitations Affects the Absorption Spectrum and Photoinduced Dynamics of Perylene Diimide Dimers: A Molecular Dynamics/Quantum Vibronic Approach. J. Chem. Theory Comput. 2022, 18, 3718–3736. [Google Scholar] [CrossRef]
- Prampolini, G.; Ingrosso, F.; Segalina, A.; Caramori, S.; Foggi, P.; Pastore, M. Dynamical and Environmental Effects on the Optical Properties of an Heteroleptic Ru(II)–Polypyridine Complex: A Multilevel Approach Combining Accurate Ground and Excited State QM-Derived Force Fields, MD and TD-DFT. J. Chem. Theory Comput. 2019, 15, 529–545. [Google Scholar] [CrossRef] [PubMed]
- Cerezo, J.; García-Iriepa, C.; Santoro, F.; Navizet, I.; Prampolini, G. Unraveling the Contributions to the Spectral Shape of Flexible Dyes in Solution: Insights on the Absorption Spectrum of an Oxyluciferin Analogue. Phys. Chem. Chem. Phys. 2023, 25, 5007–5020. [Google Scholar] [CrossRef]
- Cerezo, J.; Prampolini, G.; Cacelli, I. Developing Accurate Intramolecular Force Fields for Conjugated Systems through Explicit Coupling Terms. Theor. Chem. Acc. 2018, 137, 80. [Google Scholar] [CrossRef]
- Cacelli, I.; Prampolini, G. Parametrization and Validation of Intramolecular Force Fields Derived from DFT Calculations. J. Chem. Theory Comput. 2007, 3, 1803–1817. [Google Scholar] [CrossRef] [PubMed]
- Prampolini, G.; Campetella, M.; Ferretti, A. Solvent Effects on Catechol’s Binding Affinity: Investigating the Role of the Intra-Molecular Hydrogen Bond through a Multi-Level Computational Approach. Phys. Chem. Chem. Phys. 2023, 25, 2523–2536. [Google Scholar] [CrossRef]
- Fonseca, T.; Ladanyi, B.M. Breakdown of Linear Response for Solvation Dynamics in Methanol. J. Phys. Chem. 1991, 95, 2116–2119. [Google Scholar] [CrossRef]
- Fonseca, T.; Ladanyi, B.M. Solvation Dynamics in Methanol: Solute and Perturbation Dependence. J. Mol. Liq. 1994, 60, 1–24. [Google Scholar] [CrossRef]
- Cerezo, J.; Gao, S.; Armaroli, N.; Ingrosso, F.; Prampolini, G.; Santoro, F.; Ventura, B.; Pastore, M. Non-Phenomenological Description of the Time-Resolved Emission in Solution with Quantum–Classical Vibronic Approaches—Application to Coumarin C153 in Methanol. Molecules 2023, 28, 3910. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. G16_C01 2016, Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Mark, J.A.; Teemu, M.; Roland, S.; Szilárd, P.; Jeremy, C.S.; Berk, H.; Erik, L. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Losantos, R.; Prampolini, G.; Monari, A. A Portrait of the Chromophore as a Young System—Quantum-Derived Force Field Unraveling Solvent Reorganization upon Optical Excitation of Cyclocurcumin Derivatives. Molecules 2024, 29, 1752. https://doi.org/10.3390/molecules29081752
Losantos R, Prampolini G, Monari A. A Portrait of the Chromophore as a Young System—Quantum-Derived Force Field Unraveling Solvent Reorganization upon Optical Excitation of Cyclocurcumin Derivatives. Molecules. 2024; 29(8):1752. https://doi.org/10.3390/molecules29081752
Chicago/Turabian StyleLosantos, Raúl, Giacomo Prampolini, and Antonio Monari. 2024. "A Portrait of the Chromophore as a Young System—Quantum-Derived Force Field Unraveling Solvent Reorganization upon Optical Excitation of Cyclocurcumin Derivatives" Molecules 29, no. 8: 1752. https://doi.org/10.3390/molecules29081752
APA StyleLosantos, R., Prampolini, G., & Monari, A. (2024). A Portrait of the Chromophore as a Young System—Quantum-Derived Force Field Unraveling Solvent Reorganization upon Optical Excitation of Cyclocurcumin Derivatives. Molecules, 29(8), 1752. https://doi.org/10.3390/molecules29081752






