An Update in Computational Methods for Environmental Monitoring: Theoretical Evaluation of the Molecular and Electronic Structures of Natural Pigment–Metal Complexes
Abstract
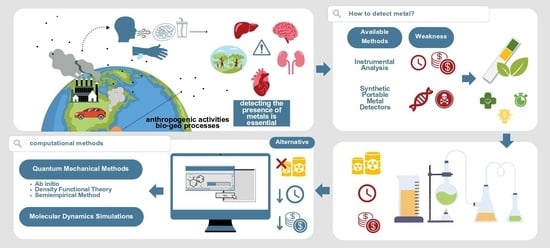
1. Introduction
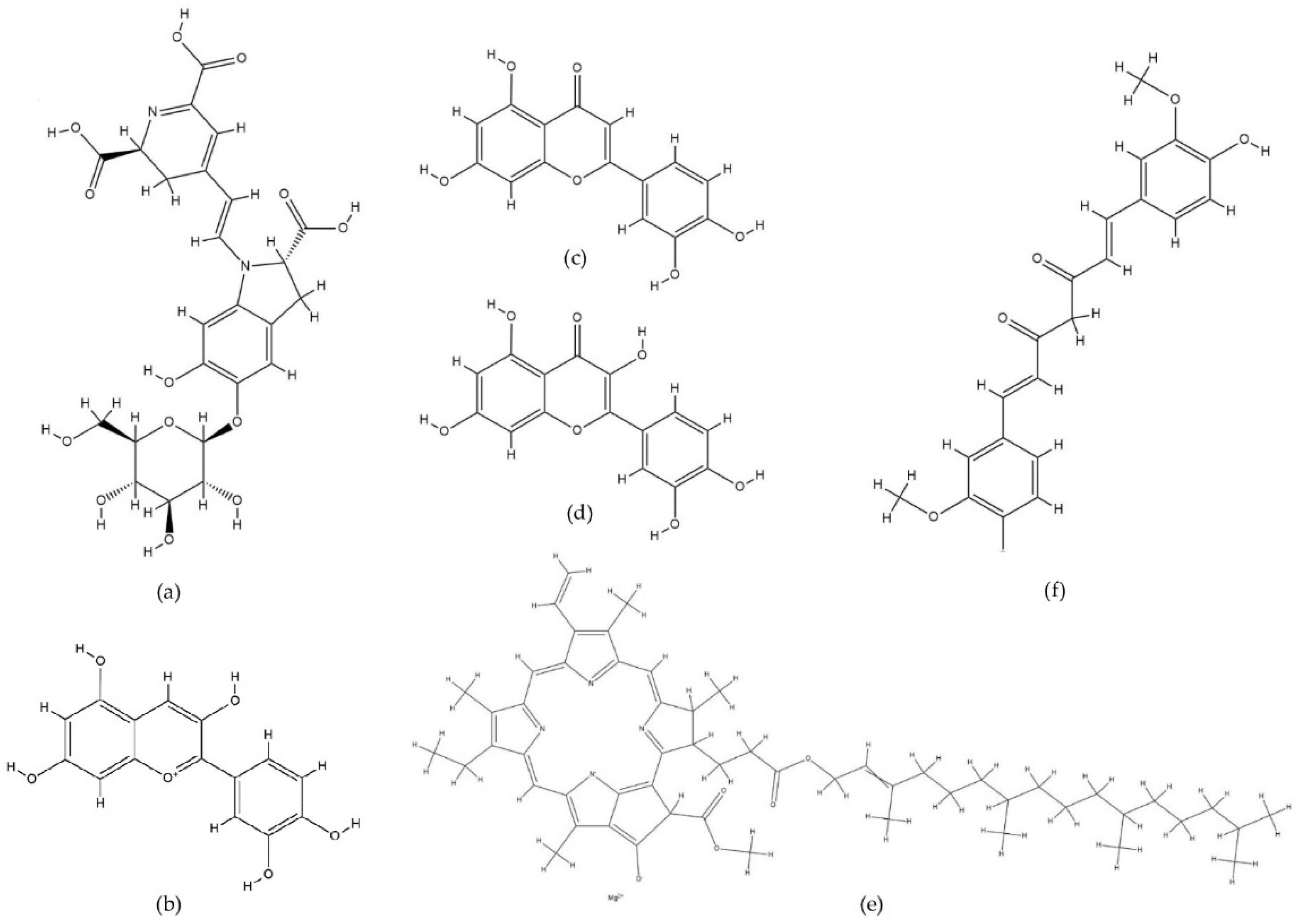
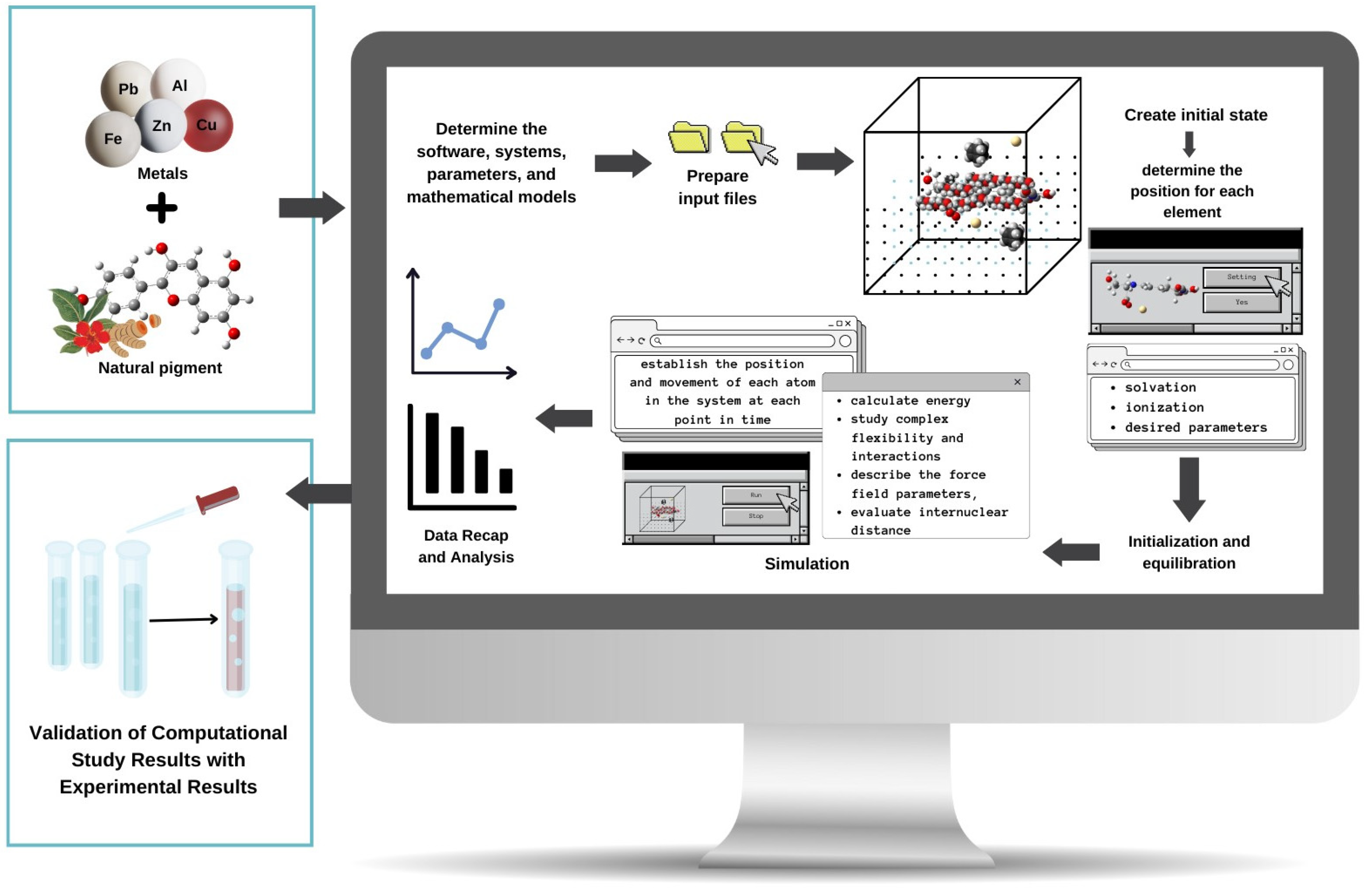
2. Computational Methods for Studying Metal–Pigment Interactions in General
3. Quantum Mechanical Methods to Study Metal–Pigment Interactions
3.1. Ab Initio Methods
3.2. Density Functional Theory (DFT)
3.3. Semiempirical Methods to Study Metal–Pigment Interactions
4. Molecular Dynamics Methods to Study Metal–Pigment Interactions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mendel, R.R.; Smith, A.G.; Marquet, A.; Warren, M.J. Metal and Cofactor Insertion. Nat. Prod. Rep. 2007, 24, 963. [Google Scholar] [CrossRef] [PubMed]
- Permyakov, E.A. Metal Binding Proteins. Encyclopedia 2021, 1, 261–292. [Google Scholar] [CrossRef]
- Fu, F.; Wang, Q. Removal of Heavy Metal Ions from Wastewaters: A Review. J. Environ. Manag. 2011, 92, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Tchounwou, P.B.; Yedjou, C.G.; Patlolla, A.K.; Sutton, D.J. Heavy Metal Toxicity and the Environment. In Molecular, Clinical and Environmental Toxicology; Springer: Berlin/Heidelberg, Germany, 2012; pp. 133–164. [Google Scholar]
- Wieczorek-Dąbrowska, M.; Tomza-Marciniak, A.; Pilarczyk, B.; Balicka-Ramisz, A. Roe and Red Deer as Bioindicators of Heavy Metals Contamination in North-Western Poland. Chem. Ecol. 2013, 29, 100–110. [Google Scholar] [CrossRef]
- Agwu, K.K.; Okoye, C.M.I.; Okeji, M.C.; Clifford, E.O. Potential Health Impacts of Heavy Metal Concentrations in Fresh and Marine Water Fishes Consumed in Southeast, Nigeria. Pak. J. Nutr. 2018, 17, 647–653. [Google Scholar] [CrossRef]
- Fu, Z.; Xi, S. The Effects of Heavy Metals on Human Metabolism. Toxicol. Mech. Methods 2020, 30, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Manoj, S.R.; Karthik, C.; Kadirvelu, K.; Arulselvi, P.I.; Shanmugasundaram, T.; Bruno, B.; Rajkumar, M. Understanding the Molecular Mechanisms for the Enhanced Phytoremediation of Heavy Metals through Plant Growth Promoting Rhizobacteria: A Review. J. Environ. Manag. 2020, 254, 109779. [Google Scholar] [CrossRef]
- Jaishankar, M.; Tseten, T.; Anbalagan, N.; Mathew, B.B.; Beeregowda, K.N. Toxicity, Mechanism and Health Effects of Some Heavy Metals. Interdiscip. Toxicol. 2014, 7, 60–72. [Google Scholar] [CrossRef] [PubMed]
- Al-Samman, T. Effect of Heavy Metal Impurities in Secondary Mg Alloys on the Microstructure and Mechanical Properties during Deformation. Mater. Des. 2015, 65, 983–988. [Google Scholar] [CrossRef]
- Rehman, K.; Fatima, F.; Waheed, I.; Akash, M.S.H. Prevalence of Exposure of Heavy Metals and Their Impact on Health Consequences. J. Cell Biochem. 2018, 119, 157–184. [Google Scholar] [CrossRef]
- He, T.; Feng, X.; Guo, Y.; Qiu, G.; Li, Z.; Liang, L.; Lu, J. The Impact of Eutrophication on the Biogeochemical Cycling of Mercury Species in a Reservoir: A Case Study from Hongfeng Reservoir, Guizhou, China. Environ. Pollut. 2008, 154, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Mazumder, M.A.J.; Al-Attas, O.; Husain, T. Heavy Metals in Drinking Water: Occurrences, Implications, and Future Needs in Developing Countries. Sci. Total Environ. 2016, 569–570, 476–488. [Google Scholar] [CrossRef]
- Asati, A.; Pichhode, M.; Nikhil, K. Effect of Heavy Metals on Plants: An Overview. Int. J. Appl. Innov. Eng. Manag. 2016, 5, 56–66. [Google Scholar]
- Ali, H.; Khan, E. What Are Heavy Metals? Long-Standing Controversy over the Scientific Use of the Term ‘Heavy Metals’—Proposal of a Comprehensive Definition. Toxicol. Environ. Chem. 2018, 100, 6–19. [Google Scholar] [CrossRef]
- Nurchi, V.; Crespo-Alonso, M.; Toso, L.; Lachowicz, J.; Crisponi, G. Chelation Therapy for Metal Intoxication: Comments from a Thermodynamic Viewpoint. Mini-Rev. Med. Chem. 2013, 13, 1541–1549. [Google Scholar] [CrossRef]
- Corrente, G.A.; Malacaria, L.; Beneduci, A.; Furia, E.; Marino, T.; Mazzone, G. Experimental and Theoretical Study on the Coordination Properties of Quercetin towards Aluminum(III), Iron(III) and Copper(II) in Aqueous Solution. J. Mol. Liq. 2021, 325, 115171. [Google Scholar] [CrossRef]
- Abd Elnabi, M.K.; Elkaliny, N.E.; Elyazied, M.M.; Azab, S.H.; Elkhalifa, S.A.; Elmasry, S.; Mouhamed, M.S.; Shalamesh, E.M.; Alhorieny, N.A.; Abd Elaty, A.E.; et al. Toxicity of Heavy Metals and Recent Advances in Their Removal: A Review. Toxics 2023, 11, 580. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Singh, N.; Rai, S.N.; Kumar, A.; Singh, A.K.; Singh, M.P.; Sahoo, A.; Shekhar, S.; Vamanu, E.; Mishra, V. Heavy Metal Contamination in the Aquatic Ecosystem: Toxicity and Its Remediation Using Eco-Friendly Approaches. Toxics 2023, 11, 147. [Google Scholar] [CrossRef]
- Luo, A.; Wang, H.; Wang, Y.; Huang, Q.; Zhang, Q. A Novel Colorimetric and Turn-on Fluorescent Chemosensor for Iron (III) Ion Detection and Its Application to Cellular Imaging. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2016, 168, 37–44. [Google Scholar] [CrossRef]
- Barbieri, M. The Importance of Enrichment Factor (EF) and Geoaccumulation Index (Igeo) to Evaluate the Soil Contamination. J. Geol. Geophys. 2016, 5, 1–4. [Google Scholar] [CrossRef]
- Patrick, L. Mercury Toxicity and Antioxidants: Part I: Role of Glutathione and Alpha-Lipoic Acid in the Treatment of Mercury Toxicity (Mercury Toxicity). Altern. Med. Rev. 2002, 7, 456–472. [Google Scholar] [PubMed]
- Castagnetto, J.M.; Hennessy, S.W.; Roberts, V.A.; Getzoff, E.D.; Tainer, J.A.; Pique, M.E. MDB: The Metalloprotein Database and Browser at the Scripps Research Institute. Nucleic Acids Res. 2002, 30, 379–382. [Google Scholar] [CrossRef] [PubMed]
- Lane, T.W.; Morel, F.M.M. A Biological Function for Cadmium in Marine Diatoms. Proc. Natl. Acad. Sci. USA 2000, 97, 4627–4631. [Google Scholar] [CrossRef] [PubMed]
- Lambing, A.; Kachalsky, E.; Mueller, M.L. The Dangers of Iron Overload: Bring in the Iron Police. J. Am. Acad. Nurse Pract. 2012, 24, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Kwiatkowski, J.L.; Cohen, A.R. Iron Chelation Therapy in Sickle-Cell Disease and Other Transfusion-Dependent Anemias. Hematol. Oncol. Clin. 2004, 18, 1355–1377. [Google Scholar] [CrossRef] [PubMed]
- Cappellini, M.D.; Taher, A. Deferasirox (Exjade®) for the Treatment of Iron Overload. Acta Haematol. 2009, 122, 165–173. [Google Scholar] [CrossRef]
- Abetz, L.; Baladi, J.-F.; Jones, P.; Rofail, D. The Impact of Iron Overload and Its Treatment on Quality of Life: Results from a Literature Review. Health Qual. Life Outcomes 2006, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization Guidelines for Drinking-Water Quality, 4th ed.; Incorporating the 1st Addendum; WHO: Geneva, Switzerland, 2017.
- USEPA (U.S. Environmental Protection Agency). National Primary Drinking Water Regulations. Available online: https://www.epa.gov/ground-water-and-drinking-water/national-primary-drinking-water-regulations (accessed on 25 November 2023).
- Khan, F.U.; Rahman, A.U.; Jan, A.; Riaz, M. Toxic and Trace Metals (Pb, Cd, Zn, Cu, Mn, Ni, Co and Cr) in Dust, Dustfall/Soil. J. Chem. Soc. Pak. 2004, 26, 453–456. [Google Scholar]
- Ali, H.; Khan, E.; Sajad, M.A. Phytoremediation of Heavy Metals—Concepts and Applications. Chemosphere 2013, 91, 869–881. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.; Khan, E. Environmental Chemistry in the Twenty-First Century. Environ. Chem. Lett. 2017, 15, 329–346. [Google Scholar] [CrossRef]
- Hashem, M.A.; Nur-A-Tomal, M.S.; Mondal, N.R.; Rahman, M.A. Hair Burning and Liming in Tanneries Is a Source of Pollution by Arsenic, Lead, Zinc, Manganese and Iron. Environ. Chem. Lett. 2017, 15, 501–506. [Google Scholar] [CrossRef]
- Ali, H.; Khan, E.; Ilahi, I. Environmental Chemistry and Ecotoxicology of Hazardous Heavy Metals: Environmental Persistence, Toxicity, and Bioaccumulation. J. Chem. 2019, 2019, 6730305. [Google Scholar] [CrossRef]
- Wang, G.; Yinglan, A.; Jiang, H.; Fu, Q.; Zheng, B. Modeling the Source Contribution of Heavy Metals in Surficial Sediment and Analysis of Their Historical Changes in the Vertical Sediments of a Drinking Water Reservoir. J. Hydrol. 2015, 520, 37–51. [Google Scholar] [CrossRef]
- Miedico, O.; Pompa, C.; Moscatelli, S.; Chiappinelli, A.; Carosielli, L.; Chiaravalle, A.E. Lead, Cadmium and Mercury in Canned and Unprocessed Tuna: Six-Years Monitoring Survey, Comparison with Previous Studies and Recommended Tolerable Limits. J. Food Compos. Anal. 2020, 94, 103638. [Google Scholar] [CrossRef]
- Abedin, M.J.; Khan, R.; Siddique, M.A.B.; Khan, A.H.A.N.; Islam, M.T.; Rashid, M.B. Metal (Loid) s in Tap-Water from Schools in Central Bangladesh (Mirpur): Source Apportionment, Water Quality, and Health Risks Appraisals. Heliyon 2023, 9, e15747. [Google Scholar] [CrossRef] [PubMed]
- Mulyaningsih, R.D.; Pratiwi, R.; Hasanah, A.N. An Update on the Use of Natural Pigments and Pigment Nanoparticle Adducts for Metal Detection Based on Colour Response. Biosensors 2023, 13, 554. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Y.; Yue, X.; Ren, D.; Liu, Y.; Yang, K. Identification and Hazard Analysis of Heavy Metal Sources in Agricultural Soils in Ancient Mining Areas: A Quantitative Method Based on the Receptor Model and Risk Assessment. J. Hazard. Mater. 2023, 445, 130528. [Google Scholar] [CrossRef]
- Singh, M.R. Impurities-Heavy Metals: IR Perspective. Int. J. Phys. Sci. 2007, 5, 1045–1058. [Google Scholar]
- Aragay, G.; Merkoci, A. Nanomaterials Application in Electrochemical Detection of Heavy Metals. Electrochim. Acta 2012, 84, 49–61. [Google Scholar] [CrossRef]
- Gong, T.; Liu, J.; Liu, X.; Liu, J.; Xiang, J.; Wu, Y. A Sensitive and Selective Sensing Platform Based on CdTe QDs in the Presence of L-Cysteine for Detection of Silver, Mercury and Copper Ions in Water and Various Drinks. Food Chem. 2016, 213, 306–312. [Google Scholar] [CrossRef]
- Chen, J.; Teo, K.C. Determination of Cadmium, Copper, Lead and Zinc in Water Samples by Flame Atomic Absorption Spectrometry after Cloud Point Extraction. Anal. Chim. Acta 2001, 450, 215–222. [Google Scholar] [CrossRef]
- Sitko, R.; Janik, P.; Zawisza, B.; Talik, E.; Margui, E.; Queralt, I. Green Approach for Ultratrace Determination of Divalent Metal Ions and Arsenic Species Using Total-Reflection X-ray Fluorescence Spectrometry and Mercapto-Modified Graphene Oxide Nanosheets as a Novel Adsorbent. Anal. Chem. 2015, 87, 3535–3542. [Google Scholar] [CrossRef] [PubMed]
- Pöykiö, R.; Perämäki, P. Acid Dissolution Methods for Heavy Metals Determination in Pine Needles. Environ. Chem. Lett. 2003, 1, 191–195. [Google Scholar] [CrossRef]
- Losev, V.N.; Buyko, O.V.; Trofimchuk, A.K.; Zuy, O.N. Silica Sequentially Modified with Polyhexamethylene Guanidine and Arsenazo I for Preconcentration and ICP–OES Determination of Metals in Natural Waters. Microchem. J. 2015, 123, 84–89. [Google Scholar] [CrossRef]
- Gałuszka, A.; Migaszewski, Z.M.; Namieśnik, J. Moving Your Laboratories to the Field—Advantages and Limitations of the Use of Field Portable Instruments in Environmental Sample Analysis. Environ. Res. 2015, 140, 593–603. [Google Scholar] [CrossRef] [PubMed]
- Sigurdson, G.T.; Tang, P.; Giusti, M.M. Natural Colorants: Food Colorants from Natural Sources. Annu. Rev. Food Sci. Technol. 2017, 8, 261–280. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Mena, A.; Ochoa-Martínez, L.A.; González-Herrera, S.M.; Rutiaga-Quiñones, O.M.; González-Laredo, R.F.; Olmedilla-Alonso, B. Natural Pigments of Plant Origin: Classification, Extraction and Application in Foods. Food Chem. 2023, 398, 133908. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, A.A.; Cichelli, A.; Lorenzo, C. Colors: Properties and Determination of Natural Pigments. In Encyclopedia of Food and Health; Elsevier: Amsterdam, The Netherlands, 2016; pp. 273–284. ISBN 0123849535. [Google Scholar]
- Oyama, K.; Yamada, T.; Ito, D.; Kondo, T.; Yoshida, K. Metal Complex Pigment Involved in the Blue Sepal Color Development of Hydrangea. J. Agric. Food Chem. 2015, 63, 7630–7635. [Google Scholar] [CrossRef]
- Fedenko, V.S.; Shemet, S.A.; Landi, M. UV–Vis Spectroscopy and Colorimetric Models for Detecting Anthocyanin-Metal Complexes in Plants: An Overview of in Vitro and in Vivo Techniques. J. Plant Physiol. 2017, 212, 13–28. [Google Scholar] [CrossRef]
- Christie, R.; Abel, A. Metal Complex Pigments. Phys. Sci. Rev. 2021, 6, 375–389. [Google Scholar] [CrossRef]
- Wybraniec, S.; Starzak, K.; Skopińska, A.; Szaleniec, M.; Słupski, J.; Mitka, K.; Kowalski, P.; Michałowski, T. Effects of Metal Cations on Betanin Stability in Aqueous-Organic Solutions. Food Sci. Biotechnol. 2013, 22, 353–363. [Google Scholar] [CrossRef]
- Saithongdee, A.; Praphairaksit, N.; Imyim, A. Electrospun Curcumin-Loaded Zein Membrane for Iron (III) Ions Sensing. Sens. Actuators B Chem. 2014, 202, 935–940. [Google Scholar] [CrossRef]
- Khaodee, W.; Aeungmaitrepirom, W.; Tuntulani, T. Effectively Simultaneous Naked-Eye Detection of Cu(II), Pb(II), Al(III) and Fe(III) Using Cyanidin Extracted from Red Cabbage as Chelating Agent. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 126, 98–104. [Google Scholar] [CrossRef]
- Yılmaz, D.D.; Demirezen, D.A.; Mıhçıokur, H. Colorimetric Detection of Mercury Ion Using Chlorophyll Functionalized Green Silver Nanoparticles in Aqueous Medium. Surf. Interfaces 2021, 22, 100840. [Google Scholar] [CrossRef]
- Mohan, A.; Prakash, J. Fabrication of Eco-Friendly Hydrogel Strips for the Simultaneous Quantification of Heavy Metal Ions in Aqueous Environment. Dye. Pigment. 2022, 199, 110045. [Google Scholar] [CrossRef]
- Raj, S.; Shankaran, D.R. Curcumin Based Biocompatible Nanofibers for Lead Ion Detection. Sens. Actuators B Chem. 2016, 226, 318–325. [Google Scholar] [CrossRef]
- Sheikhzadeh, E.; Naji-Tabasi, S.; Verdian, A.; Kolahi-Ahari, S. Equipment-Free and Visual Detection of Pb2+ Ion Based on Curcumin-Modified Bacterial Cellulose Nanofiber. J. Iran. Chem. Soc. 2022, 19, 283–290. [Google Scholar] [CrossRef]
- Kumar, P.; Paul, W.; Sharma, C.P. Curcumin Stabilized Gold Nanoparticle-Based Colorimetric Sensing of Mercury (II). Trends Biomater. Artif. Organs 2014, 28, 121–123. [Google Scholar]
- Zin, M.M.; Márki, E.; Bánvölgyi, S. Conventional Extraction of Betalain Compounds from Beetroot Peels with Aqueous Ethanol Solvent. Acta Aliment. 2020, 49, 163–169. [Google Scholar] [CrossRef]
- Malacaria, L.; La Torre, C.; Furia, E.; Fazio, A.; Caroleo, M.C.; Cione, E.; Gallelli, L.; Marino, T.; Plastina, P. Aluminum (III), Iron (III) and Copper (II) Complexes of Luteolin: Stability, Antioxidant, and Anti-Inflammatory Properties. J. Mol. Liq. 2022, 345, 117895. [Google Scholar] [CrossRef]
- Eno, E.A.; Shagal, M.H.; Godfrey, O.C.; Ngana, O.C.; Ekong, J.E.; Benjamin, I.; Ugi, B.U.; Louis, H. Computational Study of the Interaction of Metal Ions (Na+, K+, Mg2+, Ca2+, and Al3+) with Quercetin and Its Antioxidant Properties. J. Indian. Chem. Soc. 2023, 100, 101059. [Google Scholar] [CrossRef]
- Swart, M.; Gruden, M. Spinning around in Transition-Metal Chemistry. Acc. Chem. Res. 2016, 49, 2690–2697. [Google Scholar] [CrossRef] [PubMed]
- Alzahrani, E. Colorimetric Detection Based on Localized Surface Plasmon Resonance Optical Characteristics for Sensing of Mercury Using Green-Synthesized Silver Nanoparticles. J. Anal. Methods Chem. 2020, 2020, 6026312. [Google Scholar] [CrossRef] [PubMed]
- Mahimwalla, Z.; Yager, K.G.; Mamiya, J.I.; Shishido, A.; Priimagi, A.; Barrett, C.J. Azobenzene Photomechanics: Prospects and Potential Applications. Polym. Bull. 2012, 69, 967–1006. [Google Scholar] [CrossRef]
- Sousa, S.F.; Ribeiro, A.J.M.; Neves, R.P.P.; Brás, N.F.; Cerqueira, N.M.F.S.A.; Fernandes, P.A.; Ramos, M.J. Application of Quantum Mechanics/Molecular Mechanics Methods in the Study of Enzymatic Reaction Mechanisms. WIREs Comput. Mol. Sci. 2017, 7, 1281. [Google Scholar] [CrossRef]
- Starikov, A.G.; Starikova, A.A.; Minkin, V.I. Quantum-Chemical Study of (Z)-6,8-Di-Tert-Butyl-N-(4-Methoxyphenyl)-3-((4-Methoxyphenyl)Imino)-3H-Phenoxazine-2-Amine Complexation with Cobalt Bis(Chelate)s. Doklady Chem. 2017, 476, 215–218. [Google Scholar] [CrossRef]
- Ajaykamal, T.; Palaniandavar, M. Mononuclear Nickel(Ii)-Flavonolate Complexes of Tetradentate Tripodal 4N Ligands as Structural and Functional Models for Quercetin 2,4-Dioxygenase: Structures, Spectra, Redox and Dioxygenase Activity. RSC Adv. 2023, 13, 24674–24690. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Chen, W.; Cao, W.; Zhang, F.; Song, J.; Tian, C. Research on the Chelation between Quercetin and Cr (III) Ion by Density Functional Theory (DFT) Method. J. Mol. Struct. THEOCHEM 2008, 860, 40–44. [Google Scholar] [CrossRef]
- Furia, E.; Marino, T.; Russo, N. Insights into the Coordination Mode of Quercetin with the Al(III) Ion from a Combined Experimental and Theoretical Study. Dalton Trans. 2014, 43, 7269–7274. [Google Scholar] [CrossRef]
- Cornard, J.P.; Merlin, J.C. Spectroscopic and Structural Study of Complexes of Quercetin with Al(III). J. Inorg. Biochem. 2002, 92, 19–27. [Google Scholar] [CrossRef]
- Ren, J.; Meng, S.; Lekka, C.E.; Kaxiras, E. Complexation of Flavonoids with Iron: Structure and Optical Signatures. J. Phys. Chem. B 2008, 112, 1845–1850. [Google Scholar] [CrossRef] [PubMed]
- Leopoldini, M.; Russo, N.; Chiodo, S.; Toscano, M. Iron Chelation by the Powerful Antioxidant Flavonoid Quercetin. J. Agric. Food Chem. 2006, 54, 6343–6351. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R.; Yang, K.; Hashem, K.; Jiang, J. Metallated Porphyrinic Metal− Organic Frameworks for CO2 Conversion to HCOOH: A Computational Screening and Mechanistic Study. Mol. Catal. 2022, 527, 112407. [Google Scholar] [CrossRef]
- Mollaamin, F.; Mohammadian, N.T.; Najaflou, N.; Monajjemi, M. Iranian Qara Qat Fruit (Redcurrant) in Arasbaran Forests as the Resource of Anthocyanin Pigments in Formation of [ACN-Mg2+/Al3+/Ga3+/Sn2+/Cr3+/Fe3+] Chelation Clusters. SN Appl. Sci. 2021, 3, 404. [Google Scholar] [CrossRef]
- Hong, B.; Zhao, D.; Li, W.; Li, S. Generalized Energy-Based Fragmentation Approach for Structures and Properties of Periodic Condensed Phase Systems. In Comprehensive Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2024; pp. 129–138. [Google Scholar]
- Spiegel, M.; Sroka, Z. Quantum-Mechanical Characteristics of Apigenin: Antiradical, Metal Chelation and Inhibitory Properties in Physiologically Relevant Media. Fitoterapia 2023, 164, 105352. [Google Scholar] [CrossRef]
- Renger, T. Theory of Excitation Energy Transfer: From Structure to Function. Photosynth. Res. 2009, 102, 471–485. [Google Scholar] [CrossRef] [PubMed]
- Estévez, L.; Sánchez-Lozano, M.; Mosquera, R.A. Complexation of Common Metal Cations by Cyanins: Binding Affinity and Molecular Structure. Int. J. Quantum Chem. 2019, 119, 25834. [Google Scholar] [CrossRef]
- Bechaieb, R.; Fredj, A.B.; Akacha, A.B.; Gérard, H. Interactions of Copper (II) and Zinc (II) with Chlorophyll: Insights from Density Functional Theory Studies. New J. Chem. 2016, 40, 4543–4549. [Google Scholar] [CrossRef]
- Frison, G.; Ohanessian, G. A Comparative Study of Semiempirical, Ab Initio, and DFT Methods in Evaluating Metal-Ligand Bond Strength, Proton Affinity, and Interactions between First and Second Shell Ligands in Zn-Biomimetic Complexes. J. Comput. Chem. 2008, 29, 416–433. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.; Hansen, A.; Grimme, S. Best-Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. Int. Ed. 2022, 61, 5735. [Google Scholar] [CrossRef]
- Enaru, B.; Drețcanu, G.; Pop, T.D.; Stǎnilǎ, A.; Diaconeasa, Z. Anthocyanins: Factors Affecting Their Stability and Degradation. Antioxidants 2021, 10, 1967. [Google Scholar] [CrossRef]
- Ghiasi, M.; Molaei, M.; Zahedi, M. QM Study of Complexation between Natural Bilirubin and Poly-Terthiophene Carboxylic Acid-Mn(II) as a Biosensor: Temperature and Interferences Effect. J. Theor. Comput. Chem. 2015, 14, 1550048. [Google Scholar] [CrossRef]
- Fazary, A.E.; Alshihri, A.S.; Alfaifi, M.Y.; Saleh, K.A.; Elbehairi, S.E.I.; Fawy, K.F.; Abd-Rabboh, H.S.M. Gibbs Energies of Protonation and Complexation of Platinum and Vanadate Metal Ions with Naringenin and Phenolic Acids: Theoretical Calculations Associated with Experimental Values. J. Chem. Thermodyn. 2016, 100, 7–21. [Google Scholar] [CrossRef]
- Decherchi, S.; Masetti, M.; Vyalov, I.; Rocchia, W. Implicit Solvent Methods for Free Energy Estimation. Eur. J. Med. Chem. 2015, 91, 27–42. [Google Scholar] [CrossRef]
- Orzeł, Ł.; Waś, J.; Kania, A.; Susz, A.; Rutkowska-Zbik, D.; Staroń, J.; Witko, M.; Stochel, G.; Fiedor, L. Factors Controlling the Reactivity of Divalent Metal Ions towards Pheophytin a. J. Biol. Inorg. Chem. 2017, 22, 941–952. [Google Scholar] [CrossRef]
- Eilmes, A. Solvatochromic Probe in Molecular Solvents: Implicit versus Explicit Solvent Model. Theor. Chem. Acc. 2014, 133, 1–13. [Google Scholar] [CrossRef]
- Ehlert, S.; Stahn, M.; Spicher, S.; Grimme, S. Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods. J. Chem. Theory Comput. 2021, 17, 4250–4261. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Okur, A.; Wickstrom, L.; Layten, M.; Geney, R.; Song, K.; Hornak, V.; Simmerling, C. Improved Efficiency of Replica Exchange Simulations through Use of a Hybrid Explicit/Implicit Solvation Model. J. Chem. Theory Comput. 2006, 2, 420–433. [Google Scholar] [CrossRef]
- Brancato, G.; Rega, N.; Barone, V. A Hybrid Explicit/Implicit Solvation Method for First-Principle Molecular Dynamics Simulations. J. Chem. Phys. 2008, 128, 144501. [Google Scholar] [CrossRef]
- Lee, M.S.; Salsbury, F.R., Jr.; Olson, M.A. An Efficient Hybrid Explicit/Implicit Solvent Method for Biomolecular Simulations. J. Comput. Chem. 2004, 25, 1967–1978. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J.; Cai, Q. CO 2 Electroreduction Performance of a Single Transition Metal Atom Supported on Porphyrin-like Graphene: A Computational Study. Phys. Chem. Chem. Phys. 2017, 19, 23113–23121. [Google Scholar] [CrossRef]
- Pranowo, H.D. Kimia Komputasi; Universitas Gadjah Mada: Yogyakarta, Indonesia, 2000. [Google Scholar]
- Meyer, M. Ab Initio Study of Flavonoids. Int. J. Quantum Chem. 2000, 76, 724–732. [Google Scholar] [CrossRef]
- Yan, L.K.; Pomogaeva, A.; Gu, F.L.; Aoki, Y. Theoretical Study on Nonlinear Optical Properties of Metalloporphyrin Using Elongation Method. Theor. Chem. Acc. 2010, 125, 511–520. [Google Scholar] [CrossRef]
- Linnanto, J.; Korppi-Tommola, J. Structural and Spectroscopic Properties of Mg-Bacteriochlorin and Methyl Bacteriochlorophyllides a, b, g, and h Studied by Semiempirical, Ab Initio, and Density Functional Molecular Orbital Methods. J. Phys. Chem. A 2004, 108, 5872–5882. [Google Scholar] [CrossRef]
- Freitas, A.A.; Shimizu, K.; Dias, L.G.; Quina, F.H. A Computational Study of Substituted Flavylium Salts and Their Quinonoidal Conjugate-Bases: S0-> S1 Electronic Transition, Absolute PKa and Reduction Potential Calculations by DFT and Semiempirical Methods. J. Braz. Chem. Soc. 2007, 18, 1537–1546. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Z.-J.; Jiang, H.-D.; Chen, J.-Z. Computational Studies of the Regioselectivities of COMT-Catalyzed Meta-/Para.-O Methylations of Luteolin and Quercetin. J. Phys. Chem. B 2014, 118, 470–481. [Google Scholar] [CrossRef]
- Cavalheiro, E.P.; Cardoso, M.V.P.; De Souza, S.P.; Sousa, M.E.S.; Allan Leite Dos Reis, M. Correlation Between Clar Sextet Theory and Electronic Properties of Chromophores: An Ab Initio Study. J. Comput. Theor. Nanosci. 2017, 14, 1524–1527. [Google Scholar] [CrossRef]
- Yang, C.-H.; Huang, K.-S.; Wang, Y.-T.; Shaw, J.-F. A Review of Bacteriochlorophyllides: Chemical Structures and Applications. Molecules 2021, 26, 1293. [Google Scholar] [CrossRef]
- Tronrud, D.E.; Schmid, M.F.; Matthews, B.W. Structure and X-ray Amino Acid Sequence of a Bacteriochlorophyll a Protein from Prosthecochloris Aestuarii Refined at 1.9 Å Resolution. J. Mol. Biol. 1986, 188, 443–454. [Google Scholar] [CrossRef]
- Freer, A.; Prince, S.; Sauer, K.; Papiz, M.; Lawless, A.H.; McDermott, G.; Cogdell, R.; Isaacs, N.W. Pigment–Pigment Interactions and Energy Transfer in the Antenna Complex of the Photosynthetic Bacterium Rhodopseudomonas acidophila. Structure 1996, 4, 449–462. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, E.; Wrench, P.M.; Sharples, F.P.; Hiller, R.G.; Welte, W.; Diederichs, K. Structural Basis of Light Harvesting by Carotenoids: Peridinin-Chlorophyll-Protein from Amphidinium carterae. Science 1996, 272, 1788–1791. [Google Scholar] [CrossRef] [PubMed]
- Lanzo, I.; Russo, N.; Sicilia, E. First-Principle Time-Dependent Study of Magnesium-Containing Porphyrin-like Compounds Potentially Useful for Their Application in Photodynamic Therapy. J. Phys. Chem. B 2008, 112, 4123–4130. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Liu, X.; Chang, Y.; Wang, R.; Lv, T.; Cui, C.; Liu, M. Investigation of the Anti-Inflammatory and Antioxidant Activities of Luteolin, Kaempferol, Apigenin and Quercetin. S. Afr. J. Bot. 2021, 137, 257–264. [Google Scholar] [CrossRef]
- Tanaka, M.; Hayashi, T.; Morita, S. The Roles of Water Molecules at the Biointerface of Medical Polymers. Polym. J. 2013, 45, 701–710. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Zhao, S.; Huang, Q.; Xue, J. High Adsorption Capacity of Heavy Metals on Two-Dimensional MXenes: An Ab Initio Study with Molecular Dynamics Simulation. Phys. Chem. Chem. Phys. 2016, 18, 228–233. [Google Scholar] [CrossRef] [PubMed]
- Narin, P.; Abbas, J.M.A.; Atmaca, G.; Kutlu, E.; Lisesivdin, S.B.; Ozbay, E. Ab Initio Study of Electronic Properties of Armchair Graphene Nanoribbons Passivated with Heavy Metal Elements. Solid. State Commun. 2019, 296, 8–11. [Google Scholar] [CrossRef]
- Qi, C.; Xu, X.; Chen, Q.; Liu, H.; Min, X.; Fourie, A.; Chai, L. Ab Initio Calculation of the Adsorption of As, Cd, Cr, and Hg Heavy Metal Atoms onto the Illite (001) Surface: Implications for Soil Pollution and Reclamation. Environ. Pollut. 2022, 312, 120072. [Google Scholar] [CrossRef] [PubMed]
- Sousa, S.F.; Fernandes, P.A.; Ramos, M.J. General Performance of Density Functionals. J. Phys. Chem. A 2007, 111, 10439–10452. [Google Scholar] [CrossRef]
- Liu, S.-B. Conceptual Density Functional Theory and Some Recent Developments. Acta Phys. Chim. Sin. 2009, 25, 590–600. [Google Scholar]
- Guo, P.; Chen, W.; Song, J.; Cao, W.; Tian, C. A DFT Study of the Interaction between Butein Anion and Metal Cations (M= Mg2+, Cr2+, Fe2+, and Cu2+): Taking an Insight into Its Chelating Property. J. Mol. Struct. THEOCHEM 2008, 849, 33–36. [Google Scholar] [CrossRef]
- Muñoz, V.A.; Ferrari, G.V.; Sancho, M.I.; Montaña, M.P. Spectroscopic and Thermodynamic Study of Chrysin and Quercetin Complexes with Cu(II). J. Chem. Eng. Data 2016, 61, 987–995. [Google Scholar] [CrossRef]
- Amat, A.; Clementi, C.; Miliani, C.; Romani, A.; Sgamellotti, A.; Fantacci, S. Complexation of Apigenin and Luteolin in Weld Lake: A DFT/TDDFT Investigation. Phys. Chem. Chem. Phys. 2010, 12, 6672–6684. [Google Scholar] [CrossRef] [PubMed]
- Asadi, N.; Ramezanzadeh, M.; Bahlakeh, G.; Ramezanzadeh, B. Theoretical MD/DFT Computer Explorations and Surface-Electrochemical Investigations of the Zinc/Iron Metal Cations Interactions with Highly Active Molecules from Lemon Balm Extract toward the Steel Corrosion Retardation in Saline Solution. J. Mol. Liq. 2020, 310, 113220. [Google Scholar] [CrossRef]
- Ekennia, A.C.; Osowole, A.A.; Onwudiwe, D.C.; Babahan, I.; Ibeji, C.U.; Okafor, S.N.; Ujam, O.T. Synthesis, Characterization, Molecular Docking, Biological Activity and Density Functional Theory Studies of Novel 1,4-naphthoquinone Derivatives and Pd(II), Ni(II) and Co(II) Complexes. Appl. Organomet. Chem. 2018, 32, e4310. [Google Scholar] [CrossRef]
- Fiorucci, S.; Golebiowski, J.; Cabrol-Bass, D.; Antonczak, S. DFT Study of Quercetin Activated Forms Involved in Antiradical, Antioxidant, and Prooxidant Biological Processes. J. Agric. Food Chem. 2007, 55, 903–911. [Google Scholar] [CrossRef] [PubMed]
- Tanui, H.K.; Nkabyo, H.A.; Pearce, B.H.; Hussein, A.A.; Lopis, A.S.; Luckay, R.C. Iron (III) and Copper (II) Complexes Derived from the Flavonoids Morin and Quercetin: Chelation, Crystal Structure and DFT Studies. J. Mol. Struct. 2022, 1257, 132591. [Google Scholar] [CrossRef]
- Janeeshma, E.; Rajan, V.K.; Puthur, J.T. Spectral Variations Associated with Anthocyanin Accumulation; an Apt Tool to Evaluate Zinc Stress in Zea mays L. Chem. Ecol. 2021, 37, 32–49. [Google Scholar] [CrossRef]
- Beneduci, A.; Corrente, G.A.; Marino, T.; Aiello, D.; Bartella, L.; Di Donna, L.; Napoli, A.; Russo, N.; Romeo, I.; Furia, E. Insight on the Chelation of Aluminum (III) and Iron (III) by Curcumin in Aqueous Solution. J. Mol. Liq. 2019, 296, 111805. [Google Scholar] [CrossRef]
- Argaman, N.; Makov, G. Density Functional Theory: An Introduction. Am. J. Phys. 2000, 68, 69–79. [Google Scholar] [CrossRef]
- Zhang, G.; Musgrave, C.B. Comparison of DFT Methods for Molecular Orbital Eigenvalue Calculations. J. Phys. Chem. A 2007, 111, 1554–1561. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Marin, E.; Barbosa, A.; Martínez, A. The Metal Cation Chelating Capacity of Astaxanthin. Does This Have Any Influence on Antiradical Activity? Molecules 2012, 17, 1039–1054. [Google Scholar] [CrossRef] [PubMed]
- Yang, G. Density Functional Calculations: Recent Progresses of Theory and Application; BoD–Books on Demand; Intech Open: Rijeka, Croatia, 2018; ISBN 1789231329. [Google Scholar]
- Sengupta, P.; Pal, U.; Roy, P.; Samanta, T.; Chattopadhyay, N.; Sen, K.; Bose, A. Effect of a Metal Ion in Modulating the Binding Interaction of a Dietary Flavonoid with Bovine Serum Albumin and DNA: A Spectroscopic and Theoretical Approach. ACS Food Sci. Technol. 2022, 2, 114–124. [Google Scholar] [CrossRef]
- Attarki, J.; Khnifira, M.; Boumya, W.; Mahsoune, A.; Lemdek, E.M.; Sadiq, M.; Abdennouri, M.; Kaya, S.; Barka, N. Adsorption Mechanism Investigation of Methylthioninium Chloride Dye onto Some Metal Phosphates Using Monte Carlo Dynamic Simulations and DFT Calculations. Inorg. Chem. Commun. 2023, 149, 110436. [Google Scholar] [CrossRef]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Šimunková, M.; Valko, M.; Bučinský, L.; Malček, M. Structure Functionality Relationship of Flavonoids (Myricetin, Morin, Taxifolin and 3′, 4′-Dihydroxyflavone). A Computational Study via the Cupric Ion Probe. J. Mol. Struct. 2020, 1222, 128923. [Google Scholar] [CrossRef]
- Semwal, R.B.; Semwal, D.K.; Combrinck, S.; Viljoen, A. Butein: From Ancient Traditional Remedy to Modern Nutraceutical. Phytochem. Lett. 2015, 11, 188–201. [Google Scholar] [CrossRef]
- Cornard, J.P.; Dangleterre, L.; Lapouge, C. Computational and Spectroscopic Characterization of the Molecular and Electronic Structure of the Pb(II)−Quercetin Complex. J. Phys. Chem. A 2005, 109, 10044–10051. [Google Scholar] [CrossRef] [PubMed]
- Bodini, M.E.; Copia, G.; Tapia, R.; Leighton, F.; Herrera, L. Iron Complexes of Quercetin in Aprotic Medium. Redox Chemistry and Interaction with Superoxide Anion Radical. Polyhedron 1999, 18, 2233–2239. [Google Scholar] [CrossRef]
- Wu, T.-W.; Zeng, L.-H.; Wu, J.; Fung, K.-P. Morin: A Wood Pigment That Protects Three Types of Human Cells in the Cardiovascular System against Oxyradical Damage. Biochem. Pharmacol. 1994, 47, 1099–1103. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Thermodynamic and IR Spectral Study of Metal Cations–Anthocyanin Chelation: Mechanism of Formation of Pigments. Russ. J. Phys. Chem. A 2020, 94, 1887–1901. [Google Scholar] [CrossRef]
- Pratiwi, R.; Ibrahim, S.; Tjahjono, D.H. Reactivity and Stability of Metalloporphyrin Complex Formation: DFT and Experimental Study. Molecules 2020, 25, 4221. [Google Scholar] [CrossRef] [PubMed]
- Martínez, A.; Vargas, R. Electron Donor–Acceptor Properties of Metal Atoms Interacting with Pterins. New J. Chem. 2010, 34, 2988. [Google Scholar] [CrossRef]
- Linnanto, J.; Korppi-Tommola, J. Semiempirical PM5 Molecular Orbital Study on Chlorophylls and Bacteriochlorophylls: Comparison of Semiempirical, Ab Initio, and Density Functional Results. J. Comput. Chem. 2004, 25, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Dangles, O.; Elhabiri, M.; Brouillard, R. Kinetic and Thermodynamic Investigation of the Aluminium–Anthocyanin Complexation in Aqueous Solution. J. Chem. Soc. Perkin Trans. 2 1994, 2587–2596. [Google Scholar] [CrossRef]
- Elhabiri, M.; Figueiredo, P.; Toki, K.; Saito, N.; Brouillard, R. Anthocyanin–Aluminium and –Gallium Complexes in Aqueous Solution. J. Chem. Soc. Perkin Trans. 2 1997, 355–362. [Google Scholar] [CrossRef]
- Guaratini, T.; Vessecchi, R.; Pinto, E.; Colepicolo, P.; Lopes, N.P. Balance of Xanthophylls Molecular and Protonated Molecular Ions in Electrospray Ionization. J. Mass. Spectrom. 2005, 40, 963–968. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Cai, Z.-L. Theoretical Study on the Thermodynamic Properties of Chlorophyll D-Peptides Coordinating Ligand. Biochim. Biophys. Acta (BBA)—Bioenerg. 2007, 1767, 603–609. [Google Scholar] [CrossRef][Green Version]
- Chassaing, S.; Lefeuvre, D.; Jacquet, R.; Jourdes, M.; Ducasse, L.; Galland, S.; Grelard, A.; Saucier, C.; Teissedre, P.; Dangles, O.; et al. Physicochemical Studies of New Anthocyano-Ellagitannin Hybrid Pigments: About the Origin of the Influence of Oak C -Glycosidic Ellagitannins on Wine Color. Eur. J. Org. Chem. 2010, 2010, 55–63. [Google Scholar] [CrossRef]
- Phan, K.; Van Den Broeck, E.; Van Speybroeck, V.; De Clerck, K.; Raes, K.; De Meester, S. The Potential of Anthocyanins from Blueberries as a Natural Dye for Cotton: A Combined Experimental and Theoretical Study. Dye. Pigment. 2020, 176, 108180. [Google Scholar] [CrossRef]
- Cornard, J.P.; Merlin, J.C.; Boudet, A.C.; Vrielynck, L. Structural Study of Quercetin by Vibrational and Electronic Spectroscopies Combined with Semiempirical Calculations. Biospectroscopy 1997, 3, 183–193. [Google Scholar] [CrossRef]
- Daoud, I.; Mesmoudi, M.; Ghalem, S. MM/QM Study: Interactions of Copper(II) and Mercury(II) with Food Dyes in Aqueous Solutions. Int. J. Chem. Anal. Sci. 2013, 4, 49–56. [Google Scholar] [CrossRef]
- Visa, A.; Maranescu, B.; Lupa, L.; Crisan, L.; Borota, A. New Efficient Adsorbent Materials for the Removal of Cd(II) from Aqueous Solutions. Nanomaterials 2020, 10, 899. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; McCammon, J.A. Molecular Dynamics Simulations of Biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular Dynamics Simulation for All. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef] [PubMed]
- March, R.; Brodbelt, J. Analysis of Flavonoids: Tandem Mass Spectrometry, Computational Methods, and NMR. J. Mass. Spectrom. 2008, 43, 1581–1617. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, N.; Cruz, L.; Brás, N.F.; Mateus, N.; Ramos, M.J.; de Freitas, V. Structural Features of Copigmentation of Oenin with Different Polyphenol Copigments. J. Agric. Food Chem. 2013, 61, 6942–6948. [Google Scholar] [CrossRef] [PubMed]
- Moin, S.T.; Hofer, T.S. Hydration of Porphyrin and Mg-Porphyrin: Ab Initio Quantum Mechanical Charge Field Molecular Dynamics Simulations. Mol. Biosyst. 2014, 10, 117–127. [Google Scholar] [CrossRef]
- Singh, A.K.; Usman, M.; Sciortino, G.; Garribba, E.; Rath, S.P. Through-Space Spin Coupling in a Silver(II) Porphyrin Dimer upon Stepwise Oxidations: AgII···AgII, AgII···AgIII, and AgIII···AgIII Metallophilic Interactions. Chem. Eur. J. 2019, 25, 10098–10110. [Google Scholar] [CrossRef]
- Huamán Aguirre, A.A.; Salazar Salinas, K.; Quintana Cáceda, M. Molecular Interaction of Natural Dye Based on Zea mays and Bixa Orellana to Nanocrystalline TiO2 into Dye Sensitized Solar Cells. J. Electrochem. Sci. Eng. 2021, 11, 179–195. [Google Scholar] [CrossRef]
- Moradi, A.; Ranjbar, Z.; Guo, L.; Javadpour, S.; Ramezanzadeh, B. Molecular Dynamic (MD) Simulation and Electrochemical Assessments of the Satureja Hortensis Extract for the Construction of Effective Zinc-Based Protective Film on Carbon Steel. J. Mol. Liq. 2021, 338, 116606. [Google Scholar] [CrossRef]
- Hassanzadeh, M.K.; Tayarani Najaran, Z.; Nasery, M.; Emami, S.A. Summer Savory (Satureja hortensis L.) Oils. In Essential Oils in Food Preservation, Flavor and Safety; Elsevier: Amsterdam, The Netherlands, 2016; pp. 757–764. [Google Scholar]
- Dehghani, A.; Bahlakeh, G.; Ramezanzadeh, B.; Mostafatabar, A.H. Construction of a Zinc-Centered Metal–Organic Film with High Anti-Corrosion Potency through Covalent-Bonding between the Natural Flavonoid-Based Molecules (Quercetin)/Divalent-Zinc: Computer Modeling (Integrated-DFT&MC/MD)/Electrochemical-Surface Assessments. J. Ind. Eng. Chem. 2020, 88, 382–395. [Google Scholar]
- Liu, H.; Fan, B.; Fan, G.; Zhao, X.; Liu, Z.; Hao, H.; Yang, B. Long-Term Protective Mechanism of Poly (N-Methylaniline)/Phosphate One-Step Electropolymerized Coatings for Copper in 3.5% NaCl Solution. J. Alloys Compd. 2021, 872, 159752. [Google Scholar] [CrossRef]
- D’Ambrosio, M.; Santos, A.C.; Alejo-Armijo, A.; Parola, A.J.; Costa, P.M. Light-Mediated Toxicity of Porphyrin-like Pigments from a Marine Polychaeta. Mar. Drugs 2020, 18, 302. [Google Scholar] [CrossRef]
- Khoo, H.E.; Azlan, A.; Tang, S.T.; Lim, S.M. Anthocyanidins and Anthocyanins: Colored Pigments as Food, Pharmaceutical Ingredients, and the Potential Health Benefits. Food Nutr. Res. 2017, 61, 1361779. [Google Scholar] [CrossRef] [PubMed]
- Ahliha, A.H.; Nurosyid, F.; Supriyanto, A.; Kusumaningsih, T. Optical Properties of Anthocyanin Dyes on TiO 2 as Photosensitizers for Application of Dye-Sensitized Solar Cell (DSSC). IOP Conf. Ser. Mater. Sci. Eng. 2018, 333, 012018. [Google Scholar] [CrossRef]
- Hsissou, R.; Azogagh, M.; Benhiba, F.; Echihi, S.; Galai, M.; Shaim, A.; Bahaj, H.; Briche, S.; Kaya, S.; Serdaroğlu, G.; et al. Insight of Development of Two Cured Epoxy Polymer Composite Coatings as Highly Protective Efficiency for Carbon Steel in Sodium Chloride Solution: DFT, RDF, FFV and MD Approaches. J. Mol. Liq. 2022, 360, 119406. [Google Scholar] [CrossRef]
- Hsissou, R.; Benhiba, F.; El Aboubi, M.; Abbout, S.; Benzekri, Z.; Safi, Z.; Rafik, M.; Bahaj, H.; Kaba, M.; Galai, M.; et al. Synthesis and Performance of Two Ecofriendly Epoxy Resins as a Highly Efficient Corrosion Inhibition for Carbon Steel in 1 M HCl Solution: DFT, RDF, FFV and MD Approaches. Chem. Phys. Lett. 2022, 806, 139995. [Google Scholar] [CrossRef]
- Burg, J.S.; Ingram, J.R.; Venkatakrishnan, A.J.; Jude, K.M.; Dukkipati, A.; Feinberg, E.N.; Angelini, A.; Waghray, D.; Dror, R.O.; Ploegh, H.L.; et al. Structural Basis for Chemokine Recognition and Activation of a Viral G Protein–Coupled Receptor. Science 2015, 347, 1113–1117. [Google Scholar] [CrossRef]
- Dash, B.; Dash, B.; Rath, S.S. A Thorough Understanding of the Adsorption of Ni (II), Cd (II) and Zn (II) on Goethite Using Experiments and Molecular Dynamics Simulation. Sep. Purif. Technol. 2020, 240, 116649. [Google Scholar] [CrossRef]
- Giri, A.K.; Cordeiro, M.N.D.S. Heavy Metal Ion Separation from Industrial Wastewater Using Stacked Graphene Membranes: A Molecular Dynamics Simulation Study. J. Mol. Liq. 2021, 338, 116688. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, C.; Jiang, W.; Li, X.; Dai, Y.; Jia, H. Understanding the Sorption Behaviors of Heavy Metal Ions in the Interlayer and Nanopore of Montmorillonite: A Molecular Dynamics Study. J. Hazard. Mater. 2021, 416, 125976. [Google Scholar] [CrossRef] [PubMed]

| Elements | Limits (mg L−1) | ||
|---|---|---|---|
| FDA | WHO | EU | |
| Heavy metals | |||
| Antimony | 0.006 | 0.02 | 0.005 |
| Arsenic | 0.01 | 0.01 | 0.01 |
| Cadmium | 0.005 | 0.003 | 0.005 |
| Lead | 0.005 | 0.01 | 0.01 |
| Mercury | - | 0.006 | - |
| Non-heavy metals | |||
| Chromium | 0.10 | 0.05 | 0.05 |
| Cobalt | - | 0.05 | - |
| Copper | 1.00 | 2.00 | 2.00 |
| Iron | 0.30 | 2.00 | 0.20 |
| Manganese | 0.05 | 0.40 | 0.30 |
| Nickel | 0.10 | 0.02 | 0.02 |
| Zinc | 5.00 | 3.00 | 5.00 |
| Pigment | Metal | Color Change | Limit of Detection (Visually Visible) | Reference |
|---|---|---|---|---|
| Chlorophyll-based silver nanoparticle | Hg | Brown to light brown or colourless | 60 µM | [58] |
| Curcumin-anthocyanin (hydrogel strips) | Cd | White to bluish green | 0.2 µM | [59] |
| Hg | White to blue | 0.2 µM | ||
| Curcumin (cellulose acetate sensor strip) | Pb | Yellow to orange | 20 µM | [60] |
| Curcumin (cellulose nanofiber) | Pb | Orange to red | 9 µM | [61] |
| Curcumin-gold nanoparticle | Hg | Reddish wine to light blue | 2–10 µM | [62] |
| Curcumin (zein membrane) | Fe | Yellow to brown | 7.16 µM | [56] |
| Cyanidin (solution) | Al | Purple to violet to blue | 50 µM | [57] |
| Cu | Violet to blue | 50 µM | ||
| Fe | Pink to violet to blue | 200 µM | ||
| Pb | Purple to violet to blue | 80 µM | ||
| Cyanidin (dipstick sensor) | Fe | White to pink | 179–7162 µM | [63] |
| Method | Approach | Purpose | Pigment | Metal | Compatibility with Experimental Results | Reference |
|---|---|---|---|---|---|---|
| Ab initio | HF method with the 6-31G(d) basis set | Optimise structures in various conformations | Flavone and flavylium | - | Compatible in terms of internal rotation barrier | [99] |
| Ab initio | HF method with the 6-31G basis set | Calculate molecular (hyper) polarisabilities and band structures | Porphyrin | Mg, Ni, Zn | - | [100] |
| Ab initio | HF method with the 6-31G* basis set | Calculate fully optimised structures and atomic charges | Bacteriochlorin | Mg | Compatible in terms of structures, slightly differences in terms of transition energy | [101] |
| IEFPCM-ab initio | IEFPCM at the HF/6-31G(d)//mPW1PW91/6-31G(d) level | Calculate solvation free energies | Flavylium | - | - | [102] |
| Ab initio | HF method with the 6-31G* basis set | Full geometry optimisation, study the influence of methylation position, and study the influence of additional functional groups in the induction of atomic charge distribution | Quercetin | Mg | Compatible in terms of binding free energy | [103] |
| Luteolin | Mg | |||||
| Ab initio | HF method with the 6-31G basis set | Electronic characterisation | Anthracene, naphthalene, naphthacene, and pentacene | - | - | [104] |
| Application | Approach | Condition | Purpose | Pigment | Metal | Complex | BE (kcal mol−1) | ΔBE (kcal mol−1) | ΔE (kcal mol−1) | ΔG (kcal mol−1) | ΔG (binding) (kcal mol−1) | Molecular Energies (Hartree) | Ground State Energies (kcal mol−1) | Compatibility with Experimental Results | Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gaussian 09 | DFT/M052X/6-31+G(d) basis set (C, O, Al and H) and atoms - relativistic compact Stuttgart/Dres den effective core potential in conjunction with its split valence basis set for Cu and Fe atoms | Aqueous phase | Determine coordination properties | Quercetin | Al, Fe, and Cu | (4–5) Al(OH)H4Que+ | 13.7 | 0 | Compatible | [17] | |||||
| (3′-4′) AlH3Que+ | 0.0 | 4.5 | |||||||||||||
| (3′-4′s-cis) Fe(OH)2H3Que | – | 0.6 | |||||||||||||
| (4–5) CuH4Que+ | 28.2 | 0 | |||||||||||||
| (3′-4′H) CuH4Que+ | 53.4 | 4.7 | |||||||||||||
| (3–4s-cis) CuH4Que+ | 0.0 | 2 | |||||||||||||
| Gaussian 03 | DFT B3LYP/6-31+G(d)/LANL2DZ followed by single-point calculations using the 6-311+G(2d,2p) basis set | Gas phase | Locate the exact chelation site | Quercetin (3,30,40,5,7-pentahydroxylflavone) | Cr | Natural quercetin-bare Cr(III) ion | 1238.703333 | Compatible | [72] | ||||||
| Ethanol phase | Natural quercetin-bare Cr(III) ion | 668.98 | |||||||||||||
| Gas phase | Deprotonated quercetin-bare Cr(III) ion | 1514.885 | |||||||||||||
| Ethanol phase | Deprotonated quercetin-bare Cr(III) ion | 721.735 | |||||||||||||
| Gas phase | Deprotonated quercetin-hydrated Cr(III) | 469.3525 | |||||||||||||
| Ethanol phase | Deprotonated quercetin-hydrated Cr(III) | 78.4225 | |||||||||||||
| Gaussian 16 | DFT/M05–2X/6-311+G(d,p) | Study chelating properties | Apigenin | Cu and Fe | apigenin/H3A − Cu(II) | −2.2 | - | [80] | |||||||
| apigenin/H2A− − Cu(II) | −4.6 | ||||||||||||||
| apigenin/HA2− − Cu(II) | −6.9 | ||||||||||||||
| apigenin/H3A − Fe(III) | −7.0 | ||||||||||||||
| apigenin/H2A− − Fe(III) | −12.9 | ||||||||||||||
| apigenin/HA2− − Fe(III) | −18.2 | ||||||||||||||
| Gaussian 09 | DFT/UB3LYP/6-31+G(d,p)/LANL2DZ | Gas phase | Geometry optimisation | Quercetin | Cu | i-quercetin − Cu(II) | −18.00 (kJ mol−1) | Compatible | [118] | ||||||
| Solution phase | −41.03 (kJ mol−1) | ||||||||||||||
| Gas phase | ii-quercetin − Cu(II) | −9.31 (kJ mol−1) | |||||||||||||
| Solution phase | −43.29 (kJ mol−1) | ||||||||||||||
| Gas phase | iii-quercetin − Cu(II) | 334 (kJ mol−1) | |||||||||||||
| Solution phase | −22.44 (kJ mol−1) | ||||||||||||||
| Gas phase | Chrysin | chrysin − Cu(II) | −8.31 (kJ mol−1) | ||||||||||||
| Solution phase | −33.22 (kJ mol−1) | ||||||||||||||
| Gaussian 03 | DFT/B3LYP/6-31g**/CPCM | Methanol and water phase | Investigate interactions and geometry optimisation | Apigenin | Al | Al1B4,5Ap2+ | −4.95 | Compatible | [119] | ||||||
| Al1B4,5Ap12+ | 14.10 | ||||||||||||||
| Luteolin | Al1B4,5Lu12+ | 14.51 | |||||||||||||
| DMol3 code | MD/DFT/GGA/PBE functional and DNP basis set | Solution phase | Investigate metal cation–pigment interactions | Luteolin | Zn | Zn(luteolin)2 (hydroxyl complexation) | 2.585 | Compatible | [120] | ||||||
| Zn(luteolin)3 (hydroxyl complexation) | 2.550 | ||||||||||||||
| Zn(luteolin)4 (hydroxyl complexation) | 2.526 | ||||||||||||||
| Zn(luteolin)5 (hydroxyl complexation) | 2.438 | ||||||||||||||
| Zn(luteolin)2 (carbonyl complexation) | 2.035 | ||||||||||||||
| Zn(luteolin)3 (carbonyl complexation) | 2.093 | ||||||||||||||
| Zn(luteolin)4 (carbonyl complexation) | 2.170 | ||||||||||||||
| Zn(luteolin)5 (carbonyl complexation) | 2.131 | ||||||||||||||
| Gaussian 16 | DFT/B3LYP/6-31+G(d,p)/LANL2DZ | Structure optimisation | Naphthoquinone | Pd, Ni, and Co | [Co(L1)2(H2O)2].2H2O | 0.29 (eV) | −581.21 kJ mol−1 | - | [121] | ||||||
| [NiL1(H2O)2(CH3COO−)] | 0.18 (eV) | −631.88 kJ mol−1 | |||||||||||||
| [PdL1 (H2O)Cl] | 0.39 (eV) | −501.43 kJ mol−1 | |||||||||||||
| [CoL2(H2O)2(CH3COO−)] | 0.32 (eV) | −434.27 kJ mol−1 | |||||||||||||
| [NiL2(H2O)2 (CH3COO−)].H2O | 0.71 (eV) | −414.27 kJ mol−1 | |||||||||||||
| [PdL2 (H2O)Cl] | 0.34 (eV) | −301.43 kJ mol−1 | |||||||||||||
| Gaussian 09 | DFT/B3LYP/6-31++G(d,p)/PCM | Aqueous phase | Structure optimisation | Cyanin | Na+ | −12.21 | 1.16 | Compatible | [82] | ||||||
| K+ | −6.36 | 10.58 | |||||||||||||
| Mg(II) | −25.26 | −13.50 | |||||||||||||
| Ca(II) | −17.62 | −2.71 | |||||||||||||
| Cr(II) | −42.46 | −28.22 | |||||||||||||
| Mn(II) | −30.69 | −17.85 | |||||||||||||
| Fe(II) | −32.40 | −19.75 | |||||||||||||
| Co(II) | −31.26 | −19.56 | |||||||||||||
| Ni(II) | −32.40 | −20.02 | |||||||||||||
| Cu(II) | −52.04 | −37.59 | |||||||||||||
| Zn(II) | -31.74 | −19.65 | |||||||||||||
| Al(III) | −63.42 | −53.97 | |||||||||||||
| Cr(III) | −72.62 | −63.54 | |||||||||||||
| Fe(III) | −80.64 | −73.44 | |||||||||||||
| Co(III) | −108.66 | −100.94 | |||||||||||||
| Gaussian 98 | DFT/B3LYP/6-31G* basis set for C and H atoms and 6-31+G* basis set for O atoms/LanL2DZ/PCM continuum model | Solution with ε = 78.4 (corresponding to bulk water) | Structure optimisation | Quercetin | Cu | OQ1Cu | −302.7 | Compatible | [122] | ||||||
| OQ2Cu | −336.1 | ||||||||||||||
| OQ3Cu | −308.2 | ||||||||||||||
| SQ1Cu | −322.8 (−312.5) | ||||||||||||||
| SQ2Cu | −323.3 (−328.8) | ||||||||||||||
| SQ3Cu | −302.7 (−301.5) | ||||||||||||||
| D1Cu | −500.2 | ||||||||||||||
| D2Cu | −499.8 | ||||||||||||||
| DD3Cu | −676.7 | ||||||||||||||
| Gaussian 03 | DFT/M052 × 29/6-31+G(d) b/PCM | Ethanol (ε = 24.85) | For full optimisation | Quercetin | Al | a3-4eq H4QueAl(H2O)2(OH)2 | 2.9 | Compatible | [73] | ||||||
| a3-4ax H4QueAl(H2O)2(OH)2 | 3.6 | ||||||||||||||
| a4-5eq H4QueAl(H2O)2(OH)2 | 1.2 | ||||||||||||||
| a4-5ax H4QueAl(H2O)2(OH)2 | 0 | ||||||||||||||
| b3-4eq H3QueAl(H2O)3(OH) | 5.1 | ||||||||||||||
| b3-4ax H3QueAl(H2O)3(OH) | 7.4 | ||||||||||||||
| b4-5eq H3QueAl(H2O)3(OH) | 5.9 | ||||||||||||||
| b4-5ax H3QueAl(H2O)3(OH) | 7.4 | ||||||||||||||
| Gaussian 03 | DFT/B3LYP/6-31+G (d)/LANL2DZ followed by a single-point calculation using a different basis set (6-311++G(d,p)) | Water phase | Geometry optimisation | Chalcone (butein) | Mg, Cr, Fe, and Cu | Cu2+–O2′O9 | 127 | - | [117] | ||||||
| Cu2+–O4O3 | 125 | ||||||||||||||
| Fe2+–O2′O9 | 32 | ||||||||||||||
| Fe2+–O4O3 | 21 | ||||||||||||||
| Mg2+–O2′O9 | 30 | ||||||||||||||
| Mg2+–O4O3 | 22 | ||||||||||||||
| Cr2+–O2′O9 | 46 | ||||||||||||||
| Cr2+–O4O3 | 26 | ||||||||||||||
| Gas phase | Chalcone (butein) | Mg, Cr, Fe, and Cu | Cu2+–O2′O9 | 517 | 0.03187 (Hertee) | ||||||||||
| Cu2+–O4O3 | 493 | ||||||||||||||
| Fe2+–O2′O9 | 461 | 0.0716 (Hertee) | |||||||||||||
| Fe2+–O4O3 | 406 | ||||||||||||||
| Mg2+–O2′O9 | 423 | 0.06548 (Hertee) | |||||||||||||
| Mg2+–O4O3 | 370 | ||||||||||||||
| Cr2+–O2′O9 | 462 | 0.09428 (Hertee) | |||||||||||||
| Cr2+–O4O3 | 397 | ||||||||||||||
| Gaussian09W and GaussView 6.0.16 | DFT/6-31+G(d)/B3LYP | Investigate stability, reactivity, nature of interaction, and application of the complexes | Quercetin (5-hydroxy-4-keto group) | Al | 2.8297 (eV) | Compatible | [65] | ||||||||
| Mg | 1.2679 (eV) | ||||||||||||||
| Na | 3.1149 (eV) | ||||||||||||||
| K | 3.2172 (eV) | ||||||||||||||
| Ca | 0.6134 (eV) | ||||||||||||||
| Al | 2.603 (eV) | ||||||||||||||
| Mg | 1.3749 (eV) | ||||||||||||||
| Na | 3.3362 (eV) | ||||||||||||||
| K | 3.0782 (eV) | ||||||||||||||
| Ca | 1.3983 (eV) | ||||||||||||||
| Quercetin (O3′/O4′ ortho-dihydroxyl (catechol) group) | Al | 2.8828 (eV) | |||||||||||||
| Mg | 2.3431 (eV) | ||||||||||||||
| Na | 2.8488 (eV) | ||||||||||||||
| K | 3.1038 (eV) | ||||||||||||||
| Ca | 1.156 (eV) | ||||||||||||||
| Al | 1.051 (eV) | ||||||||||||||
| Mg | 1.076 (eV) | ||||||||||||||
| Na | 1.739 (eV) | ||||||||||||||
| K | 1.697 (eV) | ||||||||||||||
| Ca | 0.854 (eV) | ||||||||||||||
| Gaussian 16 | DFT/M06-2X/def2-SVP | Gas phase | Investigate electronic and structural properties of morin | Quercetin | Fe and Cu | Cu(II)M2 6 m | −2,411,782 | Compatible | [123] | ||||||
| Fe(III)M2 6 m | −2,175,328 | ||||||||||||||
| Cu(II)Q2 6 m | −2,411,784 | ||||||||||||||
| Fe(III)Q2 6 m | −2,175,331 | ||||||||||||||
| Cu(II)M2 5 m | −2,411,780 | ||||||||||||||
| Fe(III)M2 5 m | −2,175,325 | ||||||||||||||
| Cu(II)Q2 5 m | −2,411,769 | ||||||||||||||
| Fe(III)Q2 5 m | −2,175,326 | ||||||||||||||
| Gaussian 09 | DFT/B3LYP/6-31+G-(d, p) | Structural analysis | Cyanidin | Zn | 1.47 (eV) | - | [124] | ||||||||
| Gaussian 03 | DFT/B3LYP/6-31G*/LANL2DZ followed by single-point calculations using the extended 6-311++G** basis set | Gas phase | Geometry optimisation | Quercetin | Fe | I-Q-Fe2+ | 12.3 | Compatible | [76] | ||||||
| II-Q-Fe2+ | 10.1 | ||||||||||||||
| III-Q-Fe2+ | 0 | ||||||||||||||
| I-Q−-Fe2+ | 27.4 | ||||||||||||||
| II-Q−-Fe2+ | 23.6 | ||||||||||||||
| III-Q−-Fe2+ | 5.6 | ||||||||||||||
| IV-Q−-Fe2+ | 0 | ||||||||||||||
| V-Q−-Fe2+ | 34.2 | ||||||||||||||
| VI-Q−-Fe2+ | 35.3 | ||||||||||||||
| VII-Q−-Fe2+ | 48.3 | ||||||||||||||
| VIII-Q−-Fe2+ | 41.7 | ||||||||||||||
| I-Q−-Fe2+(H2O)4 | 13.8 | ||||||||||||||
| II-Q−-Fe2+(H2O)4 | 12.9 | ||||||||||||||
| III-Q−-Fe2+(H2O)4 | 0 | ||||||||||||||
| IV-Q−-Fe2+(H2O)4 | 1.8 | ||||||||||||||
| V-Q−-Fe2+(H2O)4 | 41 | ||||||||||||||
| VI-Q−-Fe2+(H2O)4 | 50.5 | ||||||||||||||
| VII-Q−-Fe2+(H2O)4 | 50.5 | ||||||||||||||
| VIII-Q−-Fe2+(H2O)4 | 42.3 | ||||||||||||||
| I-2Q−-Fe2+ | 0 | ||||||||||||||
| II-2Q−-Fe2+ | 5.9 | ||||||||||||||
| III-2Q−-Fe2+ | 1.6 | ||||||||||||||
| IV-2Q−-Fe2+ | 2.5 | ||||||||||||||
| I-2Q−-Fe2+(H2O)2 | 12.9 | ||||||||||||||
| II-2Q−-Fe2+(H2O)2 | 5.2 | ||||||||||||||
| III-2Q−-Fe2+(H2O)2 | 0 | ||||||||||||||
| IV-2Q−-Fe2+(H2O)2 | 9.3 | ||||||||||||||
| Gaussian 16 | DFT/M05-2X/6-31+G(d) (C, H, O, and Al) and relativistic compact Stuttgart/ Dresden effective core potential with its related split valence (Cu and Fe) | Aqueous phase | Properties and geometry optimisation | Luteolin | Al, Fe, and Cu | Al(OH)2(H2O)2(H3Lu) (3′-4′) | 4.9 | −89.9 | - | [64] | |||||
| Al(OH)2(H2O)2(H3Lu) (4–5) | 0 | −94.8 | |||||||||||||
| Fe(OH)2(H2O)2(H3Lu) (3′-4′) | 1.4 | −82.4 | |||||||||||||
| Fe(OH)2(H2O)2(H3Lu) (4–5) | 0 | −83.9 | |||||||||||||
| [Fe(H2O)3(OH)(H3Lu)](3′-4′) | 2.8 | −61.7 | |||||||||||||
| [Fe(H2O)3(OH)(H3Lu)](4–5) | 0 | −64.4 | |||||||||||||
| Cu(OH)2(H2O)2(H3Lu)(3′-4′) | 0.2 | −61.1 | |||||||||||||
| Cu(OH)2(H2O)2(H3Lu)(4–5) | 0 | −61.2 | |||||||||||||
| Gaussian 09 | DFT/M052X/6-31+G(d) | Water phase | Studied the complexation | Curcumin | Al and Fe | [Al(H2O)3(OH)(LA)]+ | −135.1 | Compatible | [125] | ||||||
| [Al(H2O)3(OH)(LB)] | −124.9 | ||||||||||||||
| [Fe(H2O)(OH)3(LA)] | −57.1 | ||||||||||||||
| [Fe(H2O)(OH)3(LB)] | −55.5 | ||||||||||||||
| Gaussian 09 | DFT/U-B3LYP/6-31G* and relativistic effective core potential with a valence basis set/LANL2DZ | Coordination and geometry optimisation | Quercetin | Ni | [Ni(L1)(fla)]ClO4 | 3.056 (eV) | Compatible | [71] | |||||||
| [Ni(L1)(fla)]ClO4 | 3.045 (eV) | ||||||||||||||
| [Ni(L3)(fla)]ClO4 | 3.029 (eV) | ||||||||||||||
| [Ni(ntb)(fla)]+ | 3.033 (eV) | ||||||||||||||
| Gaussian 09 | DFT/UB3LYP*/6-311++G(d,p) | Full geometry optimisation | Phenoxazines | Co | I(R = R1 = CH3)LSCoIII-SQ | 4.5 | - | [70] | |||||||
| I(R = R1 = CH3)HSCoIII-Q | |||||||||||||||
| I(R = CH3, R1 = CF3)LSCoIII-SQ | −1.7 | ||||||||||||||
| I(R = CH3, R1 = CF3)HSCoIII-Q | |||||||||||||||
| I(R = R1 = CF3)LSCoIII-SQ | −8.7 | ||||||||||||||
| I(R = R1 = CF3)HSCoIII-Q | |||||||||||||||
| II(R2 = H)LSCoIII-SQ | 14.4 | ||||||||||||||
| II(R2 = H)HSCoIII-Q | |||||||||||||||
| II(R2 = CH3)LSCoIII-SQ | 12.1 | ||||||||||||||
| II(R2 = CH3)HSCoIII-Q | |||||||||||||||
| II(R2 = Ph)LSCoIII-SQ | 3.4 | ||||||||||||||
| II(R2 = Ph)HSCoIII-Q | |||||||||||||||
| III(R2 = H)LSCoIII-SQ | 14.4 | ||||||||||||||
| III(R2 = H)HSCoIII-Q | |||||||||||||||
| III(R2 = CH3)LSCoIII-SQ | 11.9 | ||||||||||||||
| III(R2 = CH3)HSCoIII-Q | |||||||||||||||
| III(R2 = Ph)LSCoIII-SQ | 3.3 | ||||||||||||||
| III(R2 = Ph)HSCoIII-Q |
| Application | Approach | Condition | Purpose | Pigment | Metal | Complex | EE (eV) | ΔE (eV) | ΔEDIS (kJ mol−1) | Molecular Energy (Hartree) | Compatibility with Experimental Results | Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gaussian 09 | DFT/B3LYP/6- 31G/LANL2DZ | Determine the reactivity and stability of the complex | Porphyrin | Pb, Cd, Hg, Sn, and As | Pb-TMPyP | −2138.3 | Compatible | [139] | ||||
| Cd-TMPyP | −2182.9 | |||||||||||
| Hg-TMPyP | −2177.5 | |||||||||||
| Sn-TMPyP | −2137.1 | |||||||||||
| As3+-TMPyP | −2140.4 | |||||||||||
| As5+-TMPyP | −2138.9 | |||||||||||
| Pb-TDMImP | −2207.3 | |||||||||||
| Cd-TDMImP | −2251.9 | |||||||||||
| Hg-TDMImP | −246.5 | |||||||||||
| Sn-TDMImP | −2205.9 | |||||||||||
| As3+-TDMImP | −2209.3 | |||||||||||
| As5+-TDMImP | −2207.8 | |||||||||||
| Pb-TDMPzP | −2207.2 | |||||||||||
| Cd-TDMPzP | −2251.8 | |||||||||||
| Hg-TDMPzP | −2246.4 | |||||||||||
| Sn-TDMPzP | −2206.0 | |||||||||||
| As3+-TDMPzP | −2209.3 | |||||||||||
| As5+-TDMPzP | −2207.9 | |||||||||||
| Gaussian 03 | DFT/B3LYP/6-31G(d,p)/LANL2DZ | Methanol phase | Geometry optimisation | Quercetin | Pb | Pb(II)-quercetin | 0.124 | Compatible | [135] | |||
| Gaussian 09 | DFT/B3LYP/LANL2DZ followed by TD-DFT/LC-wPBE | Gas phase | Geometry optimisation and energy calculations | Astaxanthin | Pb, Cd, and Hg | [ASTA-Pb]+2 | 2.05 | Compatible | [128] | |||
| [ASTA-Pb2]+4 | 1.84 | |||||||||||
| [ASTA-Cd(H2O)2]+2 | 1.85 | |||||||||||
| [ASTA-Cd2(H2O)4]+4 | 2.08 | |||||||||||
| [ASTA-Hg(H2O)2]+2 | 1.93 | |||||||||||
| [ASTA-Hg2(H2O)4]+4 | 2.06 | |||||||||||
| Ethanol phase | [ASTA-Pb]+2 | 1.96 | ||||||||||
| [ASTA-Pb2]+4 | 1.82 | |||||||||||
| [ASTA-Cd(H2O)2]+2 | 1.68 | |||||||||||
| [ASTA-Cd2(H2O)4]+4 | 2.41 | |||||||||||
| [ASTA-Hg(H2O)2]+2 | 1.82 | |||||||||||
| [ASTA-Hg2(H2O)4]+4 | 2.40 | |||||||||||
| Gaussian 03 | DFT/B3LYP/6-311G(d,p)/LANL2DZ | Calculation of complete optimisation | Pterins, isoxanthopterin, sepiapterin | Cd, Hg | Pterins-Cd | 7.5 | Compatible | [140] | ||||
| Pterins-Cd+1 | 270.3 | |||||||||||
| Pterins-Cd+2 | 762.7 | |||||||||||
| Pterins Hg | 4.6 | |||||||||||
| Pterins-Hg+1 | 252.7 | |||||||||||
| Pterins-Hg+2 | 797.1 | |||||||||||
| Isoxanthopterin-Cd | 7.5 | |||||||||||
| Isoxanthopterin-Cd+1 | 276.6 | |||||||||||
| Isoxanthopterin-Cd+2 | 778.2 | |||||||||||
| Isoxanthopterin-Hg | 5.9 | |||||||||||
| Isoxanthopterin-Hg+1 | 258.6 | |||||||||||
| Isoxanthopterin-Hg+2 | 807.5 | |||||||||||
| Sepiapterin-Cd | 12.9 | |||||||||||
| Sepiapterin-Cd+1 | 366.9 | |||||||||||
| Sepiapterin-Cd+2 | 1018.4 | |||||||||||
| Sepiapterin-Hg | 9.2 | |||||||||||
| Sepiapterin-Hg+1 | 346.4 | |||||||||||
| Sepiapterin-Hg+2 | 1032.2 |
| Method | Approach | Purpose | Pigment | Metal | Compatibility with Experimental Results | Reference |
|---|---|---|---|---|---|---|
| Semiempirical method | AM1 using HyperChem program | Study complexation processes | Anthocyanin | Al | Compatible | [142] |
| Semiempirical method | MM+ and AM1 | Molecular calculation | Anthocyanin | Al and Ga | Compatible | [143] |
| Semiempirical method | AM1 Hamiltonian | Calculate the structural modifications caused by the chelation process | Quercetin | Al | Compatible | [74] |
| Semiempirical method | ZINDO/S CIS (40,40) or (45, 45) levels | Calculate transition energies and oscillation strengths, estimate corresponding spectroscopic transition energy values, and study the existence of dark electronic states in the system | Bacteriochlorin | Mg | Compatible | [106] |
| Semiempirical method | PM5 | Study orbitals | Bacteriochlorin, chlorin, and porphin | Mg | Compatible | [141] |
| Semiempirical method | AM1 using MOPAC17 version 6 | Geometry optimisation and electronic structure analysis | Xanthophylls, antheraxanthin, lutein, neoxanthin, violaxanthin, and zeaxanthin | - | Compatible | [144] |
| Semiempirical method | PM5 using the MOPAC 2002 package | Structure optimisation | Chlorophyll and chlorophyll d peptides | Mg | Compatible | [145] |
| Semiempirical method | AM1 (available in the AMPAC package) | Structure optimisation | Malvidin | - | Compatible | [146] |
| Semiempirical molecular dynamics | PM6 with Grimme D3 dispersion correction | Investigate intermolecular behaviour | Anthocyanins (malvidin-3-glucoside) | Al and Sn | Compatible | [147] |
| ONIOM semiempirical method | PM6 and Pm3MM | Solvation optimisation | Anthocyanins | Al, Ga, Cr, Fe, and Mg | - | [138] |
| QM/MM semiempirical method | Pm3MM | Solvation optimisation | Anthocyanins | Mg, Al, Ga, Sn, Cr, and Fe | Compatible | [78] |
| Method | Approach | Purpose | Pigment | Metal | Compatibility with Experimental Results | Reference |
|---|---|---|---|---|---|---|
| Molecular dynamics simulations | - | Calculate energy-minimised structures | Hesperidin, rutin, neodiosmin, diosmin, and neohesperidin | Co | Compatible | [153] |
| Molecular dynamics simulations | AMBER force field (GAFF) and TIP3P model using the Sander module in the Amber 10.0 simulation package | Identify several conformations of the co-pigmentation complex | Oenin | - | Compatible | [154] |
| Molecular dynamics simulations | restrained electrostatic potential (RESP) protocol implemented in the ANTECHAMBER module of AMBER 11 | Partial atomic charges determination | Quercetin and luteolin | Mg | Compatible | [108] |
| AMBER force field (GAFF) | Describe the force field parameters of the substrates | |||||
| AMBER ff99SB force field | Potential determination | |||||
| Ab initio QMCF-MD simulations | HF method with the 6-31G** basis set; Amber force field (GAFF) and restrained electrostatic potential (RESP) | Study structural and dynamic properties, and observe hydration behaviour | Porphyrin | Mg | Compatible | [155] |
| Molecular dynamics simulations | AMBER14SB force field and GAFF force field | Evaluate the possibility of increasing or decreasing internuclear distance upon low-energy conformational changes and assessing the flexibility of the complex | Porphyrin | Ag | Compatible | [156] |
| Monte Carlo/ molecular dynamics simulations | Materials Studio in the NVT ensemble with the COMPASS force field | Analyse the interaction of complexes | Luteolin–Zn complex | Fe | Compatible | [120] |
| Monte Carlo/ Molecular dynamics simulations | AMBER | Study conformation theories, thermodynamic parameters and movement rules of the molecular machine and kinetic energy to the potential energy surface | Cyanidin, delphinidin, petunidin | Mg, Al, Ga, Sn, Cr, and Fe | Compatible | [78] |
| Molecular dynamics simulations | Reax FF force field using NVT ensemble | Analyse interactions between components | Cyanidin-3-glucoside | Ti | Compatible | [157] |
| Molecular dynamics simulations | Forcite module of a Material Studio software in NVT ensemble employing universal forcefield | Study adsorption behaviour | Satureja hortensis extract (isoferulic acid, caffeic acid, kuersetin, rosmarinic acid, apigenin glucoside, and chlorogenic acid) | Zn | Compatible | [158] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maranata, G.J.; Megantara, S.; Hasanah, A.N. An Update in Computational Methods for Environmental Monitoring: Theoretical Evaluation of the Molecular and Electronic Structures of Natural Pigment–Metal Complexes. Molecules 2024, 29, 1680. https://doi.org/10.3390/molecules29071680
Maranata GJ, Megantara S, Hasanah AN. An Update in Computational Methods for Environmental Monitoring: Theoretical Evaluation of the Molecular and Electronic Structures of Natural Pigment–Metal Complexes. Molecules. 2024; 29(7):1680. https://doi.org/10.3390/molecules29071680
Chicago/Turabian StyleMaranata, Gabriella Josephine, Sandra Megantara, and Aliya Nur Hasanah. 2024. "An Update in Computational Methods for Environmental Monitoring: Theoretical Evaluation of the Molecular and Electronic Structures of Natural Pigment–Metal Complexes" Molecules 29, no. 7: 1680. https://doi.org/10.3390/molecules29071680
APA StyleMaranata, G. J., Megantara, S., & Hasanah, A. N. (2024). An Update in Computational Methods for Environmental Monitoring: Theoretical Evaluation of the Molecular and Electronic Structures of Natural Pigment–Metal Complexes. Molecules, 29(7), 1680. https://doi.org/10.3390/molecules29071680