Diffusiophoresis of Macromolecules within the Framework of Multicomponent Diffusion

Abstract

Diffusiophoresis is the isothermal migration of a colloidal particle through a liquid caused by a cosolute concentration gradient. Although diffusiophoresis was originally introduced using hydrodynamics, it can also be described by employing the framework of multicomponent diffusion. This not only enables the extraction of diffusiophoresis coefficients from measured multicomponent-diffusion coefficients but also their theoretical interpretation using fundamental thermodynamic and transport parameters. This review discusses the connection of diffusiophoresis with the 2 × 2 diffusion-coefficient matrix of ternary liquid mixtures. Specifically, diffusiophoresis is linked to the cross-term diffusion coefficient characterizing diffusion of colloidal particles due to cosolute concentration gradient. The other cross-term, which describes cosolute diffusion due to the concentration gradient of colloidal particles, is denoted as osmotic diffusion. Representative experimental results on diffusiophoresis and osmotic diffusion for polyethylene glycol and lysozyme in the presence of aqueous salts and osmolytes are described. These data were extracted from ternary diffusion coefficients measured using precision Rayleigh interferometry at 25 °C. The preferential-hydration and electrophoretic mechanisms responsible for diffusiophoresis are examined. The connection of diffusiophoresis and osmotic diffusion to preferential-interaction coefficients, Onsager reciprocal relations, Donnan equilibrium and Nernst–Planck equations are also discussed.

1. Introduction

A wide range of colloidal particles, such as inorganic nanoparticles, proteins, synthetic polymers and micelles, are subject to diffusion-based transport in complex liquids in a variety of biochemical, biotechnological, geochemical and industrial processes. These include centrifugation [1], dialysis [2], adsorption [3], crystallization [4], transport in microfluidics [5], living systems [6], gel media [7], insertion into dead-end pores [8], controlled release [9], reaction kinetics and pattern formation [10,11]. Since concentration gradients of colloidal particles and related additives such as salts, osmolytes and buffer components are normally encountered in these mass-transfer processes, diffusion coefficients play a crucial role in modeling the kinetic evolution of spatial concentration profiles of mixture constituents.

In recent years, a mass transport process known as diffusiophoresis has attracted considerable attention [12,13,14]. This is the net diffusive migration of a colloidal particle through a liquid induced by a directional concentration gradient of a cosolute at constant temperature and pressure. Although diffusiophoresis may occur in any liquid, this transport phenomenon is typically considered in the context of aqueous mixtures, in which the cosolute responsible for the migration of a water-soluble colloidal particle is a salt [14] or even a nonionic additive [15] such as an osmolyte [15,16]. As illustrated in Figure 1, diffusiophoresis is analogous to the well-known electrophoresis [15,17] of charged particles, which is caused by an external electric field, i.e., a gradient of electric potential. Correspondingly, diffusiophoresis is driven by a gradient of cosolute chemical potential. In other words, we can say that the diffusiophoresis of a colloidal particle is driven by the “chemical” field generated by the concentration gradients of a salt or osmolyte in water. Although most studies have focused on diffusiophoresis of charged colloidal particles in the presence of salt gradients [18,19,20,21,22], it is important to note that diffusiophoresis can also be observed for neutral colloidal particles [23,24,25]. Furthermore, the underlying mechanism responsible for diffusiophoresis is not unique as in the case of electrophoresis (electric field), but it can be varied by changing the chemical nature of the cosolute. This increases the complexity of diffusiophoresis as more than one mechanism can concur with the overall diffusiophoresis experienced by a colloidal particle. In this paper, the main mechanisms responsible for particle diffusiophoresis of macromolecules will be discussed.

Diffusiophoresis of a colloidal particle is characterized by the diffusiophoretic mobility, D_PS, which is typically introduced by employing the following linear relation [13,19]:

$$v_{\mathrm{PS}}=-\hspace{0.17em}\hspace{0.17em}{D}_{\mathrm{PS}} \nabla \ln C_{\mathrm{S}}$$

(1)

where v_PS is particle diffusiophoretic velocity, and C_S is cosolute concentration. Note that D_PS has the units of a diffusion coefficient (e.g., m²·s⁻¹).

The term “diffusiophoresis” was originally introduced by Derjaguin in 1947 to describe the motion of large colloidal particles in the presence of concentration gradients of small ions and molecules [15]. It was then investigated by Andersen and Prieve [15,16,26], especially in connection with deposition rates of latex particles onto porous membranes. They also derived mathematical expressions for diffusiophoretic mobilities by employing hydrodynamic models [20,27,28]. These are the same types of models that were previously employed for describing electrophoretic mobilities (Henry’s equation) [17] and also the friction encountered by Brownian particles (Stokes’ law) [29]. With the advent of microfluidic technologies, many more diffusiophoresis studies were reported, showing the value of this transport phenomenon in manipulating the motion of colloidal particles. In the chemistry field, the term “chemotaxis” sometimes replaces “diffusiophoresis”, emphasizing similarities between the migration of colloidal particles and the movement of living organisms in response to gradients of nutrient or toxic molecules [5,30,31].

Experimental studies have demonstrated that diffusiophoresis promotes particle mixing, focusing and separation in microfluidics [18,19,32,33,34], particle entrainment in dead-end pores [8,18], particle deposition on porous membranes [20,35]. Moreover, diffusiophoresis was employed to achieve membraneless water filtration [22] and remove staining agents from fibrous materials [36]. The reader should, for example, consult two recent review articles by Shim [13] and Velegol [12] describing the various applications of diffusiophoresis in mass-transfer problems.

An expert in the field of transport phenomena may realize that diffusiophoresis should be associated with the phenomenon of cross-diffusion encountered in multicomponent mixtures [37,38,39,40,41,42,43,44,45,46]. Cross-diffusion is described by employing the framework of non-equilibrium thermodynamics [47,48], which was derived primarily from the statistical mechanical investigations of Onsager in 1931 [49,50]. It has been investigated by several scientists in the fields of physical chemistry [37,39,51,52,53,54,55] and chemical engineering [45,46,56,57]. Cross-diffusion coefficients are typically defined by writing Fickian relations [58] in which the flux of a solute not only depends on its concentration gradient (main-term diffusion coefficients) but also on the concentration gradient of other solutes (cross-term diffusion coefficients) [41]. Thus, multicomponent diffusion in a ternary system is described by a 2 × 2 diffusion-coefficient matrix. The two main terms describe the diffusion of the two solutes due to their own concentration gradients, while the two cross-terms describe the diffusion of a solute due to the concentration gradient of the other solute. Thus, a diffusiophoretic mobility should be closely related to the cross-term diffusion coefficient describing flux of a large solute due to the concentration gradient of the relatively small solute.

Multicomponent-diffusion coefficients can be experimentally determined. The well-established Taylor dispersion method [38,43,59,60] and interferometric techniques [37,40,61,62] have been successfully employed for the measurements of these transport parameters. Thus, the connection of diffusiophoresis to multicomponent diffusion is important because it provides the basis for determining diffusiophoretic mobilities from measurements of multicomponent-diffusion coefficients. This was first highlighted by Shaeiwitz and Lechnick in 1983 [63]. It is surprising that previous studies on diffusiophoresis were disconnected from work on multicomponent diffusion. This is even more striking considering that the theoretical electrokinetic models describing diffusiophoresis [13,15] of charged particles are fundamentally the same as those at the heart of Nernst–Planck and related Nernst–Hartley equations [52,64,65,66], which are employed for modeling multicomponent diffusion in dilute electrolyte mixtures. Presumably, diffusiophoresis has been regarded as a transport phenomenon separated from cross-diffusion because it pertains to large colloidal particles and, consequently, was originally introduced within the framework of hydrodynamics. On the other hand, the phenomenon of multicomponent diffusion, which covers the case of solutes of various sizes, is described by employing non-equilibrium thermodynamics. It is worth mentioning that a similar separation existed in the past between multicomponent diffusion coefficients and the collective diffusion coefficient determined by dynamic light scattering (DLS) [67,68]. The extension of multicomponent-diffusion studies to mixtures containing macromolecules [69] or micelles [70] then prompted more attention to the connection between DLS and multicomponent diffusion. It is now well known that the DLS diffusion coefficient represents the lower eigenvalue of the 2×2 diffusion-coefficient matrix of ternary liquid mixtures of colloidal particles and a cosolute of low molar weight [69,70,71].

We know that diffusiophoresis should be regarded as a special case of cross-diffusion [71,72]. It describes the cross-diffusion of a solute that 1) is large compared to the other components of the mixture and 2) is present at low concentration in the mixture. There is some gray area when it comes to considering the size and concentration scales relevant to diffusiophoresis. In relation to size, the same type of uncertainty is encountered in the application of the Stokes–Einstein equation with no-slip boundary condition [73]. Since this is typically applied to particles with a radius of ≈1 nm and larger, it is reasonable to assume that this size range also pertains to diffusiophoresis. In other words, diffusiophoresis is a phenomenon that is relevant to proteins, polymers, micelles and other nanoparticles of comparable (1–10 nm) or lager (≈100 nm) size. In relation to concentration, one could readily enunciate that diffusiophoresis represents cross-diffusion in the limit of zero solute concentration. However, while this definition is conceptually correct, it is possible that the infinite-dilute limit is difficult to attain experimentally due to the complex nature of colloidal particles [23,74]. For example, there is a range of supramolecular aggregates, such as micelles, that disassemble into free units as solute concentration approaches zero [75]. From a practical point of view, it is convenient to identify sufficiently low concentrations at which cross-term diffusion coefficients can be successfully measured and verify that the extracted diffusiophoretic mobility is independent of particle concentration within the experimental error. Fortunately, as it will be discussed later, non-equilibrium thermodynamics shows that the cross-term diffusion coefficient associated with diffusiophoresis does not explicitly depend on the thermodynamic non-ideality of colloidal particles. In contrast, thermodynamic non-ideality is known to cause a significant concentration dependence of the DLS diffusion coefficient [23,68,76,77]. Note that diffusiophoresis of a colloidal particle is explicitly related to how particle chemical potential depends on the concentration of the cosolute [25]. Indeed, a gradient of cosolute concentration causes a chemical-potential gradient of the colloidal particle, which may be then responsible for its migration from high to low chemical potential.

The thermodynamic effect of cosolutes on colloidal particles has been extensively investigated in the case of proteins by introducing thermodynamic parameters known as preferential-interaction coefficients [78,79,80,81,82,83,84]. These quantify the thermodynamic affinity of a protein for either the solvent (water) or the cosolute (salt or osmolyte). Related experimental and theoretical studies have played a crucial role in understanding equilibrium dialysis [85], protein solubility and crystallization [86,87,88], conformational stability [89], Hofmeister series [90,91] and modulation of biochemical reactions [79]. The connection of preferential-interaction coefficients to diffusiophoresis will also be discussed in this paper.

As previously mentioned, two cross-term diffusion coefficients are needed to describe a ternary system, with one of them describing diffusiophoresis. The other cross-term, which describes cosolute diffusion due to the concentration gradient of colloidal particles, will be denoted as cosolute “osmotic diffusion” [25,72,92]. This term was first introduced by Toor in 1957 as an alternative name for cross-diffusion in multicomponent mixtures [93]. Using different names (“diffusiophoresis” and “osmotic diffusion”) facilitates distinction between the two related cross-diffusion processes. Interestingly, as will be discussed below, cosolute osmotic diffusion is more closely related to preferential-interaction coefficients than particle diffusiophoresis [25,72,92]. Thus, it plays an important role in understanding the thermodynamic component of particle diffusiophoresis and identifying the underlying mechanisms responsible for this transport process [25,92].

The following sections of this paper intend to provide a formulation of diffusiophoresis by employing the formalism of multicomponent diffusion and non-equilibrium thermodynamics. Representative experimental diffusiophoresis data previously obtained on two different macromolecules, polyethylene glycol (PEG) [25,92,94] and lysozyme [66,71,72,95], will also be reviewed. These sections will be organized in the following way. In Section 2, the theoretical background of non-equilibrium thermodynamics that is relevant to multicomponent diffusion in ternary systems is reviewed. In Section 3 and Section 4, the formulation of non-equilibrium thermodynamics is used to describe both diffusiophoresis and osmotic diffusion. Specifically, reduced diffusiophoresis and osmotic diffusion coefficients will be introduced. Their connection to preferential-interaction coefficients will also be discussed. In Section 5, the connection of preferential-interaction coefficients to the mechanisms of preferential solvation of colloidal particles and Donnan equilibrium [71,73] for charged particles will be discussed. In Section 6, the Nernst–Planck equations for ternary electrolyte mixtures [52,64,71] are revisited to derive mathematical expressions for diffusiophoresis and osmotic diffusion coefficients. In Section 7, the determination of these two transport parameters from measurements of multicomponent-diffusion coefficients by employing the Gosting diffusiometer operating in the Rayleigh interferometry method will be discussed. In Section 8, representative experimental results on diffusiophoresis of PEG [25,92,94], a neutral hydrophilic macromolecule in the presence of salts and osmolytes will be presented. In Section 9, a useful model [25] based on preferential hydration will be discussed. This has been employed to describe the experimental results of PEG. In Section 10, the experimental results on diffusiophoresis of lysozyme [66,71,72,95], a positively charged protein, in the presence of salts will be presented. In Section 11 and Section 12, the experimental results on lysozyme will be discussed by considering both the electrophoretic (Section 11) and preferential-hydration (Section 12) mechanisms responsible for salt-induced protein diffusiophoresis.

2. Diffusion, Onsager Transport Coefficients and Reference Frames

In this section, the words “colloidal particle” or simply “particle” will be used to generally indicate macromolecules (proteins, polymers), supramolecular aggregates (micelles, vesicles) and nanoparticles (silica, polystyrene latex), with characteristic sizes ranging from 1 nm to 1 mm. The symbols “P” for colloidal particle, “S” for cosolute (e.g., salt or osmolyte) and “W” for solvent (e.g., water) will be employed.

In the absence of advection and chemical reactions, isothermal and isobaric diffusion in a ternary particle–cosolute–solvent liquid mixture is described by two linear laws relating the fluxes of the two solutes (P and S) to the two independent thermodynamic driving forces, the gradients of particle and cosolute chemical potentials. We have the following [51,96]:

$$-J_{\mathrm{P}}=L_{\mathrm{PP}} \nabla {\mu }_{\mathrm{P}}+L_{\mathrm{PS}} \nabla {\mu }_{\mathrm{S}}$$

(2a)

$$-J_{\mathrm{S}}=L_{\mathrm{SP}} \nabla {\mu }_{\mathrm{P}}+L_{\mathrm{SS}} \nabla {\mu }_{\mathrm{S}}$$

(2b)

where J_P and J_S are the molar fluxes of particle and cosolute, and μ_P and μ_S the corresponding chemical potentials. The matrix of the four L_ijs (with i,j = P,S) is the Onsager transport coefficient [51,53]. Main-term coefficients, L_PP and L_SS, describe the flux of solutes due to their own concentration gradients, while cross-term coefficients, L_PS and L_SP, describe the flux of a solute due to the concentration gradient of the other solute.

In Equation (2a,b), molar fluxes can also be rewritten as J_P = C_P·v_P and J_S = C_S·v_S [39,96], where C_P and C_S are the molar concentrations of particle and cosolute, while v_P and vs. are the corresponding diffusion velocities, which must be defined with respect to a reference frame. In the volume-fixed reference frame, v_P and vs. are defined relative to the center of volume of the ternary mixture, which corresponds to the external laboratory coordinate if mixing can be assumed to occur in isochoric conditions (i.e., the volume of mixing is negligible). In the solvent-fixed reference frame, v_P and vs. are defined relative to solvent diffusion, i.e., solvent diffusion velocity is set to be zero [39,96]. Both reference frames are qualitatively described in Figure 2 in the case of a binary mixture for simplicity.

According to non-equilibrium thermodynamics, the matrix of the four L_ijs becomes symmetric in the solvent-fixed reference frame, with

$$L_{\mathrm{PS}}=L_{\mathrm{SP}}$$

(3)

representing the Onsager reciprocal relation (ORR) [51,53]. Thus, Equation (2a,b) are usually employed to describe diffusion in the solvent-fixed reference frame. Note that diffusive transport in ternary mixtures is characterized by three independent transport coefficients.

For completeness, it is important to note that diffusion can be equivalently described by inverting Equation (2a,b). In this description, the particle thermodynamic driving force, ▽μ_P, is written as a linear combination of the velocity differences, v_P-v_W and v_P-v_S, while cosolute thermodynamic driving force, ▽μ_S, is a linear combination of the velocity differences, v_S-v_W and v_S-v_P [97]. In the field of chemical engineering, this description corresponds to the well-known Stefan–Maxwell equations [45,46,57,72,98]. The convenience of this formalism is that the coefficients of these linear combinations can be interpreted as frictional coefficients, which are also independent of the reference frame [97,99]. There are three independent friction coefficients characterizing particle–solvent, cosolute–solvent and particle–cosolute frictional interaction. These could be, in principle, experimentally determined from measurements on the three corresponding binary mixtures and assumed to be the same in the ternary mixture. However, since the particle–cosolute binary system is not accessible experimentally, Stefan–Maxwell equations are not particularly valuable for diffusiophoresis. Moreover, multicomponent-diffusion experiments on aqueous PEG in the presence of several cosolutes (osmolytes and salts) show that the PEG–cosolute frictional coefficient in water is negative [25,92,99]. This implies that its physical interpretation as an actual friction between PEG and cosolute components is misleading. Thus, Stefan–Maxwell equations do not seem to provide noteworthy benefits over Equation (2a,b) and will not be further considered below.

According to Equation (2a,b), molar fluxes, J_P and J_S, are related to the gradient of chemical potentials, ▽μ_P and ▽μ_S. Although these are the actual thermodynamic driving forces of diffusion, it is practically convenient to describe diffusion as caused by concentration gradients, ▽C_P and ▽C_S. This description is just a generalization of the well-known Fick’s law [58,100], normally encountered when describing binary mixtures [51]. The 2 × 2 matrix of Fickian diffusion coefficients is introduced by the following:

$$-J_{\mathrm{P}}=D_{\mathrm{PP}} \nabla C_{\mathrm{P}}+D_{\mathrm{PS}} \nabla C_{\mathrm{S}}$$

(4a)

$$-J_{\mathrm{S}}=D_{\mathrm{SP}} \nabla C_{\mathrm{P}}+D_{\mathrm{SS}} \nabla C_{\mathrm{S}}$$

(4b)

where the four D_ijs (with I,j = P,S) are denoted as multicomponent-diffusion coefficients (or ternary diffusion coefficients in this case). Main-term diffusion coefficients, D_PP and D_SS, describe the flux of solutes due to their own concentration gradients, while cross-term diffusion coefficients, D_PS and D_SP, describe the flux of a solute due to the concentration gradient of the other solute. Note that D_PS in Equation (4a) is directly proportional to C_P with D_PS = 0 at C_P = 0 [72]. Thus, it is more appropriate to consider the ratio D_PS/C_P when examining particle diffusiophoresis. Indeed, the value of this ratio becomes virtually independent of C_P in dilute colloidal solutions [72].

We can write Equation (4a,b) with respect to any reference frame, but it is convenient to define them with respect to solvent-fixed reference frame so that we can more directly connect Equation (4a,b) with a symmetric matrix of Onsager transport coefficients. Comparison of Equation (2a,b) with Equation (4a,b) yields the following [53]:

$$D_{\mathrm{PP}}=L_{\mathrm{PP}}{\mu }_{\mathrm{PP}}+L_{\mathrm{PS}}{\mu }_{\mathrm{SP}}$$

(5a)

$$D_{\mathrm{PS}}=L_{\mathrm{PP}}{\mu }_{\mathrm{PS}}+L_{\mathrm{PS}}{\mu }_{\mathrm{SS}}$$

(5b)

$$D_{\mathrm{SP}}=L_{\mathrm{SP}}{\mu }_{\mathrm{PP}}+L_{\mathrm{SS}}{\mu }_{\mathrm{SP}}$$

(5c)

$$D_{\mathrm{SS}}=L_{\mathrm{SP}}{\mu }_{\mathrm{PS}}+L_{\mathrm{SS}}{\mu }_{\mathrm{SS}}$$

(5d)

where μ_ij ≡ (𝜕μ_i/𝜕C_j)_Ck,k≠j and the partial-derivative subscripts denoting temperature and pressure are omitted to alleviate notation. The four μ_ijs in Equation (5a–d) are thermodynamically linked by the following [53,101]:

$${\mu }_{\mathrm{SP}}(1-C_{\mathrm{P}}{\overline{V}}_{\mathrm{P}})+{\mu }_{\mathrm{PP}}{C}_{\mathrm{P}}{\overline{V}}_{\mathrm{S}}={\mu }_{\mathrm{PS}}(1-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}})+{\mu }_{\mathrm{SS}}{C}_{\mathrm{S}}{\overline{V}}_{\mathrm{P}}$$

(6)

where ${\overline{V}}_{\mathrm{P}}$ and ${\overline{V}}_{\mathrm{S}}$ are particle and cosolute partial molar volumes, respectively.

The limit of C_P→0 is particularly important for particle diffusiophoresis. In this limit, D_PP becomes the particle tracer-diffusion coefficient, D_P(C_S), while D_SS is the cosolute diffusion coefficient of the binary cosolute–solvent system in the solvent-fixed reference frame, D_S(C_S). We have the following:

$$D_{\mathrm{P}}\equiv \underset{C_{\mathrm{P}}\to 0}{\lim }{D}_{\mathrm{PP}}=\underset{C_{\mathrm{P}}\to 0}{\lim }(L_{\mathrm{PP}}{\mu }_{\mathrm{PP}})=\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{\mathcal{R}T{L}_{\mathrm{PP}}}{C_{\mathrm{P}}}$$

(7a)

$$D_{\mathrm{S}}\equiv \underset{C_{\mathrm{P}}\to 0}{\lim }{D}_{\mathrm{SS}}=\underset{C_{\mathrm{P}}\to 0}{\lim }(L_{\mathrm{SS}}{\mu }_{\mathrm{SS}})$$

(7b)

where T is the absolute temperature, $\mathcal{R}$ is the ideal gas constant, and we have also used μ_PP→ $\mathcal{R}$T/C_P. Note that L_PP→0 and L_PS→0 while L_PP/C_P and L_PS/L_PP remain finite in the limit of C_P→0.

Multicomponent-diffusion coefficients are typically measured in the volume-fixed frame [39,53,96]. The solvent-fixed diffusion coefficients, $D_{ij}$, can then be calculated from the corresponding volume-fixed diffusion coefficients, $D_{ij}^V$, by the following [39,51,102]:

$$\frac{D_{\mathrm{PP}}-D_{\mathrm{PP}}^V}{C_{\mathrm{P}}}=\frac{D_{\mathrm{SP}}-D_{\mathrm{SP}}^V}{C_{\mathrm{S}}}=\frac{{\overline{V}}_{\mathrm{P}}{D}_{\mathrm{PP}}^V+{\overline{V}}_{\mathrm{S}}{D}_{\mathrm{SP}}^V}{1-C_{\mathrm{P}}{\overline{V}}_{\mathrm{P}}-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}}}$$

(8a)

$$\frac{D_{\mathrm{SS}}-D_{\mathrm{SS}}^V}{C_{\mathrm{S}}}=\frac{D_{\mathrm{PS}}-D_{\mathrm{PS}}^V}{C_{\mathrm{P}}}=\frac{{\overline{V}}_{\mathrm{P}}{D}_{\mathrm{PS}}^V+{\overline{V}}_{\mathrm{S}}{D}_{\mathrm{SS}}^V}{1-C_{\mathrm{P}}{\overline{V}}_{\mathrm{P}}-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}}}$$

(8b)

In the limit of C_P→0, Equation (8a,b) yield the following:

$$\underset{C_{\mathrm{P}}\to 0}{\lim }{D}_{\mathrm{PP}}^V=\underset{C_{\mathrm{P}}\to 0}{\lim }{D}_{\mathrm{PP}}=D_{\mathrm{P}}$$

(9a)

$$\underset{C_{\mathrm{P}}\to 0}{\lim }{D}_{\mathrm{SS}}^V=D_{\mathrm{S}}(1-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}})$$

(9b)

$$\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{D_{\mathrm{PS}}}{C_{\mathrm{P}}}-\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{D_{\mathrm{PS}}^V}{C_{\mathrm{P}}}={\overline{V}}_{\mathrm{S}}{D}_{\mathrm{S}}$$

(9c)

$$\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{D_{\mathrm{SP}}}{D_{\mathrm{SS}}}-\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{D_{\mathrm{SP}}^V}{D_{\mathrm{SS}}^V}=\frac{{\overline{V}}_{\mathrm{P}}{D}_{\mathrm{P}}}{(1-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}})D_{\mathrm{S}}}$$

(9d)

The conversion terms between the two reference frames are typically small and may be comparable with experimental error in the case of cross-term diffusion coefficients.

3. Particle Diffusiophoresis from Non-Equilibrium Thermodynamics

In this section, particle diffusiophoresis is described using the framework of non-equilibrium thermodynamics in the solvent-fixed reference frame. Since the actual thermodynamic driving force of this transport process is the gradient of cosolute chemical potential, we need to replace ▽lnC_S in Equation (1) with ▽μ_S. In the limit of C_P→0, we can write the following:

$$\frac{ \nabla {\mu }_{\mathrm{S}}}{\mathcal{R}T}={\nu }_{\mathrm{S}}{y}_{\mathrm{S}} \nabla \ln C_{\mathrm{S}}$$

(10)

where ν_S is the number of cosolute particles (e.g., ν_S = 1 for non-electrolytes, ν_S = 2 for symmetric electrolytes such as NaCl or MgSO₄ and ν_S = 3 for asymmetric electrolytes such as MgCl₂ or Na₂SO₄) and y_S is a thermodynamic factor (known for many cosolutes [103,104,105,106,107]) characterizing thermodynamic non-ideality of the binary cosolute–water system, with y_S = 1 in the limit of C_S→0. Since D_PS has the units of a diffusion coefficient, it is also convenient to consider the unitless ratio, D_PS/D_P, which describes the magnitude of diffusiophoresis compared to particle Brownian mobility. Note that this ratio is also independent of fluid viscosity because both D_PS and D_P are inversely proportional [15,27,30,73,108] to the fluid viscosity coefficient. We, therefore, describe diffusiophoresis by writing the following:

$$v_{\mathrm{P}}=-D_{\mathrm{P}}\left( \nabla \ln C_{\mathrm{P}}+{\widehat{D}}_{\mathrm{PS}}\hspace{0.17em}\frac{ \nabla {\mu }_{\mathrm{S}}}{\mathcal{R}T}\right)$$

(11)

where the second term in parenthesis characterizes particle diffusiophoresis with ${\widehat{D}}_{\mathrm{PS}}$ being the reduced diffusiophoresis coefficient [25,39,102]. The first term in Equation (11) represents the restoring Brownian entropic force. The reduced coefficient, ${\widehat{D}}_{\mathrm{PS}}$, is related to D_PS by the following:

$${\mathcal{D}}_{\mathrm{PS}}=D_{\mathrm{P}}{\nu }_{\mathrm{S}}{y}_{\mathrm{S}}\hspace{0.17em}{\widehat{D}}_{\mathrm{PS}}$$

(12)

where ν_Sy_S represents the conversion factor from ∇lnC_S to ∇μ_S/$\mathcal{R}$T (see Equation (10)). Thus, the convenience of ${\widehat{D}}_{\mathrm{PS}}$ compared to D_PS is that it does not explicitly depend on the stoichiometry and thermodynamic non-ideality of cosolute. Henceforth, diffusiophoresis will be described using ${\widehat{D}}_{\mathrm{PS}}$, recognizing that it can be readily converted into D_PS by employing Equation (12).

There is a simple case in which values of ${\widehat{D}}_{\mathrm{PS}}$ have a direct physical interpretation. Specifically, we may consider a steady-state diffusion process that is appropriate for colloidal particles in the presence of relatively small ions and molecules of cosolute and solvent components [92]. We shall neglect cosolute thermodynamic non-ideality (y_S = 1) and small corrections due to changes in the reference frame for simplicity. As illustrated in Figure 3, a horizontal tube positioned between x = 0 and x = l is sandwiched between two reservoirs consisting of two different binary cosolute−solvent solutions, with cosolute concentrations, C_S^(L) (left compartment, x ≤ 0) and C_S^(R) > C_S^(L) (right compartment, x ≥ l), respectively. Two membranes, not permeable to colloidal particles, seal the two tube extremities. This type of geometries, which is needed to establish steady-state concentration gradients of cosolutes, has been indeed implemented in “H-type” microfluidic devices to investigate bacterial chemotaxis [109,110] and particle diffusiophoresis [111].

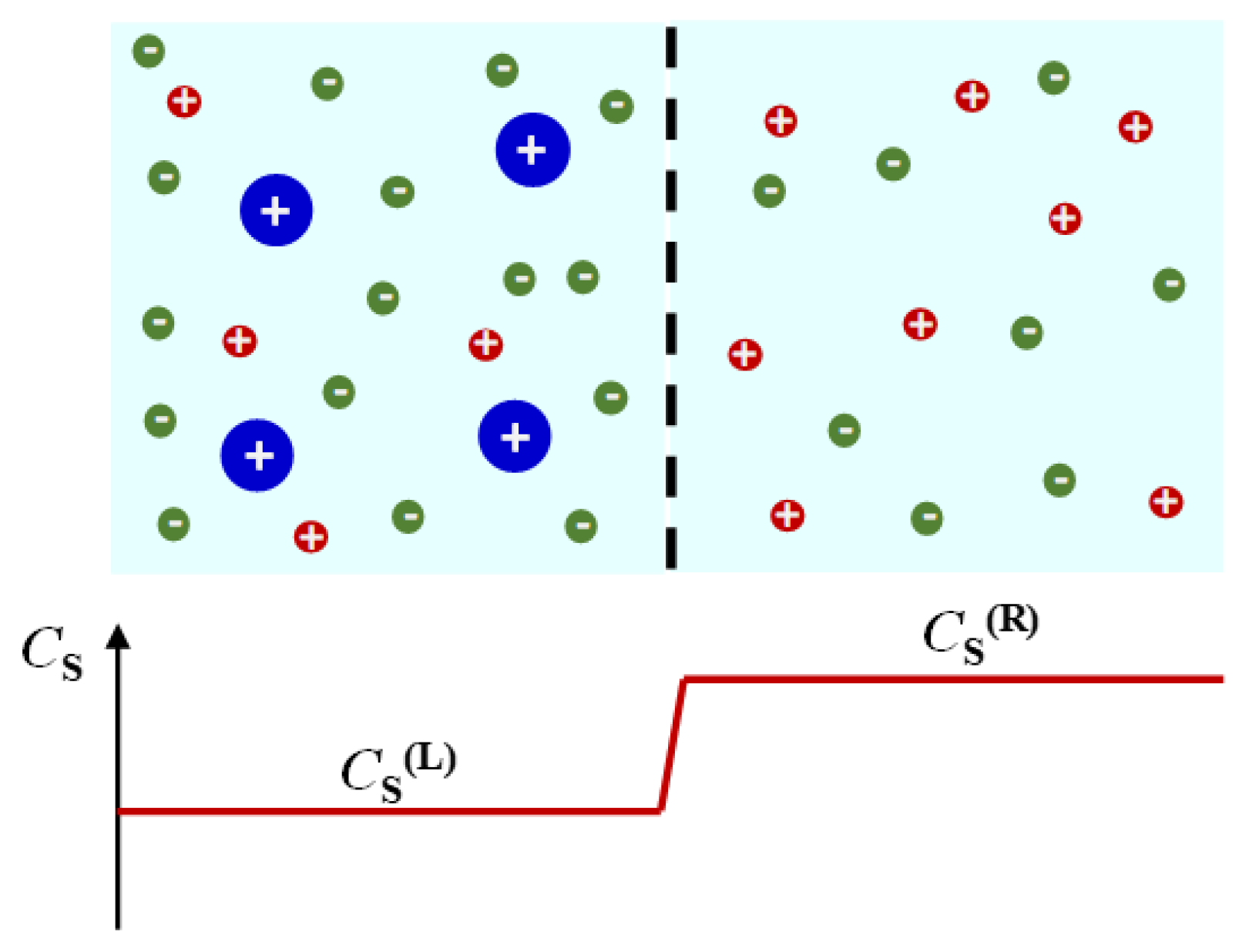
In steady-state conditions, we must have v_P = 0 throughout the tube because of the semipermeable membranes. Hence, Equation (11) becomes the following:

$$\frac{d\ln C_{\mathrm{P}}}{d({\nu }_{\mathrm{S}}{C}_{\mathrm{S}})}=-\hspace{0.17em}\frac{{\widehat{D}}_{\mathrm{PS}}}{C_{\mathrm{S}}}$$

(13)

where ν_SC_S is cosolute osmolarity. This steady-state process is analogous to equilibrium sedimentation in which sedimentation due to external gravitational field is counter-balanced by the restoring entropic force associated with Brownian diffusion.

As we shall see later, ${\widehat{D}}_{\mathrm{PS}}$/C_S is essentially a constant for neutral particles [92]. In this case, integration of Equation (13) shows that ln[C_P^(L)/C_P^(R)] ≈ (${\widehat{D}}_{\mathrm{PS}}$/C_–)·ν_SC_P^(L) − C_P^(R)]. For example, when we set the difference in cosolute osmolari–y tν_S[C_P^(L) − C_P^(R)] = 1 M, we obtain C_P^(L)/C_P^(R) ≈ 2.7 if ${\widehat{D}}_{\mathrm{PS}}$/C_S ≈ 1 M⁻¹ and C_P^(L)/C_P^(R) ≈ 150 if ${\widehat{D}}_{\mathrm{PS}}$/C_S ≈ 5 M⁻¹. For charged particles, at salt concentrations of the order of 1 mM, we can approximately assume that ${\widehat{D}}_{\mathrm{PS}}$ is a constant. In this second case, integration shows that ln[C_P^(L)/C_P^(R)] ≈ ${\widehat{D}}_{\mathrm{PS}}·$ ln[C_S^(L)/C_S^(R)]^νS. When we then set the ratio in salt concentration to C_S^(L)/C_S^(R) = 100 (e.g., C_S^(L) = 0.1 mM and C_S^(R) = 10 mM) with ν_S = 2, we obtain C_P^(L)/C_P^(R)≈100 if ${\widehat{D}}_{\mathrm{PS}}$ ≈ 0.5.

We now turn our attention to the link between the diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$, and Onsager transport coefficients. In the limit of C_P→0, Equation (7a) and J_P = C_P·v_P can be used to rewrite Equation (4a) in the following way [23]:

$$v_{\mathrm{P}}=-D_{\mathrm{P}}\left(\frac{\nabla {\mu }_{\mathrm{P}}}{\mathcal{R}T}-\hspace{0.17em}\lambda \frac{\nabla {\mu }_{\mathrm{S}}}{\mathcal{R}T}\right)$$

(14)

where λ is a reduced hydrodynamic coefficient defined by the following:

$$\lambda \equiv -\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{L_{\mathrm{PS}}}{L_{\mathrm{PP}}}$$

(15)

In Equation (14), λ describes particle migration in response to the gradient of cosolute chemical potential when ▽μ_P = 0. As it will be shown below, this does not correspond to ▽lnC_P = 0. Note that the negative sign in Equation (15) is just a convention, justified by λ being a positive hydrodynamic coefficient for colloidal particles that preferentially interact with solvent [92]. To link ${\widehat{D}}_{\mathrm{PS}}$ to λ, we need to relate ▽μ_P to ▽lnC_P. This is achieved by considering the differential of μ_P(C_P, μ_S):

$$\frac{\nabla {\mu }_{\mathrm{P}}}{RT}=\nabla \ln C_{\mathrm{P}}+\gamma \hspace{0.17em}\frac{\nabla {\mu }_{\mathrm{S}}}{\mathcal{R}T}$$

(16)

where

$$\gamma \equiv \underset{C_{\mathrm{P}}\to 0}{\lim }{\left(\frac{𝜕{\mu }_{\mathrm{P}}}{𝜕{\mu }_{\mathrm{S}}}\right)}_{C_{\mathrm{P}}}=\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{{\mu }_{\mathrm{PS}}}{{\mu }_{\mathrm{SS}}}$$

(17)

is a preferential-interaction coefficient. If the expression of ▽μ_P given by Equation (16) is inserted into Equation (14), we can finally deduce the following [71,95]:

$${\widehat{D}}_{\mathrm{PS}}=\hspace{0.17em}\gamma -\lambda$$

(18)

In summary, non-equilibrium thermodynamics is used to write particle diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$, as the difference between a thermodynamic component (γ) and a transport component (λ). It has been experimentally shown that the magnitude of λ is typically comparable with that of γ [92]. This implies that both thermodynamic and hydrodynamic interactions are equally important in shaping the behavior of ${\widehat{D}}_{\mathrm{PS}}$.

4. Cosolute Osmotic Diffusion from Non-Equilibrium Thermodynamics

Cosolute osmotic diffusion describes cosolute diffusion induced by a concentration gradient of colloidal particles. As in the case of diffusiophoresis, a reduced coefficient is introduced for osmotic diffusion. Since the diffusion of colloidal particles is slow compared to that of cosolute, it is also convenient to consider the hypothetical limit in which particle mobility is negligible compared to cosolute mobility [71]. In this case, a particle concentration gradient will dissipate after a time that is infinitely long compared to that needed for cosolute diffusion to reach a quasi-equilibrium condition. This condition is achieved when the osmotic diffusion rate, D_SP∇C_P, is counter-balanced by the cosolute diffusion rate, D_SS∇C_S, in Equation (4b). Thus, the ratio D_SP/D_SS essentially describes the equilibrium distribution of cosolute along a quasi-static concentration gradient of particles. This ratio is analogous to an equilibrium constant of a reversible reaction, which is the ratio of forward and backward kinetic constants. Cosolute osmotic diffusion is illustrated in Figure 4. Here, we can also appreciate that this transport process is also related to cosolute partitioning occurring in equilibrium dialysis. Specifically, we can consider two compartments containing a ternary particle–cosolute–solvent system and a binary cosolute–solvent system in chemical equilibrium with respect to the cosolute component through a membrane that is not permeable to particles. The difference in particle concentration between the two compartments is responsible for cosolute osmotic diffusion across the membrane, thereby leading to a difference in cosolute concentration between the two compartments at equilibrium. The connection of equilibrium dialysis to cosolute osmotic diffusion emerges from the fact that cosolute partitioning between the two compartments can also be achieved in the absence of a membrane, provided that the Brownian mobility of the colloidal particles is negligible compared to cosolute mobility.

Since the ratio D_SP/D_SS is closely connected to cosolute partitioning at equilibrium, it is convenient to define the unitless osmotic diffusion coefficient [25,71]:

$${\widehat{D}}_{\mathrm{SP}}\equiv \underset{C_{\mathrm{P}}\to 0}{\lim }\frac{D_{\mathrm{SP}}}{D_{\mathrm{SS}}}$$

(19)

We can use non-equilibrium thermodynamics to rigorously relate this coefficient to cosolute partitioning. Specifically, we first take the ratio of the expressions of D_SP (Equation (5c)) and D_SS (Equation (5d)). We then consider that we have: D_SS→L_SSμ_SS in the limit of C_P→0 (see Equation (7b)). This allows us to write D_SP/D_SS→(L_SPμ_PP)/(L_SSμ_SS)+ μ_SP/μ_SS. As will be further discussed below, it is the thermodynamic ratio, μ_SP/μ_SS, that describes cosolute partitioning. The product, L_SPμ_PP, can be rewritten as (L_PPμ_PP)(L_PS/L_PP), where we have also used the ORR (Equation (3)). According to Equation (7a,b), we can then write (L_PPμ_PP)/(L_SSμ_SS)→D_P/D_S. We finally obtain the following:

$${\widehat{D}}_{\mathrm{SP}}=C_{\mathrm{SP}}-\alpha \lambda$$

(20)

where

$$C_{\mathrm{SP}}\equiv -\hspace{0.17em}\hspace{0.17em}\underset{C_{\mathrm{P}}\to 0}{\lim }{\left(\frac{𝜕C_{\mathrm{S}}}{𝜕C_{\mathrm{P}}}\right)}_{{\mu }_{\mathrm{S}}}=\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{{\mu }_{\mathrm{SP}}}{{\mu }_{\mathrm{SS}}}$$

(21)

and we have also used (𝜕μ_S/𝜕C_P)_CS = −(𝜕μ_S/𝜕C_S)_CP(𝜕C_S/𝜕C_P)_μS. The thermodynamic factor, C_SP, characterizes the effect of particle concentration on cosolute concentration at equilibrium. The negative sign in the definition of C_SP is just a convention. It ensures that this parameter assumes positive values for colloidal particles that preferentially interact with solvent. Integration of C_SP with respect to C_P characterizes cosolute partitioning. In Equation (20), we have also defined the following:

$$\alpha \equiv \frac{D_{\mathrm{P}}}{D_{\mathrm{S}}}$$

(22)

as the particle-to-salt diffusion ratio, with typically α ≈ 0.1 or less. In Equation (22), αλ is small compared to C_SP, and ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP is a suitable approximation, which is consistent with our previous discussion. Indeed, we can state that ${\widehat{D}}_{\mathrm{SP}}$→C_SP in the limit of α→0. Note that Equation (3) allows us to introduce λ not only in Equation (18) for ${\widehat{D}}_{\mathrm{PS}}$ but also in Equation (20) for ${\widehat{D}}_{\mathrm{SP}}$. In other words, the ORR connects ${\widehat{D}}_{\mathrm{SP}}$ with ${\widehat{D}}_{\mathrm{PS}}$. However, the validity ORR is not critical because αλ in Equation (23) is small. To fully link ${\widehat{D}}_{\mathrm{SP}}$ and ${\widehat{D}}_{\mathrm{SP}}$, we also need to relate C_SP in Equation (20) to g in Equation (18). This is achieved by determining the expression of μ_SP/μ_SS from Equation (6) in the limit of C_P→0. We obtain the following [53,71,80,101,102]:

$$C_{\mathrm{SP}}\hspace{0.17em}=\hspace{0.17em}(1-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}})\hspace{0.17em}\gamma \hspace{0.17em}+C_{\mathrm{S}}{\tilde{V}}_{\mathrm{P}}$$

(23)

where ${\tilde{V}}_{\mathrm{P}}$ ≡ ${\overline{V}}_{\mathrm{P}}$ − (ν_Sy_S)⁻¹${\overline{V}}_{\mathrm{S}}$. Note that ${\tilde{V}}_{\mathrm{P}}$ = ${\overline{V}}_{\mathrm{P}}$ is an excellent approximation because ${\overline{V}}_{\mathrm{S}}$ is significantly smaller than ${\overline{V}}_{\mathrm{P}}$. It is Equation (23) that critically connects ${\widehat{D}}_{\mathrm{PS}}$ with ${\widehat{D}}_{\mathrm{SP}}$. Since both coefficients are related to γ and λ, measurements of ${\widehat{D}}_{\mathrm{PS}}$ and ${\widehat{D}}_{\mathrm{SP}}$ can be used to extract these two fundamental parameters. Although γ and λ can be rigorously calculated by combining Equations (18), (20) and (23), it is important to appreciate that ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP alone can be used to approximately extract the preferential-interaction coefficient, γ, from Equation (23). Its insertion into Equation (18) then allows the calculation of the hydrodynamic coefficient, λ.

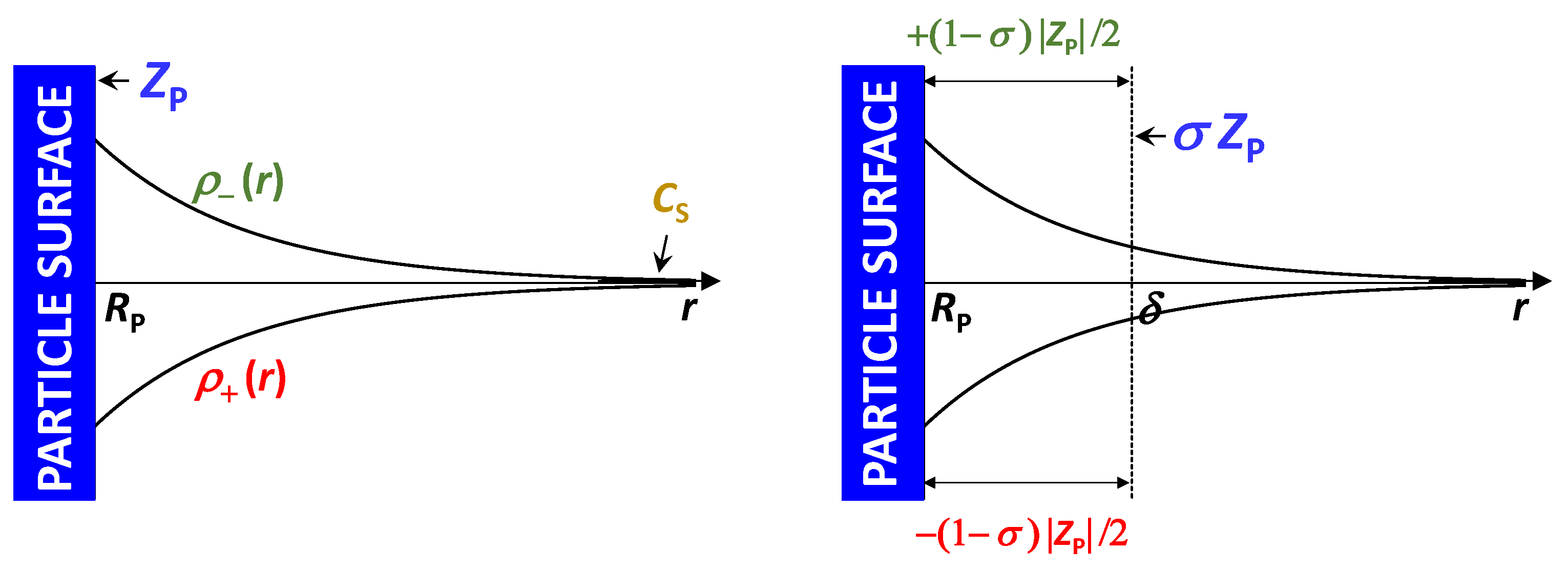
5. Interpretation of Preferential-Interaction Coefficients

In Section 4, two preferential-interaction coefficients, γ and C_SP, were introduced. They appear in the expressions of particle diffusiophoresis (Equation (18)) and cosolute osmotic diffusion (Equation (20)) and are linked to each other by Equation (23). In this section, the behavior of these thermodynamic parameters is discussed by first examining the case of a neutral colloidal particle and then considering the case of charged particles sharing a common ion with an ionic cosolute. According to the Kirkwood–Buff theory [112,113,114,115], we can write the following:

$$C_{\mathrm{SP}}=\hspace{0.17em}({\Gamma }_{\mathrm{SP}}-{\Gamma }_{\mathrm{SW}})C_{\mathrm{S}}$$

(24)

where

$${\Gamma }_{\mathrm{SP}}\equiv 4\pi N_A{\displaystyle \underset{0}{\overset{\infty }{\int }}[1-g_{\mathrm{SP}}(r)]\hspace{0.17em}{r}^{2}dr}$$

(25a)

$${\Gamma }_{\mathrm{SW}}\equiv 4\pi N_A{\displaystyle \underset{0}{\overset{\infty }{\int }}[1-g_{\mathrm{SW}}(r)]\hspace{0.17em}{r}^{2}dr}$$

(25b)

and N_A is the Avogadros’s number. The functions, g_SP(r) and g_SW(r), are angularly averaged and normalized distribution functions of cosolute as a function of distance, r, from the center of mass of the colloidal particle and solvent molecule, respectively. Note that g_SP(∞) = g_SW(∞) = 1 (bulk value). In the limit of C_P→0, g_SP(r) characterizes cosolute radial distribution around one colloidal particle. This distribution is the net result of multiple types of interactions occurring between the colloidal particles, cosolute and solvent molecules. For example, it is shaped not only by the specific binding of solvent and/or cosolute to the particle but also by particle–cosolute excluded-volume interactions. On the other hand, g_SW(r) characterizes cosolute–solvent interactions in the binary cosolute–solvent system.

The integrals, ${\Gamma }_{\mathrm{SP}}$ and ${\Gamma }_{\mathrm{SW}}$, have the units of a molar volume. According to Equation (25a), the steric presence of the colloidal particle itself yields ${\Gamma }_{\mathrm{SP}}$ = ${\overline{V}}_{\mathrm{P}}$. This allows us to appreciate that the magnitude of ${\Gamma }_{\mathrm{SP}}$ is of the order of ${\overline{V}}_{\mathrm{P}}$, while ${\Gamma }_{\mathrm{SW}}$ is small because its magnitude is comparable with cosolute and solvent molar volumes. Indeed, it can be shown that ${\Gamma }_{\mathrm{SW}}$ ≈ ${\overline{V}}_{\mathrm{S}}$ at low cosolute concentration. To understand the physical meaning of C_SP and γ, we assume that ${\Gamma }_{\mathrm{SW}}$ << ${\Gamma }_{\mathrm{SP}}$ in Equation (24) and ${\overline{V}}_{\mathrm{S}}$ << ${\overline{V}}_{\mathrm{P}}$ in Equation (23). Both G_SP and ${\tilde{V}}_{\mathrm{P}}$ = ${\overline{V}}_{\mathrm{P}}$ are regarded as constant. In this case, we can write the following:

$$C_{\mathrm{SP}}={\Gamma }_{\mathrm{SP}}{C}_{\mathrm{S}}$$

(26a)

$$\gamma =\frac{{\Gamma }_{\mathrm{SP}}-{\overline{V}}_{\mathrm{P}}}{1-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}}}{C}_{\mathrm{S}}$$

(26b)

where Equation (26a) shows that C_SP is directly proportional to cosolute concentration, C_S, with C_SP = 0 at C_S = 0. Note that Equation (26b) is obtained from Equation (26a) by using Equation (23). The preferential-interaction coefficient, g, is also approximately proportional to C_S because C_S${\overline{V}}_{\mathrm{S}}$ in the denominator of Equation (26b) is usually less than 10%. The proportionality constant, ${\Gamma }_{\mathrm{SP}}$, represents the net excluded volume experienced by cosolute, with ${\Gamma }_{\mathrm{SP}}$ = ${\overline{V}}_{\mathrm{P}}$ as the reference case in which the steric presence of the colloidal particle is the sole contribution to particle–cosolute interactions. As described in Figure 5, we have ${\Gamma }_{\mathrm{SP}}$ > ${\overline{V}}_{\mathrm{P}}$ when cosolute is depleted in the proximity of the particle (preferential solvation) and ${\Gamma }_{\mathrm{SP}}$ < ${\overline{V}}_{\mathrm{P}}$ when cosolute is enriched in the proximity of the particle (preferential binding).

Clearly, the preferential-interaction coefficient, γ, directly quantifies cosolute depletion or enrichment in the particle proximity because γ is directly proportional to ${\Gamma }_{\mathrm{SP}}$ − ${\overline{V}}_{\mathrm{P}}$, i.e., γ > 0 and γ < 0 correspond to preferential solvation and preferential binding, respectively. It is then convenient to rewrite Equation (26b) in the following way [25,79]:

$$\gamma ={\nu }_{\mathrm{W}}\frac{C_{\mathrm{S}}}{C_{\mathrm{W}}}$$

(27)

where we have used C_W${\overline{V}}_{\mathrm{W}}$ + C_S${\overline{V}}_{\mathrm{S}}$ = 1, with C_W and ${\overline{V}}_{\mathrm{W}}$ being solvent concentration and partial molar volume, respectively. Note that C_W ≈ 1/${\overline{V}}_{\mathrm{W}}$ because C_S${\overline{V}}_{\mathrm{S}}$ is small. In Equation (27), we have also introduced the solvent thermodynamic excess, ν_W, through the following equation:

$${\Gamma }_{\mathrm{SP}}={\overline{V}}_{\mathrm{P}}+{\nu }_{\mathrm{W}}{\overline{V}}_{\mathrm{W}}$$

(28)

This thermodynamic parameter, which can be approximated as a constant, represents the number of solvent molecules near the colloidal particle in excess with respect to bulk in the case of preferential solvation, and it becomes negative in the case of preferential binding. Although ν_W increases with particle solvation, it should not be confused [79] with the actual number of solvent molecules bound to the colloidal particles. The solvent thermodynamic excess, ν_W, is introduced by considering the case of a spherical colloidal particle for the sake of simplicity. It is, however, important to note that this thermodynamic formalism is rather general and can be extended to non-spherical particles, including polymer coils. In Section 8, the values of ν_W extracted for PEG in the presence of osmolytes and salts will be reported.

Preferential-interaction coefficients have been extensively investigated in connection to equilibrium dialysis [78,116]. Here, a well-stirred ternary particle–cosolute–solvent solution is in contact with a well-stirred binary cosolute–solvent reservoir through a membrane that is permeable to solvent and cosolute but not to the colloidal particles. At equilibrium, a difference in cosolute concentration between the two solutions (cosolute partitioning) emerges due to preferential solvation or preferential binding. This difference can be explained by observing that the bulk cosolute concentration in the ternary particle–cosolute–solvent compartment is the same as that in the binary cosolute–solvent compartment. This is further described in Figure 6.

Equilibrium dialysis can also be used to determine the expression of C_SP in the case of a charged colloidal particle in the presence of an ionic cosolute with the membrane permeable to both ions (e.g., Na⁺ and Cl⁻ in NaCl) [72,73]. For simplicity, we shall focus on the case of 1:1 symmetric electrolytes. The ion with a charge that is opposite to that of the particle is denoted as a counterion, while the ion with the same charge is denoted as a coion. This case of equilibrium dialysis corresponds to the well-known Donnan equilibrium and has usually been discussed for proteins in the presence of a supporting electrolyte [71,73,81]. To ensure electroneutrality, the concentrations of the two salt ions must be the same in the binary cosolute–solvent compartment. However, there must be an excess of counterions in the ternary particle–cosolute–solvent compartment due to particle charge. If the particle charge is Z_P, the difference in concentration between counterion and coion is |Z_P|C_P. Since the product of the concentrations of the two ions in the ternary compartment must be the same as that in the binary compartment at equilibrium, the excess of counterions in the ternary compartment must be invariably accompanied by a depletion of coions. This leads to a net depression of cosolute concentration in the ternary compartment relative to the binary compartment. Donnan equilibrium is further described in Figure 7. Here, cosolute concentration is assumed to be sufficiently low, so the excluded-volume effect previously illustrated in Figure 6 can be ignored for simplicity.

To take into account the Donnan effect, the expression of the preferential-interaction coefficient, C_SP, is generalized in the following way:

$$C_{\mathrm{SP}}=\frac{\left|Z_{\mathrm{P}}\right|}{2}+({\overline{V}}_{\mathrm{P}}+{\nu }_{\mathrm{W}}{\overline{V}}_{\mathrm{W}})C_{\mathrm{S}}$$

(29)

where the residual positive value of C_SP at C_S = 0 characterizes the Donnan effect, becoming zero for neutral particles. The preferential-interaction coefficient, γ, is modified in the same way because there is no difference between C_SP and γ in the limit of C_S→0 (see Equation (23)):

$$\gamma =\frac{\left|Z_{\mathrm{P}}\right|}{2}+{\nu }_{\mathrm{W}}\frac{C_{\mathrm{S}}}{C_{\mathrm{W}}}$$

(30)

6. Nernst–Planck Equations for Diffusiophoresis and Osmotic Diffusion

For aqueous mixtures containing two (or more) salt components, there exist mathematical expressions straightforwardly linking multicomponent-diffusion coefficients to tracer-diffusion coefficients and the charges of the ions, which are rigorously valid at infinite dilution. These expressions, also known as Nernst–Hartley equations, are derived by applying the electroneutrality conditions to Nernst–Planck equations for single ions [64,71,117]. Clearly, Nernst–Planck equations are also relevant to charged colloidal particles in the presence of a supporting electrolyte. Indeed, there are several multicomponent-diffusion studies on protein–salt–water systems, which have examined the application and validity of Nernst–Planck equations in the case of protein–salt–water systems [37,52,53,117]. In this section, these equations are revisited in order to derive the mathematical expressions of the particle diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$, and salt osmotic diffusion coefficient, ${\widehat{D}}_{\mathrm{PS}}$, at C_S = 0. For simplicity, the case of a positively charged particle in the presence of a 1:1 electrolyte will be considered. In this case, salt anions and cations represent particle counterions and coions, respectively. It is also important to bear in mind that we are also operating within the limit of C_P/C_S→0, i.e., we are considering one colloidal particle surrounded by a diluted sea of salt ions.

We start by considering Equation (11) in the limit of C_S→0. We have the following:

$$v_{\mathrm{P}}=-D_{\mathrm{P}}\left(\nabla \ln C_{\mathrm{P}}+2{\widehat{D}}_{\mathrm{PS}}\nabla \ln C_{\mathrm{S}}\right)$$

(31)

According to Nernst–Planck equations, the migration of a charged particle can be induced by gradients of chemical and electrical potentials [71]:

$$v_{\mathrm{P}}=-D_{\mathrm{P}}\left(\nabla \ln C_{\mathrm{P}}+Z_{\mathrm{P}}\frac{\mathcal{F} \nabla \Psi }{\mathcal{R}T}\right)$$

(32)

where $\mathcal{F}$ is Faraday’s constant, ▽lnC_P, which is the same term shown in Equation (31), represents particle chemical-potential gradient in the limit of C_P→0 and ▽Ψ represents the gradient of electrical potential, Ψ. Clearly, Equation (32) is also used to describe particle electrophoresis in response to externally imposed electrical-potential gradients. Migration of salt cations and anions can also be described by Nernst–Plank equations:

$$-J_{+}=C_{+}{D}_{+}^0\left(\nabla \ln C_{+}+\frac{\mathcal{F} \nabla \Psi }{\mathcal{R}T}\right)$$

(33a)

$$-J_{-}=C_{-}{D}_{-}^0\left(\nabla \ln C_{-}-\frac{\mathcal{F} \nabla \Psi }{\mathcal{R}T}\right)$$

(33b)

where $D_{+}^0$ and $D_{-}^0$ are the tracer-diffusion coefficients of cation and anion, J₊ and J₋ are the corresponding molar fluxes, and C₊ and C₋ are the corresponding concentrations. Note that the sign change from Equation (33a) to Equation (33b) describes the corresponding change in ion charge.

In a purely diffusive process, there is no external electric field, and the gradient of electrical-potential gradients is internally produced by the gradient of ions (remembering that C_P/C_S→0). In this case, the electrical potential is known as diffusion potential and, as it will be shown below, is directly proportional to the difference in mobility between the two ions; note that this potential is also responsible for the liquid junction potential in electrochemical cells. In the absence of external electric fields, the electroneutrality condition holds. This implies that cation and anion must have the same concentration (C₊ = C₋). Moreover, to ensure that electroneutrality is maintained during diffusion, cation and anion must also diffuse at the same diffusion rate even if the two ions have different mobility (J₊ = J₋). The observed salt diffusion coefficient can be determined by first applying C_S = C₊ = C₋ and J_S = J₊ = J₋ to Equation (33a,b). We then multiply Equation (33a) by $D_{-}^0$ and Equation (33b) by $D_{+}^0$. Finally, we add the two resulting equations to eliminate the electric term and obtain the Nernst–Hartley equation of the salt diffusion coefficient, $D_{\mathrm{S}}^0$, (D_S in the limit of C_S→0):

$$D_{\mathrm{S}}^0=\frac{2D_{+}^0{D}_{-}^0}{D_{+}^0+D_{-}^0}$$

(34)

According to Equation (34), the salt diffusion coefficient is such that ($D_{\mathrm{S}}^0$)⁻¹ is the average between ($D_{+}^0$)⁻¹ and ($D_{-}^0$)⁻¹. The expression of ▽Ψ is similarly obtained by taking the difference between Equation (33a) and Equation (33b). This yields the following:

$$\frac{\mathcal{F} \nabla \Psi }{\mathcal{R}T}=\frac{D_{-}^0-D_{+}^0}{D_{-}^0+D_{+}^0} \nabla \ln C_{\mathrm{S}}=\Delta \tau \nabla \ln C_{\mathrm{S}}$$

(35)

where Δτ = τ₋ − τ₊, τ₊ = $D_{+}^0$/($D_{+}^0$ + $D_{-}^0$) and τ₋ = $D_{-}^0$/($D_{+}^0$ + $D_{-}^0$) are cation and anion transference numbers, respectively, with τ₋ = 1 − τ₊ [105]. Tracer-diffusion coefficients are available [118] for several ions in water at 25 °C and can be used to evaluate Δτ. For example, Δτ = 0.21 for NaCl and Δτ = 0.02 for KCl. Each charged species, including the colloidal particle, will experience this internal electric field. If we insert Equation (35) into Equation (32) and compare it with Equation (31), we obtain the following:

$${\widehat{D}}_{\mathrm{PS}}=\frac{\left|Z_{\mathrm{P}}\right|}{2}\Delta \tau$$

(36)

where we have replaced Z_P with |Z_P| so that we can readily compare Equation (36) with the Donnan term, |Z_P|/2 (see Equations (29) and (30) with C_S = 0). For negatively charged particles, τ₊ and τ₋ must be inverted. Alternatively, we can directly apply Equation (36) to negative particles provided that we remember that Δτ = τ_C − τ_S is defined as the difference between the transference number of counterion (τ_C) and coion (τ_S). Since particle diffusiophoresis is induced by an internal electric field, Equation (36) characterizes the mechanism of electrophoretic diffusiophoresis in the limit of C_S→0. Nearly all studies on diffusiophoresis are based on mathematical expressions of diffusiophoresis coefficients that are generalizations of Equation (36) [12,13,16,19,20,72].

The corresponding expression of the hydrodynamic coefficient, λ, can be obtained from Equation (18). If we subtract Equation (36) to g = |Z_P|/2, we obtain the following:

$$\lambda =\left|Z_{\mathrm{P}}\right| {\tau }_{\mathrm{S}}$$

(37)

where |Z_P| represents the number of counterions and τ_S is the transference number of the coion (τ₊ if Z_P > 0 and τ₋ if Z_P < 0).

We can readily obtain also the expression of the salt osmotic diffusion coefficient. If we insert C_SP = |Z_P|/2 and Equation (37) for λ in Equation (20), we obtain the following:

$${\widehat{D}}_{\mathrm{SP}}=\frac{\left|Z_{\mathrm{P}}\right|}{2}(1-2\alpha {\tau }_{\mathrm{S}})$$

(38)

where $D_{\mathrm{S}}^0$ in α = $D_{\mathrm{P}}$/$D_{\mathrm{S}}^0$ is evaluated using Equation (34). Note that ${\widehat{D}}_{\mathrm{SP}}$ ≈ |Z_P|/2 is a suitable approximation. Since salt osmotic diffusion is approximately described by the Donnan term, |Z_P|/2, Equation (38) characterizes the mechanism of Donnan diffusion. The applicability and limitations of Equations (36)–(38) will be discussed in Section 11.

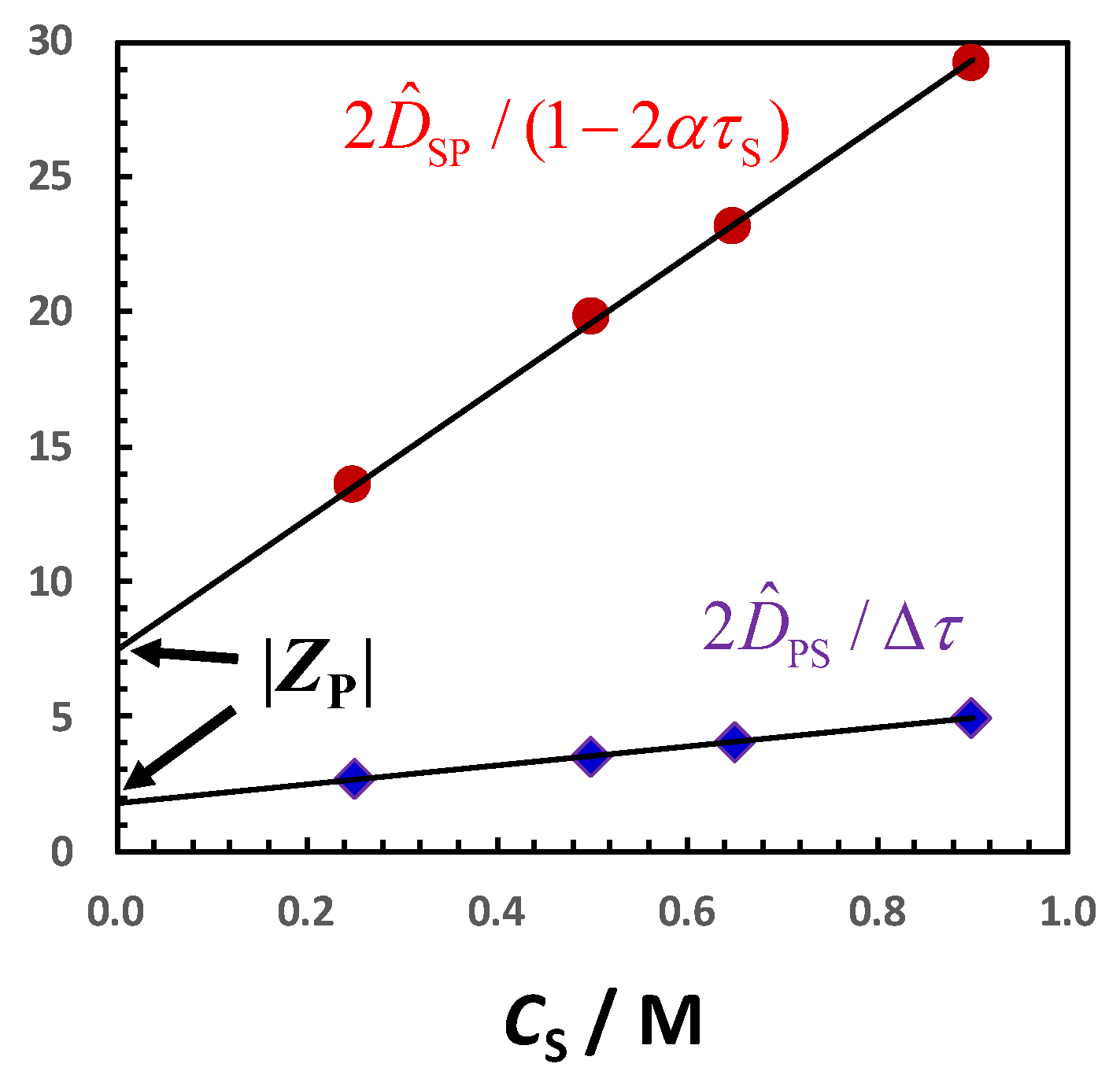
7. Extraction of ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{SP}}$(C_S) from Ternary Diffusion Coefficients

As previously mentioned, multicomponent-diffusion coefficients in the volume-fixed reference, $D_{i,j}^{\mathrm{V}}$, can be determined using Taylor’s dispersion or interferometric methods. The experimental results that are discussed in the following sections were obtained using the Gosting diffusiometer operating in the Rayleigh interferometry method at 25 °C [37,62,119,120,121,122]. This instrument, which is located at Texas Christian University in Fort Worth, Texas (USA), yields diffusion coefficients at the highest precision [37,123,124]. This instrument was initially built by Louis J. Gosting at the University of Winsconsin-Madison and then optimized by Donald G. Miller at Lawrence Livermore National Laboratory and John G. Albright at Texas Christian University [125]. Although experiments on the Gosting diffusiometer typically require specialized user training and may be time consuming, the precision of the Rayleigh interferometry method was found to be particularly important for successfully characterizing the dependence of diffusiophoresis and osmotic diffusion coefficients (${\widehat{D}}_{\mathrm{PS}}$ and ${\widehat{D}}_{\mathrm{SP}}$) on cosolute concentration, C_S [23,25,72,74,92,94,95,126].

As illustrated in Figure 8, the Gosting diffusiometer consists of a ≈9 m optical bench (5000 kg) with vibration isolation and several components [120]. The light source for generating the Rayleigh interference pattern is a He-Ne laser (543.5 nm, 5 mW). The lens components are the main lens (two-element air-spaced achromat, focal length 145 cm) and the cylinder lens (two plano-convex lenses, focal length 68 cm). A cell holder is located between these two lens components inside a water bath. The temperature of the bath was regulated at 25.00 °C with a model PTC-41 Tronac temperature controller to a precision of (0.001 °C). The cell holder has the function of supporting a Tiselius cell (where macroscopic-gradient diffusion occurs) and a mask, which consists of a double window. Here, the laser beam is split into two parts: one going through the diffusion channel of the Tiselius cell and one passing through the water bath (reference channel). The cylinder lens focuses the diffusion channel at the detector, where the Rayleigh interference pattern is observed [62]. Data from the Rayleigh interference patterns are collected with a linear CCD array (6000 pixels, 10 µm × 10 µm pixels) mounted vertically on a precision stage [37,119]. The stage with this vertical array is stepped horizontally through the 2D interference pattern to collect the data necessary to calculate the diffusion coefficients. The magnification factor is measured using a precision ruled quartz scale (100 lines/cm, accuracy 0.25 µm; Photo Sciences Inc., Torrance, CA, USA).

A typical diffusion experiment begins by preparing a sharp boundary between two solutions of different solute concentrations in the vertical diffusion channel (cell) located inside the thermostated water bath. The measured ternary diffusion coefficients correspond to the average concentrations of the two interfaced solutions. Rayleigh interferometric fringes shift horizontally as the refractive index inside the diffusion channel changes along the channel’s vertical position. This shift is directly proportional to the medium refractive index. The total number of fringes is directly proportional to the difference in refractive index between the two initial solutions and the channel width and inversely proportional to the laser wavelength. The differences in concentrations between the two interfaced solutions are typically chosen to obtain ≈50 fringes. Refractive-index profiles are typically determined at 50 different values of time during the course of each experiment. These are then rearranged as anti-symmetric and normalized sigmoidal functions, which are theoretically described as linear combinations of two error functions. A minimum of two experiments is required to determine the four diffusion coefficients at a given set of average concentrations. These two experiments must have different combinations of solute concentration differences across the diffusion boundary. To verify reproducibility, two other duplicate experiments are performed. The four ternary diffusion coefficients in the volume-fixed reference frame are then extracted by applying a method of the non-linear least squares to all normalized refractive-index profiles [127,128].

The reduced particle diffusiophoresis, ${\widehat{D}}_{\mathrm{PS}}$(C_S), is obtained from the cross-term, $D_{\mathrm{PS}}^V$, by using the following [25]:

$${\widehat{D}}_{\mathrm{PS}}=\left(\frac{1}{D_{\mathrm{P}}}\underset{C_{\mathrm{P}}\to 0}{\lim }\frac{D_{\mathrm{PS}}^V}{C_{\mathrm{P}}}+\frac{{\overline{V}}_{\mathrm{S}}}{\alpha }\right)\frac{C_{\mathrm{S}}}{{\nu }_{\mathrm{S}}{y}_{\mathrm{S}}}$$

(39)

where C_S/(ν_Sy_S) represents the conversion factor from ∇μ_S/RT to ∇C_S (see Equation (10)) and the term ${\overline{V}}_{\mathrm{S}}$/α represents a small correction (from Equation (9c)), accounting for the change from solvent- to volume-fixed reference frame. Cosolute partial molar volumes, ${\overline{V}}_{\mathrm{S}}$, and thermodynamic factors, y_S, are typically available from the literature.

The reduced cosolute osmotic diffusion coefficient, ${\widehat{D}}_{\mathrm{SP}}$(C_S), is obtained from the cross-term, $D_{\mathrm{SP}}^V$, by using the following [25]:

$${\widehat{D}}_{\mathrm{SP}}\equiv \underset{C_{\mathrm{P}}\to 0}{\lim }\hspace{0.17em}\hspace{0.17em}\frac{D_{\mathrm{SP}}^V}{D_{\mathrm{SS}}^V}+\alpha \frac{C_{\mathrm{S}}{\overline{V}}_{\mathrm{P}}}{1-C_{\mathrm{S}}{\overline{V}}_{\mathrm{S}}}$$

(40)

where the term αC_S${\overline{V}}_{\mathrm{P}}$/(1 − C_S${\overline{V}}_{\mathrm{S}}$) also represents a small correction (from Equation (9c)), accounting for the change from solvent- to volume-fixed reference frame.

According to Equations (39) and (40), ${\widehat{D}}_{\mathrm{PS}}$ and ${\widehat{D}}_{\mathrm{SP}}$ should be extracted by measuring $D_{\mathrm{PS}}^V$/C_P, $D_{\mathrm{SP}}^V$/$D_{\mathrm{SS}}^V$ as a function of C_P at a given C_S and then extrapolating these two quantities to C_P→0. However, we find that this extrapolation is not needed as long as the particle concentrations are less than ≈1% (w/w) [23,72]. In other words, $D_{\mathrm{PS}}^V$/C_P, $D_{\mathrm{SP}}^V$/$D_{\mathrm{SS}}^V$ are found to be independent of C_P within the experimental error at low particle concentration. Furthermore, measurements of cross-term diffusion coefficients at very low particle concentrations yield relatively large errors. Specifically, the relative error of $D_{\mathrm{PS}}^V$/C_P increases as C_P decreases because $D_{\mathrm{PS}}^V$ is directly proportional to C_P. Moreover, the error on the other cross-term, $D_{\mathrm{SP}}^V$, also increases as C_P decreases. This occurs because the difference in particle concentration between the two solutions in a diffusion experiment is also limited by C_P.

We now discuss why thermodynamic non-ideality associated with particle–particle interactions is not expected to significantly affect $D_{\mathrm{PS}}^V$/C_P and $D_{\mathrm{SP}}^V$/$D_{\mathrm{SS}}^V$. The thermodynamic factor, C_Pμ_PP/RT, characterizes this non-ideality effect, with C_Pμ_PP/RT→1 in the limit of C_P→0. It is important to note that this parameter can show appreciable dependence on C_P even at low particle concentrations (≈1%), especially in the proximity of a spinodal boundary [23]. Inspection of Equation (5a–d) shows that only D_PP and D_SP depend on μ_PP. This implies that $D_{\mathrm{PS}}^V$/C_P is independent of C_Pμ_PP/RT. On the other hand, the cross-term, D_SP, does depend on μ_PP. However, its contribution to ${\widehat{D}}_{\mathrm{SP}}$ is limited to the al term in Equation (20). Since this is small compared to C_SP, we deduce that the effect of C_Pμ_PP/RT on $D_{\mathrm{SP}}^V$/$D_{\mathrm{SS}}^V$ is also negligible.

The values of D_P as a function of C_S are also needed in Equation (39). According to Equation (9a), this could be extracted, at any given C_S, by measuring $D_{\mathrm{PP}}^V$ as a function of C_P and then extrapolating to C_P→0. However, a more rapid and versatile strategy to determine D_P is by extrapolation of DLS diffusion coefficients as a function of C_P [23].

8. The PEG–Osmolyte–Water and PEG–Salt–Water Systems

In this section, representative ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{SP}}$(C_S) data extracted from ternary diffusion coefficients at 25 °C using Rayleigh interferometry on aqueous PEG (nominal molecular weight, 20 kg/mol) in the presence of osmolytes and salts will be discussed [25,92,94]. PEG is a nonionic hydrophilic polymer found in many aqueous formulations relevant to pharmaceutical and biotechnological applications [129,130,131]. Furthermore, an important class of water-soluble colloidal particles is represented by neutral particles whose interfacial properties are modified or governed by PEG. Indeed, this polymer has been employed to coat the surface of inorganic nanoparticles [132,133], proteins [134], micelles [135] and vesicles [136,137]. Since diffusiophoresis is mostly an interfacial phenomenon, understanding diffusiophoresis of PEG coils is of fundamental importance for understanding diffusiophoresis of PEG-based colloidal particles [23,74].

We start by considering the effect of three osmolytes, trimethyl-N-oxide (TMAO), diethylene glycol (DEG) and urea, on PEG diffusiophoresis. Osmolytes are small organic compounds that are neutral and water soluble. They have been extensively investigated in connection with proteins because they are known to significantly affect the thermodynamic stability of the protein native state through the mechanism of preferential hydration [79,138,139]. The same type of mechanism is observed also in the case of hydrophilic macromolecules such as PEG [25].

Due to its more direct connection with the preferential-interaction coefficient, it is convenient to examine osmolyte osmotic diffusion prior to PEG diffusiophoresis. In Figure 9, the osmolyte (TMAO, DEG and urea) osmotic diffusion coefficient, ${\widehat{D}}_{\mathrm{SP}}$, as a function of osmolyte concentration, C_S, is shown. As we can see, ${\widehat{D}}_{\mathrm{SP}}$ data are positive, thereby implying that osmolyte diffuses from high to low PEG concentration. We can also see that ${\widehat{D}}_{\mathrm{SP}}$ linearly increases with C_S starting from ${\widehat{D}}_{\mathrm{SP}}$(0) = 0, consistent with ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP = (${\overline{V}}_{\mathrm{P}}$ + ν_W${\overline{V}}_{\mathrm{W}}$)·C_S (see Equation (29) with Z_P = 0). For comparison, the reference line, ${\overline{V}}_{\mathrm{P}}$C_S (with ${\overline{V}}_{\mathrm{P}}$ = 16.7 dm³·mol⁻¹) [92], is included in the same figure. Positive deviations from this line correspond to positive values of water thermodynamic excess, ν_W. We can then deduce that PEG is preferentially hydrated in the presence of TMAO and DEG. Indeed, the application of Equations (18), (20) and (23) to ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{SP}}$(C_S) data, which confirms that ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP is a suitable approximation, rigorously yields γ(C_S). We can then write γ = ν_WC_S/C_W and determine the thermodynamic excess of water molecules near PEG. This is higher for TMAO (ν_W = 1870; 4.1 per ethoxy group) than for DEG (ν_W = 970; 2.1 per ethoxy group). On the other hand, urea is preferentially binding to PEG because ${\widehat{D}}_{\mathrm{SP}}$ data are below the reference line. In this case, the water thermodynamic excess is negative (ν_W = −520; −1.1 per ethoxy group). It is interesting to observe that the effect of osmolytes on PEG follows the same type of trend observed in the case of protein. Indeed, the TMAO preferential-hydration effect on proteins is known to stabilize the protein native state. In contrast, urea preferentially binds to peptide chains. This is known to destabilize the protein native state, leading to unfolding [138].

In Figure 10, the PEG diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$, as a function of osmolyte concentration, C_S, is shown. As we can see, ${\widehat{D}}_{\mathrm{PS}}$ data are also positive, thereby implying that PEG diffusiophoresis occurs from high to low osmolyte concentration in all three cases. Moreover, as in the case of osmotic diffusion data, ${\widehat{D}}_{\mathrm{PS}}$ linearly increases with C_S starting from ${\widehat{D}}_{\mathrm{PS}}$(0) = 0. The slope trend of diffusiophoresis data is the same as that of osmotic diffusion data in Figure 9, with PEG diffusiophoresis being the largest in the TMAO case. In the urea case, ${\widehat{D}}_{\mathrm{PS}}$ values are small compared to those observed for the other two osmolytes. Interestingly, although PEG prefers to interact more with urea than water, PEG diffusiophoresis still occurs from high to low urea concentration.

According to Equation (18), ${\widehat{D}}_{\mathrm{PS}}$ is the difference between the preferential-interaction coefficient, γ, and the hydrodynamic coefficient, λ. Since both ${\widehat{D}}_{\mathrm{PS}}$ and γ are directly proportional to C_S, the ratio, ${\widehat{D}}_{\mathrm{PS}}$/γ, is a constant with ${\widehat{D}}_{\mathrm{PS}}$/γ = 1 when λ = 0. In general, the value of this ratio can be used to assess the significance of the hydrodynamic coefficient, λ. Examination of our experimental data using Equations (18), (20) and (23) yields ${\widehat{D}}_{\mathrm{PS}}$/γ = 0.14, 0.19 and −0.10 in the TMAO, DEG and urea case, respectively [25]. This implies that λ significantly contributes to the value of ${\widehat{D}}_{\mathrm{PS}}$, with λ/γ = 0.86, 0.81 and 1.10, respectively. We can also appreciate that l has the same sign as γ (e.g., positive in the presence of preferential hydration) and is directly proportional to C_S, with λ(0) = 0.

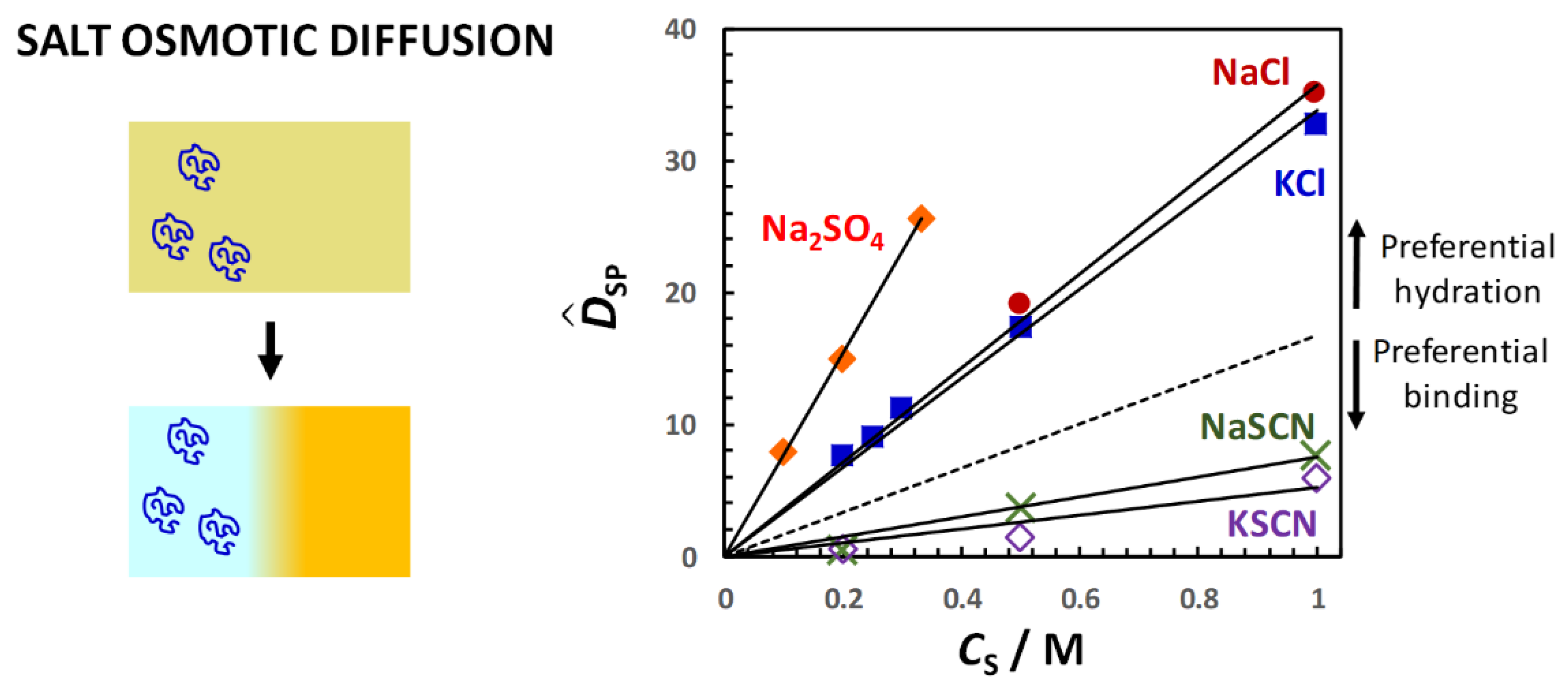
Similar results are obtained for PEG in the presence of salts [92,94]. In Figure 11, the salt osmotic diffusion coefficient, ${\widehat{D}}_{\mathrm{SP}}$, as a function of salt concentration, C_S, is shown. As previously mentioned, the salts are NaCl, KCl, NaSCN, KSCN and Na₂SO₄. All ${\widehat{D}}_{\mathrm{SP}}$ data are positive as in the osmolyte case, with ${\widehat{D}}_{\mathrm{SP}}$(0) = 0, as expected for neutral macromolecules. As in the case of osmolytes, the increase in ${\widehat{D}}_{\mathrm{SP}}$ with C_S is consistent with ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP = (${\overline{V}}_{\mathrm{P}}$ + ν_W${\overline{V}}_{\mathrm{W}}$)C_S. Comparison with the reference line, ${\overline{V}}_{\mathrm{P}}$C_S, shows that PEG is preferentially hydrated in the presence of NaCl, KCl and Na₂SO₄. Combination of ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{SP}}$(C_S) data yield a water thermodynamic excess that is significantly higher for Na₂SO₄ (ν_W = 3500; 7.7 per ethoxy group) than for NaCl (ν_W = 1100; 2.4 per ethoxy group) and KCl (ν_W = 990; 2.2 per ethoxy group) [92]. On the other hand, ${\widehat{D}}_{\mathrm{SP}}$(C_S) data exhibit negative deviations from the reference line in the case of thiocyanate salts, thereby implying preferential binding with negative n_W values for NaSCN (ν_W = −550; −1.2 per ethoxy group) and KSCN (ν_W = −690; −1.5 per ethoxy group) [94]. This is attributed to the preferential binding of thiocyanate anions on the PEG polymer chain. Clearly, changing anion nature has an effect on salt osmotic diffusion that is large compared to the effect observed by changing cation from sodium to potassium.

The observed effect of salts on PEG also follows the same type of trend observed in the case of proteins, with sulfate salts known to stabilize the protein native state while thiocyanate salts favor protein unfolding [78]. Moreover, inorganic ions have been ranked according to their effectiveness in precipitating proteins and synthetic polymers (salting-out strength), leading to the well-known Hofmeister series [140]. In this series, the sulfate anion displays a great salting-out strength, whereas chloride is approximately at the midpoint of the Hofmeister series, separating salting-out from salting-in anions such as thiocyanate, which increase the solubility of macromolecules in water. Compared to anions, the Hofmeister series for cations is significantly less pronounced, and the cation ranking can depend on the chemical nature of the macromolecule investigated, with sodium and potassium cations exhibiting similar salting-out strength. Thus, salt osmotic diffusion data are consistent with the Hofmeister series.

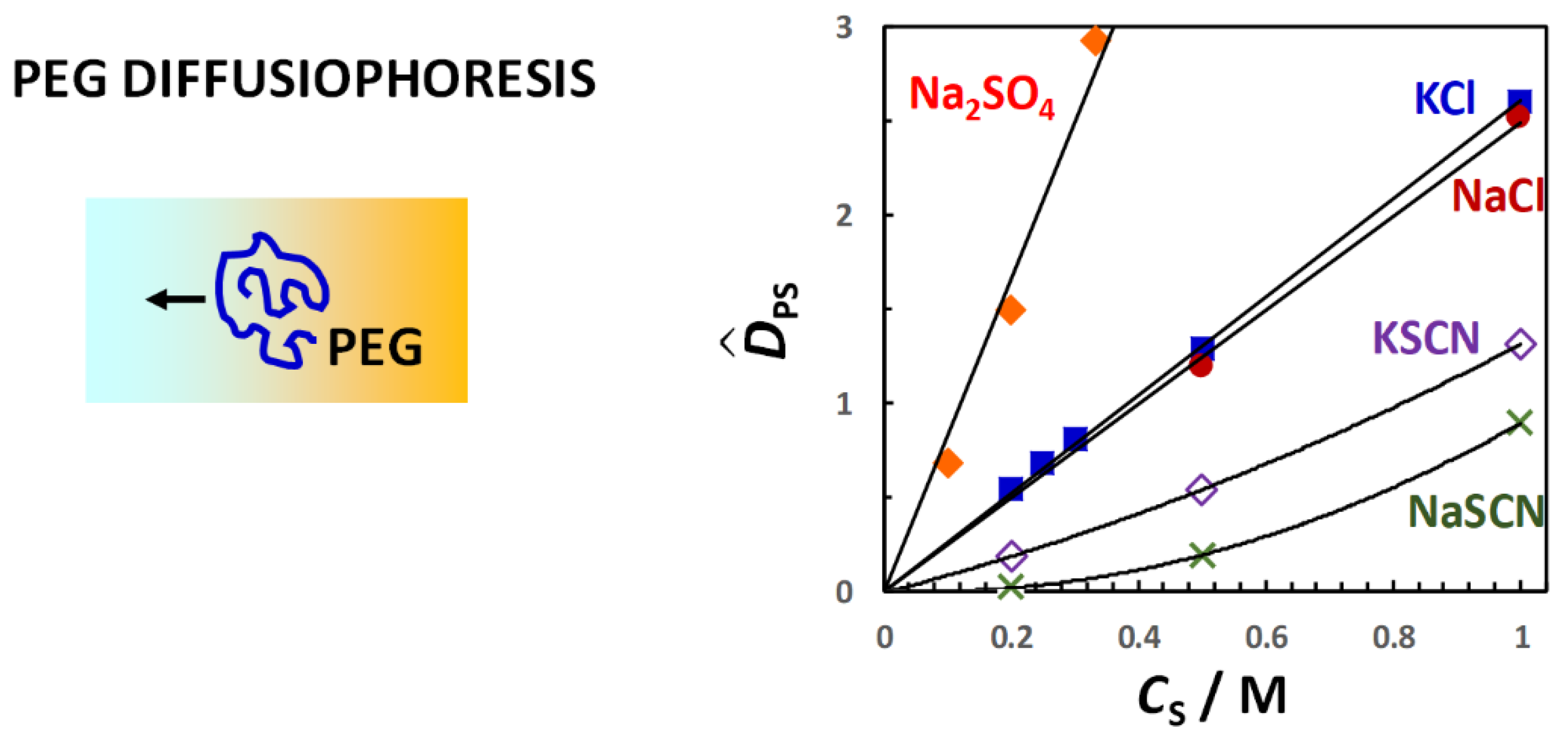
In Figure 12, the PEG diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$, as a function of salt concentration, C_S, is shown, with ${\widehat{D}}_{\mathrm{PS}}$(0) = 0. As we can see, ${\widehat{D}}_{\mathrm{PS}}$ data are positive, thereby implying that PEG diffusiophoresis occurs from high to low salt concentrations. Except for thiocyanate salts, ${\widehat{D}}_{\mathrm{PS}}$ linearly increases with C_S. This is the same behavior previously shown for PEG in the presence of osmolytes. Moreover, the slope trend of diffusiophoresis data is the same as that of osmotic diffusion data in Figure 9, with PEG diffusiophoresis being the largest in the Na₂SO₄ case. In other words, ${\widehat{D}}_{\mathrm{PS}}$ appears to be approximately proportional to γ. As in the osmolyte case, ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{PS}}$(C_S) data can be combined to determine ${\widehat{D}}_{\mathrm{PS}}$/γ. We obtain ${\widehat{D}}_{\mathrm{PS}}$/γ = 0.14, 0.13 and 0.12 in the NaCl, KCl and Na₂SO₄ cases, respectively. This implies that l significantly contributes to the observed value of ${\widehat{D}}_{\mathrm{PS}}$ also in the salt cases, with λ/γ = 0.86, 0.87 and 0.88, respectively [92]. Moreover, even if the value increases more than three-fold when going from NaCl and KCl to Na₂SO₄, the value of ${\widehat{D}}_{\mathrm{PS}}$/γ is approximately the same not only among these salts but also when comparing salts and osmolytes.

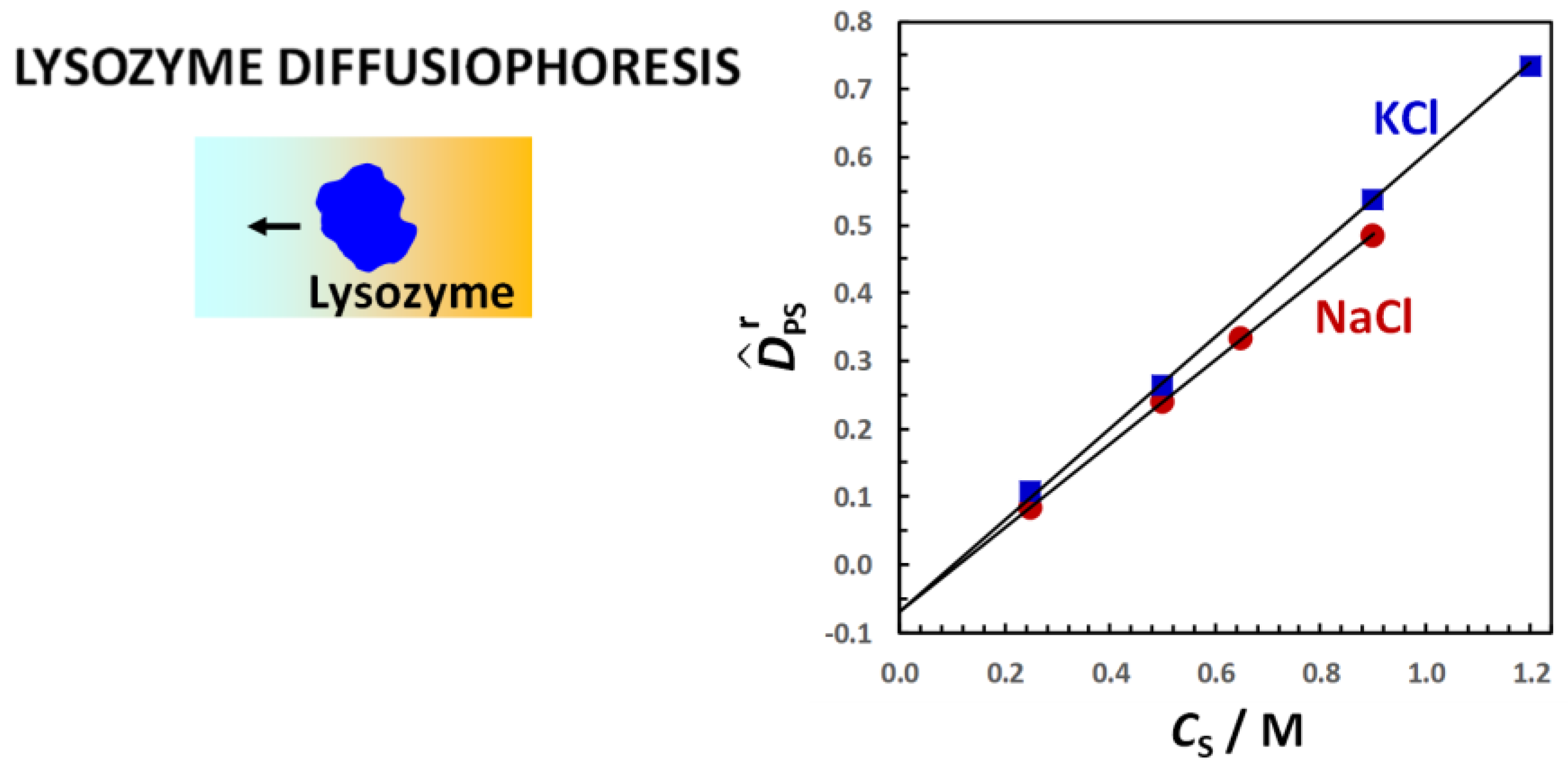
For the two thiocyanate cases, ${\widehat{D}}_{\mathrm{PS}}$ values are relatively small. However, ${\widehat{D}}_{\mathrm{PS}}$(C_S) is appreciably larger for KSCN than for NaSCN, especially at low salt concentrations. The difference between the two salt cases can be explained by considering the actual binding of thiocyanate anions to PEG [94]. This process induces a negative charge on the polymer chain, making PEG feel the diffusion potential generated by the salt gradient. The contribution of electrophoretic diffusiophoresis to total diffusiophoresis has been evaluated using Equation (36) and removed from experimental values of ${\widehat{D}}_{\mathrm{PS}}$(C_S) [94]. However, detailed calculation of electrophoretic diffusiophoresis will not be discussed here. Instead, for simplicity, we shall just focus on the difference, Δτ, between counterion (Na⁺ or K ⁺) and coion (SCN⁻) transference numbers, which is Δτ = −0.14 for NaSCN and Δτ = +0.05 for KSCN [104,118,141]. According to Equation (36), NaSCN causes a negative electrophoretic diffusiophoresis, while KSCN causes a small positive electrophoretic diffusiophoresis. Thus, the difference between the two salt cases in Figure 11 can be explained by considering that electrophoretic diffusiophoresis reduces the value of ${\widehat{D}}_{\mathrm{PS}}$ in the NaSCN case relative to the KSCN case.

In summary, experimental values of ${\widehat{D}}_{\mathrm{PS}}$ and ${\widehat{D}}_{\mathrm{SP}}$ as a function of cosolute concentration, C_S, show that both ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{SP}}$(C_S) are positive quantities for neutral PEG. In other words, PEG diffusiophoresis (cosolute osmotic diffusion) occurs from high to low cosolute (PEG) concentrations. Furthermore, these two coefficients are proportional to C_S, with ${\widehat{D}}_{\mathrm{PS}}$(0) = ${\widehat{D}}_{\mathrm{SP}}$(0) = 0. It was also verified that ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP is approximately a thermodynamic quantity directly related to the preferential-interaction coefficient, γ = ν_WC_S/C_W. The thermodynamic excess of water molecules near PEG coils, ν_W, was determined for selected osmolytes and salts and was found to follow the same trend observed for proteins. In the presence of preferential hydration (ν_W > 0), PEG diffusiophoresis, which is approximately proportional to ν_W, occurs in the direction in which PEG chemical potential is lowered as expected. According to data analysis, the ratios, λ/γ and ${\widehat{D}}_{\mathrm{PS}}$/γ = 1 − λ/γ, can be regarded as constants because the hydrodynamic coefficient, λ, is also proportional to C_S, with λ(0) = 0. In these cosolute cases (TMAO, DEG, sulfate and chloride salts), it was found that ${\widehat{D}}_{\mathrm{PS}}$/γ = 0.10–0.20. This implies that ${\widehat{D}}_{\mathrm{PS}}$ ≈ γ is not a suitable approximation. In other words, ${\widehat{D}}_{\mathrm{PS}}$ cannot be approximated as a thermodynamic quantity as in the case of ${\widehat{D}}_{\mathrm{SP}}$. Interestingly, values of λ/γ for different cosolutes tend to cluster together even if ν_W changes significantly. Another interesting result is that diffusiophoresis remains positive in the presence of cosolutes that preferentially bind to PEG, i.e., with negative ν_W (thiocyanates and urea). In other words, PEG diffusiophoresis still occurs from high to low cosolute concentrations even if PEG chemical potential tends to increase in this direction. However, the magnitude of ${\widehat{D}}_{\mathrm{PS}}$ is relatively small compared to the cases in which ν_W is positive. In the following section, a model that can explain these experimental findings will be introduced.

9. Local-Domain Model

The observed behavior of diffusiophoresis can be examined by reconsidering a local-domain model, which was previously introduced to describe preferential-interaction coefficients [25,81]. The case of a spherical colloidal particle will be considered for simplicity. However, it is important to remark that relevant equations do not rely on particle shape and are also valid for polymer coils such as PEG. According to this model, the region surrounding a colloidal particle has a composition that is different from bulk, consistent with Kirkwood–Buff theory (see Figure 5). This region, which is assumed to have a fictitious boundary, is denoted as a local domain. The remaining solution, which is a binary cosolute–solvent reservoir, represents the bulk domain. The composition of the local domain can be linked to the composition of the bulk domain by formally introducing a two-phase partitioning coefficient, K, with N_S/N_W = K C_S/C_W, where N_S and N_W are the cosolute and water number of molecules in the local domain. For salts, N_S should be taken as the average of cation and anion numbers in the local domain. The absence of preferential interaction corresponds to K = 1. Preferential hydration corresponds to K < 1, with full depletion of cosolute achieved in the local domain when K→0. Cosolute preferential binding corresponds to K > 1, with full depletion of solvent achieved when K→∞. Within the framework of this model, the solvent thermodynamic excess is ν_W = N_W(1 − K), with ν_W = N_W corresponding to the full depletion of cosolute. It is impossible to determine N_W and K separately as ν_W is the only experimentally accessible parameter. Furthermore, this model does not explicitly consider the actual binding of cosolute or solvent to the particle and excluded-volume interactions. For example, the concentration of cosolute molecules near the particle surface may be different from bulk because their size is different from that of solvent molecules [113]. If cosolute is larger than solvent, a depletion of cosolute occurs in the local domain without the need to consider other physical or chemical interactions. Nonetheless, as will be shown below, this model provides a useful conceptual picture for understanding how preferential hydration affects diffusiophoresis.

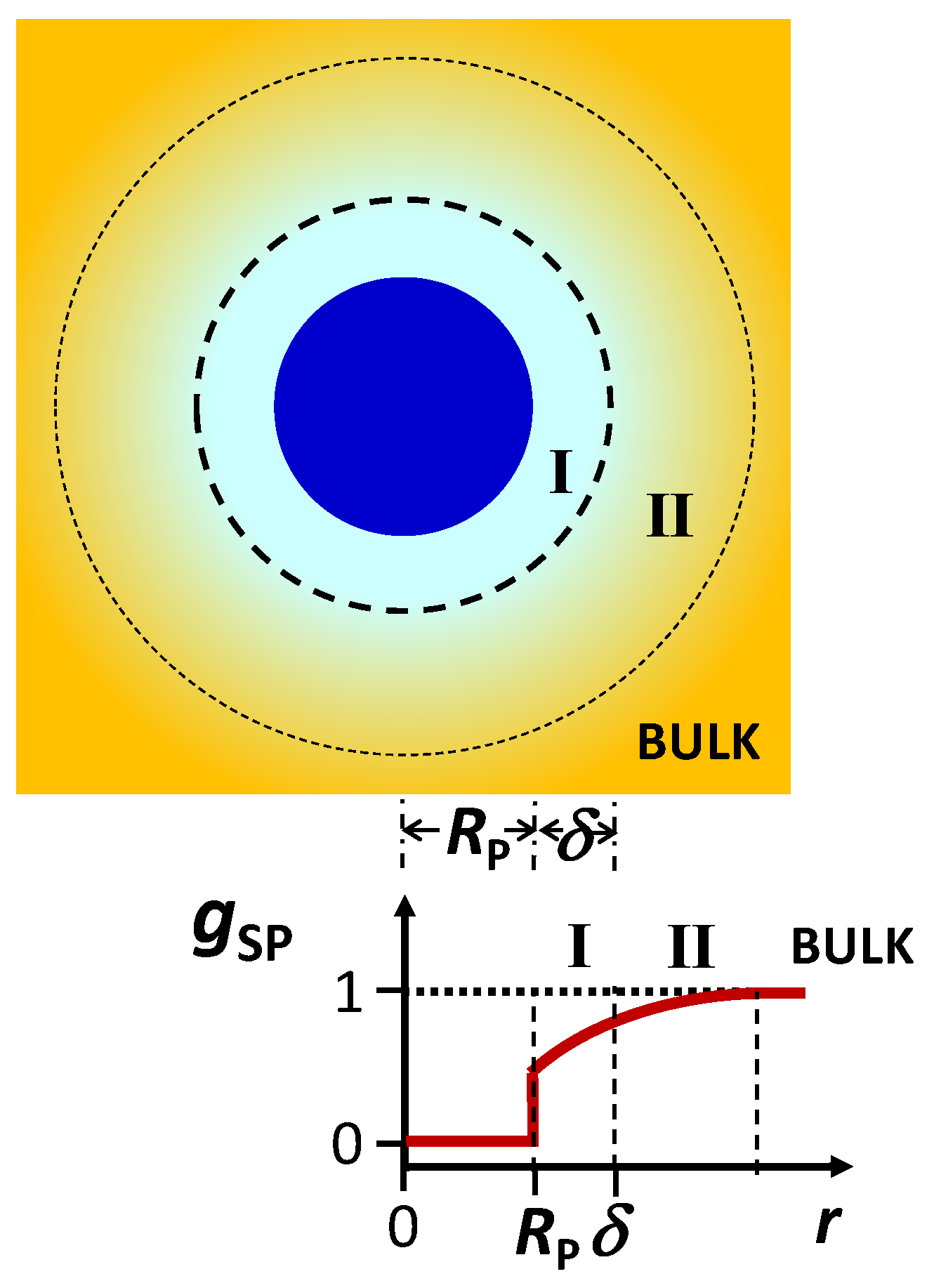
In the case of diffusiophoresis, it becomes important to distinguish between molecules (or ions) that are actually bound to the colloidal particle and those that are not bound but still contribute to the local domain [25]. Bound molecules move together with the particle during transport processes in liquids. To distinguish between these two cases, the local domain is split into an inner local domain (I), in which molecules move together with the particle, and an outer local domain (II), enclosing molecules that are still thermodynamically affected by the particle but moving together with bulk fluid. Note that a well-defined separation into two domains is a model assumption. Indeed, it is expected that there are many fluid molecules moving with intermediate velocities, consistent with hydrodynamic models. Furthermore, the division into an inner domain with bound molecules and an outer domain with non-bound molecules is certainly reasonable but not general. For example, excluded-volume interactions invariably start at the particle surface, but they are formally attributed to the outer domain [142].

The splitting of the local domain is illustrated in Figure 13 for a spherical particle. Cosolute and solvent in the inner and outer local domains are in chemical equilibrium with the binary cosolute–solvent bulk domain. As discussed below, it is only the outer domain that is responsible for diffusiophoresis.

As in the case of the original local-domain model, the composition of the inner (I) and outer (II) local domains are linked to the composition of the bulk domain by formally introducing partitioning coefficients, K^(I) and K^(II), with $N_{\mathrm{S}}^{\left(\mathrm{I}\right)}$/$N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$ = K^(I)C_S/C_W and $N_{\mathrm{S}}^{\left(\mathrm{II}\right)}$/$N_{\mathrm{W}}^{\left(\mathrm{II}\right)}$ = K^(II)C_S/C_W, where $N_{\mathrm{S}}^{\left(\mathrm{I}\right)}$ and $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$, and $N_{\mathrm{S}}^{\left(\mathrm{II}\right)}$ and $N_{\mathrm{W}}^{\left(\mathrm{II}\right)}$ are the cosolute and water number of molecules in domains I and II, respectively. The absence of preferential interaction in domains (I) and (II) corresponds to K^(I) = 1 and K^(II) = 1, respectively. Preferential hydration in the inner and outer domain corresponds to K^(I) < 1 and K^(II) < 1, with full depletion of cosolute achieved in the domains in the limits of K^(I)→0 and K^(II)→0. On the other hand, cosolute preferential binding corresponds to K^(I) > 1 and K^(II) > 1, with full depletion of solvent achieved in the limits of K^(I)→∞ and K^(II)→∞. It is expected that |1 − K^(II)| < |1 − K^(I)| as interactions with the particle are relatively weak in the outer local domain. Although |1 − K^(II)| and |1 − K^(I)| may significantly depend on cosolute nature, it is expected that the ratio, |1 − K^(II)|/|1 − K^(I)|, which describes the relative change in interaction strength between (I) and (II) domains, is a weak function of cosolute nature. Within the framework of this model, the solvent thermodynamic excesses in the inner and outer local domains are ν_W^(I) = $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$(1− K^(I)) and ν_W^(II) = $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$(1 − K^(I)), respectively, with ν_W^(I) = $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$ and ν_W^(II) = $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$ corresponding to the full depletion of cosolute in the two domains. The preferential-interaction coefficient considers cosolute–solvent partitioning in both domains. Consistent with Equation (27), we have the following:

$$\gamma =\hspace{0.17em}\left({\nu }_{\mathrm{W}}^{\left(\mathrm{I}\right)}+{\nu }_{\mathrm{W}}^{\left(\mathrm{II}\right)}\right)\frac{C_{\mathrm{S}}}{C_{\mathrm{W}}}$$

(41)

Although ν_W^(I) and ν_W^(II) may significantly depend on cosolute nature, the ratio, ν_W^(II)/ν_W^(I), which describes the relative change in interaction strength between (I) and (II) domains may be a weak function of cosolute nature.

Now that we have incorporated splitting of the local domain in the expression of the preferential-interaction coefficient, we can turn our attention to particle diffusiophoresis. It is expected that the actual particle [30] undergoing diffusion, {P}, consists of the bare particle, P, and inner local domain, with $N_{\mathrm{S}}^{\left(\mathrm{I}\right)}$ and $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$ cosolute (S) and solvent (W) molecules, respectively. We then assume that the transport of {P} is described by a simple diffusion equation [108]:

$$v_{\mathrm{P}}=-D_{\mathrm{P}}\frac{\nabla {\mu }_{\left\{\mathrm{P}\right\}}}{\mathcal{R}T}$$

(42)

where μ_{P} is the chemical potential of {P}. Note that it is assumed that no explicit dependence of v_P on ▽μ_S is considered in Equation (42). Based on {P} composition, we express ▽μ_{P} in the following way:

$$\nabla {\mu }_{\left\{\mathrm{P}\right\}}= \nabla {\mu }_{\mathrm{P}}+N_{\mathrm{W}}^{\left(\mathrm{I}\right)}\nabla {\mu }_{\mathrm{W}}+N_{\mathrm{S}}^{\left(\mathrm{I}\right)}\nabla {\mu }_{\mathrm{S}}$$

(43)

In other words, ▽μ_{P} will depend on ▽μ_W and ▽μ_S because solvent and cosolute molecules are present in the inner local domain. Since ▽μ_W and ▽μ_S are linked by the Gibbs–Duhem equation, C_S▽μ_S + C_W▽μ_W = 0, we can rewrite Equation (42) in the following way:

$$v_{\mathrm{P}}=-D_{\mathrm{P}}\left(\frac{\nabla {\mu }_{\mathrm{P}}}{\mathcal{R}T}-{\nu }_{\mathrm{W}}^{\left(\mathrm{I}\right)}\frac{C_{\mathrm{S}}}{C_{\mathrm{W}}}\frac{\nabla {\mu }_{\mathrm{S}}}{\mathcal{R}T}\right)$$

(44)

where we have also used ν_W^(I) = $N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$(1 − K^(I)) with K^(I) = ($N_{\mathrm{S}}^{\left(\mathrm{I}\right)}$/$N_{\mathrm{W}}^{\left(\mathrm{I}\right)}$)/(C_S/C_W). Finally, a comparison with Equation (14) shows that the hydrodynamic coefficient is as follows:

$$\lambda ={\nu }_{\mathrm{W}}^{\left(\mathrm{I}\right)}\frac{C_{\mathrm{S}}}{C_{\mathrm{W}}}$$

(45)

This model correctly predicts that λ is proportional to C_S. Furthermore, it is positive when there is an excess of solvent molecules binding to the particle, consistent with preferential hydration. On the other hand, λ is negative when cosolute binds to the particle. Within the framework of this model, λ/γ and ${\widehat{D}}_{\mathrm{PS}}$/γ are essentially constants representing the inner and outer domains, respectively. Specifically, they are two complementary fractions of water thermodynamic excess:

$$\frac{\lambda }{\gamma }=\frac{{\nu }_{\mathrm{W}}^{\left(\mathrm{I}\right)}}{{\nu }_{\mathrm{W}}^{\left(\mathrm{I}\right)}+{\nu }_{\mathrm{W}}^{\left(\mathrm{II}\right)}}$$

(46a)

$$\frac{{\widehat{D}}_{\mathrm{PS}}}{\gamma }=\frac{{\nu }_{\mathrm{W}}^{\left(\mathrm{II}\right)}}{{\nu }_{\mathrm{W}}^{\left(\mathrm{I}\right)}+{\nu }_{\mathrm{W}}^{\left(\mathrm{II}\right)}}$$

(46b)

Experimental results on PEG in the preferential-hydration cases can be explained using this model. For example, ν_W = 1100 and ${\widehat{D}}_{\mathrm{PS}}$/γ = 0.14 in the NaCl case corresponds to ν_W^(I) = 945 and ν_W^(II) = 155. The obtained values of ${\widehat{D}}_{\mathrm{PS}}$/γ = 0.10–0.20 represent the fraction of solvent thermodynamic excess in the outer domain. If ν_W^(II)/ν_W^(I) is a weak function of cosolute type, then ${\widehat{D}}_{\mathrm{PS}}$/γ for different cosolutes tend to be close to each other even if ν_W^(II) + ν_W^(I) vary significantly from cosolute to cosolute. This is consistent with experimental findings.

In the presence of cosolute preferential binding, experimental results show that γ < 0 and ${\widehat{D}}_{\mathrm{PS}}$/γ < 0. As discussed for PEG, in the presence of thiocyanate salts, actual cosolute binding occurs. This leads to negative values of ν_W^(I). If we then assume that ν_W^(II) of the outer domain is also negative, then we obtain ${\widehat{D}}_{\mathrm{PS}}$ < 0 and ${\widehat{D}}_{\mathrm{PS}}$/γ > 0, in disagreement with experimental results. Indeed, experimental findings can be explained only by assuming that ν_W^(II) is positive even for urea and thiocyanate salts. For example, ν_W = −520 and ${\widehat{D}}_{\mathrm{PS}}$/γ = −0.10 in the urea case leads to ν_W^(I) = −570 and ν_W^(II) = +50. This interesting result may be explained by considering that overall PEG–urea interactions are the result of an actual PEG–urea binding process (inner domain, ν_W^(I) < 0) and residual excluded-volume interactions, which are associated with the outer domain and are responsible for ν_W^(II) > 0 [142].

10. The lysozyme–Salt–Water System

Salt-induced protein diffusiophoresis, ${\widehat{D}}_{\mathrm{PS}}$, and salt osmotic diffusion, ${\widehat{D}}_{\mathrm{SP}}$, have been reported for lysozyme at pH 4.5 and 25 °C as a function of NaCl and KCl concentration, C_S [66,71,95]. Lysozyme is a globular protein with a molecular weight of 14.3 kDa that is chemically stable and commercially available at high purity. Due to these properties, this protein has been extensively studied. It is widely recognized as a model protein in the fields of biophysics and structural biology [130,143,144,145]. Since the lysozyme isoelectric point is 11, this protein is normally found to be positively charged. Indeed, lysozyme structural charge is known to be +10 at pH 4.5 [71,145], with chloride anions acting as counterions when NaCl or KCl are employed as supporting electrolytes.

The experimental behavior of salt osmotic diffusion, ${\widehat{D}}_{\mathrm{SP}}$(C_S), is shown in Figure 14. Here, we can see that ${\widehat{D}}_{\mathrm{SP}}$ linearly increases with C_S. As in the case of PEG (see Figure 11), changing NaCl with KCl has essentially no appreciable effect on ${\widehat{D}}_{\mathrm{SP}}$. However, ${\widehat{D}}_{\mathrm{SP}}$ extrapolated at C_S = 0 is not zero but remains positive. This residual intercept is attributed to protein charge. Specifically, we have ${\widehat{D}}_{\mathrm{SP}}$ ≈ |Z_P|/2 + (${\overline{V}}_{\mathrm{P}}$ + ν_W${\overline{V}}_{\mathrm{W}}$)C_S from ${\widehat{D}}_{\mathrm{SP}}$ ≈ C_SP and Equation (29).

In Figure 14, all ${\widehat{D}}_{\mathrm{SP}}$(C_S) data are above the baseline |Z_P|/2 + ${\overline{V}}_{\mathrm{P}}$C_S, thereby implying that lysozyme preferential hydration occurs in the presence of both salts. Application of Equations (18), (20) and (23) to ${\widehat{D}}_{\mathrm{PS}}$(C_S) and ${\widehat{D}}_{\mathrm{SP}}$(C_S) data, which confirms that ${\widehat{D}}_{\mathrm{SP}}$≈C_SP is a suitable approximation, rigorously yields γ(C_S). For both salt cases, the values of Z_P = 7.5 and ν_W = 150 are extracted. This charge value is somewhat lower than the protein structural charge of Z_P = 10 [145]. The observed difference is consistent with the presence of a Stern layer surrounding the charged protein with about three counterions bound to this globular macroion. Thus, the value of Z_P = 7.5 should be taken as an effective, renormalized charge, incorporating the contribution of the Stern layer [71].

The experimental behavior of lysozyme diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$(C_S), is shown in Figure 15 for both salt cases [95]. Contrary to salt osmotic diffusion, there is a marked difference between the two ${\widehat{D}}_{\mathrm{PS}}$(C_S) curves. In the KCl case, ${\widehat{D}}_{\mathrm{PS}}$ linearly increases with C_S, with a small negative intercept, which will be further discussed later. This behavior is approximately the same as that shown for PEG with the same salt (see Figure 11). In contrast, ${\widehat{D}}_{\mathrm{PS}}$ in the NaCl case is relatively large, with an evident positive intercept.

The difference between the two salt cases can be explained by considering Nernst–Planck equations. According to Equation (36), ${\widehat{D}}_{\mathrm{PS}}$ is directly proportional to the difference between counterion (Cl⁻) and coion (Na⁺ or K⁺) transference numbers, Δτ. Since Δτ = 0.21 for NaCl and Δτ = 0.02 for KCl [104,105,118], the diffusion potential (internal electric field) produced by salt gradient is significant only in the NaCl case. Thus, the difference between the two ${\widehat{D}}_{\mathrm{PS}}$(C_S) curves in Figure 15 is essentially attributed to the positive contribution of electrophoretic diffusiophoresis in the NaCl case.

11. Electrophoretic and Residual Diffusiophoresis

For lysozymes with NaCl, it is possible to determine Z_P by extrapolating 2${\widehat{D}}_{\mathrm{PS}}$/Δτ to C_S = 0 according to Equation (36). In Figure 16, 2${\widehat{D}}_{\mathrm{PS}}$/Δτ is plotted as a function of C_S. In the same figure, the plot of 2${\widehat{D}}_{\mathrm{SP}}$/(1 − 2ατ_S)≈2C_SP, which also becomes Z_P at C_S = 0 according to Equation (38), is included for comparison. This latter plot yields Z_P = 7.5 at C_S = 0, as already discussed in Section 10. Interestingly, extrapolation of 2${\widehat{D}}_{\mathrm{PS}}$/Δτ yields a value of Z_P = 1.8, in substantial disagreement with osmotic diffusion data [71]. It will be now shown that this apparently low charge is mostly related to the electrical-double-layer effect, which is predicted to give rise to a significant electrophoretic effect even at salt concentrations of the order of 1–10 mM. In other words, the value of ${\widehat{D}}_{\mathrm{PS}}$ significantly deviates from Equation (36) even at salt concentrations as low as C_S = 1 mM.

The effect of diffusion potential on diffusiophoresis of charged particles at low salt concentration can be described by applying the type of models employed in electrophoresis [17,146]. According to the electrical-double-layer (EDL) theory [147,148], the electrophoretic mobility of a particle is expected to drop dramatically as solution ionic strength increases. This effect is related to the diffuse layer surrounding charged particles in electrolyte solutions. Since an electric field tends to move the ion cloud in the opposite direction, a viscous drag applies to the macroion, thereby slowing down its motion. This electrophoretic effect can be incorporated into Equation (36) by writing the following:

$${\widehat{D}}_{\mathrm{PS}}=\sigma \frac{\left|Z_{\mathrm{P}}\right|}{2}\Delta \tau$$

(47)

where s is an electrokinetic coefficient, with σ→1 in the limit of C_S = 0, consistent with Equation (36) [71]. Note that Z_P in Equation (47) represents the charge of the particle at its slip boundary. It can be approximately assumed to be the same as Z_P = 7.5 extracted from salt osmotic diffusion data because it takes into account the contribution of small ions located within the hydrodynamic volume of the diffusion particle. As C_S increases, s sharply decreases, making s |Z_P| become a small fraction of |Z_P| at salt concentrations of the order of 0.1 M [71].

It is important to observe that the introduction of σ in the Nernst–Planck equation for ${\widehat{D}}_{\mathrm{PS}}$ does not require a modification of the Donnan expression of C_SP= |Z_P|/2 as long as the electrical potential on the macroion surface at the slip boundary, which is known as zeta potential, ζ, is weak [71]. This approximation is suitable for proteins because they have relatively low charge density on their surface. The presence of the electrophoretic effect may still be formally described using Nernst–Planck equations. However, the neutral protein component of the ternary mixture needs to be redefined. In its original description, the protein component consists of a macroion with charge, Z_P, and |Z_P| counterions. These counterions also act as common ions because they are shared with the salt component. To incorporate σ, the macroion needs to be redefined so that it has an effective charge, σZ_P, consistent with Equation (47). The newly defined macroion must formally contain the macroion itself (with charge Z_P) and a contiguous fraction of the diffuse layer, such that the net macroion charge reduces from Z_P to σZ_P. In other words, the charge of the inner fraction of the diffuse layer must be −(1 − σ)Z_P [71]. As further described in Figure 17, the inner fraction of the diffuse layer contains an excess of counterions, (1 − σ)|Z_P|/2, and a corresponding depletion of coions, −(1 − σ)|Z_P|/2. Thus, the redefined macroion is formally composed by the original macroion to which (1 − σ)|Z_P|/2 counterions are added and (1 − σ)|Z_P|/2 coions are removed. The common ions stoichiometrically balancing this macroion must consist of (1 + σ)|Z_P|/2 counterions and (1 − σ)|Z_P|/2 coions. In other words, the common ion is redefined as a combination of counterions and coions. This combination ensures that the total number of common ions is still |Z_P| and C_SP = |Z_P|/2 remains valid.

The incorporation of σ in Equation (37) also has an impact on the expression of λ given by Equation (37). After inserting the expression of ${\widehat{D}}_{\mathrm{PS}}$ given by Equation (47) in Equation (18) and setting γ = C_SP = |Z_P|/2, we obtain the following [71]:

$$\lambda =|Z_{\mathrm{P}}|\hspace{0.17em}\frac{(1+\sigma ){\tau }_{\mathrm{S}}+(1-\sigma ){\tau }_{\mathrm{C}}}{2}$$

(48)

where (1 + σ)|Z_P|τ_S/2 and (1 − σ)|Z_P|τ_C/2 terms in Equation (48) replace |Z_P|τ_S in Equation (37) as a direct consequence of the redefinition of the protein component.

The electrophoretic effect is described by the function σ(C_S) starting from σ = 1 at C_S = 0. As C_S increases, σ sharply decreases, making σZ_P become just a small fraction of Z_P. To appreciate the significance of this electrokinetic factor for proteins and globular colloidal particles in general, the following expression may be considered [71]:

$$\sigma =\frac{f(\kappa R_{\mathrm{P}})}{1+\kappa R_{\mathrm{P}}}$$

(49)

where R_P is the particle hydrodynamic radius (radius at the slip boundary), κ ≡ (8000pN_Aλ_BI)^1/2 is the Debye constant, with I being the salt ionic strength, N_A the Avogadro’s number and λ_B the Bjerrum length (0.7151 nm for water at 25 °C), and f(κR_P) is a corrective function. In Equation (49), 1/(1 + κR_P) is the dominant factor describing the electrophoretic effect. This factor also describes the effect of ionic strength on zeta potential, ζ, according to $\mathcal{F}$ζ/$\mathcal{R}$T = Z_P(λ_B/R_P)/(1 + κR_P).

One of the most employed expression of f(κR_P) is Henry’s function [17]:

$$f(x)=\frac{3}{2}-e^x\left[\frac{15}{2}{E}_7(x)-3E_5(x)\right]$$

(50)

where E_n(x) ≡ ${\displaystyle {\int }_1^{\infty }}$t⁻ⁿe^−xtdt. This takes into accounts the curvature of spherical particles with f(0) = 1 (Debye–Huckel limit) and f(∞) = 3/2 for a planar surface (Smoluckowski limit). For lysozyme, the electrophoretic factor can be evaluated as a function of salt concentration at 25 °C using Equations (49) and (50) and lysozyme hydrodynamic radius, R_P = 1.863 nm. Related data are reported in

Table 1. Electrokinetic factor, σ, as a function of salt concentration, C_S.

CS/M	κRP	f(κRP)	σ	CS/M	κRP	f(κRP)	σ
0.001	0.194	1.002	0.8392	0.30	3.357	1.113	0.2554
0.002	0.274	1.006	0.7895	0.40	3.876	1.129	0.2315
0.005	0.433	1.010	0.7045	0.50	4.334	1.142	0.2141
0.010	0.613	1.013	0.6280	0.60	4.747	1.153	0.2006
0.020	0.867	1.022	0.5476	0.70	5.128	1.163	0.1898
0.050	1.370	1.039	0.4385	0.80	5.482	1.171	0.1807
0.10	1.938	1.063	0.3617	0.90	5.814	1.179	0.1730
0.20	2.741	1.092	0.2919	1.00	6.129	1.186	0.1664

.

Note that EDL theory is expected to be accurate at relatively low salt concentrations (≈0.1 M or less) due to ion–ion steric effects and related ion–ion correlation. Nonetheless, Table 1 allows us to appreciate that the most significant change in s occurs within the reliable low salt concentration range. The 2${\widehat{D}}_{\mathrm{PS}}$/Δτ data in Figure 16 refer to salt concentrations above 0.1 M. According to Table 1, we have σ ≈ 0.2 in this concentration range. Thus, the extrapolation of these data at C_S = 0 is predicted to yield a charge that is about 20% of the value extracted from 2${\widehat{D}}_{\mathrm{SP}}$/(1 − 2ατ_S) data. This is consistent with the discrepancy observed in Figure 16. Thus, the introduction of the electrophoretic factor in Equation (47) represents a critical correction to Nernst–Planck equations so that these equations can accurately describe the limiting behavior of experimental data obtained at salt concentrations of ≈0.1 M and higher.

We are now in a position to quantitatively examine the experimental behavior of ${\widehat{D}}_{\mathrm{PS}}$(C_S) in Figure 15. It is convenient to write the following:

$${\widehat{D}}_{\mathrm{PS}}={\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{e}}+{\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$$

(51)

where ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{e}}$ is the electrophoretic contribution to diffusiophoresis, which is evaluated using Z_P = 7.5 in Equation (47). The second term in Equation (51), ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$, is a residual contribution, which is calculated from ${\widehat{D}}_{\mathrm{PS}}$–${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{e}}$ [71,95]. The corresponding plots of ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$(C_S) are shown in Figure 18 for both salts. Here, we can see that ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$ linearly increases with C_S for both salt cases. Moreover, changing NaCl with KCl now has a small effect on ${\widehat{D}}_{\mathrm{PS}}$. This analysis confirms that the difference between the two salt cases shown in Figure 14 is due to electrophoretic diffusiophoresis. Interestingly, ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$ retains a residual negative intercept, which is virtually the same for both salts, i.e., ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$(0) = −0.07 ± 0.01. This result, which is not observed in the PEG case, hardly depends on the accuracy of ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{e}}$ determination because its contribution is invariably very small in the KCl case. This negative intercept can be attributed [95] to another small EDL effect known as the chemiphoresis [15] mechanism. Specifically, a salt concentration gradient is responsible for a corresponding gradient of ionic strength within the EDL of a spherical particle, which causes particle diffusiophoresis from low to high salt concentrations. Chemiphoresis negatively contributes to diffusiophoresis and is predicted to be the same for both salts. Since it is typically small, it will be ignored in the analysis below.

The slope of ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$(C_S) in Figure 18 can be described within the framework of the preferential-hydration mechanism and the local-domain model already employed for PEG. As in the diffusiophoresis coefficient, we split the preferential-interaction coefficient, g, into two terms:

$$\gamma ={\gamma }^{\mathrm{e}}+{\gamma }^{\mathrm{r}}$$

(52)

where γ^e = |Z_P|/2 and γ^r = ν_W$\overline{V}$_WC_S. We can then determine the ratio, ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$/γ^r, for both salt cases. The obtained values of ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$/γ^r = 0.23 (NaCl) and ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$/γ^r = 0.25 (KCl) for lysozyme [108] are somewhat higher than those shown earlier for PEG. Nonetheless, they are still a small fraction of one, consistent with the local-domain model. If we use Equation (46b) with ν_W = 150 and ${\widehat{D}}_{\mathrm{PS}}^{\hspace{0.17em}\mathrm{r}}$/γ^r = 0.24 for both salts, we obtain ν_W^(I) = 115 and ν_W^(II) = 35.

12. Concluding Remarks

There is a growing number of experimental observations, applications and future opportunities related to diffusiophoresis [13]. This review has focused on the use of Rayleigh interferometry as a precise experimental technique for measuring multicomponent-diffusion coefficients on ternary aqueous mixtures of macromolecules (PEG or lysozyme) in the presence of cosolutes (salts or osmolytes). These data are employed to characterize the behavior of the diffusiophoresis coefficient, ${\widehat{D}}_{\mathrm{PS}}$, as a function of cosolute concentration, C_S. These data are also used to determine the corresponding cosolute osmotic diffusion coefficient, ${\widehat{D}}_{\mathrm{SP}}$. Examination of diffusiophoresis within the framework of non-equilibrium thermodynamics allows us to relate ${\widehat{D}}_{\mathrm{PS}}$ = γ − λ to the preferential-interaction coefficient, γ, and the Onsager transport coefficient, λ. The combination of ${\widehat{D}}_{\mathrm{PS}}$ and ${\widehat{D}}_{\mathrm{SP}}$ data enables the characterization of γ and λ. PEG diffusiophoresis in response to salt or osmolyte gradients is driven by a preferential-hydration mechanism, while lysozyme diffusiophoresis in response to salt gradients is driven by both preferential-hydration and electrophoretic mechanisms, the latter being the mechanism extensively described in the diffusiophoresis literature [12,13,19,20]. While the same effective charge (Z_P = 7.5) successfully explains both ${\widehat{D}}_{\mathrm{PS}}$ and ${\widehat{D}}_{\mathrm{SP}}$ data for lysozyme, it is not clear whether this agreement remains valid for other charged particles. Since proteins are weakly charged macromolecules, future multicomponent-diffusion studies should compare salt-induced diffusiophoresis with salt osmotic diffusion for strongly charged macromolecules such as nucleic acids, micelles and vesicles. It would also be interesting to explore diffusiophoresis for charged macromolecules in which the electrophoretic mechanism drives diffusiophoresis from low to high salt concentration while the preferential-hydration mechanism drives diffusiophoresis in the opposite direction. In this case, one can predict that there is a salt concentration at which the sign of ${\widehat{D}}_{\mathrm{PS}}$ changes from negative to positive. This implies that a steady salt concentration gradient would focus macromolecules at a specific location, corresponding to the salt concentration where ${\widehat{D}}_{\mathrm{PS}}$ = 0. This situation is analogous to isoelectric focusing in electrophoresis. It is also important to examine diffusiophoresis for neutral globular nanoparticles possessing interfacial PEG moieties. This is important for assessing the extent to which the values of preferential-hydration parameters, ν_W (per ethoxy group) and ${\widehat{D}}_{\mathrm{PS}}$/γ extracted for PEG, are applicable to PEG-based nanoparticles. Finally, future studies should also systematically investigate diffusiophoresis in the proximity of liquid–liquid phase separation (or cloud point). It is known that proteins [149,150], PEG [151] and micellar systems [152] are susceptible to phase separation in the presence of certain salts. Recent studies on tyloxapol micelles [23] indicate that salt-induced diffusiophoresis of colloidal particles dominates over their Brownian motion near phase-separation conditions due to a large osmotic compressibility. These studies would be useful for understanding the diffusiophoresis of nanoparticles in the presence of salt brines, with potential applications of diffusiophoresis to enhanced oil recovery [35].