First-Principles Study of Bimetallic Pairs Embedded on Graphene Co-Doped with N and O for N2 Electroreduction
Abstract
1. Introduction
2. Results and Discussion
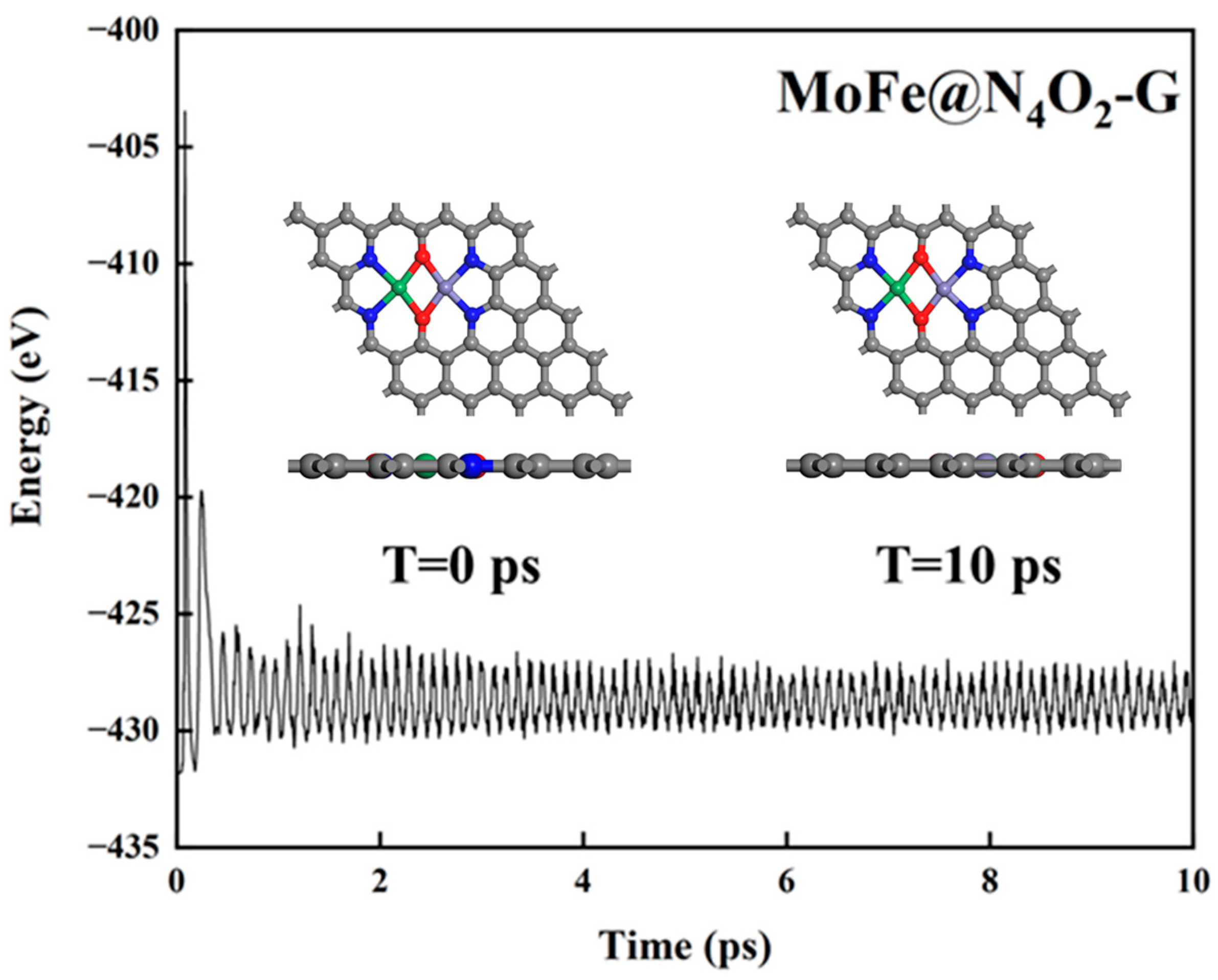
2.1. Catalyst Structure and Stability
2.2. Performance of MM′@N4O2-G for Electrocatalytic NRR
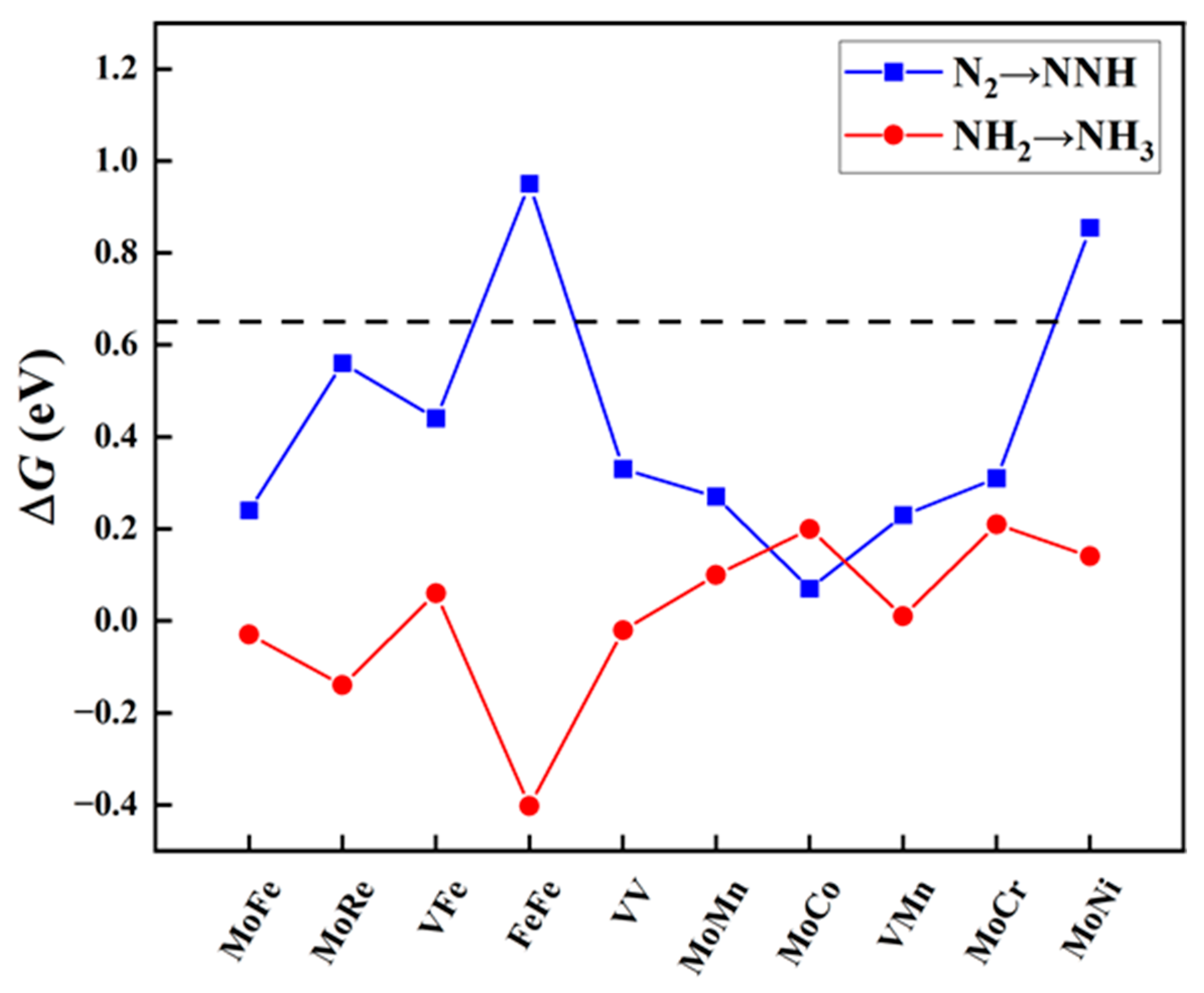
2.2.1. Screening of Catalysts
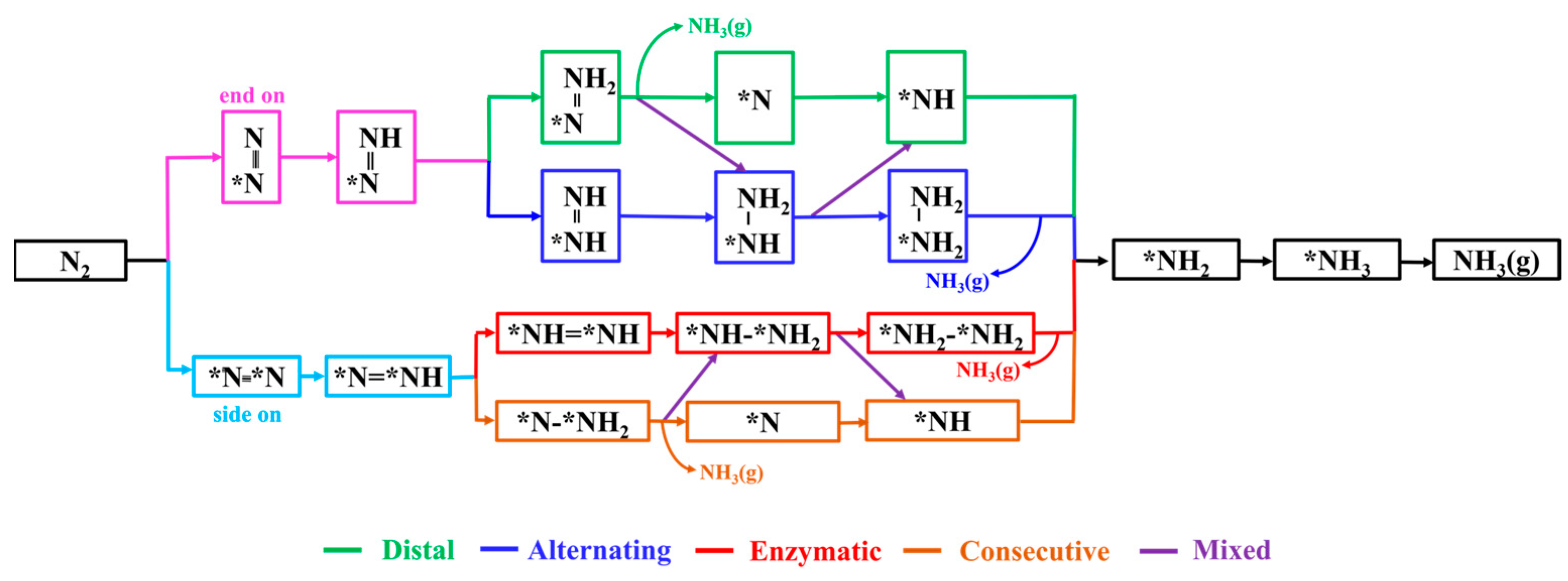
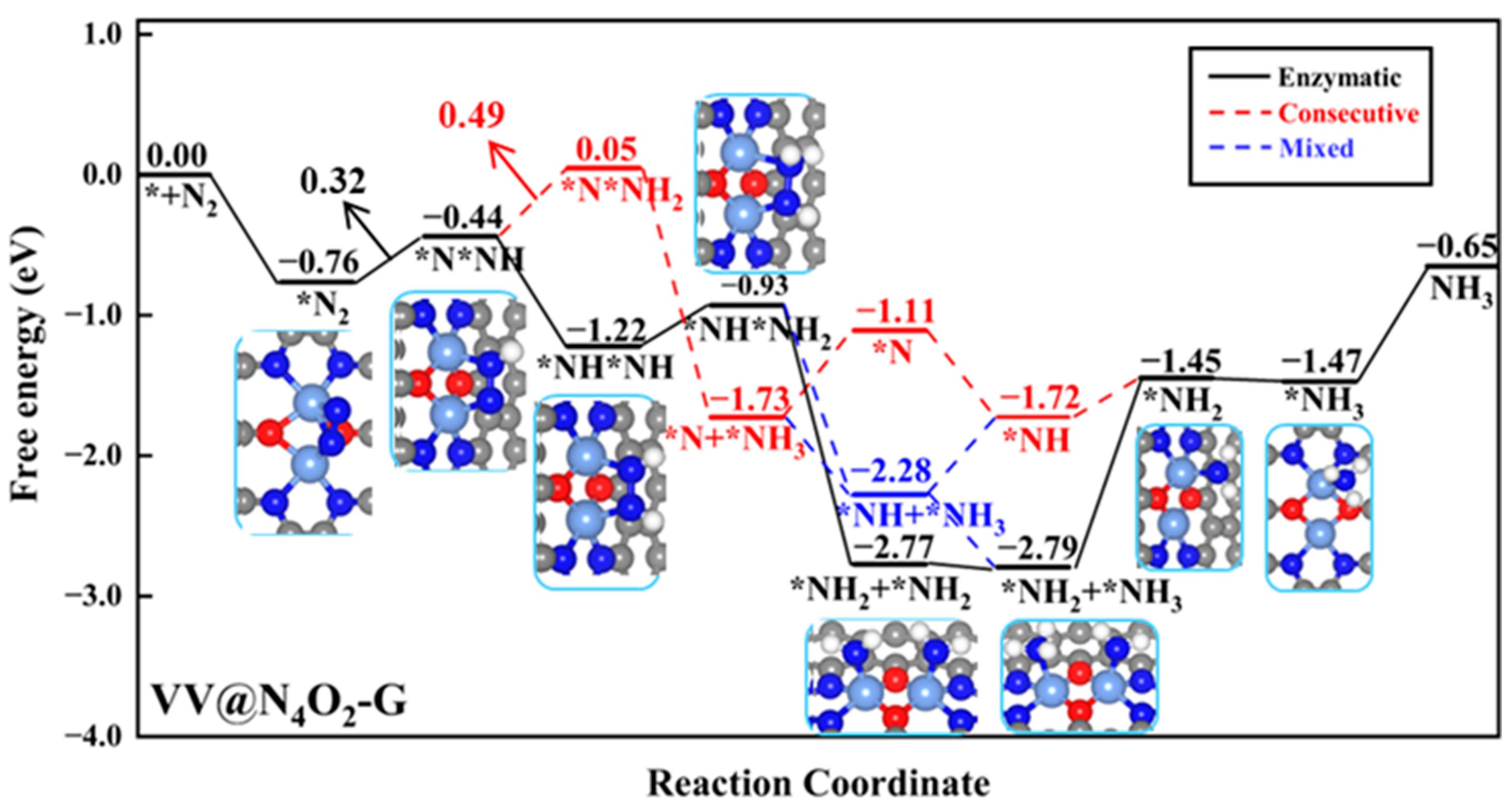
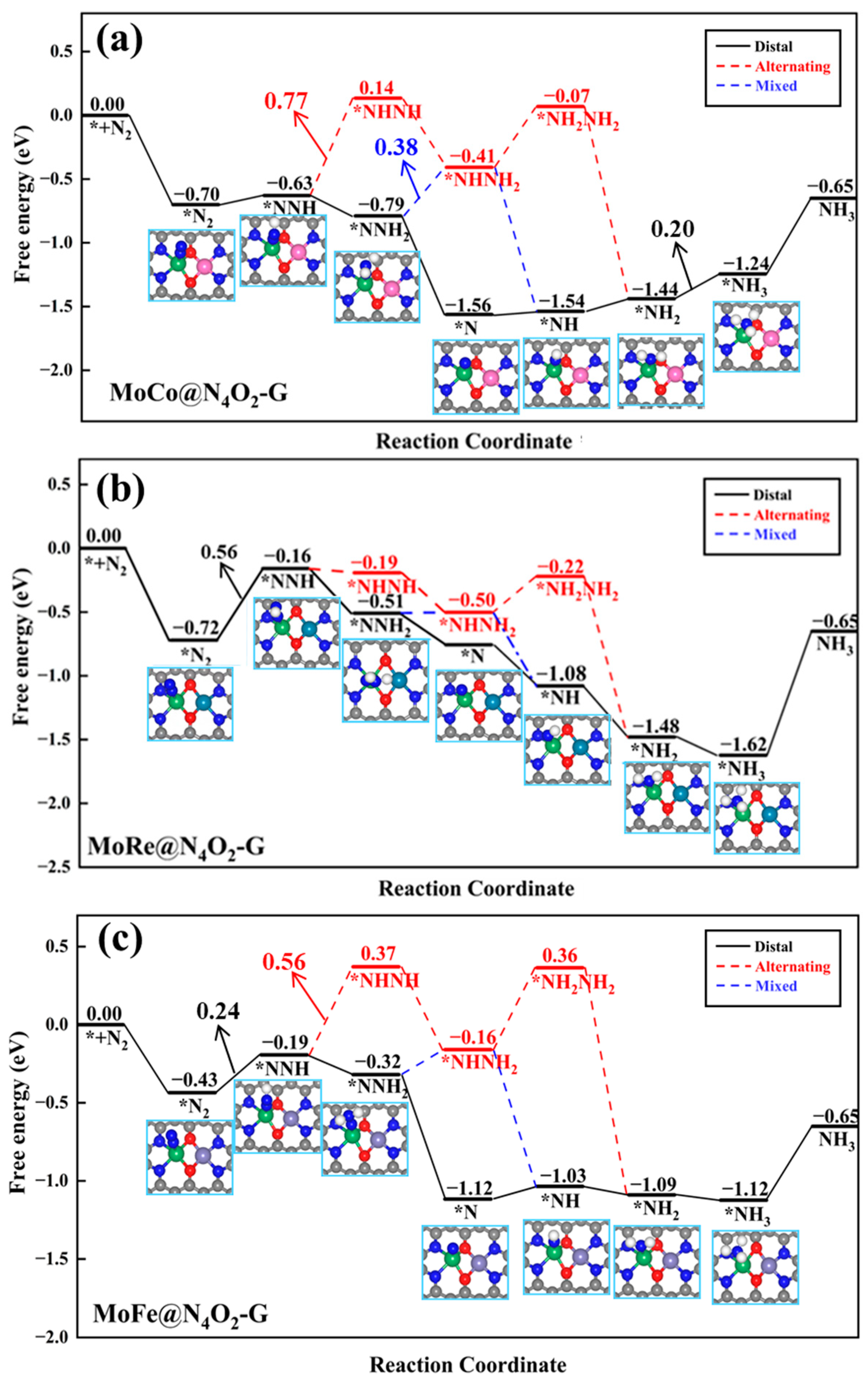
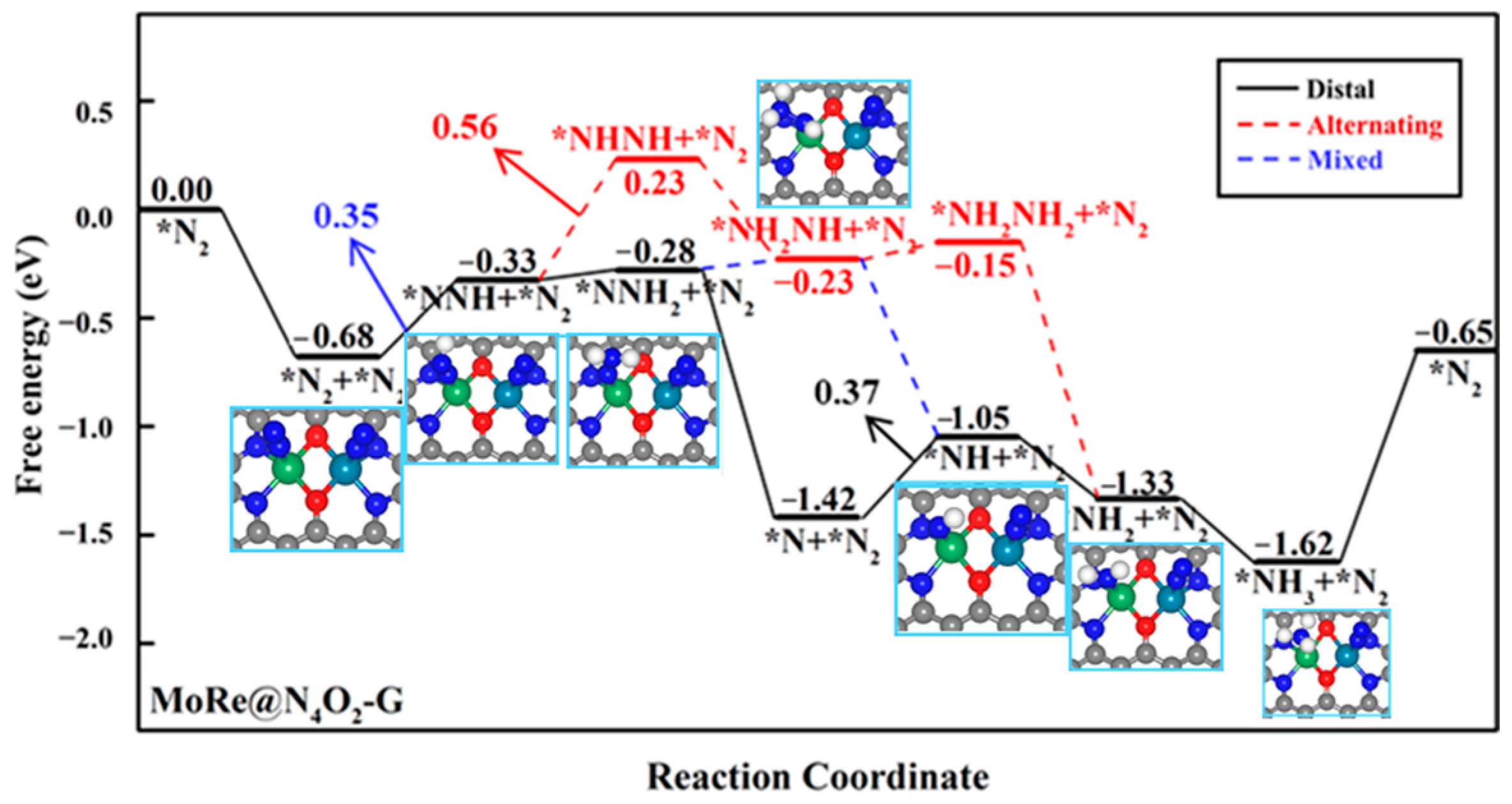
2.2.2. NRR Reaction Mechanism
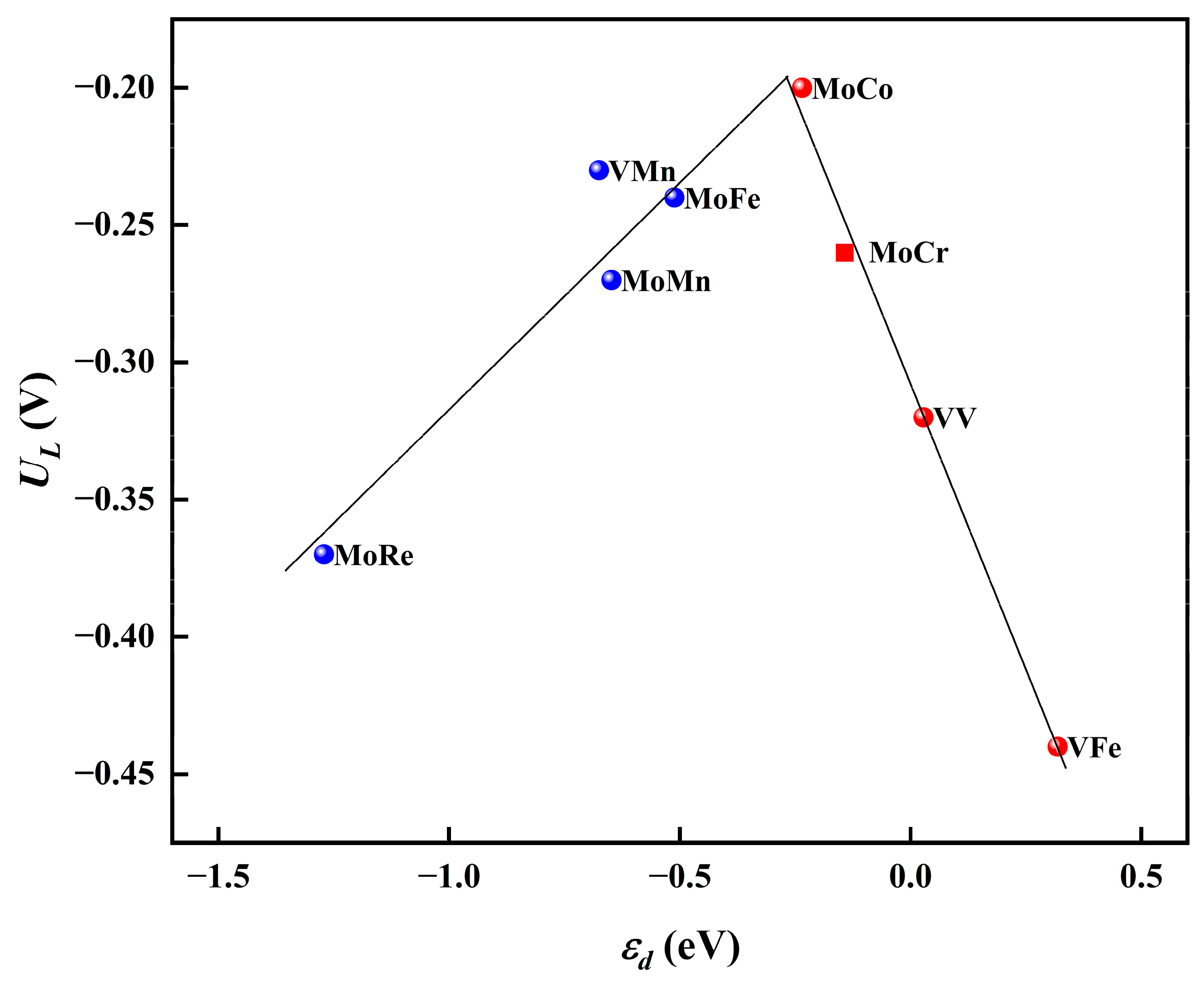
2.3. Origin of NRR Catalytic Activity
2.4. NRR Selectivity of the MM′@N4O2-G Catalysts
3. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suryanto, B.H.R.; Matuszek, K.; Choi, J.; Hodgetts, R.Y.; Du, H.-L.; Bakker, J.M.; Kang, C.S.M.; Cherepanov, P.V.; Simonov, A.N.; MacFarlane, D.R. Nitrogen reduction to ammonia at high efficiency and rates based on a phosphonium proton shuttle. Science 2021, 372, 1187–1191. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Chen, P. Catalyst: NH3 as an Energy Carrier. Chem 2017, 3, 709–712. [Google Scholar] [CrossRef]
- Chen, J.G.; Crooks, R.M.; Seefeldt, L.C.; Bren, K.L.; Bullock, R.M.; Darensbourg, M.Y.; Holland, P.L.; Hoffman, B.; Janik, M.J.; Jones, A.K.; et al. Beyond fossil fuel-driven nitrogen transformations. Science 2018, 360, eaar6611. [Google Scholar] [CrossRef]
- Rafiqul, I.; Weber, C.; Lehmann, B.; Voss, A. Energy efficiency improvements in ammonia production-perspectives and uncertainties. Energy 2005, 30, 2487–2504. [Google Scholar] [CrossRef]
- Li, K.; Andersen, S.Z.; Statt, M.J.; Saccoccio, M.; Bukas, V.J.; Krempl, K.; Sažinas, R.; Pedersen, J.B.; Shadravan, V.; Zhou, Y.; et al. Enhancement of lithium-mediated ammonia synthesis by addition of oxygen. Science 2021, 374, 1593–1597. [Google Scholar] [CrossRef]
- Foster, S.L.; Bakovic, S.I.P.; Duda, R.D.; Maheshwari, S.; Milton, R.D.; Minteer, S.D.; Janik, M.J.; Renner, J.N.; Greenlee, L.F. Catalysts for nitrogen reduction to ammonia. Nat. Catal. 2018, 1, 490–500. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Du, Y.; Zhu, X.D.; Gao, J.; Zhang, Y.C.; Wu, G. P-Block Metal-Based Electrocatalysts for Nitrogen Reduction to Ammonia: A Minireview. Small 2023, 19, 16. [Google Scholar] [CrossRef]
- Tang, X.; Wei, Z.; Liu, Q.; Ma, J. Strain engineering the D-band center for Janus MoSSe edge: Nitrogen fixation. J. Energy Chem. 2019, 33, 155–159. [Google Scholar] [CrossRef]
- Wang, C.; Shan, Y.-T.; Zheng, W.-H.; Zhang, M.; Su, Z.-M. Two-dimensional graphdiyne analogue containing Mo-coordinated porphyrin covalent organic framework as a high-performance electrocatalyst for nitrogen fixation. Appl. Surf. Sci. 2022, 580, 152359. [Google Scholar] [CrossRef]
- Yang, X.; An, P.; Wang, R.; Jia, J. Tuning the Site-to-Site Interaction of Heteronuclear Diatom Catalysts MoTM/C2N (TM = 3d Transition Metal) for Electrochemical Ammonia Synthesis. Molecules 2023, 28, 4003. [Google Scholar] [CrossRef]
- He, C.; Wang, R.; Xiang, D.; Li, X.; Fu, L.; Jian, Z.; Huo, J.; Li, S. Charge-regulated CO2 capture capacity of metal atom embedded graphyne: A first-principles study. Appl. Surf. Sci. 2020, 509, 145392. [Google Scholar] [CrossRef]
- Lang, R.; Xi, W.; Liu, J.-C.; Cui, Y.-T.; Li, T.; Lee, A.F.; Chen, F.; Chen, Y.; Li, L.; Li, L.; et al. Non defect-stabilized thermally stable single-atom catalyst. Nat. Commun. 2019, 10, 234. [Google Scholar] [CrossRef]
- Li, F.; Liu, X.; Chen, Z. 1 + 1′ > 2: Heteronuclear Biatom Catalyst Outperforms Its Homonuclear Counterparts for CO Oxidation. Small Methods 2019, 3, 1800480. [Google Scholar] [CrossRef]
- Song, W.; Fu, Z.; Liu, X.; Guo, Y.; He, C.; Fu, L. Density functional theory study of a two-atom active site transition-metal/iridium electrocatalyst for ammonia synthesis. J. Mater. Chem. A 2022, 10, 13946–13957. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.-H.; Yu, Y.-X. Single Nb or W Atom-Embedded BP Monolayers as Highly Selective and Stable Electrocatalysts for Nitrogen Fixation with Low-Onset Potentials. ACS Appl. Mater. Interfaces 2021, 13, 10026–10036. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Liu, W.; Wu, J.; Li, Q.; Feng, Q.; Chen, Z.; Xiong, X.; Wang, D.; Lei, Y. Regulating the coordination structure of metal single atoms for efficient electrocatalytic CO2 reduction. Energy Environ. Sci. 2020, 13, 4609–4624. [Google Scholar] [CrossRef]
- Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
- Guo, R.; Hu, M.; Zhang, W.; He, J. Boosting Electrochemical Nitrogen Reduction Performance over Binuclear Mo Atoms on N-Doped Nanoporous Graphene: A Theoretical Investigation. Molecules 2019, 24, 1777. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, X.; Sun, K.; Zhang, J.; Lai, W.H.; Liu, H.; Wang, G. Direct Oxygen-Oxy gen Cleavage through Optimizing Interatomic Distances in Dual Single-atom Electrocatalysts for Efficient Oxygen Reduction Reaction. Angew. Chem. Int. Ed. 2023, 62, e202301833. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, H.; Wang, T.; Guo, Z.; Zhu, F.; Xie, H.; Qin, G.; Li, H.; Li, S. The role of single-boron of N-doped graphene for effective nitrogen reduction. J. Mater. Sci. Technol. 2023, 159, 244–250. [Google Scholar] [CrossRef]
- Orek, C.; Bartolomei, M.; Coletti, C.; Bulut, N. Graphene as Nanocarrier for Gold(I)-Monocarbene Complexes: Strength and Nature of Physisorption. Molecules 2023, 28, 3941. [Google Scholar] [CrossRef]
- Wang, X.; Niu, H.; Wan, X.; Wang, J.; Kuai, C.; Zhang, Z.; Guo, Y. Identifying TM-N4 active sites for selective CO2-to-CH4 conversion: A computational study. Appl. Surf. Sci. 2022, 582, 152470. [Google Scholar] [CrossRef]
- Hu, R.; Li, Y.; Zeng, Q.; Wang, F.; Shang, J. Bimetallic Pairs Supported on Graphene as Efficient Electrocatalysts for Nitrogen Fixation: Search for the Optimal Coordination Atoms. ChemSusChem 2020, 13, 3636–3644. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Rong, H.; Zhang, J.; Wang, D.; Li, Y. Modulating the local coordination environment of single-atom catalysts for enhanced catalytic performance. Nano Res. 2020, 13, 1842–1855. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, H.; Liu, B. Coordination Engineering of Single-Atom Catalysts for the Oxygen Reduction Reaction: A Review. Adv. Energy Mater. 2020, 11, 2002473. [Google Scholar] [CrossRef]
- Qian, Y.; Liu, Y.; Zhao, Y.; Zhang, X.; Yu, G. Single vs double atom catalyst for N2 activation in nitrogen reduction reaction: A DFT perspective. EcoMat 2020, 2, e12014. [Google Scholar] [CrossRef]
- Chen, Z.W.; Yan, J.M.; Jiang, Q. Single or Double: Which Is the Altar of Atomic Catalysts for Nitrogen Reduction Reaction? Small Methods 2018, 3, 1800291. [Google Scholar] [CrossRef]
- Gao, S.; Liu, X.; Wang, Z.; Lu, Y.; Sa, R.; Li, Q.; Sun, C.; Chen, X.; Ma, Z. Spin regulation for efficient electrocatalytic N2 reduction over diatomic Fe-Mo catalyst. J. Colloid Interface Sci. 2023, 630, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Huang, X.; Xu, H. Anchoring an Fe Dimer on Nitrogen-Doped Graphene toward Highly Efficient Electrocatalytic Ammonia Synthesis. ACS Appl. Mater. Interfaces 2021, 13, 43632–43640. [Google Scholar] [CrossRef]
- Han, S.; Song, R.; Wang, M.; Gong, Q.; Xiong, J.; Xu, Z. Electrocatalytic reduction of N2 on FeRu dual-atom catalyst anchored in N-doped phosphorene. Mol. Catal. 2023, 539, 113032. [Google Scholar] [CrossRef]
- Jiang, Q.; Meng, Y.; Li, K.; Wang, Y.; Wu, Z. Theoretical insights into bimetallic atoms supported on PC6 as highly efficient electrocatalysts for N2 electroreduction to NH3. Appl. Surf. Sci. 2021, 547, 149208. [Google Scholar] [CrossRef]
- Skúlason, E.; Bligaard, T.; Gudmundsdóttir, S.; Studt, F.; Rossmeisl, J.; Abild-Pedersen, F.; Vegge, T.; Jónsson, H.; Nørskov, J.K. A theoretical evaluation of possible transition metal electro-catalysts for N2 reduction. Phys. Chem. Chem. Phys. 2012, 14, 1235–1245. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Gu, J.; Lin, S.; Zhang, S.; Chen, Z.; Huang, S. Tackling the Activity and Selectivity Challenges of Electrocatalysts toward the Nitrogen Reduction Reaction via Atomically Dispersed Biatom Catalysts. J. Am. Chem. Soc. 2020, 142, 5709–5721. [Google Scholar] [CrossRef]
- Han, L.; Liu, X.; Chen, J.; Lin, R.; Liu, H.; Lü, F.; Bak, S.; Liang, Z.; Zhao, S.; Stavitski, E.; et al. Atomically Dispersed Molybdenum Catalysts for Efficient Ambient Nitrogen Fixation. Angew. Chem. Int. Ed. 2019, 58, 2321–2325. [Google Scholar] [CrossRef]
- Han, X.-Q.; Lang, Z.-L.; Zhang, F.-Y.; Xu, H.-L.; Su, Z.-M. Computational evaluation of FeMo heteroatom coeffect induced high electroreduction activity of N2-to-NH3. Appl. Surf. Sci. 2022, 579, 152214. [Google Scholar] [CrossRef]
- Shang, H.; Zhou, X.; Dong, J.; Li, A.; Zhao, X.; Liu, Q.; Lin, Y.; Pei, J.; Li, Z.; Jiang, Z.; et al. Engineering unsymmetrically coordinated Cu-S1N3 single atom sites with enhanced oxygen reduction activity. Nat. Commun. 2020, 11, 3049. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Wu, D.; Li, H.; Song, Y.; Lv, W.; Yu, X.; Ma, D. Tailoring the coordination environment of double-atom catalysts to boost electrocatalytic nitrogen reduction: A first-principles study. Nanoscale 2023, 15, 16056–16067. [Google Scholar] [CrossRef]
- Wang, S.; Shi, L.; Bai, X.; Li, Q.; Ling, C.; Wang, J. Highly Efficient Photo-/Electrocatalytic Reduction of Nitrogen into Ammonia by Dual-Metal Sites. ACS Cent. Sci. 2020, 6, 1762–1771. [Google Scholar] [CrossRef]
- Zhang, Y.-X.; Zhang, S.; Huang, H.; Liu, X.; Li, B.; Lee, Y.; Wang, X.; Bai, Y.; Sun, M.; Wu, Y.; et al. General Synthesis of a Diatomic Catalyst Library via a Macrocyclic Precursor-Mediated Approach. J. Am. Chem. Soc. 2023, 145, 4819–4827. [Google Scholar] [CrossRef] [PubMed]
- Zafari, M.; Nissimagoudar, A.S.; Umer, M.; Lee, G.; Kim, K.S. First principles and machine learning based superior catalytic activities and selectivities for N2 reduction in MBenes, defective 2D materials and 2D π-conjugated polymer-supported single atom catalysts. J. Mater. Chem. A 2021, 9, 9203–9213. [Google Scholar] [CrossRef]
- Ling, C.; Ouyang, Y.; Li, Q.; Bai, X.; Mao, X.; Du, A.; Wang, J. A General Two-Step Strategy-Based High-Throughput Screening of Single Atom Catalysts for Nitrogen Fixation. Small Methods 2018, 3, 1800376. [Google Scholar] [CrossRef]
- Chun, H.-J.; Apaja, V.; Clayborne, A.; Honkala, K.; Greeley, J. Atomistic Insights into Nitrogen-Cycle Electrochemistry: A Combined DFT and Kinetic Monte Carlo Analysis of NO Electrochemical Reduction on Pt(100). ACS Catal. 2017, 7, 3869–3882. [Google Scholar] [CrossRef]
- Liu, C.; Li, Q.; Wu, C.; Zhang, J.; Jin, Y.; MacFarlane, D.R.; Sun, C. Single-Boron Catalysts for Nitrogen Reduction Reaction. J. Am. Chem. Soc. 2019, 141, 2884–2888. [Google Scholar] [CrossRef]
- Qi, J.; Gao, L.; Wei, F.; Wan, Q.; Lin, S. Design of a High-Performance Electrocatalyst for N2 Conversion to NH3 by Trapping Single Metal Atoms on Stepped CeO2. ACS Appl. Mater. Interfaces 2019, 11, 47525–47534. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef]
- Mathew, K.; Kolluru, V.S.C.; Mula, S.; Steinmann, S.N.; Hennig, R.G. Implicit self-consistent electrolyte model in plane-wave density-functional theory. J. Chem. Phys. 2019, 151, 234101. [Google Scholar] [CrossRef]
- Barnett, R.N.; Landman, U. AIMD-Born-Oppenheimer molecular-dynamics simulations of finite systems: Structure and dynamics of (H2O)2. Phys. Rev. B 1993, 48, 2081–2097. [Google Scholar] [CrossRef] [PubMed]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- The National Institute of Standards and Technology (NIST). Available online: http://cccbdb.nist.gov/ (accessed on 12 June 2023).




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Sun, H.; Xing, G.; Liu, S.; Duan, X.; Liu, J. First-Principles Study of Bimetallic Pairs Embedded on Graphene Co-Doped with N and O for N2 Electroreduction. Molecules 2024, 29, 779. https://doi.org/10.3390/molecules29040779
Dong H, Sun H, Xing G, Liu S, Duan X, Liu J. First-Principles Study of Bimetallic Pairs Embedded on Graphene Co-Doped with N and O for N2 Electroreduction. Molecules. 2024; 29(4):779. https://doi.org/10.3390/molecules29040779
Chicago/Turabian StyleDong, Haozhe, Hao Sun, Guanru Xing, Shize Liu, Xuemei Duan, and Jingyao Liu. 2024. "First-Principles Study of Bimetallic Pairs Embedded on Graphene Co-Doped with N and O for N2 Electroreduction" Molecules 29, no. 4: 779. https://doi.org/10.3390/molecules29040779
APA StyleDong, H., Sun, H., Xing, G., Liu, S., Duan, X., & Liu, J. (2024). First-Principles Study of Bimetallic Pairs Embedded on Graphene Co-Doped with N and O for N2 Electroreduction. Molecules, 29(4), 779. https://doi.org/10.3390/molecules29040779







