Abstract
Laser ablated Be atoms have been reacted with acetonitrile molecules in 4 K solid neon matrix. The diberyllium products BeBeNCCH3 and CNBeBeCH3 have been identified by D and 13C isotopic substitutions and quantum chemical calculations. The stabilization of the diberyllium species is rationalized from the formation of the real Be−Be single bonds with bond distances as 2.077 and 2.058 Å and binding energies as −27.1 and −77.2 kcal/mol calculated at CCSD (T)/aug-cc-pVTZ level of theory for BeBeNCCH3 and CNBeBeCH3, respectively. EDA-NOCV analysis described the interaction between Be2 and NC···CH3 fragments as Lewis “acid−base” interactions. In the complexes, the Be2 moiety carries positive charges which transfer from antibonding orbital of Be2 to the bonding fragments significantly strengthen the Be−Be bonds that are corroborated by AIM, LOL and NBO analyses. In addition, mono beryllium products BeNCCH3, CNBeCH3, HBeCH2CN and HBeNCCH2 have also been observed in our experiments.
1. Introduction
The chemistry of beryllium is predicted to be the richest among the alkaline earth metals due to its small size and the highest electronegativity and ionization energy among s-block elements [1,2], which is, however, largely unexplored due to the high toxicity of the compounds containing this element [3,4]. Over the past few decades, the very weak beryllium–beryllium interaction has been the most studied for s-block metal–metal interactions [5,6,7]. Isolated beryllium dimer was characterized as a typical weakly bound molecule with a bonding interaction of 11.2 kJ mol−1 (calc.) and a large bond distance of 2.45 Å as a result of the both doubly occupied bonding 2σg+ orbital and antibonding 2σu+ orbital [8,9,10].
Up to now, diberyllium complexes have aroused a great deal of enthusiasm among researchers, and many theoretical strategies have been proposed to enhance the strength of Be−Be bond [5,11,12,13,14,15]. Removing/adding an electron from/to this dimer by interaction with some other molecules is a general formula to stabilize the system. The complexation of Be2 with electron-withdrawing ligands such as F [16] or CN [17], or electron-deficient conjugated fragments such as cyclopentdienyl [18,19], pentadienyl [20] and phospholyl [21] is able to obtain a classical Be−Be σ single bond by pulling one or both electrons from antibonding orbital of Be2 to ligands. Despite the intrinsic electron-deficient nature of beryllium, reports indicate that the Be2 moiety in these molecules is essentially a dication Be22+, [17] which exhibits the formation of a strong bond in the presence of a counterion. Strong Be–Be bonds are also formed via electron transferring from Be atoms to CnHn (n = 3, 5, 7), π-radicals [22] and SO ligands. [23] Furthermore, a neutral odd-electron Be−Be bond is firstly identified in the tri-AMD-ligands-chelated D3h-Be2(AMD)3 complex by one AMD ligand attracting one electron from Be antibonding σ* orbital [24]. A strong 2-center-1-electron Be−Be bond is also formed by attaching one electron to 1,2-diBeX-benzene (X = H, F, Cl, CN) derivatives [25]. Be–Be double-π bonds are first achieved in the predicted octahedral cluster of Be2(μ2-X)4 (X = Li, Cu, BeF) by a novel concerted electron-donation from four s1-type electron-donating ligands [15]. The Be–Be triple bonds are formed in theoretically predicted Li6Be2 [26] species, which are stabilized by six s1-type donor ligands and in Be2X4Y2 (X = Li, Na; Y = Na, K) [27] clusters where six alkali metals are electron-donating ligands. Another way to form a Be−Be covalent bond is by adding radical ligands to an excited Be2 moiety. The neutral Be2 moiety in an excited state adding ligands such as (HCNMe)2B [28] and N-heterocyclic carbenes (NHCs) [29] can form a single or double bond, respectively.
Acetonitrile is known as an effective electron donor based on the previous research of reactions with metal atoms [30,31,32,33,34,35,36,37], and it could be a good candidate for stabilizing the Be2 dimer. In this paper, we investigated the reactions of beryllium atoms with acetonitrile by means of matrix-isolation infrared spectroscopy and theoretical calculations, in order to further supplement the reactions of alkali metal with acetonitrile, and search for stable diberyllium complexes that might be formed. Six different products were spectroscopically identified in solid neon including two complexes possessing Be−Be single bonds, and three related reaction paths were presented.
2. Results and Discussion
The infrared spectra for acetonitrile (0.5% in solid neon) on pre-deposition and the reaction products on co-deposition, annealing and stepwise photolysis in the selected regions are shown in Figure 1. The isotopic substitution experiments with CD3CN and 13CH313CN samples were performed and the infrared spectra are given in Figure 2. The absorptions of acetonitrile are extremely strong, so the changes of acetonitrile absorptions during the reaction are negligible compared with the products’ absorptions. In addition to the absorptions assigned to the precursor and common species that were also observed in other experiments with CH3CN as reagent, several new product absorptions appeared, which can be classified into six groups based on their intensity changes. Table 1 shows the observed and computed vibrational frequencies of the products along with the assignment of the modes. The full sets of B3LYP calculated harmonic and anharmonic frequencies are all collected in Tables S1−S6. The laser intensity is relatively high in our experiments that are able to directly produce beryllium dimer. The infrared intensities of diberyllium products are much weaker with low laser power, while the intensities of mono beryllium products almost remain unchanged in Figure 1a. Several new absorptions located in N−C and C−N stretching region are almost diminished with low laser intensity. We tentatively assigned these weak absorptions to Bex(CH3CN), which were generated from the reactions of Be clusters and acetonitrile with high laser power.
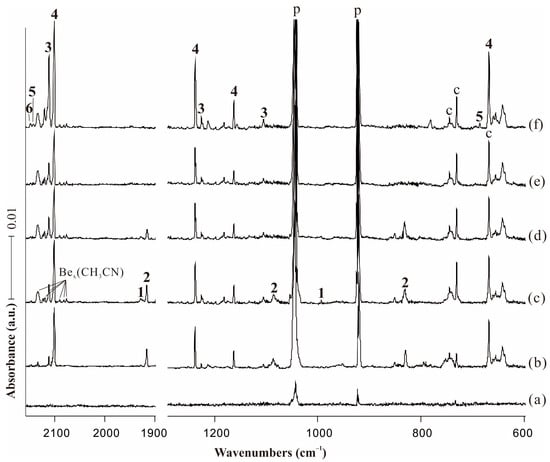
Figure 1.
Infrared spectra in the product regions from the reactions of laser-ablated Be atoms with 0.5% CH3CN in neon matrix at 4 K. (a) Pre-deposition of 0.5% CH3CN in neon for 6 min; (b) co-deposition for 60 min (weaker laser intensity); (c) co-deposition for 60 min (higher laser intensity); (d) after annealing at 8 K; (e) after visible (λ > 520 nm) irradiation for 6 min; and (f) after full arc (λ > 220 nm) irradiation for 6 min. Bands labeled p and c stand for the precursor absorptions and common absorptions in the CH3CN matrix spectra. Numbers 1, 2, 3, 4, 5, 6 denote BeBeNCCH3, BeNCCH3, CNBeBeCH3, CNBeCH3, HBeCH2CN and HBeNCCH2, respectively.
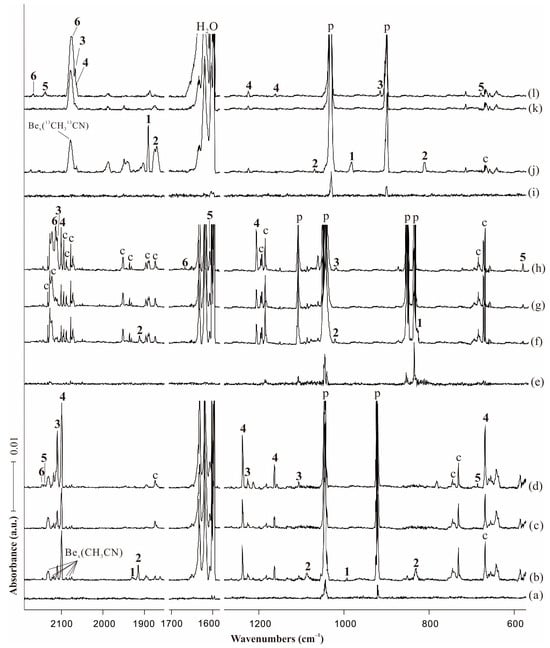
Figure 2.
Infrared spectra in the product regions from the reactions of laser-ablated Be atoms with CH3CN in neon matrix at 4 K. (a) Pre-deposition of 0.5% CH3CN in neon for 6 min; (b) co-deposition of Be + 0.5% CH3CN for 60 min; (c) after visible (λ = 520 nm) irradiation; (d) after full arc (λ > 220 nm) irradiation for 6 min; (e) pre-deposition of 0.75% CD3CN in neon for 6 min; (f) co-deposition of Be + 0.75% CD3CN for 60 min; (g) after visible (λ = 520 nm) irradiation; (h) after full arc (λ > 220 nm) irradiation for 6 min; (i) pre-deposition of 0.75% 13CH313CN in neon for 6 min; (j) co-deposition of Be + 0.75% 13CH313CN for 60 min; (k) after visible (λ = 520 nm) irradiation; and (l) after full arc (λ > 220 nm) irradiation for 6 min. Bands labeled p and c stand for the precursor absorptions and common absorptions in the CH3CN matrix spectra. Numbers 1, 2, 3, 4, 5, 6 denote BeBeNCCH3, BeNCCH3, CNBeBeCH3, CNBeCH3, HBeCH2CN and HBeNCCH2, respectively.

Table 1.
Experimentally observed (in Ne) and calculated vibrational frequencies of products from reactions of beryllium atoms with acetonitrile a.
The relatively weak absorptions in the original deposition spectra marked “1” were completely destroyed under visible irradiation. New product absorptions denoted with “2” also appeared upon sample deposition, which decreased after annealing to 8 K and totally disappeared on the first visible (λ = 520 nm) irradiation. On the opposite, the intensities of the bands marked with “3” and “4” tripled and doubled upon full arc irradiation (λ > 220 nm) compared with the co-deposition spectra. In addition, the relatively weak absorptions marked “5” and “6” only appeared after full arc irradiation.
2.1. End-On Products: BeBeNCCH3 and BeNCCH3
The absorption of C−N stretching mode for BeBeNCCH3 complex was observed at 1927.8 cm−1 on co-deposition, and its corresponding 13C counterpart was located at 1889.4 cm−1, but unfortunately the corresponding D isotopic absorption was covered by the precursor bands. The observed absorptions matched well with the computed IR frequencies with strongest intensities at 1986.0 and 1942.7 cm−1 for 12C and 13C, respectively. The band at 994.1 cm−1 is attributed to the CH3 bending mode, with D and 13C counterparts observed at 827.0 and 981.2 cm−1, respectively. The computed infrared absorptions of BeBeNCCH3 are shown in Table S1.
The assignment of the mono beryllium end-on complex BeNCCH3 was confirmed by the experimental observation of three bands at 1915.4, 1082.3 and 831.4 cm−1. The strong 1915.4 cm−1 band showed a large 13C shift to 1875.4 cm−1, exhibiting a 12C/13C isotopic frequency ratio of 1.0213, while its corresponding D counterpart was at 1911.2 cm−1. We assigned this band to the C−N stretching mode of BeNCCH3 based on the isotopic shifts and good consistence with the calculated value of 1953.5 cm−1. The bands at 1082.3, 1020.8 and 1068.7 cm−1 for 12C, D and 13C isotopes are in good agreement with the calculated results of N−Be stretching mode at 1106.0 (12C), 1043.4 (D) and 1091.5 cm−1 (13C), respectively. The absorption observed at 831.4 cm−1 with a 13C isotopic substitution at 811.6 cm−1 lays in the region expected for a C−C stretching vibration, [37] and the large 12C/13C ratio of 1.0244 was obtained to verify our assignment. The corresponding D isotopic absorption was covered by the precursor bands. All calculated frequencies of BeNCCH3 are listed in Table S2.
2.2. Insertion Products: CNBeBeCH3 and CNBeCH3
The strong band at 2111.0 cm−1 is due to the N−C stretching vibration for the diberyllium insertion product CNBeBeCH3, and the D and 13C isotopic substitutions were observed at 2111.9 and 2068.1 cm−1, respectively, conforming to the N−C stretching mode shifts. The low-intensity band of CH3 wagging mode is located at 1226.1 cm−1, the predicted value of which is at 1249.1 cm−1. The most decisive band for the diberyllium insertion product was observed at 1105.6 cm−1, which matched well with the calculated absorption for Be−Be stretching mode at 1109.8 cm−1. Unfortunately, the isotopic counterparts for these two absorptions were too weak to be observed in our experiments. The C−Be stretching mode was observed at 1013.4 and 913.4 cm−1 in D and 13C spectra, but this mode was covered by the extremely strong precursor absorption in 12C experiments.
The most intense absorption at 2100.2 cm−1 in the spectrum after full arc irradiation showed essentially no shift upon D substitution, but largely shifted to 2064.3 cm−1 on 13C. The B3LYP isotope ratio for 13C substitution of 1.0187 was in accordance with the experimental ratio of 1.0174. We therefore assigned the uniquely strong 2100.2 cm−1 band to the N−C stretching vibration of the mono beryllium insertion complex. The strong CH3 wagging absorption observed at 1237.8 cm−1 showed its D and 13C isotopic absorptions at 1205.0 and 1223.8 cm−1, and these bands are in excellent consistence with calculated values of 1269.2, 1217.9 and 1255.5 cm−1, respectively. A medium absorption was observed at 1162.9 cm−1 along with its 13C counterpart at 1160.5 cm−1, and it is indicative of the antisymmetric CBeN stretching vibration. The observed bands are in the good agreement with the calculated frequencies of 1186.4 and 1183.2 cm−1 for 12C and 13C isotopes. Though the band at 668.3 cm−1 is common in the matrix spectra of CH3CN + M reactions, it only doubled under full arc irradiation in the case of beryllium, and tracked with other bands labeled “4”. Unfortunately, its D and 13C counterparts were not detected because of our detector noise. We tentatively assigned this band to the CBeN bending mode of CNBeCH3. The B3LYP functional predicted this band at 695.6 cm−1, which is only 27.3 cm−1 higher than observed. The other infrared absorptions of CNBeCH3 are very weak, which are not observed in the experiment (Table S4).
2.3. HBeCH2CN and HBeNCCH2
The band at 2141.4 cm−1 only appeared after full arc irradiation showing almost no 13C shift at 2141.8 cm−1. The Be−D stretching mode of HBeCH2CN was calculated at 1654.6 cm−1, and was observed at 1608.3 cm−1 among the strong absorptions of water impurity existing in all our experiments. We assigned these bands to the Be−H stretching mode of HBeCH2CN. In the low frequency region, a weak absorption at 685.9 cm−1 tracked with 2141.1 cm−1 band, and it showed a large D shift to 579.9 cm−1 and very small 13C shift to 680.6 cm−1. The band position and large D shift of 106.0 cm−1 suggested a Be−H bending vibration. The observed bands are in excellent agreement with the calculated frequencies of 710.2, 596.8 and 703.2 cm−1, respectively. The observation of the Be−H bending mode overwhelmingly confirmed our assignment of HBeCH2CN.
The band at 2147.7 cm−1 exhibited its D and 13C counterparts at 2114.6 and 2075.7 cm−1. The B3LYP computed 12C/13C isotopic frequency ratios for C−N stretching mode of HBeNCCH2 was 1.0352, very slightly lower than the observed value of 1.0347. For D counterpart, the calculation result showed that the C−N stretching mode is coupled with CD2 symmetric stretching vibration, which is the reason of the large D shift observed in the experiment. The coincident coupled frequency in D substitution is decisive for the confirmation of product HBeNCCH2. The Be−H stretching mode was observed at 1661.8 and 2169.0 cm−1 for D and 13C, and the predicted values were at 1688.5 and 2197.2 cm−1, respectively. The calculated intensities of the other infrared bands are all weak in Table S6.
3. Molecular Structures and Bonding
The optimized structures of diberyllium and mono beryllium end-on and insertion complexes are shown in Figure 3, with the end-on products in Cs symmetry and the insertion complexes possessing C3v symmetry. The point groups of beryllium products happen to be reverse with the C3v point groups of N-coordination transition-metal complexes and Cs structures of transition-metal insertion complexes (except for Mn products) [30,31,32,33,34,35,36,37]. According to the NBO analysis in Table S8, the electropositive beryllium forms sp hybrid orbitals, which make σ bonds with sp hybrid orbitals on the C atoms in the insertion complexes. The higher s contributions from Be in the C−Be bond lead to the linear structures, different from the higher d characters in the carbon−metal bond leading to the bent transition-metal structures. The unpaired spin destinies of triplet state BeNCCH3 complex are most located on Be and C atoms (1.105 and 0.555, shown in Figure S1), which cause a bent structure with CCN bond angles of 134.6°.
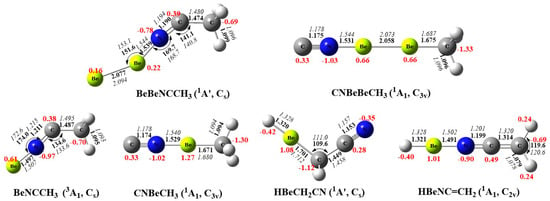
Figure 3.
Optimized structures of the reaction products at the B3LYP−D3 (bold) and CCSD (italic) levels. The aug−cc−pVTZ basis was set for all atoms. Black color: bond length in Å and bond angle in degree; red color: the atomic partial charges calculated by the NBO method.
Unlike the tiny differences in the structures, the diberyllium products are much more exothermic compared with mono beryllium complexes, which may be caused by the formation of the Be−Be real single bonds. The binding energies of the Be–Be bonds in BeBeNCCH3 and CNBeBeCH3 are calculated to be −27.1 and −77.2 kcal/mol at CCSD(T)/aug-cc-pVTZ level of theory, respectively. The Be–Be bond in CNBeBeCH3 is also quantified by the EDA, as shown in Figure 4 and Table S9. The total interaction energy ΔEint is −73.72 kcal·mol−1 between the NCBe and BeCH3 fragments, which consist of −65.54 kcal·mol−1 of electrostatic energy ΔEelstat, −41.61 kcal·mol−1 of orbital interaction energy ΔEorb, and 33.43 kcal· mol−1 of Pauli repulsion energy ΔEPauli. For BeBeNCCH3, the Be–Be bond distance is calculated to be 2.077 Å, significantly shorter than that in the free Be2 dimer of 2.509 Å. The Be−Be distance is further shortened in CNBeBeCH3 with 2.058 Å. The Be–Be distances match the single bond value of 2.05 Å in reported calculations of comparable compounds, and the bond lengths are also closer to that of Be22+ than to the neutral Be2 molecule [17]. Furthermore, the CN and CH3 moieties are both doubly occupied rather than singly occupied in HOMO-2 and HOMO-3 (Figure S2), which also indicates charge transfer from Be2 to the bonding fragments. As expected, the beryllium atoms in our diberyllium products carry positive charge and the NC and CH3 moieties are negatively charged. According to the NPA charges showed in Figure 3, the Be2 moiety carries positive charges of 0.38 and 1.32 for BeBeNCCH3 and CNBeBeCH3, respectively. More positive charges on the Be2 moiety lead to shorter Be−Be bond distances.
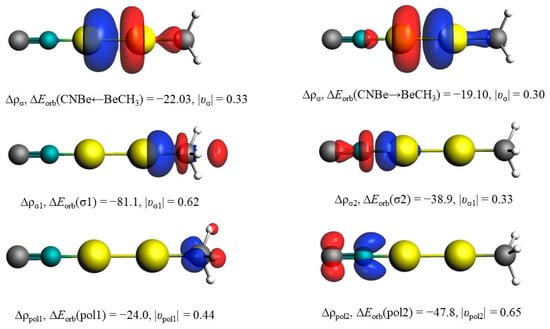
Figure 4.
Plots of the deformation densities Δρ. ΔEorb are in kcal mol−1. The direction of the charge flow is red → blue.
The energy decomposition analysis (EDA) in combination with the natural orbital for chemical valence (NOCV) theory has been carried out to further confirm the types of bonding in Table 2. There are two possibilities of interaction types in CNBeBeCH3: ionic or neutral interacting fragments. The most suitable fragments to describe the bonding situations yield the smallest amount of the orbital interaction energy (ΔEorb), because the least alteration of the electronic charge distribution is required to generate the electronic structure of the molecule. The significantly smaller ΔEorb value of ionic fragments (by 183.7 kcal/mol) convincingly shows that CNBeBeCH3 complex can be envisaged as the result of the interaction of Be22+ and (NC···CH3)2− through a donor–acceptor type of bonding rather than the electron-shared bonding between the neutral ones. The substantial electrostatic energy ΔEelstat (−640.7 kcal/mol) between the ionic interacting fragments contributes much more (75.9%) to the total attraction than the covalent contribution ΔEorb (24.0%). The polarization interaction caused by strong electrostatic interaction is also not neglectable. The corresponding deformation densities Δρ due to the electron transfer between the ionic interacting fragments are visualized in Figure 4. The direction of the charge flow is from the red region to the blue one. The colors also corroborate well with the NPA charges in Figure 3. It is obvious that the orbital interactions in CNBeBeCH3 are mainly σ donations of the Lewis base (NC···CH3)2− to the vacant σu+ orbitals of the Lewis acid Be22+.

Table 2.
EDA-NOCV results for CNBeBeCH3 obtained at the B3LYP/TZ2P/ZORA level of theory.
We also studied the topological analysis of electron density in these complexes to obtain a better understanding of the bonding situation. Figure 5 and Figure S3 display the contour plots of Laplacian of electron density (∇2ρ(r)) at the molecular plane. The red dotted lines correspond to the areas of charge concentration (∇2ρ < 0), while the blue solid lines indicate the areas of charge depletion (∇2ρ > 0). The bond critical points identified between two beryllium atoms with negative Laplacian values (∇2ρcp = −0.1176 in BeBeNCCH3, −0.1079 in CNBeBeCH3) support the formation of a real Be−Be bond, which exhibits covalent character. The negative values of the electronic energy density, E(r), as −0.3154 and −0.3997 in Table S10, also stand for the interactions with significant covalent character. All Be−N interactions present a positive bond critical point (BCP) value for the Laplacian ∇2ρ(r) (∇2ρcp = 0.6479 in BeBeNCCH3, 0.7387 in BeNCCH3, 0.6078 in CNBeBeCH3, and 0.6073 in CNBeCH3), denoting their ionic character. The negative electron energy densities at BCP (E(r)= −0.2494 in BeBeNCCH3, −0.3440 in BeNCCH3, −0.3663 in CNBeCH3 and −0.3788 in CNBeBeCH3) indicate the covalent character. Thus, the Be−N bonds are covalent polar bonds with a certain degree of both covalent and ionic contributions [38]. The localized orbital locator (LOL) map is also introduced to characterize bond effects in Figure 5 and Figure S4. The LOL values of more than 0.9e (red regions) in Be−Be region of our products are significant larger compared with isolated Be2 dimer. The strong electron localization indicates the aforementioned Be−Be covalent bonds. The strength of the Be−Be bonds in our products is also clear from the HOMO molecular orbitals involving the Be2 moiety in Figure 5. Coherently, NBO describes the Be−Be bonds as σ bonds with a population of around two electrons (Table S8). The Wiberg bond index (WBI) for the Be–Be bonds is calculated to be 0.791 in BeBeNCCH3 and 0.966 in CNBeBeCH3. It is worth noting that the strength of the Be−Be bond in CNBeBeCH3 is just slightly weaker than the C–Be and N–Be bonds, the bond orders of which are 0.976 and 0.977, respectively.
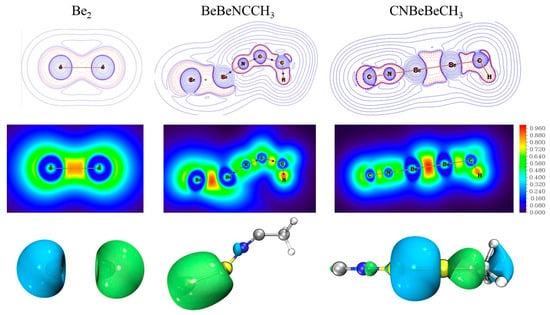
Figure 5.
Contour line diagrams of the Laplacian electronic density of the diberyllium products (first row). Blue dots stand for BCPs. The blue solid lines and red dotted lines correspond to values of ∇2ρ(r) > 0 and ∇2ρ(r) < 0, respectively; 2D Localized Orbital Locator (LOL) map of the diberyllium products (second row). The HOMO molecular orbitals involving the Be2 moiety (last row). The length unit is Bohr for Laplacian and LOL map.
For HBeCH2NC, the C−C and C–N bond distances are calculated to be 1.449 and 1.153 Å, respectively. After Be−H moiety transferring from CH2 to the N-end, the C−C bond is sizably shortened to 1.314 Å while the C−N bond is weakened (WBI from 2.923 to 1.924). The Wiberg bond order gives values of 0.985 and 1.825 for the C−C bonds of HBeCH2CN and HBeNCCH2, indicating single and double bonds, respectively.
4. Reaction Mechanism
The calculated reaction paths including energies of products and transition states at the CCSD(T)//B3LYP−D3/aug−cc−pVTZ level of theory are illustrated in Figure 6. The reactions of beryllium atoms with acetonitrile in excess neon can be divided into three separate paths. For all products both singlet and triplet states are considered; unless noted, the following discussion relates to the lower energy singlet state species.
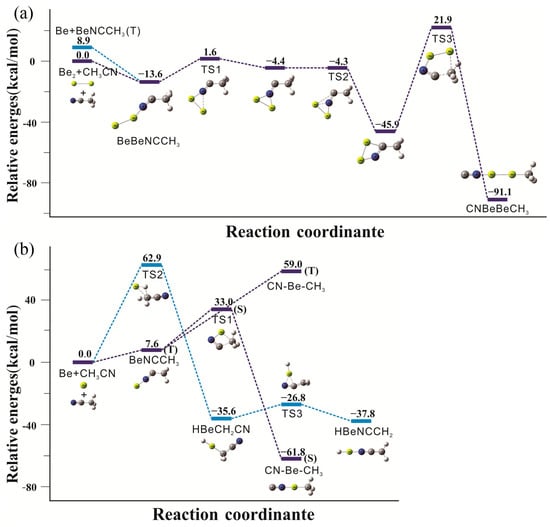
Figure 6.
Calculated reaction paths in relation to the reactants [Be/Be2 + CH3CN]. (a) diberyllium reaction paths; (b) mono beryllium reaction paths. Relative energies are given in kcal mol−1. S and T denote singlet and triplet electronic states, respectively.
The calculations indicate that beryllium dimer reacts with acetonitrile on co-deposition to form the initial structure, BeBeNCCH3. The diberyllium end-on complex is more stable in the singlet (1A’) electronic state by exothermic 13.6 kcal/mol. BeBeNCCH3 is also possible to be formed by adding another beryllium atom to the mono beryllium end-on complex in our experiments. The next step is both beryllium atoms bonding to the N atom to form a triangle intermediate (not observed), and an energetic barrier of 15.2 kcal/mol needs to be overcome. It later transfers to another energetically much lower cyclic intermediate via one beryllium atom bonding to the C atom by exothermic 45.9 kcal/mol. The infrared absorptions of this cyclic intermediate are calculated and showed in Table S7. Unfortunately, its main absorptions (1609.8, 1095.5 and 768.1 cm−1) are all close to the extremely strong bands of water or precursor, so we cannot make sure whether it existed in our experiment or not. The last energy barrier of insertion into the C−N bond is pretty high with 67.8 kcal/mol, and the most stable diberyllium product CNBeBeCH3 is finally generated.
For the mono beryllium reactions, calculations suggest that the initial end-on complex BeNCCH3 is more stable in the triplet state, and the laser power in our experiments is able to initiate this N-coordination process. The CNBeCH3 complex is calculated to be the global minimum for the mono beryllium products as 61.8 kcal/mol exothermic. The insertion process occurs in a single step involving the breaking of C−C bond and the formation of a new C−Be bond, which only requires to cross an energy barrier of 25.4 kcal/mol. The insertion reaction is also the primary reaction according to the strongest infrared absorptions of the product “4” after full arc irradiation. The C−H bond insertion products of acetonitrile in cryogenic matrix experiment were first observed in our experiment. The C−H insertion reaction proceeded with a high energetic cost of 62.9 kcal/mol, which was apparently supplied by photon energy during full arc photolysis, and in line with the experimental observation of HBeCH2CN and HBeNCCH2 only after full arc irradiation. The HBeCH2CN complex is found to be 35.6 kcal/mol more stable than the reactants. The next step involves a relatively low energy barrier of 8.8 kcal/mol to obtain the more stable product, HBeNCCH2, which is exothermic by 37.8 kcal/mol.
5. Experimental and Computational Methods
The experimental details in conjunction with matrix infrared spectroscopy investigation have been described previously [39,40,41,42]. Briefly, the Nd:YAG laser fundamental (1064 nm, 10 Hz repetition rate with 10 ns pulse width) was focused onto a rotating beryllium metal target (Alfa Aesar, Haverhill, MA, USA), and the ablated beryllium atoms were co-deposited with the gas mixture of neon and acetonitrile (Sinopharm Chemical Reagent Co., Ltd., Shanghai, China) onto a substrate (CsI) maintained at 4 K using a closed-cycle helium refrigerator (Sumitomo Heavy Industries Model RDK 205D, Tokyo, Japan) for normally 60 min. Matrix samples then were annealed and subjected to LED lights or a high-pressure mercury arc lamp (Philips, 175 W, Beijing, China) with the globe removed, and the products were confirmed by IR spectra recorded on a Bruker 80 V spectrometer in the range from 400 to 4000 cm−1 at 0.5 cm−1 resolution. The experiments were repeated using CD3CN (Sigma-Aldrich, St. Louis, MO, USA) and 13CH313CN (Cambridge Isotope Laboratories, Cambridge, Britain) samples to further confirm our assignment of the products.
Quantum chemical calculations were carried out using the Gaussian 09 software package [43]. The geometry optimization and frequency calculations were performed using the hybrid B3LYP [44,45] functional including Grimme’s D3-dispersion correction [46] with aug-cc-pVTZ [47,48] basis set employed for all atoms. The second-order vibrational perturbation theory (VPT2) was used to calculate the anharmonic values of the spectral parameters [49,50]. Geometries of products were reoptimized using the more strenuous CCSD method [51] and the single-point energy calculations were separately performed at the CCSD(T) [52,53,54]/aug-cc-pVTZ level with B3LYP-D3-optimized geometries. Bonding analyses were carried out considering Quantum Theory of Atoms in Molecules (AIM) [38], localized orbital locator (LOL) map [55] and Natural Bond Orbital (NBO) [56]. The AIM and LOL analyses were performed using Multiwfn code [57] and the NBO analysis was computed using the NBO 3.1 program. The Multiwfn and VMD [58] programs were applied for plots of HOMO molecular orbitals. The energy decomposition analysis (EDA) [59,60] combined with the natural orbital for chemical valence (NOCV) theory [61,62] was performed using the ADF 2020.101 program packages to analyze the interaction nature of the bonding fragments [63,64]. Uncontracted triple-ζ Slatertype orbital (STO) basis sets plus two sets of polarization functions (TZ2P) [65] were used for all elements. The scalar relativistic effects were included via the zeroth-order regular approximation (ZORA) Hamiltonian [66].
6. Conclusions
Beryllium atom reactions with CH3CN give six new products. The diberyllium complexes BeBeNCCH3 and CNBeBeCH3 were found to be 30 kcal/mol more exothermic than the mono beryllium products because of the formation of the Be−Be single bonds. The calculated binding energies of the Be–Be bonds are −27.1 and −77.2 kcal/mol for BeBeNCCH3 and CNBeBeCH3 at CCSD(T)/aug−cc−pVTZ level of theory, respectively. In spite of the fact that Be is an electron-deficient element, the Be2 moiety shows a distinct cationic character and the electron transfer from Be2 antibonding orbitals to the bonding fragments strengthens the Be−Be bonds. AIM, LOL and NBO analyses confirm the existence of the covalent Be−Be bonds. EDA-NOCV analysis demonstrates clearly that the CNBeBeCH3 complex can be seen as a result of the interaction between Be22+ and (H3C···NC)2− anions. The bonding interactions between Be and N atoms are identified as covalent polar bonds because of the coexisting ionic and covalent characters from AIM analyses. Lower yields of HBeCH2CN and HBeNCCH2 have also been observed after full arc irradiation, and the double C=C and C=N bonds are formed after Be−H moiety transferring from CH2 to the N-end. Finally, we hope the present study can further extend knowledge of the reactions and bonding investigations of beryllium complexes, and attract further theoretical and experimental research about beryllium chemistry.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules29010177/s1, Figure S1: The Spin Density Plots of BeNCCH3 at the B3LYP−D3/aug−cc−pVTZ Level of Theory. Figure S2: Selected frontier molecular orbitals of CNBeBeCH3 calculated at B3LYP−D3/aug−cc−pVTZ level of theory. Figure S3: Contour line diagrams of the Laplacian of the electronic density of the mono beryllium products. Figure S4: 2D Localized Orbital Locator (LOL) map of the mono beryllium products. Table S1: Observed and Calculated Fundamental Frequencies of BeBeNCCH3 Isotopomers in the Ground 3A’ State. Table S2: Observed and Calculated Fundamental Frequencies of BeNCCH3 Isotopomers in the Ground 3A1 State. Table S3: Observed and Calculated Fundamental Frequencies of CNBeBeCH3 Isotopomers in the Ground 1A1 State. Table S4: Observed and Calculated Fundamental Frequencies of CNBeCH3 Isotopomers in the Ground 1A1 State. Table S5: Observed and Calculated Fundamental Frequencies of HBeCH2CN Isotopomers in the Ground 1A’ State. Table S6: Observed and Calculated Fundamental Frequencies of HBeNCCH2 Isotopomers in the Ground 1A1 State. Table S7: Calculated Fundamental Frequencies of the cyclic intermediate in the Ground 1A1 State. Table S8: NBO Analysis of Products Using the B3LYP−D3/aug−cc−pVTZ Level of Theory. Table S9: EDA-NOCV Results at the B3LYP/TZ2P/ZORA Level of Theory for CNBeBeCH3. Table S10: AIM Analysis of BeN, BeC and BeBe bonds in Products.
Author Contributions
Conceptualization, F.C. and X.W.; methodology, F.C. and X.W.; software, Z.P. and X.W.; validation, F.C., J.C. and L.C.; formal analysis, X.W.; investigation, F.C.; resources, X.W. data curation, F.C.; writing—original draft preparation, F.C.; writing—review and editing, F.C., Z.P. and X.W.; visualization, X.W.; supervision, X.W.; project administration, X.W.; funding acquisition, National Natural Science Foundation of China. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number No. 22273066.
Data Availability Statement
Data are contained within the article and supplementary materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, S.; Jana, G.; Saha, R.; Zhao, L.L.; Chattaraj, P.K. Intriguing structural, bonding and reactivity features in some beryllium containing complexes. Phys. Chem. Chem. Phys. 2020, 22, 27476–27495. [Google Scholar] [CrossRef] [PubMed]
- Dutton, J.L.; Frenking, G. New Avenues in s-Block Chemistry: Beryllium(0) Complexes. Angew. Chem. Int. Ed. 2016, 55, 13380–13382. [Google Scholar] [CrossRef] [PubMed]
- Sutton, M.; Burastero, S.R. Beryllium chemical speciation in elemental human biological fluids. Chem. Res. Toxicol. 2003, 16, 1145–1154. [Google Scholar] [CrossRef] [PubMed]
- Puchta, R. A brighter beryllium. Nat. Chem. 2011, 3, 416. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.X.; Zhao, X.F.; Wu, Y.B.; Wang, X.T. Ultrashort Beryllium-Beryllium Distances Rivalling Those of Metal-Metal Quintuple Bonds Between Transition Metals. Angew. Chem. Int. Ed. 2016, 55, 15651–15655. [Google Scholar] [CrossRef] [PubMed]
- Kalemos, A. The nature of the chemical bond in Be2+, Be2, Be2−, and Be3. J. Chem. Phys. 2016, 145, 214302. [Google Scholar] [CrossRef]
- Zhang, Q.N.; Li, W.L.; Zhao, L.L.; Chen, M.H.; Zhou, M.F.; Li, J.; Frenking, G. A Very Short Be-Be Distance but No Bond: Synthesis and Bonding Analysis of Ng-Be2O2-Ng’ (Ng, Ng’ = Ne, Ar, Kr, Xe). Chem.-Eur. J. 2017, 23, 2035–2039. [Google Scholar] [CrossRef]
- Patkowski, K.; Spirko, V.; Szalewicz, K. On the Elusive Twelfth Vibrational State of Beryllium Dimer. Science 2009, 326, 1382–1384. [Google Scholar] [CrossRef]
- Merritt, J.M.; Bondybey, V.E.; Heaven, M.C. Beryllium Dimer-Caught in the Act of Bonding. Science 2009, 324, 1548–1551. [Google Scholar] [CrossRef]
- Bondybey, V.E. Electronic-Structure and Bonding of Be2. Chem. Phys. Lett. 1984, 109, 436–441. [Google Scholar] [CrossRef]
- Qin, Z.Z.; Wang, Q.; Yuan, C.X.; Yang, Y.T.; Zhao, X.F.; Li, D.B.; Liu, P.; Wu, Y.B. Combining covalent bonding and electrostatic attraction to achieve highly viable species with ultrashort beryllium-beryllium distances: A computational design. Dalton Trans. 2018, 47, 4707–4713. [Google Scholar] [CrossRef] [PubMed]
- Nijesh, K.; De, S.; Parameswaran, P. Homopolar dihydrogen bonding in ligand stabilized diberyllium hydride complexes, Be2(CH3)2H2L2 (L = H−, CO, N-heterocyclic carbene and CN−). Dalton Trans. 2016, 45, 7836–7846. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.N.; Jerabek, P.; Chen, M.H.; Zhou, M.; Frenking, G. The Oxygen-Rich Beryllium Oxides BeO4 and BeO6. Angew. Chem. Int. Ed. 2016, 55, 10863–10867. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.; Tague, T.J.; Kushto, G.P.; Davy, R.D. Infrared-Spectra of Beryllium Carbonyls from Reactions of Beryllium Atoms with Carbon-Monoxide in Solid Argon. Inorg. Chem. 1995, 34, 2952–2961. [Google Scholar] [CrossRef]
- Liu, X.M.; Zhang, M.; Yu, S.; Geng, Y.; Zhang, X.X.; Ding, Y.H.; Su, Z.M. Beryllium-beryllium double-pi bonds in the octahedral cluster of Be2(μ2-X)4 (X = Li, Cu, BeF). Phys. Chem. Chem. Phys. 2018, 20, 23898–23902. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.H.; Yang, W.S.; Zhao, L.L.; Ding, Y.H.; Frenking, G. Unusually Short Be-Be Distances with and without a Bond in Be2F2 and in the Molecular Discuses Be2B8 and Be2B7−. Angew. Chem. Int. Ed. 2016, 55, 7841–7846. [Google Scholar] [CrossRef]
- Brea, O.; Corral, I. Super Strong Be−Be Bonds: Theoretical Insight into the Electronic Structure of Be-Be Complexes with Radical Ligands. J. Phys. Chem. A 2018, 122, 2258–2265. [Google Scholar] [CrossRef]
- Boronski, J.T.; Crumpton, A.E.; Wales, L.L.; Aldridge, S. Diberyllocene, a stable compound of Be(I) with a Be-Be bond. Science 2023, 380, 1147–1149. [Google Scholar] [CrossRef]
- West, T. The elusive Be–Be bond. Nat. Synth 2023, 2, 696. [Google Scholar] [CrossRef]
- Li, X.Y.; Huo, S.H.; Zeng, Y.L.; Sun, Z.; Zheng, S.J.; Meng, L.P. Metal-Metal and Metal-Ligand Bonds in (η5-C5H5)2M2 (M = Be, Mg, Ca, Ni, Cu, Zn). Organometallics 2013, 32, 1060–1066. [Google Scholar] [CrossRef]
- Wu, S.L.; Su, J.H.; Lu, Y.; Chen, B.W.; Huang, C.Y.; Wen, Z.H.; Kuo, Y.H.; Sheu, J.H. Simplexins J-O, Eunicellin-Based Diterpenoids from a Dongsha Atoll Soft Coral Klyxum simplex. B Chem. Soc. Jpn. 2011, 84, 626–632. [Google Scholar] [CrossRef]
- Vos, E.; Montero-Campillo, M.M.; Corral, I.; Yanez, M.; Alkorta, I.; Elguero, J. From Very Strong to Inexistent Be-Be Bonds in the Interactions of Be2 with pi-Systems. ChemPhysChem 2020, 21, 2701–2708. [Google Scholar] [CrossRef] [PubMed]
- Rezaie, F.; Noorizadeh, S. Strong Be-Be bonds in double-aromatic bridged Be2(μ-SO) molecules. Dalton Trans. 2022, 51, 12596–12603. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.M.; Zhang, M.; Zhong, R.L.; Wu, S.X.; Liu, Y.Y.; Geng, Y.; Su, Z.M. Computational Study of spx(x = 1–3)-Hybridized Be-Be Bonds Stabilized by Amidinate Ligands. Chem.-Eur. J. 2020, 26, 10891–10895. [Google Scholar] [CrossRef] [PubMed]
- Sarmah, K.; Kalita, A.J.; Guha, A.K. A theoretical investigation of Zn-Zn and Be-Be one electron bond. Int. J. Quantum Chem. 2023, 123, e27006. [Google Scholar] [CrossRef]
- Rohman, S.S.; Kashyap, C.; Ullah, S.S.; Guha, A.K.; Mazumder, L.J.; Sharma, P.K. Ultra-Weak Metal-Metal Bonding: Is There a Beryllium-Beryllium Triple Bond? ChemPhysChem 2019, 20, 516–518. [Google Scholar] [CrossRef]
- Liu, X.M.; Zhong, R.L.; Zhang, M.; Wu, S.X.; Geng, Y.; Su, Z.M. Be≡Be triple bond in Be2X4Y2 clusters (X = Li, Na and Y = Li, Na, K) and a perfect classical Be≡Be triple bond presented in Be2Na4K2. Dalton Trans. 2019, 48, 14590–14594. [Google Scholar] [CrossRef]
- Saha, R.; Pan, S.; Merino, G.; Chattaraj, P.K. Unprecedented Bonding Situation in Viable E2(NHBMe)2 (E=Be, Mg; NHBMe=(HCNMe)2B) Complexes: Neutral E2 Forms a Single E-E Covalent Bond. Angew. Chem. Int. Ed. 2019, 58, 8372–8377. [Google Scholar] [CrossRef]
- Couchman, S.A.; Holzmann, N.; Frenking, G.; Wilson, D.J.D.; Dutton, J.L. Beryllium chemistry the safe way: A theoretical evaluation of low oxidation state beryllium compounds. Dalton Trans. 2013, 42, 11375–11384. [Google Scholar] [CrossRef]
- Cho, H.G.; Andrews, L. Infrared spectra and density functional calculations of the M←NCCCH3, M-η2-(NC)-CH3, CH3-MNC, CH2=M(H)NC, and CH≡M(H)2NC complexes produced by reactions of Group 6 metal atoms with acetonitrile. J. Organomet. Chem. 2012, 703, 25–33. [Google Scholar] [CrossRef]
- Cho, H.G.; Andrews, L. IR Spectra and DFT Calculations of M-η2-(NC)-CH3, CH3-MNC, and CH2=M(H)NC Prepared by Reactions of Laser-Ablated Hf and Ti Atoms with Acetonitrile. Eur. J. Inorg. Chem. 2015, 2015, 4379–4387. [Google Scholar] [CrossRef]
- Cho, H.G.; Andrews, L. Infrared Spectra of the Complexes Os←NCCH3, Re←NCCH3, CH3-ReNC, CH2=Re(H)NC, and CH≡Re(H)2NC and their Mn Counterparts Prepared by Reactions of Laser-Ablated Os, Re, and Mn Atoms with Acetonitrile in Excess Argon. Organometallics 2012, 31, 6095–6105. [Google Scholar] [CrossRef]
- Cho, H.G.; Andrews, L. Infrared Spectra of CH2=M(H)NC, CH3-MNC, and M-η2-(NC)-CH3 Produced by Reactions of Laser-Ablated Group 5 Metal Atoms with Acetonitrile. J. Phys. Chem. A 2010, 114, 5997–6006. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.G.; Andrews, L. Infrared Spectra of CH2=Zr(H)NC, CH3-ZrNC, and Zr-η2-(NC)-CH3 Produced by Reactions of Laser-Ablated Zr Atoms with Acetonitrile. J. Phys. Chem. A 2010, 114, 891–897. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.G.; Andrews, L. Infrared Spectra of CH3CN→M, M-η2-(NC)-CH3, CH3-MNC Prepared by Reactions of Laser-Ablated Fe, Ru, and Pt Atoms with Acetonitrile in Excess Argon. Inorg. Chem. 2019, 58, 16194–16204. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.G.; Andrews, L. Infrared Spectra of the M-η2-(NC)-CH3, CH3-MNC, and CH2=M(H)NC Complexes Prepared by Reactions of Thorium and Uranium Atoms with Acetonitrile. Organometallics 2012, 31, 535–544. [Google Scholar] [CrossRef]
- Cong, F.; Cheng, J.J.; Cho, H.G.; Huang, T.F.; Wang, X.F.; Andrews, L. M←NCCH3, M-η2-(NC)-CH3, and CN−M-CH3 Prepared by Reactions of Ce, Sm, Eu, and Lu Atoms with Acetonitrile: Matrix Infrared Spectra and Theoretical Calculations. Inorg. Chem. 2021, 60, 17649–17656. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Cong, F.; Cai, L.Y.; Cheng, J.J.; Wang, X.F.; Andrews, L. Boron-Mediated C-C and C-N Bond Cleavage of Acetonitrile: Matrix Infrared Spectra and Theoretical Calculations. Organometallics 2023, 42, 995–1004. [Google Scholar] [CrossRef]
- Huang, T.F.; Yu, W.J.; Cheng, J.J.; Cong, F.; Xu, B.; Wang, X.F. CO2 activation by ligand-free manganese hydrides in a parahydrogen matrix. Chem. Commun. 2021, 57, 2301–2304. [Google Scholar] [CrossRef]
- Xu, B.; Beckers, H.; Ye, H.Y.; Lu, Y.; Cheng, J.J.; Wang, X.F.; Riedel, S. Cleavage of the N≡N Triple Bond and Unpredicted Formation of the Cyclic 1,3-Diaza-2,4-Diborete (FB)2N2 from N2 and Fluoroborylene BF. Angew. Chem. Int. Ed. 2021, 60, 17205–17210. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.J.; Cai, L.Y.; Cong, F.; Qiu, R.Z.; Pan, C.W.; Xu, B.; Wang, X.F. Complex with Linear B-B-B Skeleton Trapped in Dinitrogen Matrix: Matrix Infrared Spectra and Quantum Chemical Calculations. Inorg. Chem. 2023, 62, 6314–6322. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. 3. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations. 1. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron-Affinities of the 1st-Row Atoms Revisited—Systematic Basis-Sets and Wave-Functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Bloino, J. A VPT2 Route to Near-Infrared Spectroscopy: The Role of Mechanical and Electrical Anharmonicity. J. Phys. Chem. A 2015, 119, 5269–5287. [Google Scholar] [CrossRef]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Schaefer, H.F. The Unimolecular Triple Dissociation of Glyoxal—Transition-State Structures Optimized by Configuration-Interaction and Coupled Cluster-Methods. J. Am. Chem. Soc. 1989, 111, 7761–7765. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musial, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Headgordon, M. A 5th-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Purvis, G.D.; Bartlett, R.J. A Full Coupled-Cluster Singles and Doubles Model—The Inclusion of Disconnected Triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Schmider, H.L.; Becke, A.D. Chemical content of the kinetic energy density. J. Mol. Struc. THEOCHEM 2000, 527, 51–61. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Zhao, L.L.; von Hopffgarten, M.; Andrada, D.M.; Frenking, G. Energy decomposition analysis. Wires Comput. Mol. Sci. 2018, 8, e1345. [Google Scholar] [CrossRef]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A. Natural orbitals for chemical valence as descriptors of chemical bonding in transition metal complexes. J. Mol. Model 2007, 13, 347–355. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A. Applications of natural orbitals for chemical valence in a description of bonding in conjugated molecules. J. Mol. Model 2008, 14, 681–687. [Google Scholar] [CrossRef] [PubMed]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Guerra, C.F.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ziegler, T.; Autschbach, J.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; Cavallo, L.; Chong, D.P.; et al. ADF2020.101, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands 2020. Available online: http://www.scm.com (accessed on 1 June 2023).
- Van Lenthe, E.; Baerends, E.J. Optimized slater-type basis sets for the elements 1-118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-Component Hamiltonians Relativistic Regular Two Component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).