The Effect of Crude Oil Stripped by Surfactant Action and Fluid Free Motion Characteristics in Porous Medium
Abstract
1. Introduction
2. Results and Discussion
2.1. Motion Characteristics of Crude Oil in Porous Medium under Spontaneous Imbibition
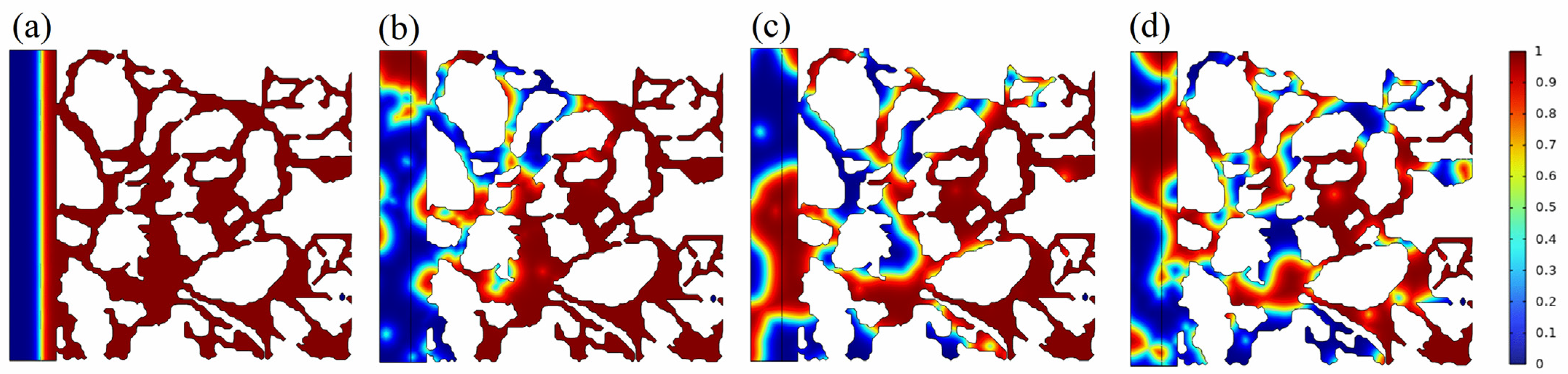
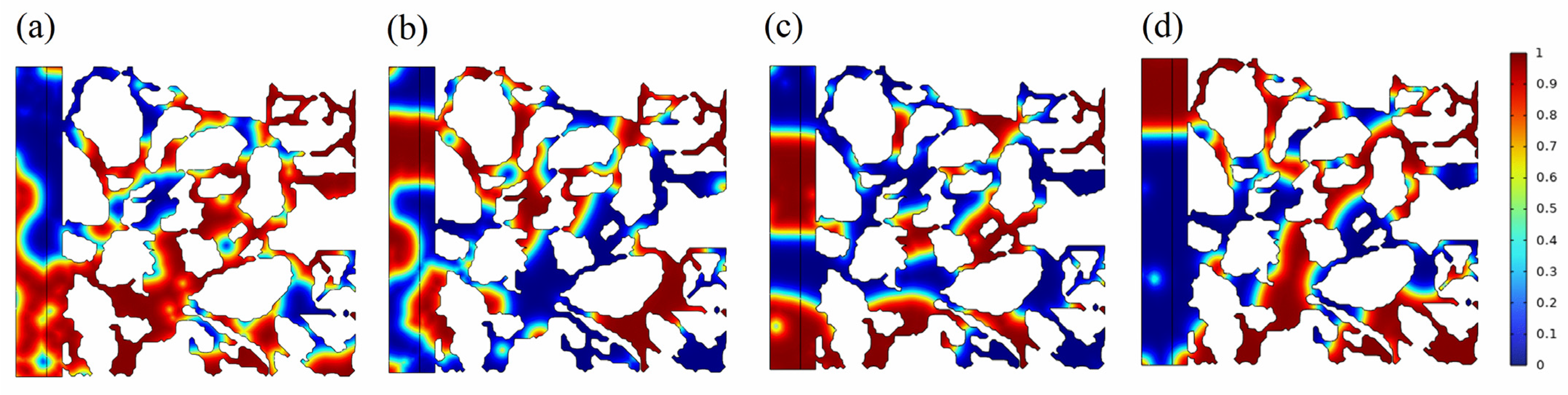
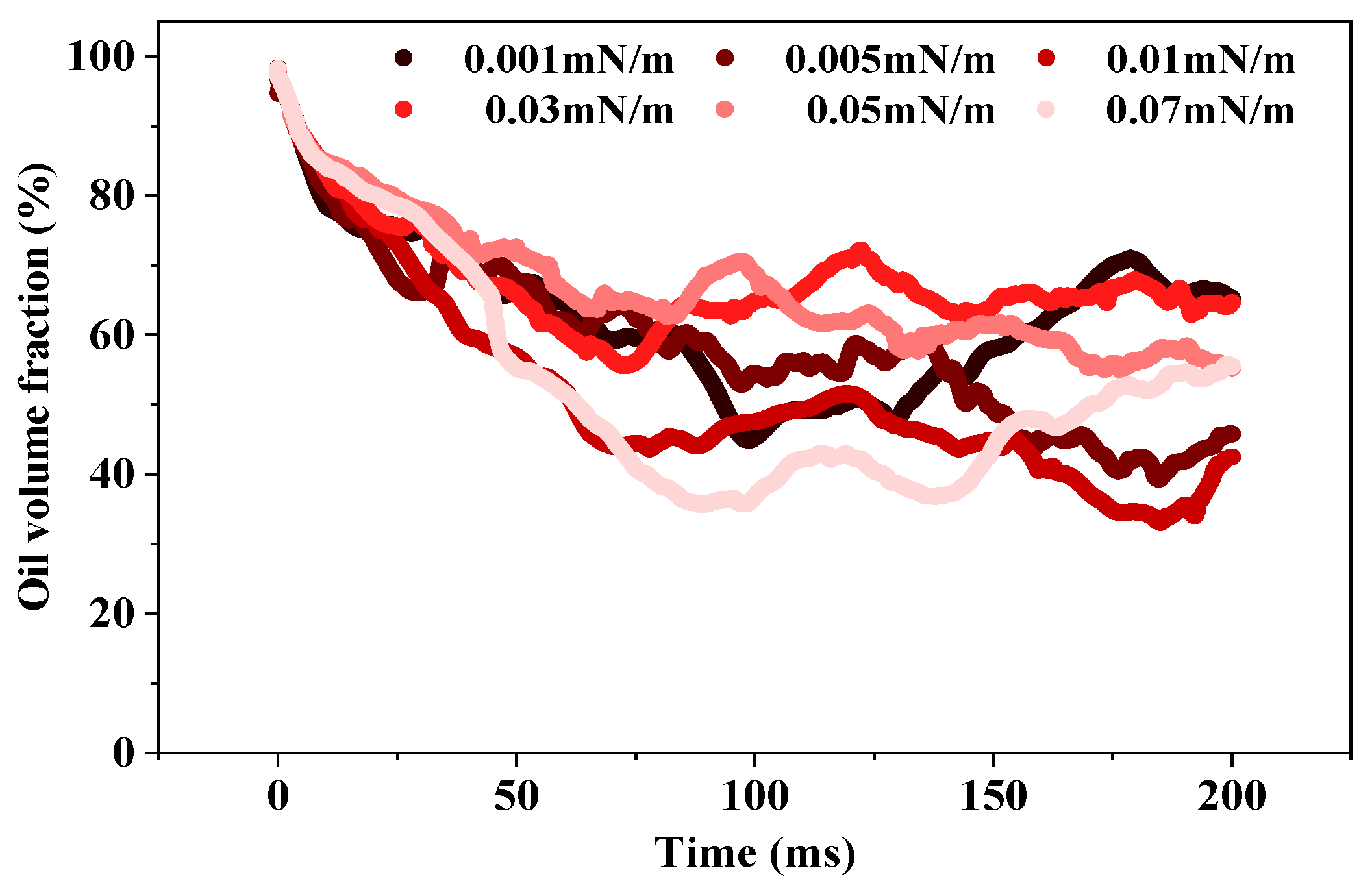
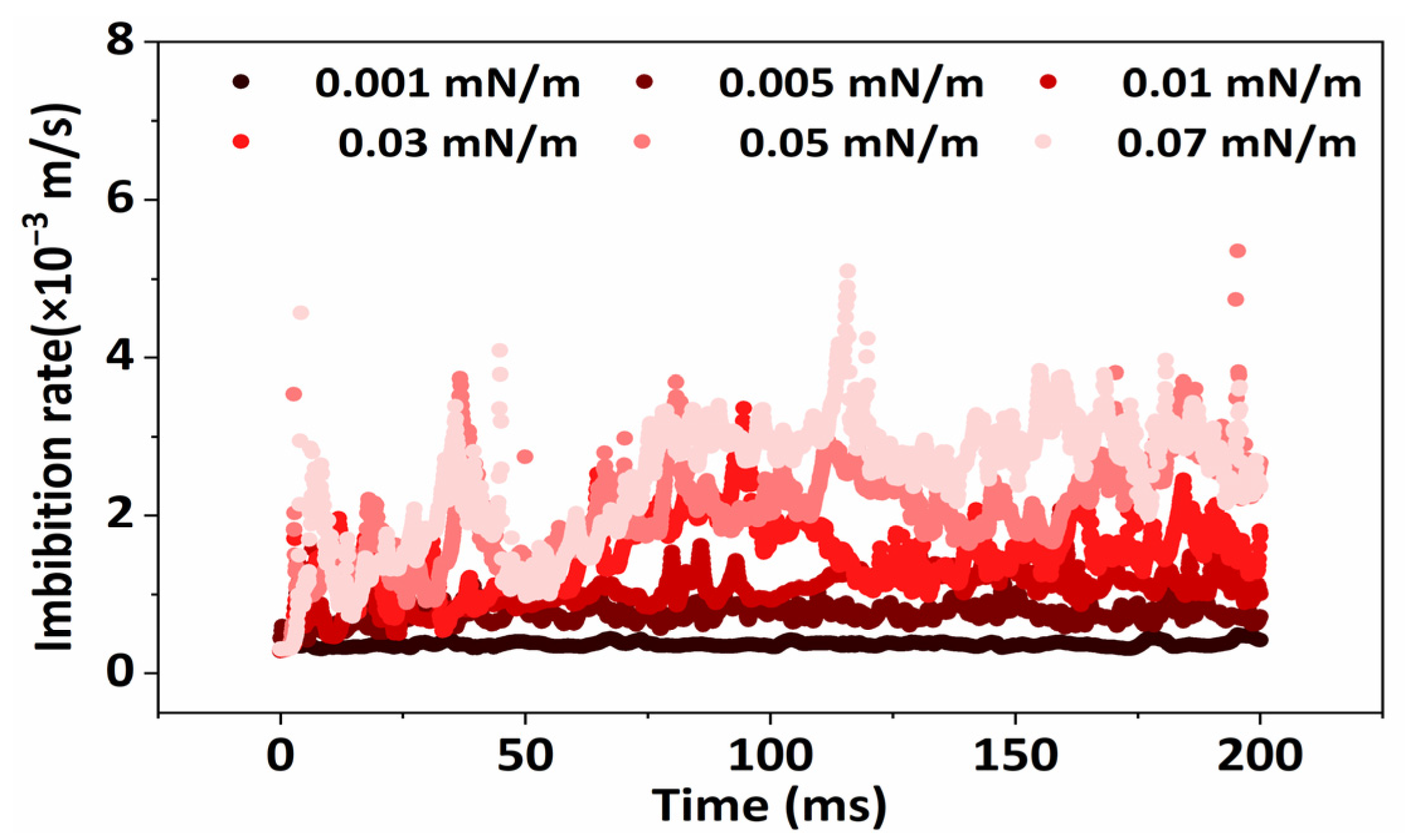
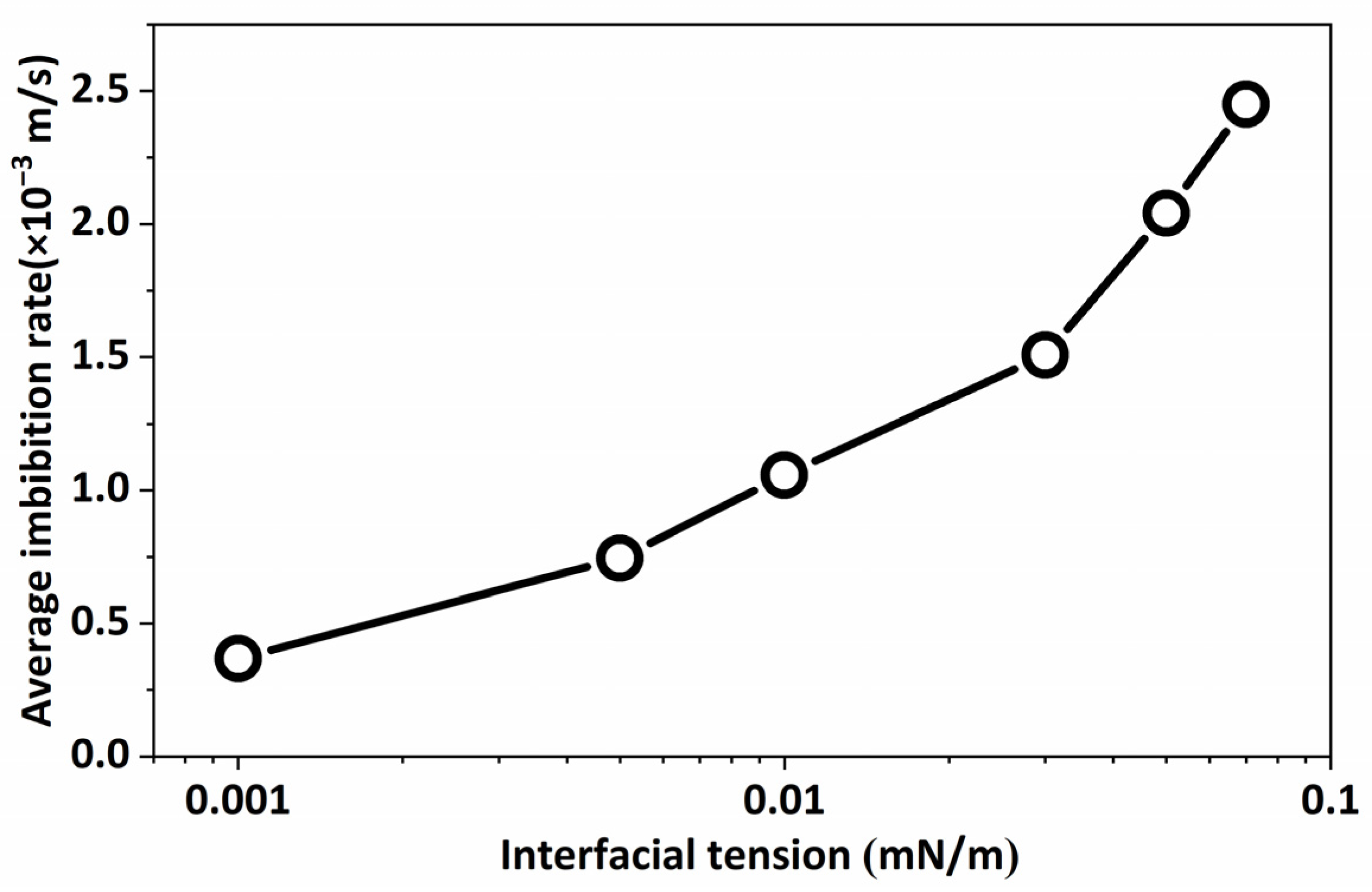
2.1.1. Effect of Interfacial Tension on Crude Oil Flow
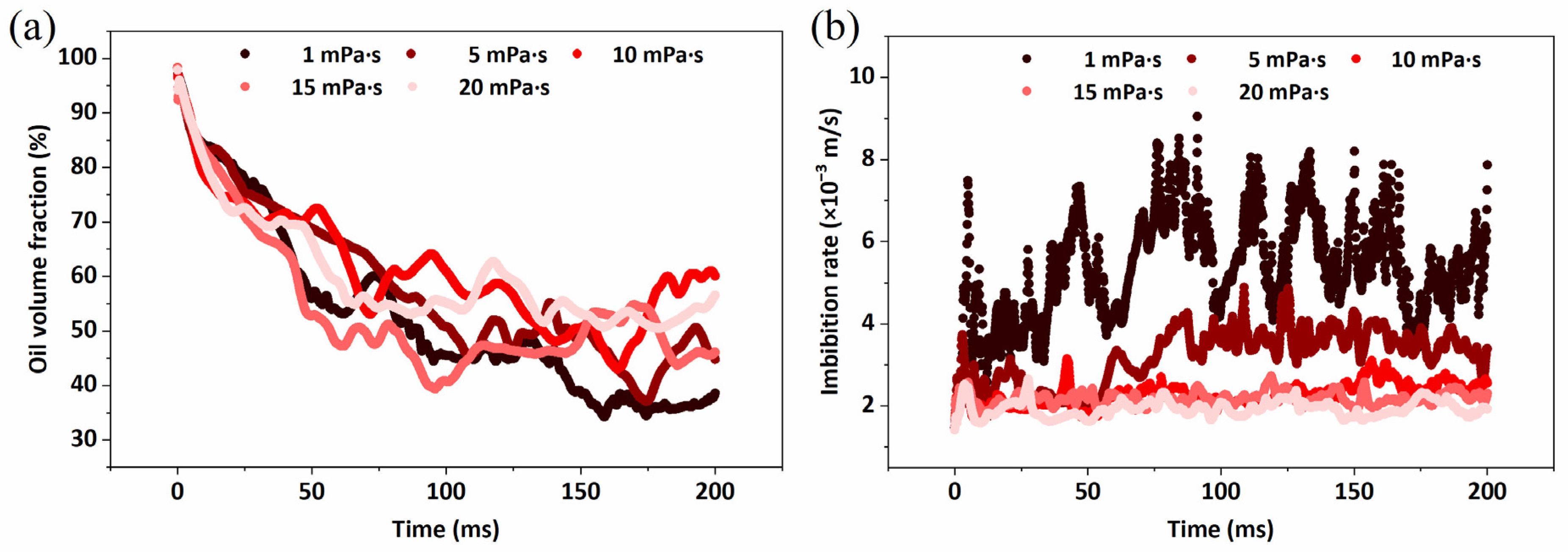
2.1.2. Effect of Viscosity on Crude Oil Flow
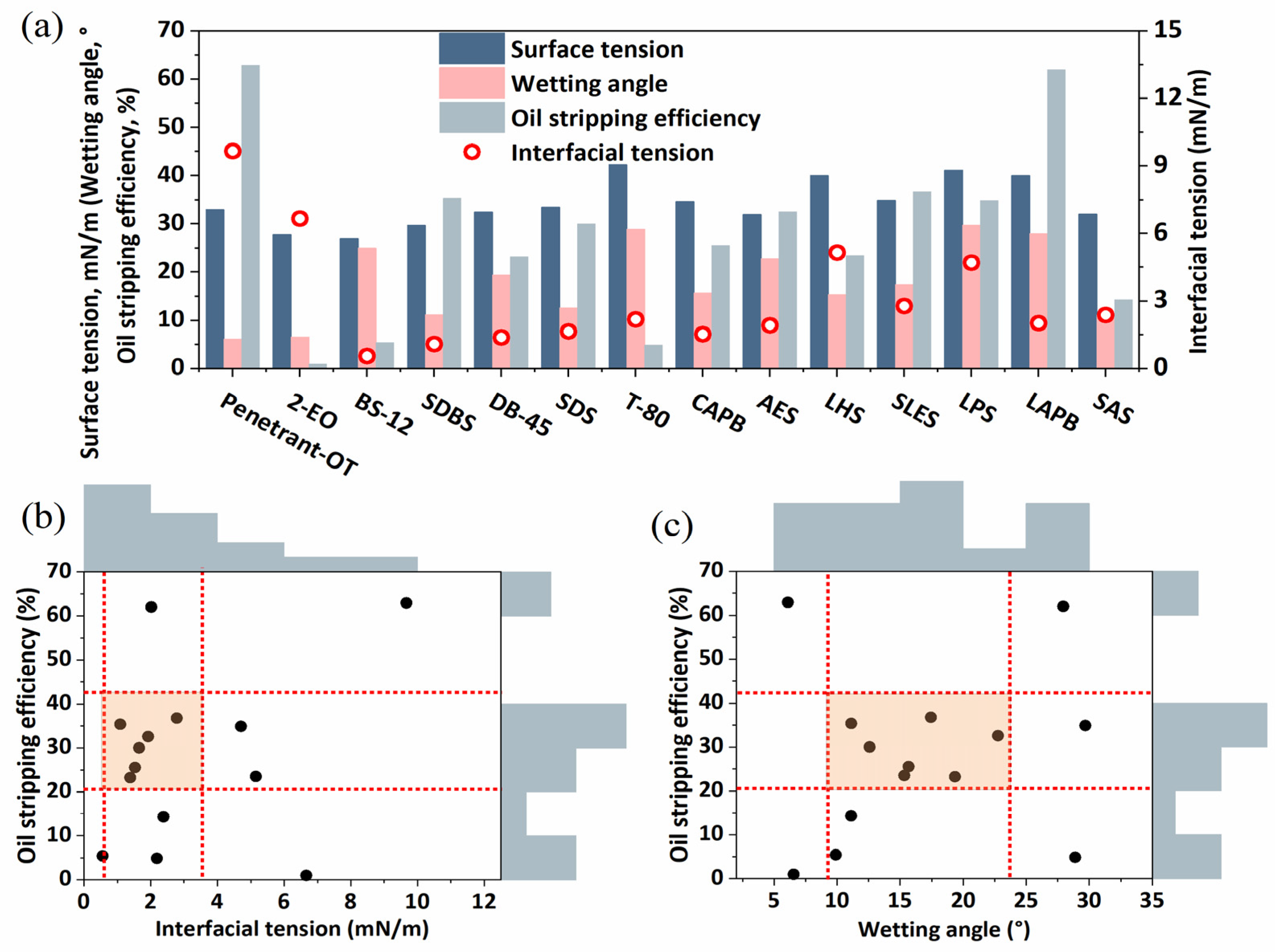
2.2. Factors Affecting Stripping Efficiency of Crude Oil
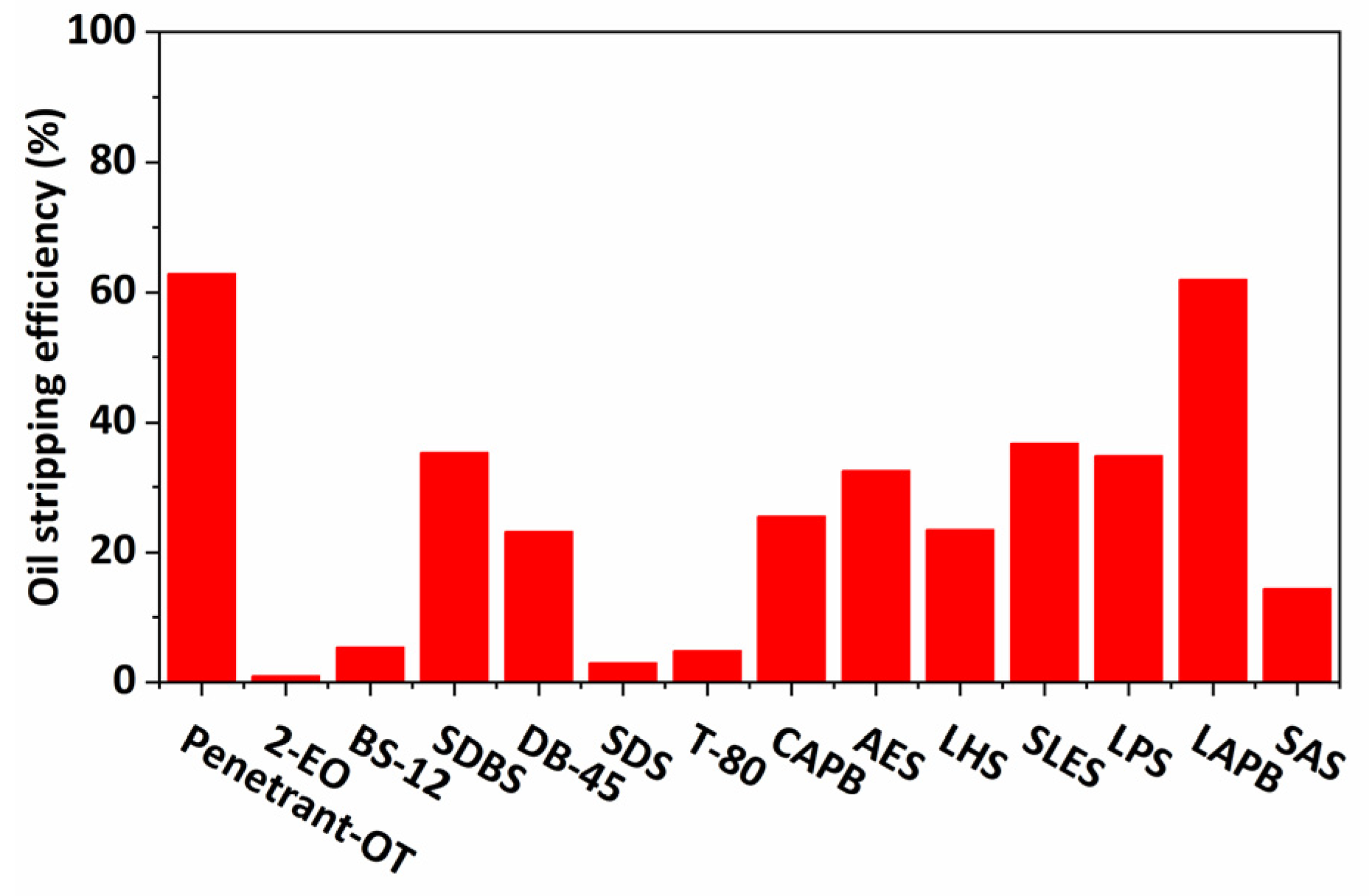
2.2.1. Effect of Surfactant Types on Oil-Stripping Efficiency
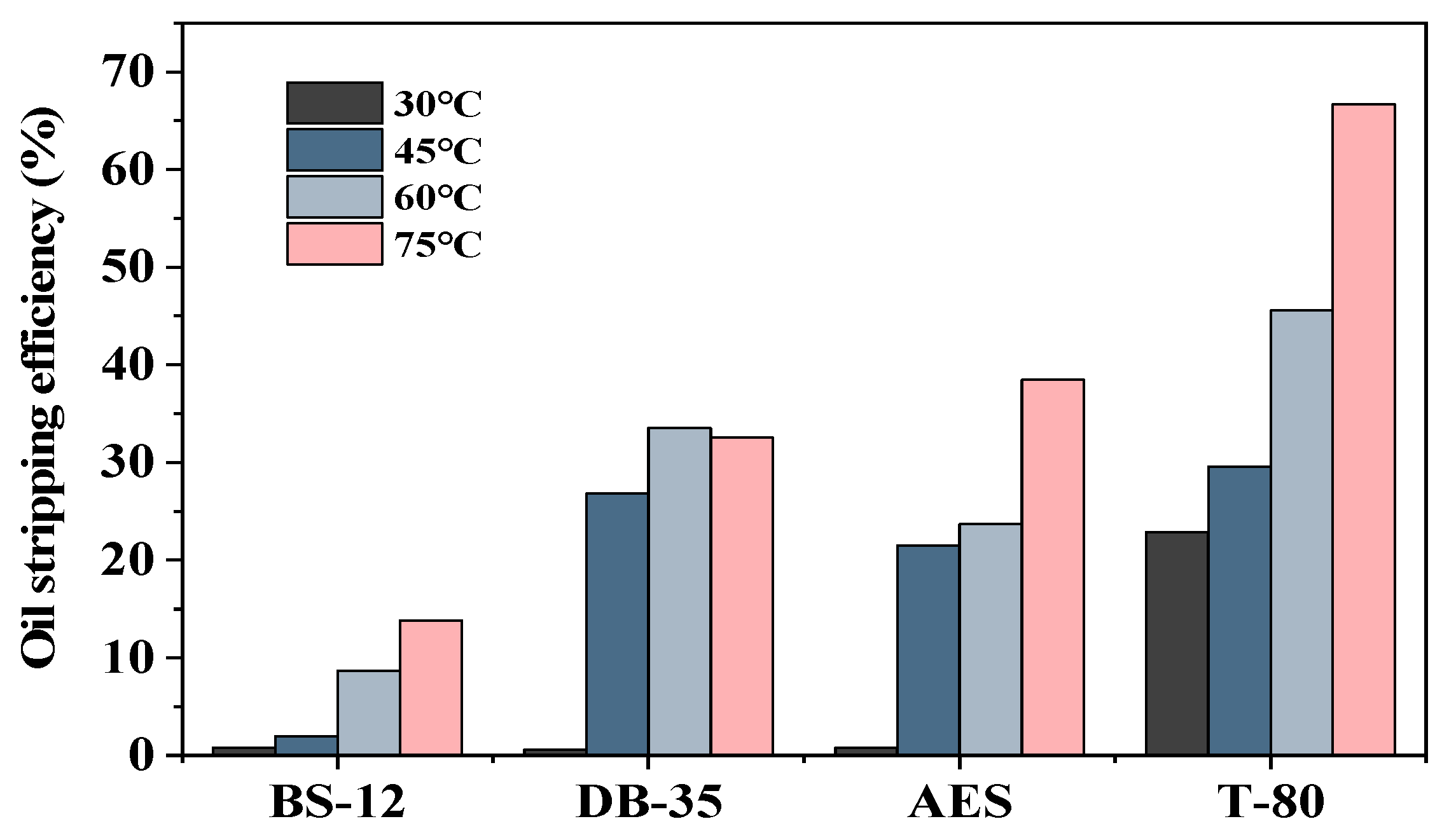
2.2.2. Effect of Temperature on Oil-Stripping Efficiency
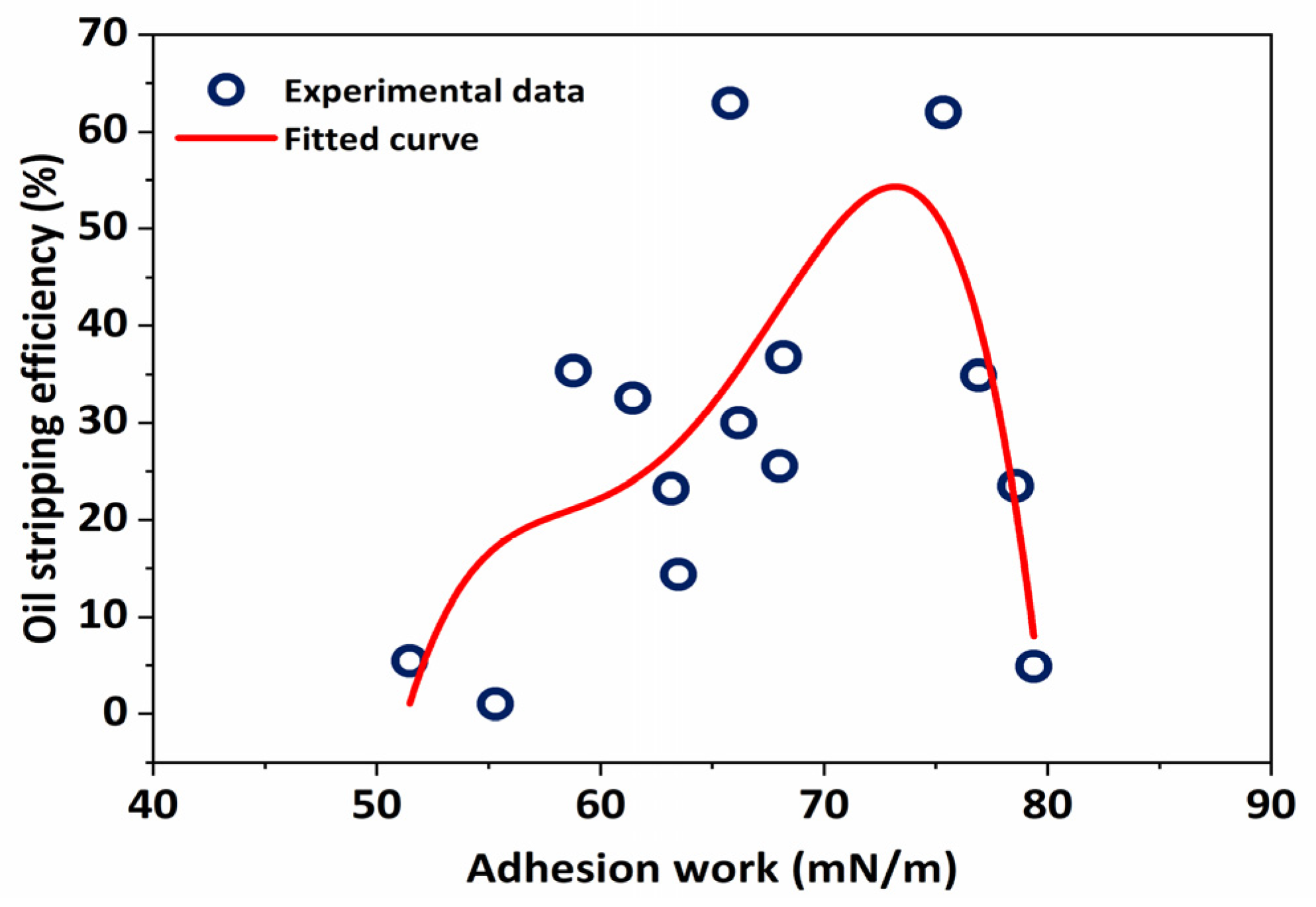
2.2.3. Effect of Fluid–Rock Interface Properties on Oil Stripping Efficiency
3. Theory and Experiment
3.1. Theory
- Fluid flow does not involve heat transfer;
- The viscosity of the oil and water remains constant during the flow;
- The rock surface is required to not adsorb the fluid;
- The effect of the surfactant structure on the interfacial tension between oil and water is not taken into account.
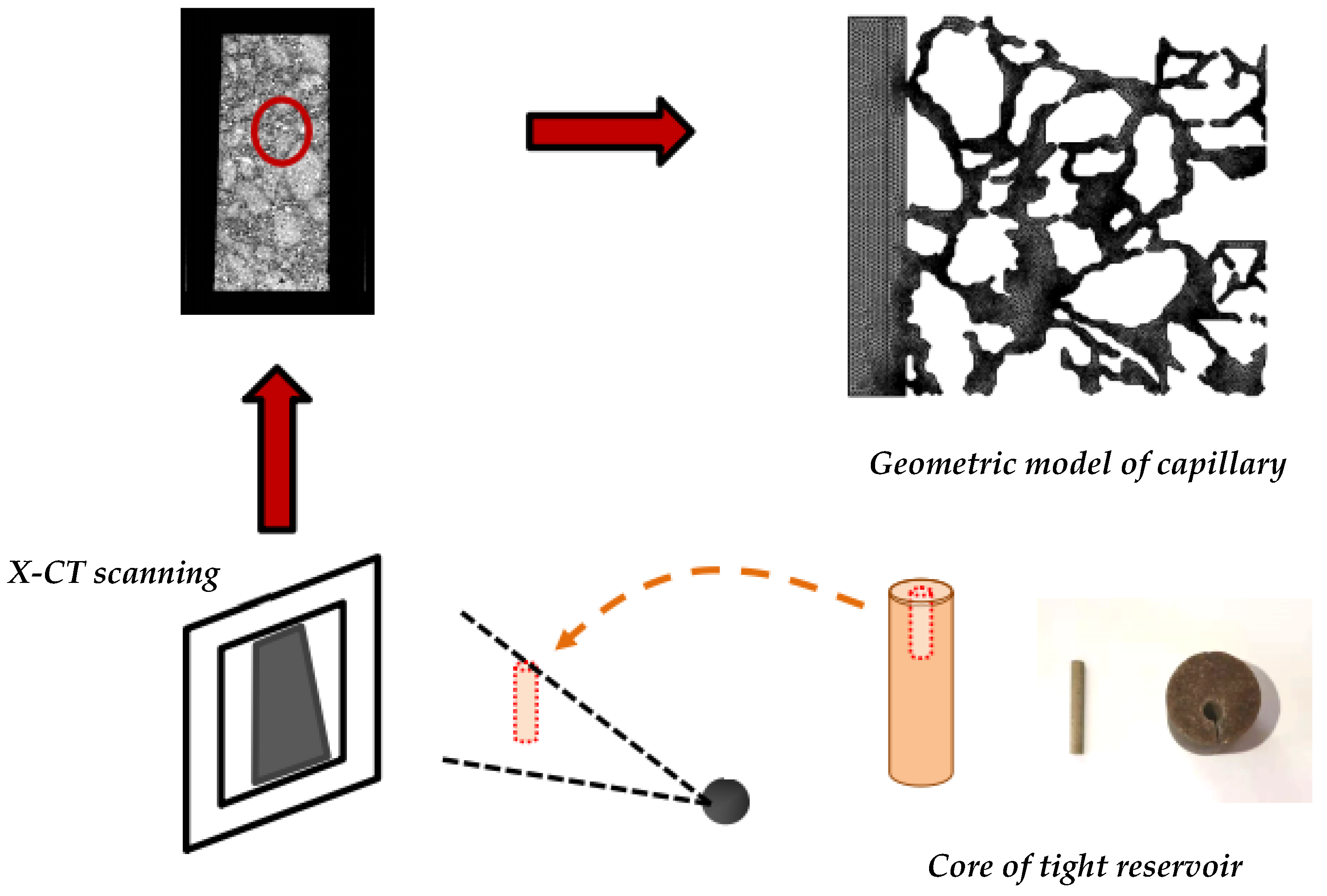
3.2. Experiment
3.2.1. Materials and Reagents
3.2.2. Oil-Stripping Efficiency Experiment
- (1)
- Quartz sand was combined in a 1:6 ratios with crude oil and aged for 24 h at 60 °C;
- (2)
- Deionized water was combined with the surfactant solution, which had a mass concentration of 0.2%;
- (3)
- The centrifuge tube was filled with the oil sand (m1 = 15 g), and the surfactant was added at a mass ratio of 1:2 to the oil sand. The samples were placed in a centrifuge, which compressed the oil sand and produced the effect of a static stripping test;
- (4)
- Once the oil sand was filtered through the centrifuge tube in Step 3, it was encased and desiccated for a duration of 24 h in an oven;
- (5)
- In step 4, the oil sand was weighed, and Equation (5) was used to determine the oil-stripping efficiency.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamal, M.S.; Hussein, I.A.; Sultan, A.S. Review on surfactant flooding: Phase behavior, retention, IFT, and field applications. Energy Fuels 2017, 31, 7701–7720. [Google Scholar] [CrossRef]
- Hirasaki, G.; Miller, C.A.; Puerto, M.; Puerto, M. Recent advances in surfactant EOR. SPE J. 2011, 16, 889–907. [Google Scholar] [CrossRef]
- Olatunji, K.; Zhang, J.; Wang, D.M. Effect of the rock dimension on surfactant imbibition rate in the Middle Member of Bakken: Creating a model for frac design. J. Pet. Sci. Eng. 2018, 169, 416–420. [Google Scholar] [CrossRef]
- Xu, D.R.; Li, Z.; Bai, B.J.; Chen, X.; Wu, H.R.; Hou, J.R.; Kang, W.L. A systematic research on spontaneous imbibition of surfactant solutions for low permeability sandstone reservoirs. J. Pet. Sci. Eng. 2021, 206, 109003. [Google Scholar] [CrossRef]
- Kumar, A.; Mandal, A. Critical investigation of zwitterionic surfactant for enhanced oil recovery from both sandstone and carbonate reservoirs: Adsorption, wettability alteration and imbibition studies. Chem. Eng. Sci. 2019, 209, 115222. [Google Scholar] [CrossRef]
- Kumar, N.; Mandal, A. Wettability alteration of sandstone rock by surfactant stabilized nanoemulsion for enhanced oil recovery—A mechanistic study. Colloids Surf. A 2020, 601, 125043. [Google Scholar] [CrossRef]
- Cao, G.; Cheng, Q.; Liu, Y.; Bu, R.; Zhang, N.; Wang, P. Influencing factors of surfactant stripping crude oil and spontaneous imbibition mechanism of surfactants in a tight reservoir. ACS Omega 2022, 7, 19010–19020. [Google Scholar] [CrossRef]
- Liang, T.B.; Zhou, F.J.; Lu, J. Evaluation of wettability alteration and IFT reduction on mitigating water blocking for low-permeability oil-wet rocks after hydraulic fracturing. Fuel 2017, 209, 650–660. [Google Scholar] [CrossRef]
- Cheng, Z.; Ning, Z.; Yu, X.; Wang, Q.; Zhang, W. New insights into spontaneous imbibition in tight oil sandstones with NMR. J. Pet. Sci. Eng. 2019, 179, 455–464. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, Y.; Wu, Y.; Dai, C.; Gao, M.; Yan, R.; Guo, X. Enhanced oil recovery mechanism by surfactant-silica nanoparticles imbibition in ultra-low permeability reservoirs. J. Mol. Liq. 2022, 348, 118010. [Google Scholar] [CrossRef]
- Dai, C.; Cheng, R.; Sun, X.; Liu, Y.; Zhou, H.; Wu, Y.; Sun, Y. Oil migration in nanometer to micrometer sized pores of tight oil sandstone during dynamic surfactant imbibition with online NMR. Fuel 2019, 245, 544–553. [Google Scholar] [CrossRef]
- Alvarez, J.O.; Saputra, I.W.; Schechter, D.S. The impact of surfactant imbibition and adsorption for improving oil recovery in the Wolfcamp and Eagle Ford Reservoirs. SPE J. 2018, 23, 2103–2117. [Google Scholar] [CrossRef]
- Wang, D.; Butler, R.; Zhang, J.; Seright, R. Wettability survey in Bakken shale with surfactant-formulation imbibition. SPE Reserv. Eval. Eng. 2012, 15, 695–705. [Google Scholar] [CrossRef]
- Starov, V.M.; Zhdanov, S.A.; Velarde, M.G. Capillary imbibition of surfactant solutions in porous media and thin capillaries: Partial wetting case. J. Colloid Interface Sci. 2004, 273, 589–595. [Google Scholar] [CrossRef] [PubMed]
- Austad, T.; Standnes, D.C. Spontaneous imbibition of water into oil-wet carbonates. J. Pet. Sci. Eng. 2003, 39, 363–376. [Google Scholar] [CrossRef]
- Schechter, D.S.; Zhou, D.; Orr, F.M. Low IFT drainage and imbibition. J. Pet. Sci. Eng. 1994, 11, 283–300. [Google Scholar] [CrossRef]
- Liu, J.; Sheng, J.J.; Wang, X.; Ge, H.; Yao, E. Experimental study of wettability alteration and spontaneous imbibition in Chinese shale oil reservoirs using anionic and nonionic surfactants. J. Pet. Sci. Eng. 2019, 175, 624–633. [Google Scholar] [CrossRef]
- Akin, S.; Schembre, J.M.; Bhat, S.K.; Kovscek, A.R. Spontaneous imbibition characteristics of diatomite. J. Pet. Sci. Eng. 2000, 25, 149–165. [Google Scholar] [CrossRef]
- Kathel, P.; Mohanty, K.K. Wettability Alteration in a Tight Oil Reservoir. Energy Fuels 2013, 27, 6460–6468. [Google Scholar] [CrossRef]
- Negin, C.; Ali, S.; Xie, Q. Most common surfactants employed in chemical enhanced oil recovery. Petroleum 2017, 3, 197–211. [Google Scholar] [CrossRef]
- Qin, W.; Guo, Y.; Sun, L.; Shi, J.; Bao, B. Spontaneous Imbibition in Nanomatrix–Fracture of Low Permeability Using Multiscale Nanofluidic Chips. Langmuir 2023, 39, 17972–17983. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Xiong, S.; Liu, Y.; He, Y.; Chu, S.; Liu, S. Spontaneous imbibition in tight porous media with different wettability: Pore-scale simulation. Phys. Fluids 2021, 33, 032013. [Google Scholar] [CrossRef]
- Cai, J.; Perfect, E.; Cheng, C.L.; Hu, X. Generalized modeling of spontaneous imbibition based on Hagen–Poiseuille flow in tortuous capillaries with variably shaped apertures. Langmuir 2014, 30, 5142–5151. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, H.O.; Gokmen, M.; Cesur, Y. Effect of shape factor, characteristic length, and boundary conditions on spontaneous imbibition. J. Pet. Sci. Eng. 2006, 53, 158–170. [Google Scholar] [CrossRef]
- Shi, Y.; Yassin, M.R.; Dehghanpour, H. A modified model for spontaneous imbibition of wetting phase into fractal porous media. Colloids Surf. A 2018, 543, 64–75. [Google Scholar] [CrossRef]
- Qin, C.Z.; van Brummelen, H. A dynamic pore-network model for spontaneous imbibition in porous media. Adv. Water Resour. 2019, 133, 103420. [Google Scholar] [CrossRef]
- Meng, Q.; Cai, J. Recent advances in spontaneous imbibition with different boundary conditions. Capillarity 2018, 1, 19–26. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Q.; Cao, G.; Bai, Y.; Liu, Y. The Effect of Crude Oil Stripped by Surfactant Action and Fluid Free Motion Characteristics in Porous Medium. Molecules 2024, 29, 288. https://doi.org/10.3390/molecules29020288
Cheng Q, Cao G, Bai Y, Liu Y. The Effect of Crude Oil Stripped by Surfactant Action and Fluid Free Motion Characteristics in Porous Medium. Molecules. 2024; 29(2):288. https://doi.org/10.3390/molecules29020288
Chicago/Turabian StyleCheng, Qingchao, Guangsheng Cao, Yujie Bai, and Ying Liu. 2024. "The Effect of Crude Oil Stripped by Surfactant Action and Fluid Free Motion Characteristics in Porous Medium" Molecules 29, no. 2: 288. https://doi.org/10.3390/molecules29020288
APA StyleCheng, Q., Cao, G., Bai, Y., & Liu, Y. (2024). The Effect of Crude Oil Stripped by Surfactant Action and Fluid Free Motion Characteristics in Porous Medium. Molecules, 29(2), 288. https://doi.org/10.3390/molecules29020288






