Insights on the Bonding Mechanism, Electronic and Optical Properties of Diamond Nanothread–Polymer and Cement–Boron Nitride Nanotube Composites
Abstract
1. Introduction
2. Results and Discussion
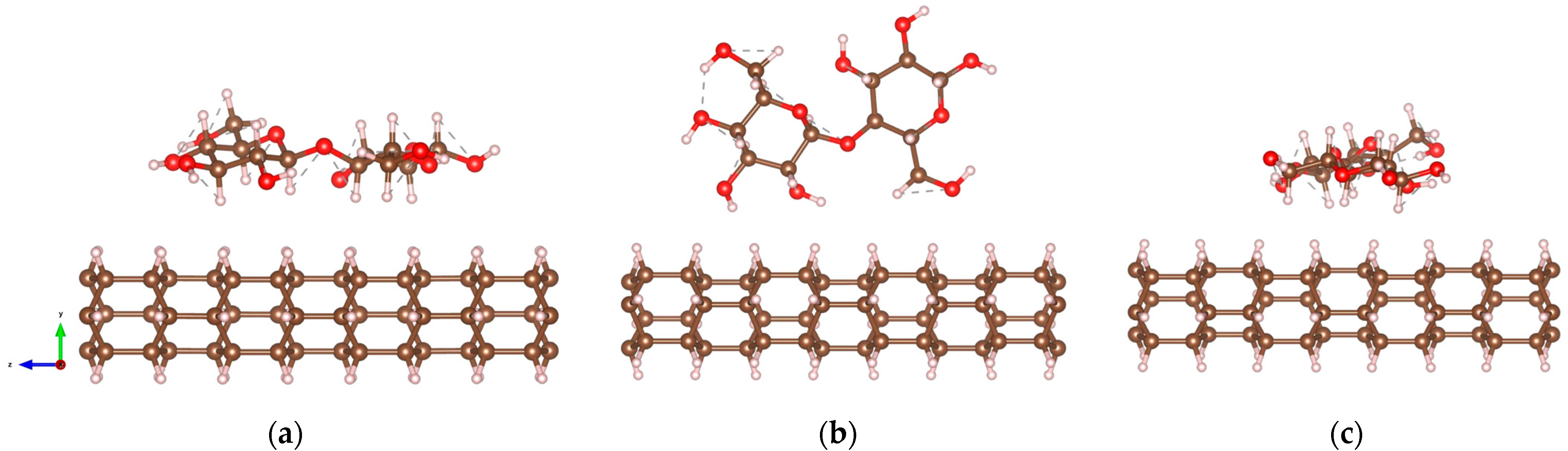
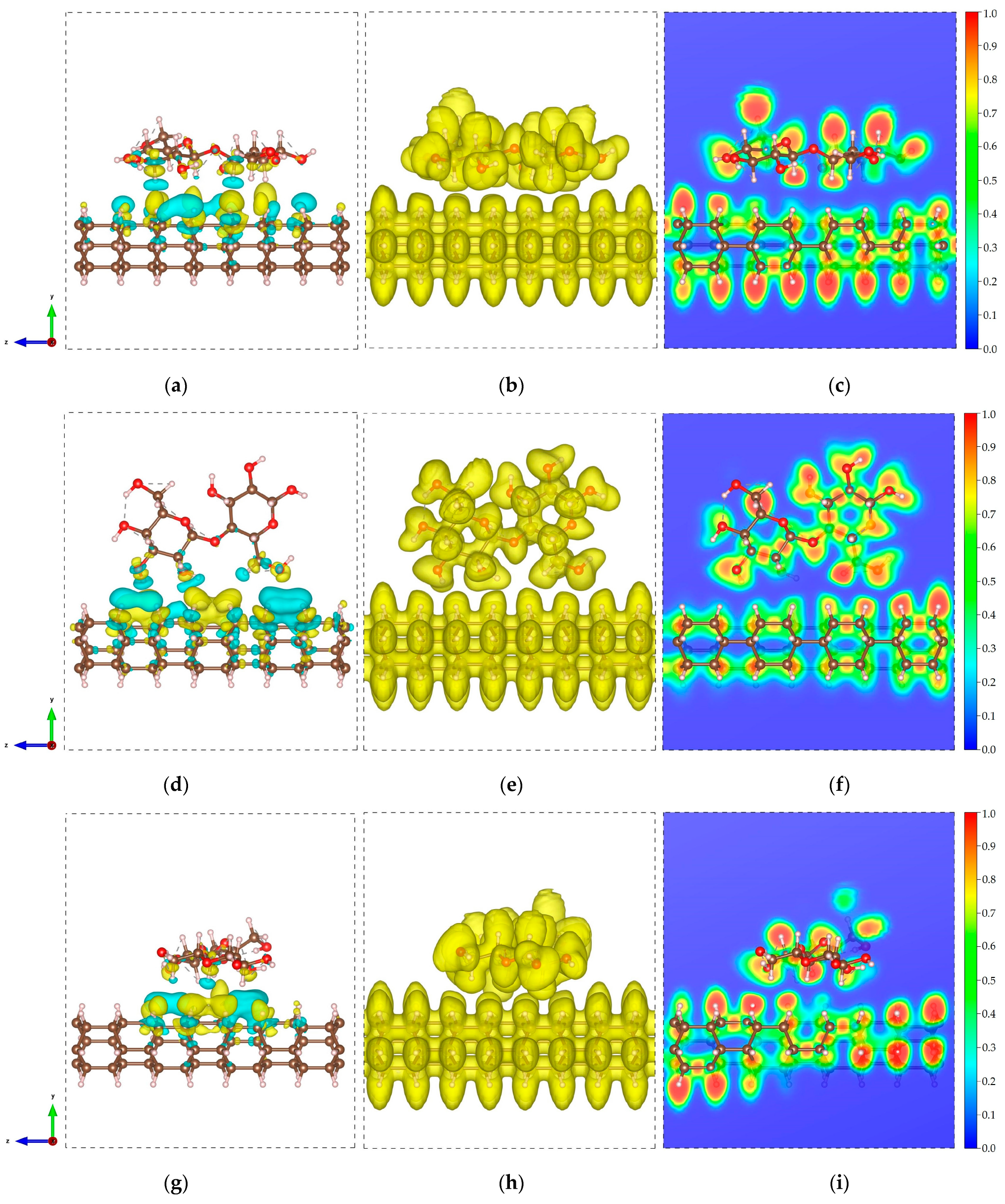
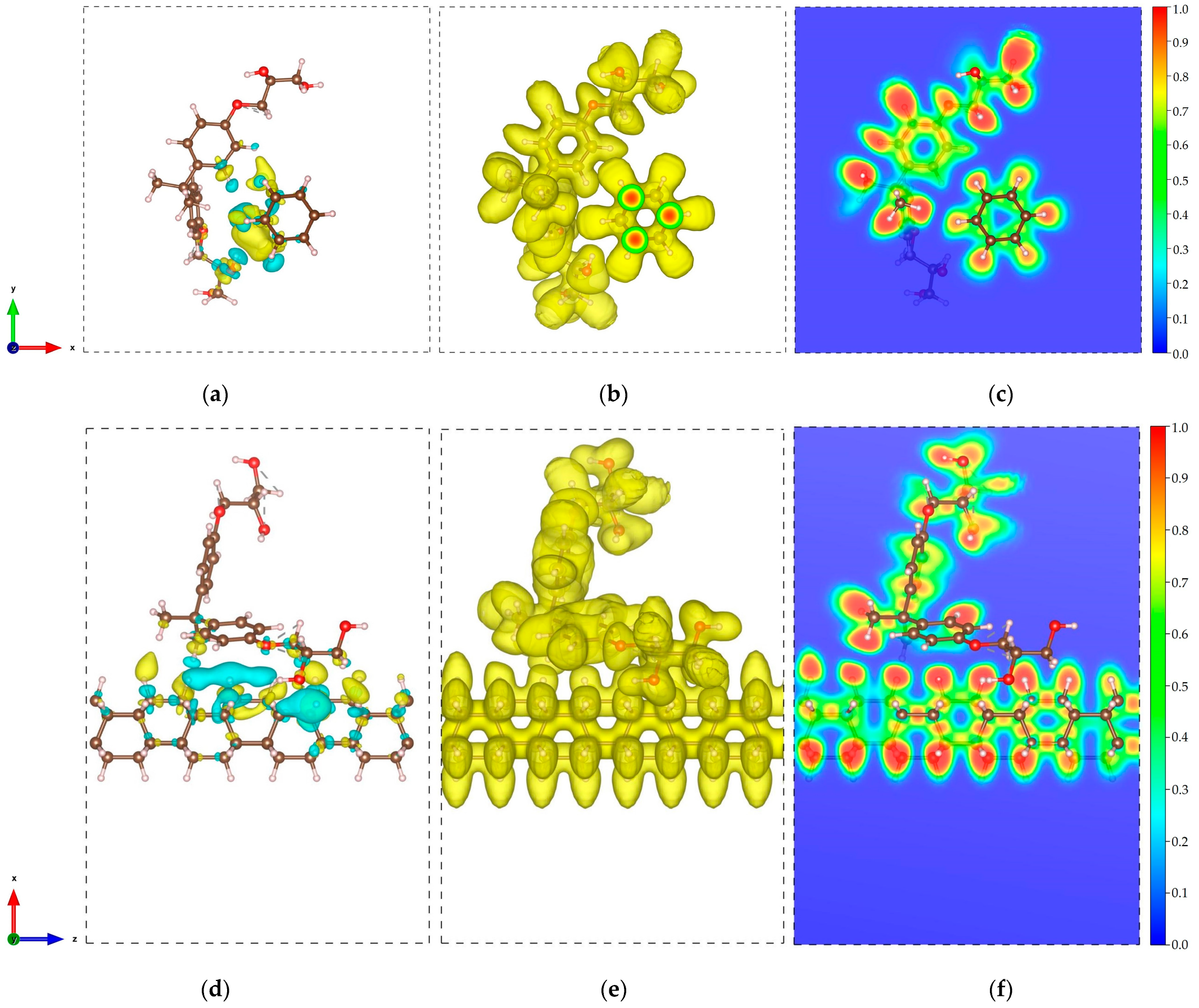
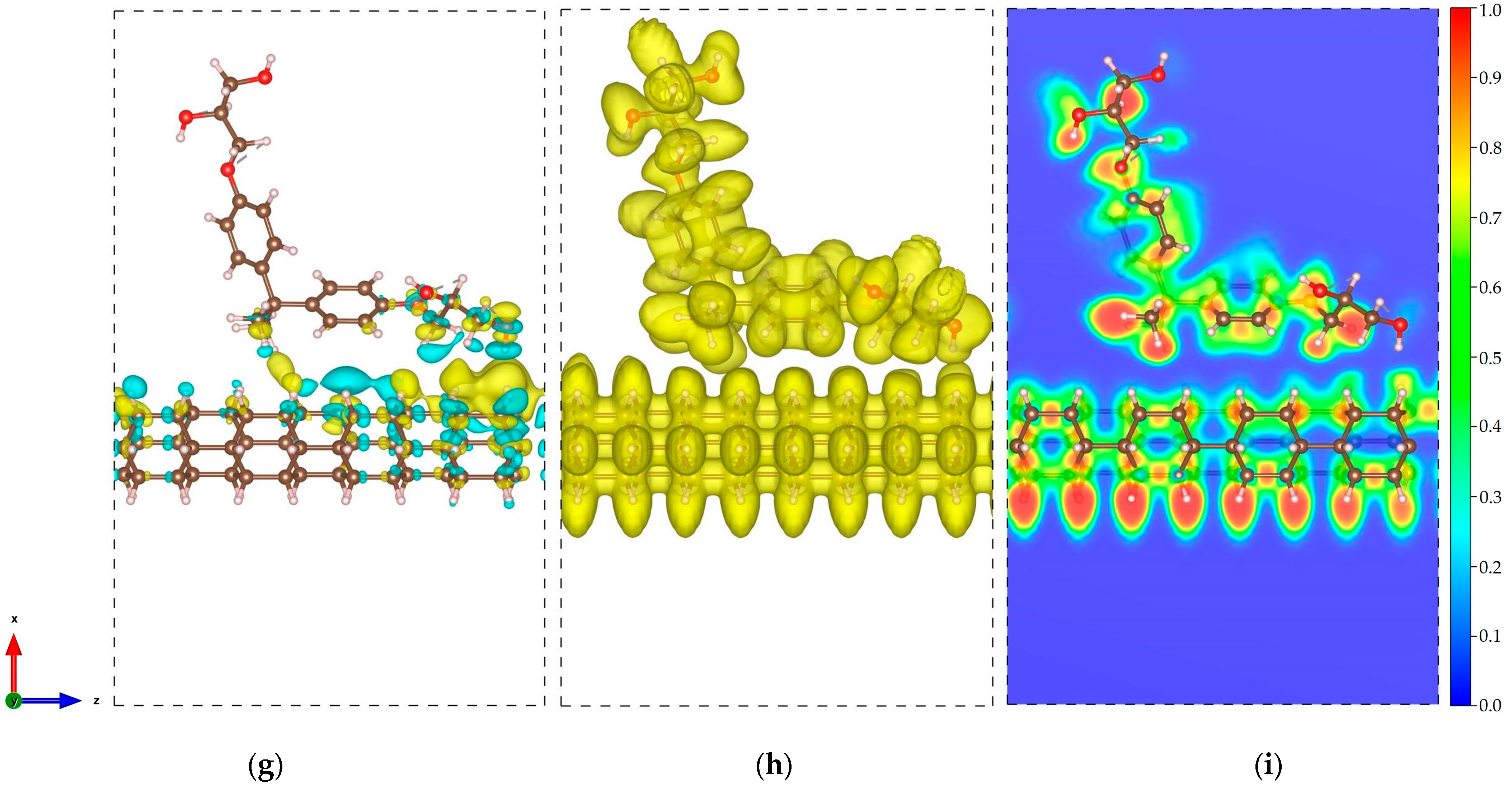
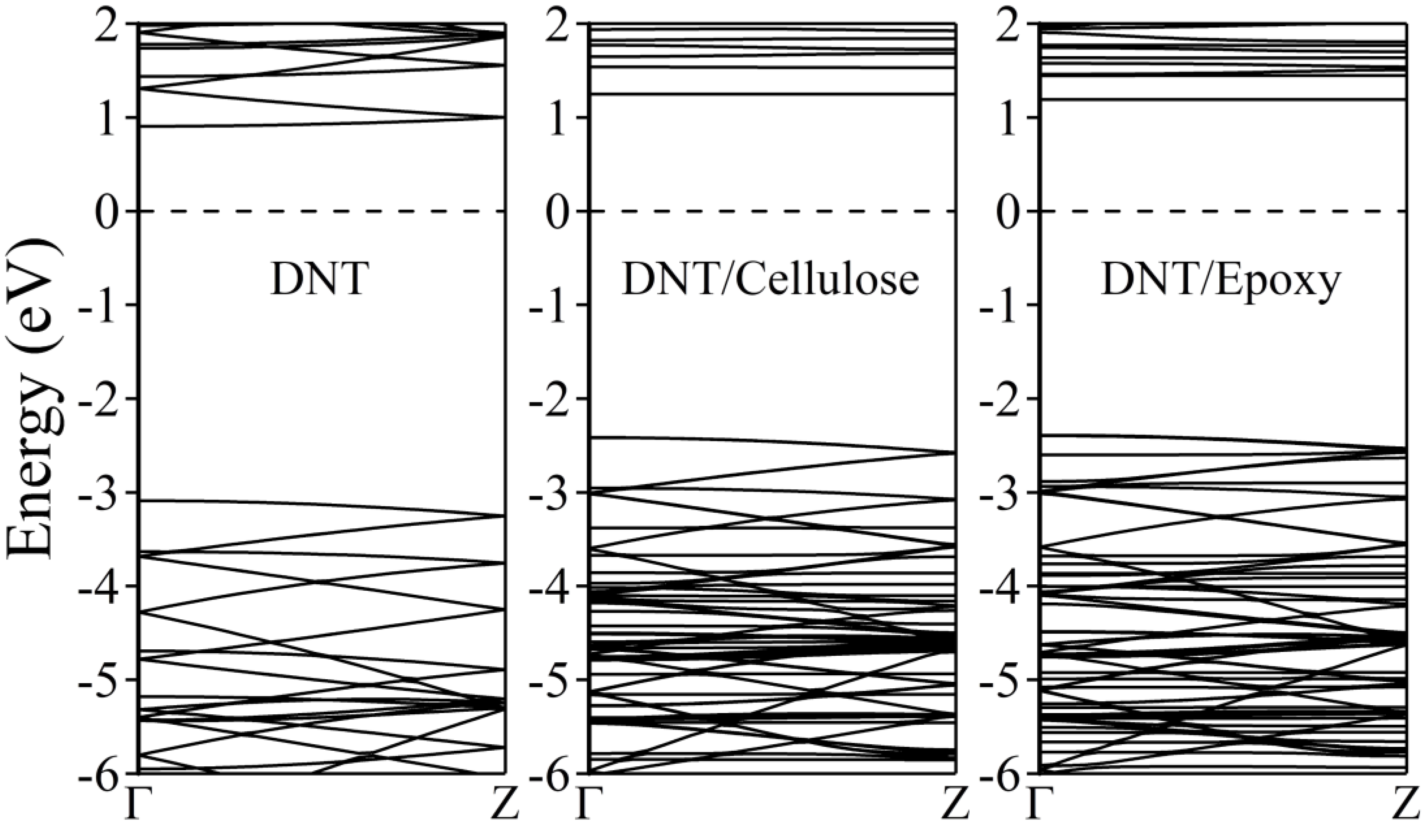
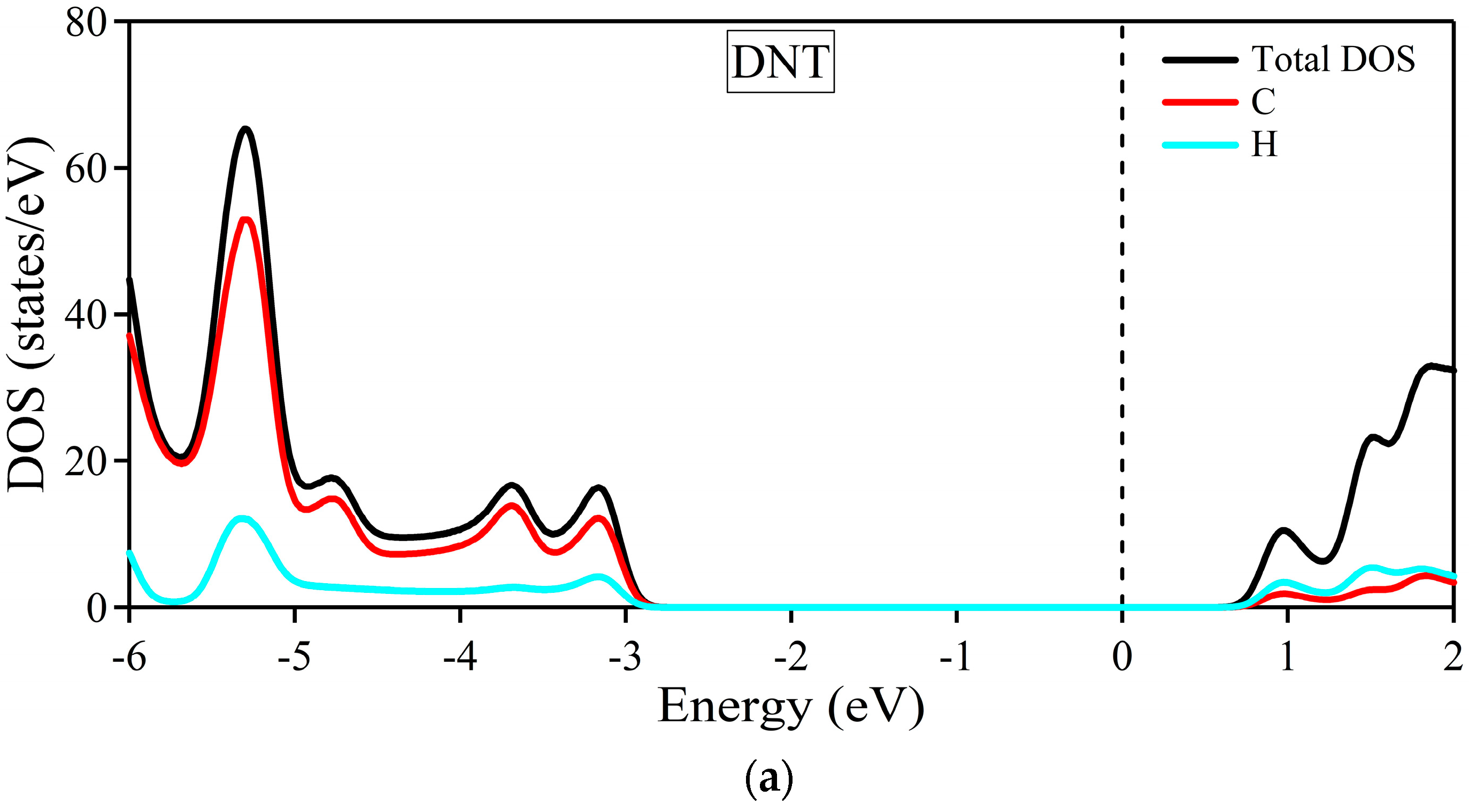
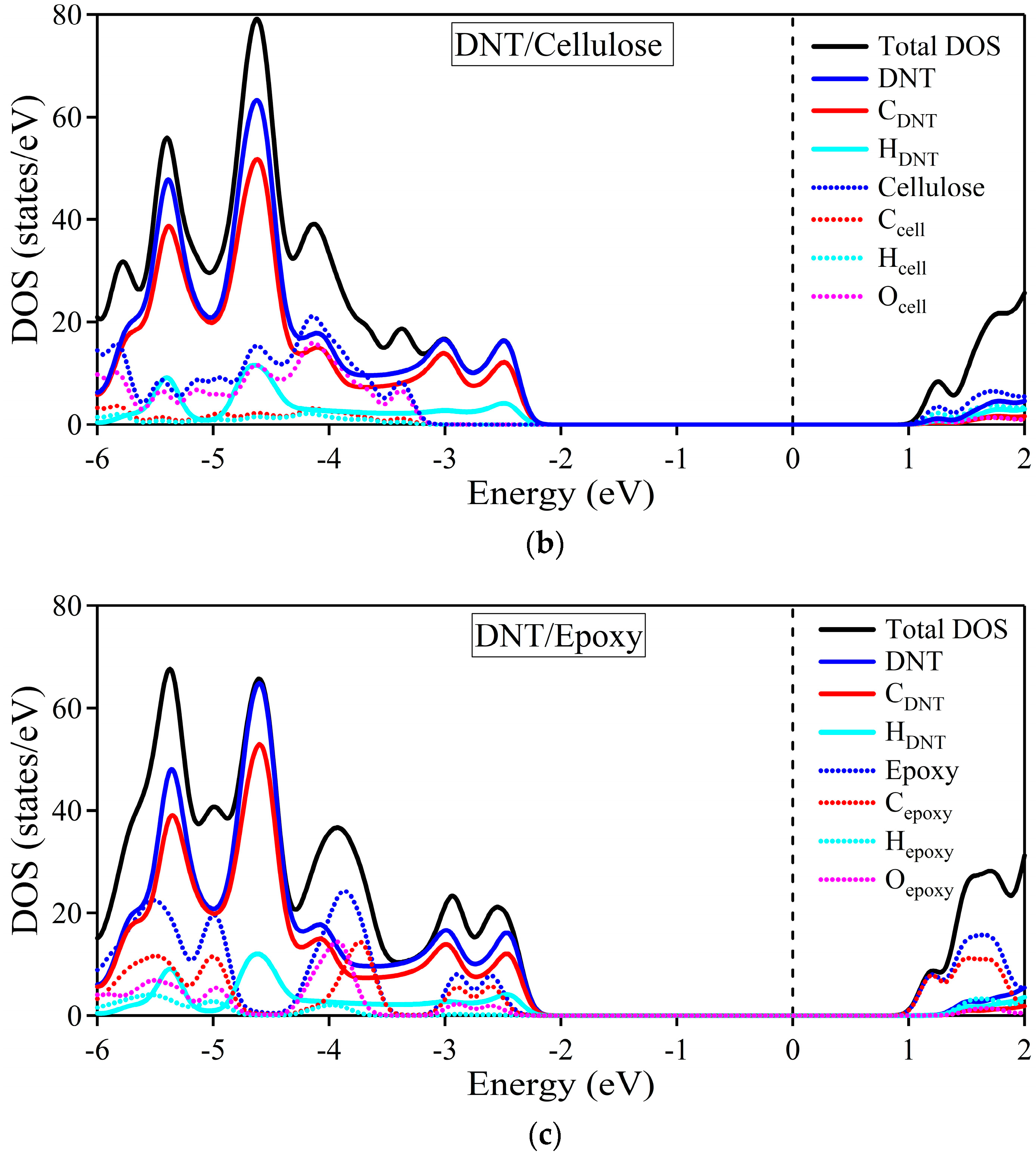
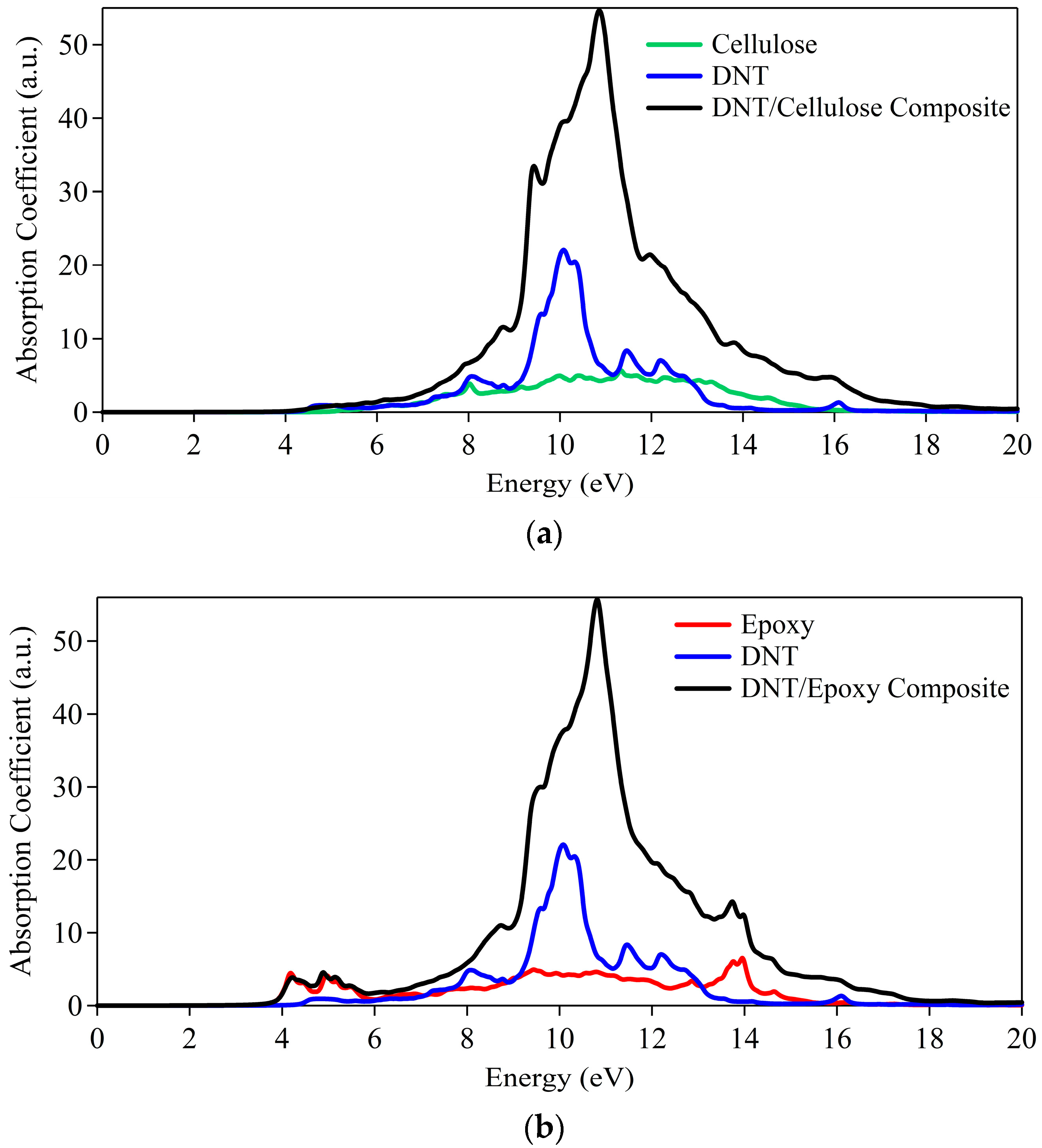
2.1. DNT/Cellulose and DNT/Epoxy Nanocomposites
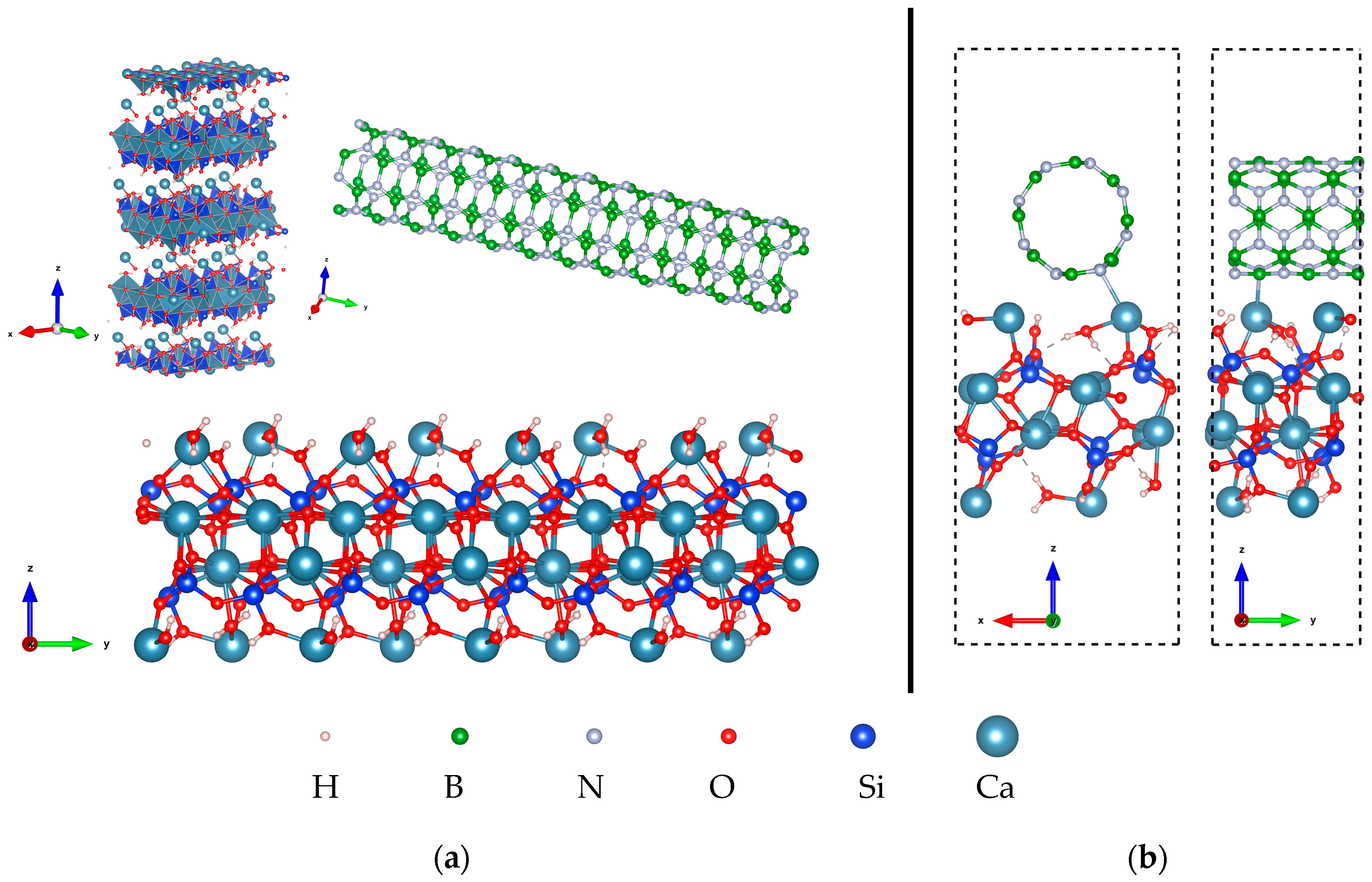
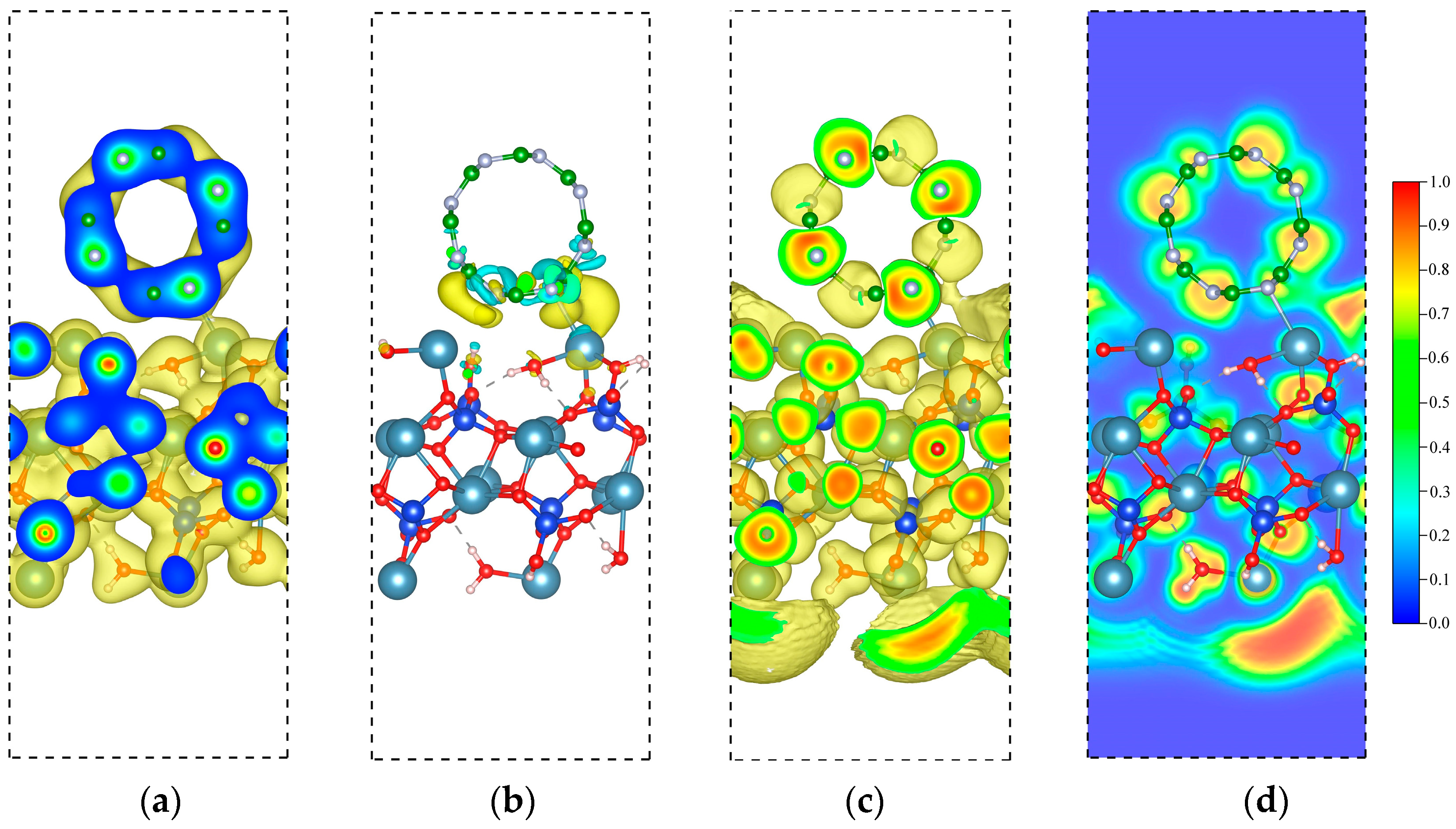
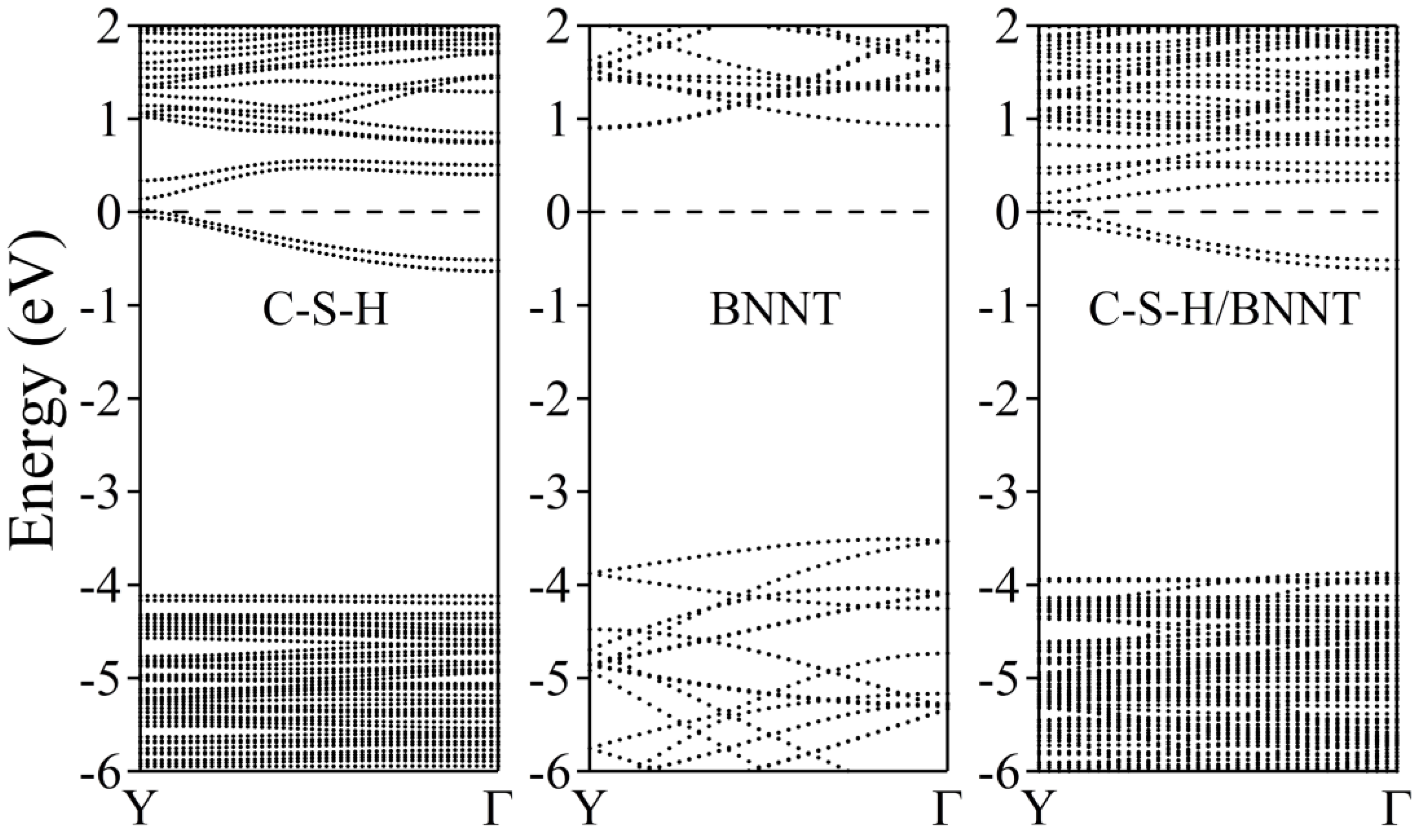
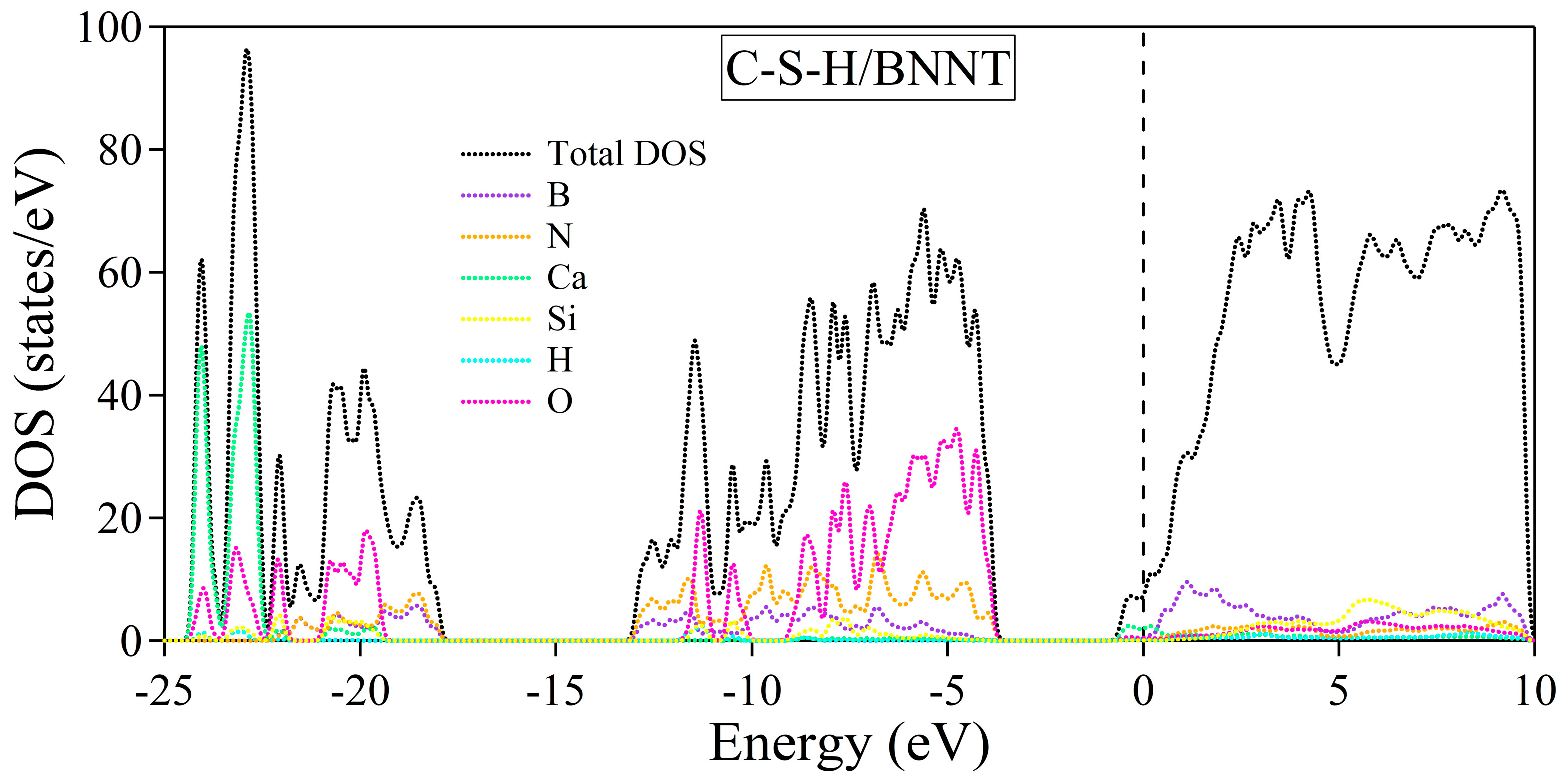
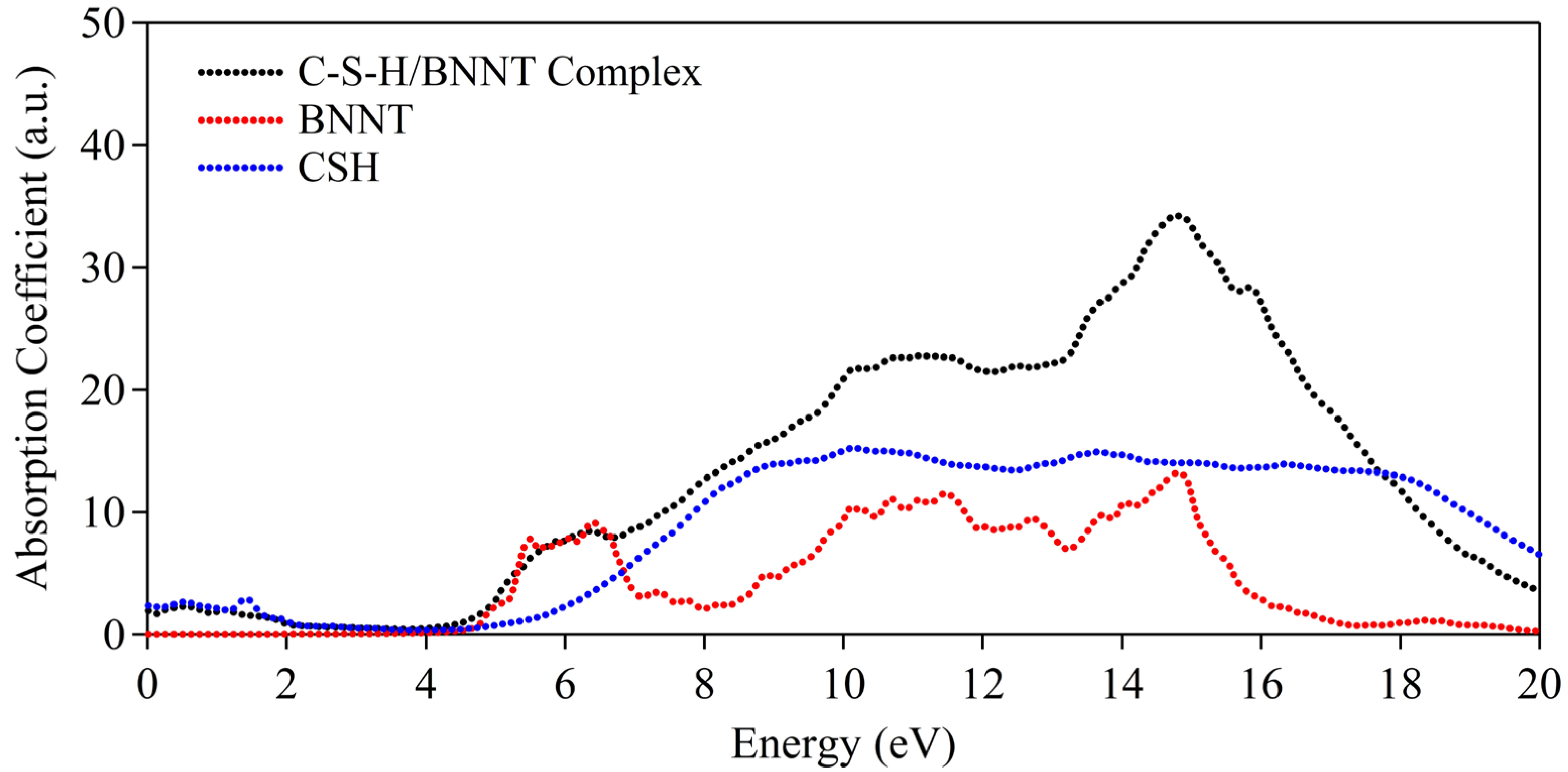
2.2. Calcium Silicate Hydrate and Boron Nitride Nanotube Nanocomposites
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Egbo, M.K. A Fundamental Review on Composite Materials and Some of Their Applications in Biomedical Engineering. J. King Saud. Univ.—Eng. Sci. 2020, 33, 557–568. [Google Scholar] [CrossRef]
- Li, W.; Dong, W.; Guo, Y.; Wang, K.; Shah, S.P. Advances in Multifunctional Cementitious Composites with Conductive Carbon Nanomaterials for Smart Infrastructure. Cem. Concr. Compos. 2022, 128, 104454. [Google Scholar] [CrossRef]
- Umar, K.; Yaqoob, A.A.; Ibrahim, M.N.M.; Parveen, T.; Safian, M.T. Chapter Thirteen—Environmental Applications of Smart Polymer Composites. In Smart Polymer Nanocomposites; Bhawani, S.A., Khan, A., Jawaid, M., Eds.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Sawston, UK, 2021; pp. 295–312. ISBN 978-0-12-819961-9. [Google Scholar]
- Ali, A.; Andriyana, A. Properties of Multifunctional Composite Materials Based on Nanomaterials: A Review. RSC Adv. 2020, 10, 16390–16403. [Google Scholar] [CrossRef] [PubMed]
- Bekzhanova, Z.; Memon, S.A.; Kim, J.R. Self-Sensing Cementitious Composites: Review and Perspective. Nanomaterials 2021, 11, 2355. [Google Scholar] [CrossRef] [PubMed]
- Basquiroto de Souza, F.; Yao, X.; Lin, J.; Naseem, Z.; Tang, Z.Q.; Hu, Y.; Gao, W.; Sagoe-Crentsil, K.; Duan, W. Effective Strategies to Realize High-Performance Graphene-Reinforced Cement Composites. Constr. Build. Mater. 2022, 324, 126636. [Google Scholar] [CrossRef]
- Sreenivasulu, B.; Ramji, B.; Nagaral, M. A Review on Graphene Reinforced Polymer Matrix Composites. Mater. Today Proc. 2018, 5, 2419–2428. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M. Carbon-Based Polymer Nanocomposites for High-Performance Applications. Polymers 2020, 12, 872. [Google Scholar] [CrossRef] [PubMed]
- Harussani, M.M.; Sapuan, S.M.; Nadeem, G.; Rafin, T.; Kirubaanand, W. Recent Applications of Carbon-Based Composites in Defence Industry: A Review. Def. Technol. 2022, 18, 1281–1300. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Zhang, Y.; Huang, Y.; Liu, J.; Zhang, X.; Liu, X.; Teng, H.; Zhang, X.; Zhang, J.; et al. A Review of Graphene-Based Materials/Polymer Composite Aerogels. Polymers 2023, 15, 1888. [Google Scholar] [CrossRef]
- Seydibeyoğlu, M.Ö.; Dogru, A.; Wang, J.; Rencheck, M.; Han, Y.; Wang, L.; Seydibeyoğlu, E.A.; Zhao, X.; Ong, K.; Shatkin, J.A.; et al. Review on Hybrid Reinforced Polymer Matrix Composites with Nanocellulose, Nanomaterials, and Other Fibers. Polymers 2023, 15, 984. [Google Scholar] [CrossRef] [PubMed]
- Latif, Z.; Ali, M.; Lee, E.-J.; Zubair, Z.; Lee, K.H. Thermal and Mechanical Properties of Nano-Carbon-Reinforced Polymeric Nanocomposites: A Review. J. Compos. Sci. 2023, 7, 441. [Google Scholar] [CrossRef]
- Amraei, J.; Jam, J.E.; Arab, B.; Firouz-Abadi, R.D. Modeling the Interphase Region in Carbon Nanotube-reinforced Polymer Nanocomposites. Polym. Compos. 2019, 40, E1219–E1234. [Google Scholar] [CrossRef]
- Fitzgibbons, T.C.; Guthrie, M.; Xu, E.; Crespi, V.H.; Davidowski, S.K.; Cody, G.D.; Alem, N.; Badding, J.V. Benzene-Derived Carbon Nanothreads. Nat. Mater. 2015, 14, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Baldini, M.; Wang, T.; Chen, B.; Xu, E.; Vermilyea, B.; Crespi, V.H.; Hoffmann, R.; Molaison, J.J.; Tulk, C.A.; et al. Mechanochemical Synthesis of Carbon Nanothread Single Crystals. J. Am. Chem. Soc. 2017, 139, 16343–16349. [Google Scholar] [CrossRef] [PubMed]
- Duan, P.; Li, X.; Wang, T.; Chen, B.; Juhl, S.J.; Koeplinger, D.; Crespi, V.H.; Badding, J.V.; Schmidt-Rohr, K. The Chemical Structure of Carbon Nanothreads Analyzed by Advanced Solid-State NMR. J. Am. Chem. Soc. 2018, 140, 7658–7666. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Duan, P.; Xu, E.-S.; Vermilyea, B.; Chen, B.; Li, X.; Badding, J.V.; Schmidt-Rohr, K.; Crespi, V.H. Constraining Carbon Nanothread Structures by Experimental and Calculated Nuclear Magnetic Resonance Spectra. Nano Lett. 2018, 18, 4934–4942. [Google Scholar] [CrossRef] [PubMed]
- Nobrega, M.M.; Teixeira-Neto, E.; Cairns, A.B.; Temperini, M.L.A.; Bini, R. One-Dimensional Diamondoid Polyaniline-like Nanothreads from Compressed Crystal Aniline. Chem. Sci. 2018, 9, 254–260. [Google Scholar] [CrossRef] [PubMed]
- Fanetti, S.; Nobrega, M.M.; Teixeira-Neto, E.; Temperini, M.L.A.; Bini, R. Effect of Structural Anisotropy in High-Pressure Reaction of Aniline. J. Phys. Chem. C 2018, 122, 29158–29164. [Google Scholar] [CrossRef]
- Li, X.; Wang, T.; Duan, P.; Baldini, M.; Huang, H.-T.; Chen, B.; Juhl, S.J.; Koeplinger, D.; Crespi, V.H.; Schmidt-Rohr, K.; et al. Carbon Nitride Nanothread Crystals Derived from Pyridine. J. Am. Chem. Soc. 2018, 140, 4969–4972. [Google Scholar] [CrossRef] [PubMed]
- Fanetti, S.; Santoro, M.; Alabarse, F.; Enrico, B.; Bini, R. Modulating the H-Bond Strength by Varying the Temperature for the High Pressure Synthesis of Nitrogen Rich Carbon Nanothreads. Nanoscale 2020, 12, 5233–5242. [Google Scholar] [CrossRef] [PubMed]
- Oburn, S.M.; Huss, S.; Cox, J.; Gerthoffer, M.C.; Wu, S.; Biswas, A.; Murphy, M.; Crespi, V.H.; Badding, J.V.; Lopez, S.A.; et al. Photochemically Mediated Polymerization of Molecular Furan and Pyridine: Synthesis of Nanothreads at Reduced Pressures. J. Am. Chem. Soc. 2022, 144, 22026–22034. [Google Scholar] [CrossRef] [PubMed]
- Biswas, A.; Ward, M.D.; Wang, T.; Zhu, L.; Huang, H.-T.; Badding, J.V.; Crespi, V.H.; Strobel, T.A. Evidence for Orientational Order in Nanothreads Derived from Thiophene. J. Phys. Chem. Lett. 2019, 10, 7164–7171. [Google Scholar] [CrossRef] [PubMed]
- Huss, S.; Wu, S.; Chen, B.; Wang, T.; Gerthoffer, M.C.; Ryan, D.J.; Smith, S.E.; Crespi, V.H.; Badding, J.V.; Elacqua, E. Scalable Synthesis of Crystalline One-Dimensional Carbon Nanothreads through Modest-Pressure Polymerization of Furan. ACS Nano 2021, 15, 4134–4143. [Google Scholar] [CrossRef] [PubMed]
- Ward, M.D.; Tang, W.S.; Zhu, L.; Popov, D.; Cody, G.D.; Strobel, T.A. Controlled Single-Crystalline Polymerization of C10H8·C10F8 under Pressure. Macromolecules 2019, 52, 7557–7563. [Google Scholar] [CrossRef]
- Friedrich, A.; Collings, I.E.; Dziubek, K.F.; Fanetti, S.; Radacki, K.; Ruiz-Fuertes, J.; Pellicer-Porres, J.; Hanfland, M.; Sieh, D.; Bini, R.; et al. Pressure-Induced Polymerization of Polycyclic Arene–Perfluoroarene Cocrystals: Single Crystal X-Ray Diffraction Studies, Reaction Kinetics, and Design of Columnar Hydrofluorocarbons. J. Am. Chem. Soc. 2020, 142, 18907–18923. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Tang, X.; Xu, J.; Yang, X.; Zhang, P.; Che, G.; Wang, Y.; Chen, Y.; Gao, X.; Dong, X.; et al. Crystalline C3N3H3 Tube (3,0) Nanothreads. Proc. Natl. Acad. Sci. USA 2022, 119, e2201165119. [Google Scholar] [CrossRef] [PubMed]
- Dunning, S.G.; Zhu, L.; Chen, B.; Chariton, S.; Prakapenka, V.B.; Somayazulu, M.; Strobel, T.A. Solid-State Pathway Control via Reaction-Directing Heteroatoms: Ordered Pyridazine Nanothreads through Selective Cycloaddition. J. Am. Chem. Soc. 2022, 144, 2073–2078. [Google Scholar] [CrossRef] [PubMed]
- Xu, E.; Lammert, P.E.; Crespi, V.H. Systematic Enumeration of Sp3 Nanothreads. Nano Lett. 2015, 15, 5124–5130. [Google Scholar] [CrossRef] [PubMed]
- Silveira, J.F.R.V.; Muniz, A.R. Functionalized Diamond Nanothreads from Benzene Derivatives. Phys. Chem. Chem. Phys. 2017, 19, 7132–7137. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wang, T.; Crespi, V.H.; Li, X.; Badding, J.; Hoffmann, R. All the Ways To Have Substituted Nanothreads. J. Chem. Theory Comput. 2018, 14, 1131–1140. [Google Scholar] [CrossRef] [PubMed]
- Roman, R.E.; Kwan, K.; Cranford, S.W. Mechanical Properties and Defect Sensitivity of Diamond Nanothreads. Nano Lett. 2015, 15, 1585–1590. [Google Scholar] [CrossRef] [PubMed]
- Zhan, H.; Zhang, G.; Tan, V.B.C.; Cheng, Y.; Bell, J.M.; Zhang, Y.; Gu, Y. Diamond Nanothread as a New Reinforcement for Nanocomposites. Adv. Funct. Mater. 2016, 26, 5279–5283. [Google Scholar] [CrossRef]
- Zhang, L.W.; Ji, W.M.; Liew, K.M. Mechanical Properties of Diamond Nanothread Reinforced Polymer Composites. Carbon. 2018, 132, 232–240. [Google Scholar] [CrossRef]
- Ji, W.M.; Zhang, L.W. Diamond Nanothread Reinforced Polymer Composites: Ultra-High Glass Transition Temperature and Low Density. Compos. Sci. Technol. 2019, 183, 107789. [Google Scholar] [CrossRef]
- Duan, K.; Zhang, J.; Li, L.; Hu, Y.; Zhu, W.; Wang, X. Diamond Nanothreads as Novel Nanofillers for Cross-Linked Epoxy Nanocomposites. Compos. Sci. Technol. 2019, 174, 84–93. [Google Scholar] [CrossRef]
- Zhan, H.; Zhang, G.; Tan, V.B.C.; Gu, Y. The Best Features of Diamond Nanothread for Nanofibre Applications. Nat. Commun. 2017, 8, 14863. [Google Scholar] [CrossRef] [PubMed]
- Klemm, D.; Heublein, B.; Fink, H.; Bohn, A. Cellulose: Fascinating Biopolymer and Sustainable Raw Material. Angew. Chem. Int. Ed. 2005, 44, 3358–3393. [Google Scholar] [CrossRef] [PubMed]
- Tapia-Orozco, N.; Ibarra-Cabrera, R.; Tecante, A.; Gimeno, M.; Parra, R.; Garcia-Arrazola, R. Removal Strategies for Endocrine Disrupting Chemicals Using Cellulose-Based Materials as Adsorbents: A Review. J. Environ. Chem. Eng. 2016, 4, 3122–3142. [Google Scholar] [CrossRef]
- Miyashiro, D.; Hamano, R.; Umemura, K. A Review of Applications Using Mixed Materials of Cellulose, Nanocellulose and Carbon Nanotubes. Nanomaterials 2020, 10, 186. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.-D.; Zhang, H.; Zhong, G.-J.; Yao, G.; Lai, B. Cellulose/Carbon Composites and Their Applications in Water Treatment—A Review. Chem. Eng. J. 2021, 405, 126980. [Google Scholar] [CrossRef]
- Yang, K.; Yazawa, K.; Tsuchiya, K.; Numata, K.; Guan, J. Molecular Interactions and Toughening Mechanisms in Silk Fibroin–Epoxy Resin Blend Films. Biomacromolecules 2019, 20, 2295–2304. [Google Scholar] [CrossRef] [PubMed]
- Yu, A.; Itkis, M.E.; Bekyarova, E.; Haddon, R.C. Effect of Single-Walled Carbon Nanotube Purity on the Thermal Conductivity of Carbon Nanotube-Based Composites. Appl. Phys. Lett. 2006, 89, 133102. [Google Scholar] [CrossRef]
- Rana, S.; Alagirusamy, R.; Joshi, M. A Review on Carbon Epoxy Nanocomposites. J. Reinf. Plast. Compos. 2009, 28, 461–487. [Google Scholar] [CrossRef]
- Gantayat, S.; Rout, D.; Swain, S.K. Carbon Nanomaterial–Reinforced Epoxy Composites: A Review. Polym.-Plast. Technol. Eng. 2018, 57, 1–16. [Google Scholar] [CrossRef]
- Singh, N.P.; Gupta, V.K.; Singh, A.P. Graphene and Carbon Nanotube Reinforced Epoxy Nanocomposites: A Review. Polymer 2019, 180, 121724. [Google Scholar] [CrossRef]
- Khostavan, S.; Fazli, M.; Ahangari, M.G.; Rostamiyan, Y. The Effect of Interaction between Nanofillers and Epoxy on Mechanical and Thermal Properties of Nanocomposites: Theoretical Prediction and Experimental Analysis. Adv. Polym. Technol. 2019, 2019, 8156718. [Google Scholar] [CrossRef]
- Prasanthi, P.P.; Kumar, M.S.R.N.; Chowdary, M.S.; Madhav, V.V.V.; Saxena, K.K.; Mohammed, K.A.; Khan, M.I.; Upadhyay, G.; Eldin, S.M. Mechanical Properties of Carbon Fiber Reinforced with Carbon Nanotubes and Graphene Filled Epoxy Composites: Experimental and Numerical Investigations. Mater. Res. Express 2023, 10, 025308. [Google Scholar] [CrossRef]
- Zeng, K.; Jibril Ibrahim, A.; Muter Saleh, Z.; Altimari, U.S.; Turki Jalil, A.; Kadhim, M.M.; Hussain Dilfy, S.; Taheri Andani, M.; Alizadeh, A.; Hekmatifar, M. Investigation of Mechanical and Thermal Characteristics of Epoxy/Graphene Oxide Nanocomposites by Molecular Dynamics Simulation. Mater. Sci. Eng. B 2023, 287, 116087. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Kamal, A.; Otabil, A.; Mamoun, O.; Liao, K. Graphene/Epoxy Nanocomposites for Improved Fracture Toughness: A Focused Review on Toughening Mechanism. Chem. Eng. J. Adv. 2023, 16, 100537. [Google Scholar] [CrossRef]
- Hu, P.; Alizadeh, A.; Jasim, D.J.; Nasajpour-Esfahani, N.; Shamsborhan, M.; Sabetvand, R. The Effect of Graphene Oxide Nanosheet Size and Initial Temperature on the Mechanical and Thermal Properties of Epoxy/Graphene Oxide Structure Using Molecular Dynamics Simulation. J. Phys. Chem. Solids 2024, 184, 111713. [Google Scholar] [CrossRef]
- Cassese, P.; Rainieri, C.; Occhiuzzi, A. Applications of Cement-Based Smart Composites to Civil Structural Health Monitoring: A Review. Appl. Sci. 2021, 11, 8530. [Google Scholar] [CrossRef]
- Rao, R.K.; Sasmal, S. Nanoengineered Smart Cement Composite for Electrical Impedance-Based Monitoring of Corrosion Progression in Structures. Cem. Concr. Compos. 2022, 126, 104348. [Google Scholar] [CrossRef]
- Suryanto, B.; McCarter, W.J.; Starrs, G.; Wilson, S.A.; Traynor, R.M. Smart Cement Composites for Durable and Intelligent Infrastructure. Procedia Eng. 2015, 125, 796–803. [Google Scholar] [CrossRef]
- Yang, H.; Cui, H.; Tang, W.; Li, Z.; Han, N.; Xing, F. A Critical Review on Research Progress of Graphene/Cement Based Composites. Compos. Part. A Appl. Sci. Manuf. 2017, 102, 273–296. [Google Scholar] [CrossRef]
- Huseien, G. A Review on Concrete Composites Modified with Nanoparticles. J. Compos. Sci. 2023, 7, 67. [Google Scholar] [CrossRef]
- Kedir, A.; Gamachu, M.; Alex, A.G. Cement-Based Graphene Oxide Composites: A Review on Their Mechanical and Microstructure Properties. J. Nanomater. 2023, 2023, e6741000. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, M.; Han, X.; Zheng, Y. A Review on Properties of Cement-Based Composites Doped with Graphene. J. Build. Eng. 2023, 70, 106367. [Google Scholar] [CrossRef]
- Bagheri, A.; Negahban, E.; Asad, A.; Ali Abbasi, H.; Muhammad Raza, S. Graphene Oxide-Incorporated Cementitious Composites: A Thorough Investigation. Mater. Adv. 2022, 3, 9040–9051. [Google Scholar] [CrossRef]
- Cho, B.H.; Nam, B.H. Concrete Composites Reinforced with Graphene Oxide Nanoflake (GONF) and Steel Fiber for Application in Rigid Pavement. Case Stud. Constr. Mater. 2022, 17, e01346. [Google Scholar] [CrossRef]
- Murali, M.; Alaloul, W.S.; Mohammed, B.S.; Musarat, M.A.; Salaheen, M.A.; Al-Sabaeei, A.M.; Isyaka, A. Utilizing Graphene Oxide in Cementitious Composites: A Systematic Review. Case Stud. Constr. Mater. 2022, 17, e01359. [Google Scholar] [CrossRef]
- Xu, Y.; Zeng, J.; Chen, W.; Jin, R.; Li, B.; Pan, Z. A Holistic Review of Cement Composites Reinforced with Graphene Oxide. Constr. Build. Mater. 2018, 171, 291–302. [Google Scholar] [CrossRef]
- Du, M.; Jing, H.; Gao, Y.; Su, H.; Fang, H. Carbon Nanomaterials Enhanced Cement-Based Composites: Advances and Challenges. Nanotechnol. Rev. 2020, 9, 115–135. [Google Scholar] [CrossRef]
- Cho, B.H.; Chung, W.; Nam, B.H. Molecular Dynamics Simulation of Calcium-Silicate-Hydrate for Nano-Engineered Cement Composites—A Review. Nanomaterials 2020, 10, 2158. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Zhong, J. Carbon-Based Nanomaterials Engineered Cement Composites: A Review. J. Infrastruct. Preserv. Resil. 2022, 3, 2. [Google Scholar] [CrossRef]
- Du, H.; Pang, S. Transport of Water and Chloride Ion in Cement Composites Modified with Graphene Nanoplatelet. Key Eng. Mater. 2015, 629, 162–167. [Google Scholar] [CrossRef]
- Maselugbo, A.O.; Harrison, H.B.; Alston, J.R. Boron Nitride Nanotubes: A Review of Recent Progress on Purification Methods and Techniques. J. Mater. Res. 2022, 37, 4438–4458. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, K.; Cai, Q.; Wang, N.; Wu, L.; He, Q.; Wang, H.; Zhang, Y.; Xie, Y.; Yao, Y.; et al. Advances in Synthesis and Applications of Boron Nitride Nanotubes: A Review. Chem. Eng. J. 2022, 431, 134118. [Google Scholar] [CrossRef]
- Roudi, M.R.R.; Ranjkesh, M.; Korayem, A.H.; Shahsavary, R. Review of Boron Nitride Nanosheet-Based Composites for Construction Applications. ACS Appl. Nano Mater. 2022, 5, 17356–17372. [Google Scholar] [CrossRef]
- Liu, J.; Jian, W.; Lau, D. Boron Nitride Nanosheet as a Promising Reinforcement for Cementitious Composites. Appl. Surf. Sci. 2022, 572, 151395. [Google Scholar] [CrossRef]
- Falin, A.; Cai, Q.; Santos, E.J.G.; Scullion, D.; Qian, D.; Zhang, R.; Yang, Z.; Huang, S.; Watanabe, K.; Taniguchi, T.; et al. Mechanical Properties of Atomically Thin Boron Nitride and the Role of Interlayer Interactions. Nat. Commun. 2017, 8, 15815. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Dmuchowski, C.M.; Park, C.; Fay, C.C.; Ke, C. Quantitative Characterization of Structural and Mechanical Properties of Boron Nitride Nanotubes in High Temperature Environments. Sci. Rep. 2017, 7, 11388. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Koumpouras, K.; Larsson, J.A. Distinguishing between Chemical Bonding and Physical Binding Using Electron Localization Function (ELF). J. Phys. Condens. Matter 2020, 32, 315502. [Google Scholar] [CrossRef]
- Zhang, L.-W.; Ji, W.-M.; Hu, Y.; Liew, K.M. Atomistic Insights into the Tunable Transition from Cavitation to Crazing in Diamond Nanothread-Reinforced Polymer Composites. Research 2020, 2020, 7815462. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhou, Y.; Zhan, H.; Bai, J.; Gu, Y. Effective Enhancement of a Carbon Nanothread on the Mechanical Properties of the Polyethylene Nanocomposite. J. Phys. Chem. C 2021, 125, 5781–5792. [Google Scholar] [CrossRef]
- Zhan, H.; Zhou, Y.; Zhang, G.; Zhu, J.; Zhang, W.; Lü, C.; Gu, Y. Carbon Nanothreads Enable Remarkable Enhancement in the Thermal Conductivity of Polyethylene. Nanoscale 2021, 13, 6934–6943. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Tai, B.; Guan, S.; Yang, S.A.; Zhang, G. Hybrid Structures and Strain-Tunable Electronic Properties of Carbon Nanothreads. J. Phys. Chem. C 2018, 122, 3101–3106. [Google Scholar] [CrossRef]
- Chen, M.-M.; Xiao, J.; Cao, C.; Zhang, D.; Cui, L.-L.; Xu, X.-M.; Long, M.-Q. Theoretical Prediction Electronic Properties of Group-IV Diamond Nanothreads. AIP Adv. 2018, 8, 075107. [Google Scholar] [CrossRef]
- Demingos, P.G.; Muniz, A.R. Electronic and Mechanical Properties of Partially Saturated Carbon and Carbon Nitride Nanothreads. J. Phys. Chem. C 2019, 123, 3886–3891. [Google Scholar] [CrossRef]
- Xiao, J.; Chen, M.-M.; Liu, W.-J.; He, J.; Pan, C.-N.; Long, M.-Q. Perfect Mechanical and Robust Electronic Properties of New Carbon Nanothreads: A First Principles Study. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 111, 37–43. [Google Scholar] [CrossRef]
- Miao, Z.; Cao, C.; Zhang, B.; Duan, H.; Long, M. First-Principles Study on the Effects of Doping and Adsorption on the Electronic and Magnetic Properties of Diamond Nanothreads. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 118, 113949. [Google Scholar] [CrossRef]
- Munio, A.A.Z.; Domato, D.C.; Pido, A.A.G. Non-Covalent Functionalization of Biphenylene Network by Cellulose and Nylon-6: A First-Principles Study. Biointerface Res. Appl. Chem. 2023, 13, 548. [Google Scholar]
- Munio, A.A.Z.; Pido, A.A.G.; Ambolode Ii, L.C.C. First-Principles Insights on the Bonding Mechanism and Electronic Structure of SWCNT and Oxygenated-SWCNT Functionalized by Cellulose Biopolymer. Nano Hybrids Compos. 2023, 40, 51–63. [Google Scholar] [CrossRef]
- Jilili, J.; Abdurahman, A.; Gülseren, O.; Schwingenschlögl, U. Non-Covalent Functionalization of Single Wall Carbon Nanotubes and Graphene by a Conjugated Polymer. Appl. Phys. Lett. 2014, 105, 013103. [Google Scholar] [CrossRef]
- Pido, A.A.G.; Munio, A.A.Z.; Ambolode Ii, L.C.C. Ab Initio Calculations of the Atomic Structure, Stability, and Electronic Properties of (C6H10O5)2 Encapsulation into Hydrogen-Doped Carbon Nanotube. Nano Hybrids Compos. 2023, 38, 53–62. [Google Scholar] [CrossRef]
- Selvam, R.P.; Subramani, V.J.; Murray, S. Potential Application of Nanotechnology on Cement Based Materials. Available online: https://trid.trb.org/View/898967 (accessed on 1 June 2023).
- Soyer-Uzun, S.; Chae, S.R.; Benmore, C.J.; Wenk, H.; Monteiro, P.J.M. Compositional Evolution of Calcium Silicate Hydrate (C–S–H) Structures by Total X-Ray Scattering. J. Am. Ceram. Soc. 2012, 95, 793–798. [Google Scholar] [CrossRef]
- Munio, A.A.Z.; Domato, D.C.; Pido, A.A.G.; Ambolode Ii, L.C.C. On the Nanoscale Interface, Electronic Structure, and Optical Properties of Nanocarbon-Reinforced Calcium Silicate Hydrates. Phys. Scr. 2024, 99, 015927. [Google Scholar] [CrossRef]
- Ju, S.-P.; Wang, Y.-C.; Lien, T.-W. Tuning the Electronic Properties of Boron Nitride Nanotube by Mechanical Uni-Axial Deformation: A DFT Study. Nanoscale Res. Lett. 2011, 6, 160. [Google Scholar] [CrossRef] [PubMed]
- Izadifar, M.; Dolado, J.S.; Thissen, P.; Ayuela, A. Interactions between Reduced Graphene Oxide with Monomers of (Calcium) Silicate Hydrates: A First-Principles Study. Nanomaterials 2021, 11, 2248. [Google Scholar] [CrossRef]
- Movlarooy, T.; Minaie, B. First Principles Study of Structural and Electronic Properties of BNNTs. J. Comput. Electron. 2018, 17, 1441–1449. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, X.; Bian, Y.; Nie, K.; Liu, S.; Tang, K.; Zhang, R.; Zheng, Y.; Gu, S. First-Principles Insights on the Electronic and Optical Properties of ZnO@CNT Core@shell Nanostructure. Sci. Rep. 2018, 8, 15464. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Hamann, D.R. Optimized Norm-Conserving Vanderbilt Pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Stojkovic, D.; Zhang, P.; Crespi, V.H. Smallest Nanotube: Breaking the Symmetry of sp3 Bonds in Tubular Geometries. Phys. Rev. Lett. 2001, 87, 125502. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved Grid-based Algorithm for Bader Charge Allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Sanville, E.; Henkelman, G. A Grid-Based Bader Analysis Algorithm without Lattice Bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Trinkle, D.R. Accurate and Efficient Algorithm for Bader Charge Integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef] [PubMed]


| System | (Å) | (eV) | (e) |
|---|---|---|---|
| DNT/cellulose—1 | 3.67 | −0.797 | −0.008 |
| DNT/cellulose—2 | 3.42 | −0.730 | 0.004 |
| DNT/cellulose—3 | 3.48 | −0.726 | −0.006 |
| System | (Å) | (eV) | (e) |
|---|---|---|---|
| DNT/Epoxy—1 | 3.56 | −0.224 | −0.003 |
| DNT/Epoxy—2 | 3.64 | −0.236 | −0.019 |
| DNT/Epoxy—3 | 3.60 | −0.168 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domato, D.C.; Munio, A.A.Z.; Jacosalem, N.J.P.; Fuentes, D.R.T.; Ambolode, L.C.C., II. Insights on the Bonding Mechanism, Electronic and Optical Properties of Diamond Nanothread–Polymer and Cement–Boron Nitride Nanotube Composites. Molecules 2024, 29, 4693. https://doi.org/10.3390/molecules29194693
Domato DC, Munio AAZ, Jacosalem NJP, Fuentes DRT, Ambolode LCC II. Insights on the Bonding Mechanism, Electronic and Optical Properties of Diamond Nanothread–Polymer and Cement–Boron Nitride Nanotube Composites. Molecules. 2024; 29(19):4693. https://doi.org/10.3390/molecules29194693
Chicago/Turabian StyleDomato, Diamond C., Art Anthony Z. Munio, Naomi Jane P. Jacosalem, Dexter Rhys T. Fuentes, and Leo Cristobal C. Ambolode, II. 2024. "Insights on the Bonding Mechanism, Electronic and Optical Properties of Diamond Nanothread–Polymer and Cement–Boron Nitride Nanotube Composites" Molecules 29, no. 19: 4693. https://doi.org/10.3390/molecules29194693
APA StyleDomato, D. C., Munio, A. A. Z., Jacosalem, N. J. P., Fuentes, D. R. T., & Ambolode, L. C. C., II. (2024). Insights on the Bonding Mechanism, Electronic and Optical Properties of Diamond Nanothread–Polymer and Cement–Boron Nitride Nanotube Composites. Molecules, 29(19), 4693. https://doi.org/10.3390/molecules29194693






