Reproducing the Solvatochromism of Merocyanines by PCM Calculations
Abstract
1. Introduction
2. Results
2.1. Calculations of Betaines 1–3
N = 27, r2 = 0.96
N = 27, r2 = 0.60
N = 7, r2 = 0.79
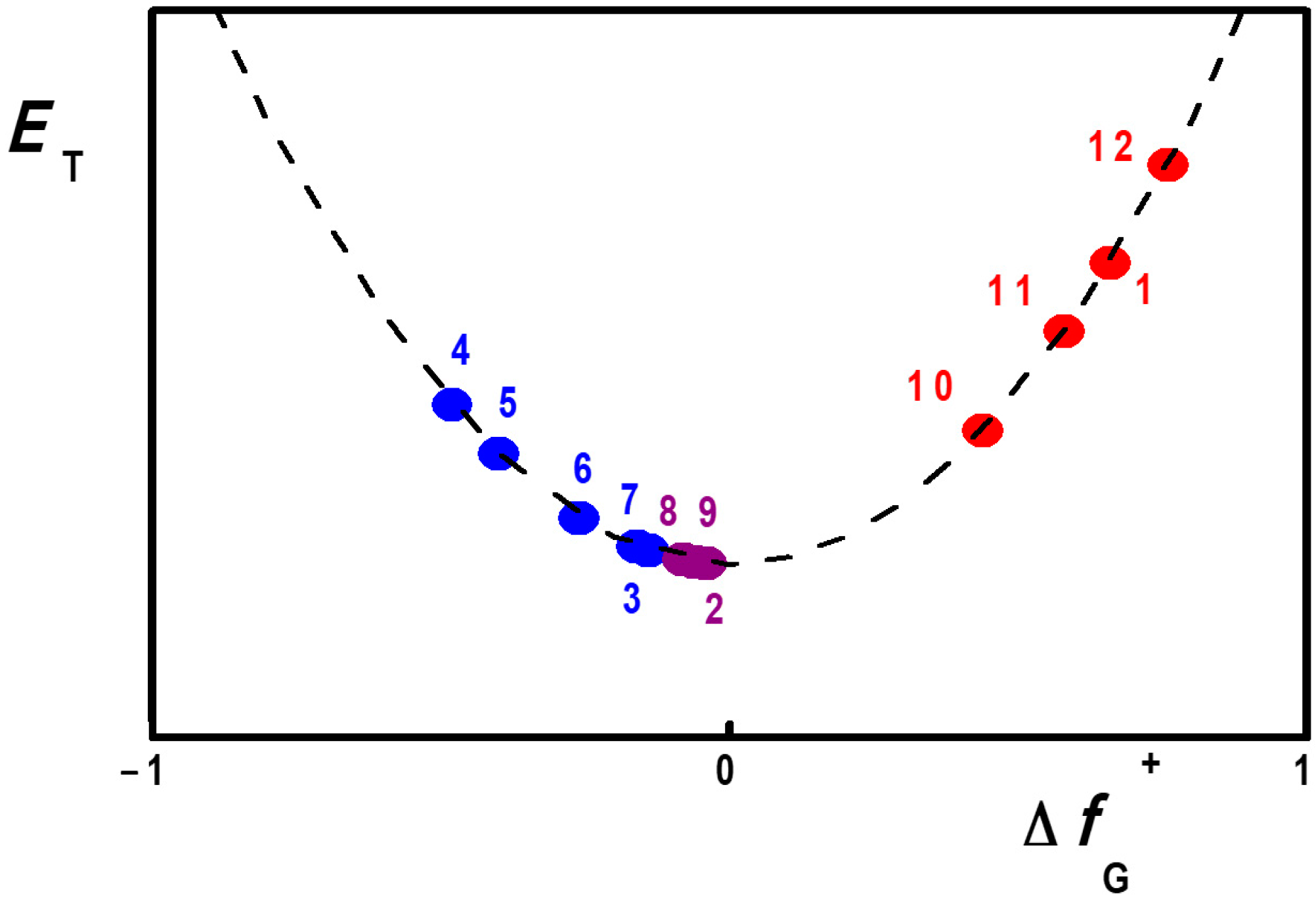
2.2. Consequences of Continuum Model Limitations
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herbert, J.M. Dielectric continuum methods for quantum chemistry. WIREs Comput. Mol. Sci. 2021, 11, e1519. [Google Scholar] [CrossRef]
- Caricato, M.; Mennucci, B.; Tomasi, J. Solvent polarity scales revisited: A ZINDO-PCM study of the solvatochromism of betaine-30. Mol. Phys. 2006, 104, 875. [Google Scholar] [CrossRef]
- Eilmes, A. Solvatochromic probe in molecular solvents: Implicit versus explicit solvent model. Theor. Chem. Acc. 2014, 133, 1538. [Google Scholar] [CrossRef]
- Kulinich, A.V.; Derevyanko, N.A.; Mikitenko, E.K.; Ischchenko, A.A. Merocyanines based on 1,3-indanedione: Electronic structure and solvatochromism. J. Phys. Org. Chem. 2011, 24, 732–742. [Google Scholar] [CrossRef]
- Pedone, A. Role of Solvent on Charge Transfer in 7-Aminocoumarin Dyes: New Hints from TD-CAM-B3LYP and State Specific PCM Calculations. J. Chem. Theory Comput. 2013, 9, 4087–4096. [Google Scholar] [CrossRef]
- Krawczyk, P. Time-dependent density functional theory calculations of the solvatochromism of some azo sulfonamide fluorochromes. J. Mol. Model. 2015, 21, 118. [Google Scholar] [CrossRef]
- Wada, T.; Nakano, H.; Sato, H. Solvatochromic Shift of Brooker’s Merocyanine: Hartree-Fock Exchange in Time Dependent Density Functional Calculation and Hydrogen Bonding Effect. J. Chem. Theory Comput. 2014, 10, 4535–4547. [Google Scholar] [CrossRef]
- Pawlowska, Z.; Lietard, A.; Aloise, S.; Sliwa, M.; Idrissi, A.; Poizat, O.; Buntinx, G.; Delbaere, S.; Perrier, A.; Maurel, F.; et al. The excited state dipole moments of betaine pyridinium investigated by an innovative solvatochromic analysis and TDDFT calculations. Phys. Chem. Chem. Phys. 2011, 13, 13185–13195. [Google Scholar] [CrossRef]
- Lalevee, J.; Allonas, X.; Jacques, P. Electronic distribution and solvatochromism investigation of a model radical (2,2,6,6-tetramethylpiperidine N-oxyl:tempo) through TD-DFT calculations including PCM solvation. J. Mol. Struct. THEOCHEM 2006, 767, 143–147. [Google Scholar] [CrossRef]
- Nemykin, V.N.; Makarova, E.A.; Grosland, J.O.; Hadt, R.G.; Koposov, A.Y. Preparation, characterization, molecular and electronic structures, TDDFT, and TDDFT/PCM study of the solvatochromism in cyanovinylferrocenes. Inorg. Chem. 2007, 46, 9591–9601. [Google Scholar] [CrossRef]
- Zhao, W.; Bian, W. Investigation of the structures and electronic spectra for coumarin 6 through TD-DFT calculations including PCM solvation. J. Mol. Struct. THEOCHEM 2007, 818, 43–49. [Google Scholar] [CrossRef]
- Fukuda, R.; Ehara, M. Mechanisms for Solvatochromic Shifts of Free-Base Porphine Studied with Polarizable Continuum Models and Explicit Solute-Solvent Interactions. J. Chem. Theory Comput. 2013, 9, 470–480. [Google Scholar] [CrossRef]
- Kulinich, A.V.; Kurdyukov, V.V.; Ishchenko, A.A. Effect of bulky substituents in the donor and acceptor terminal groups on solvatochromism of Brooker’s merocyanine. New J. Chem. 2019, 43, 7379–7385. [Google Scholar] [CrossRef]
- Budzak, S.; Jaunet-Lahary, T.; Laurent, A.D.; Laurence, C.; Medved’, M.; Jacquemin, D. Exploring the Solvatochromism of Betaine 30 with Ab Initio Tools: From Accurate Gas-Phase Calculations to Implicit and Explicit Solvation Models. Chem. Eur. J. 2017, 23, 4108–4119. [Google Scholar] [CrossRef]
- Ceron-Carrasco, J.P.; Jacquemin, D.; Laurence, C.; Planchat, A.; Reichardt, C.; Sraidi, K. Determination of a Solvent Hydrogen-Bond Acidity Scale by Means of the Solvatochromism of Pyridinium-N-phenolate Betaine Dye 30 and PCM-TD-DFT Calculations. J. Phys. Chem. B 2014, 118, 4605–4614. [Google Scholar] [CrossRef]
- Etienne, T.; Michaux, C.; Monari, A.; Assfeld, X.; Perpète, E.A. Theoretical computation of Betain B30 solvatochromism using a Polarizable Continnum Model. Dye. Pigment. 2014, 100, 24–31. [Google Scholar] [CrossRef]
- Mera-Adasme, R.; Moraga, D.; Medina, R.; Domínguez, M. Mapping the solute–solvent interactions for the interpretation of the three types of solvatochromism exhibited by phenolate-based dyes. J. Mol. Liq. 2022, 359, 119302. [Google Scholar] [CrossRef]
- Catalán, J. Toward a Generalized Treatment of the Solvent Effect Based on Four Empirical Scales: Dipolarity (SdP, a New Scale), Polarizability (SP), Acidity (SA), and Basicity (SB) of the Medium. J. Phys. Chem. B 2009, 113, 5951–5960. [Google Scholar] [CrossRef]
- Ormazábal-Toledo, R.; Rezende, M.C.; Vidal, M. The Simulation of Solvent Polarizabilities and Dipolarities with Polarizable Continuum Model. J. Phys. Chem. B 2024, 128, 7208–7218. [Google Scholar] [CrossRef]
- Martins, C.T.; El Seoud, O.A. Thermo-Solvatochromism of Merocyanine Polarity Probes—What Are the Consequences of Increasing Probe Lipophilicity through Annelation? Eur. J. Org. Chem. 2008, 2008, 1165–1180. [Google Scholar] [CrossRef]
- Hünig, S.; Rosenthal, O. Farbe und Konstitution II: Phenolbetainfarbstoffe. Justus Liebigs Ann. Chem. 1955, 592, 161–179. [Google Scholar] [CrossRef]
- Dimroth, K.; Reichardt, C.; Siepmann, T.; Bohlmann, F. Über Pyridinium-N-phenol-betaine und ihre Verwendung zur Charakterisierung der Polarität von Lösungsmitteln. Justus Liebigs Ann. Chem. 1963, 661, 1–37. [Google Scholar] [CrossRef]
- Reichardt, C. Solvatochromic Dyes as Solvent Polarity Indicators. Chem. Rev. 1994, 94, 2319–2358. [Google Scholar] [CrossRef]
- Machado, V.G.; Stock, R.I.; Reichardt, C. Pyridinium N-Phenolate Betaine Dyes. Chem. Rev. 2014, 114, 10429–10475. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry, 4th ed.; Wiley-VCH Verlag: Weinheim, Germany, 2011; pp. 455–461. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Rezende, M.C. A generalized reversal model for the solvatochromism of merocyanines. J. Phys. Org. Chem. 2016, 29, 460–467. [Google Scholar] [CrossRef]
- Rezende, M.C.; Dominguez, M.; Aracena, A.; Millán, D. Solvatochromism and electrophilicity. Chem. Phys. Lett. 2011, 514, 267–273. [Google Scholar] [CrossRef]
- Rezende, M.C.; Aracena, A. Electrophilicity and solvatochromic reversal of pyridinium phenolate betaine dyes. Chem. Phys. Lett. 2012, 542, 147–152. [Google Scholar] [CrossRef]
- Keum, S.-R.; Hur, M.-S.; Kazmaier, P.M.; Buncel, E. Thermo- and photochromic dyes: Indolino-benzospiropyrans. Part 1. UV–VIS spectroscopic studies of 1,3,3-spiro(2H-1-benzopyran-2,2′-indolines) and the open-chain merocyanine forms; solvatochromism and medium effects on spiro ring formation. Can. J. Chem. 1991, 69, 1940–1947. [Google Scholar] [CrossRef]
- Le Beuze, A.; Samat, A.; Botrel, A.; Appriou, P.; Guglielmetti, R. Détermination expérimentale du moment dipolaire de mérocyanines hétérocycliques. J. Chim. Phys. 1978, 75, 46–52. [Google Scholar] [CrossRef]
- Rajagopal, S.; Buncel, E. Synthesis and Electronic Spectral Characteristics of Some New Azo Merocyanine Dyes. Dye. Pigment. 1991, 17, 303–321. [Google Scholar] [CrossRef]
- Diemer, V.; Chaumeil, H.; Defoin, A.; Jacques, P.; Carré, C. Synthesis of 4-[N-methyl-4-pyridinio]-phenolate (POMP) and negative solvatochromism of this model molecule in view of nonlinear optical applications. Tetrahedron Lett. 2005, 46, 4737–4740. [Google Scholar] [CrossRef]
- Jacques, P. On the Relative Contributions of Nonspecific and Specific Interactions to the Unusual Solvatochromism of a Typical Merocyanine Dye. J. Phys. Chem. 1986, 90, 5535–5539. [Google Scholar] [CrossRef]
- Minkovska, S.; Jeliazkova, B.; Borisova, E.; Avramov, L.; Deligeorgiev, T. Substituent and solvent effect on the photochromic properties of a series of spiroindolinonaphthooxazines. J. Photochem. Photobiol. A Chem. 2004, 163, 121–126. [Google Scholar] [CrossRef][Green Version]
- Paley, M.S.; Meehan, E.J.; Smith, C.D.; Rosenberger, F.E.; Howard, S.C.; Harris, J.M. Synthesis and characterization of a novel betaine dye: 2,4-dimethyl-6-(2,4,6-triphenyl-N-pyridinio)phenolate. J. Org. Chem. 1989, 54, 3432–3436. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Yang, W.; Mortier, W.J. The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines. J. Am. Chem. Soc. 1986, 108, 5708–5711. [Google Scholar] [CrossRef]
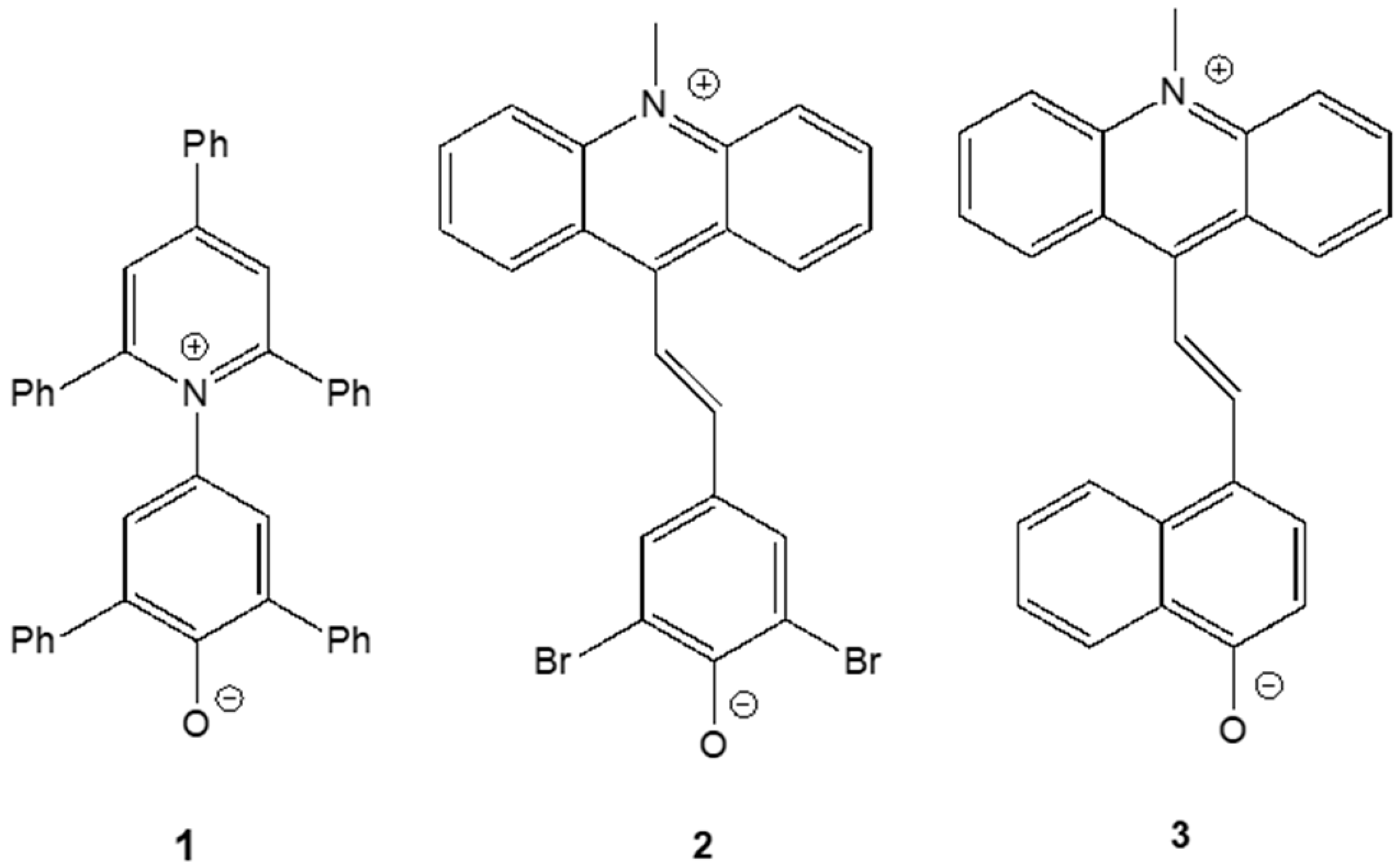

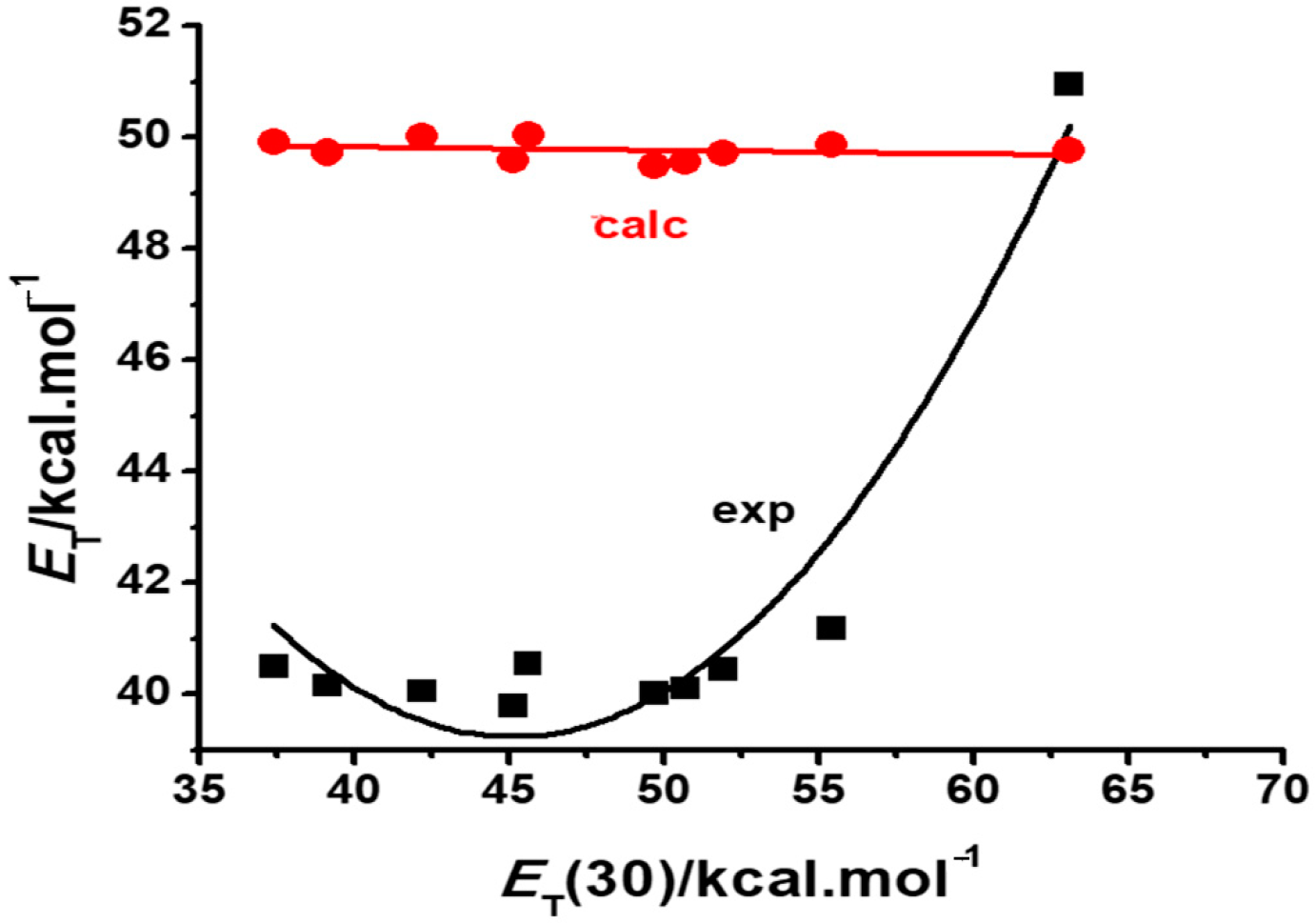

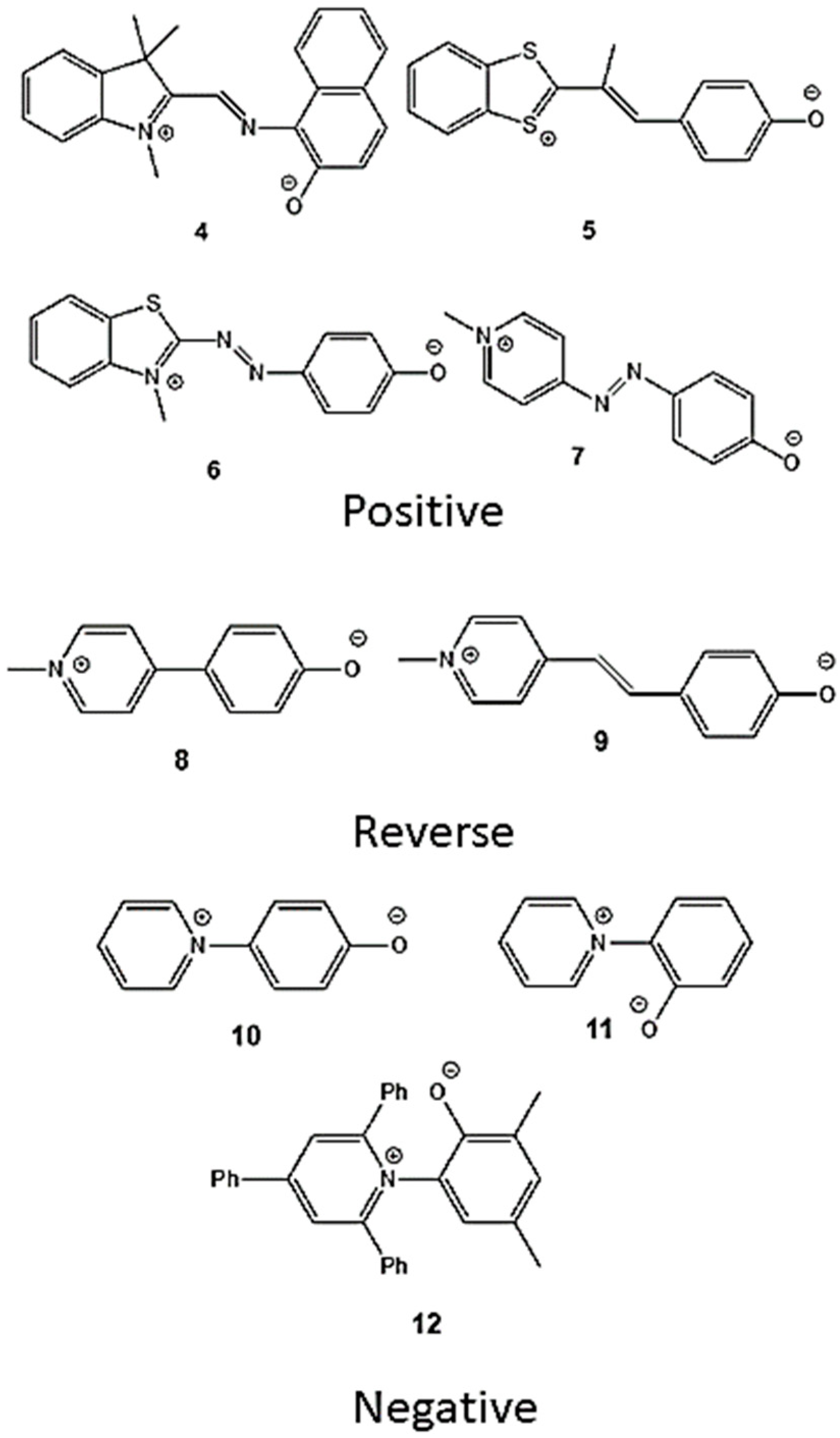
| Solvent | Solvent ET(30) Value/kcal·mol−1 | Dye 1 | Dye 2 a | Dye 3 a | |
|---|---|---|---|---|---|
| PCM | SMD | SMD | SMD | ||
| Cyclohexane | 30.9 | - | - | - | (54.98) |
| Benzene | 34.3 | - | - | - | (52.94) |
| Tetrahydrofuran | 37.4 | 33.66 | 34.51 | 49.93 (40.50) | 50.89 |
| Chloroform | 39.1 | 32.42 | 33.13 | 49.73 (40.16) | 50.73 (51.51) |
| Acetone | 42.2 | 35.63 | 37.41 | 50.02 (40.06) | 50.68 (51.51) |
| Dimethylsulfoxide | 45.1 | 36.57 | 38.42 | 49.60 (39.78) | 50.21 |
| Acetonitrile | 45.6 | 36.30 | 38.51 | 50.05 (40.54) | 50.60 |
| 1-Butanol | 49.7 | 35.46 | 39.73 | 49.48 (40.02) | 49.60 |
| Benzyl alcohol | 50.4 | - | - | - | (46.49) |
| 1-Propanol | 50.7 | 35.60 | 40.24 | 49.56 (40.11) | 49.63 |
| Ethanol | 51.9 | 35.88 | 40.74 | 49.72 (40.44) | 49.75 |
| Methanol | 55.4 | 36.23 | 42.27 | 49.86 (41.18) | 49.71 (46.49) |
| Formamide | 55.8 | - | - | - | (46.49) |
| Water | 63.1 | 37.00 | 43.64 | 49.78 (50.96) | 49.48 |
| Compound | fG+ (Phenolate) | fG+ (Heterocyclic) | ΔfG+ |
|---|---|---|---|
| 1 | 0.17 | 0.83 | 0.66 |
| 2 | 0.54 | 0.46 | −0.08 |
| 3 | 0.57 | 0.43 | −0.14 |
| 4:00 a | 0.74 | 0.26 | −0.48 |
| 5:00 a | 0.7 | 0.3 | −0.4 |
| 6:00 a | 0.63 | 0.37 | −0.26 |
| 7:00 a | 0.58 | 0.42 | −0.16 |
| 8 b | 0.48 | 0.52 | −0.04 |
| 9 b | 0.53 | 0.47 | −0.06 |
| 10 a | 0.28 | 0.72 | 0.44 |
| 11 a | 0.21 | 0.79 | 0.58 |
| 12 a | 0.12 | 0.88 | 0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aracena, A.; Rezende, M.C.; Pizarro, S. Reproducing the Solvatochromism of Merocyanines by PCM Calculations. Molecules 2024, 29, 4103. https://doi.org/10.3390/molecules29174103
Aracena A, Rezende MC, Pizarro S. Reproducing the Solvatochromism of Merocyanines by PCM Calculations. Molecules. 2024; 29(17):4103. https://doi.org/10.3390/molecules29174103
Chicago/Turabian StyleAracena, Andrés, Marcos Caroli Rezende, and Sebastián Pizarro. 2024. "Reproducing the Solvatochromism of Merocyanines by PCM Calculations" Molecules 29, no. 17: 4103. https://doi.org/10.3390/molecules29174103
APA StyleAracena, A., Rezende, M. C., & Pizarro, S. (2024). Reproducing the Solvatochromism of Merocyanines by PCM Calculations. Molecules, 29(17), 4103. https://doi.org/10.3390/molecules29174103






