Magnetic Exchange Mechanism and Quantized Anomalous Hall Effect in Bi2Se3 Film with a CrWI6 Monolayer
Abstract
1. Introduction
2. Model and Computational Details
3. Results and Discussion
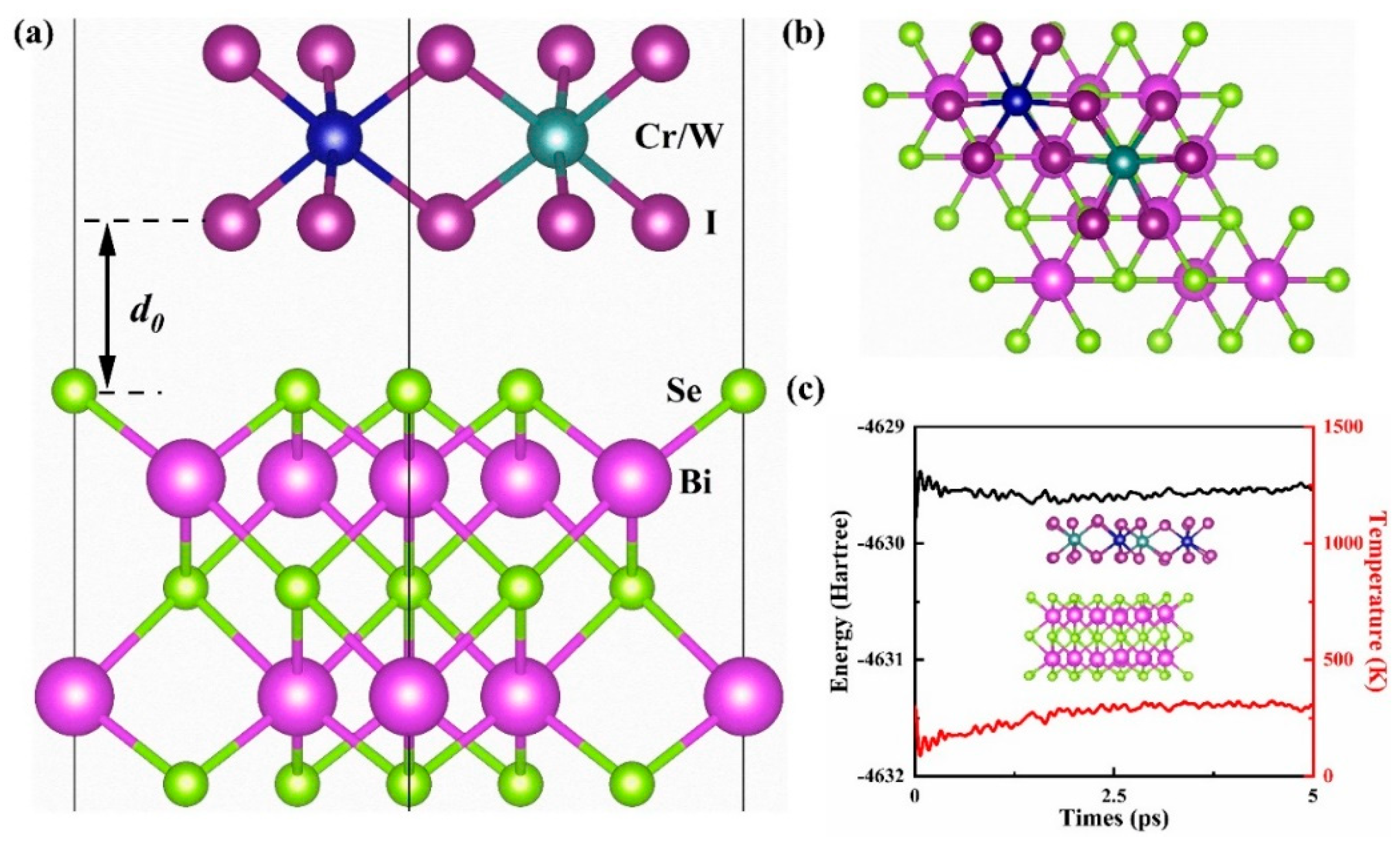
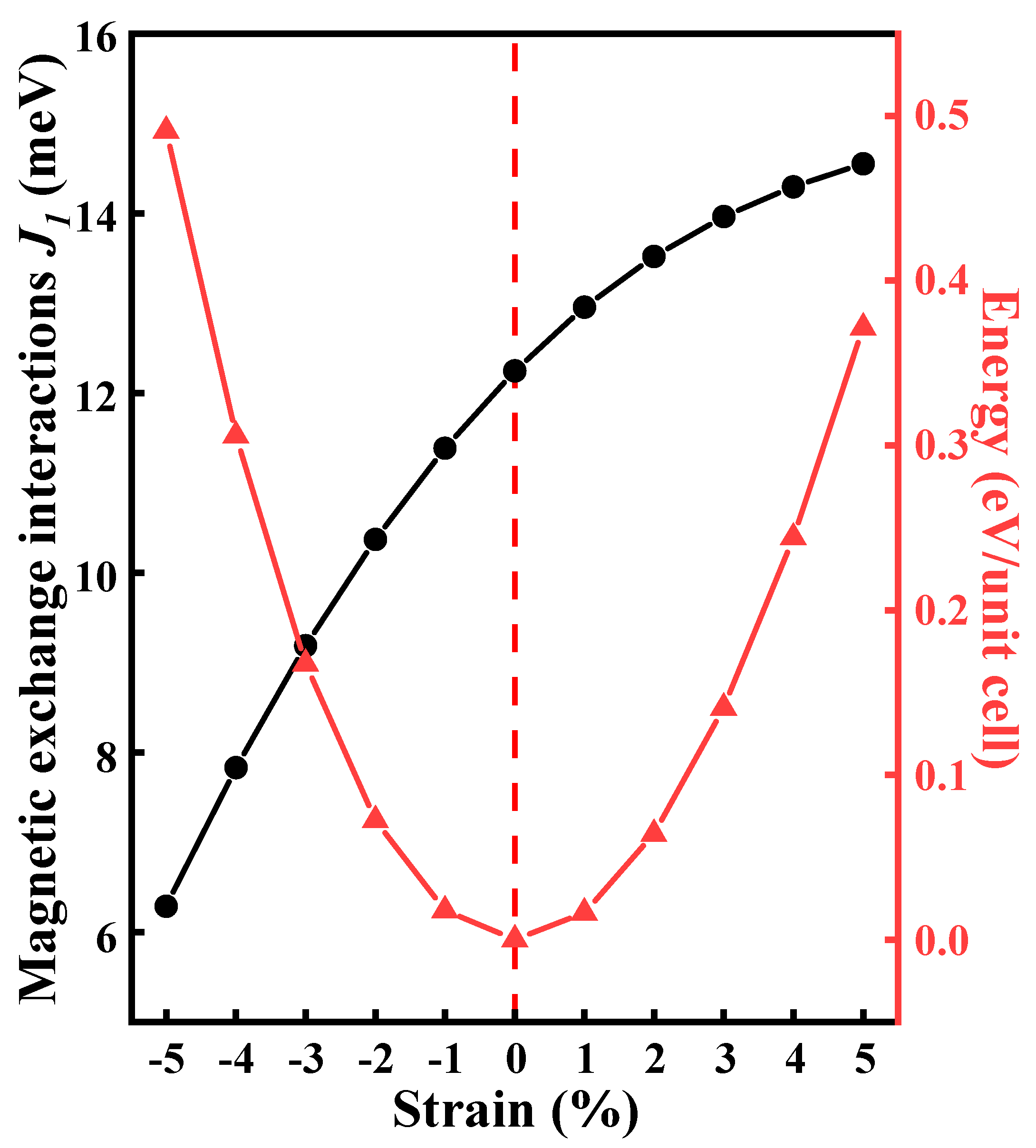
3.1. Magnetism and Structure of CrWI6
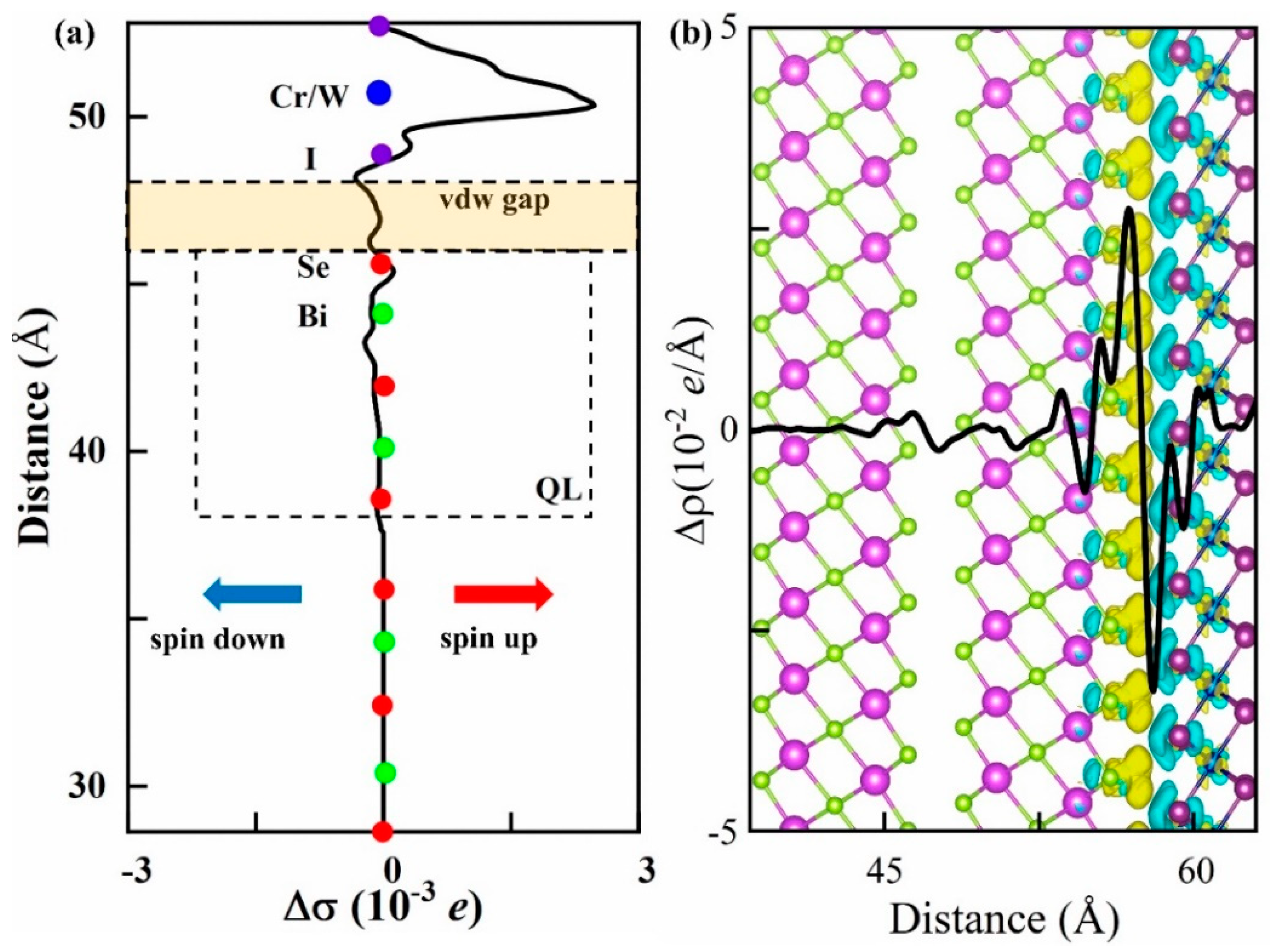
3.2. Electronic Properties of Heterojunction
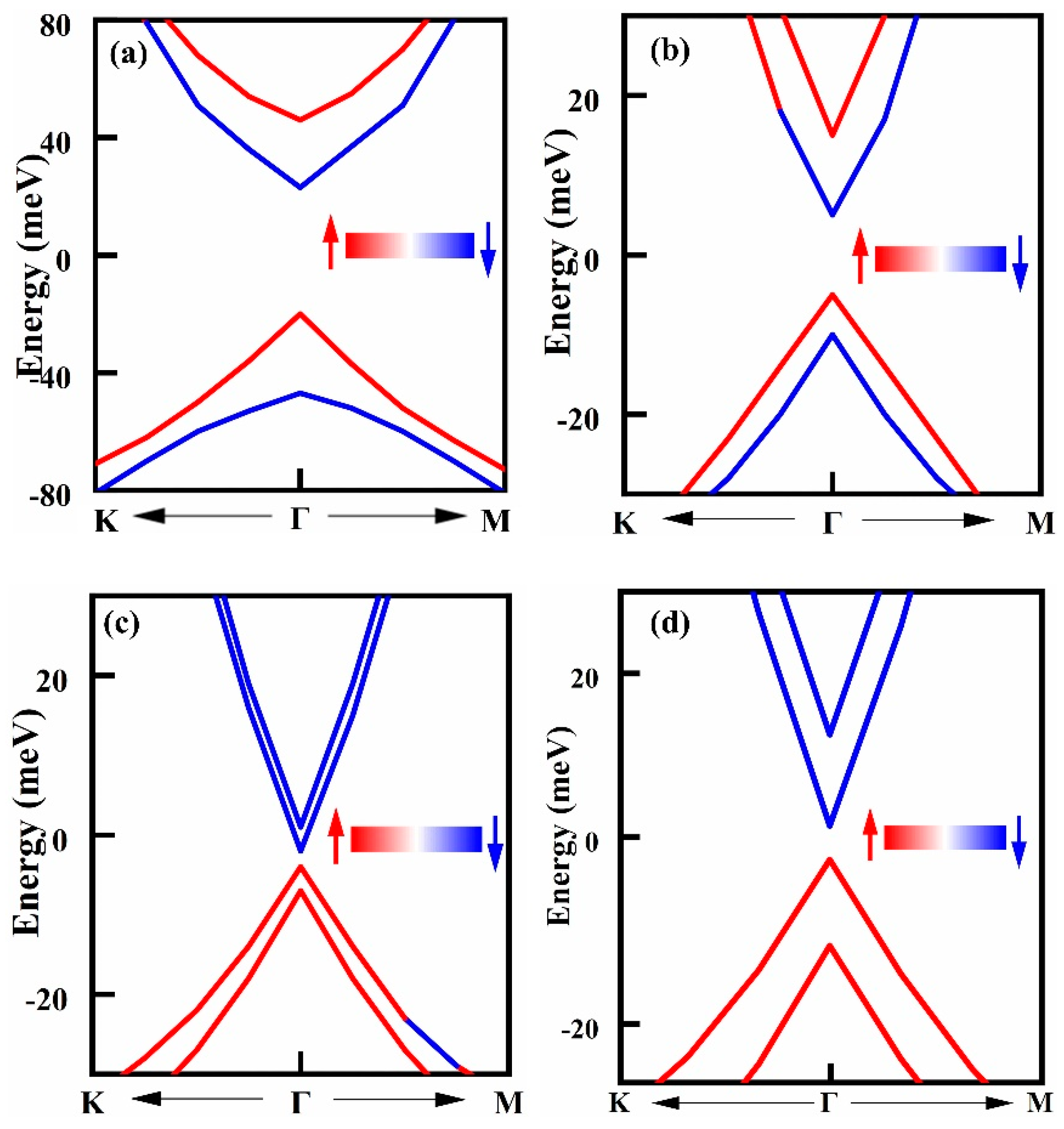
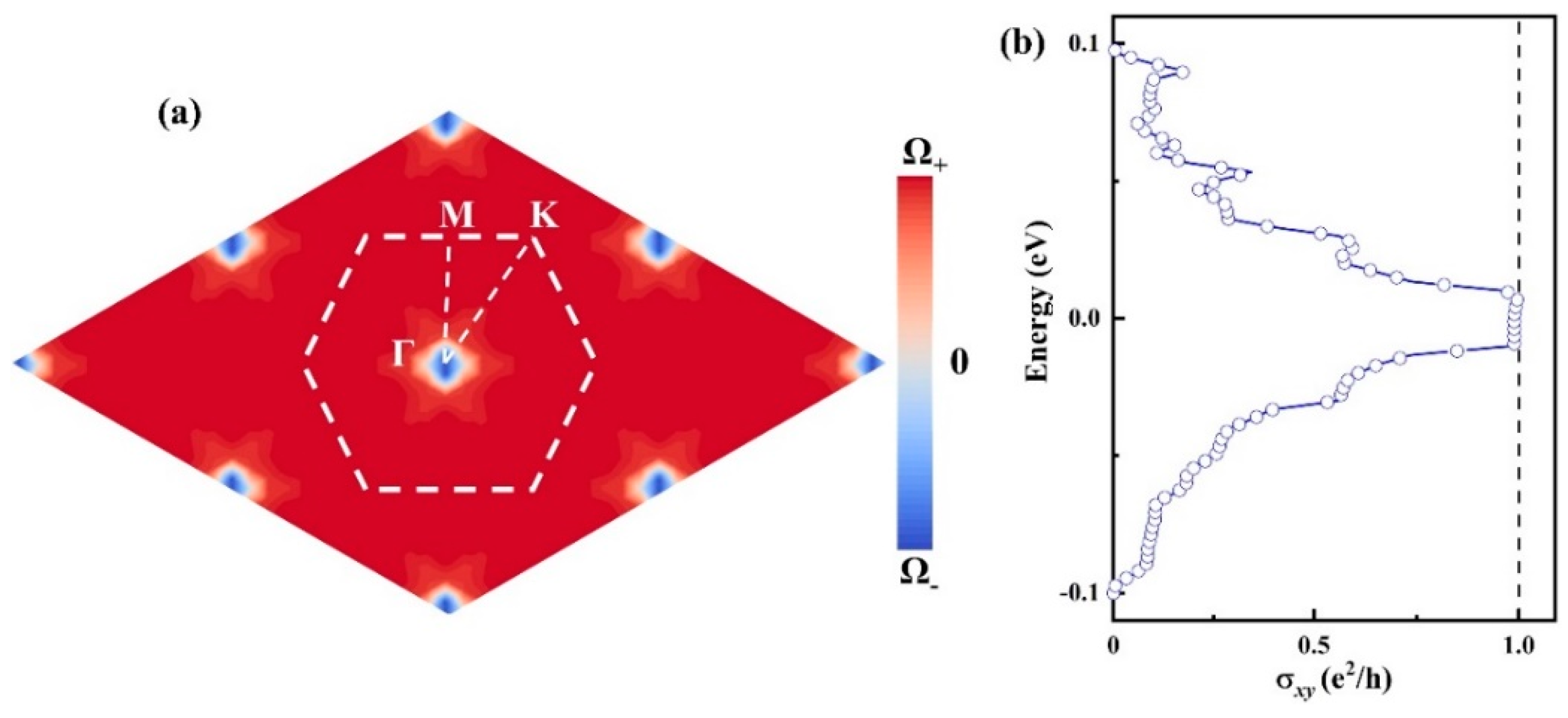
3.3. Topological Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Hesjedal, T. Magnetic Topological Insulator Heterostructures: A Review. Adv. Mater. 2023, 35, 2102427. [Google Scholar] [CrossRef]
- Li, X.-G.; Zhang, G.-F.; Wu, G.-F.; Chen, H.; Culcer, D.; Zhang, Z.-Y. Proximity effects in topological insulator heterostructures. Chin. Phys. B 2013, 22, 097306. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, W.; Zhang, H.J.; Zhang, S.C.; Dai, X.; Fang, Z. Quantized Anomalous Hall Effect in Magnetic Topological Insulators. Science 2010, 329, 61–64. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Feng, X.; Wang, J.; Lian, B.; Zhang, J.; Chang, C.; Guo, M.; Ou, Y.; Feng, Y.; Zhang, S.-C.; et al. Magnetic quantum phase transition in Cr-doped Bi2(SexTe1−x)3 driven by the Stark effect. Nat. Nanotechnol. 2017, 12, 953–957. [Google Scholar] [CrossRef]
- Wei, P.; Katmis, F.; Assaf, B.A.; Steinberg, H.; Jarillo-Herrero, P.; Heiman, D.; Moodera, J.S. Exchange-Coupling-Induced Symmetry Breaking in Topological Insulators. Phys. Rev. Lett. 2013, 110, 186807. [Google Scholar] [CrossRef]
- Pan, L.; Grutter, A.; Zhang, P.; Che, X.; Nozaki, T.; Stern, A.; Street, M.; Zhang, B.; Casas, B.; He, Q.L.; et al. Observation of Quantum Anomalous Hall Effect and Exchange Interaction in Topological Insulator/Antiferromagnet Heterostructure. Adv. Mater. 2020, 32, 2001460. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Xiao, D.; Wang, F.; Shin, J.-H.; Andreoli, D.; Zhang, J.; Xiao, R.; Zhao, Y.-F.; Kayyalha, M.; Zhang, L.; et al. Concurrence of quantum anomalous Hall and topological Hall effects in magnetic topological insulator sandwich heterostructures. Nat. Mater. 2020, 19, 732–737. [Google Scholar] [CrossRef] [PubMed]
- Kanagaraj, M.; Yizhe, S.; Ning, J.; Zhao, Y.; Tu, J.; Zou, W.; He, L. Topological quantum weak antilocalization limit and anomalous Hall effect in semimagnetic Bi2−xCrxSe3/Bi2Se3−y Tey heterostructure. Mater. Res. Express 2020, 7, 016401. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, D.; Zang, Y.; Yuan, Y.; Jiang, G.; Liao, M.; Zhang, D.; He, K.; Ma, X.; Xue, Q.; et al. Ferromagnetism in vanadium-doped Bi2Se3 topological insulator films. APL Mater. 2017, 5, 076106. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Tang, P.; Wang, Y.-L.; Feng, X.; Li, K.; Zhang, Z.; Wang, Y.; Wang, L.-L.; Chen, X.; Liu, C.; et al. Chemical-Potential-Dependent Gap Opening at the Dirac Surface States of Bi2Se3 Induced by Aggregated Substitutional Cr Atoms. Phys. Rev. Lett. 2014, 112, 056801. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, S.; Akhgar, G.; Gebert, M.; Karel, J.; Edmonds, M.T.; Fuhrer, M.S. Recent Progress in Proximity Coupling of Magnetism to Topological Insulators. Adv. Mater. 2021, 33, 2007795. [Google Scholar] [CrossRef] [PubMed]
- Mathimalar, S.; Sasmal, S.; Bhardwaj, A.; Abhaya, S.; Pothala, R.; Chaudhary, S.; Satpati, B.; Raman, K.V. Signature of gate-controlled magnetism and localization effects at Bi2Se3/EuS interface. Npj Quantum Mater. 2020, 5, 64. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Men, V.N.; Tugushev, V.V.; Chulkov, E.V. Interface induced states at the boundary between a 3D topological insulator Bi2Se3 and a ferromagnetic insulator EuS. J. Magn. Magn. Mater. 2015, 383, 30–33. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Otrokov, M.M.; Chulkov, E.V. New Universal Type of Interface in the Magnetic Insulator/Topological Insulator Heterostructures. Nano Lett. 2018, 18, 6521–6529. [Google Scholar] [CrossRef]
- Lee, A.T.; Han, M.J.; Park, K. Magnetic proximity effect and spin-orbital texture at the Bi2Se3/EuS interface. Phys. Rev. B 2014, 90, 155103. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Men’shov, V.N.; Tugushev, V.V.; Echenique, P.M.; Chulkov, E.V. Magnetic proximity effect at the three-dimensional topological insulator/magnetic insulator interface. Phys. Rev. B 2013, 88, 144430. [Google Scholar] [CrossRef]
- Luo, W.; Qi, X.-L. Massive Dirac surface states in topological insulator/magnetic insulator heterostructures. Phys. Rev. B 2013, 87, 085431. [Google Scholar] [CrossRef]
- Hou, Y.; Kim, J.; Wu, R. Magnetizing topological surface states of Bi2Se3 with a CrI3 monolayer. Sci. Adv. 2019, 5, eaaw1874. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Gong, C.; Zhang, X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science 2019, 363, eaav4450. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Feng, J.; Wu, F.; Ahmed, D.; Huang, B.; Xiang, H.; Deng, K.; Kan, E. Toward Intrinsic Room-Temperature Ferromagnetism in Two-Dimensional Semiconductors. J. Am. Chem. Soc. 2018, 140, 11519–11525. [Google Scholar] [CrossRef] [PubMed]
- Kanamori, J. Superexchange Interaction and Symmetry Properties of Electron Orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 1955, 100, 564. [Google Scholar] [CrossRef]
- Anderson, P.W. Antiferromagnetism. Theory of Superexchange Interaction. Phys. Rev. 1950, 79, 350–356. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. CP2K: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Wang, Y.; Qiu, Z.Q.; Cava, R.J.; et al. Discovery of Intrinsic Ferromagnetism in Two-Dimensional van Der Waals Crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Wang, X.; Wu, R.; Wang, D.; Freeman, A.J. Torque method for the theoretical determination of magnetocrystalline anisotropy. Phys. Rev. B 1996, 54, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.-B.; Qu, Q.; Zhu, P.; Lam, C.-H. Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides. J. Mater. Chem. C 2015, 3, 12457–12468. [Google Scholar] [CrossRef]
- Wang, H.; Fan, F.; Zhu, S.; Wu, H. Doping enhanced ferromagnetism and induced half-metallicity in CrI3 monolayer. EPL 2016, 114, 47001. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Chen, L.; Shi, C.; Jiang, C.; Liu, H.; Cui, G.; Wang, D.; Li, X.; Gao, K.; Zhang, X. Realization of quantized anomalous Hall effect by inserting CrI3 layer in Bi2Se3 film. New J. Phys. 2020, 22, 073005. [Google Scholar] [CrossRef]
- Zhang, Y.; He, K.; Chang, C.-Z.; Song, C.-L.; Wang, L.-L.; Chen, X.; Jia, J.-F.; Fang, Z.; Dai, X.; Shan, W.-Y.; et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 2010, 6, 584–588. [Google Scholar] [CrossRef]
- Kim, S.-W.; Kim, H.-J.; Cheon, S.; Kim, T.-H. Circular dichroism of emergent chiral stacking orders in quasi-one-dimensional charge density waves. Phys. Rev. Lett. 2022, 128, 046401. [Google Scholar] [CrossRef]
- Yao, Y.; Kleinman, L.; MacDonald, A.H.; Sinova, J.; Jungwirth, T.; Wang, D.; Wang, E.; Niu, Q. First Principles Calculation of Anomalous Hall Conductivity in Ferromagnetic bcc Fe. Phys. Rev. Lett. 2004, 92, 037204. [Google Scholar] [CrossRef]
- Qi, X.-L.; Wu, Y.-S.; Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 2006, 74, 085308. [Google Scholar] [CrossRef]
- Li, P.; You, Y.; Huang, K.; Luo, W. Quantum Anomalous Hall Effect in Cr2Ge2Te6/Bi2Se3/Cr2Ge2Te6 Heterostructures. J. Phys.: Condens. Matter 2021, 33, 465003. [Google Scholar] [CrossRef]
- Li, P.; Yu, J.; Wang, Y.; Luo, W. Electronic Structure and Topological Phases of the Magnetic Layered Materials MnBi2Te4. MnBi2Se4 and MnSb2Te4. Phys. Rev. B 2021, 103, 155118. [Google Scholar] [CrossRef]

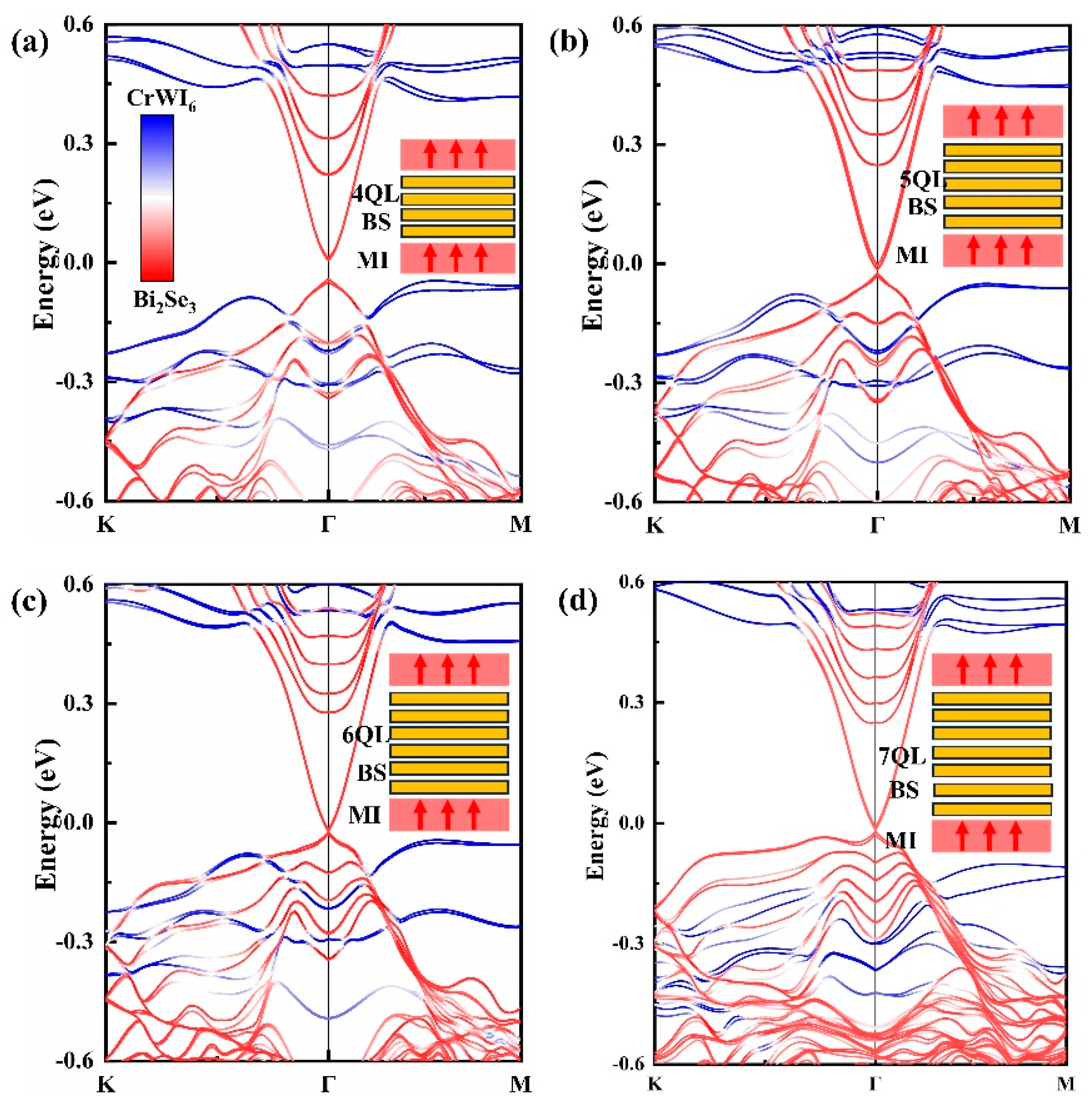
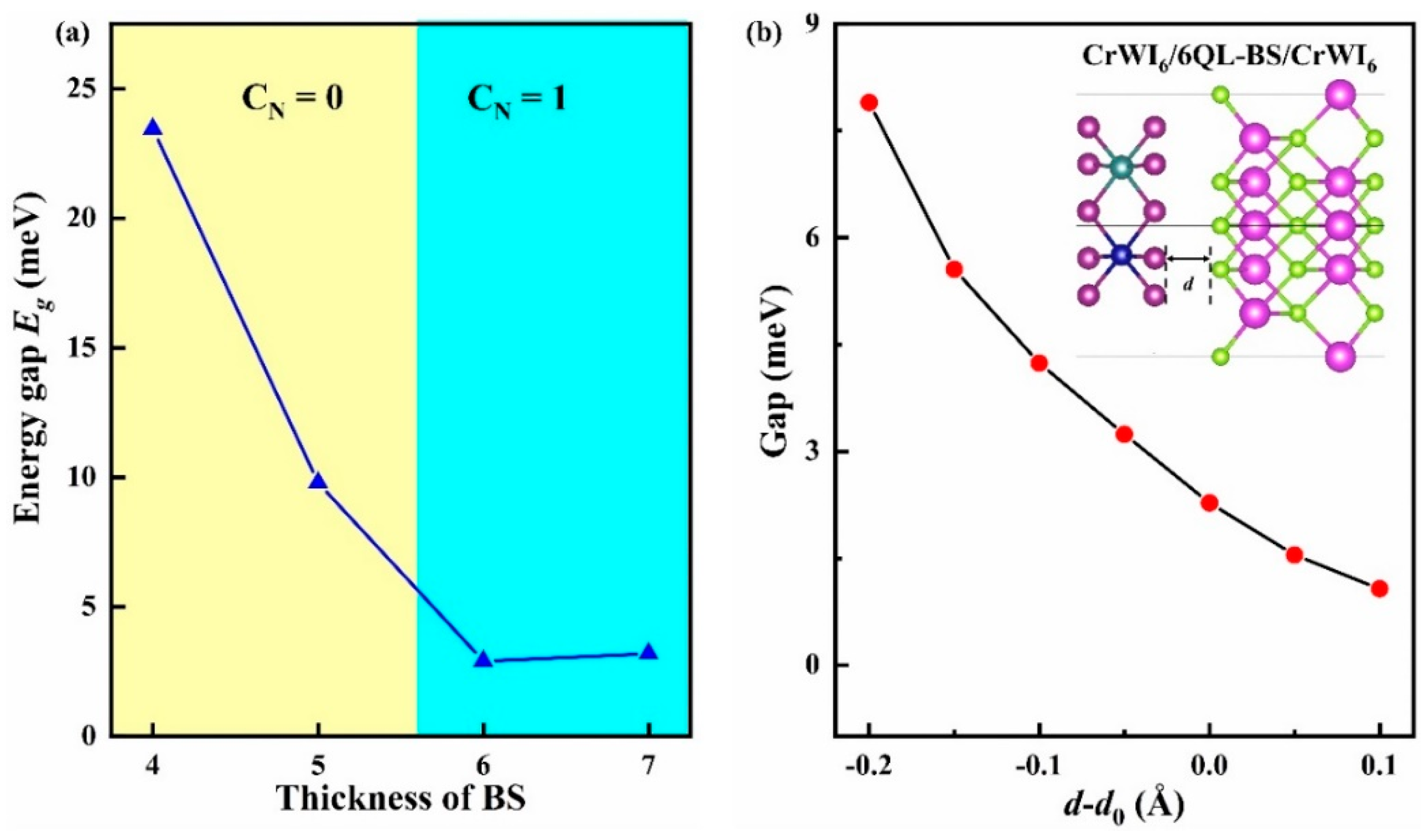
| Thickness of BS | Energy Gaps Eg (meV) |
|---|---|
| 4QLs | 23.5 (Se site) |
| 5QLs | 9.8 (Se site) |
| 6QLs | 2.9 (Se site) 1.4 (Bi site) 1.1 (Hole site) |
| 7QLs | 3.2 (Se site) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; He, F.; Liu, Q.; Yu, Y.; Zhang, M. Magnetic Exchange Mechanism and Quantized Anomalous Hall Effect in Bi2Se3 Film with a CrWI6 Monolayer. Molecules 2024, 29, 4101. https://doi.org/10.3390/molecules29174101
Huang H, He F, Liu Q, Yu Y, Zhang M. Magnetic Exchange Mechanism and Quantized Anomalous Hall Effect in Bi2Se3 Film with a CrWI6 Monolayer. Molecules. 2024; 29(17):4101. https://doi.org/10.3390/molecules29174101
Chicago/Turabian StyleHuang, He, Fan He, Qiya Liu, You Yu, and Min Zhang. 2024. "Magnetic Exchange Mechanism and Quantized Anomalous Hall Effect in Bi2Se3 Film with a CrWI6 Monolayer" Molecules 29, no. 17: 4101. https://doi.org/10.3390/molecules29174101
APA StyleHuang, H., He, F., Liu, Q., Yu, Y., & Zhang, M. (2024). Magnetic Exchange Mechanism and Quantized Anomalous Hall Effect in Bi2Se3 Film with a CrWI6 Monolayer. Molecules, 29(17), 4101. https://doi.org/10.3390/molecules29174101








