Time-Resolved Circular Dichroism in Molecules: Experimental and Theoretical Advances
Abstract
1. Introduction
2. TRCD: Experimental Aspects
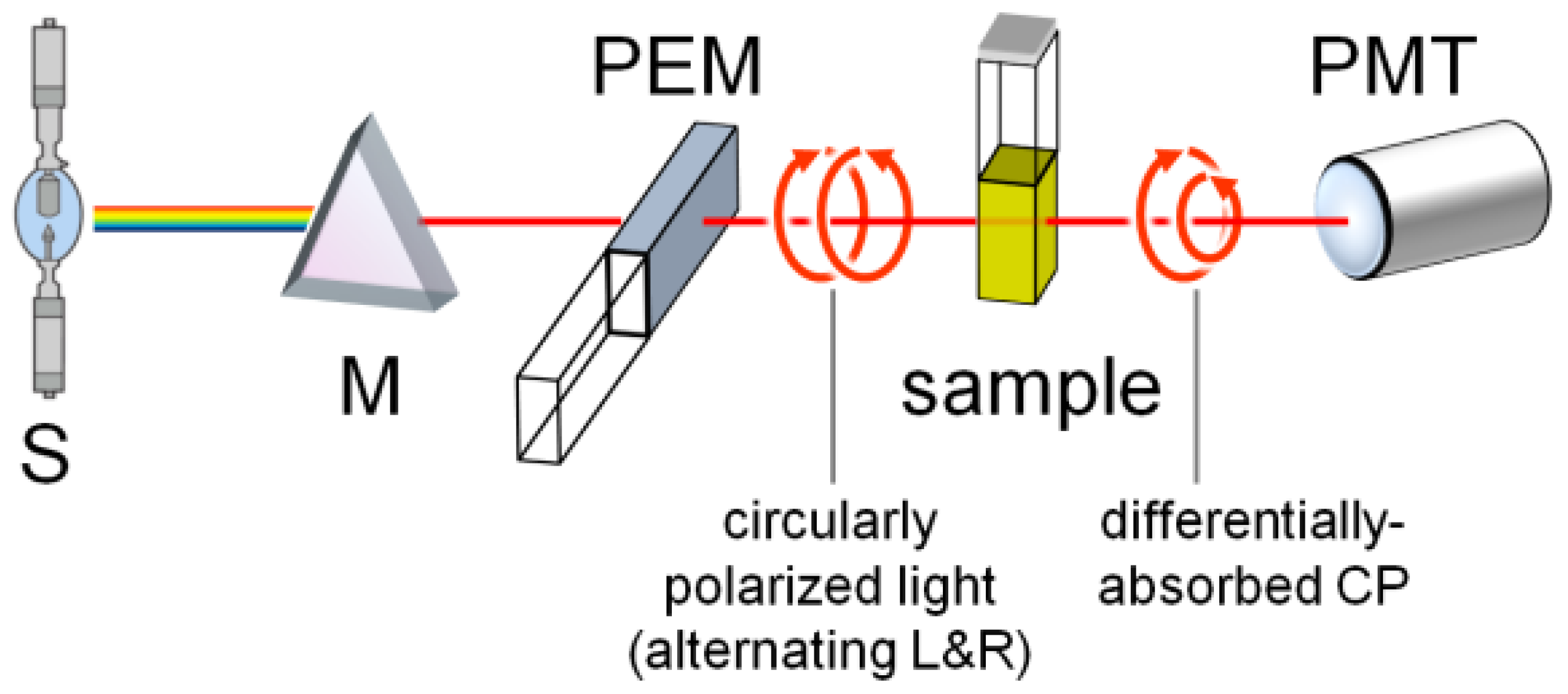
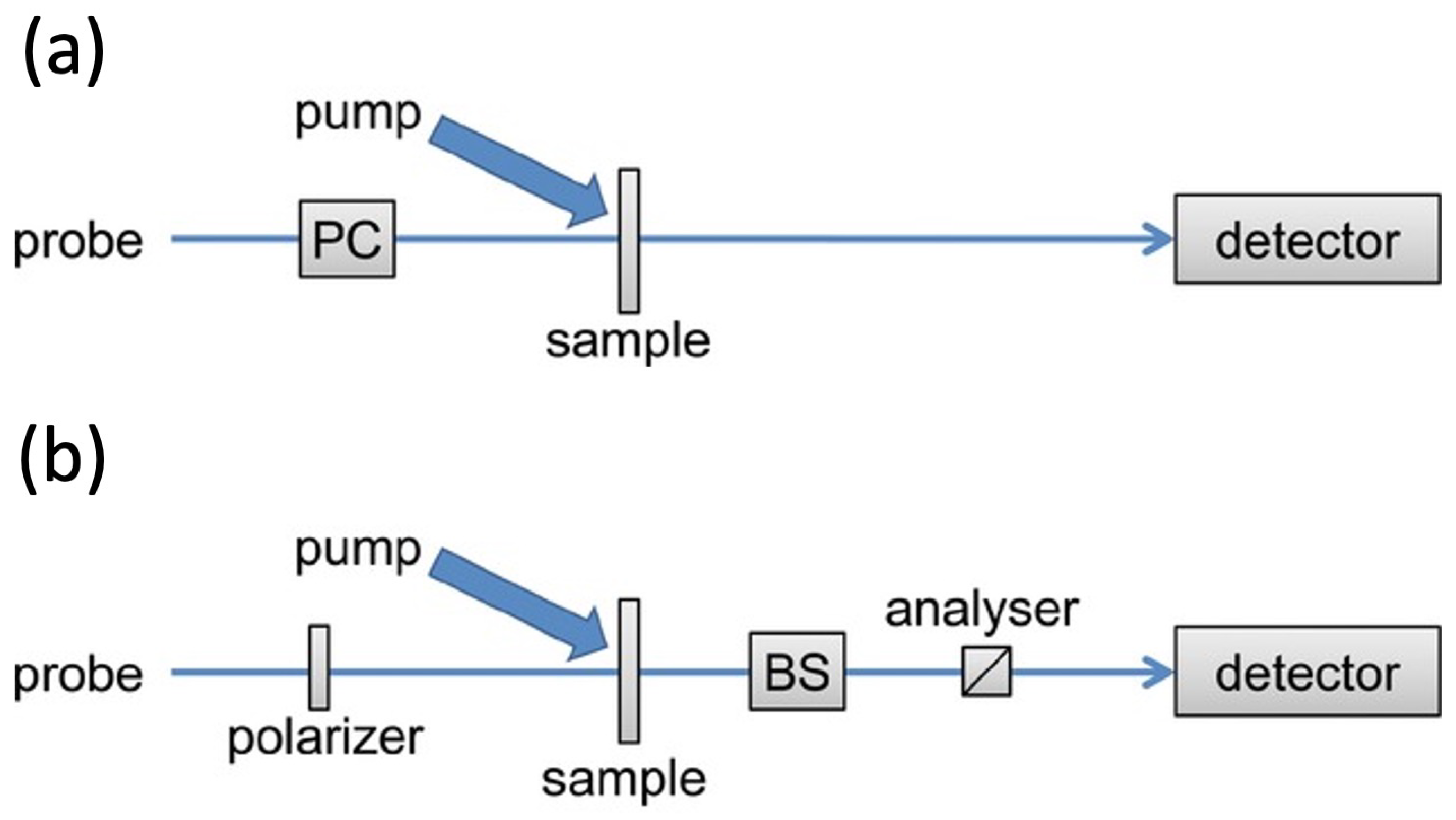
2.1. Ultrafast TRCD: Differential Absorption and Ellipsometric Setup
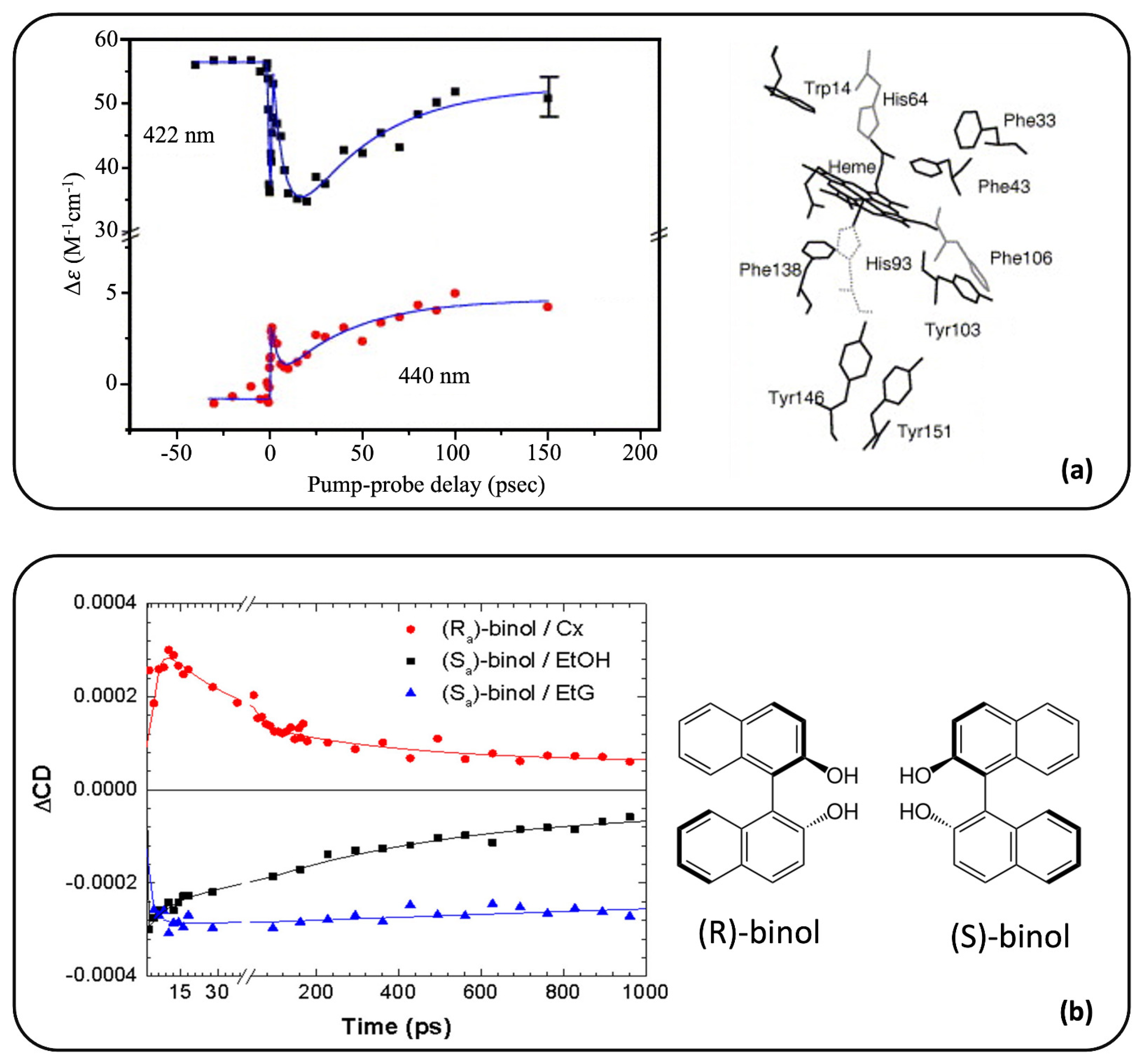
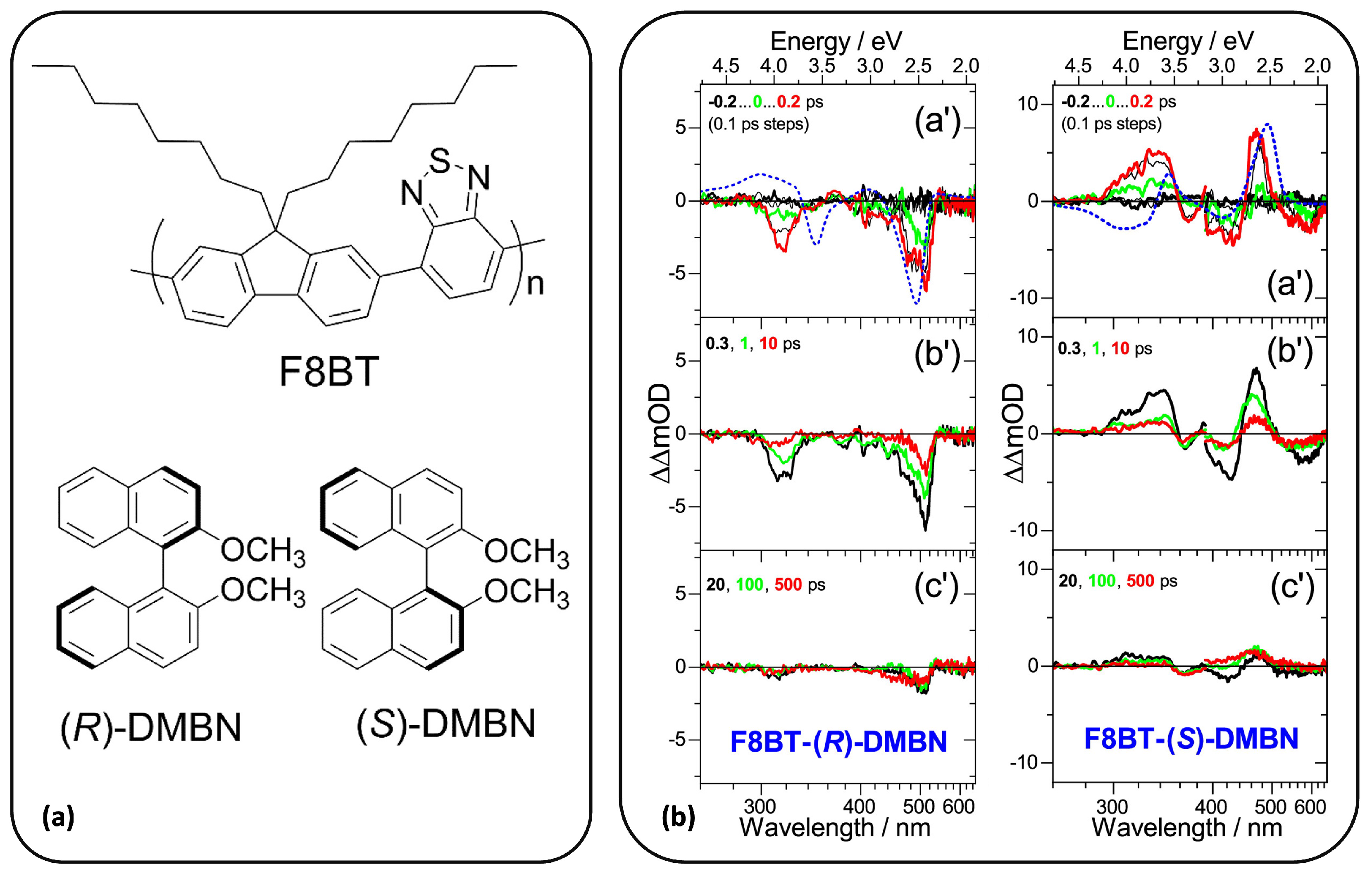
2.2. Broadband TRCD Detection
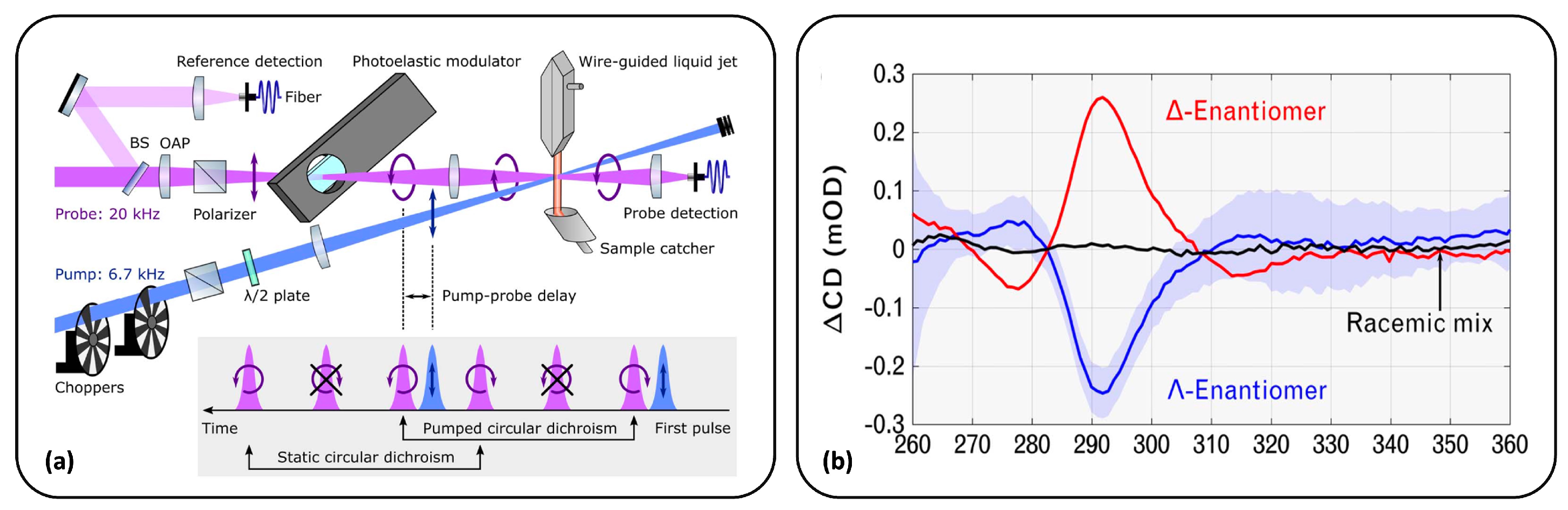
2.3. Single-Shot Ellipsometric TRCD
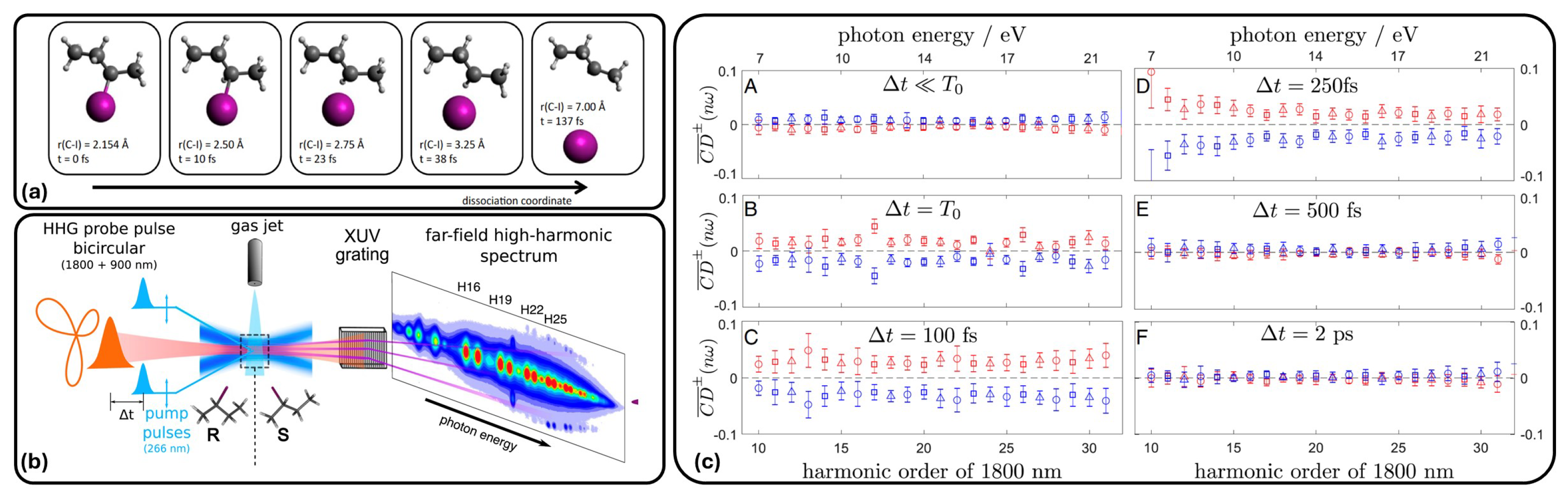
2.4. High-Harmonic Generation and Photoelectron Measurements for CD Applications
3. TRCD: Theoretical Methods
3.1. Non-Adiabatic Molecular Dynamics
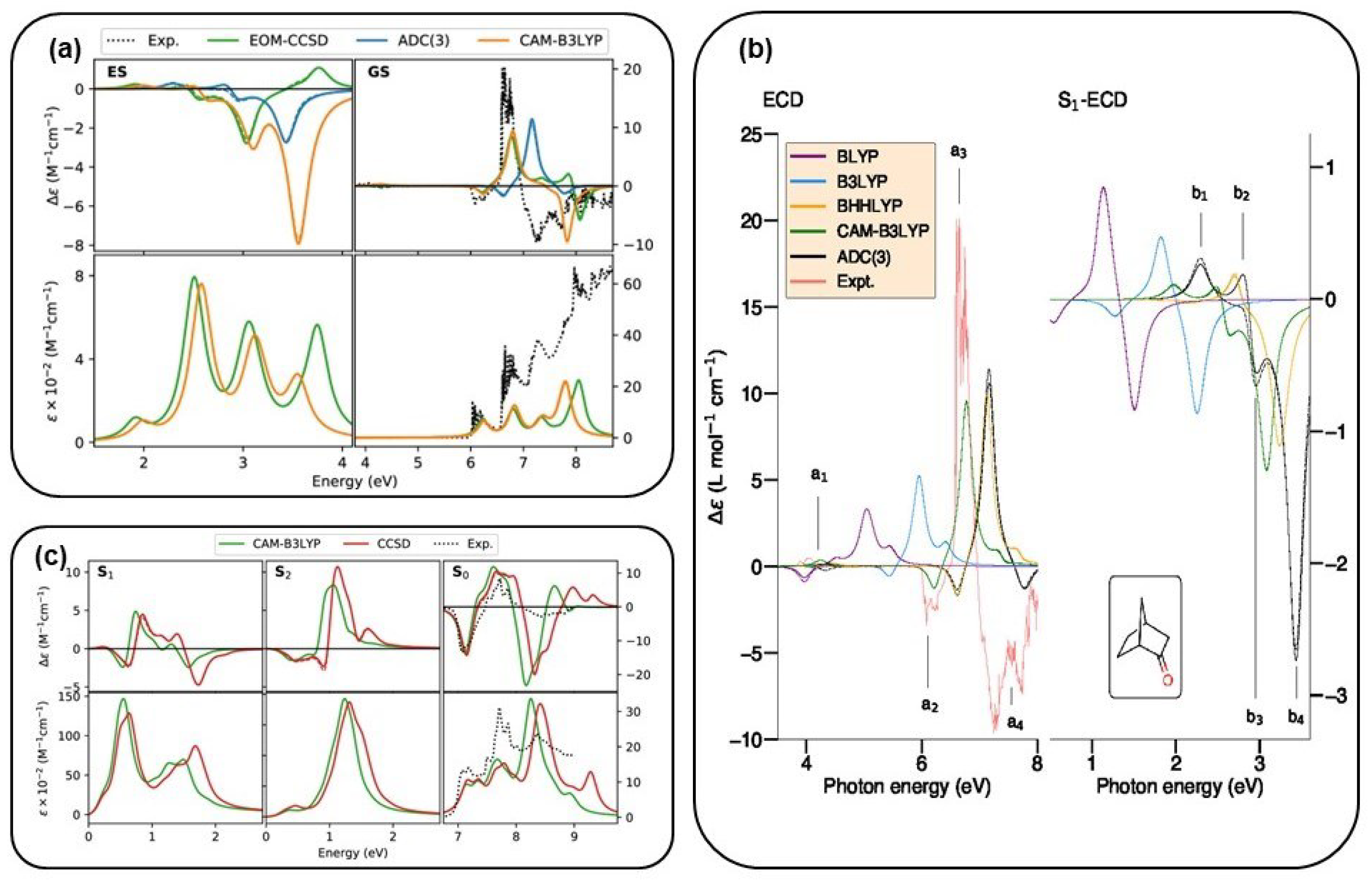
3.2. Excited-State CD Spectra
4. Discussion and Outlook
- coupling techniques such as NAMD, which explore excited-state PESs, with approaches that compute ESCD spectra, with explicit focus on the population of excited states over time;
- using the time-resolved version of methods such as LR-TDDFT to easily calculate ESCD in a general way, once an excited-state geometry is provided (from dynamics or geometry optimization).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pelayo, J.J.; Valencia, I.; García, A.P.; Chang, L.; López, M.; Toffoli, D.; Stener, M.; Fortunelli, A.; Garzón, I.L. Chirality in bare and ligand-protected metal nanoclusters. Adv. Phys. X 2018, 3, 1509727. [Google Scholar] [CrossRef]
- Gray, L.E., Jr.; Ostby, J.; Furr, J.; Price, M.; Veeramachaneni, D.R.; Parks, L. Perinatal exposure to the phthalates DEHP, BBP, and DINP, but not DEP, DMP, or DOTP, alters sexual differentiation of the male rat. Toxicol. Sci. 2000, 58, 350–365. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Scialli, A.R. Thalidomide: The tragedy of birth defects and the effective treatment of disease. Toxicol. Sci. 2011, 122, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Brooks, W.H.; Guida, W.C.; Daniel, K.G. The significance of chirality in drug design and development. Curr. Top. Med. Chem. 2011, 11, 760. [Google Scholar] [CrossRef]
- Müller, C.; Bauer, A.; Bach, T. Licht-getriebene enantioselektive Organokatalyse. Angew. Chem. 2009, 121, 6767–6769. [Google Scholar] [CrossRef]
- Kameta, N.; Masuda, M.; Shimizu, T. Qualitative/chiral sensing of amino acids by naked-eye fluorescence change based on morphological transformation and hierarchizing in supramolecular assemblies of pyrene-conjugated glycolipids. Chem. Commun. 2015, 51, 11104–11107. [Google Scholar] [CrossRef]
- Frank, F.C. On spontaneous asymmetric synthesis. Biochim. Biophys. Acta 1953, 11, 459–463. [Google Scholar] [CrossRef] [PubMed]
- Budin, I.; Szostak, J.W. Expanding roles for diverse physical phenomena during the origin of life. Annu. Rev. Biophys. 2010, 39, 245–263. [Google Scholar] [CrossRef]
- Meierhenrich, U.J. Amino acids and the asymmetry of life. Eur. Rev. 2013, 21, 190–199. [Google Scholar] [CrossRef]
- Pavlov, V.A.; I Klabunovskii, E. Homochirality origin in nature: Possible versions. Curr. Org. Chem. 2014, 18, 93–114. [Google Scholar] [CrossRef]
- Berova, N.; Nakanishi, K.; Woody, R.W. Circular Dichroism: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Stephens, P.J. Theory of vibrational circular dichroism. J. Phys. Chem. 1985, 89, 748–752. [Google Scholar] [CrossRef]
- Riehl, J.P.; Richardson, F.S. Circularly polarized luminescence spectroscopy. Chem. Rev. 1986, 86, 1–16. [Google Scholar] [CrossRef]
- Kuball, H.G. Chiroptical Analysis. In Encyclopedia of Analytical Science, 3rd ed.; Worsfold, P., Poole, C., Townshend, A., Miró, M., Eds.; Academic Press: Oxford, UK, 2013; pp. 1–21. [Google Scholar]
- Berova, N.; Di Bari, L.; Pescitelli, G. Application of electronic circular dichroism in configurational and conformational analysis of organic compounds. Chem. Soc. Rev. 2007, 36, 914–931. [Google Scholar] [CrossRef] [PubMed]
- Fasman, G.D. Circular Dichroism and the Conformational Analysis of Biomolecules; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Serber, R. The Theory of the Faraday Effect in Molecules. Phys. Rev. 1932, 41, 489. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Stephens, P.J. Magnetic Optical Activity. Annu. Rev. Phys. Chem. 1966, 17, 399. [Google Scholar] [CrossRef]
- Mason, W.R. A Practical Guide to Magnetic Circular Dichroism Spectroscopy; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Piepho, S.B.; Schatz, P.N. Group Theory in Spectroscopy: With Applications to Magnetic Circular Dichroism; Wiley-Interscience: Hoboken, NJ, USA, 1983. [Google Scholar]
- Elove, G.A.; Chaffotte, A.F.; Roder, H.; Goldberg, M.E. Early steps in cytochrome c folding probed by time-resolved circular dichroism and fluorescence spectroscopy. Biochemistry 1992, 31, 6876–6883. [Google Scholar] [CrossRef]
- Jones, C.M.; Henry, E.R.; Hu, Y.; Chan, C.K.; Luck, S.D.; Bhuyan, A.; Roder, H.; Hofrichter, J.; Eaton, W.A. Fast events in protein folding initiated by nanosecond laser photolysis. Proc. Natl. Acad. Sci. USA 1993, 90, 11860–11864. [Google Scholar] [CrossRef]
- van der Laan, G.; Figueroa, A.I. X-ray magnetic circular dichroism—A versatile tool to study magnetism. Coord. Chem. Rev. 2014, 277–278, 95. [Google Scholar] [CrossRef]
- Fan, T.; Grychtol, P.; Knut, R.; Hernandez-Garcia, C.; Hickstein, D.D.; Zusin, D.; Gentry, C.; Dollar, F.J.; Mancuso, C.A.; Hogle, C.W.; et al. Bright circularly polarized soft X-ray high harmonics for X-ray magnetic circular dichroism. Proc. Natl. Acad. Sci. USA 2015, 112, 14206. [Google Scholar] [CrossRef]
- Stamm, C.; Kachel, T.; Pontius, N.; Mitzner, R.; Quast, T.; Holldack, K.; Khan, S.; Lupulescu, C.; Aziz, E.F.; Wietstruk, M.; et al. Femtosecond modification of electron localization and transfer of angular momentum in nickel. Nat. Mater. 2007, 6, 740. [Google Scholar] [CrossRef]
- Boeglin, C.; Beaurepaire, E.; Halté, V.; López-Flores, V.; Stamm, C.; Pontius, N.; Dürr, H.A.; Bigot, J.Y. Distinguishing the ultrafast dynamics of spin and orbital moments in solids. Nature 2010, 465, 458. [Google Scholar] [CrossRef]
- Sun, S.; Gu, B.; Hu, H.; Lu, L.; Tang, D.; Chernyak, V.Y.; Li, X.; Mukamel, S. Direct Probe of Conical Intersection Photochemistry by Time-Resolved X-ray Magnetic Circular Dichroism. J. Am. Chem. Soc. 2024, 146, 19863. [Google Scholar] [CrossRef] [PubMed]
- Bayley, P. Fast kinetic studies with chiroptical techniques: Stopped flow circular dichroism and related methods. Prog. Biophys. Mol. Biol. 1981, 37, 149–180. [Google Scholar] [CrossRef]
- Anson, M.; Martin, S.R.; Bayley, P.M. Transient CD measurements at submillisecond time resolution—Application to studies of temperature-jump relaxation of equilibria of chiral biomolecules. Rev. Sci. Instrum. 1977, 48, 953–962. [Google Scholar] [CrossRef]
- Ferrone, F.; Hopfield, J.; Schnatterly, S. The measurement of transient circular dichroism: A new kinetic technique. Rev. Sci. Instrum. 1974, 45, 1392–1396. [Google Scholar] [CrossRef]
- Laouer, K.; Schmid, M.; Wien, F.; Changenet, P.; Hache, F. Folding Dynamics of DNA G-Quadruplexes Probed by Millisecond Temperature Jump Circular Dichroism. J. Phys. Chem. B 2021, 125, 8088–8098. [Google Scholar] [CrossRef]
- Khuc, M.T.; Mendonça, L.; Sharma, S.; Solinas, X.; Volk, M.; Hache, F. Measurement of circular dichroism dynamics in a nanosecond temperature-jump experiment. Rev. Sci. Instrum. 2011, 82, 054302. [Google Scholar] [CrossRef]
- Mendonça, L.; Steinbacher, A.; Bouganne, R.; Hache, F. Comparative Study of the Folding/Unfolding Dynamics of Poly(glutamic acid) in Light and Heavy Water. J. Phys. Chem. B 2014, 118, 5350–5356. [Google Scholar] [CrossRef] [PubMed]
- Chen, E.; Wittung-Stafshede, P.; Kliger, D.S. Far-UV Time-Resolved Circular Dichroism Detection of Electron-Transfer-Triggered Cytochrome c Folding. J. Am. Chem. Soc. 1999, 121, 3811–3817. [Google Scholar] [CrossRef]
- Kuwajima, K.; Yamaya, H.; Miwa, S.; Sugai, S.; Nagamura, T. Rapid formation of secondary structure framework in protein folding studied by stopped-flow circular dichroism. FEBS Lett. 1987, 221, 115–118. [Google Scholar] [CrossRef]
- Thomas, Y.G.; Szundi, I.; Lewis, J.W.; Kliger, D.S. Microsecond Time-Resolved Circular Dichroism of Rhodopsin Photointermediates. Biochemistry 2009, 48, 12283–12289. [Google Scholar] [CrossRef] [PubMed]
- Clinger, J.A.; Chen, E.; Kliger, D.S.; Phillips, G.N.J. Pump–Probe Circular Dichroism Spectroscopy of Cyanobacteriochrome TePixJ Yields: Insights into Its Photoconversion. J. Chem. Phys. B 2021, 125, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Milder, S.; Bjorling, S.; Kuntz, I.; Kliger, D. Time-resolved circular dichroism and absorption studies of the photolysis reaction of (carbonmonoxy) myoglobin. Biophys. J. 1988, 53, 659–664. [Google Scholar] [CrossRef]
- Chen, E.; Kliger, D.S. Time-resolved near UV circular dichroism and absorption studies of carbonmonoxymyoglobin photolysis intermediates. Inorg. Chim. Acta 1996, 242, 149–158. [Google Scholar] [CrossRef]
- Björling, S.C.; Goldbeck, R.A.; Paquette, S.J.; Milder, S.J.; Kliger, D.S. Allosteric Intermediates in Hemoglobin. 1. Nanosecond Time-Resolved Circular Dichroism Spectroscopy. Biochemistry 1996, 35, 8619–8627. [Google Scholar] [CrossRef]
- Lewis, J.W.; Goldbeck, R.A.; Kliger, D.S.; Xie, X.; Dunn, R.C.; Simon, J.D. Time-resolved circular dichroism spectroscopy: Experiment, theory, and applications to biological systems. J. Phys. Chem. 1992, 96, 5243–5254. [Google Scholar] [CrossRef]
- Goldbeck, R.A.; Kim-Shapiro, D.B.; Kliger, D.S. Fast Natural and Magnetic Circular Dichroism Spectroscopy. Annu. Rev. Phys. Chem. 1997, 48, 453–479. [Google Scholar] [CrossRef]
- Chen, E.; Goldbeck, R.A.; Kliger, D.S. Nanosecond time-resolved polarization spectroscopies: Tools for probing protein reaction mechanisms. Methods 2010, 52, 3–11. [Google Scholar] [CrossRef]
- Hache, F.; Changenet, P. Multiscale conformational dynamics probed by time-resolved circular dichroism from seconds to picoseconds. Chirality 2021, 33, 747–757. [Google Scholar] [CrossRef]
- Meyer-Ilse, J.; Akimov, D.; Dietzek, B. Recent advances in ultrafast time-resolved chirality measurements: Perspective and outlook. Laser Photonics Rev. 2013, 7, 495–505. [Google Scholar] [CrossRef]
- Changenet, P.; Hache, F. Recent advances in the development of ultrafast electronic circular dichroism for probing the conformational dynamics of biomolecules in solution. Eur. Phys. J. Spec. Top. 2023, 232, 2117–2129. [Google Scholar] [CrossRef]
- Lewis, J.; Tilton, R.; Einterz, C.; Milder, S.; Kuntz, I.; Kliger, D. New technique for measuring circular dichroism changes on a nanosecond time scale. Application to (carbonmonoxy) myoglobin and (carbonmonoxy) hemoglobin. J. Phys. Chem. 1985, 89, 289–294. [Google Scholar] [CrossRef]
- Xie, X.; Simon, J.D. Picosecond time-resolved circular dichroism spectroscopy: Experimental details and applications. Rev. Sci. Instrum. 1989, 60, 2614–2627. [Google Scholar] [CrossRef]
- Dartigalongue, T.; Hache, F. Observation of sub-100ps conformational changes in photolyzed carbonmonoxy-myoglobin probed by time-resolved circular dichroism. Chem. Phys. Lett. 2005, 415, 313–316. [Google Scholar] [CrossRef]
- Niezborala, C.; Hache, F. Measuring the dynamics of circular dichroism in a pump-probe experiment with a Babinet-Soleil Compensator. J. Opt. Soc. Am. B 2006, 23, 2418–2424. [Google Scholar] [CrossRef]
- Dartigalongue, T.; Hache, F. Time-resolved circular dichroism in carbonmonoxy-myoglobin: The central role of the proximal histidine. Chirality 2006, 18, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Dartigalongue, T.; Niezborala, C.; Hache, F. Subpicosecond UV spectroscopy of carbonmonoxy-myoglobin: Absorption and circular dichroism studies. Phys. Chem. Chem. Phys. 2007, 9, 1611–1615. [Google Scholar] [CrossRef]
- Hache, F.; Khuc, M.T.; Brazard, J.; Plaza, P.; Martin, M.M.; Checcucci, G.; Lenci, F. Picosecond transient circular dichroism of the photoreceptor protein of the light-adapted form of Blepharisma japonicum. Chem. Phys. Lett. 2009, 483, 133–137. [Google Scholar] [CrossRef]
- Mendonça, L.; Hache, F.; Changenet-Barret, P.; Plaza, P.; Chosrowjan, H.; Taniguchi, S.; Imamoto, Y. Ultrafast carbonyl motion of the photoactive yellow protein chromophore probed by femtosecond circular dichroism. J. Am. Chem. Soc. 2013, 135, 14637–14643. [Google Scholar] [CrossRef]
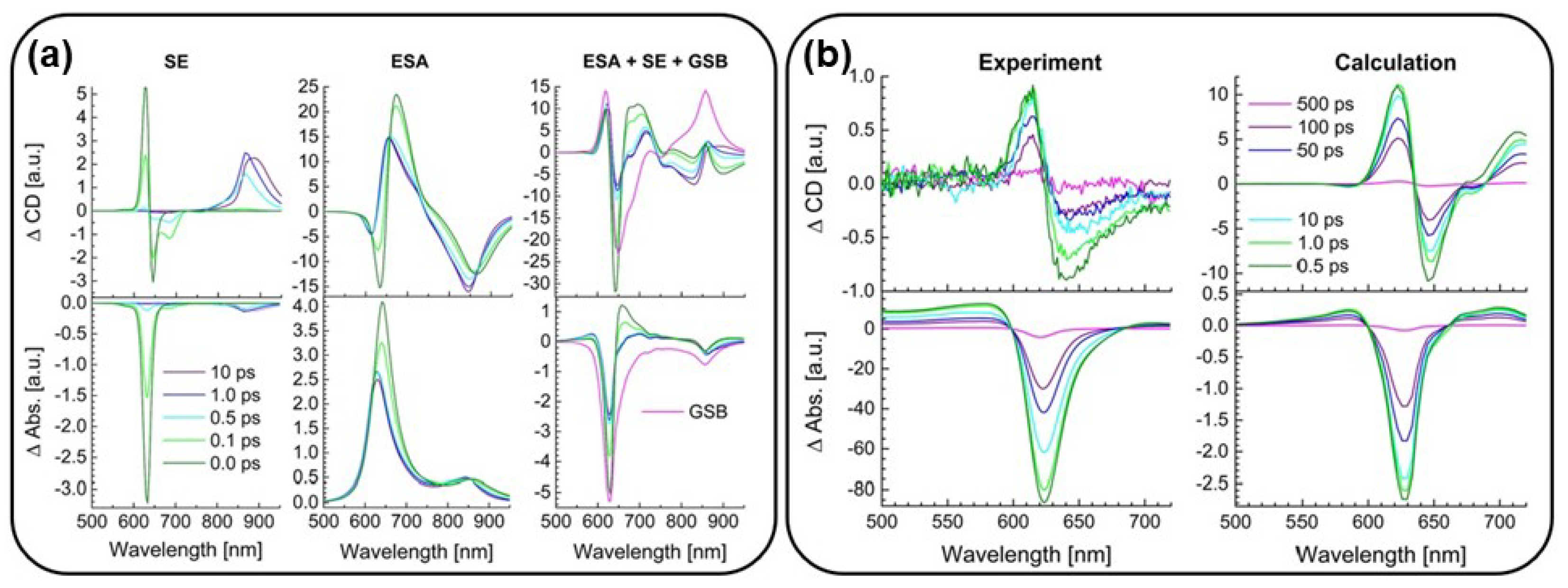
- Schmid, M.; Martinez-Fernandez, L.; Markovitsi, D.; Santoro, F.; Hache, F.; Improta, R.; Changenet, P. Unveiling excited-state chirality of binaphthols by femtosecond circular dichroism and quantum chemical calculations. J. Phys. Chem. Lett. 2019, 10, 4089–4094. [Google Scholar] [CrossRef]
- Dartigalongue, T.; Hache, F. Calculation of the circular dichroism spectra of carbon monoxy- and deoxy myoglobin: Interpretation of a time-resolved circular dichroism experiment. J. Chem. Phys. 2005, 123, 184901. [Google Scholar] [CrossRef]
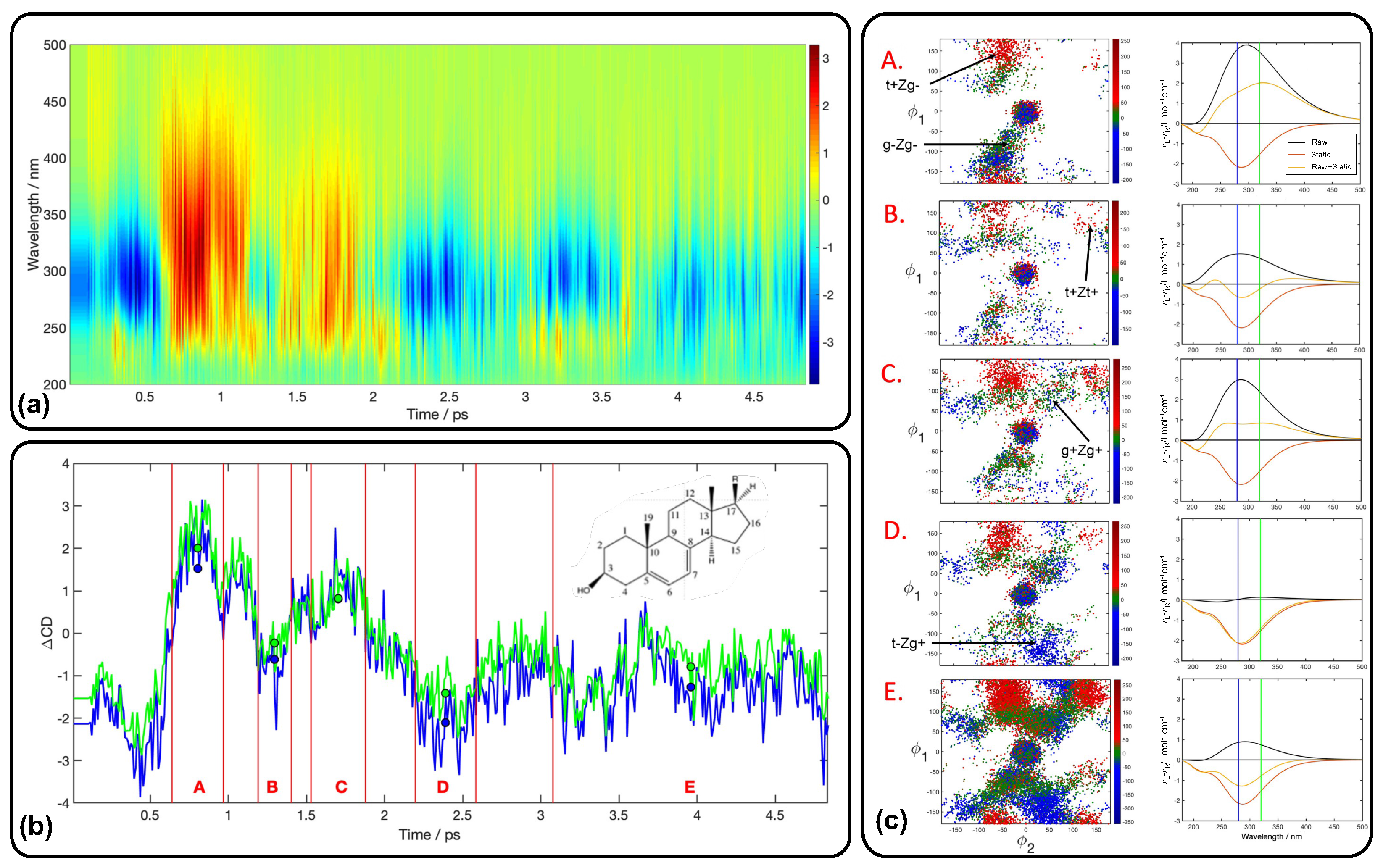
- Meyer-Ilse, J.; Akimov, D.; Dietzek, B. Ultrafast Circular Dichroism Study of the Ring Opening of 7-Dehydrocholesterol. J. Phys. Chem. Lett. 2012, 3, 182–185. [Google Scholar] [CrossRef]
- Tapavicza, E.; Reutershan, T.; Thompson, T. Ab Initio Simulation of the Ultrafast Circular Dichroism Spectrum of Provitamin D Ring-Opening. J. Phys. Chem. Lett. 2023, 14, 5061. [Google Scholar] [CrossRef]
- Trifonov, A.; Buchvarov, I.; Lohr, A.; Würthner, F.; Fiebig, T. Broadband femtosecond circular dichroism spectrometer with white-light polarization control. Rev. Sci. Instrum. 2010, 81, 043104. [Google Scholar] [CrossRef] [PubMed]
- Scholz, M.; Morgenroth, M.; Cho, M.J.; Choi, D.H.; Oum, K.; Lenzer, T. Ultrafast Broadband Transient Absorption and Circular Dichroism Reveal Relaxation of a Chiral Copolymer. J. Phys. Chem. Lett. 2019, 10, 5160–5166. [Google Scholar] [CrossRef] [PubMed]
- Morgenroth, M.; Scholz, M.; Lenzer, T.; Oum, K. Ultrafast UV–Vis Transient Absorption and Circular Dichroism Spectroscopy of a Polyfluorene Copolymer Showing Large Chiral Induction. J. Phys. Chem. C 2020, 124, 10192–10200. [Google Scholar] [CrossRef]
- Jespersen, K.G.; Beenken, W.J.D.; Zaushitsyn, Y.; Yartsev, A.; Andersson, M.; Pullerits, T.; Sundström, V. The electronic states of polyfluorene copolymers with alternating donor-acceptor units. J. Chem. Phys. 2004, 121, 12613–12617. [Google Scholar] [CrossRef] [PubMed]
- Morgenroth, M.; Scholz, M.; Cho, M.J.; Choi, D.H.; Oum, K.; Lenzer, T. Mapping the broadband circular dichroism of copolymer films with supramolecular chirality in time and space. Nat. Commun. 2022, 13, 210. [Google Scholar] [CrossRef]
- Gust, D.; Scholz, M.; Schumacher, V.; Mulatier, J.C.; Pitrat, D.; Guy, L.; Oum, K.; Lenzer, T. Annealing temperature-dependent induced supramolecular chiroptical response of copolymer thin films studied by pump-modulated transient circular dichroism spectroscopy. Sci. Rep. 2024, 14, 12694. [Google Scholar] [CrossRef]
- Ress, L.; Malỳ, P.; Landgraf, J.B.; Lindorfer, D.; Hofer, M.; Selby, J.; Lambert, C.; Renger, T.; Brixner, T. Time-resolved circular dichroism of excitonic systems: Theory and experiment on an exemplary squaraine polymer. Chem. Sci. 2023, 14, 9328–9349. [Google Scholar] [CrossRef]
- Oppermann, M.; Bauer, B.; Rossi, T.; Zinna, F.; Helbing, J.; Lacour, J.; Chergui, M. Ultrafast broadband circular dichroism in the deep ultraviolet. Optica 2019, 6, 56–60. [Google Scholar] [CrossRef]
- Gold, J.S.; Milder, S.J.; Lewis, J.W.; Kliger, D.S. Transient circular dichroism of the luminescent state of Ru(bpy)32+. J. Am. Chem. Soc. 1985, 107, 8285–8286. [Google Scholar] [CrossRef]
- Milder, S.J.; Gold, J.S.; Kliger, D.S. Time-resolved circular dichroism of the lowest excited state of (Δ)-Ru(bpy)32+. Chem. Phys. Lett. 1988, 144, 269–272. [Google Scholar] [CrossRef]
- Oppermann, M.; Spekowius, J.; Bauer, B.; Pfister, R.; Chergui, M.; Helbing, J. Broad-Band Ultraviolet CD Spectroscopy of Ultrafast Peptide Backbone Conformational Dynamics. J. Phys. Chem. Lett. 2019, 10, 2700–2705. [Google Scholar] [CrossRef]
- Mangot, L.; Taupier, G.; Romeo, M.; Boeglin, A.; Cregut, O.; Dorkenoo, K.D.H. Broadband transient dichroism spectroscopy in chiral molecules. Opt. Lett. 2010, 35, 381–383. [Google Scholar] [CrossRef]
- Eom, I.; Ahn, S.H.; Rhee, H.; Cho, M. Single-Shot Electronic Optical Activity Interferometry: Power and Phase Fluctuation-Free Measurement. Phys. Rev. Lett. 2012, 108, 103901. [Google Scholar] [CrossRef]
- Hiramatsu, K.; Nagata, T. Communication: Broadband and ultrasensitive femtosecond time-resolved circular dichroism spectroscopy. J. Chem. Phys. 2015, 143, 121102. [Google Scholar] [CrossRef]
- Preda, F.; Perri, A.; Réhault, J.; Dutta, B.; Helbing, J.; Cerullo, G.; Polli, D. Time-domain measurement of optical activity by an ultrastable common-path interferometer. Opt. Lett. 2018, 43, 1882–1885. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Ishikawa, S.; Nagatani, H. Phase-stable optical activity measurement by common-path spectral interferometry. Opt. Lett. 2020, 45, 5868–5871. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Herink, G.; Perri, A.; Preda, F.; Manzoni, C.; Polli, D.; Cerullo, G. Broadband Optical Activity Spectroscopy with Interferometric Fourier-Transform Balanced Detection. ACS Photonics 2021, 8, 2234–2242. [Google Scholar] [CrossRef] [PubMed]
- Changenet, P.; Hache, F. Artifact-free balanced detection for the measurement of circular dichroism with a sub-picosecond time resolution. Opt. Express 2023, 31, 21296–21310. [Google Scholar] [CrossRef] [PubMed]
- Niezborala, C.; Hache, F. Excited-State Absorption and Circular Dichroism of Ruthenium(II) Tris(phenanthroline) in the Ultraviolet Region. J. Phys. Chem. A 2007, 111, 7732–7735. [Google Scholar] [CrossRef]
- Ayuso, D.; Ordonez, A.F.; Smirnova, O. Ultrafast chirality: The road to efficient chiral measurements. Phys. Chem. Chem. Phys. 2022, 24, 26962. [Google Scholar] [CrossRef]
- Powis, I. Photoelectron Circular Dichroism in Chiral Molecules. Adv. Chem. Phys. 2008, 138, 267. [Google Scholar]
- Cireasa, R.; Boguslavskiy, A.E.; Pons, B.; Wong, M.C.H.; Descamps, D.; Petit, S.; Ruf, H.; Thiré, N.; Ferré, A.; Suarez, J.; et al. Probing molecular chirality on a sub-femtosecond timescale. Nat. Phys. 2015, 11, 654. [Google Scholar] [CrossRef]
- Harada, Y.; Haraguchi, E.; Kaneshima, K.; Sekikawa, T. Circular dichroism in high-order harmonic generation from chiral molecules. Phys. Rev. A 2018, 98, 021401. [Google Scholar] [CrossRef]
- Baykusheva, D.; Wörner, H.J. Chiral Discrimination through Bielliptical High-Harmonic Spectroscopy. Phys. Rev. X 2018, 9, 031060. [Google Scholar] [CrossRef]
- Baykusheva, D.; Zindel, D.; Svoboda, V.; Bommeli, E.; Ochsner, M.; Tehlar, A.; Wörner, H.J. Real-time probing of chirality during a chemical reaction. Proc. Natl. Acad. Sci. USA 2019, 116, 23923. [Google Scholar] [CrossRef]
- Svoboda, V.; Ram, N.B.; Baykusheva, D.; Zindel, D.; Waters, M.D.J.; Spenger, B.; Ochsner, M.; Herburger, H.; Stohner, J.; Wörner, H.J. Femtosecond photoelectron circular dichroism of chemical reactions. Sci. Adv. 2022, 8, 28. [Google Scholar] [CrossRef]
- Faccialà, D.; Devetta, M.; Beauvarlet, S.; Besley, N.; Calegari, F.; Callegari, C.; Catone, D.; Cinquanta, E.; Ciriolo, A.G.; Colaizzi, L.; et al. Time-Resolved Chiral X-Ray Photoelectron Spectroscopy with Transiently Enhanced Atomic Site Selectivity: A Free-Electron Laser Investigation of Electronically Excited Fenchone Enantiomers. Phys. Rev. X 2023, 13, 011044. [Google Scholar] [CrossRef]
- Tikhonov, D.S.; Blech, A.; Leibscher, M.; Greenman, L.; Schnell, M.; Koch, C.P. Pump-probe spectroscopy of chiral vibrational dynamics. Sci. Adv. 2022, 8, 49. [Google Scholar] [CrossRef] [PubMed]
- Comby, A.; Beaulieu, S.; Boggio-Pasqua, M.; Descamps, D.; Légaré, F.; Nahon, L.; Petit, S.; Pons, B.; Fabre, B.; Mairesse, Y.; et al. Relaxation Dynamics in Photoexcited Chiral Molecules Studied by Time-Resolved Photoelectron Circular Dichroism: Toward Chiral Femtochemistry. J. Phys. Chem. Lett. 2016, 7, 4514. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, S.; Comby, A.; Fabre, B.; Descamps, D.; Ferré, A.; Garcia, G.; Géneaux, R.; Légaré’, F.; Nahon, L.; Petit, S.; et al. Probing Ultrafast Dynamics of Chiral Molecules Using Time-Resolved Photoelectron Circular Dichroism. Faraday Discuss. 2016, 194, 325. [Google Scholar] [CrossRef]
- Blanchet, V.; Descamps, D.; Petit, S.; Mairesse, Y.; Pons, B.; Fabre, B. Ultrafast Relaxation Investigated by Photoelectron Circular Dichroism: An Isomeric Comparison of Camphor and Fenchone. Phys. Chem. Chem. Phys. 2021, 23, 25612. [Google Scholar] [CrossRef]
- Rouxel, J.R.; Kowalewski, M.; Mukamel, S. Photoinduced molecular chirality probed by ultrafast resonant x-ray spectroscopy. Struct. Dyn. 2017, 4, 044006. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Rouxel, J.R.; Autschbach, J.; Govind, N.; Mukamel, S. X-ray circular dichroism signals: A unique probe of local molecular chirality. Chem. Sci. 2017, 8, 5969–5978. [Google Scholar] [CrossRef]
- Rouxel, J.R.; Zhang, Y.; Mukamel, S. X-ray Raman optical activity of chiral molecules. Chem. Sci. 2019, 10, 898–908. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond Science. Nat. Phys. 2007, 3, 381. [Google Scholar] [CrossRef]
- Turchini, S.; Catone, D.; Zema, N.; Contini, G.; Prosperi, T.; Decleva, P.; Stener, M.; Rondino, F.; Piccirillo, S.; Prince, K.C.; et al. Conformational Sensitivity in Photoelectron Circular Dichroism of 3-Methylcyclopentanone. ChemPhysChem 2013, 14, 1723. [Google Scholar] [CrossRef] [PubMed]
- Ilchen, M.; Hartmann, G.; Rupprecht, P.; Artemyev, A.N.; Coffee, R.N.; Li, Z.; Ohldag, H.; Ogasawara, H.; Osipov, T.; Ray, D.; et al. Emitter-Site-Selective Photoelectron Circular Dichroism of Trifluoromethyloxirane. Phys. Rev. A 2017, 95, 053423. [Google Scholar] [CrossRef]
- Schuetz, G.; Wagner, W.; Wilhelm, W.; Kienle, P.; Zeller, R.; Frahm, R.; Materlik, G. Absorption of circularly polarized x-rays in iron. Phys. Rev. Lett. 1987, 58, 737. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Idzerda, Y.; Lin, H.J.; Smith, N.; Meigs, G.; Chaban, E.; Ho, G.; Pellegrin, E.; Sette, F. Experimental Confirmation of the X-ray Magnetic Circular Dichroism Sum Rules for Iron and Cobalt. Phys. Rev. Lett. 1995, 75, 152. [Google Scholar] [CrossRef]
- Funk, T.; Deb, A.; George, S.J.; Wang, H.; Cramer, S.P. X-ray magnetic circular dichroism—A high energy probe of magnetic properties. Coordin. Chem. Rev. 2005, 249, 3. [Google Scholar] [CrossRef]
- Zamudio-Bayer, V.; Hirsch, K.; Langenberg, A.; Niemeyer, M.; Vogel, M.; Ławicki, A.; Terasaki, A.; Lau, J.T.; Von Issendorff, B. Maximum Spin Polarization in Chromium Dimer Cations as Demonstrated by X-ray Magnetic Circular Dichroism Spectroscopy. Angew. Chem. Int. Ed. 2015, 54, 4498. [Google Scholar] [CrossRef][Green Version]
- Wilhelm, F.; Sanchez, J.P.; Rogalev, A. Magnetism of uranium compounds probed by XMCD spectroscopy. J. Phys. D Appl. Phys. 2018, 51, 333001. [Google Scholar] [CrossRef]
- Bar, A.K.; Kalita, P.; Singh, M.K.; Rajaraman, G.; Chandrasekhar, V. Low-coordinate mononuclear lanthanide complexes as molecular nanomagnets. Coord. Chem. Rev. 2018, 367, 163. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Meihaus, K.R.; Rogalev, A.; Wilhelm, F.; Aravena, D.; Amoza, M.; Ruiz, E.; Long, J.R.; Bendix, J.; Clérac, R. [UF6]2−: A Molecular Hexafluorido Actinide(IV) Complex with Compensating Spin and Orbital Magnetic Moments. Angew. Chem. Int. Ed. 2019, 58, 15650. [Google Scholar] [CrossRef]
- Kowalska, J.K.; Henthorn, J.T.; Van Stappen, C.; Trncik, C.; Einsle, O.; Keavney, D.; DeBeer, S. X-ray Magnetic Circular Dichroism Spectroscopy Applied to Nitrogenase and Related Models: Experimental Evidence for a Spin-Coupled Molybdenum (III) Center. Angew. Chem. Int. Ed. 2019, 58, 9373. [Google Scholar]
- Jungcharoen, P.; Pédrot, M.; Choueikani, F.; Pasturel, M.; Hanna, K.; Heberling, F.; Tesfa, M.; Marsac, R. Probing the effects of redox conditions and dissolved Fe2+ on nanomagnetite stoichiometry by wet chemistry, XRD, XAS and XMCD. Environ. Sci. Nano 2021, 8, 2098. [Google Scholar] [CrossRef]
- N’Diaye, A.; Bordage, A.; Nataf, L.; Baudelet, F.; Rivière, E.; Bleuzen, A. Interplay between Transition-Metal K-edge XMCD and Magnetism in Prussian Blue Analogs. ACS Omega 2022, 7, 36366. [Google Scholar] [CrossRef]
- Takubo, K.; Yamamoto, K.; Hirata, Y.; Yokoyama, Y.; Kubota, Y.; Yamamoto, S.; Yamamoto, S.; Matsuda, I.; Shin, S.; Seki, T.; et al. Capturing ultrafast magnetic dynamics by time-resolved soft x-ray magnetic circular dichroism. Appl. Phys. Lett. 2017, 110, 162401. [Google Scholar] [CrossRef]
- Ishii, Y.; Yamasaki, Y.; Kozuka, Y.; Lustikova, J.; Nii, Y.; Onose, Y.; Yokoyama, Y.; Mizumaki, M.; ichi Adachi, J.; Nakao, H.; et al. Microscopic evaluation of spin and orbital moment in ferromagnetic resonance. Sci. Rep. 2024, 14, 15504. [Google Scholar] [CrossRef] [PubMed]
- Emori, S.; Maizel, R.E.; Street, G.T.; Jones, J.L.; Arena, D.A.; Shafer, P.; Klewe, C. Quantifying the orbital-to-spin moment ratio under dynamic excitation. Appl. Phys. Lett. 2024, 124, 122404. [Google Scholar] [CrossRef]
- Iftimie, R.; Minary, P.; Tuckerman, M.E. Ab initio molecular dynamics: Concepts, recent developments, and future trends. Proc. Natl. Acad. Sci. USA 2005, 102, 6654. [Google Scholar] [CrossRef]
- Tully, J.C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061–1071. [Google Scholar] [CrossRef]
- Tapavicza, E.; Tavernelli, I.; Rothlisberger, U. Trajectory Surface Hopping within Linear Response Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 2007, 98, 023001. [Google Scholar] [CrossRef]
- McWeeny, R. Methods of Molecular Quantum Mechanics, 2nd ed.; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Schellman, J.A. Circular dichroism and optical rotation. Chem. Rev. 1975, 75, 323–331. [Google Scholar] [CrossRef]
- Tapavicza, E.; Bellchambers, G.D.; Vincent, J.C.; Furche, F. Ab initio non-adiabatic molecular dynamics. Phys. Chem. Chem. Phys. 2013, 15, 18336–18348. [Google Scholar] [CrossRef]
- Liu, J.; Neukirch, A.J.; Prezhdo, O.V. Non-radiative electron–hole recombination in silicon clusters: Ab initio non-adiabatic molecular dynamics. J. Phys. Chem. C 2014, 118, 20702–20709. [Google Scholar] [CrossRef]
- Chapman, S. The Classical Trajectory-Surface-Hopping Approach to Charge-Transfer Processes. In Advances in Chemical Physics: State-Selected and State-To-State Ion-Molecule Reaction Dynamics, Part 2, Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1992; Volume 82, pp. 423–483. [Google Scholar]
- Subotnik, J.E.; Jain, A.; Landry, B.; Petit, A.; Ouyang, W.; Bellonzi, N. Understanding the surface hopping view of electronic transitions and decoherence. Annu. Rev. Phys. Chem. 2016, 67, 387–417. [Google Scholar] [CrossRef]
- Malhado, J.P.; Bearpark, M.J.; Hynes, J.T. Non-adiabatic dynamics close to conical intersections and the surface hopping perspective. Front. Chem. 2014, 2, 97. [Google Scholar] [CrossRef] [PubMed]
- Barbatti, M. Nonadiabatic dynamics with trajectory surface hopping method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 620–633. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R. Adiabatic time-dependent density functional methods for excited state properties. J. Chem. Phys. 2002, 117, 7433–7447. [Google Scholar] [CrossRef]
- Send, R.; Furche, F. First-order nonadiabatic couplings from time-dependent hybrid density functional response theory: Consistent formalism, implementation, and performance. J. Chem. Phys. 2010, 132, 044107. [Google Scholar] [CrossRef]
- Tavernelli, I.; Curchod, B.F.; Rothlisberger, U. On nonadiabatic coupling vectors in time-dependent density functional theory. J. Chem. Phys. 2009, 131, 196101. [Google Scholar] [CrossRef]
- Sofferman, D.L.; Konar, A.; Spears, K.G.; Sension, R.J. Ultrafast excited state dynamics of provitamin D3 and analogs in solution and in lipid bilayers. J. Chem. Phys. 2021, 154, 094309. [Google Scholar] [CrossRef] [PubMed]
- Tapavicza, E.; Meyer, A.M.; Furche, F. Unravelling the details of vitamin D photosynthesis by non-adiabatic molecular dynamics simulations. Phys. Chem. Chem. Phys. 2011, 13, 20986–20998. [Google Scholar] [CrossRef]
- Sałek, P.; Vahtras, O.; Helgaker, T.; Ågren, H. Density-functional theory of linear and nonlinear time-dependent molecular properties. J. Chem. Phys. 2002, 117, 9630–9645. [Google Scholar] [CrossRef]
- Jansik, B.; Sałek, P.; Jonsson, D.; Vahtras, O.; Ågren, H. Cubic response functions in time-dependent density functional theory. J. Chem. Phys. 2005, 122, 054107. [Google Scholar] [CrossRef] [PubMed]
- Gaw, J.; Handy, N. Ab initio quadratic, cubic and quartic force constants for the calculation of spectroscopic constants. Chem. Phys. Lett. 1985, 121, 321–329. [Google Scholar] [CrossRef]
- Rizzo, A.; Vahtras, O. Ab initio study of excited state electronic circular dichroism. Two prototype cases: Methyl oxirane and R-(+)-1, 1′-bi (2-naphthol). J. Chem. Phys. 2011, 134, 244109. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent advances in wave function-based methods of molecular-property calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef]
- Koch, H. Coupled cluster response functions. J. Chem. Phys. 1990, 93, 3333–3344. [Google Scholar] [CrossRef]
- Christiansen, O.; Jørgensen, P.; Hättig, C. Response functions from Fourier component variational perturbation theory applied to a time-averaged quasienergy. Int. J. Quantum Chem. 1998, 68, 1–52. [Google Scholar] [CrossRef]
- Andersen, J.H.; Nanda, K.D.; Krylov, A.I.; Coriani, S. Probing Molecular Chirality of Ground and Electronically Excited States in the UV–vis and X-ray Regimes: An EOM-CCSD Study. J. Chem. Theory Comput. 2022, 18, 1748–1764. [Google Scholar] [CrossRef]
- Pescitelli, G.; Bruhn, T. Good computational practice in the assignment of absolute configurations by TDDFT calculations of ECD spectra. Chirality 2016, 28, 466–474. [Google Scholar] [CrossRef]
- Bannwarth, C.; Seibert, J.; Grimme, S. Electronic circular dichroism of [16]Helicene with simplified TD-DFT: Beyond the single structure approach. Chirality 2016, 28, 365–369. [Google Scholar] [CrossRef]
- Jang, H.; Kim, N.J.; Heo, J. Benchmarking study on time-dependent density functional theory calculations of electronic circular dichroism for gas-phase molecules. Comput. Theor. Chem. 2018, 1125, 63–68. [Google Scholar] [CrossRef]
- Bannwarth, C.; Grimme, S. A simplified time-dependent density functional theory approach for electronic ultraviolet and circular dichroism spectra of very large molecules. Comput. Theor. Chem. 2014, 1040, 45–53. [Google Scholar] [CrossRef]
- Mikhailov, I.A.; Tafur, S.; Masunov, A.E. Double excitations and state-to-state transition dipoles in π-π* excited singlet states of linear polyenes: Time-dependent density-functional theory versus multiconfigurational methods. Phys. Rev. A 2008, 77, 012510. [Google Scholar] [CrossRef]
- Tretiak, S.; Mukamel, S. Density matrix analysis and simulation of electronic excitations in conjugated and aggregated molecules. Chem. Rev. 2002, 102, 3171–3212. [Google Scholar] [CrossRef]
- Nayyar, I.H.; Masunov, A.E.; Tretiak, S. Comparison of TD-DFT methods for the calculation of two-photon absorption spectra of oligophenylvinylenes. J. Chem. Phys. C 2013, 117, 18170–18189. [Google Scholar] [CrossRef]
- Segatta, F.; Russo, M.; Nascimento, D.R.; Presti, D.; Rigodanza, F.; Nenov, A.; Bonvicini, A.; Arcioni, A.; Mukamel, S.; Maiuri, M.; et al. In Silico Ultrafast Nonlinear Spectroscopy Meets Experiments: The Case of Perylene Bisimide Dye. J. Chem. Theory Comput. 2021, 17, 7134–7145. [Google Scholar] [CrossRef]
- Casida, M.E. Time-dependent density-functional theory for molecules and molecular solids. J. Mol. Struc. THEOCHEM 2009, 914, 3–18. [Google Scholar] [CrossRef]
- Monti, M.; Stener, M.; Coccia, E. Electronic circular dichroism from real-time propagation in state space. J. Chem. Phys 2023, 158, 084102. [Google Scholar] [CrossRef] [PubMed]
- Biancorosso, L.; D’Antoni, P.; Corni, S.; Stener, M.; Coccia, E. Time-dependent quantum/continuum modelling of plasmon-enhanced electronic circular dichroism. J. Chem. Phys. 2024; submitted. [Google Scholar]
- Coccia, E.; Fregoni, J.; Guido, C.A.; Marsili, M.; Corni, S. Hybrid theoretical models for molecular nanoplasmonics. J. Chem. Phys. 2020, 153, 200901. [Google Scholar] [CrossRef]
- Grobas Illobre, P.; Marsili, M.; Corni, S.; Stener, M.; Toffoli, D.; Coccia, E. Time-Resolved Excited-State Analysis of Molecular Electron Dynamics by TDDFT and Bethe–Salpeter Equation Formalisms. J. Chem. Theory Comput. 2021, 17, 6314. [Google Scholar] [CrossRef]
- Scott, M.; Rehn, D.R.; Norman, P.; Dreuw, A. Ab initio excited-state electronic circular dichroism spectra exploiting the third-order algebraic-diagrammatic construction scheme for the polarization propagator. J. Phys. Chem. Lett. 2021, 12, 5132–5137. [Google Scholar] [CrossRef]
- Schirmer, J. Beyond the random-phase approximation: A new approximation scheme for the polarization propagator. Phys. Rev. A 1982, 26, 2395. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Dickhoff, W.H.; Van Neck, D.V. Many-Body Theory Exposed! Propagator Description of Quantum Mechanics in Many-Body Systems; World Scientific Publishing Company: Singapore, 2008. [Google Scholar]
- Dreuw, A.; Wormit, M. The algebraic diagrammatic construction scheme for the polarization propagator for the calculation of excited states. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 82–95. [Google Scholar] [CrossRef]
- Dreuw, A.; Dempwolff, A.L. Algebraic diagrammatic construction schemes for the simulation of electronic spectroscopies. In Theoretical and Computational Photochemistry; Elsevier: Amsterdam, The Netherlands, 2023; pp. 119–134. [Google Scholar]
- Sokolov, A.Y. Multi-reference algebraic diagrammatic construction theory for excited states: General formulation and first-order implementation. J. Chem. Phys. 2018, 149, 204113. [Google Scholar] [CrossRef] [PubMed]
- Mertins, F.; Schirmer, J. Algebraic propagator approaches and intermediate-state representations. I. The biorthogonal and unitary coupled-cluster methods. Phys. Rev. A 1996, 53, 2140. [Google Scholar] [CrossRef] [PubMed]
- Knippenberg, S.; Rehn, D.; Wormit, M.; Starcke, J.; Rusakova, I.; Trofimov, A.; Dreuw, A. Calculations of nonlinear response properties using the intermediate state representation and the algebraic-diagrammatic construction polarization propagator approach: Two-photon absorption spectra. J. Chem. Phys. 2012, 136, 064107. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, J. Closed-form intermediate representations of many-body propagators and resolvent matrices. Phys. Rev. A 1991, 43, 4647. [Google Scholar] [CrossRef]
- Schirmer, J.; Trofimov, A.B. Intermediate state representation approach to physical properties of electronically excited molecules. J. Chem. Phys. 2004, 120, 11449–11464. [Google Scholar] [CrossRef]
- Stanton, J.F.; Bartlett, R.J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029–7039. [Google Scholar] [CrossRef]
- Krylov, A.I. Equation-of-motion coupled-cluster methods for open-shell and electronically excited species: The hitchhiker’s guide to Fock space. Annu. Rev. Phys. Chem. 2008, 59, 433–462. [Google Scholar] [CrossRef]
- Nascimento, D.R.; DePrince III, A.E. Linear absorption spectra from explicitly time-dependent equation-of-motion coupled-cluster theory. J. Chem. Theory Comput. 2016, 12, 5834–5840. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, D.R.; DePrince, A.E. A general time-domain formulation of equation-of-motion coupled-cluster theory for linear spectroscopy. J. Chem. Phys. 2019, 151, 204107. [Google Scholar] [CrossRef]
- Friese, D.H.; Hättig, C.; Rizzo, A. Origin-independent two-photon circular dichroism calculations in coupled cluster theory. Phys. Chem. Chem. Phys. 2016, 18, 13683–13692. [Google Scholar] [CrossRef] [PubMed]
- Faber, R.; Ghidinelli, S.; Hättig, C.; Coriani, S. Magnetic circular dichroism spectra from resonant and damped coupled cluster response theory. J. Chem. Phys. 2020, 153, 114105. [Google Scholar] [CrossRef]
- Vidal, M.L.; Feng, X.; Epifanovsky, E.; Krylov, A.I.; Coriani, S. New and efficient equation-of-motion coupled-cluster framework for core-excited and core-ionized states. J. Chem. Theory Comput. 2019, 15, 3117–3133. [Google Scholar] [CrossRef] [PubMed]
- Nanda, K.D.; Krylov, A.I. The effect of polarizable environment on two-photon absorption cross sections characterized by the equation-of-motion coupled-cluster singles and doubles method combined with the effective fragment potential approach. J. Chem. Phys. 2018, 149, 164109. [Google Scholar] [CrossRef] [PubMed]
- Coriani, S.; Koch, H. Communication: X-ray absorption spectra and core-ionization potentials within a core-valence separated coupled cluster framework. J. Chem. Phys. 2015, 143, 181103. [Google Scholar] [CrossRef]
- Pulm, F.; Schramm, J.; Hormes, J.; Grimme, S.; Peyerimhoff, S.D. Theoretical and experimental investigations of the electronic circular dichroism and absorption spectra of bicyclic ketones. Chem. Phys. 1997, 224, 143–155. [Google Scholar] [CrossRef]
- Hoerner, P.; Lee, M.K.; Schlegel, H.B. Angular dependence of strong field ionization of N2 by time-dependent configuration interaction using density functional theory and the Tamm-Dancoff approximation. J. Chem. Phys. 2019, 151, 054102. [Google Scholar] [CrossRef]
- Rüger, R.; Franchini, M.; Trnka, T.; Yakovlev, A.; van Lenthe, E.; Philipsen, P.; van Vuren, T.; Klumpers, B.; Soini, T. AMS 2022.1, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2022. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monti, M.; Biancorosso, L.; Coccia, E. Time-Resolved Circular Dichroism in Molecules: Experimental and Theoretical Advances. Molecules 2024, 29, 4049. https://doi.org/10.3390/molecules29174049
Monti M, Biancorosso L, Coccia E. Time-Resolved Circular Dichroism in Molecules: Experimental and Theoretical Advances. Molecules. 2024; 29(17):4049. https://doi.org/10.3390/molecules29174049
Chicago/Turabian StyleMonti, Marta, Leonardo Biancorosso, and Emanuele Coccia. 2024. "Time-Resolved Circular Dichroism in Molecules: Experimental and Theoretical Advances" Molecules 29, no. 17: 4049. https://doi.org/10.3390/molecules29174049
APA StyleMonti, M., Biancorosso, L., & Coccia, E. (2024). Time-Resolved Circular Dichroism in Molecules: Experimental and Theoretical Advances. Molecules, 29(17), 4049. https://doi.org/10.3390/molecules29174049




