Tuning Ferulic Acid Solubility in Choline-Chloride- and Betaine-Based Deep Eutectic Solvents: Experimental Determination and Machine Learning Modeling
Abstract
1. Introduction
2. Results and Discussion
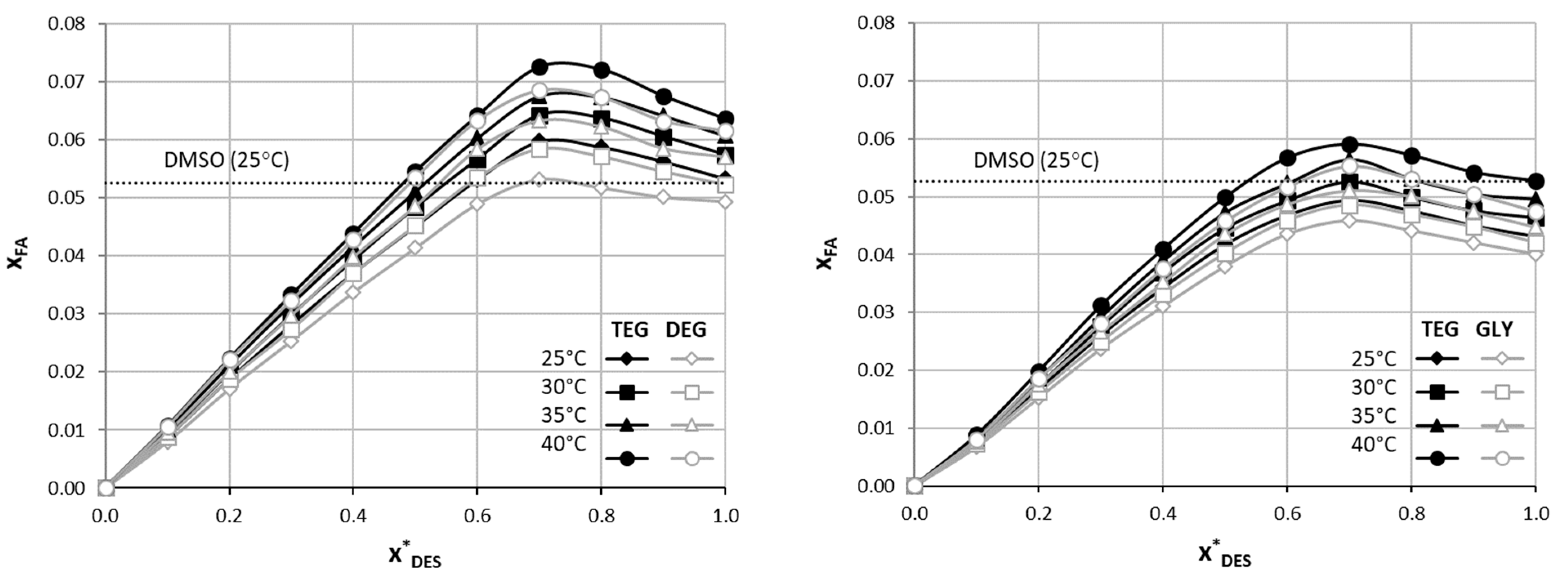
2.1. Solubility of Ferulic Acid in DESs and DES–Water Mixtures
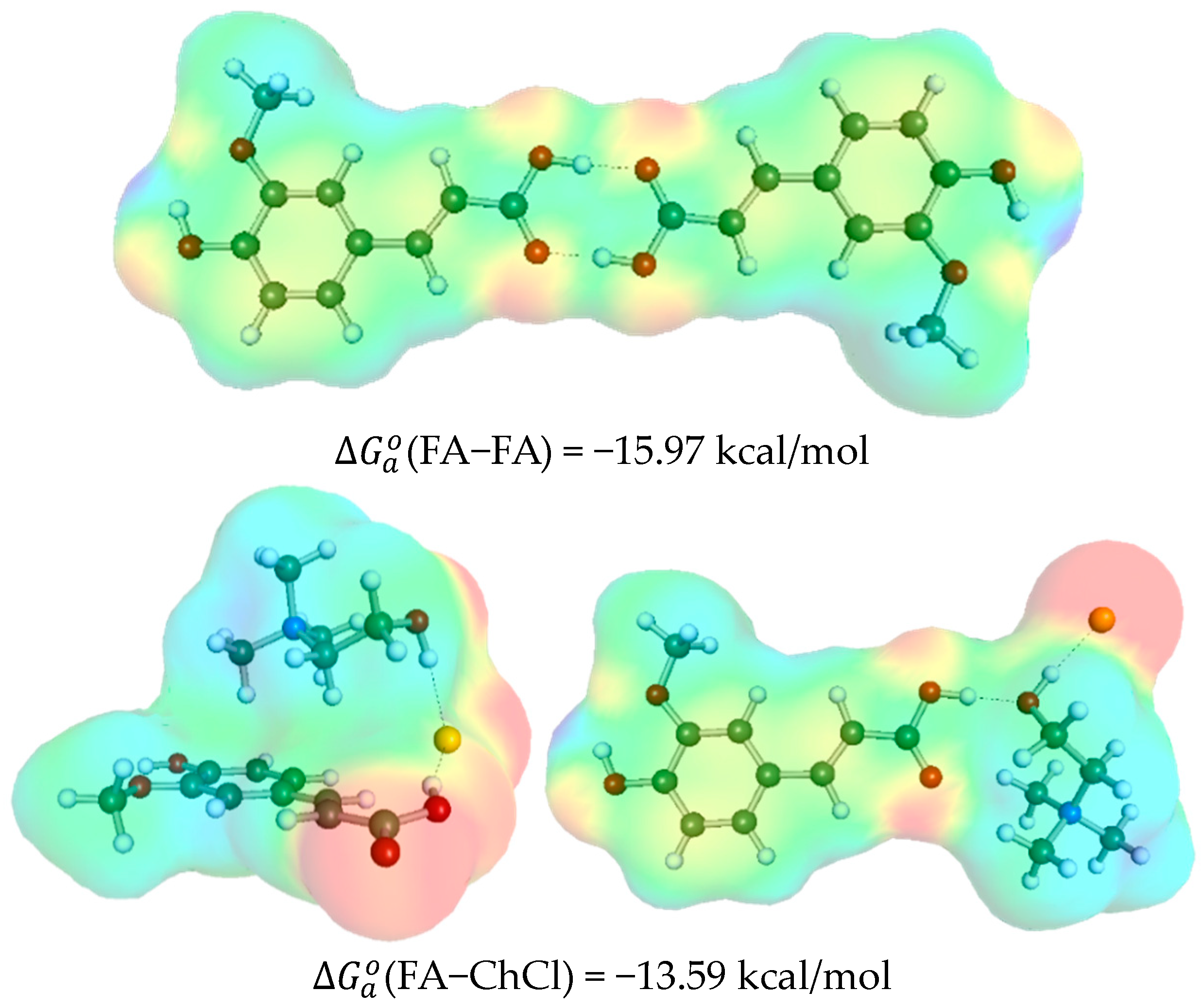
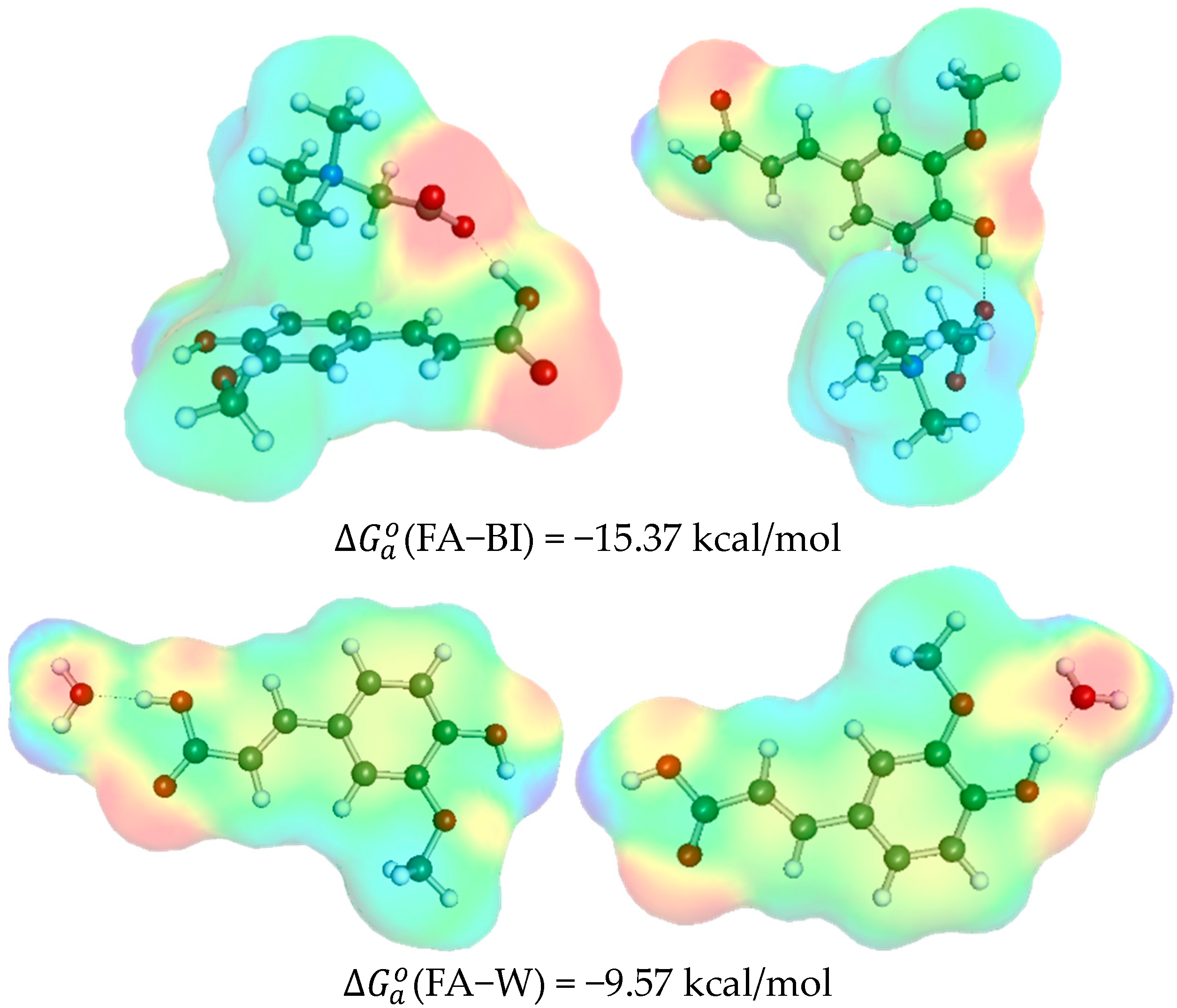
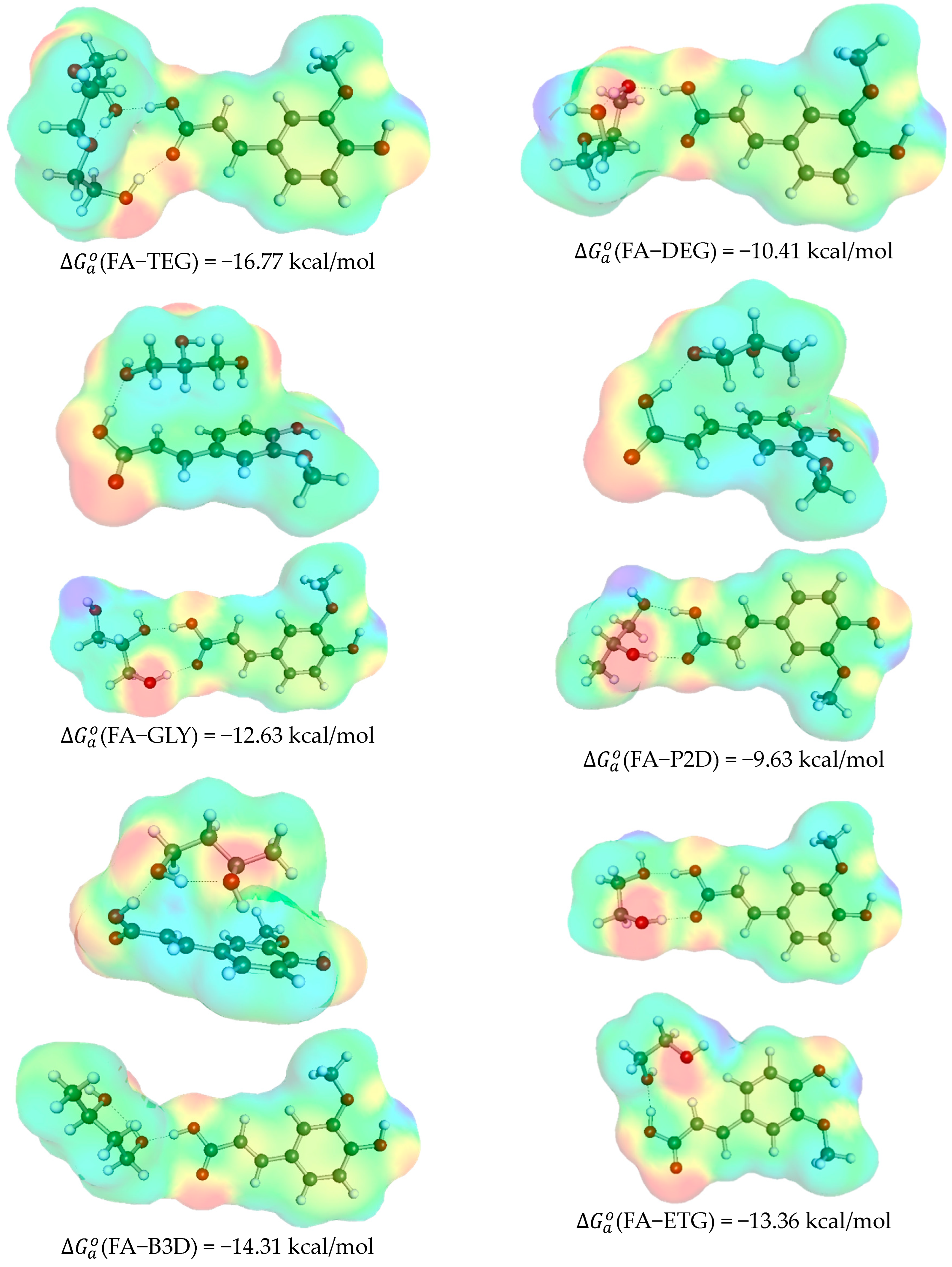
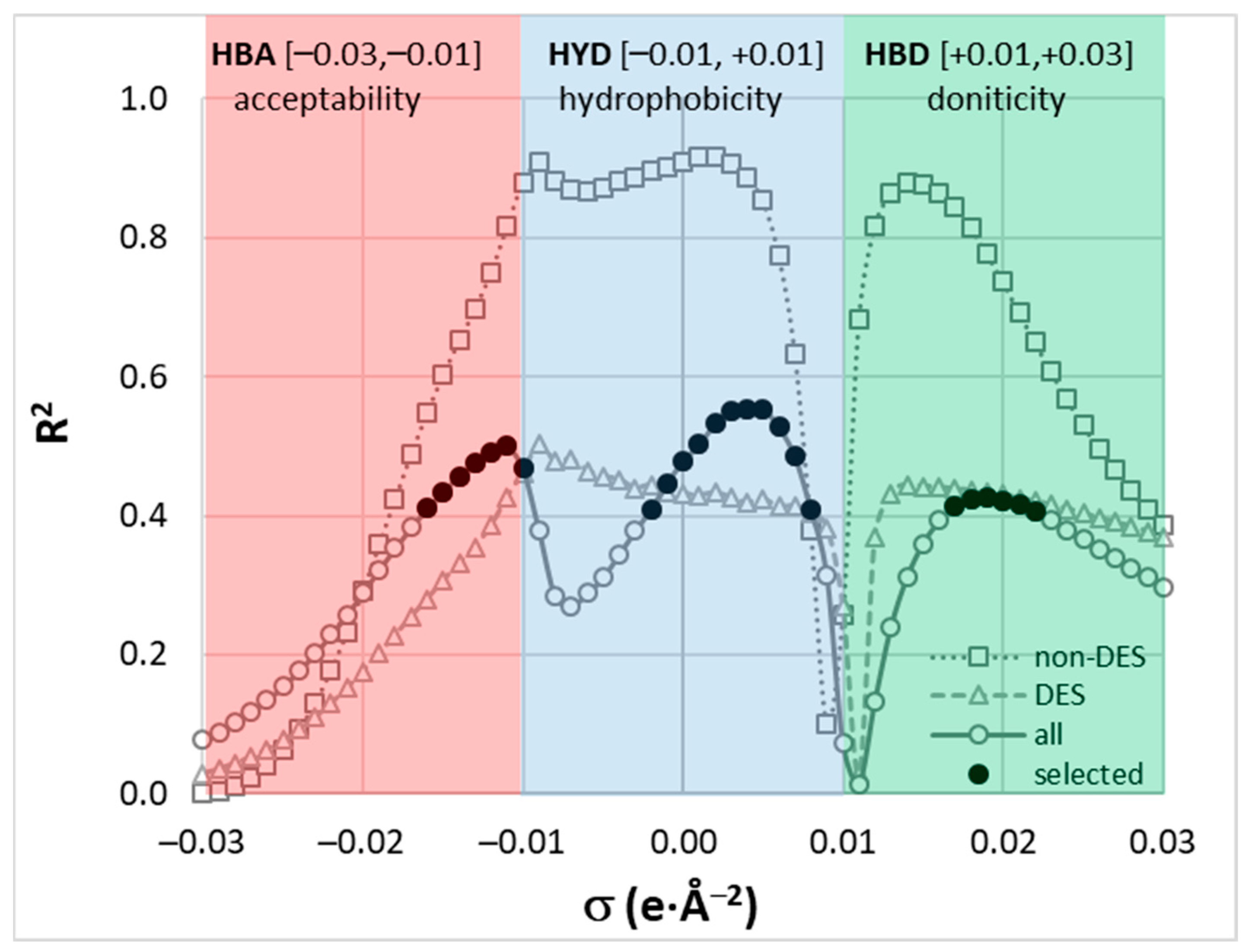
2.2. Ferulic Acid Intermolecular Interactions in DES
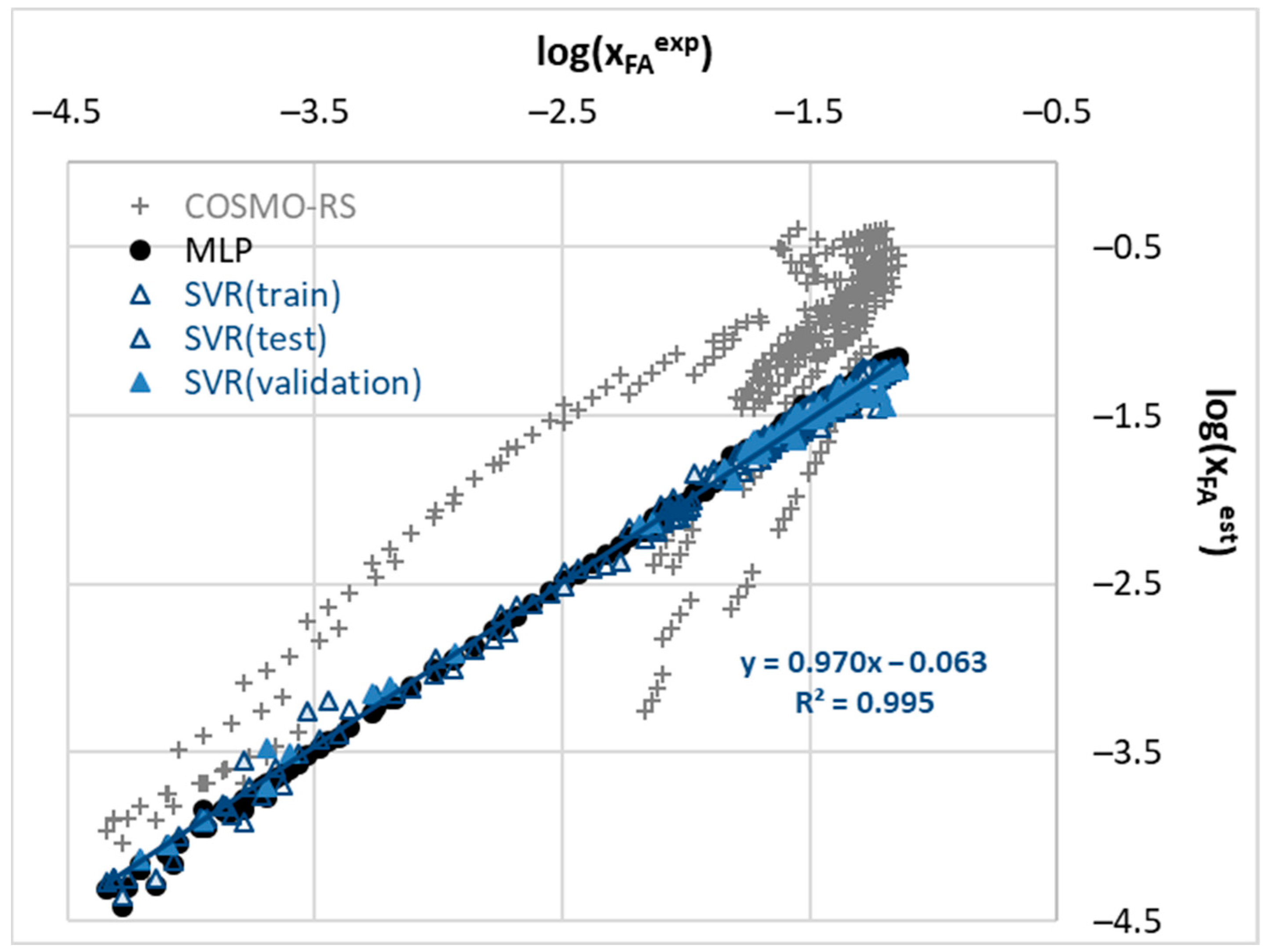
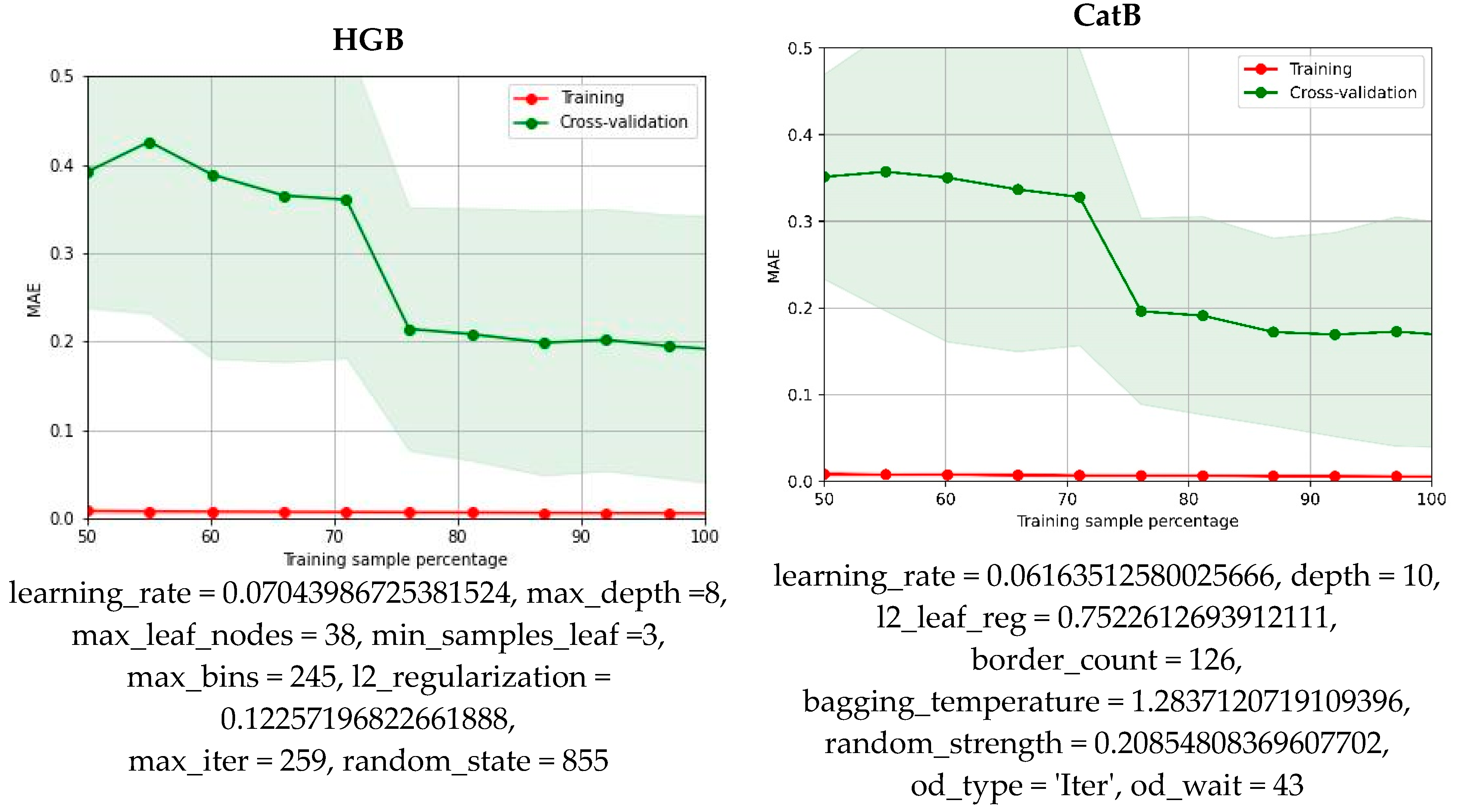
2.3. Machine Learning Model
3. Materials and Methods
3.1. Materials
3.2. Preparation of the Calibration Curve
3.3. Preparation of the Samples and Solubility Measurements
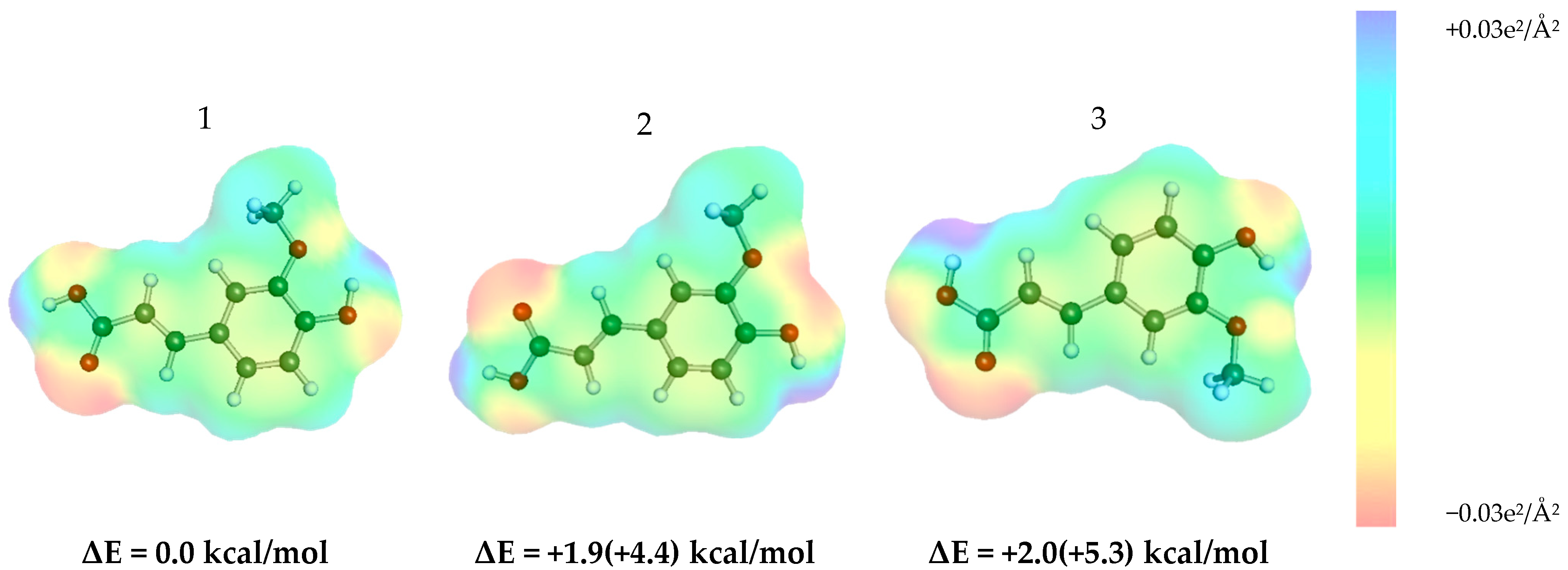
3.4. Conformational Analysis
3.5. Solubility Dataset
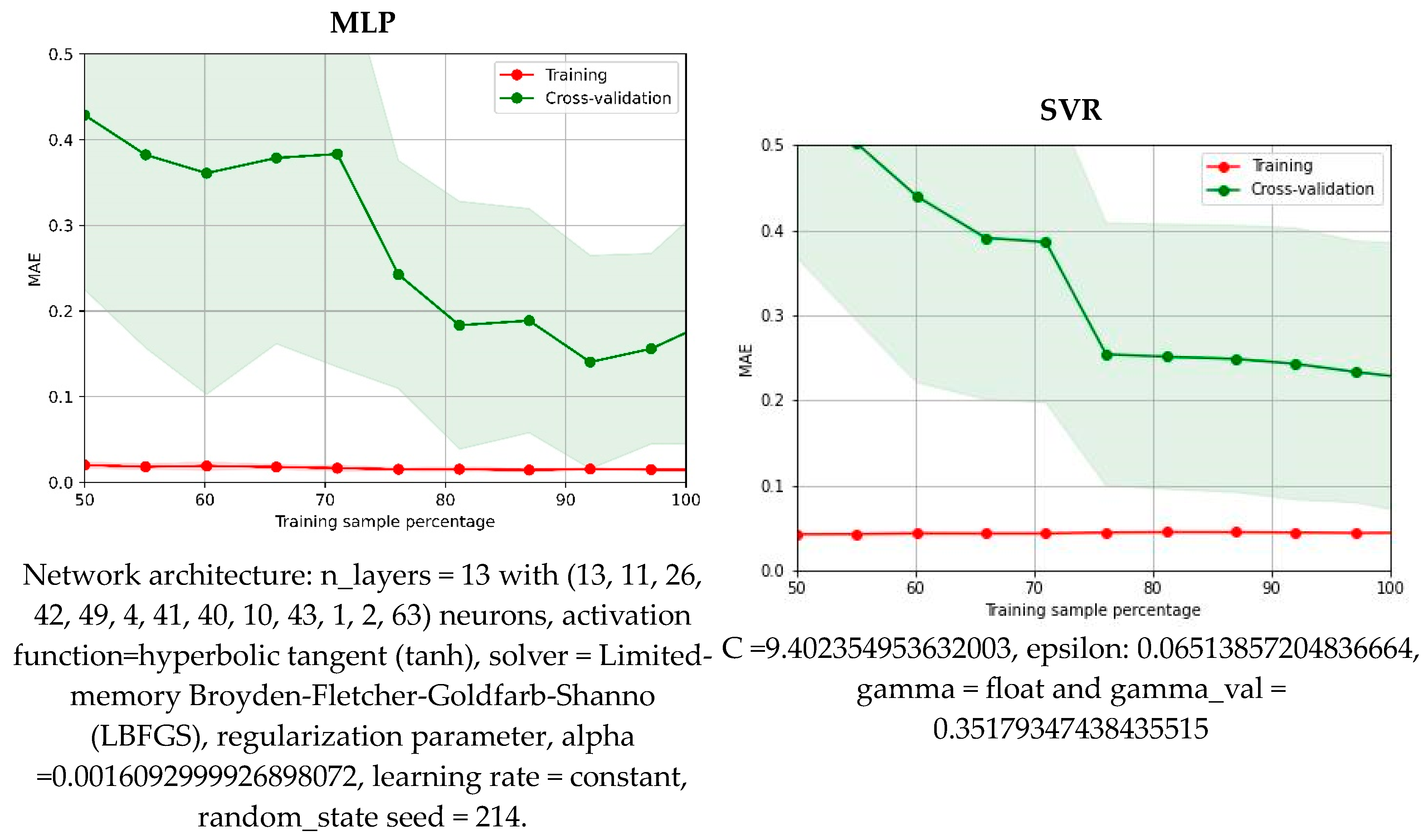
3.6. Machine Learning Protocol
3.7. Molecular Descriptors
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ou, S.; Kwok, K.C. Ferulic acid: Pharmaceutical functions, preparation and applications in foods. J. Sci. Food Agric. 2004, 84, 1261–1269. [Google Scholar] [CrossRef]
- Mancuso, C.; Santangelo, R. Ferulic acid: Pharmacological and toxicological aspects. Food Chem. Toxicol. 2014, 65, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Rui, Y.X.; Guo, S.; Luan, F.; Liu, R.; Zeng, N. Ferulic acid: A review of its pharmacology, pharmacokinetics and derivatives. Life Sci. 2021, 284, 119921. [Google Scholar] [CrossRef] [PubMed]
- Babbar, R.; Dhiman, S.; Grover, R.; Kaur, A.; Arora, S. A Comprehensive Review on Therapeutic Applications of Ferulic Acid and its Novel Analogues: A Brief Literature. Mini-Rev. Med. Chem. 2021, 21, 1578–1593. [Google Scholar] [CrossRef]
- Kumar, N.; Pruthi, V. Potential applications of ferulic acid from natural sources. Biotechnol. Rep. 2014, 4, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Sakai, S.; Kawamata, H.; Kogure, T.; Mantani, N.; Terasawa, K.; Umatake, M.; Ochiai, H. Inhibitory Effect of Ferulic Acid and Isoferulic Acid on the Production of Macrophage Inflammatory Protein-2 in Response to Respiratory Syncytial Virus Infection in RAW264.7 Cells. Mediat. Inflamm. 1999, 8, 173–175. [Google Scholar] [CrossRef]
- Graf, E. Antioxidant potential of ferulic acid. Free Radic. Biol. Med. 1992, 13, 435–448. [Google Scholar] [CrossRef]
- Zduńska, K.; Dana, A.; Kolodziejczak, A.; Rotsztejn, H. Antioxidant Properties of Ferulic Acid and Its Possible Application. Ski. Pharmacol. Physiol. 2018, 31, 332–336. [Google Scholar] [CrossRef]
- Kikuzaki, H.; Hisamoto, M.; Hirose, K.; Akiyama, K.; Taniguchi, H. Antioxidant properties of ferulic acid and its related compounds. J. Agric. Food Chem. 2002, 50, 2161–2168. [Google Scholar] [CrossRef]
- Urbaniak, A.; Szelag, M.; Molski, M. Theoretical investigation of stereochemistry and solvent influence on antioxidant activity of ferulic acid. Comput. Theor. Chem. 2013, 1012, 33–40. [Google Scholar] [CrossRef]
- Borges, F.; Lima, J.L.F.C.; Pinto, I.; Reis, S.; Siquet, C. Application of a Potentiometric System with Data-Analysis Computer Programs to the Quantification of Metal-Chelating Activity of Two Natural Antioxidants: Caffeic Acid and Ferulic Acid. Helv. Chim. Acta 2003, 86, 3081–3087. [Google Scholar] [CrossRef]
- Truong, D.H.; Nhung, N.T.A.; Dao, D.Q. Iron ions chelation-based antioxidant potential vs. pro-oxidant risk of ferulic acid: A DFT study in aqueous phase. Comput. Theor. Chem. 2020, 1185, 112905. [Google Scholar] [CrossRef]
- Hosoda, A.; Ozaki, Y.; Kashiwada, A.; Mutoh, M.; Wakabayashi, K.; Mizuno, K.; Nomura, E.; Taniguchi, H. Syntheses of Ferulic Acid Derivatives and Their Suppressive Effects on Cyclooxygenase-2 Promoter Activity. Bioorg. Med. Chem. 2002, 10, 1189–1196. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Pruthi, V. Structural elucidation and molecular docking of ferulic acid from Parthenium hysterophorus possessing COX-2 inhibition activity. 3 Biotech 2015, 5, 541–551. [Google Scholar] [CrossRef] [PubMed]
- Amić, A.; Marković, J.M.D.; Marković, Z.; Milenković, D.; Milanović, Ž.; Antonijević, M.; Cagardová, D.M.; Pedregal, J.R.G. Theoretical study of radical inactivation, lox inhibition, and iron chelation: The role of ferulic acid in skin protection against uva induced oxidative stress. Antioxidants 2021, 10, 1303. [Google Scholar] [CrossRef]
- Zhao, J.; Suyama, A.; Tanaka, M.; Matsui, T. Ferulic acid enhances the vasorelaxant effect of epigallocatechin gallate in tumor necrosis factor-alpha-induced inflammatory rat aorta. J. Nutr. Biochem. 2014, 25, 807–814. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, R.; Rasool, M. Ferulic acid inhibits interleukin 17-dependent expression of nodal pathogenic mediators in fibroblast-like synoviocytes of rheumatoid arthritis. J. Cell. Biochem. 2019, 120, 1878–1893. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yuan, Z.; Zhao, H.; Ju, D.; Chen, Y.; Chen, X.; Zhang, J. Ferulic acid promotes endothelial cells proliferation through up-regulating cyclin D1 and VEGF. J. Ethnopharmacol. 2011, 137, 992–997. [Google Scholar] [CrossRef] [PubMed]
- Serreli, G.; Le Sayec, M.; Thou, E.; Lacour, C.; Diotallevi, C.; Dhunna, M.A.; Deiana, M.; Spencer, J.P.E.; Corona, G. Ferulic Acid Derivatives and Avenanthramides Modulate Endothelial Function through Maintenance of Nitric Oxide Balance in HUVEC Cells. Nutrients 2021, 13, 2026. [Google Scholar] [CrossRef]
- Ali, S.A.; Saifi, M.A.; Pulivendala, G.; Godugu, C.; Talla, V. Ferulic acid ameliorates the progression of pulmonary fibrosis via inhibition of TGF-β/smad signalling. Food Chem. Toxicol. 2021, 149, 111980. [Google Scholar] [CrossRef]
- Zhao, X.M.; Zhang, J.; Liang, Y.N.; Niu, Y.C. Astragaloside IV Synergizes with Ferulic Acid to Alleviate Hepatic Fibrosis in Bile Duct-Ligated Cirrhotic Rats. Dig. Dis. Sci. 2020, 65, 2925–2936. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Singh, A.K.; Loka, M.; Pandey, A.K.; Bishayee, A. Ferulic acid-mediated modulation of apoptotic signaling pathways in cancer. Adv. Protein Chem. Struct. Biol. 2021, 125, 215–257. [Google Scholar]
- Nakayama, H.; Nakahara, M.; Matsugi, E.; Soda, M.; Hattori, T.; Hara, K.; Usami, A.; Kusumoto, C.; Higashiyama, S.; Kitaichi, K. Protective Effect of Ferulic Acid against Hydrogen Peroxide Induced Apoptosis in PC12 Cells. Molecules 2020, 26, 90. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Shen, X.; Yang, L.; Chen, Q.; Wang, N.; Li, Y.; Song, P.; Jiang, M.; Bai, G.; Yang, P.; et al. Exploring the Q-markers of Angelica sinensis (Oliv.) Diels of anti-platelet aggregation activity based on spectrum–effect relationships. Biomed. Chromatogr. 2022, 36, e5422. [Google Scholar] [CrossRef]
- Nguyen, T.M.H.; Le, H.L.; Ha, T.T.; Bui, B.H.; Le, N.T.; Nguyen, V.H.; Nguyen, T.V.A. Inhibitory effect on human platelet aggregation and coagulation and antioxidant activity of C. edulis Ker Gawl rhizome and its secondary metabolites. J. Ethnopharmacol. 2020, 263, 113136. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.Y.; Li, J.N.; Liu, W.L.; Huang, Q.; Li, W.X.; Tan, Y.H.; Liu, F.; Song, Z.H.; Wang, M.Y.; Xie, N.; et al. Ferulic Acid Ameliorates Alzheimer’s Disease-like Pathology and Repairs Cognitive Decline by Preventing Capillary Hypofunction in APP/PS1 Mice. Neurotherapeutics 2021, 18, 1064–1080. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Huang, R. Ferulic acid: An extraordinarily neuroprotective phenolic acid with anti-depressive properties. Phytomedicine 2022, 105, 154355. [Google Scholar] [CrossRef]
- Bourne, L.C.; Rice-Evans, C. Bioavailability of Ferulic Acid. Biochem. Biophys. Res. Commun. 1998, 253, 222–227. [Google Scholar] [CrossRef]
- Lafay, S.; Gil-Izquierdo, A. Bioavailability of phenolic acids. Phytochem. Rev. 2008, 7, 301–311. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Zhang, K.; Yang, G.; Wang, Z.; Zhao, J.; Hu, R.; Feng, N. Ethyl oleate-containing nanostructured lipid carriers improve oral bioavailability of trans-ferulic acid ascompared with conventional solid lipid nanoparticles. Int. J. Pharm. 2016, 511, 57–64. [Google Scholar] [CrossRef]
- Hassanzadeh, P.; Arbabi, E.; Atyabi, F.; Dinarvand, R. Ferulic acid-loaded nanostructured lipid carriers: A promising nanoformulation against the ischemic neural injuries. Life Sci. 2018, 193, 64–76. [Google Scholar] [CrossRef] [PubMed]
- Hithamani, G.; Srinivasan, K. Bioavailability of finger millet (Eleusine coracana) phenolic compounds in rat as influenced by co-administered piperine. Food Biosci. 2017, 19, 101–109. [Google Scholar] [CrossRef]
- Scholz, S.; Williamson, G. Interactions Affecting the Bioavailability of Dietary Polyphenols in Vivo. Int. J. Vitam. Nutr. Res. 2013, 77, 224–235. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.W.; Al-Suwayeh, S.A.; Hsieh, P.W.; Fang, J.Y. A comparison of skin delivery of ferulic acid and its derivatives: Evaluation of their efficacy and safety. Int. J. Pharm. 2010, 399, 44–51. [Google Scholar] [CrossRef]
- Chen, M.; Liu, X.; Fahr, A. Skin delivery of ferulic acid from different vesicular systems. J. Biomed. Nanotechnol. 2010, 6, 577–585. [Google Scholar] [CrossRef]
- Zduńska-Pęciak, K.; Dębowska, R.; Kołodziejczak, A.; Rotsztejn, H. Ferulic acid—A novel topical agent in reducing signs of photoaging. Dermatol. Ther. 2022, 35, e15543. [Google Scholar] [CrossRef]
- Janus, E.; Pinheiro, L.R.; Nowak, A.; Kucharska, E.; Świątek, E.; Podolak, N.; Perużyńska, M.; Piotrowska, K.; Duchnik, W.; Kucharski, Ł.; et al. New Ferulic Acid and Amino Acid Derivatives with Increased Cosmeceutical and Pharmaceutical Potential. Pharmaceutics 2023, 15, 117. [Google Scholar] [CrossRef]
- Cavalcanti, G.R.; Duarte, F.I.C.; Converti, A.; de Lima, Á.A.N. Ferulic Acid Activity in Topical Formulations: Technological and Scientific Prospecting. Curr. Pharm. Des. 2020, 27, 2289–2298. [Google Scholar] [CrossRef]
- Martínez, F.; Jouyban, A.; Acree, W.E. Pharmaceuticals solubility is still nowadays widely studied everywhere. Pharm. Sci. 2017, 23, 1–2. [Google Scholar] [CrossRef]
- Savjani, K.T.; Gajjar, A.K.; Savjani, J.K. Drug Solubility: Importance and Enhancement Techniques. ISRN Pharm. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Coltescu, A.R.; Butnariu, M.; Sarac, I. The importance of solubility for new drug molecules. Biomed. Pharmacol. J. 2020, 13, 577–583. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, Y.; Xia, M.; Dai, W.; Zhu, B.; Mei, X. Improving the dissolution behaviors and bioavailability of abiraterone acetate via multicomponent crystal forms. Int. J. Pharm. 2022, 614, 121460. [Google Scholar] [CrossRef] [PubMed]
- Kalam, M.A.; Alshamsan, A.; Alkholief, M.; Alsarra, I.A.; Ali, R.; Haq, N.; Anwer, M.K.; Shakeel, F. Solubility Measurement and Various Solubility Parameters of Glipizide in Different Neat Solvents. ACS Omega 2020, 5, 1708–1716. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kim, C.-M.; Jo, A.-N.; Kim, J.-E. Studies on Preformulation and Formulation of JIN-001 Liquisolid Tablet with Enhanced Solubility. Pharmaceuticals 2022, 15, 412. [Google Scholar] [CrossRef]
- Khadka, P.; Ro, J.; Kim, H.; Kim, I.; Kim, J.T.; Kim, H.; Cho, J.M.; Yun, G.; Lee, J. Pharmaceutical particle technologies: An approach to improve drug solubility, dissolution and bioavailability. Asian J. Pharm. Sci. 2014, 9, 304–316. [Google Scholar] [CrossRef]
- Müller, C.E. Prodrug Approaches for Enhancing the Bioavailability of Drugs with Low Solubility. Chem. Biodivers. 2009, 6, 2071–2083. [Google Scholar] [CrossRef]
- Das, T.; Mehta, C.H.; Nayak, U.Y. Multiple approaches for achieving drug solubility: An in silico perspective. Drug Discov. Today 2020, 25, 1206–1212. [Google Scholar] [CrossRef]
- Tian, Y.; Shi, C.; Sun, Y.; Zhu, C.; Sun, C.C.; Mao, S. Designing micellar Nanocarriers with improved drug loading and stability based on solubility parameter. Mol. Pharm. 2015, 12, 816–825. [Google Scholar] [CrossRef] [PubMed]
- Lipinski, C.A. Drug-like properties and the causes of poor solubility and poor permeability. J. Pharmacol. Toxicol. Methods 2000, 44, 235–249. [Google Scholar] [CrossRef]
- Da Silva, F.L.O.; Marques, M.B.D.F.; Kato, K.C.; Carneiro, G. Nanonization techniques to overcome poor water-solubility with drugs. Expert Opin. Drug Discov. 2020, 15, 853–864. [Google Scholar] [CrossRef]
- Das, B.; Baidya, A.T.K.; Mathew, A.T.; Yadav, A.K.; Kumar, R. Structural modification aimed for improving solubility of lead compounds in early phase drug discovery. Bioorg. Med. Chem. 2022, 56, 116614. [Google Scholar] [CrossRef] [PubMed]
- Bergström, C.A.S.; Avdeef, A. Perspectives in solubility measurement and interpretation. ADMET DMPK 2019, 7, 88–105. [Google Scholar] [CrossRef] [PubMed]
- Black, S.; Dang, L.; Liu, C.; Wei, H. On the measurement of solubility. Org. Process Res. Dev. 2013, 17, 486–492. [Google Scholar] [CrossRef]
- Boobier, S.; Hose, D.R.J.; Blacker, A.J.; Nguyen, B.N. Machine learning with physicochemical relationships: Solubility prediction in organic solvents and water. Nat. Commun. 2020, 11, 5753. [Google Scholar] [CrossRef] [PubMed]
- Lovrić, M.; Pavlović, K.; Žuvela, P.; Spataru, A.; Lučić, B.; Kern, R.; Wong, M.W. Machine learning in prediction of intrinsic aqueous solubility of drug-like compounds: Generalization, complexity, or predictive ability? J. Chemom. 2021, 35, e3349. [Google Scholar] [CrossRef]
- Bhalani, D.V.; Nutan, B.; Kumar, A.; Singh Chandel, A.K. Bioavailability Enhancement Techniques for Poorly Aqueous Soluble Drugs and Therapeutics. Biomedicines 2022, 10, 2055. [Google Scholar] [CrossRef] [PubMed]
- Manallack, D.T.; Yuriev, E.; Chalmers, D.K. The influence and manipulation of acid/base properties in drug discovery. Drug Discov. Today Technol. 2018, 27, 41–47. [Google Scholar] [CrossRef]
- Merisko-Liversidge, E.; Liversidge, G.G. Nanosizing for oral and parenteral drug delivery: A perspective on formulating poorly-water soluble compounds using wet media milling technology. Adv. Drug Deliv. Rev. 2011, 63, 427–440. [Google Scholar] [CrossRef] [PubMed]
- Brewster, M.E.; Loftsson, T. Cyclodextrins as pharmaceutical solubilizers. Adv. Drug Deliv. Rev. 2007, 59, 645–666. [Google Scholar] [CrossRef]
- Korn, C.; Balbach, S. Compound selection for development—Is salt formation the ultimate answer? Experiences with an extended concept of the “100mg approach” . Eur. J. Pharm. Sci. 2014, 57, 257–263. [Google Scholar]
- Seedher, N.; Kanojia, M. Co-solvent solubilization of some poorly-soluble antidiabetic drugs. Pharm. Dev. Technol. 2009, 14, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Hahnenkamp, I.; Graubner, G.; Gmehling, J. Measurement and prediction of solubilities of active pharmaceutical ingredients. Int. J. Pharm. 2010, 388, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H.; Smith, R.E.; Luchtefeld, R.; Boorem, A.J.; Lou, R.; Acree, W.E. Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 2010, 99, 1500–1515. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, M.; Cronin, M.T.D.; Enoch, S.J.; Madden, J.C.; Roberts, D.W.; Dearden, J.C. In silico prediction of aqueous solubility: The solubility challenge. J. Chem. Inf. Model. 2009, 49, 2572–2587. [Google Scholar] [CrossRef] [PubMed]
- Lenoir, D.; Schramm, K.W.; Lalah, J.O. Green Chemistry: Some important forerunners and current issues. Sustain. Chem. Pharm. 2020, 18, 100313. [Google Scholar] [CrossRef]
- Kopach, M.; Leahy, D.; Manley, J. The green chemistry approach to pharma manufacturing. Innov. Pharm. Technol. 2012, 43, 72–75. [Google Scholar]
- Becker, J.; Manske, C.; Randl, S. Green chemistry and sustainability metrics in the pharmaceutical manufacturing sector. Curr. Opin. Green Sustain. Chem. 2022, 33, 100562. [Google Scholar] [CrossRef]
- Mishra, M.; Sharma, M.; Dubey, R.; Kumari, P.; Ranjan, V.; Pandey, J. Green synthesis interventions of pharmaceutical industries for sustainable development. Curr. Res. Green Sustain. Chem. 2021, 4, 100174. [Google Scholar] [CrossRef]
- DeSimone, J.M. Practical approaches to green solvents. Science 2002, 297, 799–803. [Google Scholar] [CrossRef]
- Häckl, K.; Kunz, W. Some aspects of green solvents. Comptes Rendus Chim. 2018, 21, 572–580. [Google Scholar] [CrossRef]
- Santana-Mayor, Á.; Rodríguez-Ramos, R.; Herrera-Herrera, A.V.; Socas-Rodríguez, B.; Rodríguez-Delgado, M.Á. Deep eutectic solvents. The new generation of green solvents in analytical chemistry. TrAC Trends Anal. Chem. 2021, 134, 116108. [Google Scholar] [CrossRef]
- Vanda, H.; Dai, Y.; Wilson, E.G.; Verpoorte, R.; Choi, Y.H. Green solvents from ionic liquids and deep eutectic solvents to natural deep eutectic solvents. Comptes Rendus Chim. 2018, 21, 628–638. [Google Scholar] [CrossRef]
- Omar, K.A.; Sadeghi, R. Physicochemical properties of deep eutectic solvents: A review. J. Mol. Liq. 2022, 360, 119524. [Google Scholar] [CrossRef]
- Paiva, A.; Craveiro, R.; Aroso, I.; Martins, M.; Reis, R.L.; Duarte, A.R.C. Natural Deep Eutectic Solvents—Solvents for the 21st Century. ACS Sustain. Chem. Eng. 2014, 2, 1063–1071. [Google Scholar] [CrossRef]
- Espino, M.; de los Ángeles Fernández, M.; Gomez, F.J.V.; Silva, M.F. Natural designer solvents for greening analytical chemistry. TrAC Trends Anal. Chem. 2016, 76, 126–136. [Google Scholar] [CrossRef]
- Xu, G.; Shi, M.; Zhang, P.; Tu, Z.; Hu, X.; Zhang, X.; Wu, Y. Tuning the composition of deep eutectic solvents consisting of tetrabutylammonium chloride and n-decanoic acid for adjustable separation of ethylene and ethane. Sep. Purif. Technol. 2022, 298, 121680. [Google Scholar] [CrossRef]
- Cao, Y.; Tao, X.; Jiang, S.; Gao, N.; Sun, Z. Tuning thermodynamic properties of deep eutectic solvents for achieving highly efficient photothermal sensor. J. Mol. Liq. 2020, 308, 113163. [Google Scholar] [CrossRef]
- Pedro, S.N.; Freire, C.S.R.; Silvestre, A.J.D.; Freire, M.G. Deep Eutectic Solvents and Pharmaceuticals. Encyclopedia 2021, 1, 942–963. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Experimental and Theoretical Insights into the Intermolecular Interactions in Saturated Systems of Dapsone in Conventional and Deep Eutectic Solvents. Molecules 2024, 29, 1743. [Google Scholar] [CrossRef]
- Bazzo, G.C.; Pezzini, B.R.; Stulzer, H.K. Eutectic mixtures as an approach to enhance solubility, dissolution rate and oral bioavailability of poorly water-soluble drugs. Int. J. Pharm. 2020, 588, 119741. [Google Scholar] [CrossRef]
- Kapre, S.; Palakurthi, S.S.; Jain, A.; Palakurthi, S. DES-igning the future of drug delivery: A journey from fundamentals to drug delivery applications. J. Mol. Liq. 2024, 400, 124517. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Mianowana, M.; Misiak, K.; Cysewski, P. Deep Eutectic Solvents as Agents for Improving the Solubility of Edaravone: Experimental and Theoretical Considerations. Molecules 2024, 29, 1261. [Google Scholar] [CrossRef] [PubMed]
- Duarte, A.R.C.; Ferreira, A.S.D.; Barreiros, S.; Cabrita, E.; Reis, R.L.; Paiva, A. A comparison between pure active pharmaceutical ingredients and therapeutic deep eutectic solvents: Solubility and permeability studies. Eur. J. Pharm. Biopharm. 2017, 114, 296–304. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.-H.; Augis, L.; Fourmentin, S.; Barratt, G.; Legrand, F.-X. Deep Eutectic Solvents for Innovative Pharmaceutical Formulations; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Liu, Y.; Wu, Y.; Liu, J.; Wang, W.; Yang, Q.; Yang, G. Deep eutectic solvents: Recent advances in fabrication approaches and pharmaceutical applications. Int. J. Pharm. 2022, 622, 121811. [Google Scholar] [CrossRef] [PubMed]
- García-Roldán, A.; Piriou, L.; Jauregi, P. Natural deep eutectic solvents as a green extraction of polyphenols from spent coffee ground with enhanced bioactivities. Front. Plant Sci. 2023, 13, 1072592. [Google Scholar] [CrossRef] [PubMed]
- Cysewski, P.; Przybyłek, M.; Jeliński, T. Predicting sulfanilamide solubility in the binary mixtures using a reference solvent approach. Polym. Med. 2024, 54, 27–34. [Google Scholar]
- Hammond, O.S.; Bowron, D.T.; Edler, K.J.; Hammond, S.; Edler, K.J.; Bowron, D.T. The Effect of Water upon Deep Eutectic Solvent Nanostructure: An Unusual Transition from Ionic Mixture to Aqueous Solution. Angew. Chem. Int. Ed. 2017, 56, 9782–9785. [Google Scholar] [CrossRef] [PubMed]
- Gabriele, F.; Chiarini, M.; Germani, R.; Tiecco, M.; Spreti, N. Effect of water addition on choline chloride/glycol deep eutectic solvents: Characterization of their structural and physicochemical properties. J. Mol. Liq. 2019, 291, 111301. [Google Scholar] [CrossRef]
- Mota, F.L.; Queimada, A.J.; Pinho, S.P.; Macedo, E.A. Aqueous solubility of some natural phenolic compounds. Ind. Eng. Chem. Res. 2008, 47, 5182–5189. [Google Scholar] [CrossRef]
- Shakeel, F.; Salem-Bekhit, M.M.; Haq, N.; Siddiqui, N.A. Solubility and thermodynamics of ferulic acid in different neat solvents: Measurement, correlation and molecular interactions. J. Mol. Liq. 2017, 236, 144–150. [Google Scholar] [CrossRef]
- Manic, M.S.; Villanueva, D.; Fornari, T.; Queimada, A.J.; MacEdo, E.A.; Najdanovic-Visak, V. Solubility of high-value compounds in ethyl lactate: Measurements and modeling. J. Chem. Thermodyn. 2012, 48, 93–100. [Google Scholar] [CrossRef]
- Haq, N.; Siddiqui, N.A.; Shakeel, F. Solubility and molecular interactions of ferulic acid in various (isopropanol + water) mixtures. J. Pharm. Pharmacol. 2017, 69, 1485–1494. [Google Scholar] [CrossRef]
- Vilas-Boas, S.M.; Alves, R.S.; Brandão, P.; Campos, L.M.A.; Coutinho, J.A.P.; Pinho, S.P.; Ferreira, O. Solid-liquid phase equilibrium of trans-cinnamic acid, p-coumaric acid and ferulic acid in water and organic solvents: Experimental and modelling studies. Fluid Phase Equilib. 2020, 521, 112747. [Google Scholar] [CrossRef]
- Przybyłek, M.; Recki, Ł.; Mroczyńska, K.; Jeliński, T.; Cysewski, P. Experimental and theoretical solubility advantage screening of bi-component solid curcumin formulations. J. Drug Deliv. Sci. Technol. 2019, 50, 125–135. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Cysewski, P. Solubility advantage of sulfanilamide and sulfacetamide in natural deep eutectic systems: Experimental and theoretical investigations. Drug Dev. Ind. Pharm. 2019, 45, 1120–1129. [Google Scholar] [CrossRef]
- Jeliński, T.; Stasiak, D.; Kosmalski, T.; Cysewski, P. Experimental and theoretical study on theobromine solubility enhancement in binary aqueous solutions and ternary designed solvents. Pharmaceutics 2021, 13, 1118. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Application of COSMO-RS-DARE as a Tool for Testing Consistency of Solubility Data: Case of Coumarin in Neat Alcohols. Molecules 2022, 27, 5274. [Google Scholar] [CrossRef] [PubMed]
- Dassault Systèmes. COSMOconf, Version 24.0.0, Dassault Systèmes; Biovia: San Diego, CA, USA, 2022. [Google Scholar]
- COSMOtherm, Version 24.0.0, Dassault Systèmes; Biovia: San Diego, CA, USA, 2022.
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Intermolecular Interactions of Edaravone in Aqueous Solutions of Ethaline and Glyceline Inferred from Experiments and Quantum Chemistry Computations. Molecules 2023, 28, 629. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Różalski, R.; Cysewski, P. Solubility of dapsone in deep eutectic solvents: Experimental analysis, molecular insights and machine learning predictions. Polym. Med. 2024, 54, 15–25. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M.; Mai, A.; Kułak, J. Experimental and Machine-Learning-Assisted Design of Pharmaceutically Acceptable Deep Eutectic Solvents for the Solubility Improvement of Non-Selective COX Inhibitors Ibuprofen and Ketoprofen. Molecules 2024, 29, 2296. [Google Scholar] [CrossRef]
- Jeliński, T.; Cysewski, P. Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation. Int. J. Mol. Sci. 2022, 23, 7832. [Google Scholar] [CrossRef] [PubMed]
- Witte, J.; Neaton, J.B.; Head-Gordon, M. Effective empirical corrections for basis set superposition error in the def2-SVPD basis: gCP and DFT-C. J. Chem. Phys. 2017, 146, 234105. [Google Scholar] [CrossRef] [PubMed]
- TURBOMOLE GmbH. TURBOMOLE, Version 7.8; TURBOMOLE GmbH: Karlsruhe, Germany, 2023. [Google Scholar]
- Bitencourt, R.G.; Cabral, F.A.; Meirelles, A.J.A. Ferulic acid solubility in supercritical carbon dioxide, ethanol and water mixtures. J. Chem. Thermodyn. 2016, 103, 285–291. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Finding the Right Solvent: A Novel Screening Protocol for Identifying Environmentally Friendly and Cost-Effective Options for Benzenesulfonamide. Molecules 2023, 28, 5008. [Google Scholar] [CrossRef] [PubMed]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799. [Google Scholar] [CrossRef]
- Acree, W.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds and Ionic Liquids. Sublimation, Vaporization, and Fusion Enthalpies from 1880 to 2015. Part 2. C11–C192. J. Phys. Chem. Ref. Data 2017, 46, 013104. [Google Scholar]
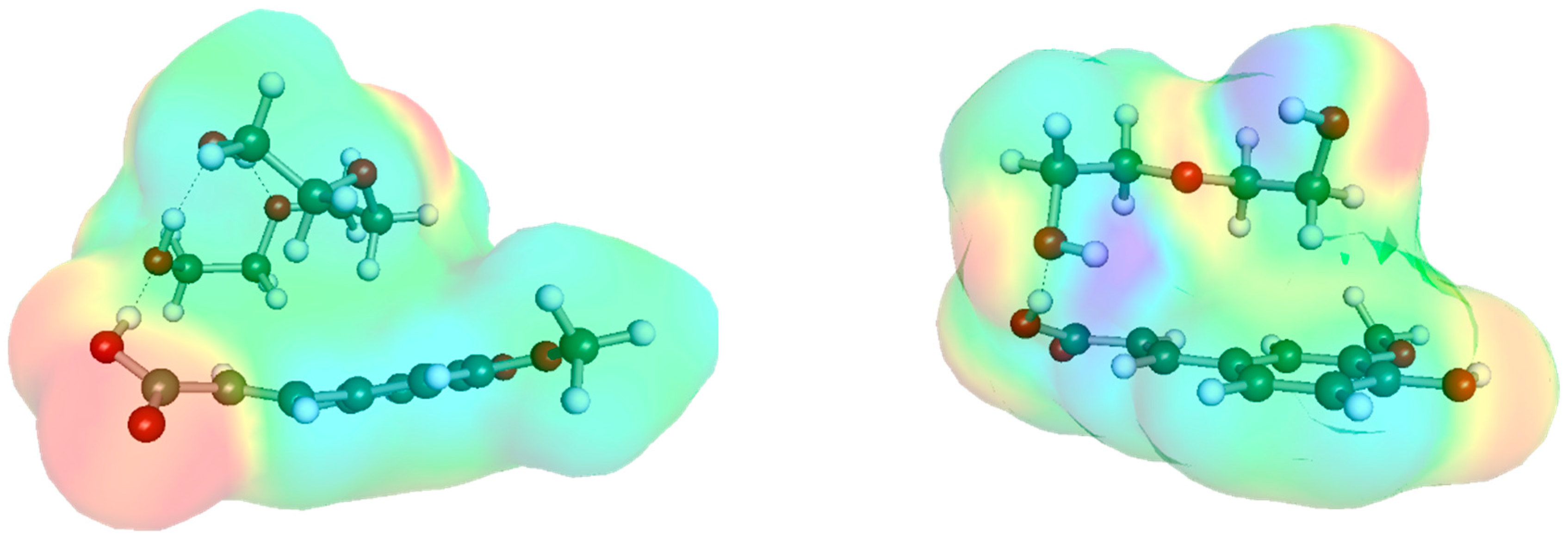
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeliński, T.; Przybyłek, M.; Różalski, R.; Romanek, K.; Wielewski, D.; Cysewski, P. Tuning Ferulic Acid Solubility in Choline-Chloride- and Betaine-Based Deep Eutectic Solvents: Experimental Determination and Machine Learning Modeling. Molecules 2024, 29, 3841. https://doi.org/10.3390/molecules29163841
Jeliński T, Przybyłek M, Różalski R, Romanek K, Wielewski D, Cysewski P. Tuning Ferulic Acid Solubility in Choline-Chloride- and Betaine-Based Deep Eutectic Solvents: Experimental Determination and Machine Learning Modeling. Molecules. 2024; 29(16):3841. https://doi.org/10.3390/molecules29163841
Chicago/Turabian StyleJeliński, Tomasz, Maciej Przybyłek, Rafał Różalski, Karolina Romanek, Daniel Wielewski, and Piotr Cysewski. 2024. "Tuning Ferulic Acid Solubility in Choline-Chloride- and Betaine-Based Deep Eutectic Solvents: Experimental Determination and Machine Learning Modeling" Molecules 29, no. 16: 3841. https://doi.org/10.3390/molecules29163841
APA StyleJeliński, T., Przybyłek, M., Różalski, R., Romanek, K., Wielewski, D., & Cysewski, P. (2024). Tuning Ferulic Acid Solubility in Choline-Chloride- and Betaine-Based Deep Eutectic Solvents: Experimental Determination and Machine Learning Modeling. Molecules, 29(16), 3841. https://doi.org/10.3390/molecules29163841








