Self-Association and Microhydration of Phenol: Identification of Large-Amplitude Hydrogen Bond Librational Modes
Abstract
1. Introduction
2. Results
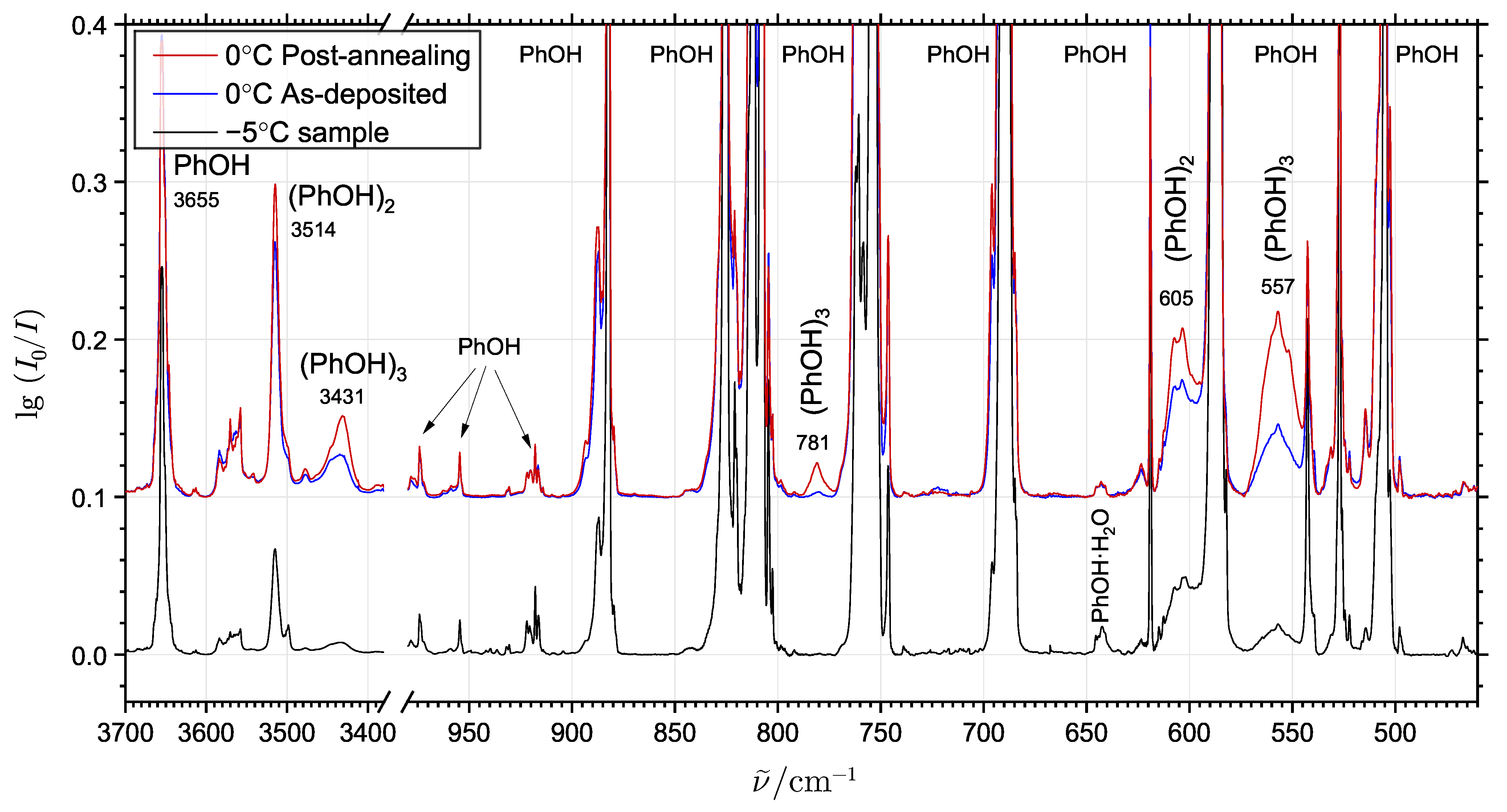
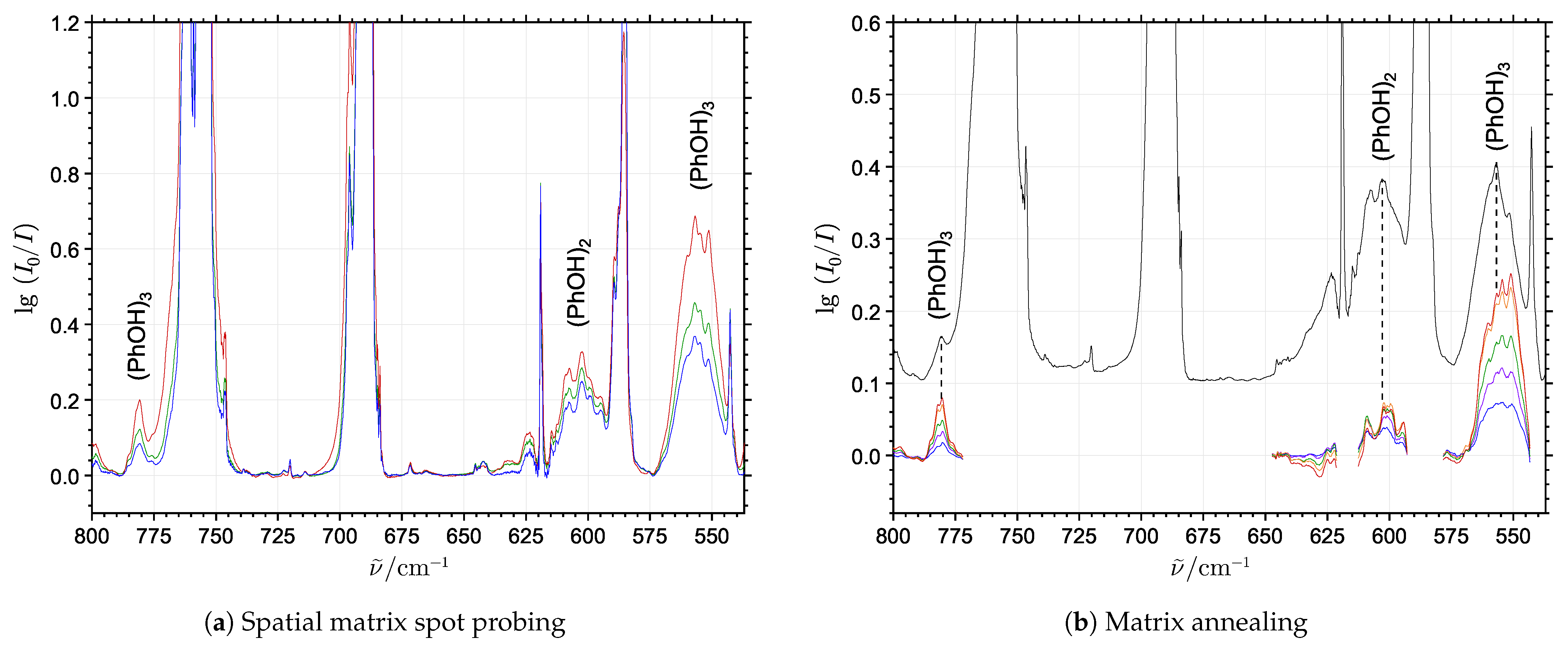
2.1. Phenol Cluster Molecules
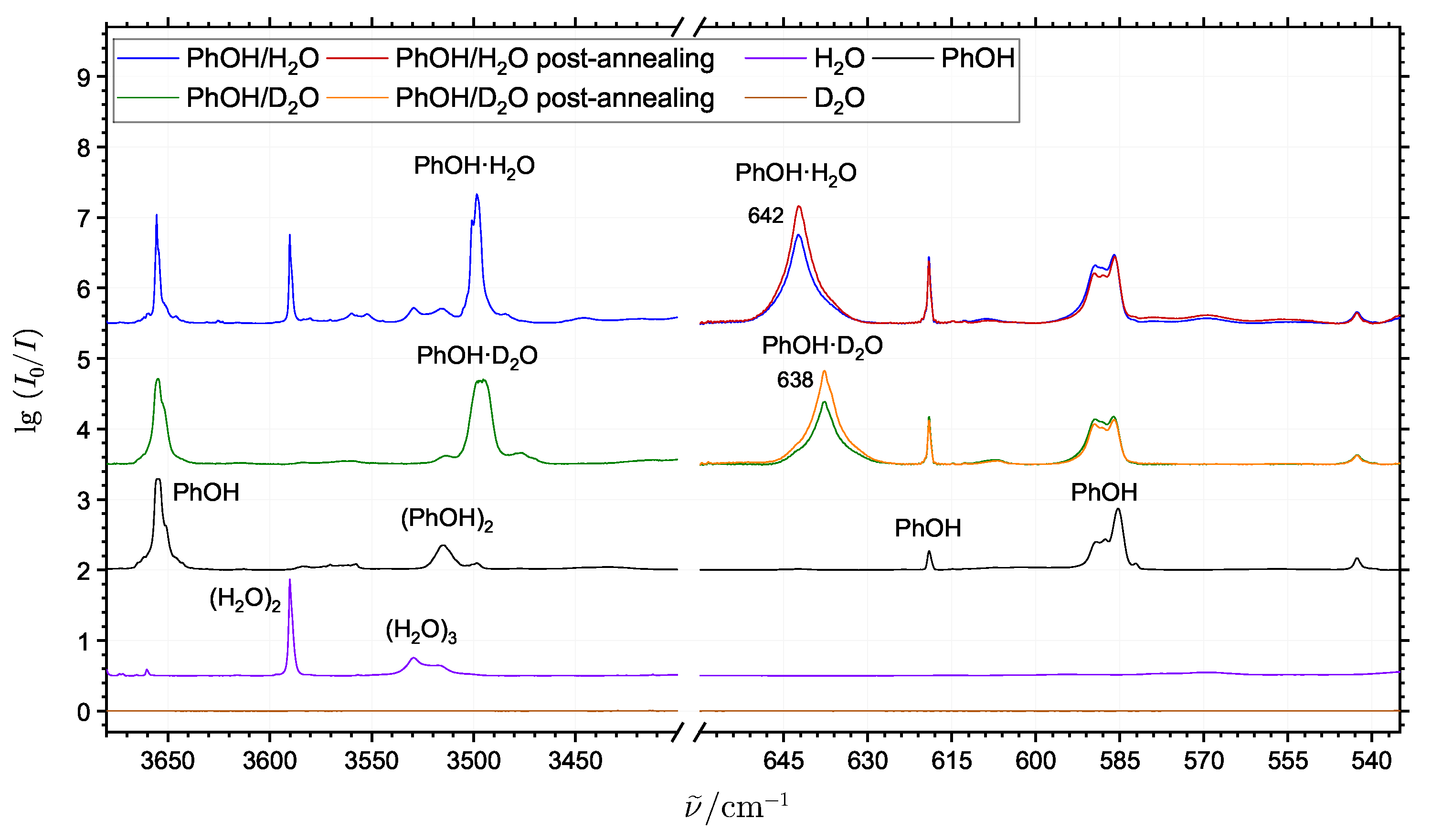
2.2. The Phenol Monohydrate
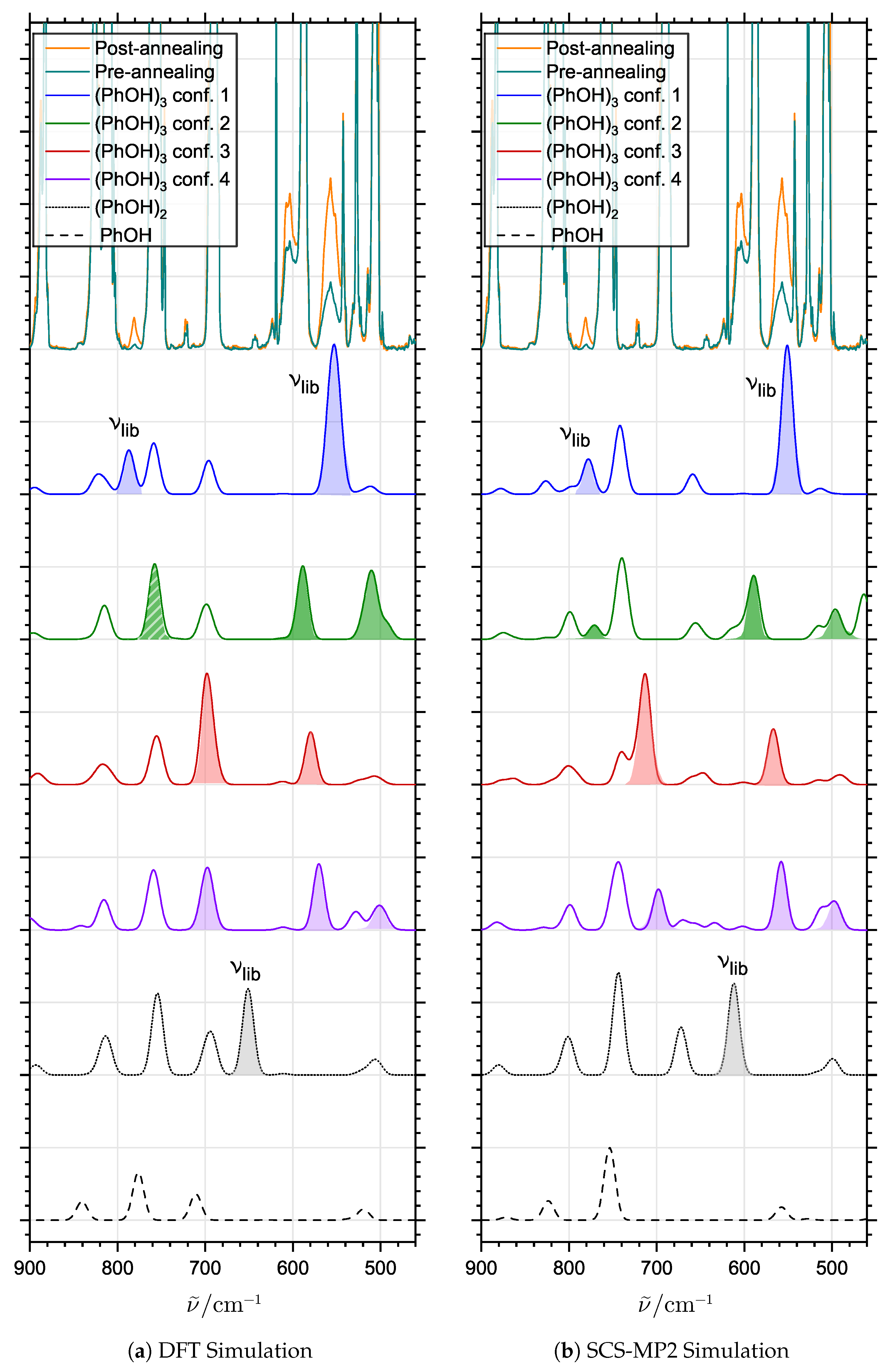
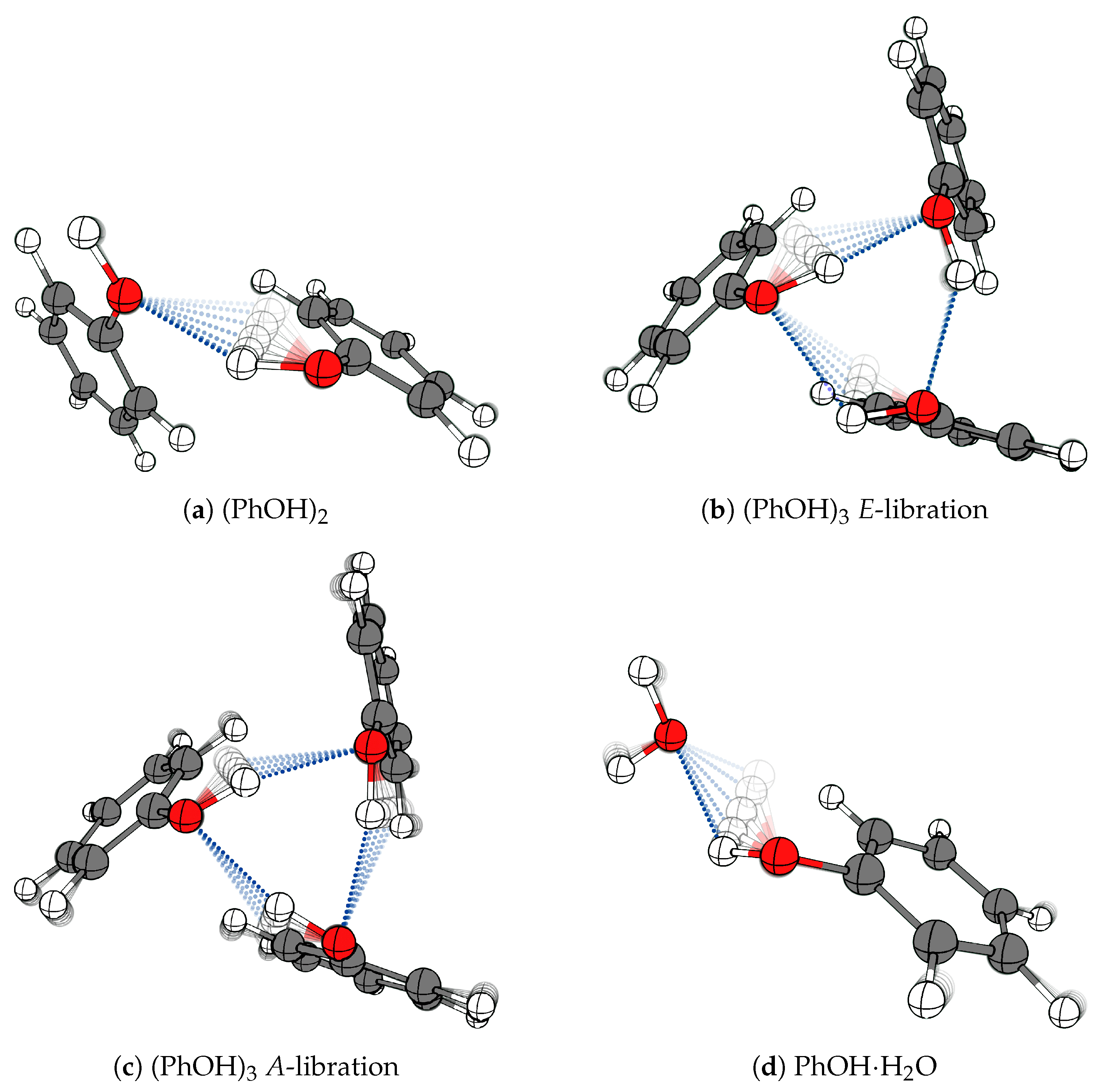
2.3. Supporting Theoretical Analysis
3. Materials and Methods
3.1. Experimental Details
3.2. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chand, A.; Sahoo, D.K.; Rana, A.; Jena, S.; Biswal, H.S. The Prodigious Hydrogen Bonds with Sulfur and Selenium in Molecular Assemblies, Structural Biology, and Functional Materials. Accounts Chem. Res. 2020, 53, 1580–1592. [Google Scholar] [CrossRef] [PubMed]
- Mata, R.A.; Zhanabekova, T.; Obenchain, D.A.; Suhm, M.A. Dispersion Control over Molecule Cohesion: Exploiting and Dissecting the Tipping Power of Aromatic Rings. Accounts Chem. Res. 2024, 57, 1077–1086. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.; Heimdal, J.; Nelander, B.; Larsen, R.W. Competition between weak OH⋯π and CH⋯O hydrogen bonds: THz spectroscopy of the C2H2—H2O and C2H4—H2O complexes. J. Chem. Phys. 2017, 146, 194302. [Google Scholar] [CrossRef] [PubMed]
- Řezáč, J.; Hobza, P. Describing Noncovalent Interactions beyond the Common Approximations: How Accurate Is the “Gold Standard”, CCSD(T) at the Complete Basis Set Limit? J. Chem. Theory Comput. 2013, 9, 2151–2155. [Google Scholar] [CrossRef] [PubMed]
- Mehta, N.; Martin, J.M.L. Explicitly Correlated Double-Hybrid DFT: A Comprehensive Analysis of the Basis Set Convergence on the GMTKN55 Database. J. Chem. Theory Comput. 2022, 18, 5978–5991. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Santra, G.; Martin, J.M.L. A double-hybrid density functional based on good local physics with outstanding performance on the GMTKN55 database. J. Chem. Phys. 2023, 158, 151103. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Jurečka, P.; Šponer, J.; Černý, J.; Hobza, P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef] [PubMed]
- León, I.; Lesarri, A.; Fernández, J.A. Noncovalent interactions in isolated molecular aggregates: From single molecules to nanostructures. In Intra- and Intermolecular Interactions Between Non-Covalently Bonded Species; Elsevier: Amsterdam, The Netherlands, 2021; pp. 143–188. [Google Scholar] [CrossRef]
- Kolář, M.; Hobza, P. Accurate Theoretical Determination of the Structure of Aromatic Complexes Is Complicated: The Phenol Dimer and Phenol·Methanol Cases. J. Phys. Chem. A 2007, 111, 5851–5854. [Google Scholar] [CrossRef]
- Plokhotnichenko, A.M.; Radchenko, E.D.; Blagoi, Y.P.; Karachevtsev, V.A. Dimers of phenol in argon and neon matrices. Low Temp. Phys. 2001, 27, 666–675. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Subramanian, V.; Sathyamurthy, N. Hydrogen Bonding in Phenol, Water, and Phenol–Water Clusters. J. Phys. Chem. A 2005, 109, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Bödecker, M.; Mihrin, D.; Suhm, M.A.; Wugt Larsen, R. Regularities and anomalies in neon matrix shifts of hydrogen-bonded O-H stretching fundamentals. J. Phys. Chem. A 2024. [Google Scholar]
- Gor, G.Y.; Tapio, S.; Domanskaya, A.V.; Räsänen, M.; Nemukhin, A.V.; Khriachtchev, L. Matrix-isolation study of the phenol–water complex and phenol dimer. Chem. Phys. Lett. 2011, 517, 9–15. [Google Scholar] [CrossRef]
- Ebata, T.; Watanabe, T.; Mikami, N. Evidence for the Cyclic Form of Phenol Trimer: Vibrational Spectroscopy of the OH Stretching Vibrations of Jet-Cooled Phenol Dimer and Trimer. J. Phys. Chem. 1995, 99, 5761–5764. [Google Scholar] [CrossRef]
- Ebata, T.; Kayano, M.; Sato, S.; Mikami, N. Picosecond IR-UV Pump-Probe Spectroscopy. IVR of OH Stretching Vibration of Phenol and Phenol Dimer. J. Phys. Chem. A 2001, 105, 8623–8628. [Google Scholar] [CrossRef]
- Weichert, A.; Riehn, C.; Brutschy, B. High-Resolution Rotational Coherence Spectroscopy of the Phenol Dimer. J. Phys. Chem. A 2001, 105, 5679–5691. [Google Scholar] [CrossRef]
- Schmitt, M.; Böhm, M.; Ratzer, C.; Krügler, D.; Kleinermanns, K.; Kalkman, I.; Berden, G.; Meerts, W.L. Determining the Intermolecular Structure in the S0 and S1 States of the Phenol Dimer by Rotationally Resolved Electronic Spectroscopy. ChemPhysChem 2006, 7, 1241–1249. [Google Scholar] [CrossRef] [PubMed]
- Seifert, N.A.; Steber, A.L.; Neill, J.L.; Pérez, C.; Zaleski, D.P.; Pate, B.H.; Lesarri, A. The interplay of hydrogen bonding and dispersion in phenol dimer and trimer: Structures from broadband rotational spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 11468. [Google Scholar] [CrossRef]
- Tanabe, S.; Ebata, T.; Fujii, M.; Mikami, N. OH stretching vibrations of phenol—(H2O)n (n=1-3) complexes observed by IR-UV double-resonance spectroscopy. Chem. Phys. Lett. 1993, 215, 347–352. [Google Scholar] [CrossRef]
- Yu, Z.; Klemperer, W. Asymmetry in angular rigidity of hydrogen-bonded complexes. Proc. Natl. Acad. Sci. USA 2005, 102, 12667–12669. [Google Scholar] [CrossRef]
- Andersen, J.; Heimdal, J.; Wugt Larsen, R. The influence of large-amplitude librational motion on the hydrogen bond energy for alcohol–water complexes. Phys. Chem. Chem. Phys. 2015, 17, 23761–23769. [Google Scholar] [CrossRef] [PubMed]
- Mihrin, D.; Andersen, J.; Jakobsen, P.W.; Larsen, R.W. Highly localized H2O librational motion as a far-infrared spectroscopic probe for microsolvation of organic molecules. Phys. Chem. Chem. Phys. 2019, 21, 1717–1723. [Google Scholar] [CrossRef] [PubMed]
- Wugt Larsen, R.; Suhm, M.A. The benefits of alternation and alkylation: Large amplitude hydrogen bond librational modes of alcohol trimers and tetramers. Phys. Chem. Chem. Phys. 2010, 12, 8152–8157. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.; Heimdal, J.; Wugt Larsen, R. Spectroscopic identification of ethanol-water conformers by large-amplitude hydrogen bond librational modes. J. Chem. Phys. 2015, 143, 224315. [Google Scholar] [CrossRef] [PubMed]
- Mihrin, D.; Voute, A.; Jakobsen, P.W.; Feilberg, K.L.; Wugt Larsen, R. The effect of alkylation on the micro-solvation of ethers revealed by highly localized water librational motion. J. Chem. Phys. 2022, 156, 084305. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.; Voute, A.; Mihrin, D.; Heimdal, J.; Berg, R.W.; Torsson, M.; Larsen, R.W. Probing the global potential energy minimum of (CH2O)2: THz absorption spectrum of (CH2O)2 in solid neon and para-hydrogen. J. Chem. Phys. 2017, 146, 244311. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.; Heimdal, J.; Mahler, D.W.; Nelander, B.; Larsen, R.W. Communication: THz absorption spectrum of the CO2–H2O complex: Observation and assignment of intermolecular van der Waals vibrations. J. Chem. Phys. 2014, 140, 091103. [Google Scholar] [CrossRef] [PubMed]
- Mihrin, D.; Jakobsen, P.W.; Voute, A.; Manceron, L.; Wugt Larsen, R. High-resolution synchrotron terahertz investigation of the large-amplitude hydrogen bond librational band of (HCN)2. Phys. Chem. Chem. Phys. 2018, 20, 8241–8246. [Google Scholar] [CrossRef] [PubMed]
- Wugt Larsen, R.; Suhm, M.A. Cooperative organic hydrogen bonds: The librational modes of cyclic methanol clusters. J. Chem. Phys. 2006, 125, 154314. [Google Scholar] [CrossRef]
- Schneider, W.B.; Bistoni, G.; Sparta, M.; Saitow, M.; Riplinger, C.; Auer, A.A.; Neese, F. Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework. J. Chem. Theory Comput. 2016, 12, 4778–4792. [Google Scholar] [CrossRef]
- Altun, A.; Neese, F.; Bistoni, G. Effect of Electron Correlation on Intermolecular Interactions: A Pair Natural Orbitals Coupled Cluster Based Local Energy Decomposition Study. J. Chem. Theory Comput. 2018, 15, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Kollipost, F.; Andersen, J.; Mahler, D.W.; Heimdal, J.; Heger, M.; Suhm, M.A.; Wugt Larsen, R. The effect of hydrogen bonding on torsional dynamics: A combined far-infrared jet and matrix isolation study of methanol dimer. J. Chem. Phys. 2014, 141, 174314. [Google Scholar] [CrossRef] [PubMed]
- Pracht, P.; Bohle, F.; Grimme, S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef] [PubMed]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Bernholdt, D.E.; Harrison, R.J. Large-scale correlated electronic structure calculations: The RI-MP2 method on parallel computers. Chem. Phys. Lett. 1996, 250, 477–484. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Xu, X.; Truhlar, D.G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Accounts 2010, 128, 295–305. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Pinski, P.; Becker, U.; Valeev, E.F.; Neese, F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef] [PubMed]
- Liakos, D.G.; Sparta, M.; Kesharwani, M.K.; Martin, J.M.L.; Neese, F. Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Hartree–Fock exchange fitting basis sets for H to Rn. J. Comput. Chem. 2007, 29, 167–175. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057. [Google Scholar] [CrossRef]
- Weigend, F.; Köhn, A.; Hättig, C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175–3183. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Kossmann, S.; Neese, F. Efficient Structure Optimization with Second-Order Many-Body Perturbation Theory: The RIJCOSX-MP2 Method. J. Chem. Theory Comput. 2010, 6, 2325–2338. [Google Scholar] [CrossRef] [PubMed]
- DTU Computing Center. DTU Computing Center Resources; Technical University of Denmark: Kongens Lyngby, Denmark, 2021. [Google Scholar] [CrossRef]

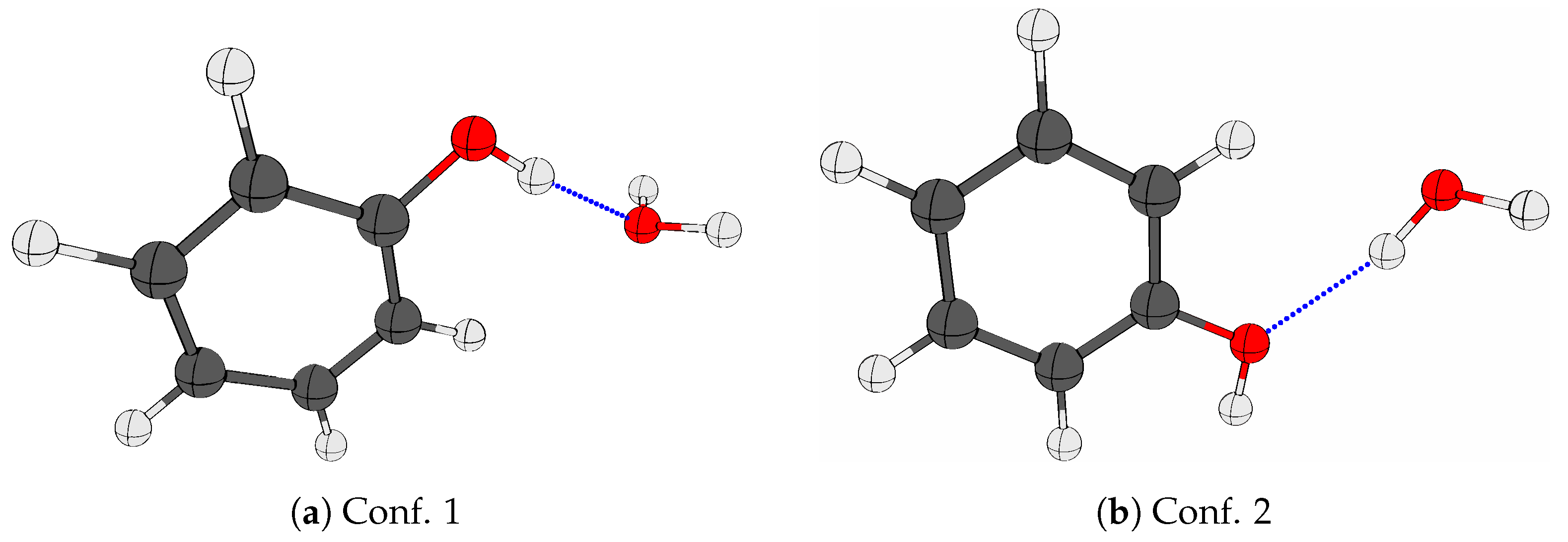
| DFT | SCS-MP2 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PhOH·H2O | (PhOH)2 | (PhOH)3 | PhOH·H2O | (PhOH)2 | (PhOH)3 | |||||||||
| Conf. 1 | Conf. 2 | Conf. 1 | Conf. 2 | Conf. 3 | Conf. 4 | Conf. 1 | Conf. 2 | Conf. 1 | Conf. 2 | Conf. 3 | Conf. 4 | |||
| De | 27.9 | 18.3 | 27.8 | 76.3 | 74.4 | 71.7 | 73.1 | 26.6 | 17.8 | 31.7 | 95.5 | 85.4 | 85.2 | 87.0 |
| De(CC) | 28.9 | 19.8 | 30.0 | 89.2 | 80.8 | 78.0 | 81.6 | 28.8 | 19.7 | 30.1 | 90.1 | 81.7 | 78.5 | 82.4 |
| * 30.4 | ||||||||||||||
| D0 | 20.9 | 11.7 | 22.5 | 66.6 | 63.2 | 61.0 | 62.4 | 19.7 | 11.6 | 24.5 | 79.6 | 70.6 | 71.2 | 71.9 |
| D0(CC) | 21.8 | 13.2 | 24.8 | 79.5 | 69.6 | 67.3 | 70.9 | 22.0 | 13.6 | 23.0 | 74.3 | 66.9 | 64.5 | 67.3 |
| ZPE | 7.1 | 6.5 | 5.2 | 9.7 | 11.2 | 10.7 | 10.7 | 6.9 | 6.2 | 7.2 | 15.8 | 14.7 | 14.0 | 15.1 |
| * 4.2 | ||||||||||||||
| Edisp, frag | 8.5 | 9.1 | 17.8 | 15.7 | 25.6 | 27.0 | 18.6 | 8.3 | 8.5 | 21.8 | 20.5 | 26.3 | 31.8 | 20.8 |
| 15.9 | 12.6 | 17.5 | 14.3 | 20.1 | 12.9 | 18.5 | 17.9 | |||||||
| 15.9 | 12.2 | 15.5 | 13.1 | 20.1 | 12.5 | 16.9 | 14.1 | |||||||
| ∑Edisp | 8.5 | 9.1 | 17.8 | 47.6 | 50.4 | 59.9 | 46.0 | 8.3 | 8.5 | 21.8 | 60.7 | 51.6 | 67.2 | 52.8 |
| * 19.7 | ||||||||||||||
| ∑EN/D | 20.4 | 10.7 | 12.3 | 41.7 | 30.5 | 18.1 | 35.7 | 20.6 | 11.3 | 8.3 | 29.4 | 30.0 | 11.3 | 29.6 |
| * 10.6 | ||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihrin, D.; Feilberg, K.L.; Larsen, R.W. Self-Association and Microhydration of Phenol: Identification of Large-Amplitude Hydrogen Bond Librational Modes. Molecules 2024, 29, 3012. https://doi.org/10.3390/molecules29133012
Mihrin D, Feilberg KL, Larsen RW. Self-Association and Microhydration of Phenol: Identification of Large-Amplitude Hydrogen Bond Librational Modes. Molecules. 2024; 29(13):3012. https://doi.org/10.3390/molecules29133012
Chicago/Turabian StyleMihrin, Dmytro, Karen Louise Feilberg, and René Wugt Larsen. 2024. "Self-Association and Microhydration of Phenol: Identification of Large-Amplitude Hydrogen Bond Librational Modes" Molecules 29, no. 13: 3012. https://doi.org/10.3390/molecules29133012
APA StyleMihrin, D., Feilberg, K. L., & Larsen, R. W. (2024). Self-Association and Microhydration of Phenol: Identification of Large-Amplitude Hydrogen Bond Librational Modes. Molecules, 29(13), 3012. https://doi.org/10.3390/molecules29133012







