Unique Use of Dibromo–L–Tyrosine Ligand in Building of Cu(II) Coordination Polymer—Experimental and Theoretical Investigations
Abstract
1. Introduction
2. Results and Discussion
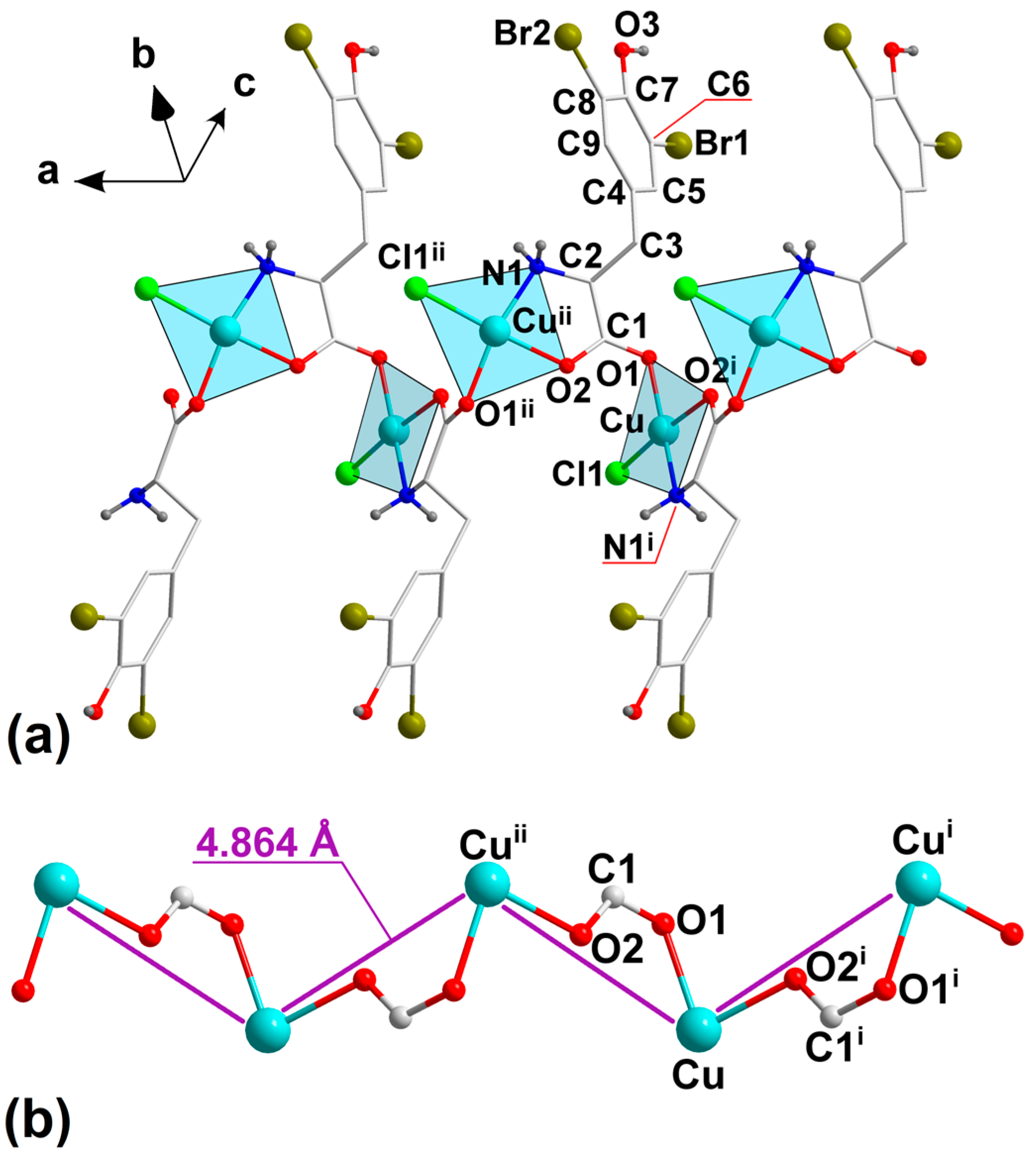
2.1. Crystal Structure Description of 1
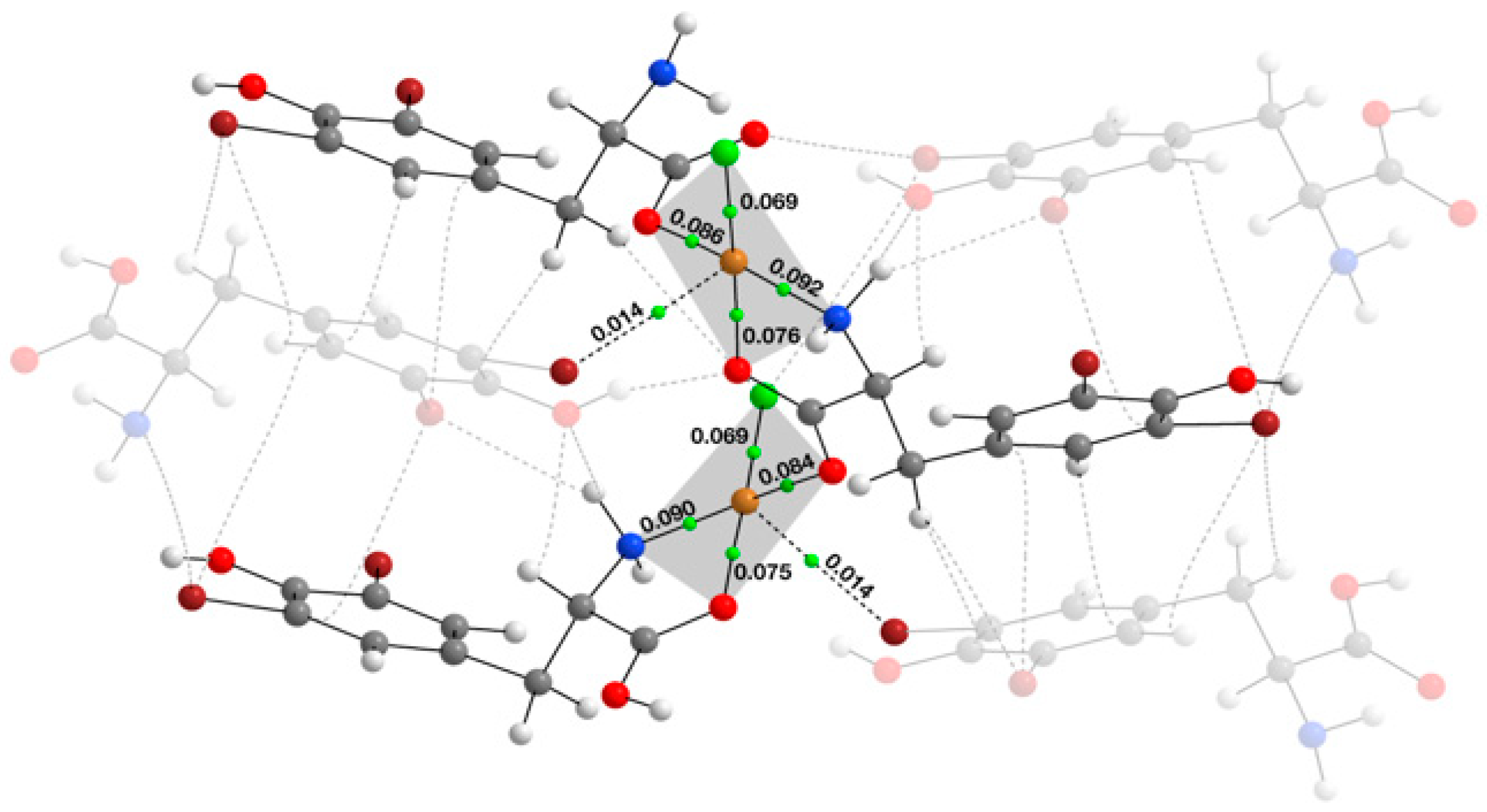
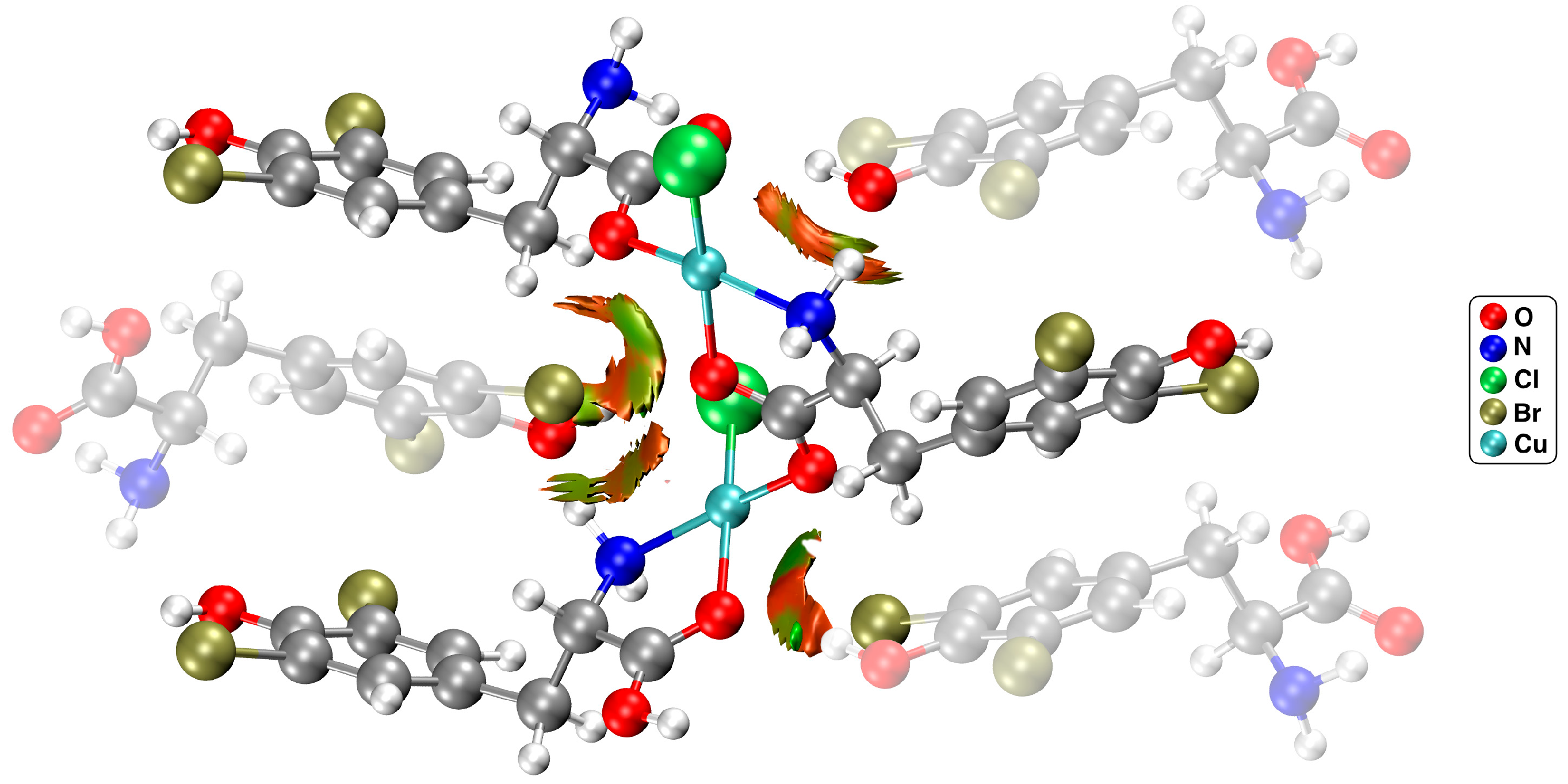
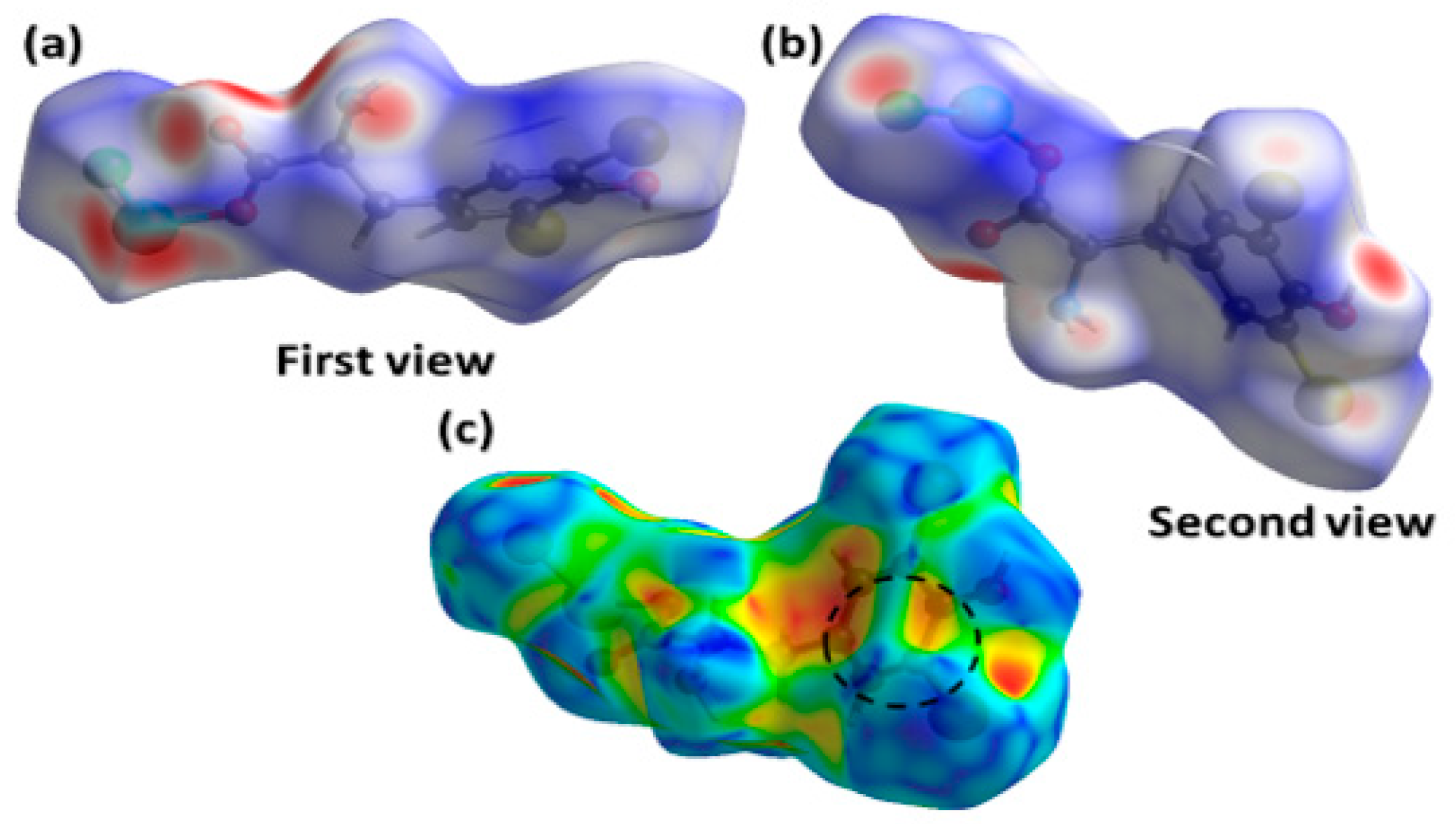
2.2. Theoretical Quantum Chemistry AIM, NCI, and NBO Calculations
2.3. Hirshfeld Surface Analysis
2.4. Spectroscopic Studies
2.4.1. FT–IR and Raman Spectra
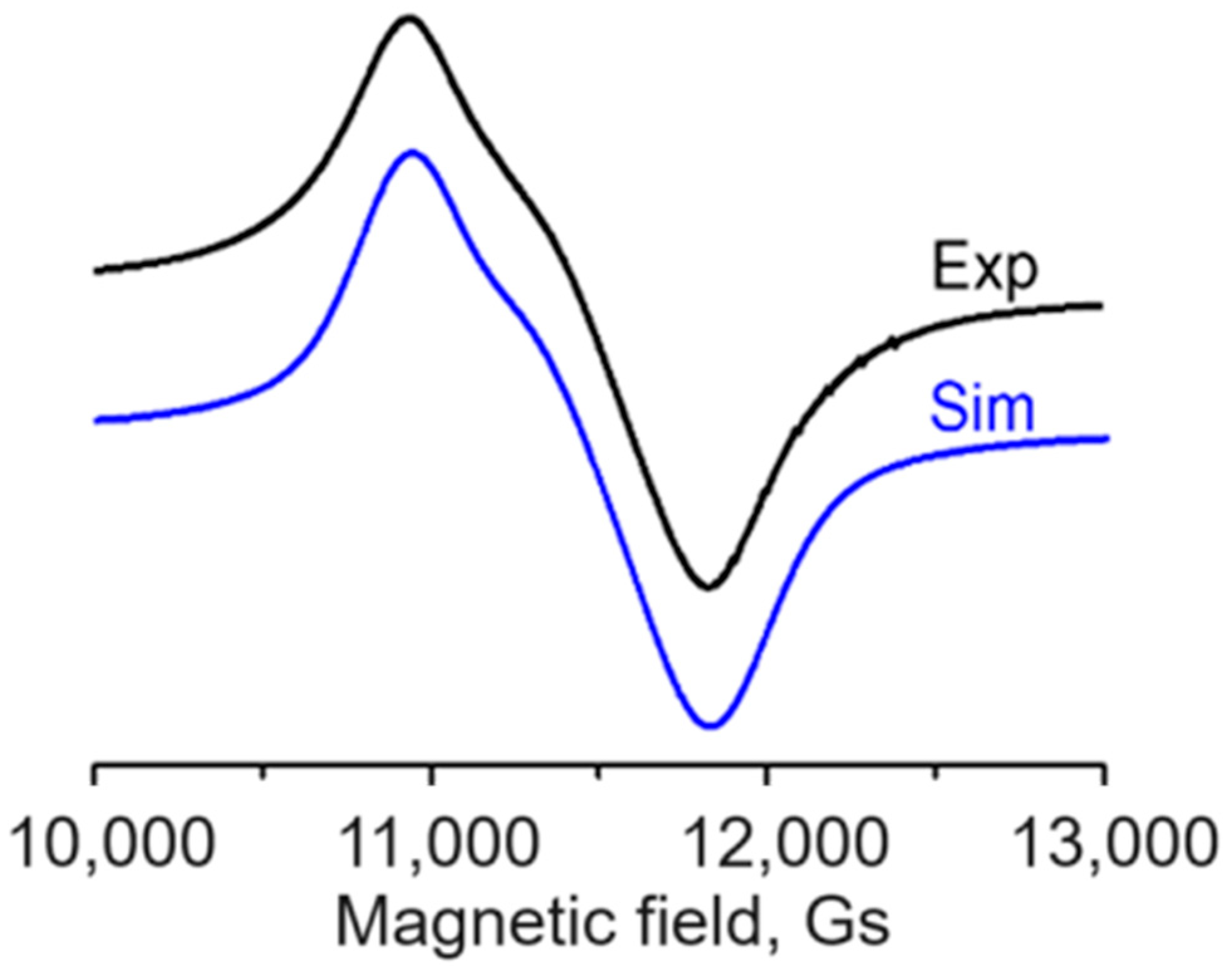
2.4.2. X- and Q-Band EPR Spectra
2.4.3. NIR–Vis–UV Electronic Spectra
3. Materials and Methods
3.1. Materials
3.2. The Synthesis of {[CuCl(μ–O,O’–l–Br2Tyr)]}n (1)
3.3. Methods
3.3.1. Single-Crystal and Powder X-ray Data Collection
3.3.2. Theoretical Calculations—QTAIM, NCI, and NBO
3.3.3. Hirshfeld Surface Analysis
3.3.4. Spectroscopic Methods (FT–IR, FT–Raman, X- and Q-Band EPR, NIR–VIS–UV)
4. Conclusions
5. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- New, S.Y.; Wu, X.; Bai, S.-Q.; Koh, L.L.; Hor, T.S.A.; Xue, F. Lipid-bilayer-mimicking solid-state structures of Cu(II) and Ni(II) with L-tryptophan and L-tyrosine Schiff base derivatives. CrystEngComm 2011, 13, 4228–4235. [Google Scholar] [CrossRef]
- Ebel, M.; Rehder, D. Interaction of vanadyl (VO2+) with ligands containing serine, tyrosine, and threonine. Inorg. Chem. 2006, 45, 7083–7090. [Google Scholar] [CrossRef]
- Kiss, T.; Gergely, A. Complex-forming properties of tyrosine isomers with transition metal ions. J. Chem. Soc. Dalton Trans. 1984, 9, 1951–1957. [Google Scholar] [CrossRef]
- Ye, Q.; Li, Y.-H.; Wu, Q.; Song, Y.-M.; Wang, J.-X.; Zhao, H.; Xiong, R.-G.; Xue, Z. The First Metal (Nd3+, Mn2+, and Pb2+) Coordination compounds of 3,5-dinitrotyrosine and their nonlinear optical properties. Chem.—Eur. J. 2005, 11, 988–994. [Google Scholar] [CrossRef]
- Li, D.Q.; Zhou, J.; Liu, X. The one-dimensional chain polymer of aqua(tyrosinato)zinc(II). Acta Crystallogr. C 2007, 63, m371–m373. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Islam, S.M.R.; Noman, A.S.M.; Khanam, J.A.; Ali, S.M.M.; Alam, S.; Lee, M.W. Biological screening of a novel nickel (II) tyrosine complex. Mycobiology 2007, 35, 25–29. [Google Scholar] [CrossRef]
- Kirk, K.L. Convenient synthesis of 3-fluoro-L-tyrosine and 3,5-difluoro-L-tyrosine. J. Organic Chem. 1980, 45, 2015–2016. [Google Scholar] [CrossRef]
- Leong, W.L.; Vittal, J.J. Synthesis, characterization and structures of copper(II) complexes containing carboxylate and sulfonate groups. J. Incl. Phenom. Macrocycl. Chem. 2011, 71, 557–566. [Google Scholar] [CrossRef]
- Imaz, I.; Rubio-Martínez, M.; An, J.; Solé-Font, I.; Rosi, N.L.; Maspoch, D. Metal–biomolecule frameworks (MBioFs). Chem. Comm. 2011, 47, 7287–7302. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Hong, M.; Shi, Q.; Cao, R.; Chan, A.S.C. Chiral supramolecular assemblies derived from the insertion of a segmental ligand into a copper-tyrosine framework. Eur. J. Inorg. Chem. 2002, 2002, 2553–2556. [Google Scholar] [CrossRef]
- Van der Helm, D.; Tatsch, C.E. The crystal structure of bis-(L-tyrosinato)copper(II). Acta Crystallogr. B 1972, 28, 2307–2312. [Google Scholar] [CrossRef]
- Wojciechowska, A.; Daszkiewicz, M.; Bieńko, A. Polymeric Zn(II) and Cu(II) complexes with exobidentate bridging L-tyrosine: Synthesis, structural and spectroscopic properties. Polyhedron 2009, 28, 1481–1489. [Google Scholar] [CrossRef]
- Zhou, B.; Silva, N.J.O.; Shi, F.-N.; Palacio, F.; Mafra, L.; Rocha, J. CoII/ZnII–(L-tyrosine) magnetic metal–organic frameworks. E. J. Inorg. Chem. 2012, 2012, 5259–5268. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, N.-H. Poly[[diaqua-μ-4,4′-bipyridine-dinitratodi-μ-L-tyrosinato-dicopper(II)]: A chiral two-dimensional coordination polymer. Acta Crystallogr. C 2008, 65, m7–m9. [Google Scholar] [CrossRef] [PubMed]
- Okabe, N.; Hokaze, M. Crystal structure of the copper(II) chloride complex of 3, 5-diiodo-L-tyrosine. Chem. Pharm. Bull. 1993, 41, 605–607. [Google Scholar] [CrossRef]
- Walker, W.R.; Shaw, Y.-H.L.; Li, N.C. Nature of copper(II) interaction with thyroxine and analogs. J. Am. Chem. Soc. 1973, 95, 3015–3017. [Google Scholar] [CrossRef]
- Zhang, F.; Odani, A.; Masuda, H.; Yamauchi, O. Structures and stabilities of ternary copper(II) complexes with 3,5-diiodo-L-tyrosinate. Weak interactions involving iodo groups. Inorg. Chem. 1996, 35, 7148–7155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Yajima, T.; Masuda, H.; Odani, A.; Yamauchi, O. Weak interactions in ternary copper(II) complexes with iodotyrosinates. biological significance of the iodines in thyroid hormones. Inorg. Chem. 1997, 36, 5777–5784. [Google Scholar] [CrossRef]
- Wojciechowska, A.; Rojek, T.; Malik−Gajewska, M.; Jerzykiewicz, M.; Wysokiński, R.; Gągor, A.; Rytlewski, P.; Staszak, Z.; Duczmal, M. Crystal and molecular structure stabilized by weak interaction in unique 3,5-diiodo-L-tyrosinato copper(II) complex—Synthesis, experimental and theoretical studies. Mater. Sci. Eng. B 2020, 262, 114723. [Google Scholar] [CrossRef]
- Wojciechowska, A.; de Graaf, C.; Rojek, T.; Jerzykiewicz, M.; Malik, M.; Gągor, A.; Duczmal, M. A rare diiodo-L-tyrosine copper(II) complexes—Crystal and molecular structure of materials stabilized by weak interactions. Polyhedron 2022, 219, 115780. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, X.; Fan, Y.; Bi, C.; Yan, X.; Zhang, Z.; Zhang, N. Synthesis, Crystal structure and theoretical calculation of a novel nickel(II) complex with dibromotyrosine and 1,10-phenanthroline. Bull. Korean Chem. Soc. 2013, 34, 2889–2894. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Han, L.-H.; Lin, J.-X.; Cao, R. Supramolecular Organic Frameworks of Brominated Bisphenol Derivatives with Organoamines. Cryst. Growth Des. 2011, 11, 3551–3557. [Google Scholar] [CrossRef]
- Bruno, I.J.; Cole, J.C.; Edgington, P.R.; Kessler, M.; Macrae, C.F.; McCabe, P.; Pearson, J.; Taylor, R. New software for searching the Cambridge Structural Database and visualizing crystal structures. Acta Crystallogr. B 2002, 58, 389–397. [Google Scholar] [CrossRef] [PubMed]
- İnci, D.; Aydın, R.; Vatan, Ö.; Yılmaz, D.; Gençkal, H.M.; Zorlu, Y.; Cavaş, T. Binary and ternary new water soluble copper(II) complexes of L-tyrosine and substituted 1,10-phenanthrolines: Effect of substitution on DNA interactions and cytotoxicities. Spectr. Acta Part A 2015, 145, 313–324. [Google Scholar] [CrossRef]
- İnci, D.; Aydın, R.; Vatan, Ö.; Huriyet, H.; Zorlu, Y.; Çoşut, B.; Çinkılıç, N. Cu (II) tyrosinate complexes containing methyl substituted phenanthrolines: Synthesis, X-ray crystal structures, biomolecular interactions, antioxidant activity, ROS generation and cytotoxicity. Appl. Organomet. Chem. 2019, 33, e4652. [Google Scholar] [CrossRef]
- Arularasan, P.; Sivakumar, B.; Chakkaravarthi, G.; Mohan, R. Bis(μ-l-arginine-κ3N2,O:O’)bis-(L-arginine-κ3N2,O)tetra- μ-chlorido-tetra-chlorido-tetra-copper(II). Acta Crystallogr. E 2013, 69, m583–m584. [Google Scholar] [CrossRef]
- Colyvas, K.; Tietze, H.R.; Egri, S.K.J. The structure of dichloro(L-histidine)copper(II). Australian J. Chem. 1982, 35, 1581–1586. [Google Scholar] [CrossRef]
- Bujacz, A.; Turek, M.; Majzner, W.; Lodyga-Chruscinska, E. X-ray structure of a novel histidine-copper(II) complex. Russian J. Coord. Chem. 2010, 36, 430–435. [Google Scholar] [CrossRef]
- Nelyubina, Y.V.; Korlyukov, A.A.; Fedyanin, I.V.; Lyssenko, K.A. Extremely long Cu⋯O contact as a possible pathway for magnetic interactions in Na2Cu(CO3)2. Inorg. Chem. 2013, 52, 14355–14363. [Google Scholar] [CrossRef]
- Barszcz, B.; Głowiak, T.; Jezierska, J. Crystal and molecular structures of eight-coordinate (CuN4O4) and six-coordinate (CuN4O2) Cu(II) complexes with 4-methyl-5-imidazole-carboxaldehyde or 1-benzyl-2-hydroxymethylimidazole, respectively: Spectroscopic and potentiometric studies. Polyhedron 1999, 18, 3713–3721. [Google Scholar] [CrossRef]
- Degtyarenko, A.S.; Solntsev, P.V.; Rusanov, E.B.; Chernega, A.N.; Domasevitch, K.V. Copper(II) bromide and copper(II) acetate complexes of 4,4’-(p-phenylene)bipyridazine. Acta Crystallogr. C 2008, 64, m254–m258. [Google Scholar] [CrossRef] [PubMed]
- Stassen, A.F.; Kooijman, H.; Spek, A.L.; de Jongh, L.J.; Haasnoot, J.G.; Reedijk, J. Strongly isolated ferromagnetic layers in poly-trans-mu-dichloro- and poly-trans-mu-dibromobis(1-(2-chloroethyl)-tetrazole-N4)copper(II) complexes. Inorg. Chem. 2002, 41, 6468–6473. [Google Scholar] [CrossRef] [PubMed]
- Lane, J.R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B.J.; Kjaergaard, H.G. Are Bond Critical Points Really Critical for Hydrogen Bonding? J. Chem. Theory Comput. 2013, 9, 3263–3266. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Bianchi, R.; Gervasio, G.; Marabello, D. Experimental Electron Density Analysis of Mn2(CO)10: Metal−Metal and Metal−Ligand Bond Characterization. Inorg. Chem. 2000, 39, 2360–2366. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. On the reliability of atoms in molecules, noncovalent index, and natural bond orbital to identify and quantify noncovalent bonds. J. Comput. Chem. 2022, 43, 1814–1824. [Google Scholar] [CrossRef] [PubMed]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem. Commun. 2007, 37, 3814–3816. [Google Scholar] [CrossRef] [PubMed]
- Jelsch, C.; Ejsmont, K.; Huder, L. The enrichment ratio of atomic contacts in crystals, an indicator derived from the Hirshfeld surface analysis. IUCrJ 2014, 1, 119–128. [Google Scholar] [CrossRef]
- Piovesan, D.; Minervini, G.; Tosatto Silvio, C.E. The RING 2.0 web server for high quality residue interaction networks. Nucleic Acids Res. 2016, 44, W367–W374. [Google Scholar] [CrossRef]
- Burley, S.K.; Petsko, G.A. Aromatic-Aromatic Interaction: A Mechanism of Protein Structure Stabilization. Science 1985, 229, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.J.; McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Visualisation and characterisation of voids in crystalline materials. CrystEngComm. 2011, 13, 1804–1813. [Google Scholar] [CrossRef]
- Nakamoto, K. Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part B: Applications in Coordination, Organometallic, and Bioinorganic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 64–72. [Google Scholar]
- Whiffen, D.H. Vibrational frequencies and thermodynamic properties of fluoro-, chloro-, bromo-, and iodo-benzene. J. Chem. Soc. 1956, 1350–1356. [Google Scholar] [CrossRef]
- Olalekan, T.E.; Beukes, D.R.; Van Brecht, B.; Watkins, G.M. Copper(II) Complexes of 2-(Methylthiomethyl)anilines: Spectral and Structural Properties and In Vitro Antimicrobial Activity. J. Inorg. Chem. 2014, 2014, 769573. [Google Scholar] [CrossRef][Green Version]
- Plesch, G.; Friebel, C.; Warda, S.A.; Sivy’, J.I.; SŠvajlenova’, O.G. Coordination geometries and cooperative ordering effects in copper(II) complexes with tridentate Schiff base dianions 5 E.p.r. spectra of [N-salicylidene-(R,S)-alaninato]copper(II) complexes with derivatives of imidazole and pyrazole and structure of 1-methylimidazole[N-salicylidene-(R,S)-valinato]copper(II). Trans. Met. Chem. 1997, 22, 433–440. [Google Scholar] [CrossRef]
- Halcrow, M.A. Interpreting and controlling the structures of six-coordinate copper(ii) centres—When is a compression really a compression? Dalton Trans. 2003, 4375–4384. [Google Scholar] [CrossRef]
- Hathaway, B.J.; Billing, D.E. The electronic properties and stereochemistry of mono-nuclear complexes of the copper(II) ion. Coord. Chem. Rev. 1970, 5, 143–207. [Google Scholar] [CrossRef]
- Akitsu, T.; Komorita, S.; Urushiyama, A. Assignment of d–d Transitions of Square Planar [CuIIN4] Complexes Containing Imidate and Amine Ligands by Means of Polarized Crystal Spectra. Bull. Chem. Soc. Jpn. 2001, 74, 851–860. [Google Scholar] [CrossRef]
- Belford, R.L.; Hitchman, M.A. Single-crystal polarized spectrum of bis(benzoylacetonato)copper(II). Sources of intensity. Inorg. Chem. 1971, 10, 984–988. [Google Scholar] [CrossRef]
- Walsh, A.; Hathaway, B.J. The crystal structure of bis(NN-diethylethylenediamine)copper(II) dinitrate and the electronic properties of some square planar CuN4 chromophores. J. Chem. Soc. Dalton Trans. 1984, 1, 15–18. [Google Scholar] [CrossRef]
- Belford, R.L.; Carmichael, J.W., Jr. Bis(3-Phenyl−2,4-Pentanedionato)Copper. II. Polarized Crystal Spectra. J. Chem. Phys. 1967, 46, 4515–4522. [Google Scholar] [CrossRef]
- Atanasov, M.A.; Hitchman, M.A. d-Orbital energies inbeta.-ketoenolate copper(II) complexes. Inorg. Chem. 1993, 32, 3973–3975. [Google Scholar] [CrossRef]
- McDonald, R.G.; Riley, M.J.; Hitchman, M.A. Analysis of the vibrational fine structure in the electronic spectrum of the planar tetrachlorocuprate(II) ion in N-(2-ammonioethyl)morpholinium tetrachlorocuprate(II): Evidence for a pseudo tetrahedral distortion in the 2A1g excited electronic state. Inorg. Chem. 1989, 28, 752–758. [Google Scholar] [CrossRef]
- Reddy, S.L.; Endo, T.; Reddy, G.S. Advanced Aspects of Spectroscopy; IntechOpen: Rijeka, Croatia, 2012. [Google Scholar]
- Buluggiu, E.; Dascola, G.; Giori, D.C.; Vera, A. ESR Studies of Covalent Copper Complexes with a Rhombic Arrangement. J. Chem. Phys. 1971, 54, 2191–2196. [Google Scholar] [CrossRef]
- Oxford Diffraction Poland. CrysAlis CCD and CrysAlis Red; Version 1.171.33.42; Oxford Diffraction Limited: London, UK, 2009. [Google Scholar]
- Sheldrick, G.M. Structure determination revisited. Acta Crystallogr. A Found. Adv. 2015, 71, s9. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Crystal Impact GbR. DIAMOND; Version 3.1 e; Crystal Impact GbR: Bonn, Germany, 2006. [Google Scholar]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H.; Hay, P.J. Gaussian Basis Sets for Molecular Calculations. In Methods of Electronic Structure Theory; Schaefer, H.F., Ed.; Springer: Boston, MA, USA, 1977; pp. 1–27. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Keith, T.A. AIMAll (Version 19.10.12); TK Gristmill Software: Overland Park, KS, USA, 2019. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
- Chemcraft. Graphical Software for Visualization of Quantum Chemistry Computations, Version 1.8, Build 682. Available online: https://www.chemcraftprog.com (accessed on 30 May 2024).
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm 2002, 4, 378–392. [Google Scholar] [CrossRef]
- Ozarowski, A. DoubletExactAdv (S=1/2) Program; National High Magnetic Field Laboratory, Florida, University: Tallahassee, FL, USA, 2023. [Google Scholar]

| Bond Lengths (Å) | Bond Angles (°) | ||||
|---|---|---|---|---|---|
| Cu–O1 | 1.944(4) | Cu–O2i | 1.981(4) | O1–Cu–N1i | 164.46(19) |
| Cu–N1i | 1.972(4) | Cu–Cl1 | 2.2217(15) | O1–Cu–O2i | 85.81(17) |
| O1–C1 | 1.242(7) | O2–C1 | 1.276(6) | N1i–Cu–O2i | 82.68(17) |
| C6–Br1 | 1.907(5) | C2–N1 | 1.482(7) | O1–Cu–Cl1 | 96.80(13) |
| C8–Br2 | 1.896(5) | N1i–Cu–Cl1 | 95.46(14) | ||
| O2i–Cu–Cl1 | 175.11(12) | ||||
| D–H···A | D–H | H···A | D···A | D–H···A | I(J) | Me | I···Me | Cg(I) | Cg(J) | Cg···Cg | Cg(I) | I(J) | Cg···I |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O3–H3···O2iii | 0.88 | 1.98 | 2.804 (5) | 151 | O3vi | Cu | 3.131(8) | Cg(1) | Cg(1)iv | 5.798(3) | Cg(1) | Br2iv | 3.450(2) |
| N1–H1A···Br2iv | 0.81 | 2.93 | 3.651 (4) | 149 | Br1vii | Cu | 3.168(8) | Cg(1) | Cg(1)viii | 5.161(3) | |||
| N1–H1B···Cl1v | 0.87 | 2.42 | 3.280 (5) | 171 |
| ρ | ∇2ρ | H | G | V | |
|---|---|---|---|---|---|
| Cu–N | 0.092 | +0.443 | −0.016 | +0.126 | −0.142 |
| Cu–O1 | 0.086 | +0.512 | −0.008 | +0.136 | −0.144 |
| Cu–O2 | 0.076 | +0.498 | −0.003 | +0.128 | −0.131 |
| Cu–Cl | 0.069 | +0.281 | −0.004 | +0.074 | −0.078 |
| Cu···Br | 0.014 | +0.027 | −0.002 | +0.008 | −0.010 |
| Donor → Acceptor | ΣE2 | |
|---|---|---|
| O2–Cu | LP (O) → σ* (Cu-Cl) (70) a | 72.52 |
| O1–Cu | LP (O) → LV (Cu) (86) | 69.41 |
| N–Cu | LP (N) → LV (Cu) (84) | 62.89 |
| Br···Cu | LP (Br) → LV (Cu) (79) | 10.65 |
| HO···Cu | LP (O) → LV (Cu) (67) | 1.16 |
| 1 | [CuCl(L–I2Tyr) (phen)]∙2H2O [20] | [Cu(L–I2Tyr)(H2O) (phen)]∙(NO3) [20] | [Cu(L–I2TyrO−)(H2O) (phen)]∙2H2O [19] | |||||
|---|---|---|---|---|---|---|---|---|
| modes | FIR | Raman | FIR | Raman | FIR | Raman | FIR | Raman |
| ν(Cu–NL-X2Tyr) | 425 m | 425 m | 431 m | 433 s | 433 m | 434 s | 425 m | 432 m |
| ν(Cu–OL-X2Tyr) | 336/320 s | 323 w | 353 m | 361 vw | 358/349 m | 362 vvw | 350 m | 354 vw |
| ν(Cu–Cl) * | 264 m | 263 m | ov | ov | − | − | − | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wojciechowska, A.; Janczak, J.; Rojek, T.; Ashfaq, M.; Malik, M.; Trzęsowska, N.; Wysokiński, R.; Jezierska, J. Unique Use of Dibromo–L–Tyrosine Ligand in Building of Cu(II) Coordination Polymer—Experimental and Theoretical Investigations. Molecules 2024, 29, 2709. https://doi.org/10.3390/molecules29112709
Wojciechowska A, Janczak J, Rojek T, Ashfaq M, Malik M, Trzęsowska N, Wysokiński R, Jezierska J. Unique Use of Dibromo–L–Tyrosine Ligand in Building of Cu(II) Coordination Polymer—Experimental and Theoretical Investigations. Molecules. 2024; 29(11):2709. https://doi.org/10.3390/molecules29112709
Chicago/Turabian StyleWojciechowska, Agnieszka, Jan Janczak, Tomasz Rojek, Muhammad Ashfaq, Magdalena Malik, Natasza Trzęsowska, Rafał Wysokiński, and Julia Jezierska. 2024. "Unique Use of Dibromo–L–Tyrosine Ligand in Building of Cu(II) Coordination Polymer—Experimental and Theoretical Investigations" Molecules 29, no. 11: 2709. https://doi.org/10.3390/molecules29112709
APA StyleWojciechowska, A., Janczak, J., Rojek, T., Ashfaq, M., Malik, M., Trzęsowska, N., Wysokiński, R., & Jezierska, J. (2024). Unique Use of Dibromo–L–Tyrosine Ligand in Building of Cu(II) Coordination Polymer—Experimental and Theoretical Investigations. Molecules, 29(11), 2709. https://doi.org/10.3390/molecules29112709









