Finite Temperature String with Order Parameter as Collective Variables for Molecular Crystal: A Case of Polymorphic Transformation of TNT under External Electric Field
Abstract
1. Introduction
2. Theory
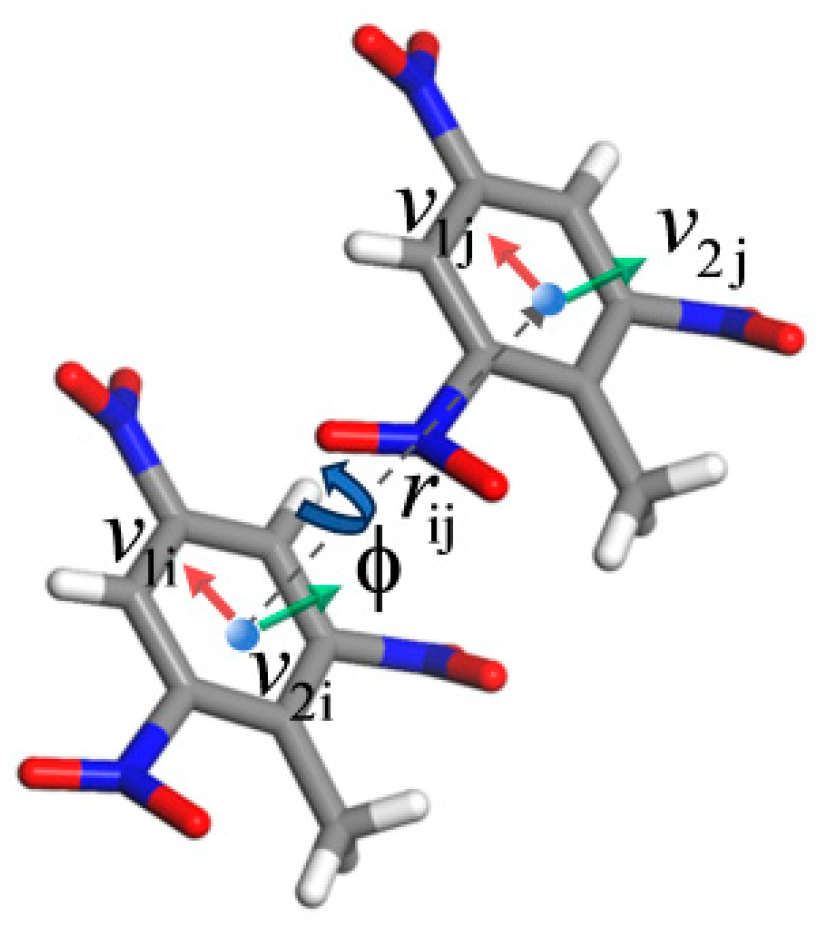
2.1. Order Parameter
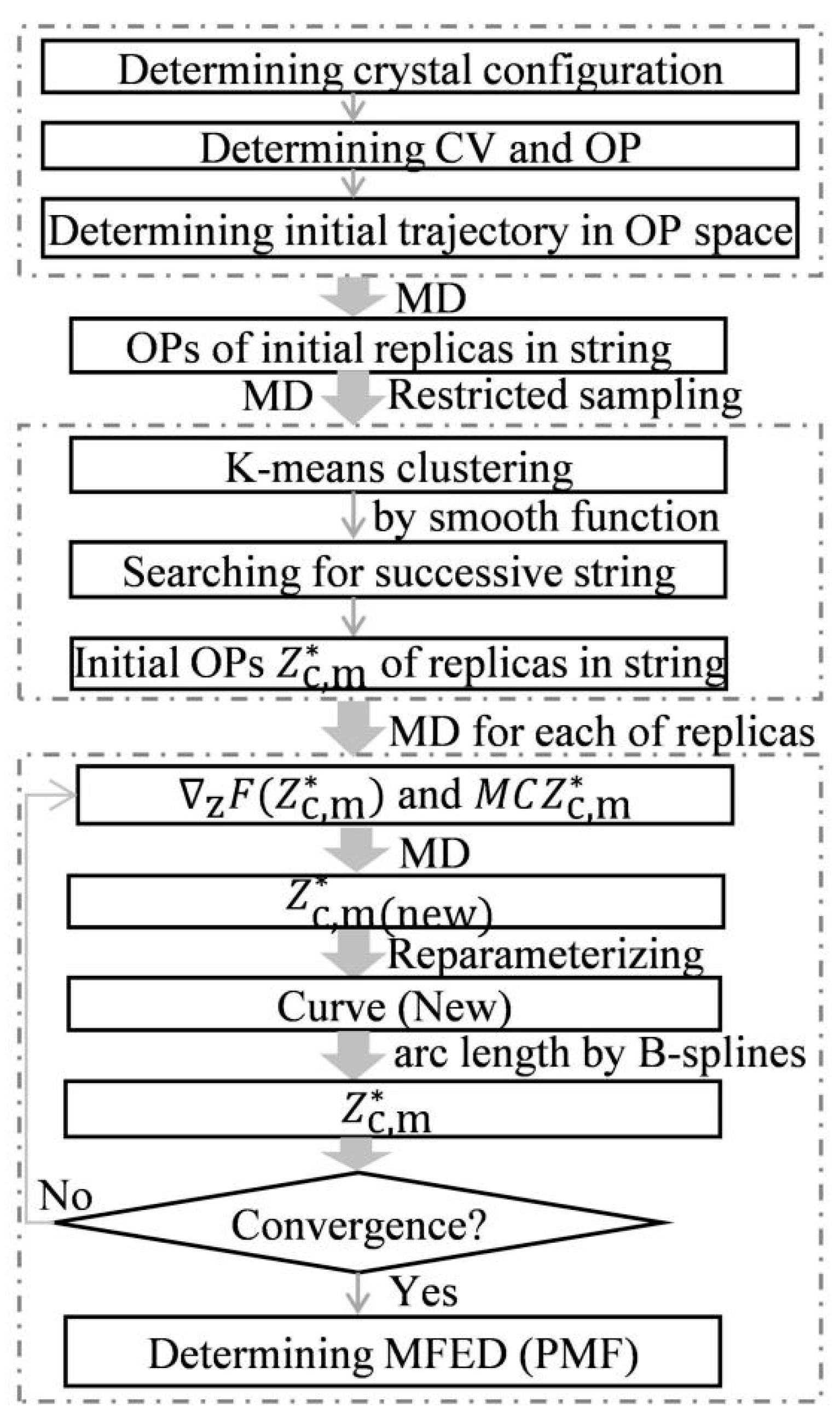
2.2. Finite Temperature String
2.3. Minimum Free-Energy Path from Finite Temperature String
2.4. External Electric Field Effect on Nucleation
3. Polymorphic Transformation of TNT
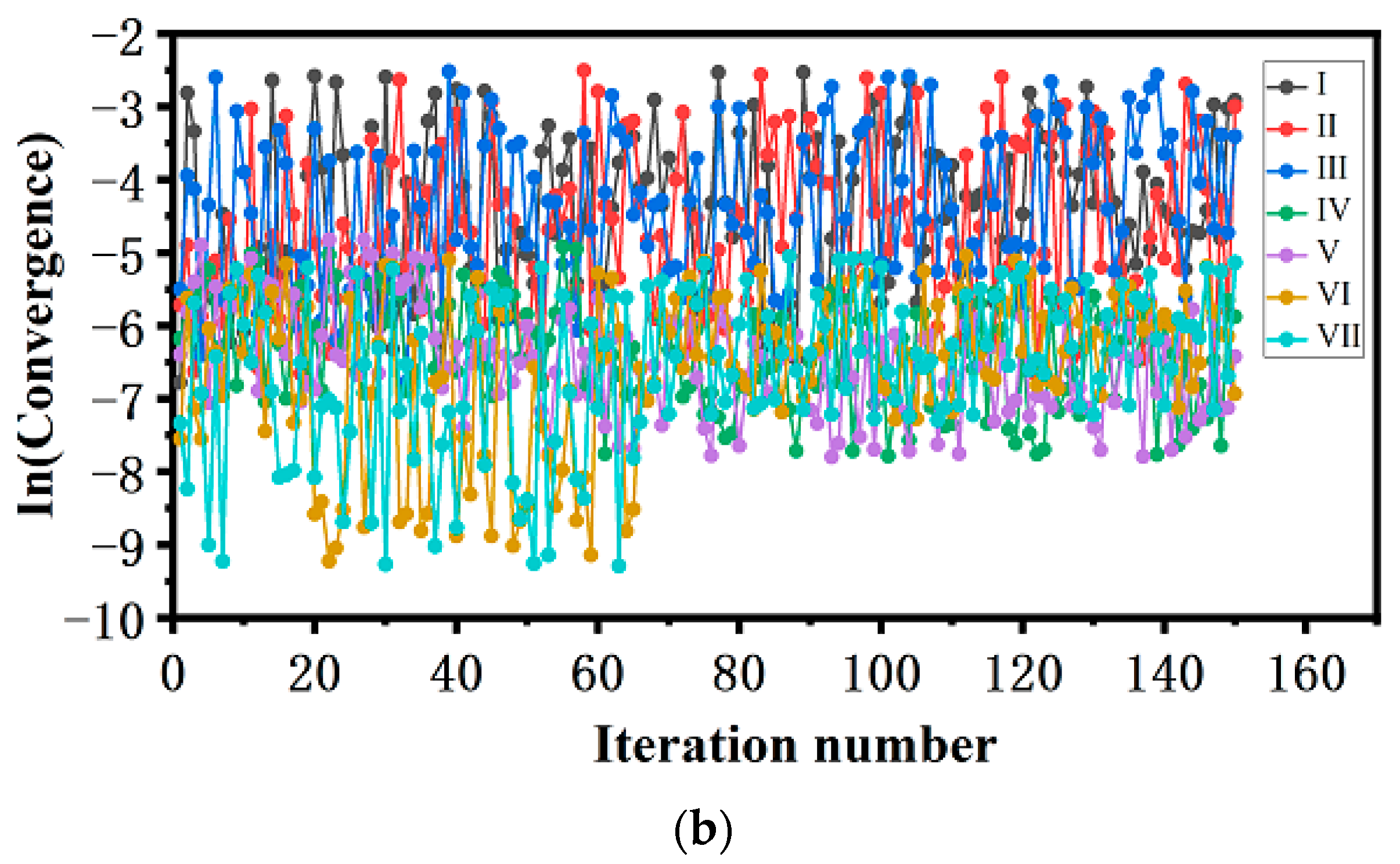
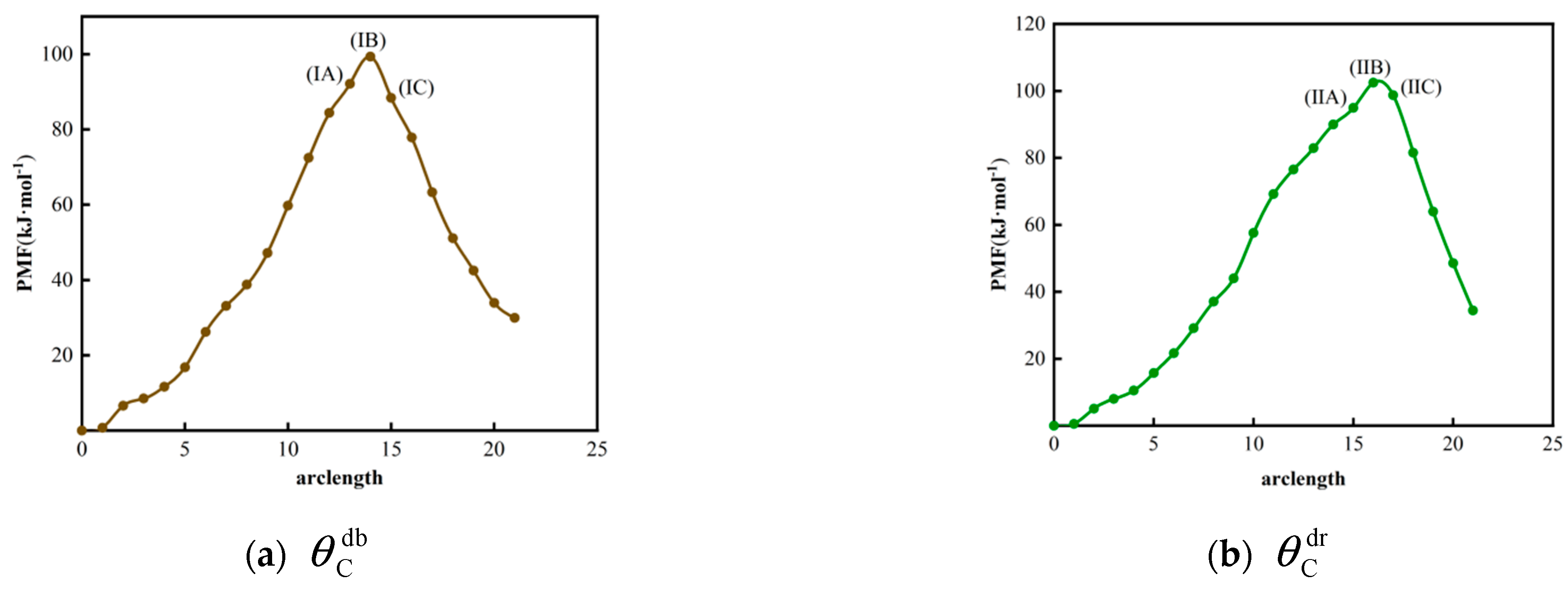
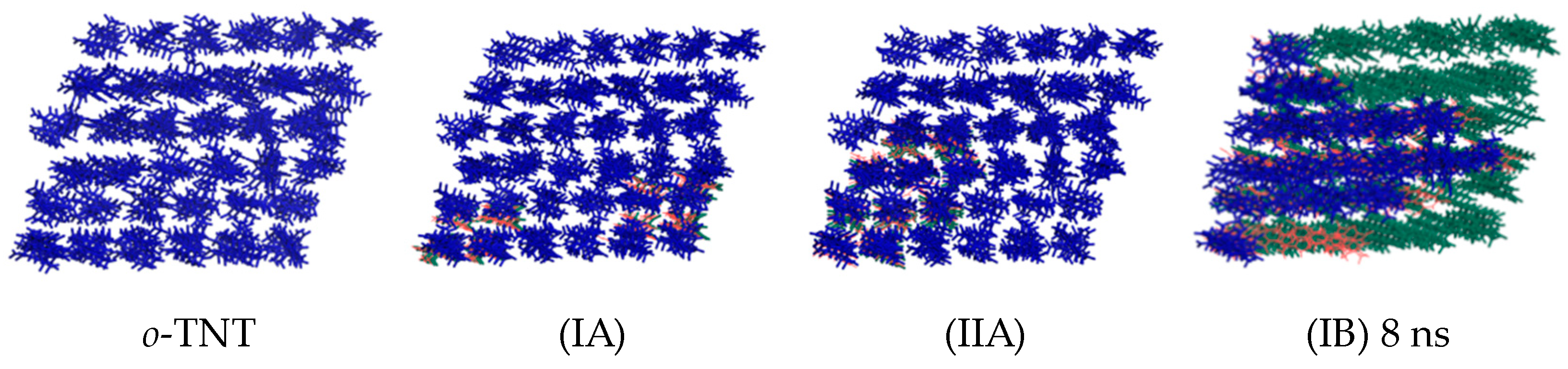
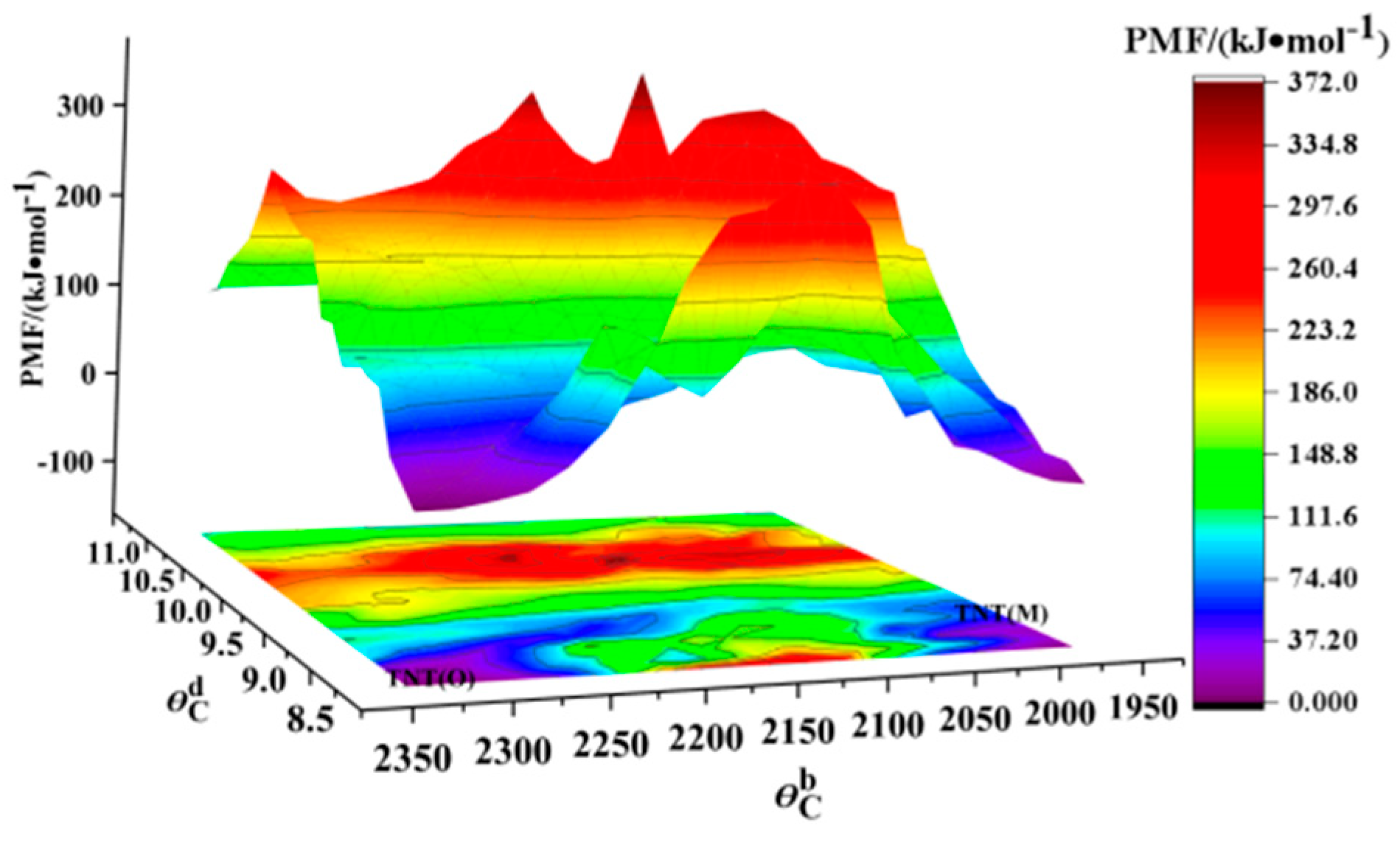
3.1. Convergence of FTS and Polymorphic Transformation without Electric Field
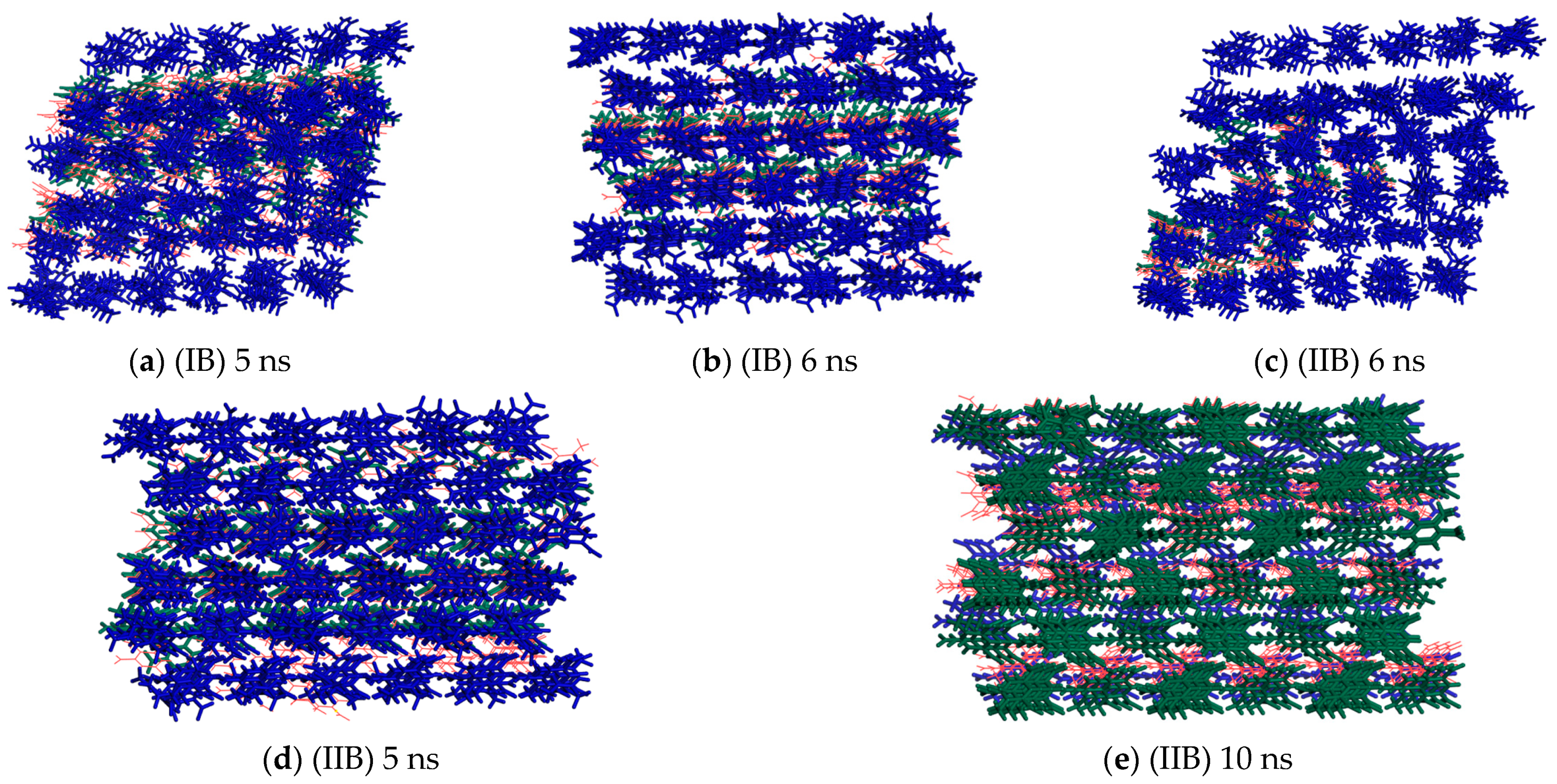
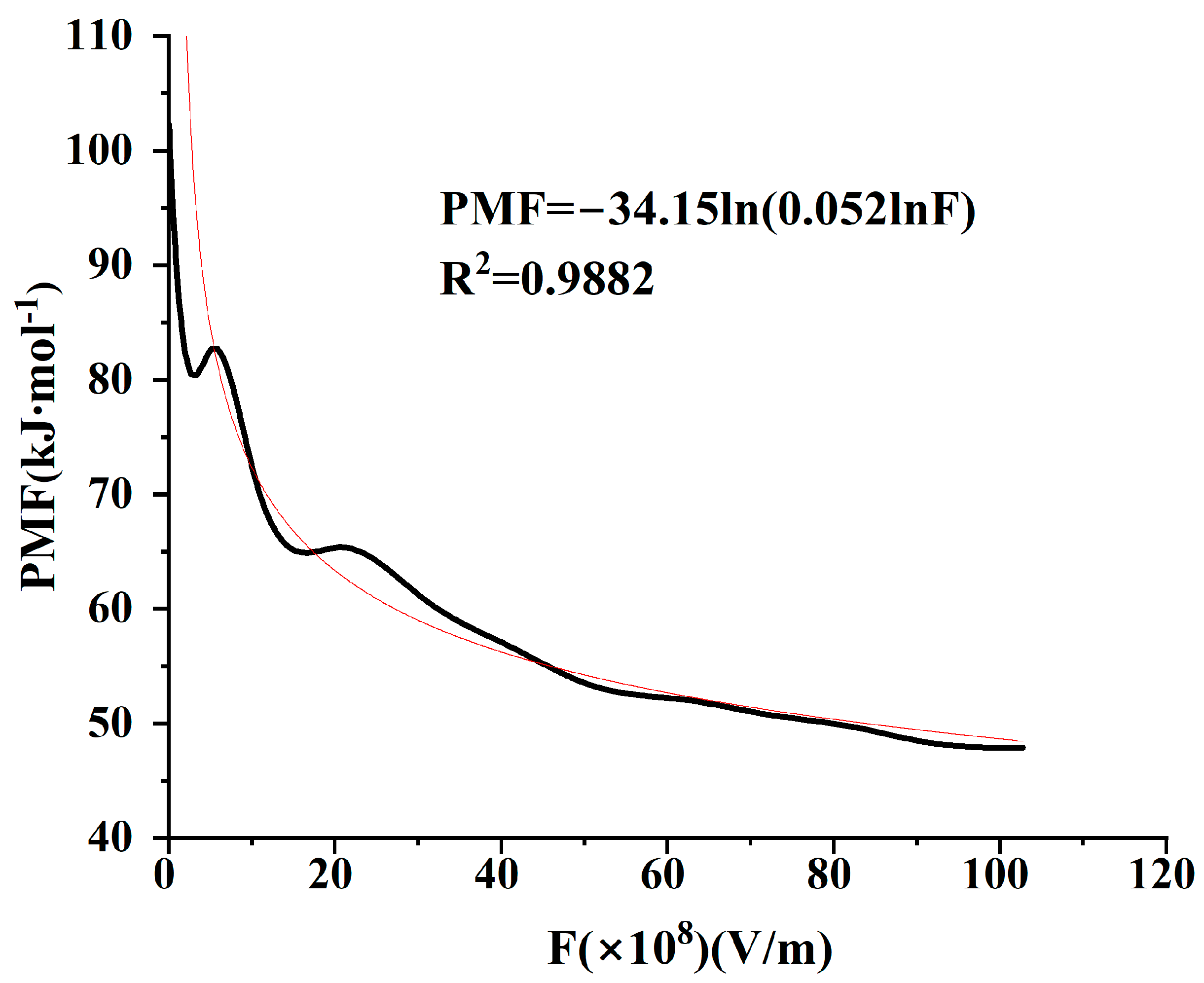
3.2. Polymorphic Transformation of TNT under the External Electric Fields
4. MD Simulation Details
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Ren, D.; Cheng, X. The theoretical investigation of the β-crystobalite structure under the effect of electric field. Comp. Mater. Sci. 2015, 96, 306–311. [Google Scholar] [CrossRef]
- Simura, R.; Nakamura, K.; Uda, S. Change of melting temperature of non-doped and Mg-doped lithium niobate underan external electric field. J. Cryst. Growth 2008, 310, 3873–3877. [Google Scholar] [CrossRef]
- Roland, C.M.; Fragiadakis, D.; Bogoslovov, R.; Urban, S.; Dabrowski, R.; Tykarska, M.; Osiecka, N.; Czub, J. Volumetric, dielectric, calorimetric and X-ray studies of smectogenic 10PBO8 at atmospheric and elevated pressures. Liq. Cryst. Rev. 2012, 39, 993–1001. [Google Scholar] [CrossRef]
- Mukherjee, P.K.; Rahman, M. Electric-field induced isotropic to smectic-Cphase transition. J. Mol. Liq. 2014, 196, 204–207. [Google Scholar] [CrossRef]
- Mahmood, A.; Chan, M.S.Y.; Saleemi, A.S.; Guo, J.; Lee, S.L. Synergic effect: Temperature-assisted electric-field-induced supramolecular phase transitions at the liquid/solid Interface. Langmuir 2019, 35, 8031–8037. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Zhang, P.; Zhang, Q.; Qiao, R.; He, Q.; Li, H.B.; Wang, Y.; Guo, J.; Zhang, D.; Duan, Z.; et al. Electric-field control of tri-statephase transformation with a selective dual-ion switch. Nature 2017, 546, 124–128. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Aetukuri, N.; Graf, T.; Schladt, T.D.; Samant, M.G.; Parkin, S.S.P. Suppression of metal-insulator transition in VO2 by electric field-induced oxygen vacancy formation. Science 2013, 339, 1402–1405. [Google Scholar] [CrossRef] [PubMed]
- Tai, B.T.; Andrew, J.S.; David, A.K. Efficient calculation of α- and β-nitrogen free energies and coexistence conditions viaoverlap sampling with targeted perturbation. J. Chem. Phys. 2011, 135, 044125. [Google Scholar]
- Beckham, G.T.; Peters, B.; Starbuck, C.; Variankaval, N.; Trout, B.L. Surface-mediated nucleation in the solid-state polymorph transformation of terephthalic acid. J. Am. Chem. Soc. 2007, 129, 4714–4723. [Google Scholar] [CrossRef] [PubMed]
- Davey, R.J.; Maginn, S.J.; Andrews, S.J.; Buckley, A.M.; Cottier, D.; Dempsay, P.; Rout, J.E.; Stanley, D.R.; Taylor, A. Stabilization of a metastable crystalline phase by twinning. Nature 1993, 366, 248–250. [Google Scholar] [CrossRef]
- Morris, K.R.; Griesser, U.J.; Eckhardt, C.J.; Stowell, J.G. Theoretical approaches to physical transformations of active pharmaceutical ingredients during manufacturing processes. Adv. Drug. Deliv. Rev. 2001, 48, 91–114. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.G.Z.; Gu, C.; Zell, M.T.; Burkhardt, R.T.; Munson, E.J.; Grant, D.J.W. Crystallization and transitions of sulfamerazine polymorphs. J. Pharm. Sci. 2002, 91, 1089–1100. [Google Scholar] [CrossRef]
- Kim, Y.S.; Paskow, H.C.; Rousseau, R.W. Propagation of solid-state transformations by dehvdration and stabilization of pseudopolymorphic crystals of sodium naproxen. Cryst. Growth Des. 2005, 5, 1623–1632. [Google Scholar] [CrossRef]
- Herbstein, F.H. On the mechanism of some first-order enantiotropic solid-state phase transitions: From Simon through Ubbelohde to Mnyukh. Acta Crystallogr. 2006, B62, 341–383. [Google Scholar] [CrossRef] [PubMed]
- Tonauer, C.M.; Bauer, M.; Loerting, T. The impact of temperature and unwanted impurities on slow compression of ice. Phys. Chem. Chem. Phys. 2022, 24, 35–41. [Google Scholar] [CrossRef]
- Bao, J.N.; Fan, H.B.; Xue, X.J.; Xie, Q.; Pan, P.J. Temperature-dependent crystalline structure and phasetransition of poly(butylene adipate) end-functionalized by multiple hydrogen-bonding groups. Phys. Chem. Chem. Phys. 2018, 20, 26479–26488. [Google Scholar] [CrossRef]
- Handle, P.H.; Loerting, T. Temperature-induced amorphisation of hexagonal ice. Phys. Chem. Chem. Phys. 2015, 17, 5403–5412. [Google Scholar] [CrossRef]
- Mutailipu, M.; Zhang, M.; Wu, H.; Yang, Z.; Shen, Y.; Sun, J.; Pan, S. Ba3Mg3(BO3)3F3 polymorphs with reversible phase transition and high performances as ultraviolet nonlinear optical materials. Nat. Commun. 2018, 9, 3089. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Han, J.; Baiheti, T.; Li, F.; Wei, Z.; Yang, Z.; Mutailipu, M.; Pan, S. Finding a series of BaBOF3 fluorooxoborate polymorphs with tunable symmetries: A simple but flexible case. Chem. Mater. 2021, 33, 7905–7913. [Google Scholar] [CrossRef]
- Xiao, G.; Zhu, Q.; Cui, Y.; Yang, W.; Li, B.; Song, S.; Cao, G.-H.; Ren, Z. Polymorphism, structural transition, and superconductivity in the equiatomic ternary germanide ThRhGe. Chem. Mater. 2022, 34, 1235–1244. [Google Scholar] [CrossRef]
- Diana, H.; Pilar, C.; Rico, G.; Benjamin, W.; Rajadurai, C.; Svetlana, K.; Mario, R.; Carlos, S.R.; Klaus, K.; Doris, G. Polymorphism and metal-induced structural transformation in 5,5′-bis(4-pyridyl)(2,2′-bispyrimidine) adlayers on Au(111). Phys. Chem. Chem. Phys. 2018, 20, 15960–15969. [Google Scholar]
- Venugopal, K.; Deepak, D.; Suresh, D.; Sunil, V. Transformation of photophysical properties from solution to solid state in alkoxy-cyano-diphenylacetylene molecules. Phys. Chem. Chem. Phys. 2015, 17, 18768–18779. [Google Scholar]
- Beckham, G.T.; Peters, B.; Trout, B.L. Evidence for a size dependent nucleation mechanism in solid state polymorph transformations. J. Phys. Chem. B 2008, 112, 7460–7466. [Google Scholar] [CrossRef] [PubMed]
- Dickson, A.; Warmflash, A.; Dinner, A.R. Nonequilibrium umbrella sampling in spaces of many order parameters. J. Chem. Phys. 2009, 130, 074104. [Google Scholar] [CrossRef] [PubMed]
- Faradjian, A.K.; Elber, R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys. 2004, 120, 10880–10889. [Google Scholar] [CrossRef] [PubMed]
- Santiso, E.E.; Trout, B.L. A general set of order parameters for molecular crystals. J. Chem. Phys. 2011, 134, 064109. [Google Scholar] [CrossRef] [PubMed]
- Carter, E.; Ciccotti, G.; Hynes, J.; Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 1989, 156, 472–477. [Google Scholar] [CrossRef]
- Anwar, J.; Zahn, D. Uncovering molecular processes in crystal nucleation and growth by using molecular simulation. Angew. Chem. Int. Ed. 2011, 50, 1996–2013. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E.; Ren, W.; Vanden-Eijnden, E. String method for the study of rare events. Phys. Rev. B Condens. Matter Mater. Phys. 2002, 66, 052301. [Google Scholar]
- Weinan, E.; Ren, W.; Vanden-Eijnden, E. Finite temperature string method for the study of rare events. J. Phys. Chem. B 2005, 109, 6688–6693. [Google Scholar]
- Vanden-Eijnden, E.; Venturoli, M. Revisiting the finite temperature string method for the calculation of reaction tubes and free energies. J. Chem. Phys. 2009, 130, 194103. [Google Scholar] [CrossRef] [PubMed]
- Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
- Maragliano, L.; Fischer, A.; Vanden-Eijnden, E.; Ciccotti, G. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 2006, 125, 024106. [Google Scholar] [CrossRef] [PubMed]
- Zinovjev, K.; Tuñón, I. Adaptive finite temperature string method in collective variables. J. Phys. Chem. A 2017, 121, 9764–9772. [Google Scholar] [CrossRef] [PubMed]
- Dickson, B.M.; Huang, H.; Post, C.B. Unrestrained computation of free energy along a path. J. Phys. Chem. B 2012, 116, 11046–11055. [Google Scholar] [CrossRef] [PubMed]
- Díaz, L.G.; Ensing, B. Path finding on high-dimensional free energy landscapes. Phys. Rev. Lett. 2012, 109, 020601. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, L.; Roux, B.; Vanden-Eijnden, E. Comparison between mean forces and swarms-of-trajectories string methods. J. Chem. Theory Comput. 2014, 10, 524–533. [Google Scholar] [CrossRef] [PubMed]
- Song, H.-D.; Zhu, F.-Q. Finite temperature string method with umbrella sampling: Application on a side chain flipping in Mhp1 transporter. J. Phys. Chem. B 2017, 121, 3376–3386. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.R.; Lv, C.; Yang, W. Hidden conformation events in DNA Base extrusions: A generalized-ensemble path optimization and equilibrium simulation study. J. Chem. Theory Comput. 2013, 9, 3756–3768. [Google Scholar] [CrossRef] [PubMed]
- Bellucci, M.A.; Trout, B.L. Bezier curve string method for the study of rare events in complex chemical systems. J. Chem. Phys. 2014, 141, 074110. [Google Scholar] [CrossRef] [PubMed]
- Shah, M.; Santiso, E.E.; Trout, B.L. Computer simulations of homogeneous nucleation of benzene from the melt. J. Phys. Chem. B 2011, 115, 10400–10412. [Google Scholar] [CrossRef] [PubMed]
- Gobbo, G.; Bellucci, M.A.; Tribello, G.A.; Ciccotti, G.; Trout, B.L. Nucleation of molecular crystals driven by relative information entropy. J. Chem. Theory Comput. 2018, 14, 959–972. [Google Scholar] [CrossRef]
- Mac, Q.J. Some methods for classification and analysis of multivariate observations. In Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967. [Google Scholar]
- Nawaz, M.; Mehmood, Z.; Nazir, T.; Naqvi, R.A.; Rehman, A.; Iqbal, M.; Saba, T. Skin cancer detection from dermoscopic images using deeplearning and fuzzy k-means clustering. Microsc. Res. Tech. 2021, 85, 339–351. [Google Scholar] [CrossRef] [PubMed]
- Abo-Elnaga, Y.; Nasr, S. K-means cluster interactive algorithm-based evolutionary approach for solving bilevel multi-objective programming problems. Alex. Eng. J. 2021, 61, 811–827. [Google Scholar] [CrossRef]
- Rong, H.; Ramirez-Serrano, A.; Guan, L.; Gao, Y. lmage object extraction based on semantic detection and improved K-Means agorithm. IEEE Access 2020, 8, 171129–171139. [Google Scholar] [CrossRef]
- Ren, F.-D.; Liu, Y.-Z.; Ding, K.-W.; Chang, L.-L.; Cao, D.-L.; Liu, S.-B. Finite temperature string by K-means clustering sampling with order parameter as collective variables for molecular crystal: Application to polymorphic transformation between β-CL-20 and ε-CL-20. Phys. Chem. Chem. Phys. 2024, 26, 3500–3515. [Google Scholar] [CrossRef] [PubMed]
- Ren, F.D.; Wang, X.L.; Zhang, Q.; Wang, X.J.; Chang, L.L.; Zhang, Z.T. Experimental and theoretical investigation of external electric-field-induced crystallization of TKX-50 from solution by finite-temperature string with order parameters as collective variables for ionic crystals. Molecules 2024, 29, 1159. [Google Scholar] [CrossRef] [PubMed]
- Bernshtein, J. Polymorphism in Molecular Crystals; Clarendon Press: Oxford, UK, 2002. [Google Scholar]
- Sikder, A.K.; Sikder, N. A review of advanced high performance, insensitive and thermally stable energetic materials emerging for military and space applications. J. Hazard. Mater. 2004, 112, 1–15. [Google Scholar] [CrossRef]
- Sivabalan, R.; Gore, G.M.; Nair, U.R.; Saikia, A.; Venugopalan, S.; Gandhe, B.R. Study on ultrasound assisted precipitation of CL-20 and its effect on morphology and sensitivity. J. Hazard. Mater. 2007, 139, 199–203. [Google Scholar] [CrossRef]
- Vrcelj, R.M.; Gallagher, H.G.; Sherwood, J.N. Polymorphism in 2,4,6-trinitrotoluene crystallized from solution. J. Am. Chem. Soc. 2001, 123, 2291–2295. [Google Scholar] [CrossRef]
- Parrish, D.A.; Deschamps, J.R.; Gilardi, R.D.; Butcher, R.J. Part of the special issue: Facets of polymorphism in crystals. Cryst. Growth Des. 2008, 8, 57–62. [Google Scholar] [CrossRef]
- Ranko, V.; Sherwood, J.N.; Alan, R.K.; Hugh, G.G. Polymorphism in 2-4-6 trinitrotoluene. Cryst. Growth Des. 2003, 3, 1027–1032. [Google Scholar]
- Santiso, E.E.; Trout, B.L. A general method for molecular modeling of nucleation from the melt. J. Chem. Phys. 2015, 143, 174109. [Google Scholar] [CrossRef] [PubMed]
- Alexander, L.F.; Radacsi, N. Application of electric fields for controlling crystallization. CrystEngComm 2019, 21, 5014–5031. [Google Scholar] [CrossRef]
- Kulshrestha, A.; Punnathanam, S.N.; Ayappa, K.G. Finite temperature string method with umbrella sampling using path collective variables: Application to secondary structure change in a protein. Soft Matter 2022, 18, 7593–7603. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, L.; Vanden-Eijnden, E. On-the-fly string method for minimum free energy paths calculation. Chem. Phys. Lett. 2007, 446, 182–190. [Google Scholar] [CrossRef]
- Radacsi, N. Process Intensification in Crystallization: Submicron Particle Generation Using Alternative Energy Forms; IPSKAMP DRUKKERS: Enschede, The Netherlands, 2012. [Google Scholar]
- Hammadi, Z.; Astier, J.P.; Morin, R.; Veesler, S. Protein Crystallization Induced by a Localized Voltage. Cryst. Growth Des. 2007, 7, 1472–1475. [Google Scholar] [CrossRef]
- Mirkin, N.; Frontana-Uribe, B.A.; Rodríguez-Romero, A.; Hernández-Santoyo, A.; Moreno, A. The influence of an internal electric field upon protein crystallization using the gel-acupuncture method. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, 59, 1533–1538. [Google Scholar] [CrossRef] [PubMed]
- Aber, J.E.; Arnold, S.; Garetz, B.A.; Myerson, A.S. Strong dc electric field applied to supersaturated aqueous glycine solution induces nucleation of the γ polymorph. Phys. Rev. Lett. 2005, 94, 145503. [Google Scholar] [CrossRef] [PubMed]
- Profio, G.D.; Reijonen, M.T.; Caliandro, R.; Guagliardi, A.; Curcio, E.; Drioli, E. Insights into the polymorphism of glycine: Membrane crystallization in an electric field. Phys. Chem. Chem. Phys. 2013, 15, 9271. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer, R.C.; Morris, J.B. Improved quantitative structure property relationships for the prediction of dielectric constants for a set of diverse compounds by subsetting of the data set. J. Chem. Inf. Comput. Sci. 2000, 40, 1253–1261. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.C.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.V.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingford CT, USA, 2009. [Google Scholar]



| Sample | r(Å) | 1/σ2(Å−1) | (°) | (°) | ||
|---|---|---|---|---|---|---|
| 5.68(5.65) a | 22.03 | 74.67(71.53) | 23.18 | 10.55(12.31) | 8.93 | |
| o-TNT | 6.22(6.26) | 19.28 | 68.43(66.28) | 11.53 | 57.79(56.29) | 15.62 |
| 6.68(6.67) | 28.32 | 49.62(53.10) | 19.18 | 85.62(84.17) | 13.17 | |
| 5.63(5.64) | 61.25 | 41.18(42.53) | 22.36 | 172.88(169.17) | 19.32 | |
| m-TNT | 5.72(5.65) | 9.02 | 85.37(82.11) | 18.52 | 163.27(165.02) | 15.78 |
| 7.43(7.46) | 11.25 | 51.28(53.62) | 21.87 | 44.50(45.13) | 27.62 |
| r(Å) | 1/σ2(Å−1) | (°) | (°) | |||
|---|---|---|---|---|---|---|
| o-TNT | 5.67 a (5.67) b 5.79 c | 24.18(25.33) 27.62 | 67.82(65.31) 62.16 | 20.23(20.56) 23.51 | 8.12(6.62) 9.93 | 7.88(8.39) 6.26 |
| 6.25(6.24) 6.26 | 17.63(19.81) 15.17 | 65.17(62.76) 69.35 | 13.18(9.03) 17.63 | 53.16(51.87) 49.27 | 13.98(13.25) 16.07 | |
| 6.67(6.63) 6.65 | 26.55(24.89) 20.12 | 52.88(57.13) 49.21 | 22.56(24.12) 27.80 | 82.35(86.18) 76.22 | 15.26(17.53) 19.18 | |
| m-TNT | 5.66(5.63) 5.92 | 71.37(75.28) 63.12 | 46.26(49.17) 50.89 | 20.15(23.62) 20.83 | 141.40(123.79) 165.18 | 21.52(24.31) 20.17 |
| 5.70(5.71) 5.73 | 11.18(15.62) 13.79 | 67.28(65.39) 61.04 | 16.31(18.15) 16.27 | 149.01(153.82) 157.25 | 18.92(20.13) 17.65 | |
| 7.46(7.42) 7.45 | 14.31(13.29) 12.10 | 55.97(51.18) 60.12 | 19.31(21.83) 16.72 | 45.23(46.18) 40.35 | 25.31(27.02) 24.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, S.-J.; Ren, F.-D. Finite Temperature String with Order Parameter as Collective Variables for Molecular Crystal: A Case of Polymorphic Transformation of TNT under External Electric Field. Molecules 2024, 29, 2549. https://doi.org/10.3390/molecules29112549
Niu S-J, Ren F-D. Finite Temperature String with Order Parameter as Collective Variables for Molecular Crystal: A Case of Polymorphic Transformation of TNT under External Electric Field. Molecules. 2024; 29(11):2549. https://doi.org/10.3390/molecules29112549
Chicago/Turabian StyleNiu, Shi-Jie, and Fu-De Ren. 2024. "Finite Temperature String with Order Parameter as Collective Variables for Molecular Crystal: A Case of Polymorphic Transformation of TNT under External Electric Field" Molecules 29, no. 11: 2549. https://doi.org/10.3390/molecules29112549
APA StyleNiu, S.-J., & Ren, F.-D. (2024). Finite Temperature String with Order Parameter as Collective Variables for Molecular Crystal: A Case of Polymorphic Transformation of TNT under External Electric Field. Molecules, 29(11), 2549. https://doi.org/10.3390/molecules29112549





