Comparison of Various Theoretical Measures of Aromaticity within Monosubstituted Benzene
Abstract
1. Introduction
2. Results
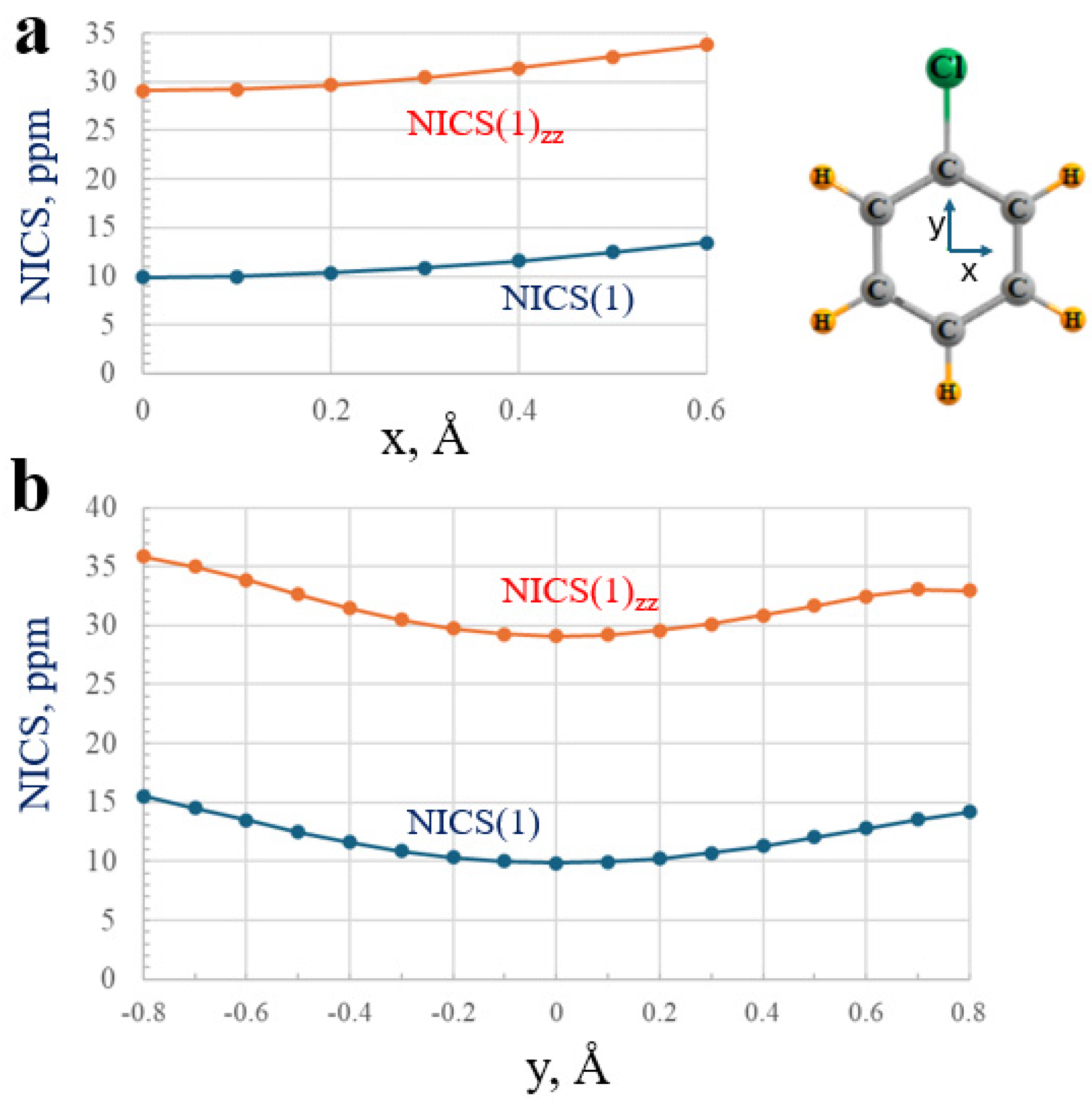
2.1. Magnetic Properties
2.2. Bond Length Uniformity
2.3. Energetic Measures
3. Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hofmann, A.W.I. On insolinic acid. Proc. R. Soc. Lond. 1857, 8, 1–3. [Google Scholar]
- Krygowski, T.M.; Cyrañski, M.K.; Czarnocki, Z.; Häfelinger, G.; Katritzky, A.R. Aromaticity: A Theoretical Concept of Immense Practical Importance. Tetrahedron 2000, 56, 1783–1796. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.V. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef]
- Baranac-Stojanović, M. 4π-Electron B–N Monocycles: Stability and (Anti)aromaticity. Eur. J. Org. Chem. 2017, 2017, 5163–5169. [Google Scholar] [CrossRef]
- Stanger, A. Obtaining Relative Induced Ring Currents Quantitatively from NICS. J. Org. Chem. 2010, 75, 2281–2288. [Google Scholar] [CrossRef]
- Stanger, A. What is… aromaticity: A critique of the concept of aromaticity—Can it really be defined? Chem. Commun. 2009, 1939–1947. [Google Scholar] [CrossRef]
- Szatylowicz, H.; Jezuita, A.; Krygowski, T.M. On the relations between aromaticity and substituent effect. Struct. Chem. 2019, 30, 1529–1548. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Barczynski, P.; Musumarra, G.; Pisano, D.; Szafran, M. Aromaticity as a quantitative concept. 1. A statistical demonstration of the orthogonality of classical and magnetic aromaticity in five- and six-membered heterocycles. J. Am. Chem. Soc. 1989, 111, 7–15. [Google Scholar] [CrossRef]
- Jiao, H.; von Ragué Schleyer, P. The Cope Rearrangement Transition Structure Is Not Diradicaloid, but Is It Aromatic? Angew. Chem. Int. Ed. Engl. 1995, 34, 334–337. [Google Scholar] [CrossRef]
- Cysewski, P.; Jelinski, T.; Krygowski, M.T.; Oziminski, P.W. Factors Influencing Aromaticity: PCA Studies of Monosubstituted Derivatives of Pentafulvene, Benzene and Heptafulvene. Curr. Org. Chem. 2012, 16, 1920–1933. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Stanger, A. Magnetic criteria of aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
- Gomes, J.A.N.F.; Mallion, R.B. Aromaticity and Ring Currents. Chem. Rev. 2001, 101, 1349–1384. [Google Scholar] [CrossRef]
- Leyva-Parra, L.; Pino-Rios, R.; Inostroza, D.; Solà, M.; Alonso, M.; Tiznado, W. Aromaticity and Magnetic Behavior in Benzenoids: Unraveling Ring Current Combinations. Chem. Eur. J. 2024, 30, e202302415. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of magnetically induced current densities: Theory and applications. WIREs Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef]
- Herges, R.; Geuenich, D. Delocalization of Electrons in Molecules. J. Phys. Chem. A 2001, 105, 3214–3220. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of .pi.-electron systems. J. Chem. Inf. Comp. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Mischie, A.; Toader, A.M.; Buta, M.C.; Cimpoesu, F. Harmonic oscillator model of aromaticity (HOMA) in conjugated radicals and cations. Comput. Theor. Chem. 2023, 1230, 114370. [Google Scholar] [CrossRef]
- Stawski, W.; Zhu, Y.; Wei, Z.; Petrukhina, M.A.; Anderson, H.L. Crystallographic evidence for global aromaticity in the di-anion and tetra-anion of a cyclophane hydrocarbon. Chem. Sci. 2023, 14, 14109–14114. [Google Scholar] [CrossRef] [PubMed]
- Arpa, E.M.; Durbeej, B. HOMER: A reparameterization of the harmonic oscillator model of aromaticity (HOMA) for excited states. Phys. Chem. Chem. Phys. 2023, 25, 16763–16771. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M. Separation of the energetic and geometric contributions to the aromaticity. Part IV. A general model for the π-electron systems. Tetrahedron 1996, 52, 10255–10264. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Ejsmont, K.; Stepień, B.T.; Cyrański, M.K.; Poater, J.; Solà, M. Relation between the Substituent Effect and Aromaticity. J. Org. Chem. 2004, 69, 6634–6640. [Google Scholar] [CrossRef]
- Herndon, W.C.; Mills, N.S. Aromatic Stabilization Energy Calculations for the Antiaromatic Fluorenyl Cation. Issues in the Choice of Reference Systems for Positively Charged Species. J. Org. Chem. 2005, 70, 8492–8496. [Google Scholar] [CrossRef] [PubMed]
- Cyrański, M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef]
- Aihara, J.-i. Graph Theory of Aromatic Stabilization. Bull. Chem. Soc. Jpn. 2016, 89, 1425–1454. [Google Scholar] [CrossRef]
- Kemula, W.; Krygowski, T.M. Substituent effects in poorly aromatic system: Dichloro-anthraquinones and related semi-antrhraquinone radicals. Tetrahedron Lett. 1968, 9, 5135–5140. [Google Scholar] [CrossRef]
- Stanger, A. The Different Aromatic Characters of Some Localized Benzene Derivatives. J. Phys. Chem. A 2008, 112, 12849–12854. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Pühlhofer, F. Recommendations for the Evaluation of Aromatic Stabilization Energies. Org. Lett. 2002, 4, 2873–2876. [Google Scholar] [CrossRef] [PubMed]
- Patra, S.G.; Mondal, H.; Bhattacharjya, M.J.; Chetia, N.; Chattaraj, P.K. On the aromaticity of substituted benzene. Theor. Chem. Acc. 2023, 142, 91. [Google Scholar] [CrossRef]
- Stanger, A. Reexamination of NICSπ,zz: Height Dependence, Off-Center Values, and Integration. J. Phys. Chem. A 2019, 123, 3922–3927. [Google Scholar] [CrossRef] [PubMed]
- Stanger, A. NICS—Past and Present. Eur. J. Org. Chem. 2020, 2020, 3120–3127. [Google Scholar] [CrossRef]
- Baranac-Stojanović, M. Substituent Effect on Triplet State Aromaticity of Benzene. J. Org. Chem. 2020, 85, 4289–4297. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Chen, S.; Chen, D.; Lin, L.; Xiao, K.; Zhao, L.; Solà, M.; Zhu, J. The application of aromaticity and antiaromaticity to reaction mechanisms. Fundam. Res. 2023, 3, 926–938. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules, A Quantum Theory; Clarendon Press: Oxford, UK, 1990; Volume 22, p. 438. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
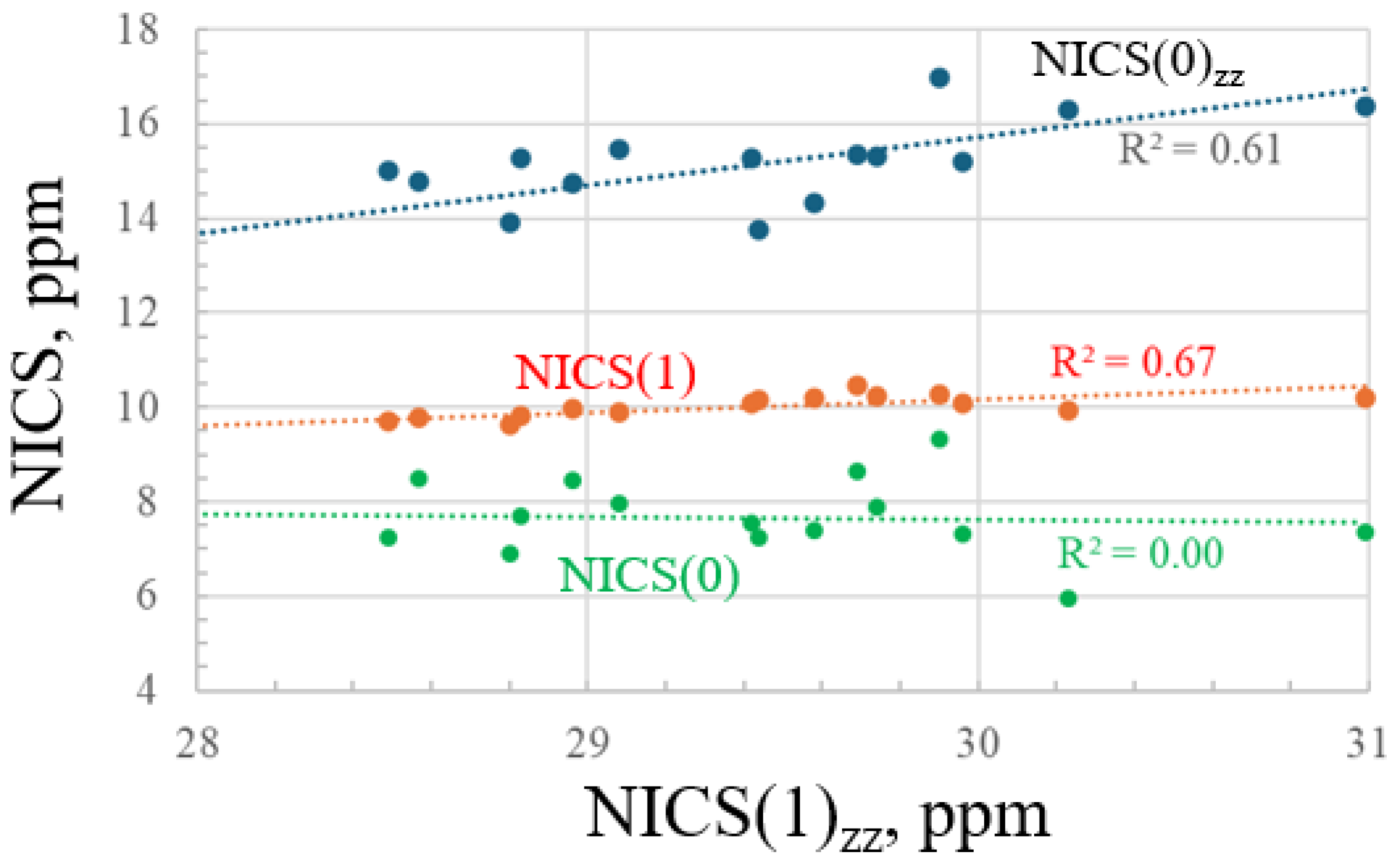

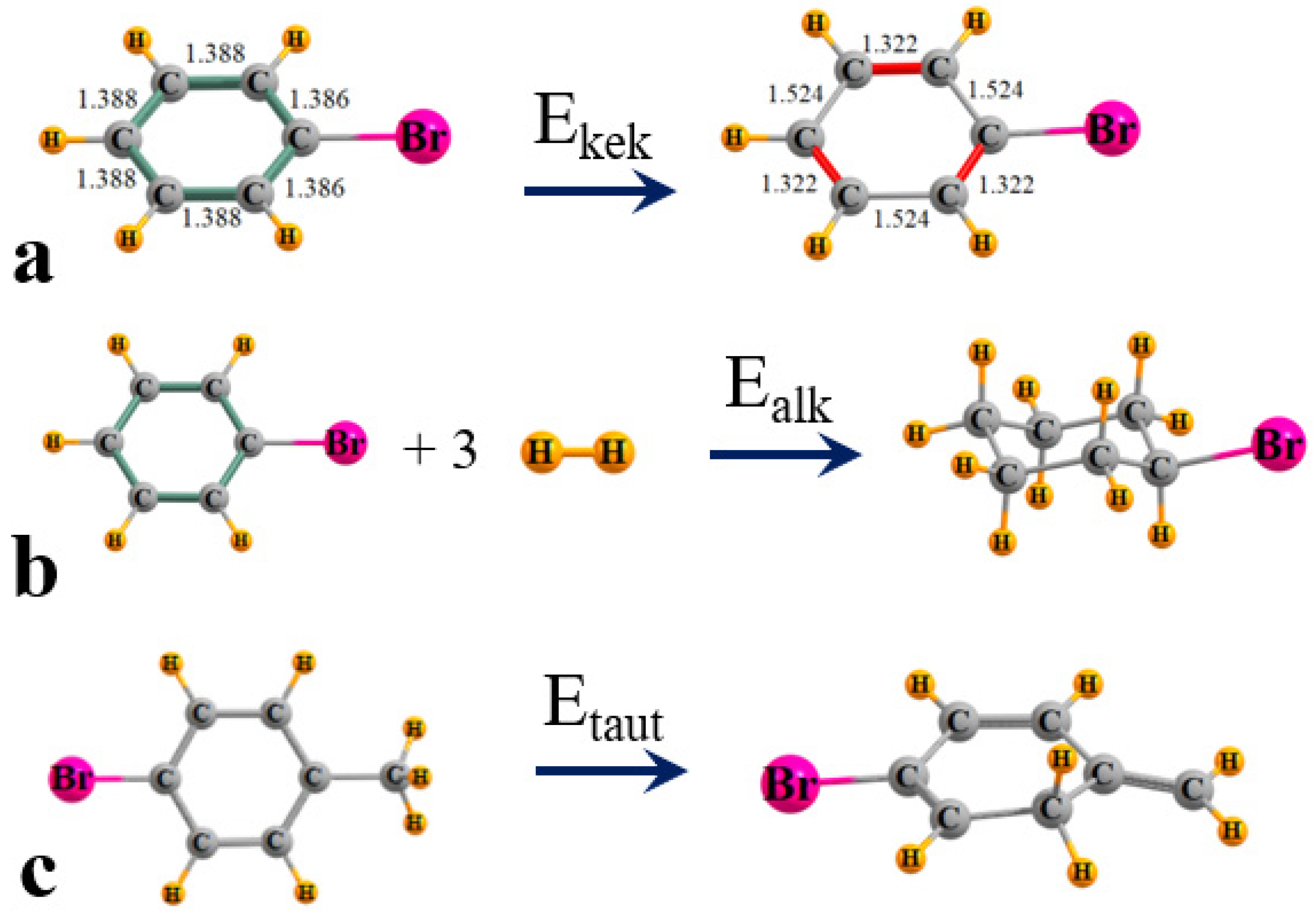
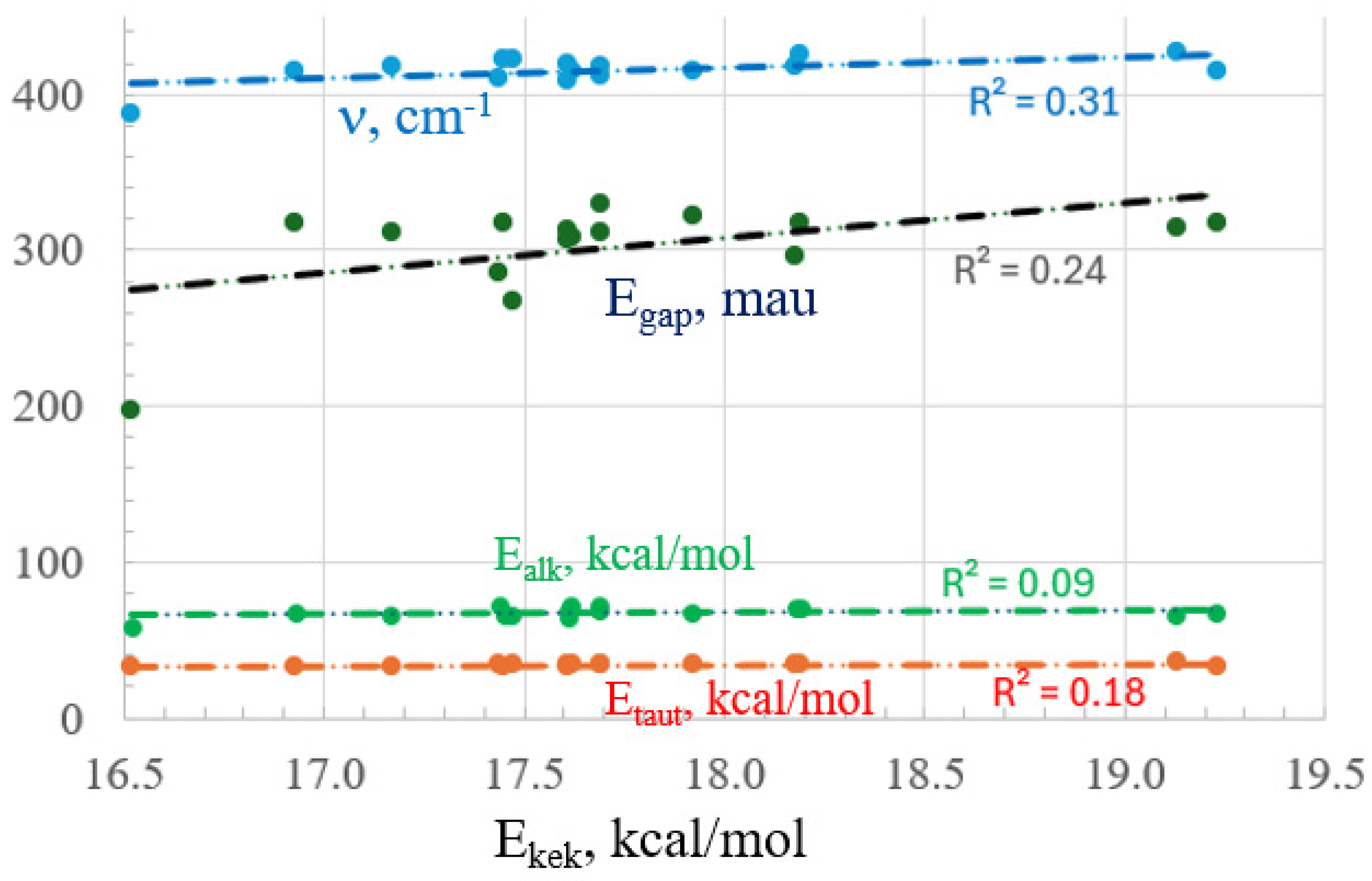
| NICS(1)zz | NICS(0)zz | NICS(1) | NICS(0) | |
|---|---|---|---|---|
| H | 30.99 | 16.37 | 10.21 | 7.35 |
| Li | 30.23 | 16.30 | 9.92 | 5.97 |
| Me | 29.96 | 15.19 | 10.07 | 7.33 |
| F | 29.90 | 16.98 | 10.27 | 9.31 |
| CN | 29.74 | 15.33 | 10.24 | 7.88 |
| NO2 | 29.69 | 15.36 | 10.46 | 8.64 |
| COOH | 29.58 | 14.34 | 10.18 | 7.38 |
| CHO | 29.44 | 13.76 | 10.17 | 7.23 |
| n-propyl | 29.42 | 15.27 | 10.07 | 7.53 |
| Cl | 29.08 | 15.46 | 9.88 | 7.95 |
| OMe | 28.96 | 14.73 | 9.97 | 8.45 |
| Br | 28.83 | 15.28 | 9.82 | 7.70 |
| Ph | 28.80 | 13.91 | 9.62 | 6.91 |
| OH | 28.57 | 14.78 | 9.77 | 8.49 |
| I | 28.49 | 14.99 | 9.70 | 7.25 |
| NH2 | 27.06 | 12.02 | 9.23 | 7.42 |
| σ(R) | σ(ρBCP) | 100× ρRCP | |
|---|---|---|---|
| H | 0.00 | 0.00 | 2.44 |
| I | 1.48 | 1.93 | 2.46 |
| Br | 2.40 | 2.59 | 2.45 |
| Cl | 2.62 | 3.44 | 2.44 |
| OH | 4.95 | 4.15 | 2.41 |
| n-propyl | 5.29 | 2.13 | 2.44 |
| Me | 5.55 | 2.16 | 2.44 |
| NO2 | 5.90 | 4.11 | 2.47 |
| COOH | 5.96 | 3.38 | 2.45 |
| F | 7.91 | 11.31 | 2.43 |
| CHO | 8.35 | 4.74 | 2.46 |
| CN | 8.92 | 6.18 | 2.42 |
| Ph | 9.07 | 5.19 | 2.44 |
| NH2 | 10.84 | 3.47 | 2.41 |
| OMe | 12.51 | 6.38 | 2.41 |
| Li | 20.46 | 14.77 | 2.48 |
| Ekek | Ealk | Etaut | Egap | ν | |
|---|---|---|---|---|---|
| n-propyl | 19.23 | 67.04 | 32.54 | 317 | 415.47 |
| OMe | 19.13 | 65.96 | 36.30 | 315 | 426.41 |
| F | 18.19 | 70.58 | 33.88 | 318 | 425.44 |
| NO2 | 18.18 | 70.95 | 34.07 | 296 | 418.61 |
| COOH | 17.92 | 67.04 | 34.35 | 322 | 414.88 |
| Cl | 17.69 | 71.23 | 33.81 | 312 | 417.87 |
| H | 17.69 | 68.25 | 34.11 | 329 | 412.06 |
| Br | 17.62 | 72.11 | 33.76 | 308 | 414.25 |
| CN | 17.61 | 69.06 | 34.20 | 307 | 409.10 |
| NH2 | 17.61 | 63.86 | 33.66 | 313 | 418.85 |
| Ph | 17.47 | 65.69 | 34.17 | 267 | 422.28 |
| OH | 17.45 | 65.95 | 33.25 | 317 | 422.26 |
| I | 17.44 | 72.17 | 33.73 | 285 | 409.91 |
| CHO | 17.17 | 65.68 | 32.78 | 311 | 417.35 |
| Me | 16.93 | 67.88 | 33.04 | 317 | 414.98 |
| Li | 16.52 | 58.25 | 33.18 | 198 | 387.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swain, C.K.; Scheiner, S. Comparison of Various Theoretical Measures of Aromaticity within Monosubstituted Benzene. Molecules 2024, 29, 2260. https://doi.org/10.3390/molecules29102260
Swain CK, Scheiner S. Comparison of Various Theoretical Measures of Aromaticity within Monosubstituted Benzene. Molecules. 2024; 29(10):2260. https://doi.org/10.3390/molecules29102260
Chicago/Turabian StyleSwain, Caleb K., and Steve Scheiner. 2024. "Comparison of Various Theoretical Measures of Aromaticity within Monosubstituted Benzene" Molecules 29, no. 10: 2260. https://doi.org/10.3390/molecules29102260
APA StyleSwain, C. K., & Scheiner, S. (2024). Comparison of Various Theoretical Measures of Aromaticity within Monosubstituted Benzene. Molecules, 29(10), 2260. https://doi.org/10.3390/molecules29102260







