Extreme Gradient Boosting Combined with Conformal Predictors for Informative Solubility Estimation
Abstract
:1. Introduction
- (1)
- On the reference web page [27], among many stated articles, one is related to the applicability domain [29] from 2008. The independent literature search results found only a web link [30] last updated in 2014, where they cite Ref. [29] stating that the prediction accuracy of an unknown set is estimated using “ASNN-STD” under the AD section. However, that link [30] was not cited by Drugbank. Instead, under Drugbank publications, the last update related to solubility prediction was in 2007 [31] and they only referenced the AlogPS2.1 program from 2002 [32]. In Ref. [32], only similarity measures between compounds were considered.
- (2)
- Ref. [28] displays in one of its figures the dependency of the prediction accuracy on the compound’s number of nonhydrogen atoms. This means that based on their own used reference for solubility extrapolation to the Drugbank database, molecules with different molecular properties (e.g., molecular mass) must have a different difficulty of being predicted. When prediction models are extrapolated to large databases, this must be accounted for each compound. Thus, besides the predicted solubility, there should also be a difficulty class related to that prediction. But there are no signs of any such solubility classification in Drugbank or any other database [33,34].
- (3)
- There is no approximative statistic (e.g., median prediction interval at a certain confidence level) given for the successfulness of the whole solubility extrapolation to large databases.
2. Results and Discussion
2.1. Model Accuracy and Variable Selection on Data Sets (1–6)
2.2. Applicability Domain Results on External Databases
2.3. Conformal Predictor (CP) Results on Data Sets (1–6)
2.4. Extrapolation of AqSolDB Models to External Databases
3. Materials and Methods
3.1. Data Sets, Data Curation, and Preprocessing
3.1.1. AD for Train–Test Split
3.1.2. Molecular Descriptors
3.2. Machine Learning
3.2.1. Variable Selection Procedure for XGB
- Upon obtaining a grid-optimized XGB model on all variables, sort out the descriptors based on their statistical importance in decreasing order.
- Starting from the top three variables, perform a 5-fold CV in each step by parallelly adding the next top important variable in the forward stepwise (one by one) manner, and limit such forward addition to the top m variables (m = 30). Use the normal grid search in XGB for each addition of a variable.
- After adding m variables, continue the forward stepwise addition until RMSECV(new step) > RMSECV(ex-step), then stop and select the number of variables of the RMSECV global minimum.
3.2.2. Conformal Predictors
Absolute Residual (AR)
Absolute Residual Stability (ARS) and Absolute Residual Semistability (ARSS)
Error Model and Log-Error Model
k-Nearest Neighbours from Euclidean Distances (kNN-EuD)
RMSE × t-Value
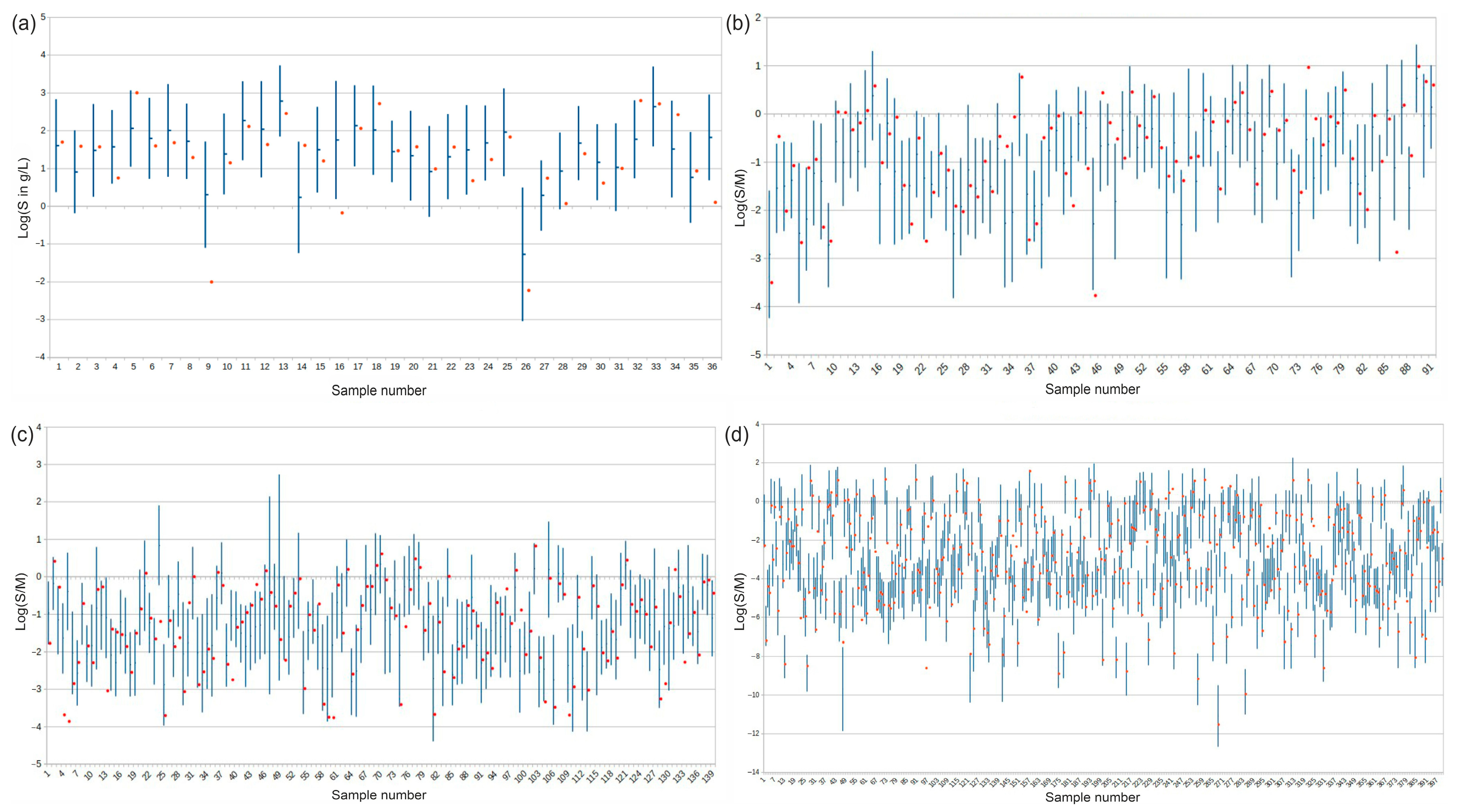
3.2.3. Validation of Prediction Intervals
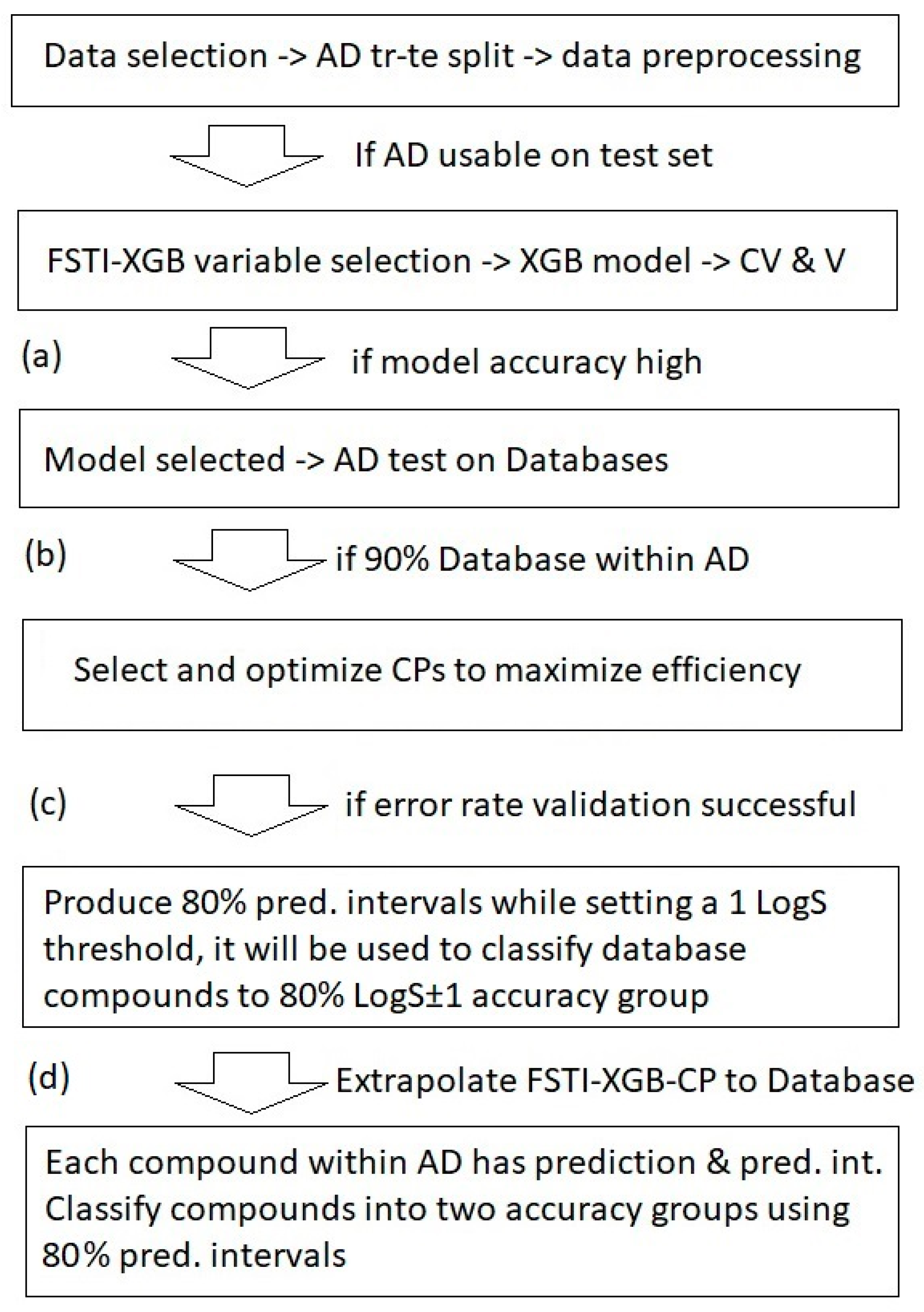
3.3. Extrapolation to the Drugbank, PubChem and COCONUT Databases
4. Conclusions
- (1)
- The FSTI-XGB model, having at most 34 descriptors, outperformed in accuracy five different data sets which included two ML studies of uncurated and curated AqSolDB sets. The obtained accuracy for the Acetone data set could be put in line with other top-performing non-TL Log(S) prediction results. For the AqSolDB-n data set, the obtained total CV and test accuracy (RMSEtot) was lower than any water Log(S) CV literature train(all-CV)–test(all-independent) split’s RMSEtot known to date, if very small independent test-size data of ca. 20 compounds and CV results on all data sets as “final tests” are neglected. It was obtained only with Pvars, which underperformed when QMvars (e.g., melting points) were also available (Table 3). Additionally, we proved that XGB was a stronger ML method than RF, and that FSTI-XGB correctly selected important descriptors.
- (2)
- For the first time, conformal predictors were extensively calculated to produce prediction intervals for Log(S) in water and organic solvents using the XGB algorithm. This study revealed that they could be utilized to approximatively assess the important %LogS ± 1 accuracy measure of the data set. The calculations was feasible with the ARSS when β was targeted between 0.5 and 1.5 median(σ) if the data of molecular descriptors were scaled when used to predict Log(S). The ARSS significant interval efficiency gain was successfully validated on experimental solubility data sets (1–6) and on one external test set (900), ranging from 135 examples (data set (1)) to 9709 cases (data set (2)).
- (3)
- The normalized half-width intervals were not only correlated with the absolute residuals but were more correlated with the absolute residuals than any single molecular descriptor in the model. That information marks the background support of CP application to the informative solubility estimation of any targeted compound. The informativeness of varying individual half-width intervals offers either reliable estimates of individual Log(S) for narrow intervals or at least carries an indication of less reliable estimates for the cases of wide intervals. This is important for individual compound Log(S) estimation in the process and product development of potential new drugs and with regards to any solvent.
- (4)
- We predicted 473,276 Log(S)’s (11,130 DrugBank + 71,808 PubChem + 390,338 COCONUT) values, evaluated their individual error margins, and classified them into four accuracy groups. We also assessed the approximative general accuracy of the databases. The obtained final estimated LogS ± 1 was in the range 79.9–81.6% while the RMSE for the three databases was <1.0 Log(S), which was very solid when considering the difference in molecular weights between our model data set and public domains.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Krudy, G.; Hou, T.; Zhang, W.; Holland, G.; Xu, X. Development of reliable aqueous solubility models and their application in druglike analysis. J. Chem. Inf. Model. 2007, 47, 1395–1404. [Google Scholar] [CrossRef] [PubMed]
- Lusci, A.; Pollastri, G.; Baldi, P. Deep architectures and deep learning in chemoinformatics: The prediction of aqueous solubility for drug-like molecules. J. Chem. Inf. Model. 2013, 53, 1563–1575. [Google Scholar] [CrossRef] [PubMed]
- Francoeur, G.P.; Koes, D.R. SolTranNet—A Machine Learning Tool for Fast Aqueous Solubility Prediction. J. Chem. Inf. Model. 2021, 61, 2530–2536. [Google Scholar] [CrossRef] [PubMed]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Hildebrand, J.H. Solubility of non-electrolytes. Nature 1936, 138, 742. [Google Scholar]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectricscreening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. 1993, 5, 799–805. [Google Scholar] [CrossRef]
- Bara, J.E.; Moon, J.D.; Reclusado, K.R.; Whitley, J.W. COSMOTherm as a Tool for Estimating the Thermophysical Properties of Alkylimidazoles as Solvents for CO2 Separations. Ind. Eng. Chem. Res. 2013, 52, 5498–5506. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1941, 9, 660. [Google Scholar] [CrossRef]
- Huggins, M.L. Solutions of long chain compounds. J. Chem. Phys. 1941, 9, 440. [Google Scholar] [CrossRef]
- Gracin, S.; Brinck, T.; Rasmuson, Å.C. Prediction of solubility of solid organic compounds in solvents by UNIFAC. Ind. Eng. Chem. Res. 2002, 41, 5114–5124. [Google Scholar] [CrossRef]
- Ye, Z.; Ouyang, D. Prediction of small-molecule compound solubility in organic solvents by machine learning algorithms. J. Cheminform. 2021, 13, 98. [Google Scholar] [CrossRef]
- Boobier, S.; Hose, D.R.J.; Blacker, A.J.; Nguyen, B.N. Machine learning with physicochemical relationships: Solubility prediction in organic solvents and water. Nat. Commun. 2020, 11, 5753. [Google Scholar] [CrossRef] [PubMed]
- Huuskonen, J.; Salo, M.; Taskinen, J. Aqueous solubility prediction of drugs based on molecular topology and neural network modeling. J. Chem. Inf. Comput. Sci. 1998, 38, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Ge, K.; Ji, Y. Novel Computational Approach by Combining Machine Learning with Molecular Thermodynamics for Predicting Drug Solubility in Solvents. Ind. Eng. Chem. Res. 2021, 60, 9259–9268. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, J.; Lai, R.; Wang, Y.; Mao, B.; Wu, H.; Tian, L.; Shao, Y. Machine Learning Predicting Optimal Preparation of Silica-Coated Gold Nanorods for Photothermal Tumor Ablation. Nanomaterials 2023, 13, 1024. [Google Scholar] [CrossRef] [PubMed]
- Nikolova-Jeliazkova, N.; Jaworska, J. An approach to determining applicability domains for QSAR group contribution models: An analysis of SRC KOWWIN. Altern. Lab. Anim. 2005, 33, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, R.P.; Feuston, B.P.; Maiorov, V.N.; Kearsley, S. Similarity to molecules in the training set is a good discriminator for prediction accuracy in QSAR. J. Chem. Inf. Comput. Sci. 2004, 44, 1912–1928. [Google Scholar] [CrossRef] [PubMed]
- Sahigara, F.; Mansouri, K.; Ballabio, D.; Mauri, A.; Consonni, V.; Todeschini, R. Comparison of different approaches to define the applicability domain of QSAR models. Molecules 2012, 17, 4791–4810. [Google Scholar] [CrossRef]
- Netzeva, T.I.; Worth, A.; Aldenberg, T.; Benigni, R.; Cronin, M.T.; Gramatica, P.; Jaworska, J.S.; Kahn, S.; Klopman, G.; Marchant, C.A.; et al. Current status of methods for defining the applicability domain of (quantitative) structure-activity relationships: The report and recommendations of ECVAM Workshop 52. Altern. Lab. Anim. 2005, 33, 155–173. [Google Scholar] [CrossRef]
- Jaworska, J.; Nikolova-Jeliazkova, N.; Aldenberg, T. QSAR applicabilty domain estimation by projection of the training set descriptor space: A review. Altern. Lab. Anim. 2005, 33, 445–459. [Google Scholar] [CrossRef]
- Löfström, T.; Ryasik, A.; Johansson, U. Tutorial for using conformal prediction in KNIME, Conformal and Probabilistic Prediction and Applications. Proc. Mach. Learn. Res. 2022, 179, 4–23. [Google Scholar]
- Papadopoulos, H.; Vovk, V.; Gammerman, A. Regression Conformal Prediction with Nearest Neighbours. J. Artif. Intell. Res. 2011, 40, 815–840. [Google Scholar] [CrossRef]
- Lapins, M.; Arvidsson, S.; Lampa, S.; Berg, A.; Schaal, W.; Alvarsson, J.; Spjuth, O. A confidence predictor for LogD using conformal regression and a support-vector machine. J. Cheminform. 2018, 10, 17. [Google Scholar] [CrossRef] [PubMed]
- Johansson, U.; Boström, H.; Löfström, T.; Linusson, H. Regression conformal prediction with random forests. Mach. Learn. 2014, 97, 155–176. [Google Scholar] [CrossRef]
- Sluga, J.; Venko, K.; Drgan, V.; Novič, M. QSPR Models for Prediction of Aqueous Solubility: Exploring the Potency of Randić-type Indices. Croat. Chem. Acta 2020, 93, 311–319. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2017, 46, D1074–D1082. [Google Scholar] [CrossRef]
- Tetko, I.V. Welcome to the ALOGPS 2.1 Home Page! Available online: https://vcclab.org/lab/alogps/ (accessed on 5 June 2023).
- Tetko, I.V.; Tanchuk, V.Y.; Kasheva, T.N.; Villa, A.E.P. Estimation of Aqueous Solubility of Chemical Compounds Using E-State Indices. J. Chem. Inf. Comput. Sci. 2001, 41, 1488–1493. [Google Scholar] [CrossRef]
- Tetko, I.V.; Sushko, I.; Pandey, A.K.; Zhu, H.; Tropsha, A.; Papa, E.; Öberg, T.; Todeschini, R.; Fourches, D.; Varnek, A. Critical Assessment of QSAR Models of Environmental Toxicity against Tetrahymena pyriformis: Focusing on Applicability Domain and Overfitting by Variable Selection. J. Chem. Inf. Model. 2008, 48, 1733–1746. [Google Scholar] [CrossRef]
- Tetko, I.V. AlogPS (Aqueous Solubility and Octanol/Water Partition Coefficient). Available online: https://docs.ochem.eu/x/OoGZ.html (accessed on 6 June 2023).
- Wishart, D.S.; Knox, C.; Guo, A.C.; Cheng, D.; Shrivastava, S.; Tzur, D.; Gautam, B.; Hassanali, M. DrugBank: A knowledgebase for drugs, drug actions and drug targets. Nucleic Acids Res. 2008, 36, D901–D906. [Google Scholar] [CrossRef]
- Tetko, I.V.; Tanchuk, V.Y. Application of Associative Neural Networks for Prediction of Lipophilicity in ALOGPS 2.1 Program. J. Chem. Inf. Comput. Sci. 2002, 42, 1136–1145. [Google Scholar] [CrossRef]
- PubChem Classification Browser. With Selection of 72,852 Crystal Structures. Available online: https://pubchem.ncbi.nlm.nih.gov/classification/#hid=72 (accessed on 18 June 2023).
- COCONUT. Collection of Open Natural Products. With Selection of Canonical Smiles Format. Available online: https://coconut.naturalproducts.net/download (accessed on 18 June 2023).
- Huuskonen, J. Estimation of Aqueous Solubility for a Diverse Set of Organic Compounds Based on Molecular Topology. J. Chem. Inf. Comput. Sci. 2000, 40, 773–777. [Google Scholar] [CrossRef]
- Oja, M.; Sild, S.; Piir, G.; Maran, U. Intrinsic Aqueous Solubility: Mechanistically Transparent Data-Driven Modeling of Drug Substances. Pharmaceutics 2022, 14, 2248. [Google Scholar] [CrossRef] [PubMed]
- Sahigara, F.; Ballabio, D.; Todeschini, R.; Consonni, V. Defining a novel k-nearest neighbours approach to assess the applicability domain of a QSAR model for reliable predictions. J. Cheminform. 2013, 5, 27. [Google Scholar] [CrossRef] [PubMed]
- Aliev, T.A.; Belyaev, V.E.; Pomytkina, A.V.; Nesterov, P.V.; Shityakov, S.; Sadovnichii, R.V.; Novikov, A.S.; Orlova, O.Y.; Masalovich, M.S.; Skorb, E.V. Electrochemical Sensor to Detect Antibiotics in Milk Based on Machine Learning Algorithms. ACS Appl. Mater. Interfaces 2023, 15, 52010–52020. [Google Scholar] [CrossRef] [PubMed]
- Shahab, M.; Zheng, G.; Khan, A.; Wei, D.; Novikov, A.S. Machine Learning-Based Virtual Screening and Molecular Simulation Approaches Identified Novel Potential Inhibitors for Cancer Therapy. Biomedicines 2023, 11, 2251. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, A.S.; Nikolaev, K.G.; Novikov, A.S.; Yurchenko, S.O.; Novoselov, K.S.; Andreeva, D.V.; Skorb, E.V. Programmable soft-matter electronics. J. Phys. Chem. Lett. 2021, 12, 2017–2022. [Google Scholar] [CrossRef] [PubMed]
- Stokes, J.M.; Yang, K.; Swanson, K.; Jin, W.; Cubillos-Ruiz, A.; Donghia, N.M.; MacNair, C.R.; French, S.; Carfrae, L.A.; Bloom-Ackermann, Z.; et al. A Deep Learning Approach to Antibiotic Discovery. Cell 2020, 180, 688–702. [Google Scholar] [CrossRef] [PubMed]
- Pereira, J.C.; Ca, E.R.; dos Santos, C.N. Boosting Docking-Based Virtual Screening with Deep Learning. J. Chem. Inf. Model. 2016, 56, 2495–2506. [Google Scholar] [CrossRef] [PubMed]
- Vermeire, F.H.; Green, W.H. Transfer learning for solvation free energies: From quantum chemistry to experiments. Chem. Eng. J. 2021, 418, 129307. [Google Scholar] [CrossRef]
- Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.; Gi, E.M. Extreme Gradient Boosting as a Method for Quantitative Structure—Activity Relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Kim, N.; Lee, T.; Quagliato, L. Extreme gradient boosting-inspired process optimization algorithm for manufacturing engineering applications. Mater. Des. 2023, 226, 111625. [Google Scholar] [CrossRef]
- Tran-Nguyen, V.-K.; Junaid, M.; Simeon, S.; Ballester, P.J. A practical guide to machine-learning scoring for structure-based virtual screening. Nat. Protoc. 2023, 18, 3460–3511. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zhang, C.; Cheng, Y.; Yang, Y.-F.; She, Y.-B.; Liu, F.; Su, W.; Su, A. SolvBERT for solvation free energy and solubility prediction: A demonstration of an NLP model for predicting the properties of molecular complexes. Digit. Discov. 2023, 2, 409–421. [Google Scholar] [CrossRef]
- Sorkun, M.C.; Khetan, A.; Er, S. AqSolDB, a curated reference set of aqueous solubility and 2D descriptors for a diverse set of compounds. Sci. Data 2019, 6, 143. [Google Scholar] [CrossRef] [PubMed]
- Vassileiou, A.D.; Robertson, M.N.; Wareham, B.G.; Soundaranathan, M.; Ottoboni, S.; Florence, A.J.; Hartwigd, T.; Johnston, B.F. A unified ML framework for solubility prediction across organic solvents. Digit. Discov. 2023, 2, 356–367. [Google Scholar] [CrossRef]
- Wang, J.; Hou, T.; Xu, X. Aqueous Solubility Prediction Based on Weighted Atom Type Counts and Solvent Accessible Surface Areas. J. Chem. Inf. Model. 2009, 49, 571–581. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Bian, Y.; Xu, T.; Xie, W.; Wei, Y.; Huang, W.; Huang, J. Self-Supervised Graph Transformer on Large-Scale Molecular Data. Adv. Neural Inf. Process. Syst. 2020, 33, 12559–12571. [Google Scholar]
- PaDELPy: A Python Wrapper for PaDEL-Descriptor Software. Available online: https://github.com/ecrl/padelpy (accessed on 31 December 2022).
- Pharmacopeia Online. Available online: http://www.uspbpep.com/ (accessed on 4 April 2023).
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- ORCA DFT Version 5.0.3. Manual, Chapter 9.41.3, The SMD Solvation Model. pp. 1073–1077. Available online: https://orcaforum.kofo.mpg.de (accessed on 22 February 2023).
- R: RandomForest: Breiman and Cutler’s Random Forests for Classification and Regression. Available online: https://cran.r-project.org/web/packages/randomForest/index.html (accessed on 2 February 2023).
- R: Xgboost: Extreme Gradient Boosting. Available online: https://cran.r-project.org/web/packages/xgboost/index.html (accessed on 2 February 2023).
- Vovk, V. Cross-conformal predictors. Ann. Math. Artif. Intell. 2015, 74, 9–28. [Google Scholar] [CrossRef]
- Andries, J.P.M.; Heyden, Y.V.; Buydens, L.M.C. Improved variable reduction in partial least squares modelling by global-minimum error Uninformative-Variable Elimination. Anal. Chim. Acta 2017, 982, 37–47. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.-L. Elimination of Uninformative Variables for Multivariate Calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef]
- Papadopoulos, H.; Haralambous, H. Reliable prediction intervals with regression neural networks. Neural Netw. 2011, 24, 842–851. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, D. Mean-Square-Error. Available online: https://dtkaplan.github.io/SDS-book/mean-square-error.html (accessed on 30 March 2023).
- Hyndman, R.J.; Athanasopoulos, G. Chapter 3.5. Prediction Intervals. In Forecasting: Princliple and Praxis; Otexts: Melbourne, Australia, 2018; Available online: https://otexts.com/fpp2/prediction-intervals.html (accessed on 30 March 2023).
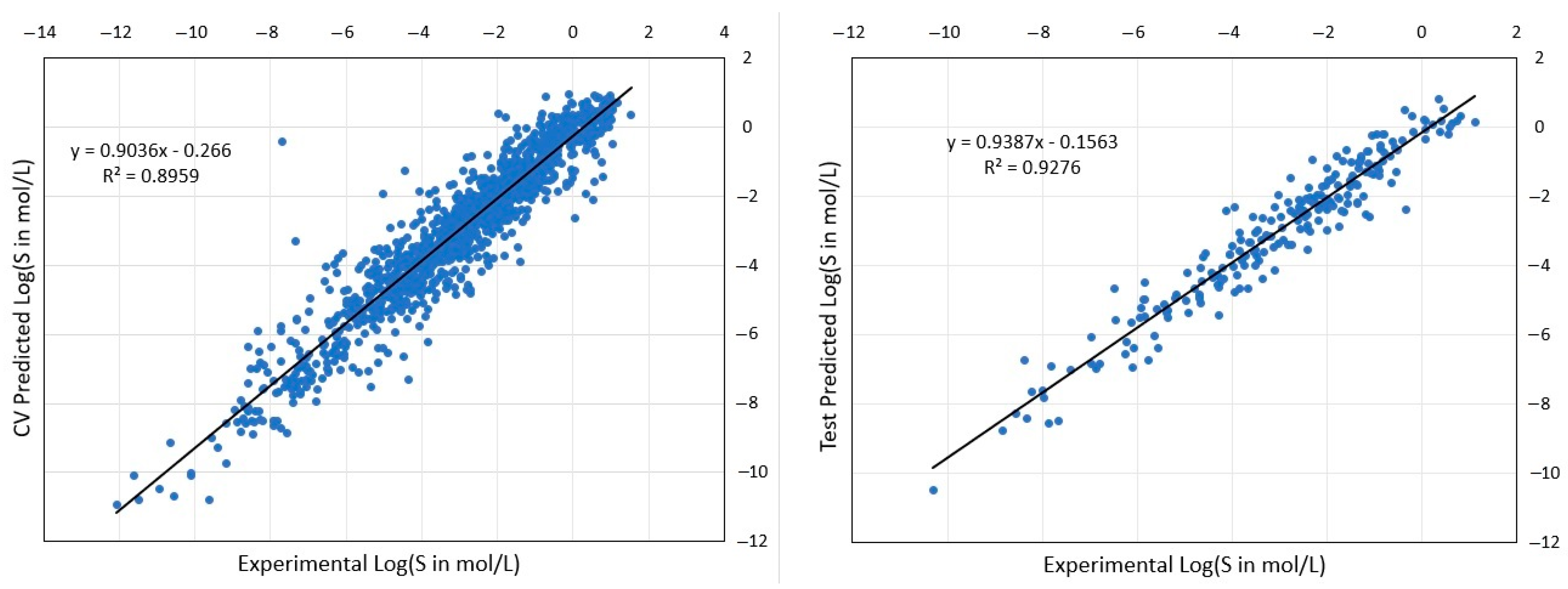

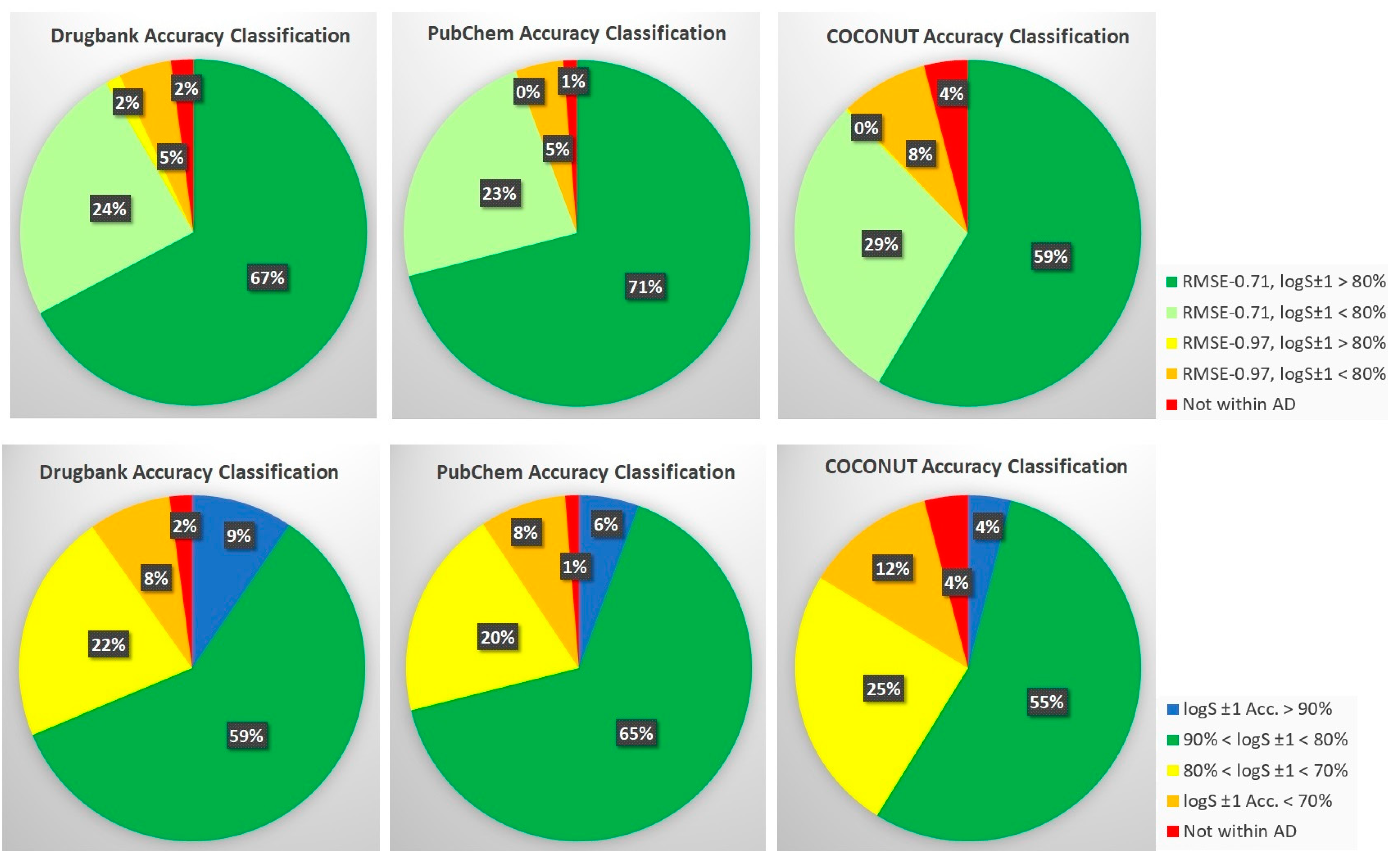
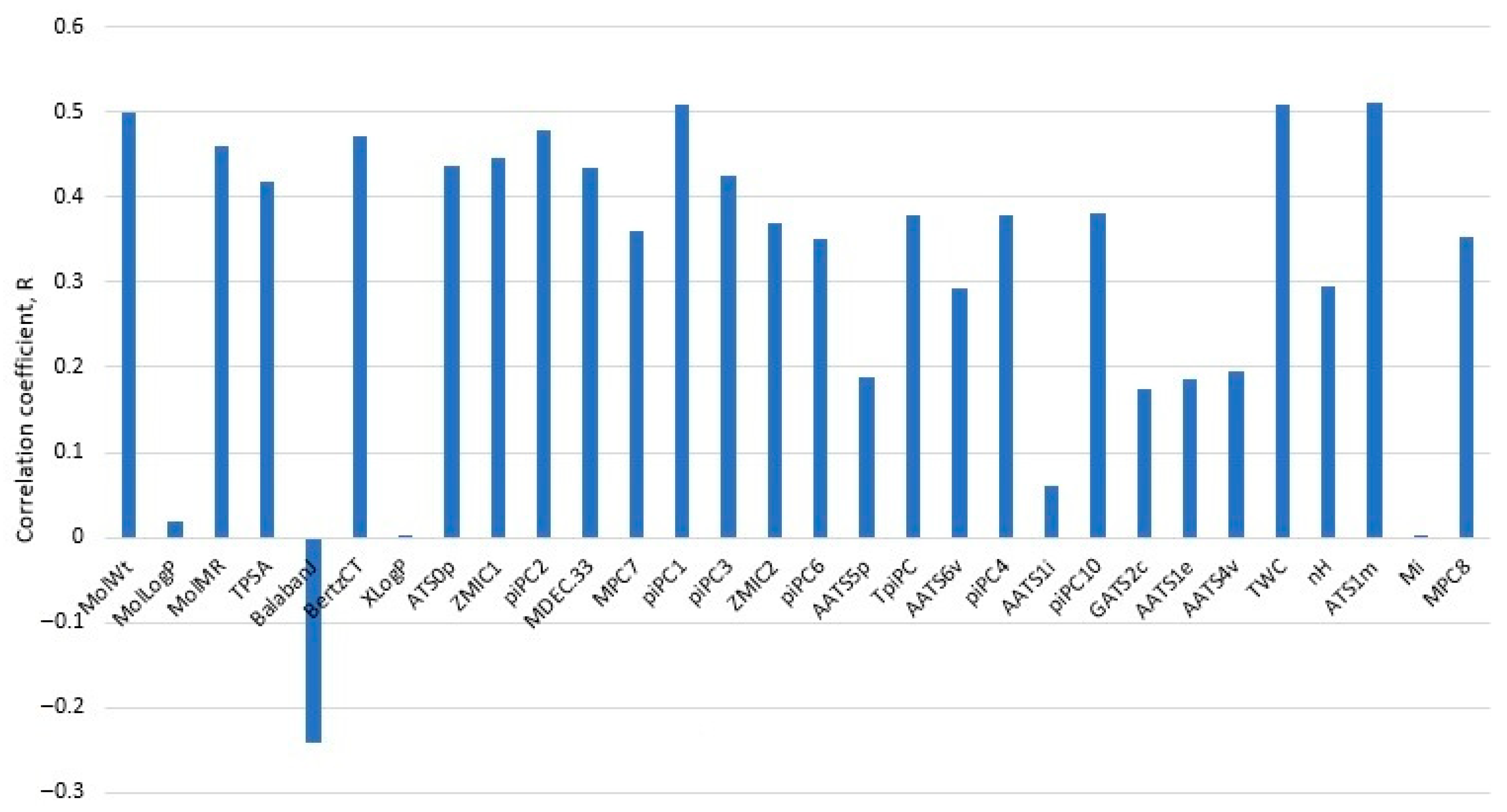
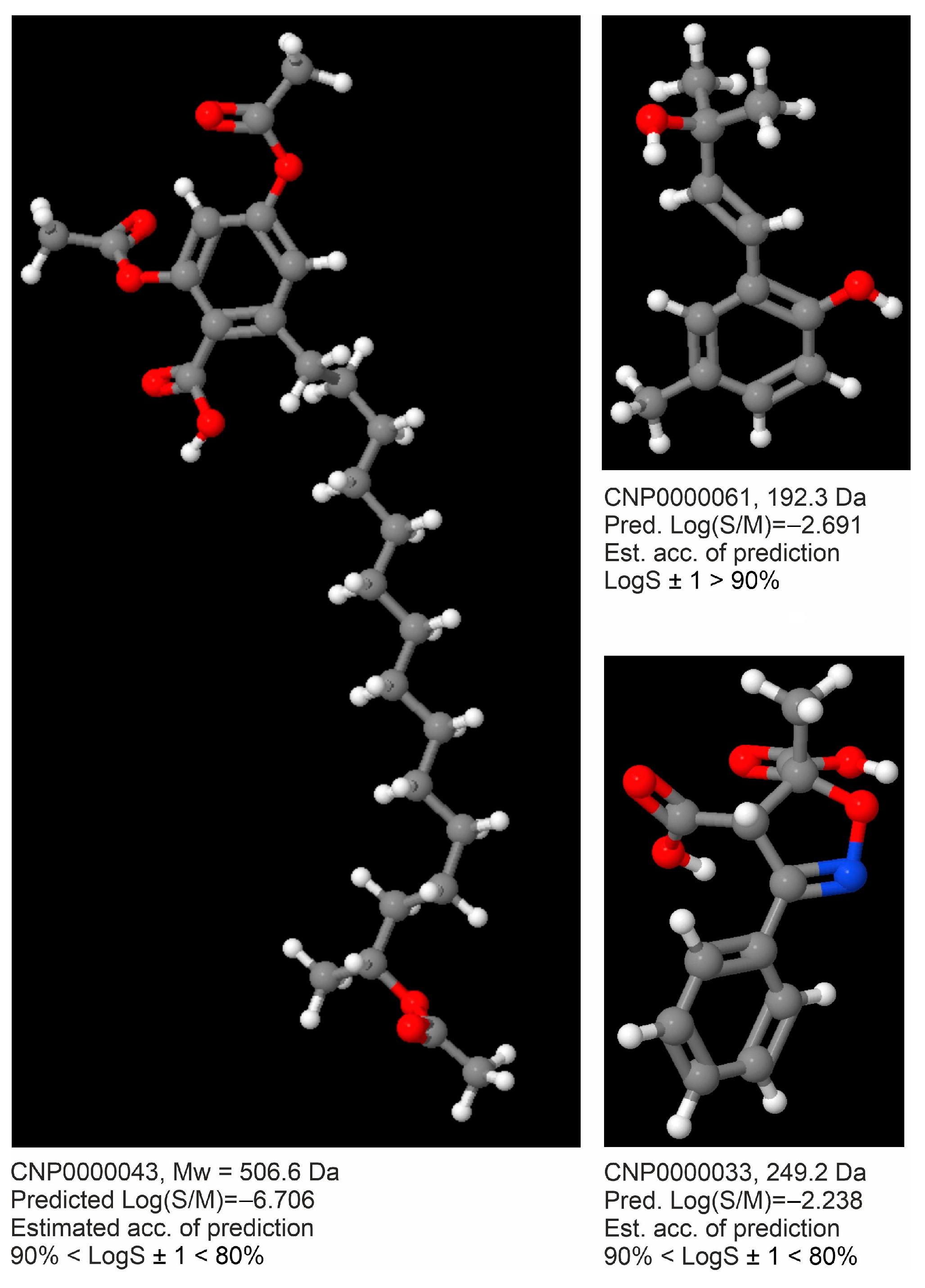

| Method | RMSECV | R2(CV) | CV-%LogS ± 0.7 | CV-%LogS ± 1.0 | RMSEV | R2(V) | V-%LogS ± 0.7 | V-%LogS ± 1.0 |
| RF | 0.757 * | 0.890 | 73.5 | 84.3 | 0.596 | 0.929 | 77.7 | 90.9 |
| RF fine-t. | 0.753 * | 0.890 | 73.8 | 84.5 | 0.594 | 0.929 | 79.5 | 90.0 |
| XGB | 0.711 | 0.901 | 77.1 | 88.3 | 0.558 | 0.936 | 83.6 | 92.7 |
| Method | RMSEP (T) | R2(T) | T-%LogS ± 0.7 | T-%LogS ± 1.0 | Method | RMSEtot | %LogS ± 0.7tot | %LogS ± 1.0tot |
| RF | 0.790 * | 0.899 | 72.1 | 84.4 | RF | 0.755 | 73.1 | 84.9 |
| RF fine-t. | 0.781 ** | 0.900 | 73.1 | 84.3 | RF-fine-t. | 0.749 | 74.0 | 84.9 |
| XGB | 0.755 | 0.905 | 75.2 | 86.0 | XGB | 0.713 | 77.0 | 87.9 |
| Method | RMSECV | R2(CV) | CV-%LogS ± 0.7 | CV-%LogS ± 1.0 | RMSEV | R2(V) | V-%LogS ± 0.7 | V-%LogS ± 1.0 |
|---|---|---|---|---|---|---|---|---|
| RF fine-t. | 1.060 * | 0.798 | 62.9 | 75.6 | 0.958 ** | 0.836 | 66.9 | 79.2 |
| XGB | 0.943 * | 0.838 | 69.0 | 80.9 | 0.924 ** | 0.845 | 69.8 | 81.5 |
| Data Set, vars Type as P/QM/P + QM (Number of Variables) | FSTI-XGB | |
|---|---|---|
| RMSECV | RMSEV | |
| Methanol, P (17) | 0.7007 | 0.8480 |
| Methanol, QM (6) | 1.0541 * | 0.8471 |
| Methanol, P + QM (34) | 0.6893 * | 0.7883 |
| Ethanol, P (32) | 0.7303 | 0.8923 |
| Ethanol, QM (16) | 0.7363 * | 0.8727 |
| Ethanol, P + QM (33) | 0.6503 * | 0.7902 |
| Acetone, P (30) | 0.7337 | 0.7969 |
| Acetone, QMvars (12) | 0.7097 * | 0.6975 |
| Acetone, P + QMvars (31) | 0.6164 * | 0.7018 |
| Data Set | Set Size | Method | nvars | RMSECV/ RMSE-Test * | RMSEV | RMSEtot | R2(V) ** CV | %LogS ± 0.7, CV-Set/V-Set | %LogS ± 1.0, CV-Set/V-Set | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AqSolDB-w | 9982 | SolTranNet [3] | - | 1.459 | 1.711 | - | 0.68 ** | - | - | - | - |
| AqSolDB-w | 9709 | FSTI-XGB * | 32 | 0.966 | 0.966 | 0.966 | 0.831 | 68.6 | 67.2 | 79.7 | 79.7 |
| AqSolDB-n | 1674 | NN-A [25] | 7 | 0.72 * | 0.76 | 0.74 * | 0.88 | - | - | - | - |
| AqSolDB-n | 1665 | NN-D [25] | 22 | 1.07 * | 0.96 | 1.00 * | 0.80 | - | - | - | - |
| AqSolDB-n | 1619 | FSTI-XGB * | 26 | 0.730 | 0.594 | 0.712 | 0.928 | 76.3 | 76.8 | 87.3 | 92.7 |
| AqSolDB-n | 1619 | FSTI-XGB * | Ext. test set, RMSEP = 0.764, R2(T) = 0.902, %LogS ± 0.7 = 75.7, %LogS ± 1.0 = 85.3% | ||||||||
| Data Set | Set Size | Method | nvars | RMSECV | RMSEV | RMSEtot | R2(V) | %LogS ± 0.7, CV-Set/V-Set | %LogS ± 1.0, CV-Set/V-Set | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Water-wide | 900 | SVM [12] | 41 | 0.85 | 0.85 | 0.85 | 0.89 | 68.3 | 71.6 | 81.7 | 78.9 |
| Water-wide | 900 | GP [12] | 41 | 0.86 | 0.89 | 0.86 | 0.88 | 67.0 | 68.4 | 79.2 | 73.7 |
| Water-wide | 900 | FSTI-XGB | 33 | 0.779 | 0.833 | 0.803 | 0.883 | 70.4 | 70.5 | 83.2 | 82.2 |
| Ethanol | 695 | RF [12] | 41 | 0.76 | 0.79 | 0.76 | 0.53 | 68.5 | 64.8 | 82.2 | 82.4 |
| Ethanol | 695 | Bag [12] | 41 | 0.76 | 0.80 | 0.77 | 0.52 | 69.1 | 65.5 | 82.7 | 79.6 |
| Ethanol | 695 | FSTI-XGB | 33 | 0.650 | 0.790 | 0.678 | 0.528 | 78.1 | 67.6 | 89.7 | 82.0 |
| Acetone | 452 | SVM [12] | 41 | 0.69 | 0.84 | 0.72 | 0.42 | 76.3 | 72.8 | 84.3 | 81.5 |
| Acetone | 452 | Bag [12] | 41 | 0.70 | 0.83 | 0.72 | 0.41 | 73.7 | 62.0 | 84.9 | 80.4 |
| Acetone | 452 | FSTI-XGB | 31 | 0.616 | 0.702 | 0.633 | 0.558 | 78.9 | 71.4 | 88.9 | 83.5 |
| Methanol | 135 | FSTI-XGB | 34 | 0.689 | 0.788 | 0.715 | 0.524 | 70.7 | 66.7 | 84.8 | 86.1 |
| Method | 99% | 95% | 90% | 80% | Average of 8 Statistics | Average of All 4 Means | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CP | β | Mean | Median | Mean | Median | Mean | Median | Mean | Median | ||
| AR | - | 3.439 | 3.439 | 2.043 | 2.043 | 1.489 | 1.489 | 1.006 | 1.006 | 1.994 | 1.994 |
| ARS | 0 | 3.193 | 2.733 | 1.856 | 1.588 | 1.425 | 1.220 | 1.033 | 0.885 | 1.742 | 1.877 |
| ARS | 0.2 | 2.906 | 2.720 | 1.751 | 1.639 | 1.350 | 1.264 | 0.959 | 0.898 | 1.686 | 1.742 |
| ARS | 0.5 × Q2(σ) | 2.905 | 2.612 | 1.717 | 1.544 | 1.364 | 1.226 | 0.977 | 0.879 | 1.653 | 1.741 |
| ARSS | 0.5 × Q2(σ) | 2.806 | 2.524 | 1.744 | 1.568 | 1.390 | 1.250 | 0.993 | 0.893 | 1.646 | 1.733 |
| EM-N | 0 | 2.811 | 2.359 | 1.830 | 1.536 | 1.428 | 1.198 | 1.031 | 0.866 | 1.632 | 1.775 |
| EM-N | 0.5 × Q2(σ) | 2.657 | 2.355 | 1.735 | 1.537 | 1.350 | 1.196 | 0.971 | 0.860 | 1.583 | 1.678 |
| EM-N | 0.3 × Q2(σ) | 2.667 | 2.323 | 1.742 | 1.517 | 1.360 | 1.185 | 0.987 | 0.860 | 1.580 | 1.689 |
| EM-Log | 0.5 × Q2(σ) | 2.734 | 2.461 | 1.761 | 1.585 | 1.350 | 1.215 | 0.984 | 0.886 | 1.622 | 1.707 |
| knn-EuD | 0 | 3.454 | 2.815 | 2.167 | 1.766 | 1.633 | 1.331 | 1.125 | 0.917 | 1.901 | 2.095 |
| knn-EuD | 1× Q2(σ) | 3.123 | 2.805 | 1.968 | 1.768 | 1.489 | 1.768 | 1.022 | 0.918 | 1.858 | 1.901 |
| Confidence Level: | 99% | 95% | 90% | 80% |
|---|---|---|---|---|
| AqSolDB-w, AR(Q2), AR/CP(Q2) | 3.439, 48.0% | 2.043, 32.3% | 1.489, 20.3% | 1.006, 12.0% |
| CP, CP mean, CP(Q2) | EM-N, 2.657, 2.323 * | ARS, 1.717, 1.544 * | EM-Log, 1.342, 1.238 * | ARS, 0.959, 0.898 * |
| AqSolDB-n (int. t. set), AR, AR/CP | 2.335, 32.9% | 1.534, 27.9% | 1.176, 18.5% | 0.783, 7.1% |
| CP, CP mean, CP(Q2) | EM-N, 1.831, 1.757 * | EM-N, 1.267, 1.199 * | EM-N, 1.034, 0.992 * | ARSS, 0.755, 0.731 ** |
| AqSolDB-n (ext. t. set), AR, AR/CP | 2.335, 24.3% | 1.534, 23.9% | 1.176, 17.7% | 0.783, 6.1% |
| CP, CP mean, CP(Q2) | ARS, 1.935, 1.878 * | ARS, 1.276, 1.238 * | ARSS, 1.029, 0.999 * | ARSS, 0.751, 0.738 ** |
| Water-w (int. t. set), AR, AR/CP | 2.367, 15.5% | 1.496, 7.6% | 1.230, 8.6% | 0.918, 8.0% * |
| CP, CP mean, CP(Q2) | ARS, 2.177, 2.05 * | ARSS, 1.445, 1.391 * | EM-N, 1.155, 1.133 * | knn-EuD, 0.879, 0.85 |
| Ethanol (int. t. set), AR, AR/CP | 2.034, 17.1% | 1.361, 11.7% | 1.040, 11.1% | 0.732, 0% |
| CP, CP mean, CP(Q2) | EM-N, 1.832, 1.737 * | ARS, 1.318, 1.228 ** | EM-N, 1.014, 0.936 | AR, 0.732, 0.732 |
| Acetone int. test set, AR, AR/CP | 1.801, 3.7% | 1.344, 11.4% | 1.047, 8.8% | 0.741, 8.7% |
| CP, CP mean, CP(Q2) | ARSS, 1.797, 1.737 | EM-N, 1.240, 1.206 * | EM-N, 1.001, 0.962 | EM-N, 0.701, 0.682 ** |
| Methanol int. test set, AR, AR/CP | 2.392, 26.8% | 1.351, 11.1% | 1.194, 15.0% | 0.810, 1.1% |
| CP, CP mean, CP(Q2) | EM-N, 1.938, 1.886 * | EM-N, 1.232, 1.216 * | ARS, 1.041, 1.038 * | ARS, 0.802, 0.801 |
| LogD: AR, AR/CP (a) CP, CP(Q2) [23]: | 3.841, 32.8% EM-N, 2.892 | 2.237, 35.7% EM-N, 1.649 | 1.245, 3.8% EM-N, 1.200 | 0.843, 6.8% EM-N, 0.789 |
| Data Set | Q2(MW) | Total Size | In AD, Assessed | 80% Q2(h-w)/Mean | LogS ± 1.0 > 80% | Est. LogS ± 1.0 * |
|---|---|---|---|---|---|---|
| AqSolDB-n | 186.6 | 1619 | 900 (ext. test set) | 0.738/0.751 | 93.3% | 85.3% (true) |
| DrugBank | 338.2 | 11,370 | 10,413 | 0.888/0.906 | 73.6% | 82.8% |
| PubChem | 323.4 | 72,739 | 68,535 | 0.885/0.912 | 75.4% | 82.7% |
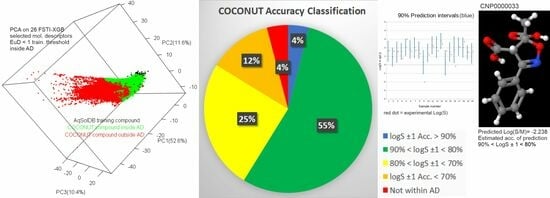
| COCONUT | 390.5 | 406,919 | 356,277 | 0.918/0.946 | 66.9% | 81.7% |
| Data set | Q2(MW) | In AD | Assessed (MW) | 80% Q2(h-w)/mean | LogS ± 1.0 > 80% | Est. LogS ± 1.0 * |
| AqSolDB-w | 232.2 | 9709 | 1611 (int. test) | 0.860/0.971 | 65.51% | 80.0% (true) |
| DrugBank | 340.4 | 11,130 | 717 (585.9) | 1.478/1.493 | 22.6% | 63.3% |
| PubChem | 329.8 | 71,808 | 3273 (689.0) | 1.779/1.790 | 1.25% | 55.3% |
| COCONUT | 406.4 | 390,338 | 34,061 (863.3) | 1.491/1.546 | 2.86% | 61.7% |
| Drugbank | PubChem | COCONUT | ||||
| Final estimated LogS ±1.0 (Aq-n + Aq-w): * | 81.6% | 81.5% | 79.9% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jovic, O.; Mouras, R. Extreme Gradient Boosting Combined with Conformal Predictors for Informative Solubility Estimation. Molecules 2024, 29, 19. https://doi.org/10.3390/molecules29010019
Jovic O, Mouras R. Extreme Gradient Boosting Combined with Conformal Predictors for Informative Solubility Estimation. Molecules. 2024; 29(1):19. https://doi.org/10.3390/molecules29010019
Chicago/Turabian StyleJovic, Ozren, and Rabah Mouras. 2024. "Extreme Gradient Boosting Combined with Conformal Predictors for Informative Solubility Estimation" Molecules 29, no. 1: 19. https://doi.org/10.3390/molecules29010019
APA StyleJovic, O., & Mouras, R. (2024). Extreme Gradient Boosting Combined with Conformal Predictors for Informative Solubility Estimation. Molecules, 29(1), 19. https://doi.org/10.3390/molecules29010019