Size-Independent Nucleation and Growth Model of Potassium Sulfate from Supersaturated Solution Produced by Stirred Crystallization
Abstract
:1. Introduction
2. Result and Discussion
2.1. Primary Nucleation Kinetics
2.1.1. Crystal Morphology
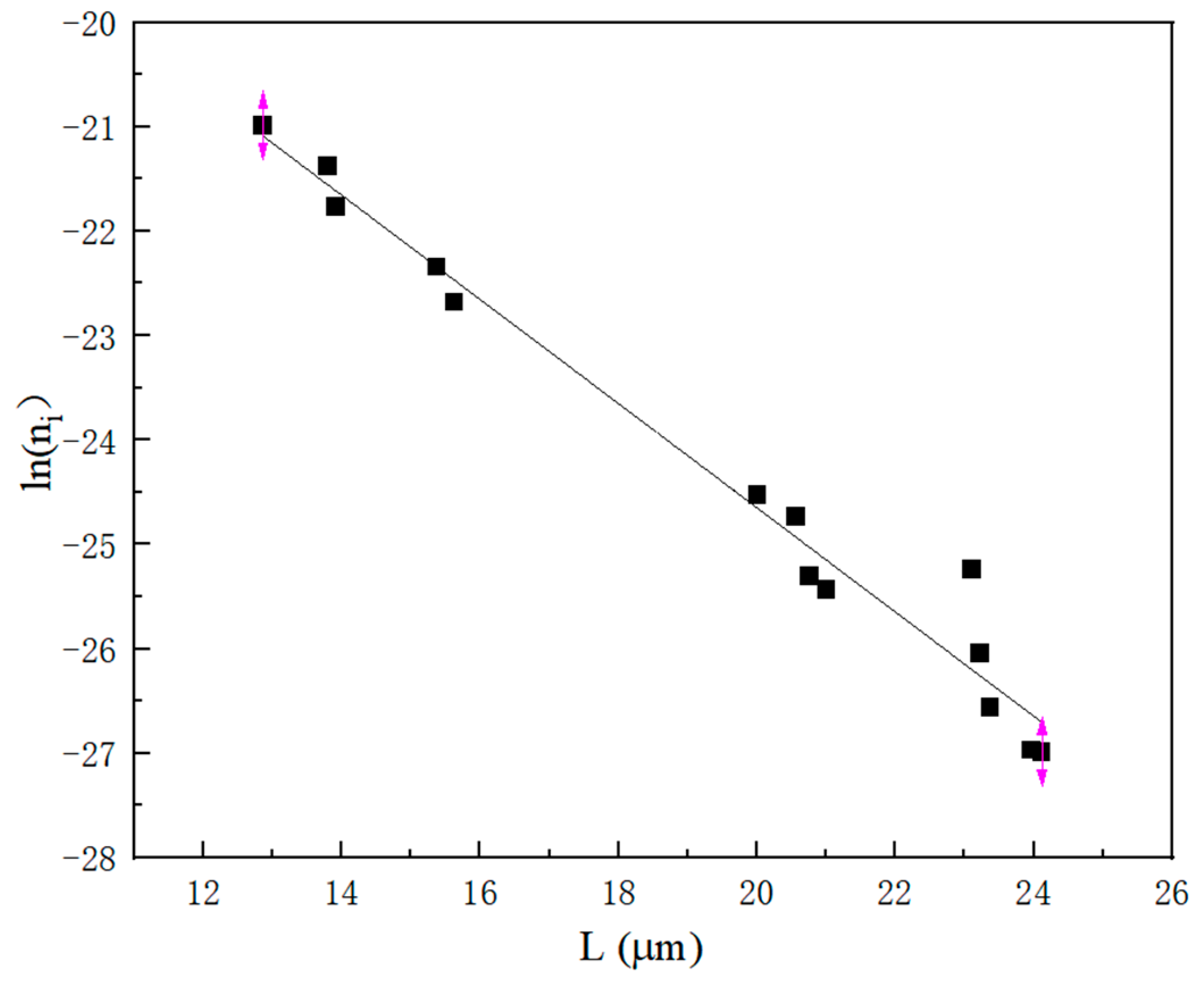
2.1.2. Nucleation Mechanism
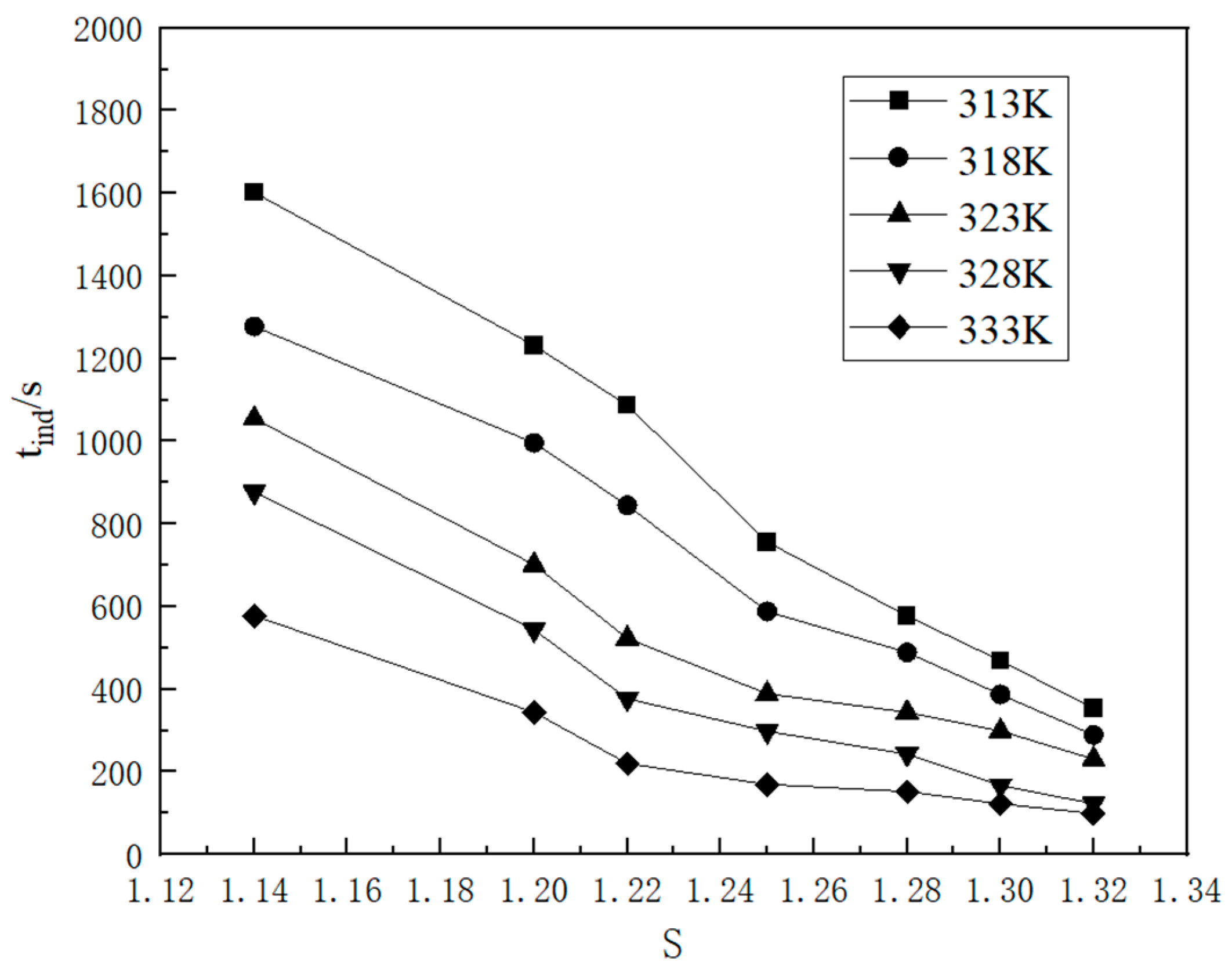
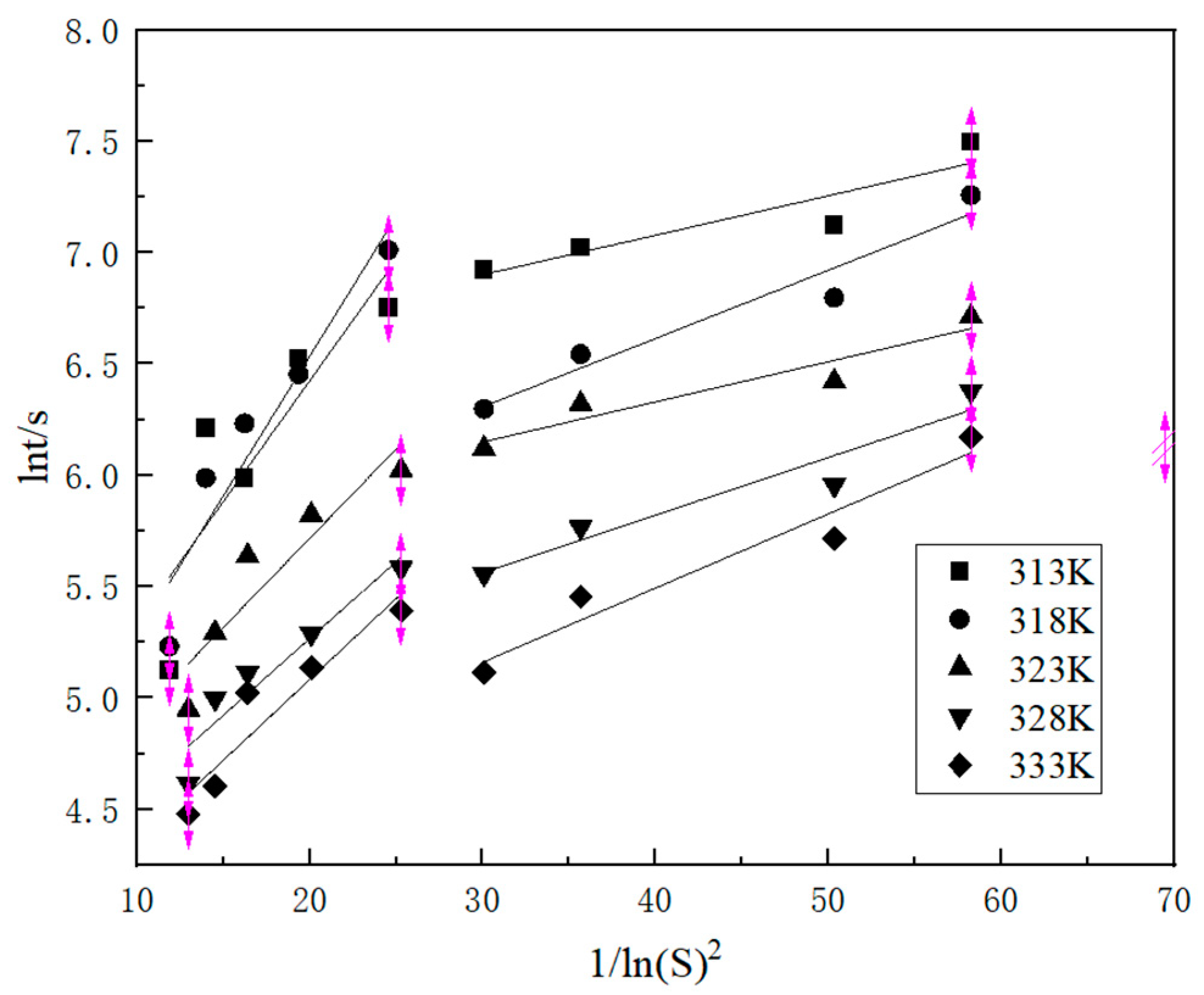
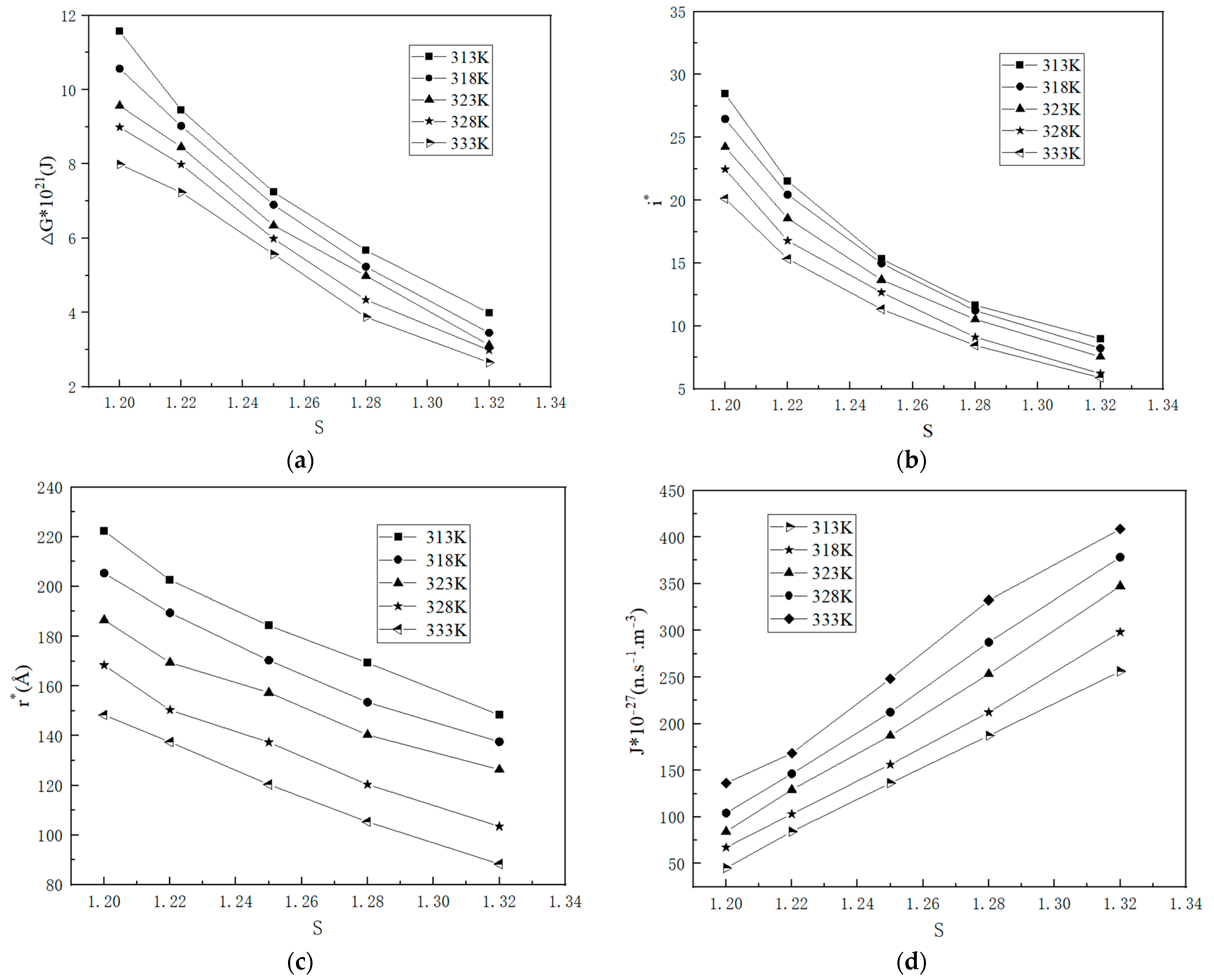
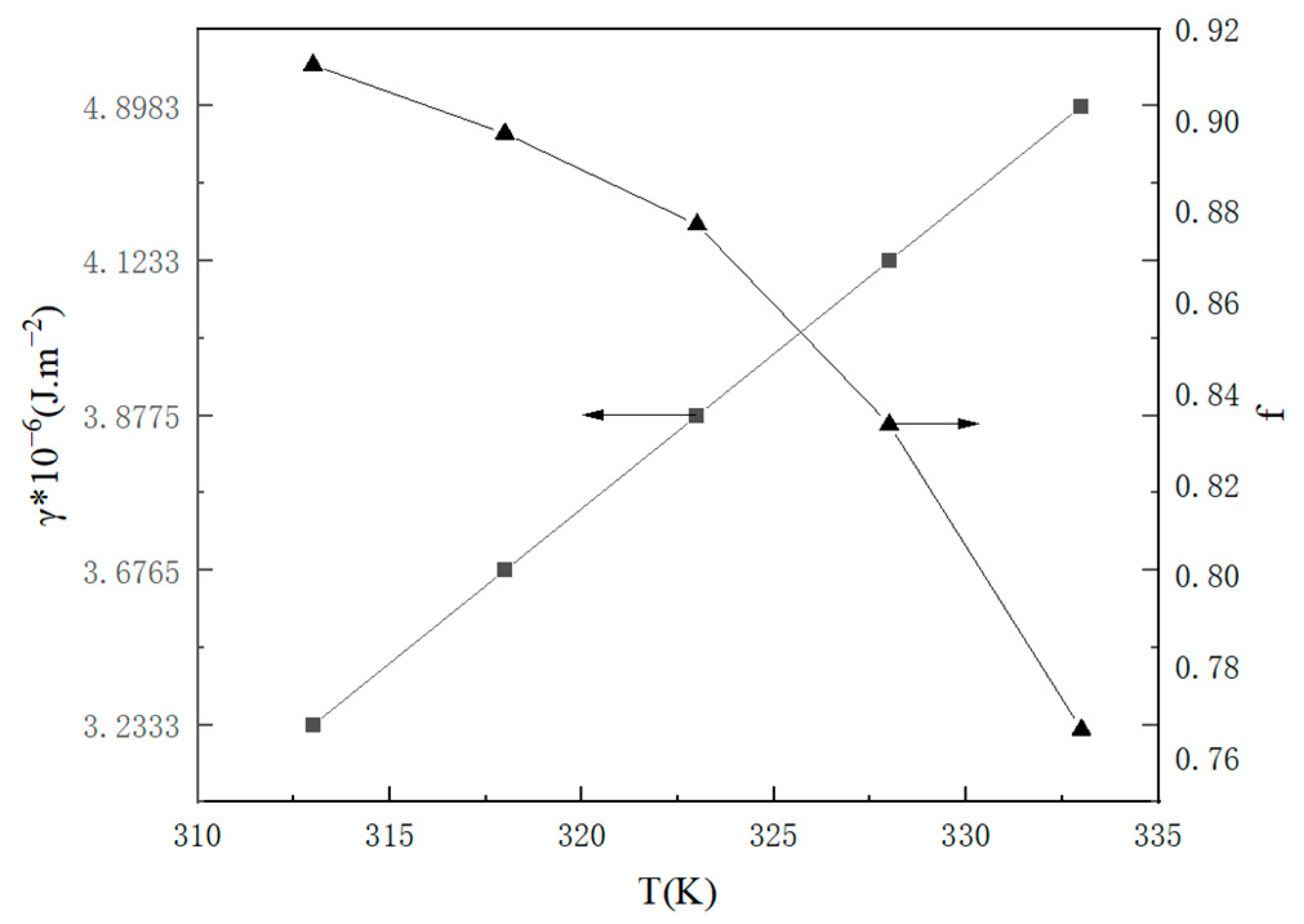
2.1.3. Nucleation Parameters
2.2. Stirring Crystallization Kinetics
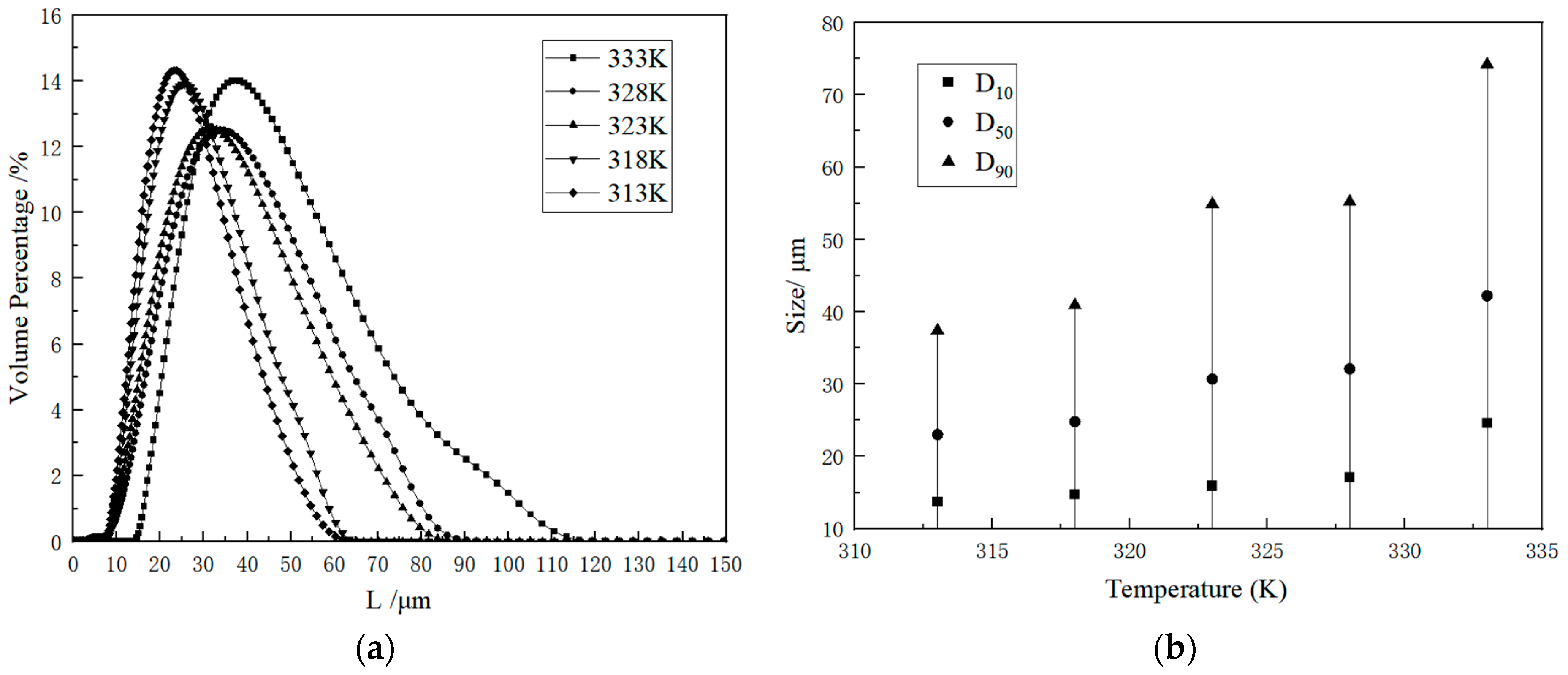
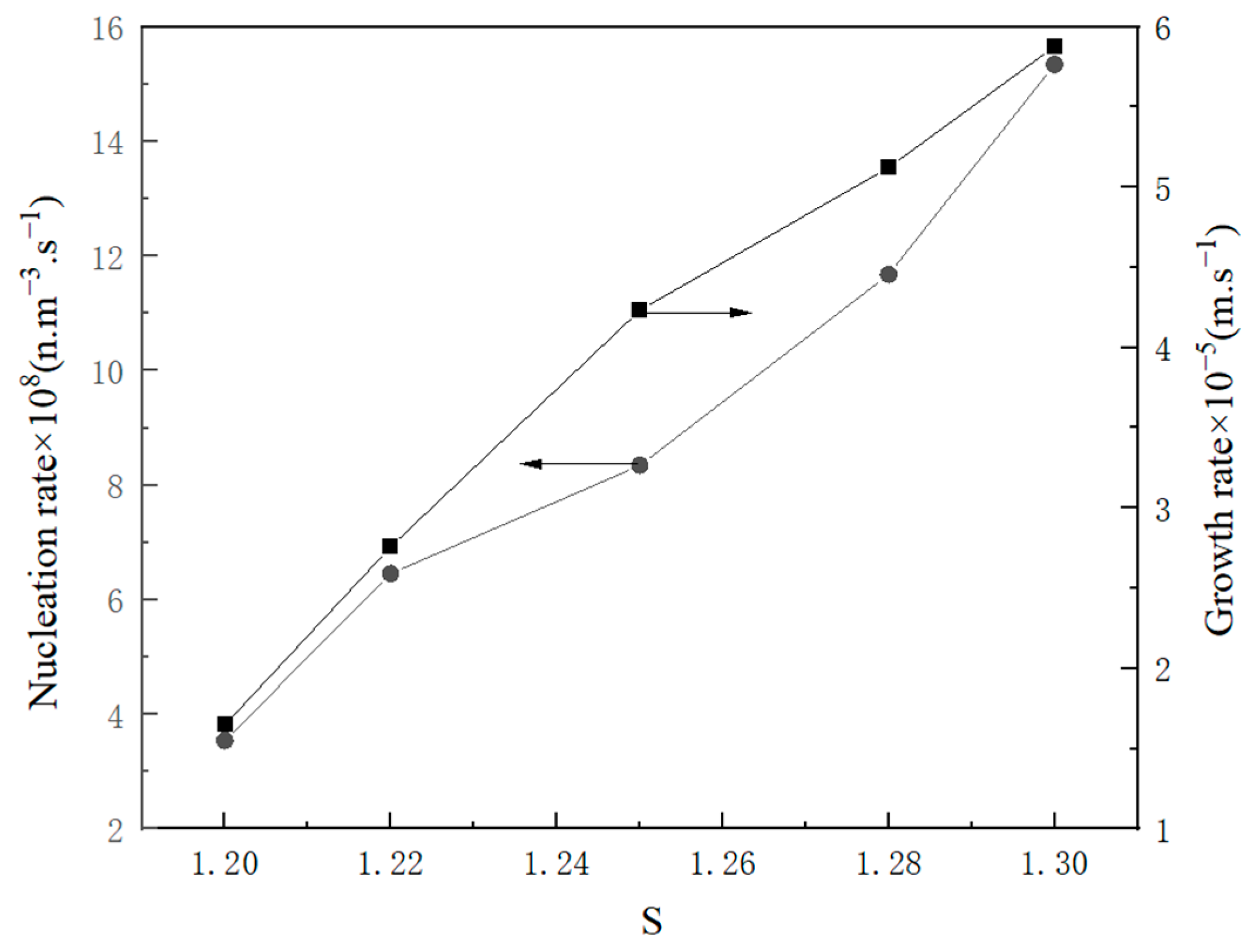
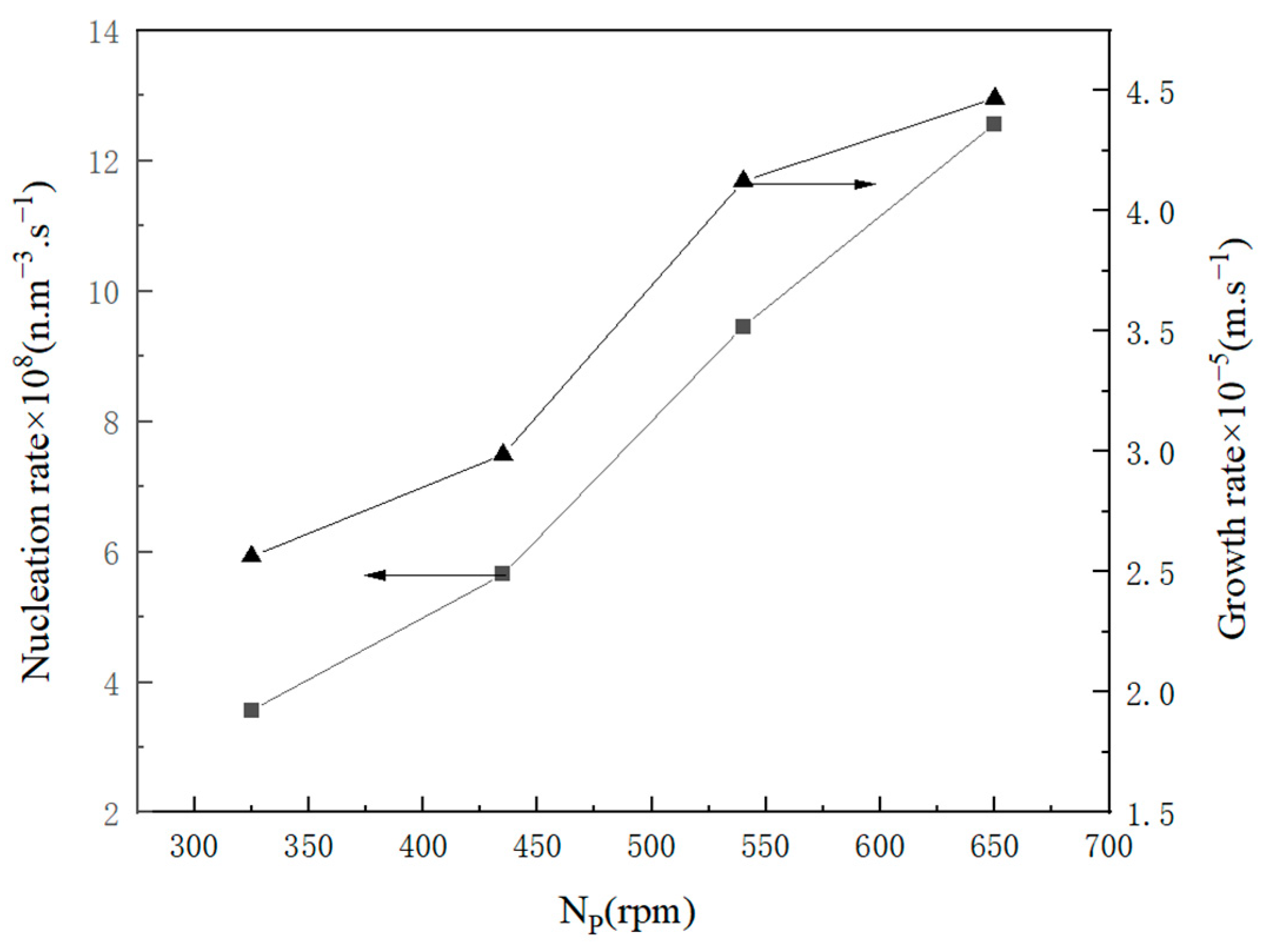
2.2.1. Kinetic Data
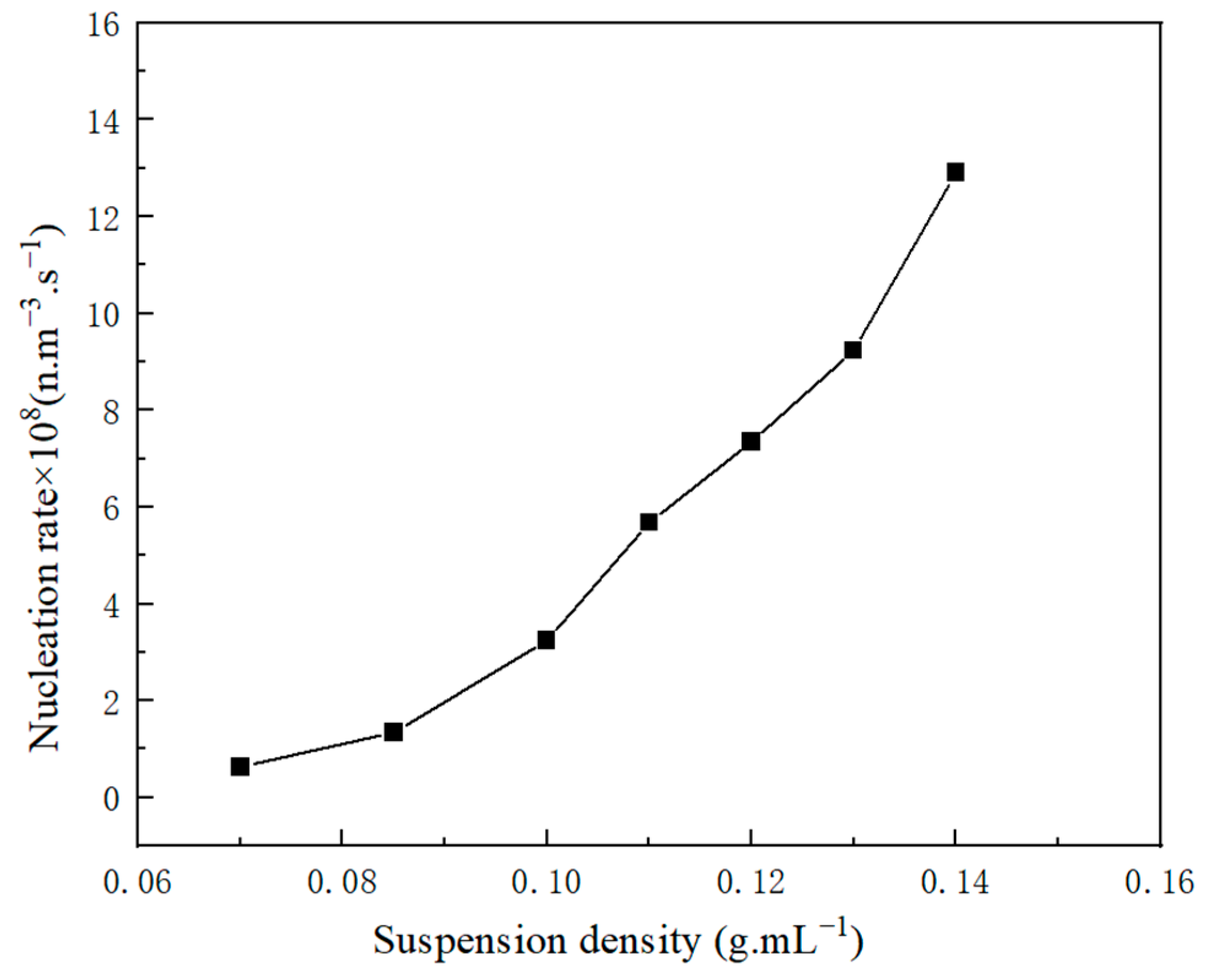
2.2.2. Influence Factor
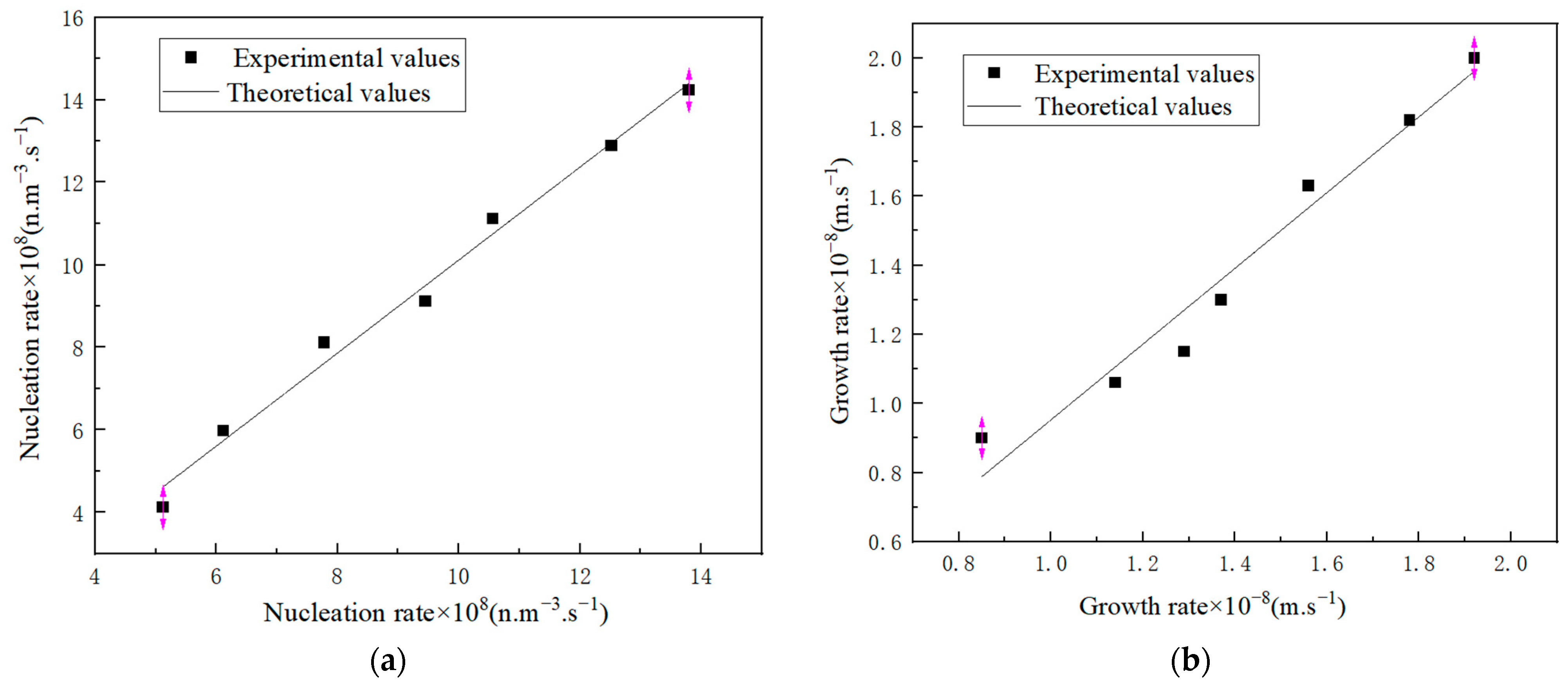
2.2.3. Statistical Analysis of Crystal Parameters
3. Material and Methods
3.1. Materials
3.1.1. Experimental Procedure
3.1.2. SEM
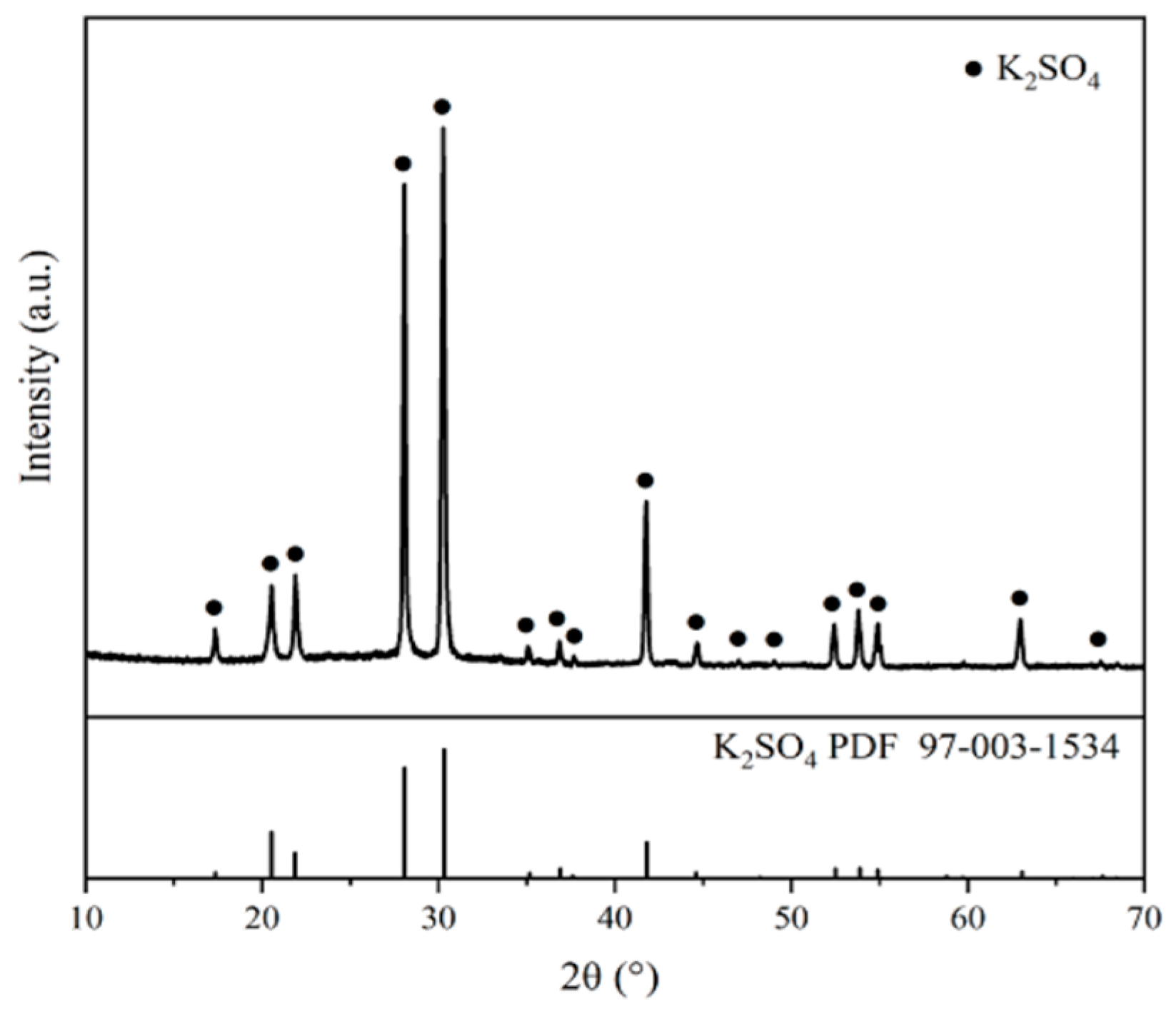
3.1.3. XRD
3.2. Mathematical Modeling
3.2.1. Population Balance Equations (PBEs)
3.2.2. Nucleation and Growth
3.2.3. Nucleation Theory
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jones, A.G.; Budz, J.; Mullin, J.W. Crystallization kinetics of potassium sulfate in an MSMPR agitated vessel. AIChE J. 1986, 32, 2002–2009. [Google Scholar] [CrossRef]
- Randolph, A.D.; Rajagopal, K. Direct Measurement of Crystal Nucleation and Growth Rate Kinetics in Backmixed Crystal Slurry. Study of the K2SO4System. Ind. Eng. Chem. Res. 1970, 9, 165–171. [Google Scholar] [CrossRef]
- Cournil, M.; Gohar, P. Thermodynamic model of supersaturated liquid solutions: Application to the homogeneous nucleation of potassium sulfate. J. Colloid Interface Sci. 1989, 132, 188–199. [Google Scholar] [CrossRef]
- Randolph, A.D.; Cise, M.D. Nucleation kinetics of the potassium sulfate-water system. AIChE J. 1972, 18, 798–807. [Google Scholar] [CrossRef]
- Zheng, D.; Zou, W.; Peng, C.; Fu, Y.; Yan, J.; Zhang, F. CFD-PBM Coupled Simulation of Liquid-Liquid Dispersions in Spray Fluidized Bed Extractor: Comparison of Three Numerical Methods. Int. J. Chem. Eng. 2019, 2019, 4836213. [Google Scholar] [CrossRef]
- Zheng, D.; Huang, T.H.; Yan, J.; Yang, H.; Peng, C.; Fu, Y.; Li, B. Coupling of abrasion attrition theory with mechanical characteristics for particle attrition in fluidized bed reactor. Asia-Pac. J. Chem. Eng. 2020, 15, 2544. [Google Scholar] [CrossRef]
- Zheng, D.; Li, J.; Jin, Y.; Zou, D.; Zhu, X. Coupling of CFD with PBM for growth behavior of potassium sulphate in spray fluidized-bed crystallizer. Powder Technol. 2017, 314, 427–441. [Google Scholar] [CrossRef]
- Kobari, M.; Kubota, N.; Hirasawa, I. Computer simulation of metastable zone width for unseeded potassium sulfate aqueous solution. J. Cryst. Growth 2011, 317, 64–69. [Google Scholar] [CrossRef]
- Nemdili, L.; Koutchoukali, O.; Mameri, F.; Gouaou, I.; Koutchoukali, M.S.; Ulrich, J. Crystallization study of potassium sulfate-water system, metastable zone width and induction time measurements using ultrasonic, turbidity and 3D-ORM techniques-ScienceDirect. J. Cryst. Growth 2018, 500, 44–51. [Google Scholar] [CrossRef]
- Tseng, Y.T. Determination of Critical Seed Loading From Nucleation Kinetics. AIChE J. 2014, 60, 1645–1653. [Google Scholar] [CrossRef]
- Botsaris, G.D.; Qian, R.-Y.; Barrett, A. New insights into nucleation through chiral crystallization. AIChE J. 1999, 45, 201–203. [Google Scholar] [CrossRef]
- Sung, C.Y.; Estrin, J.; Youngquist, G.R. Secondary nucleation of magnesium sulfate by fluid shear. AIChE J. 1973, 19, 957–962. [Google Scholar] [CrossRef]
- Garside, J.; Larson, M. Direct observation of secondary nuclei production. J. Cryst. Growth 1978, 43, 694–704. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Jin, Y.; Luo, J.; Chen, M.; Yan, C. Mixing efficiency of a rotor-stator spinning disc extractor. Chem. Eng. J. 2019, 362, 357–363. [Google Scholar] [CrossRef]
- Hulburt, H.; Katz, S. Some problems in particle technology: A statistical mechanical formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Giulietti, M.; Seckler, M.; Derenzo, S.; Ré, M.; Cekinski, E. Industrial crystallization and precipitation from solutions: State of the technique. Braz. J. Chem. Eng. 2001, 18, 423–440. [Google Scholar] [CrossRef]
- Gordon, R.G. Error bounds in equilibrium statistical mechanics. J. Math. Phys. 1968, 9, 655–663. [Google Scholar] [CrossRef]
- Li, X.; Song, X.; Liu, G. Size-dependent nucleation and growth kinetics model for KCI—Application in Qarhan salt lake. J. Cryst. Growth 2009, 311, 3167–3173. [Google Scholar] [CrossRef]
- Peng, H.; Vaughan, J. Aluminate effect on desilication product phase transformation. J. Cryst. Growth 2018, 492, 84–91. [Google Scholar] [CrossRef]
- Kuldipkumar, A.; Kwon, G.S.; Zhang, G.G.Z. Determining the growth mechanism of tolazamide by induction time measurement. Cryst. Growth Des. 2007, 7, 234–242. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Fujiwara, M.; Woo, X.Y.; Braatz, R.D. Determination of the kinetic parameters for the crystallization of paracetamol from water using metastable zone width experiments. Ind. Eng. Chem. Res. 2008, 47, 1245–1252. [Google Scholar] [CrossRef]
- Liu, X.J.; Xu, D.; Ren, M.J.; Zhang, G.H.; Wei, X.Q.; Wang, J. An examination of the growth kinetics of L-arginine trifluoroacetate(LATF) crystals from induction period and atomic force microscopy investigations. Cryst. Growth Des. 2010, 10, 3442–3447. [Google Scholar] [CrossRef]
- Xu, S.; Chen, Y.; Gong, J.; Wang, J. Interplay between kinetics and thermodynamics on the probability nucleation rate of a urea—Water crystallization system. Cryst. Growth Des. 2018, 18, 2305–2315. [Google Scholar] [CrossRef]
- Yu, J.; Li, A.; Chen, X.; Chen, Y.; Xie, J.; Wu, J.; Ying, H. Experimental determination of metastable zone width, induction period, and primary nucleation kinetics of cytidine 5′-monophosphate disodium salt in an ethanol-aqueous mixture. J. Chem. Eng. Data 2013, 58, 1244–1248. [Google Scholar] [CrossRef]
- White, E.T.; Bending, L.L.; Larson, M.A. The effect of size on the growth rate of potassium sulphate crystals. AIChE J. Symp. Ser. 1976, 72, 41. [Google Scholar]
- Fytopoulos, A.A.; Kavousanakis, M.E.; Van Gerven, T.; Boudouvis, A.G.; Stefanidis, G.D.; Xiouras, C. Crystal Growth, Dissolution, and Agglomeration Kinetics of Sodium Chlorate. Ind. Eng. Chem. Res. 2021, 60, 7367–7384. [Google Scholar] [CrossRef]
- Lopes, A.; Farelo, F. Growth kinetics of potassium chloride, I: Pure aqueous solutions. J. Cryst. Growth 2006, 290, 213–219. [Google Scholar] [CrossRef]





| Coefficients | Nucleation Rate (B0) | Growth Rate (G) |
|---|---|---|
| kB | 7.344 × 106 | |
| kG | 3.233 × 10−6 | |
| E | 1.4555 × 104 | 5.433 × 103 |
| i | 0.3445 | |
| j | 1.6522 | |
| k | 1.9876 | |
| m | 0.4655 | |
| n | 0.7455 | |
| R2 | 0.989 | 0.978 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y. Size-Independent Nucleation and Growth Model of Potassium Sulfate from Supersaturated Solution Produced by Stirred Crystallization. Molecules 2024, 29, 141. https://doi.org/10.3390/molecules29010141
Zheng Y. Size-Independent Nucleation and Growth Model of Potassium Sulfate from Supersaturated Solution Produced by Stirred Crystallization. Molecules. 2024; 29(1):141. https://doi.org/10.3390/molecules29010141
Chicago/Turabian StyleZheng, Yayuan. 2024. "Size-Independent Nucleation and Growth Model of Potassium Sulfate from Supersaturated Solution Produced by Stirred Crystallization" Molecules 29, no. 1: 141. https://doi.org/10.3390/molecules29010141
APA StyleZheng, Y. (2024). Size-Independent Nucleation and Growth Model of Potassium Sulfate from Supersaturated Solution Produced by Stirred Crystallization. Molecules, 29(1), 141. https://doi.org/10.3390/molecules29010141








