Theoretical Study of Phase Behaviors of Symmetric Linear B1A1B2A2B3 Pentablock Copolymer
Abstract
1. Introduction
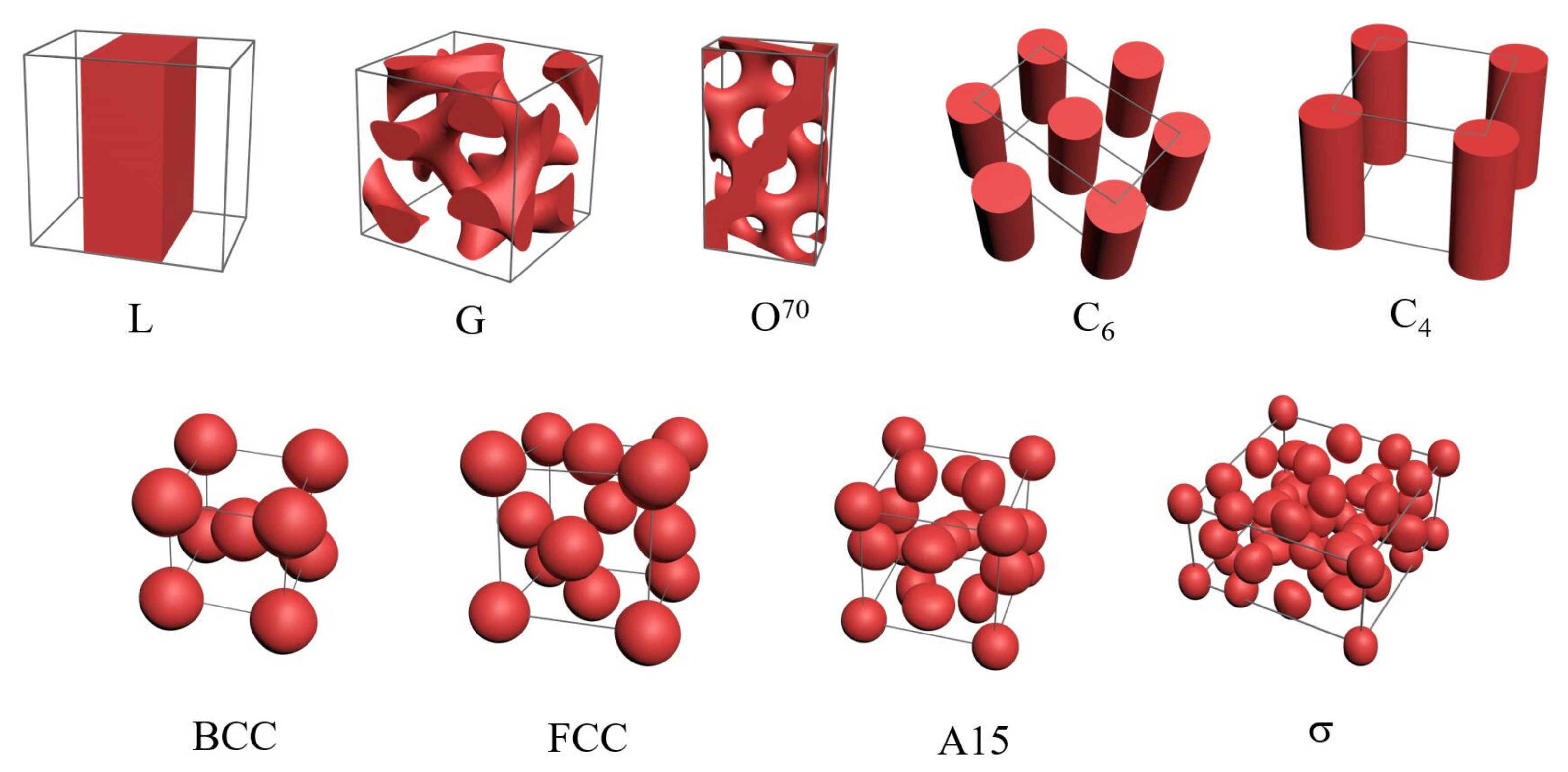
2. Result and Discussion
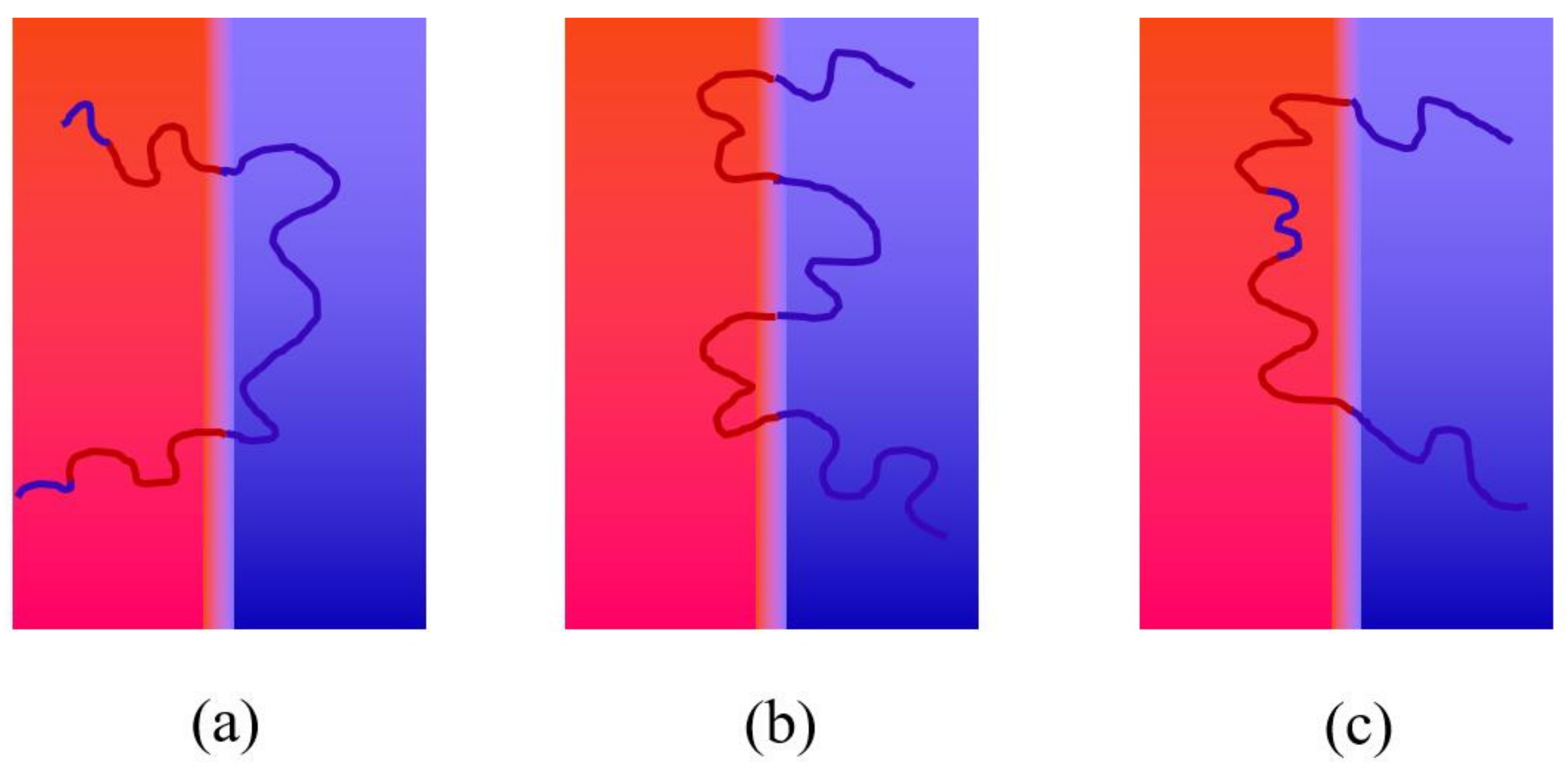
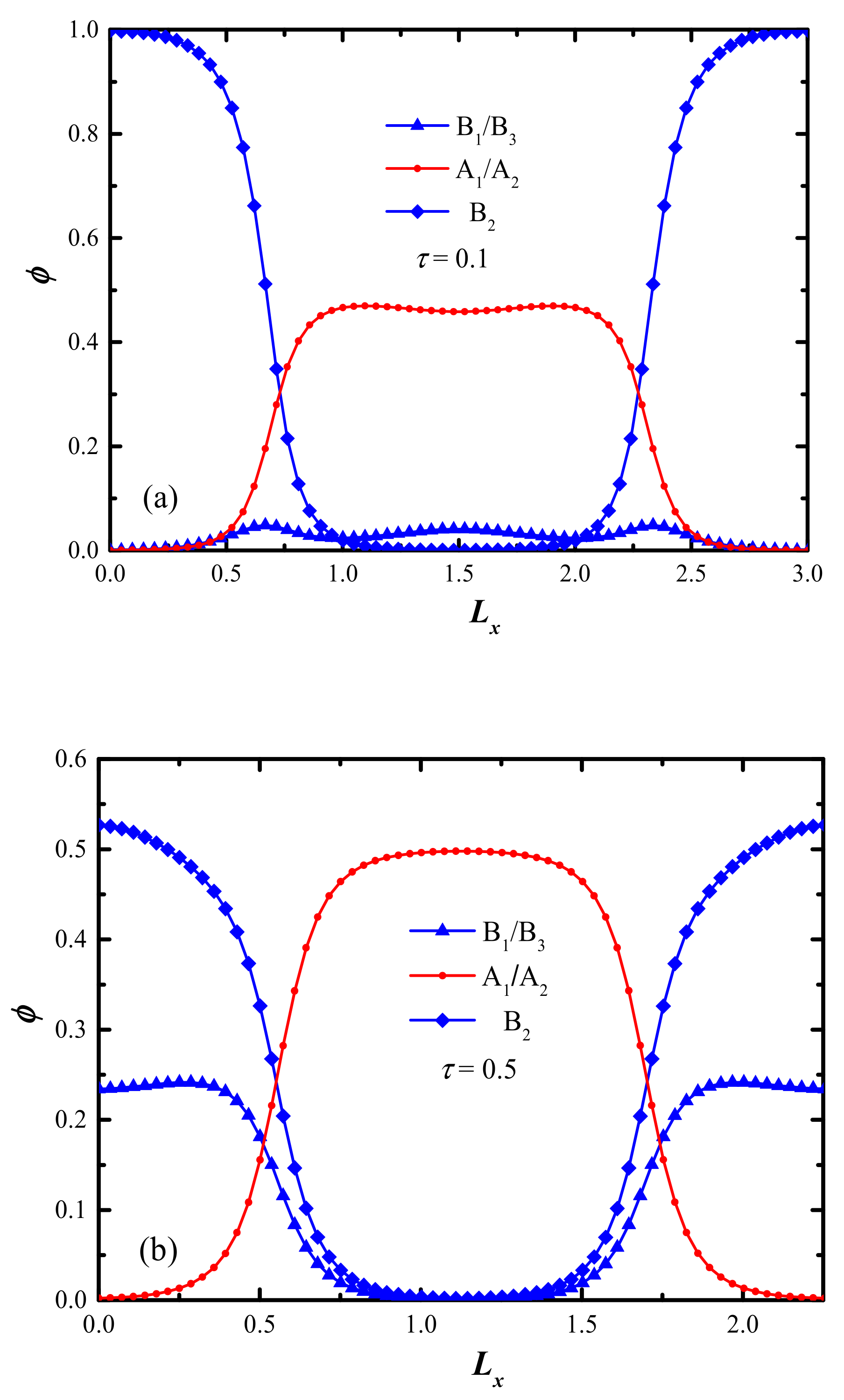
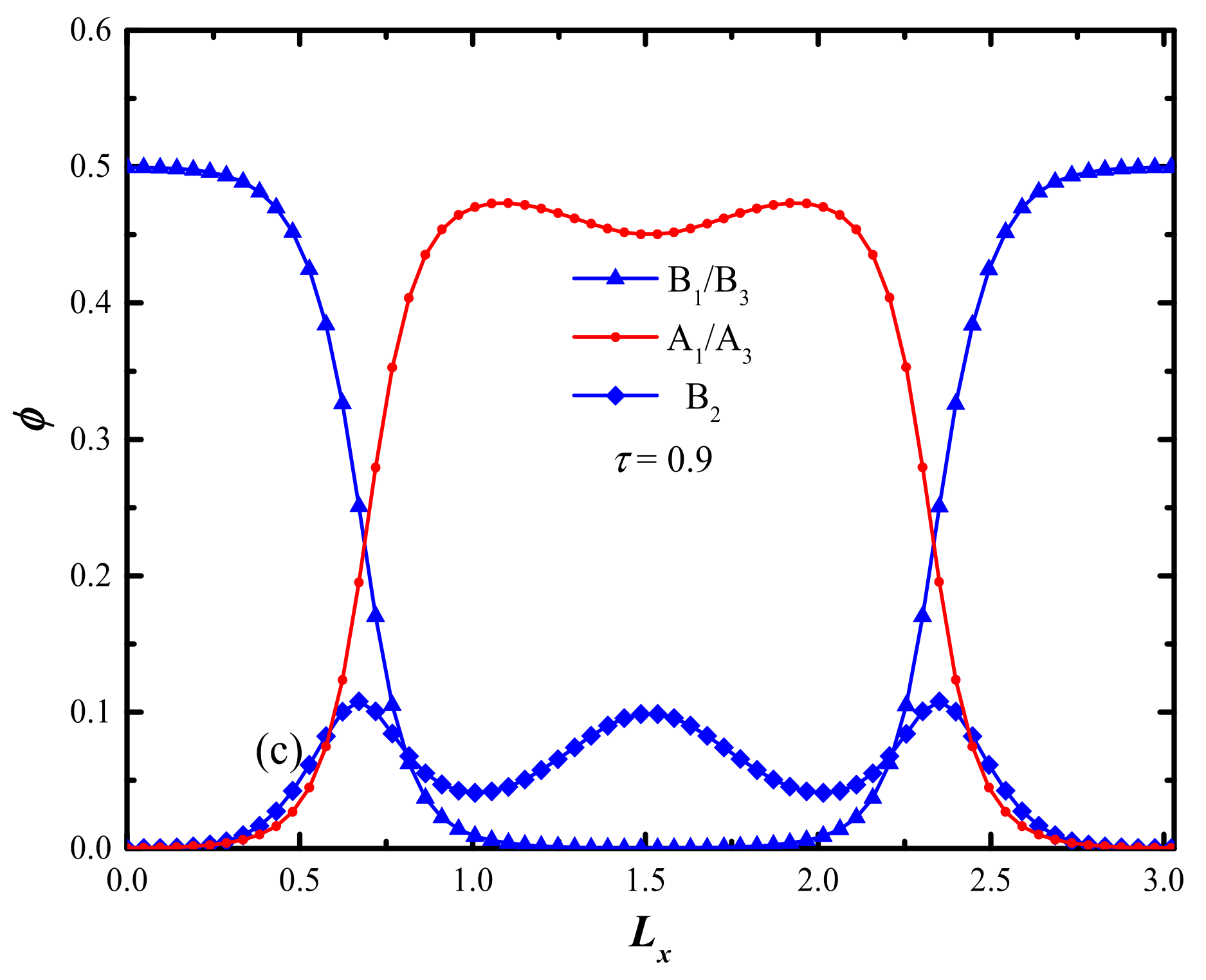
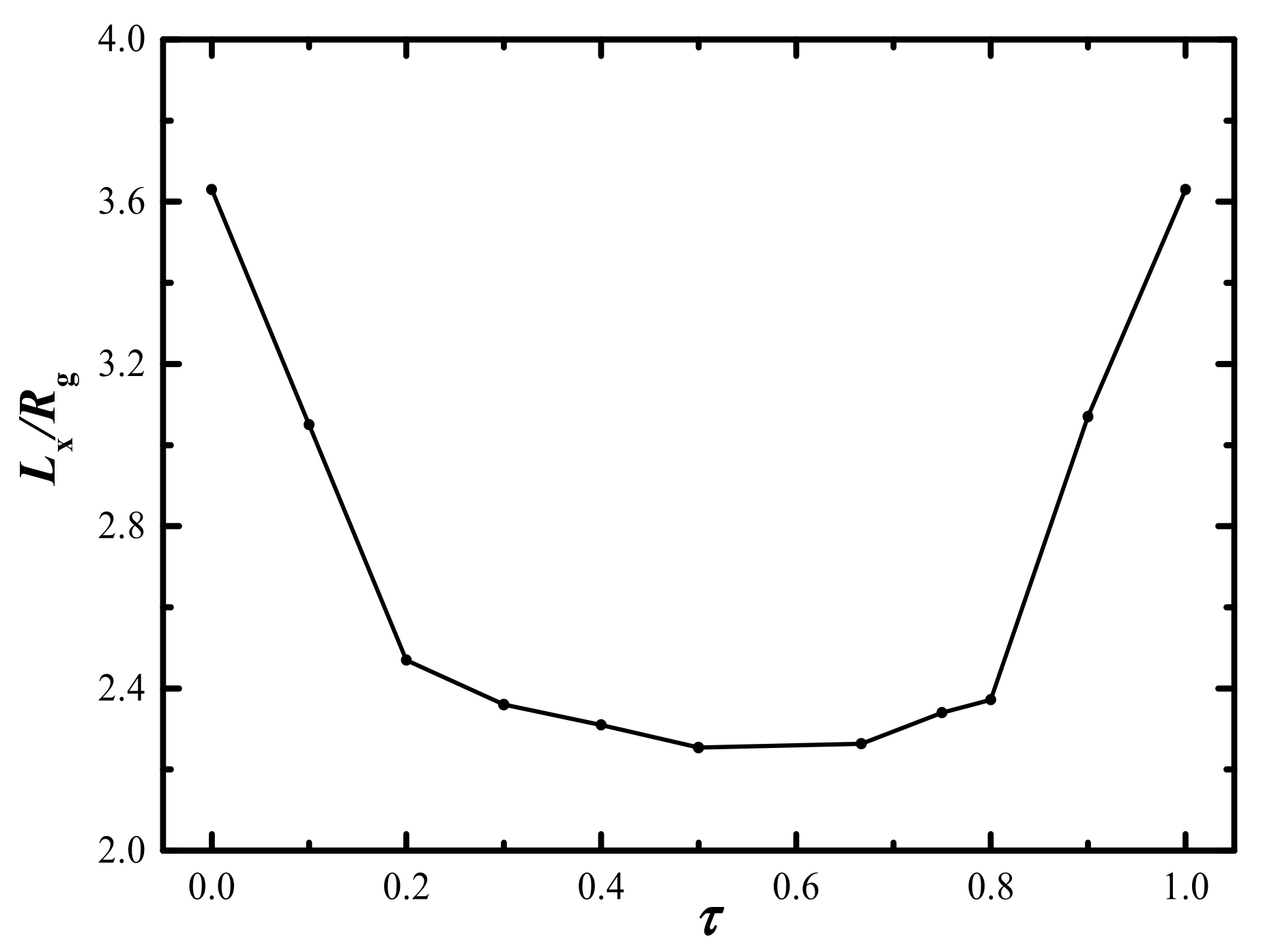
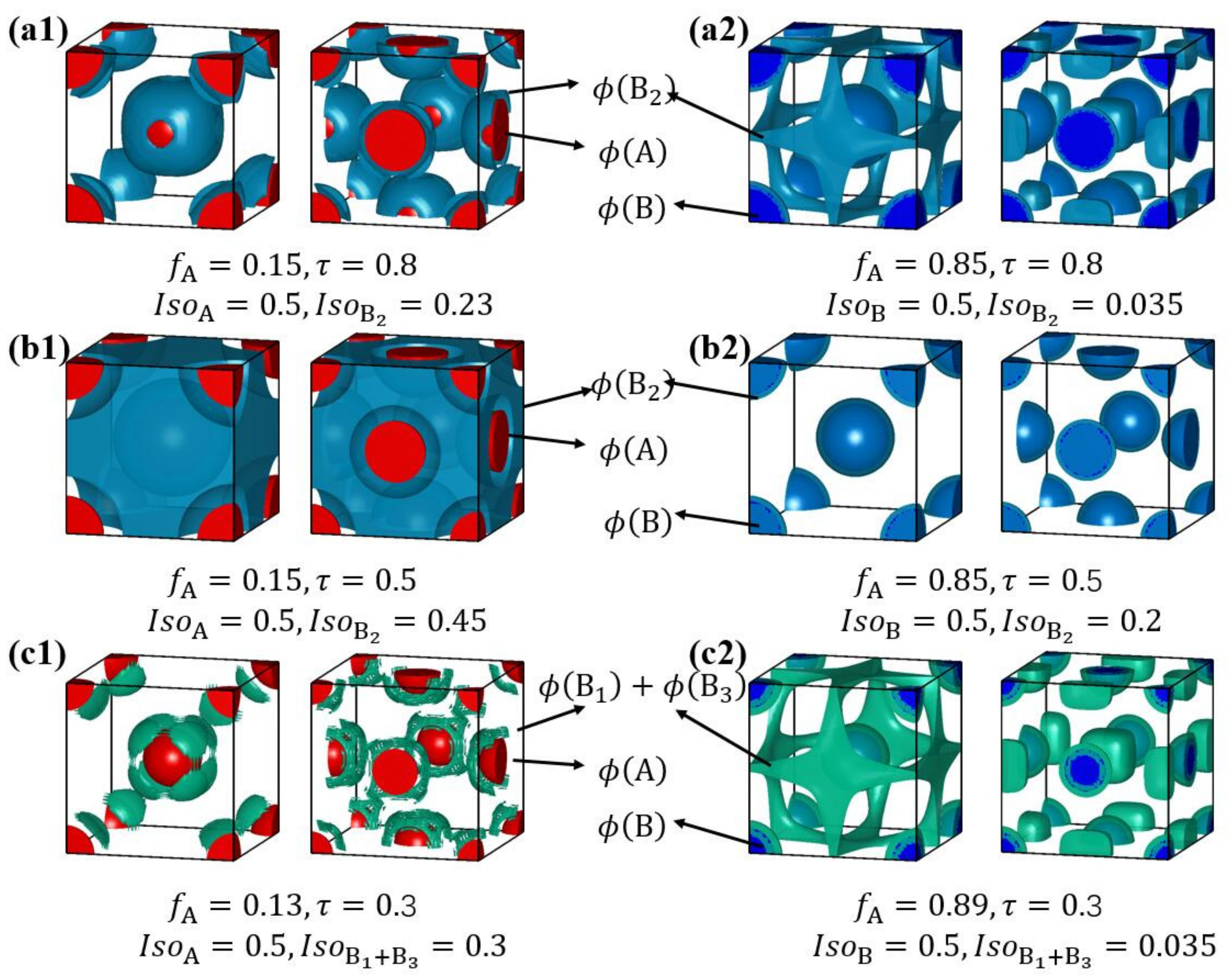
2.1. Effect of Length Ratio of B2-Block on the Formation of L Structure
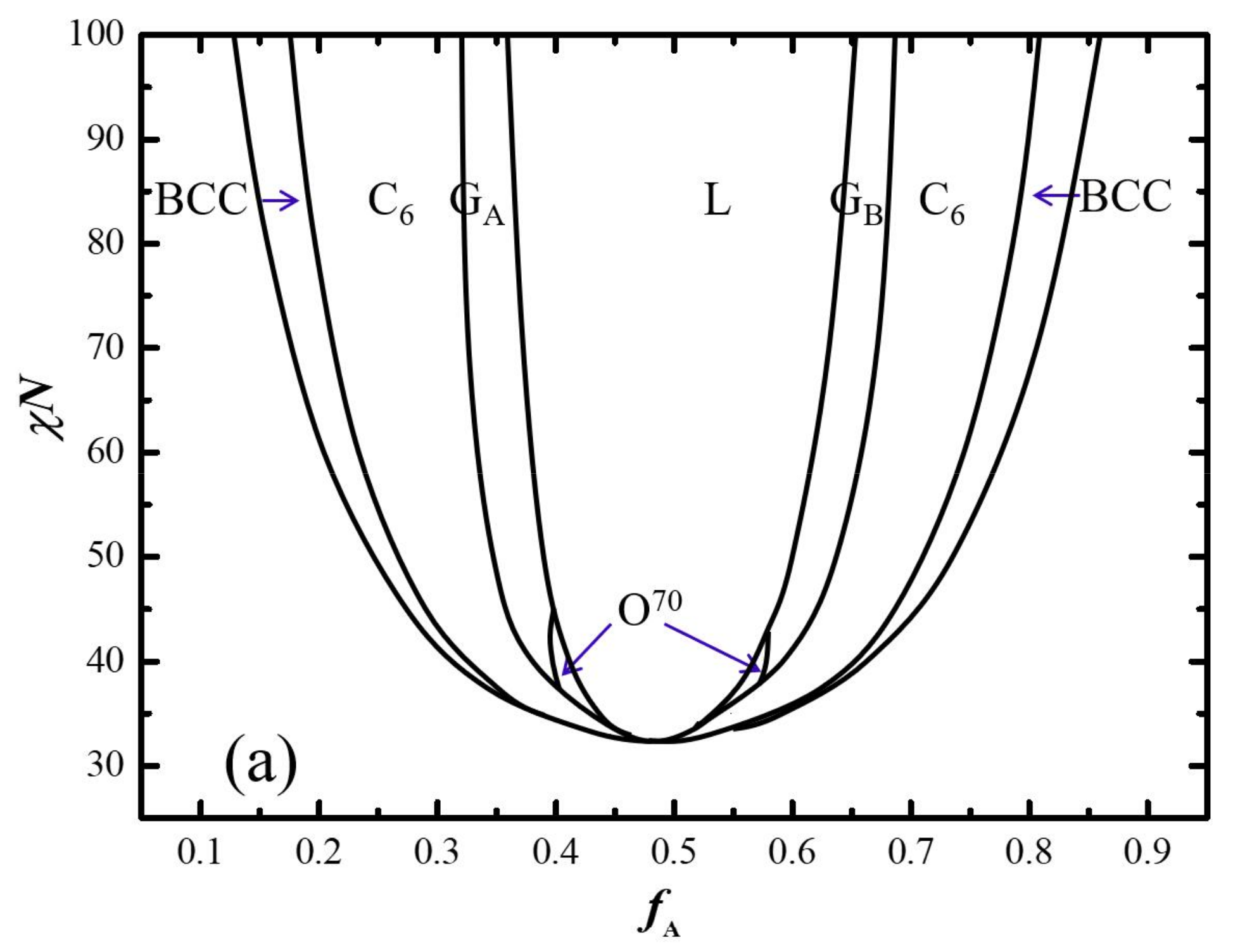
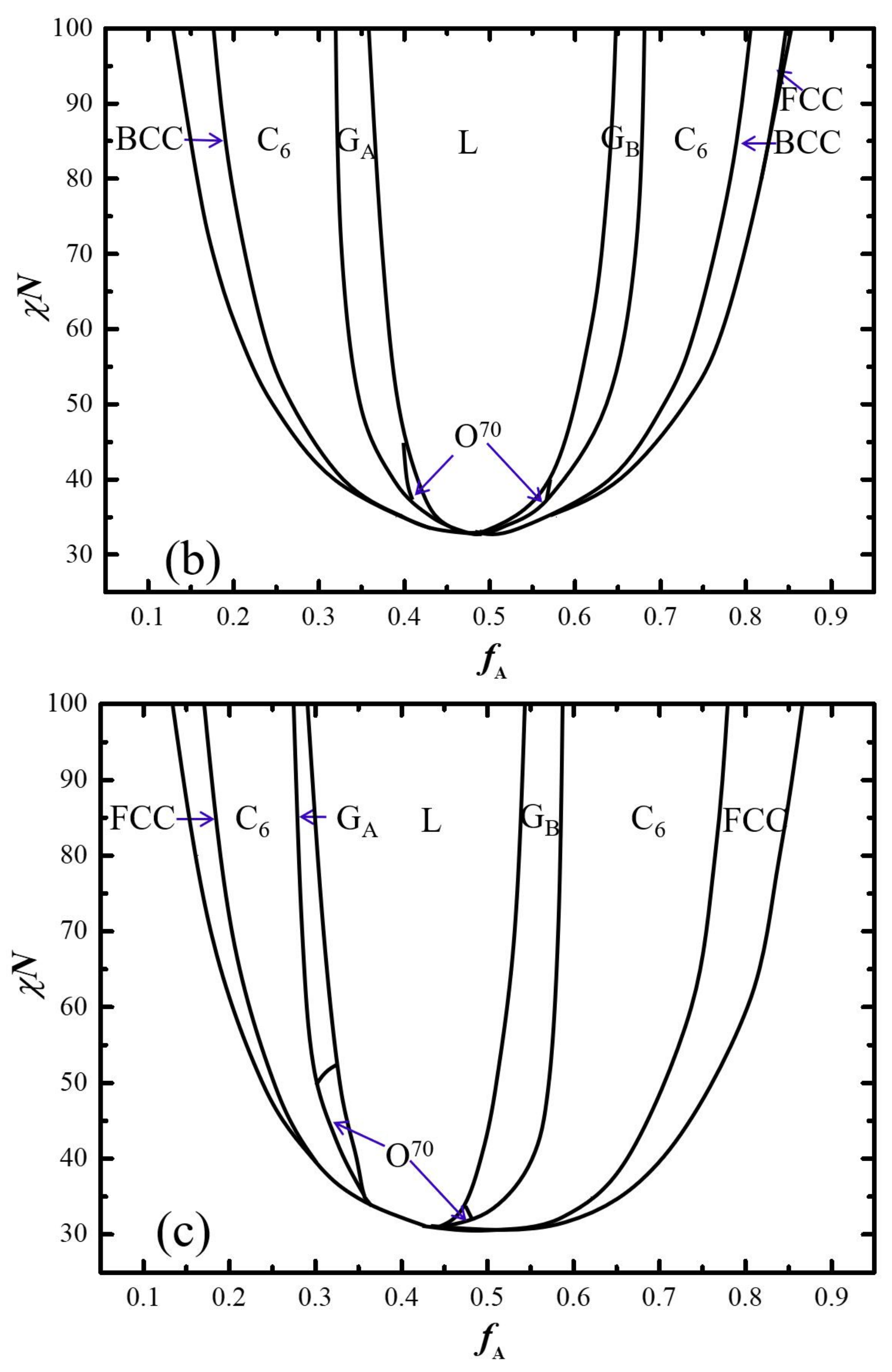
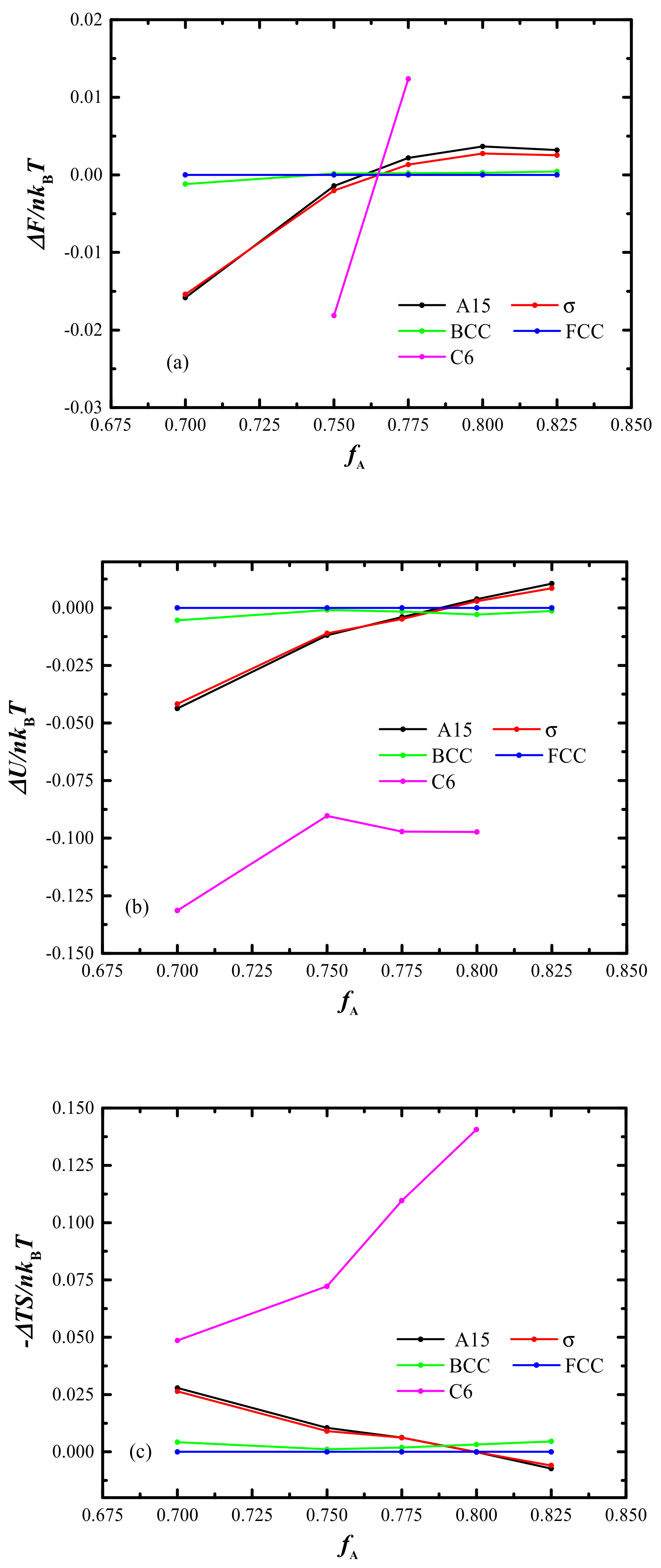
2.2. Phase Diagram in fA-χN Plane with Three Typical τ
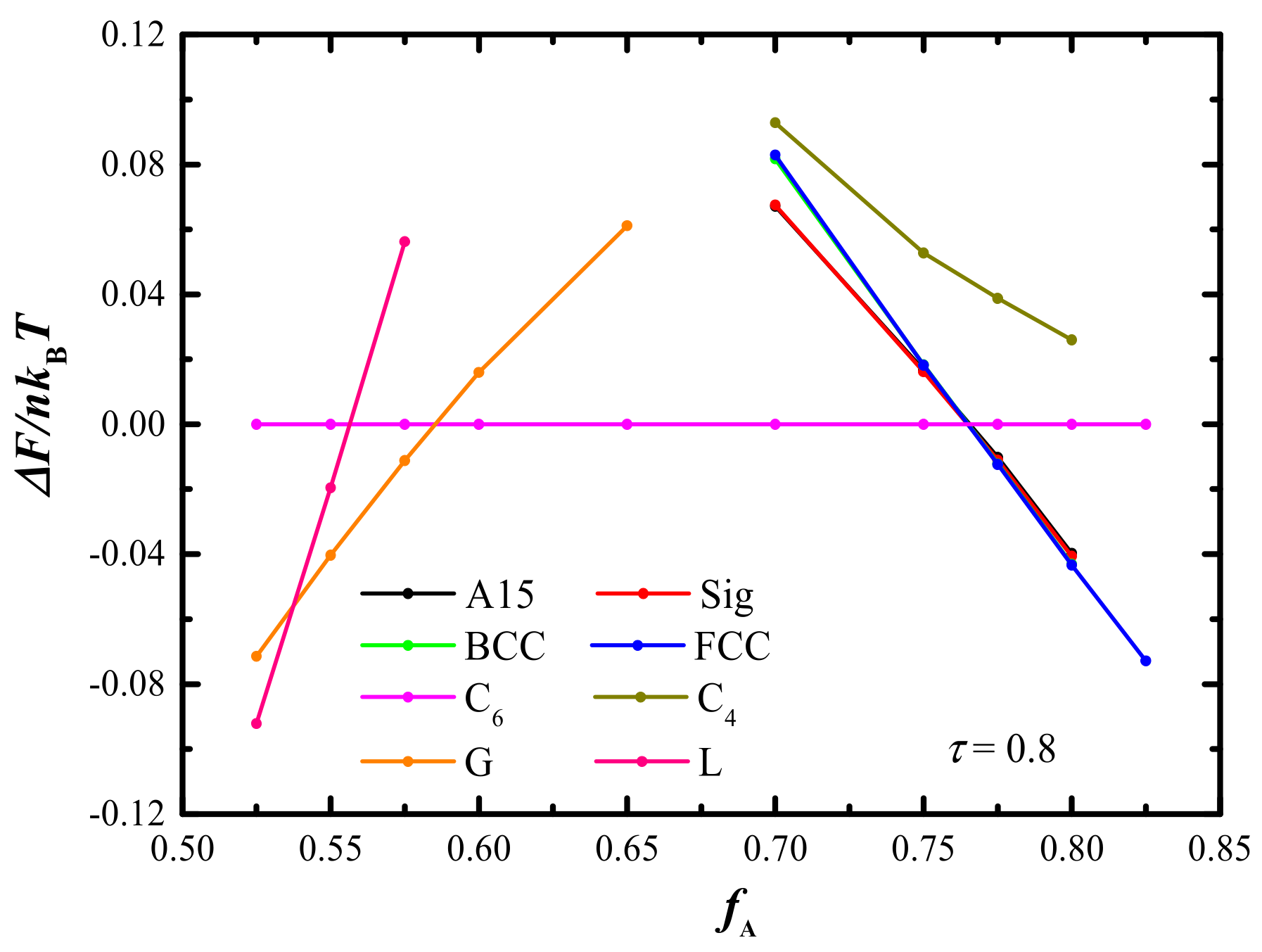
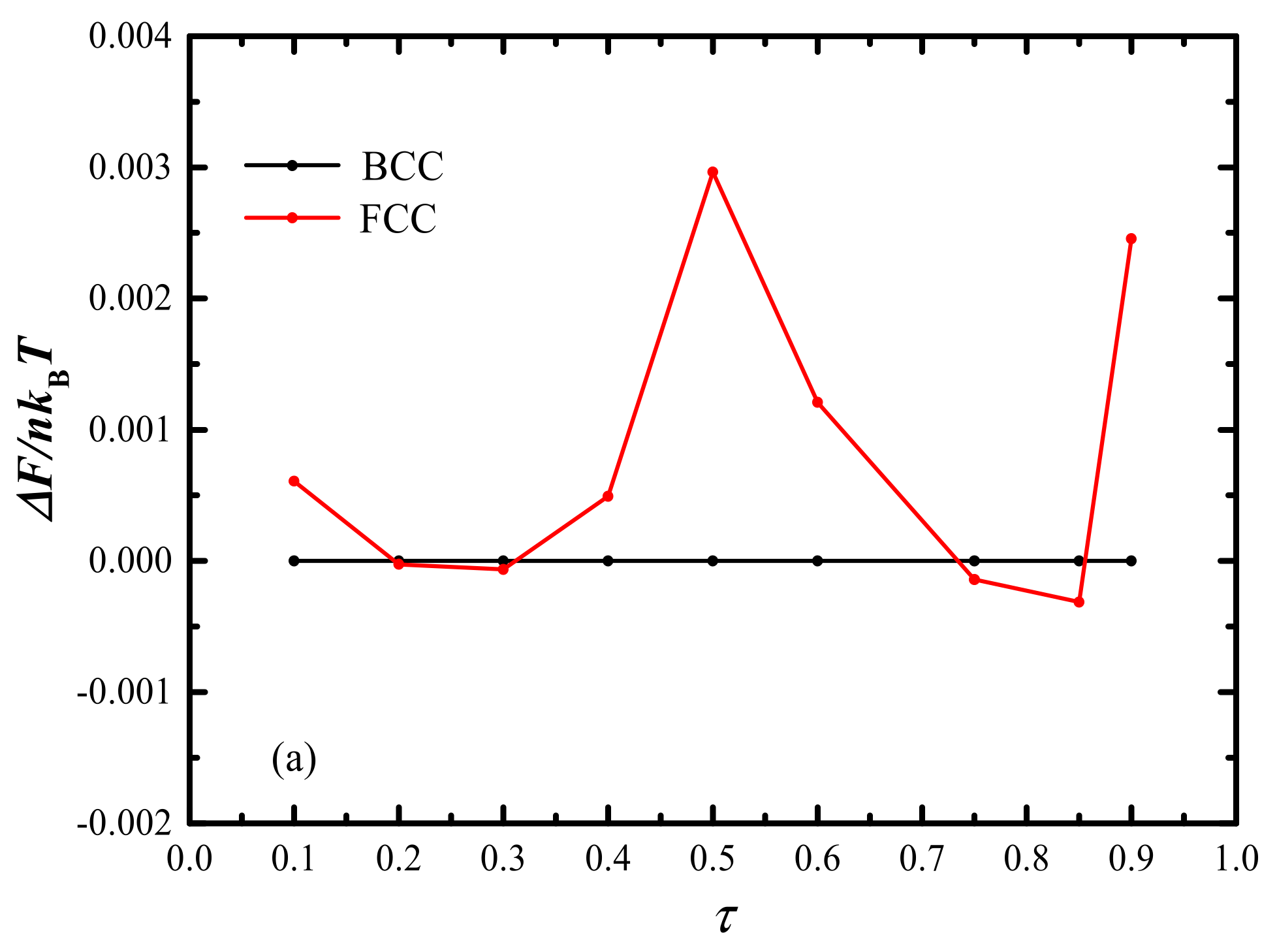
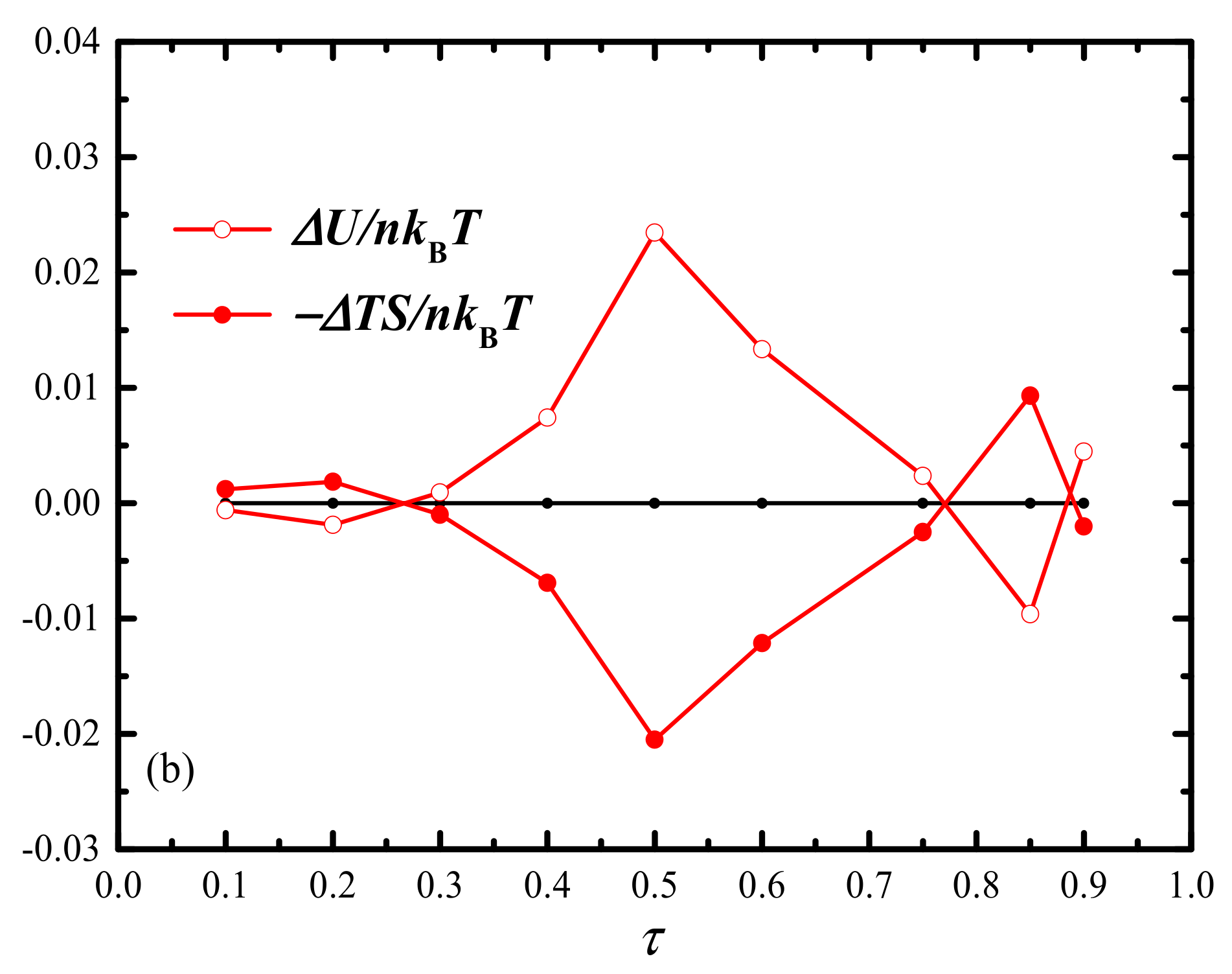
2.3. Phase Diagram in fA-τ Plane with Fixed cN
3. Theory and Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Darling, S.B. Directing the Self-assembly of Block Copolymers. Prog. Polym. Sci. 2017, 32, 1152–1204. [Google Scholar] [CrossRef]
- Li, W.H.; Muller, M. Directed Self-Assembly of Block Copolymers by Chemical or Topographical Guiding Patterns: Optimizing Molecular Architecture, Thin-Film Properties, and Kinetics. Prog. Polym. Sci. 2016, 54–55, 47–75. [Google Scholar] [CrossRef]
- Mai, Y.; Eisenberg, A. Self-assembly of Block Copolymers. Chem. Soc. Rev. 2012, 41, 5969–5985. [Google Scholar] [CrossRef] [PubMed]
- Bates, C.M.; Bates, F.S. 50th Anniversary Perspective: Block Polymers-Pure Potential. Macromolecules 2017, 50, 3–22. [Google Scholar] [CrossRef]
- Thurn-Albrecht, T.; Schotter, J.; Kastle, C.A.; Emley, N.; Shibauchi, T.; Krusin-Elbaum, L.; Guarini, K.; Black, C.T.; Tuominen, M.T.; Russell, T.P. Ultrahigh-density Nanowire Arrays Grown in Self-assembled Diblock Copolymer Templates. Science 2000, 290, 2126–2129. [Google Scholar] [CrossRef]
- Crossland, E.J.; Kamperman, M.; Nedelcu, M.; Ducati, C.; Wiesner, U.; Smilgies, D.M.; Toombes, G.E.; Hillmyer, M.A.; Ludwigs, S.; Steiner, U.; et al. A Bicontinuous Double Gyroid Hybrid Solar Cell. Nano Lett. 2009, 9, 2807–2812. [Google Scholar]
- Hampu, N.; Werber, J.R.; Chan, W.Y.; Feinberg, E.C.; Hillmyer, M.A. Next-Generation Ultrafiltration Membranes Enabled by Block Polymers. ACS Nano 2020, 14, 16446–16471. [Google Scholar] [CrossRef]
- Gong, C.; Sun, S.; Zhang, Y.; Sun, L.; Su, Z.; Wu, A.; Wei, G. Hierarchical Nanomaterials via Biomolecular Self-assembly and Bioinspiration for Energy and Environmental Applications. Nanoscale 2019, 11, 4147–4182. [Google Scholar] [CrossRef]
- Morgan, S.; Stefan, G.; Silvia, V.; Ulrich, W.; Ullrich, S. Block Copolymer Self-assembly for Nanophotonics. Chem. Soc. Rev. 2015, 44, 5076–5091. [Google Scholar]
- Gaucher, G.; Dufresne, M.H.; Sant, V.P.; Kang, N.; Maysinger, D.; Leroux, J.C. Block Copolymer Micelles: Preparation, Characterization and Application in Drug Delivery. J. Control. Release 2005, 109, 169–188. [Google Scholar] [CrossRef]
- Kaori, M.T.; Yuichi, Y.; Anjaneyulu, D.; Sorato, I.; Theofilus, A.; Tockary, K.T.; Kensuke, O.; Kazunori, K. Effect of Shear Stress on Structure and Function of Polyplex Micelles from Poly(ethylene glycol)-poly(L-lysine) Block Copolymers as Systemic Gene Delivery Carrier. Biomaterials 2017, 126, 31–38. [Google Scholar]
- Matsen, M.W.; Schick, M. Stable and Unstable Phases of a Diblock Copolymer Melt. Phys. Rev. Lett. 1994, 72, 2660–2663. [Google Scholar] [CrossRef]
- Bates, F.S.; Fredrickson, G.H. Block Copolymers-Designer Soft Materials. Phys. Today 1999, 52, 32–38. [Google Scholar] [CrossRef]
- Matsen, M.W.; Bates, F.S. Origins of Complex Self-Assembly in Block Copolymers. Macromolecules 1996, 29, 7641–7644. [Google Scholar] [CrossRef]
- Tyler, C.A.; Morse, D.C. Orthorhombic Fddd Network in Triblock and Diblock Copolymer Melts. Phys. Rev. Lett. 2005, 94, 208302. [Google Scholar] [CrossRef] [PubMed]
- Jinnai, H.; Kaneko, T.; Matsunaga, K.; Abetz, C.; Abetz, V. A Double Helical Structure Formed from an Amorphous, Achiral ABC Triblock Terpolymer. Soft Matter 2009, 5, 2042–2046. [Google Scholar] [CrossRef]
- Dobriyal, P.; Xiang, H.Q.; Kazuyuki, M.; Chen, J.T.; Jinnai, H.; Russell, T.P. Cylindrically Confined Diblock Copolymers. Macromolecules 2009, 42, 9082–9088. [Google Scholar] [CrossRef]
- Yu, B.; Sun, P.C.; Chen, T.H.; Jin, Q.H.; Ding, D.T.; Li, B.H.; Shi, A.-C. Confinement-Induced Novel Morphologies of Block Copolymers. Phys. Rev. Lett. 2006, 96, 138306. [Google Scholar] [CrossRef]
- Li, W.H.; Qiu, F.; Shi, A.-C. Emergence and Stability of Helical Superstructures in ABC Triblock Copolymers. Macromolecules 2011, 45, 503–509. [Google Scholar] [CrossRef]
- Hayashida, K.; Dotera, T.; Takano, A.; Matsushita, Y. Polymeric Quasicrystal: Mesoscopic Quasicrystalline Tiling in ABC Star Polymers. Phys. Rev. Lett. 2007, 98, 195502. [Google Scholar] [CrossRef]
- Miyamori, Y.; Suzuki, J.; Takano, A.; Matsushita, Y. Periodic and Aperiodic Tiling Patterns from a Tetrablock Terpolymer System of the A1BA2C Type. ACS Macro Lett. 2020, 9, 32–37. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.; Zhao, M.T.; Qiang, Y.C.; Chen, L.; Li, W.H.; Qiu, F.; Shi, A.-C. Stability of Two-Dimensional Dodecagonal Quasicrystalline Phase of Block Copolymers. ACS Macro Lett. 2018, 51, 7713–7721. [Google Scholar] [CrossRef]
- Nap, R.; Sushko, N.; Erukhimovich, I.; Ten Brinke, G. Double Periodic Lamellar-in-Lamellar Structure in Multiblock Copolymer Melts with Competing Length Scales. Macromolecules 2006, 39, 6765–6770. [Google Scholar] [CrossRef]
- Fleury, G.; Bates, F.S. Perpendicular Lamellae in Parallel Lamellae in a Hierarchical CECEC-P Hexablock Terpolymer. Macromolecules 2009, 42, 1691–1694. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, J. Hierarchically Ordered Nanocomposites Self-Assembled from Linear-Alternating Block Copolymer/Nanoparticle Mixture. Macromolecules 2009, 42, 1410–1414. [Google Scholar] [CrossRef]
- Xu, Y.C.; Qian, M.S. Formation of Perpendicular Three-Dimensional Network Nanostructures in ABC-Star Copolymers. Langmuir 2022, 38, 7889–7897. [Google Scholar]
- Lee, S.; Bluemle, M.J.; Bates, F.S. Discovery of a Frank-Kasper σ Phase in Sphere-Forming Block Copolymer Melts. Science 2010, 330, 349–353. [Google Scholar] [CrossRef]
- Schulze, M.W.; Lewis, R.M.; Lettow, J.H.; Hickey, R.J.; Timothy, M.G.; Marc, A.H.; Bates, F.S. Conformational Asymmetry and Quasicrystal Approximants in Linear Diblock Copolymers. Phys. Rev. Lett. 2017, 118, 207801. [Google Scholar] [CrossRef] [PubMed]
- Xie, N.; Li, W.H.; Qiu, F.; Shi, A.-C. σ Phase Formed in Conformationally Asymmetric AB-Type Block Copolymers. ACS Macro Lett. 2014, 3, 906–910. [Google Scholar] [CrossRef]
- Liu, M.J.; Qiang, Y.C.; Li, W.H.; Qiu, F.; Shi, A.-C. Stabilizing the Frank-Kasper Phases via Binary Blends of AB Diblock Copolymers. ACS Macro Lett. 2016, 5, 1167–1171. [Google Scholar] [CrossRef] [PubMed]
- Dorfman, K.D. Frank–Kasper Phases in Block polymers. Macromolecules 2021, 54, 10251–10270. [Google Scholar] [CrossRef]
- Matsen, M.W. Effect of Architecture on the Phase Behavior of AB-Type Block Copolymer Melts. Macromolecules 2012, 45, 2161–2165. [Google Scholar] [CrossRef]
- Sakurai, S.; Shirouchi, K.; Munakata, S.; Kurimura, H.; Suzuki, S.; Watanabe, J.; Oda, T.; Shimizu, N.; Tanida, K.; Yamamoto, K. Morphology Reentry with a Change in Degree of Chain Asymmetry in Neat Asymmetric Linear A1BA2 Triblock Copolymers. Macromolecules 2017, 50, 8647–8657. [Google Scholar] [CrossRef]
- Matsen, M.W. Equilibrium Behavior of Asymmetric ABA Triblock Copolymer Melts. J. Chem. Phys. 2000, 113, 5539–5544. [Google Scholar] [CrossRef]
- Ahn, S.; Kim, J.K.; Zhao, B.; Duan, C.; Li, W.H. Morphology Transitions of Linear A1B1A2B2 Tetrablock Copolymers at Symmetric Overall Volume Fraction. Macromolecules 2018, 51, 4415–4421. [Google Scholar] [CrossRef]
- Zhao, B.; Jiang, W.B.; Chen, L.; Li, W.H.; Qiu, F.; Shi, A.-C. Emergence and Stability of a Hybrid Lamella-Sphere Structure from Linear ABAB Tetrablock Copolymers. ACS Macro Lett. 2018, 7, 95–99. [Google Scholar] [CrossRef]
- Matsen, M.W. The Standard Gaussian Model for Block Copolymer Melts. J. Phys. Condens. Matter 2002, 14, R21–R47. [Google Scholar] [CrossRef]
- Drolet, F.; Fredrickson, G.H. Combinatorial Screening of Complex Block Copolymer Assembly with Self-Consistent Field Theory. Phys. Rev. Lett. 1999, 83, 4317. [Google Scholar] [CrossRef]
- Matsen, M.W. Self-Consistent Field Theory and Its Applications. In Soft Matter; Polymer Melts and Mixtures; Gompper, G., Schick, M., Eds.; Wiley-VCH: Weinheim, Germany, 2007; Volume 1, pp. 87–178. [Google Scholar]
- Grason, G.M.; DiDonna, B.A.; Kamien, R.D. Geometric Theory of Diblock Copolymer Phases. Phys. Rev. Lett. 2003, 91, 058304. [Google Scholar] [CrossRef]
- Xie, N.; Liu, M.J.; Deng, H.L.; Li, W.H.; Qiu, F.; Shi, A.-C. Macromolecular Metallurgy of Binary Mesocrystals via Designed Multiblock Terpolymers. J. Am. Chem. Soc. 2014, 136, 2974–2977. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, C.; Chen, Y.; Liu, M.J. Frank–Kasper Phases Self-Assembled from a Linear A1B1A2B2 Tetrablock Copolymer. Langmuir 2021, 37, 5642–5650. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.W.; Li, W.H. Control the Self-assembly of Block Copolymers by Tailoring the Packing Frustration. Chin. J. Chem. 2022, 40, 1083–1090. [Google Scholar]
- Gao, Y.; Deng, H.L.; Li, W.H.; Qiu, F.; Shi, A.-C. Formation of Nonclassical Ordered Phases of AB-Type Multiarm Block Copolymers. Phys. Rev. Lett. 2016, 116, 068304. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Qiang, Y.C.; Li, W.H. Single Gyroid Self-Assembled by Linear BABAB Pentablock Copolymer. ACS Macro Lett. 2022, 11, 205–209. [Google Scholar] [CrossRef]
- Lynd, N.A.; Oyerokun, F.T.; O’Donoghue, D.L.; Handlin, D.L., Jr.; Fredrickson, G.H. Design of Soft and Strong Thermoplastic Elastomers Based on Nonlinear Block Copolymer Architectures Using Self-Consistent-Field Theory. Macromolecules 2010, 43, 3479–3486. [Google Scholar] [CrossRef]
- Chen, L.; Qiang, Y.C.; Li, W.H. Tuning Arm Architecture Leads to Unusual Phase Behaviors in a (BAB)5 Star Copolymer Melt. Macromolecules 2018, 51, 9890–9900. [Google Scholar] [CrossRef]
- Matsen, M.W. Fast and Accurate SCFT Calculations for Periodic Block Copolymer Morphologies Using the Spectral Method with Anderson Mixing. Eur. Phys. J. E 2009, 30, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Shi, A.-C. Developments in Block Copolymer Science and Technology; John Wiley & Sons, Ltd.: New York, NY, USA, 2004; pp. 265–293. [Google Scholar]
- Fredrickson, G.H. The Equilibrium Theory of Inhomogeneous Polymers; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Tzeremes, G.; Rasmussen, K.Ø.; Lookman, T.; Saxena, A. Efficient Computation of the Structural Phase Behavior of Block Copolymers. Phys. Rev. E 2002, 65, 041806. [Google Scholar] [CrossRef]
- Rasmussen, K.Ø.; Kalosakas, G. Improved Numerical Algorithm for Exploring Block Copolymer Mesophases. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 1777–1783. [Google Scholar] [CrossRef]
- Thompson, R.; Rasmussen, K.; Lookman, T. Improved Convergence in Block Copolymer Self-Consistent Field Theory by Anderson Mixing. J. Chem. Phys. 2004, 120, 31–34. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Dong, Q.; Yang, W.; Xu, Y. Theoretical Study of Phase Behaviors of Symmetric Linear B1A1B2A2B3 Pentablock Copolymer. Molecules 2023, 28, 3536. https://doi.org/10.3390/molecules28083536
Zhao B, Dong Q, Yang W, Xu Y. Theoretical Study of Phase Behaviors of Symmetric Linear B1A1B2A2B3 Pentablock Copolymer. Molecules. 2023; 28(8):3536. https://doi.org/10.3390/molecules28083536
Chicago/Turabian StyleZhao, Bin, Qingshu Dong, Wei Yang, and Yuci Xu. 2023. "Theoretical Study of Phase Behaviors of Symmetric Linear B1A1B2A2B3 Pentablock Copolymer" Molecules 28, no. 8: 3536. https://doi.org/10.3390/molecules28083536
APA StyleZhao, B., Dong, Q., Yang, W., & Xu, Y. (2023). Theoretical Study of Phase Behaviors of Symmetric Linear B1A1B2A2B3 Pentablock Copolymer. Molecules, 28(8), 3536. https://doi.org/10.3390/molecules28083536




