Properties of Naked Silver Clusters with Up to 100 Atoms as Found with Embedded-Atom and Density-Functional Calculations
Abstract
1. Introduction
2. Computational Methods
2.1. The Embedded-Atom Method
2.2. The Basin-Hopping Method
2.3. DFT Calculations
3. Results and Discussion
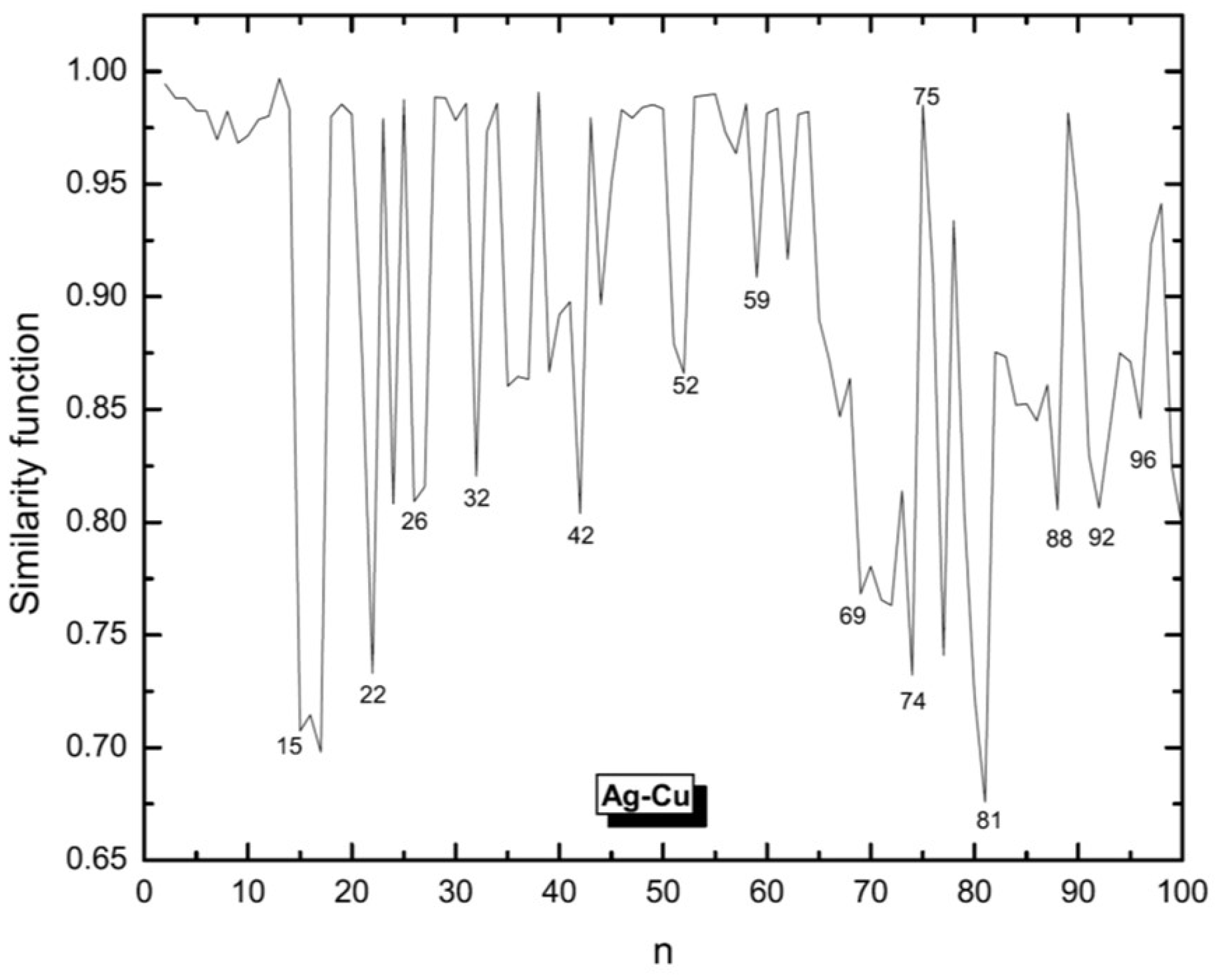
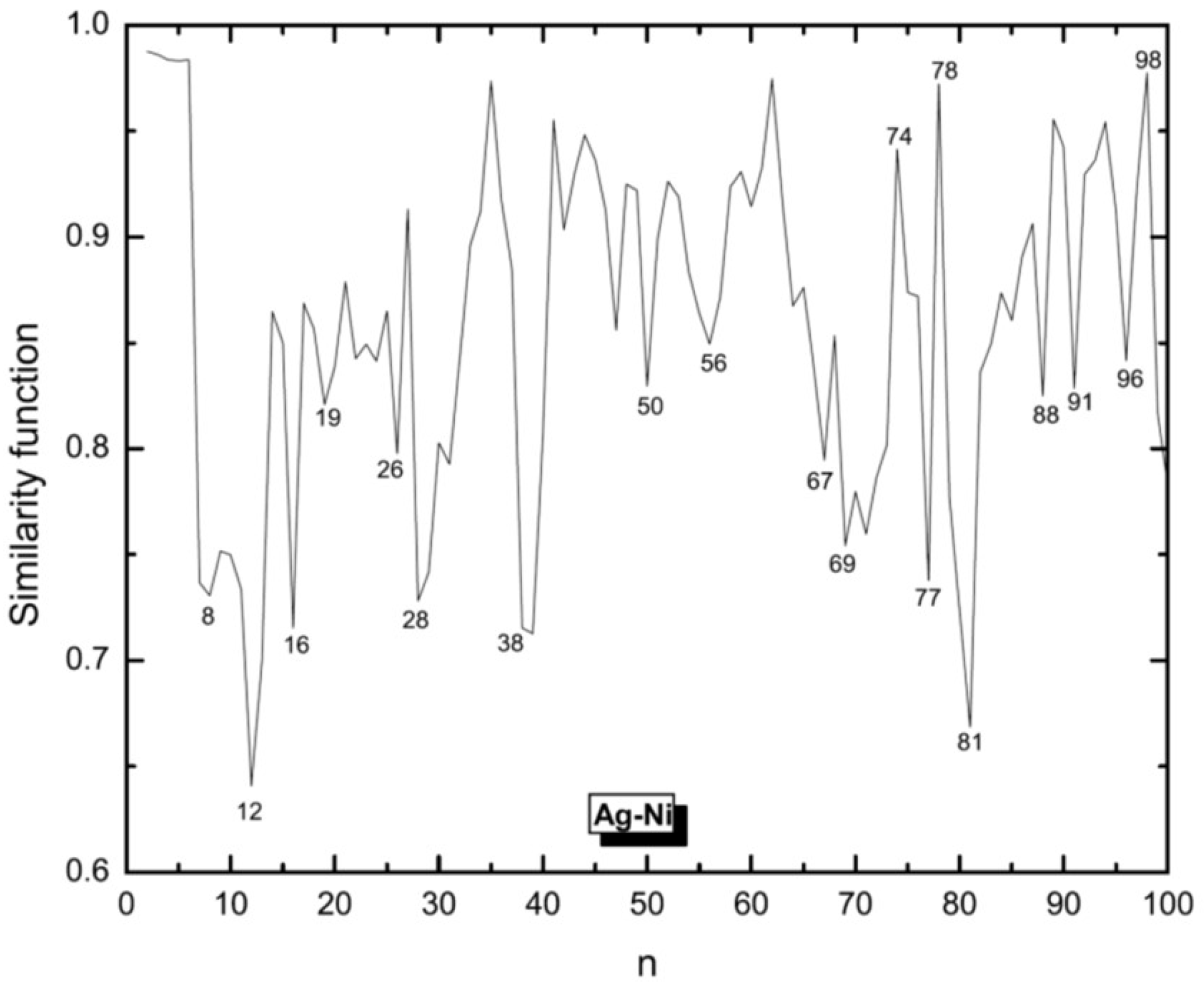
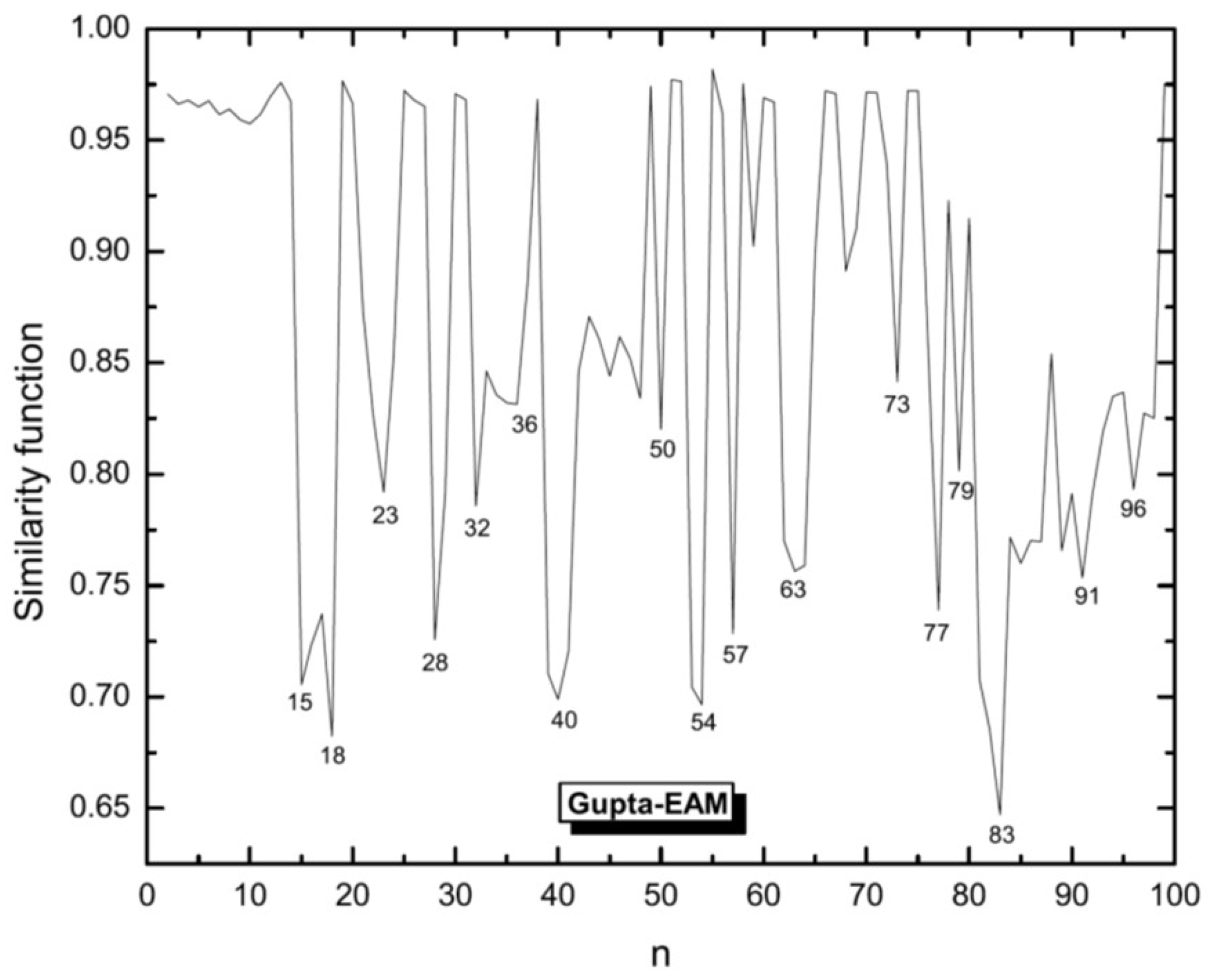
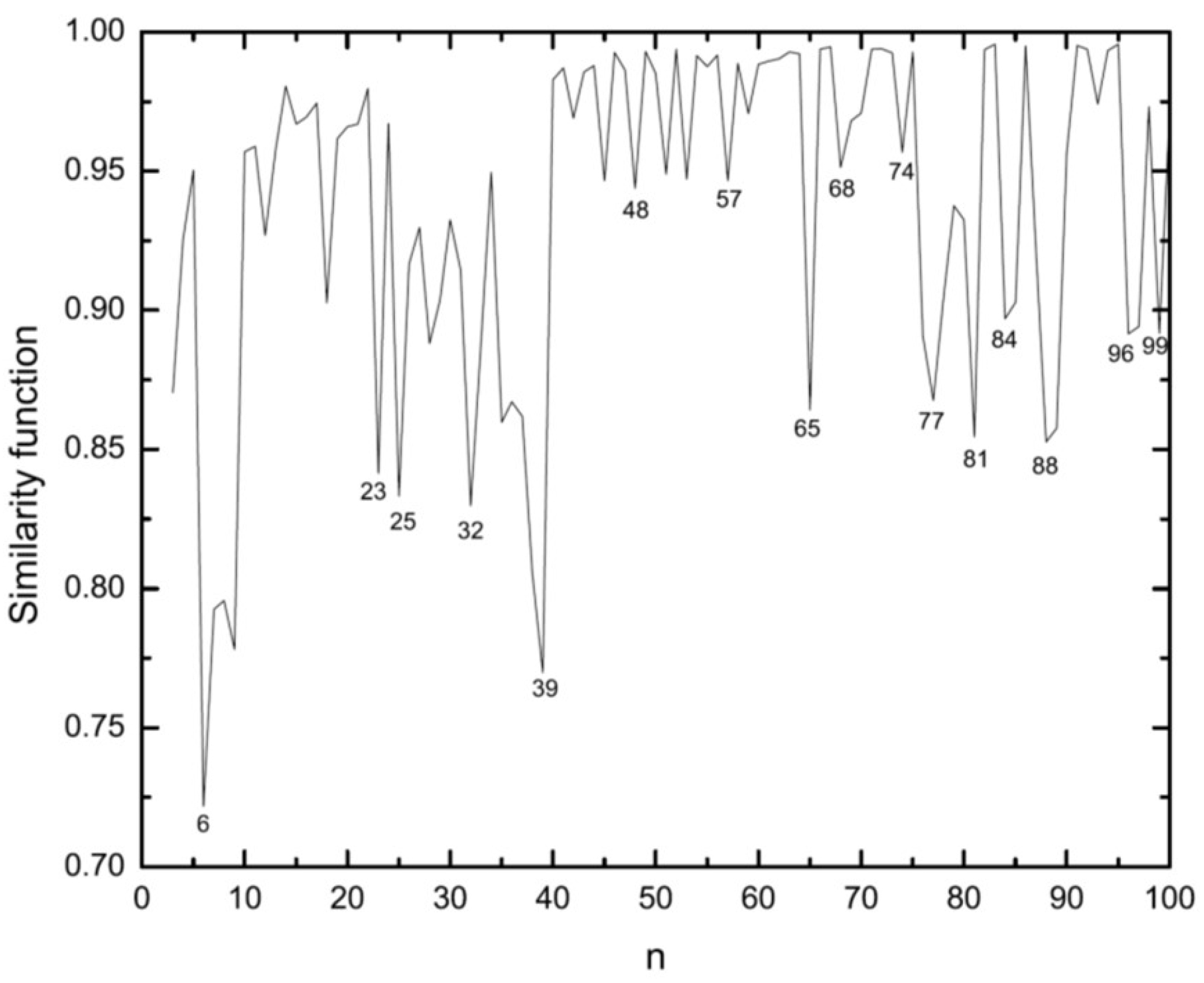
3.1. Structural Properties
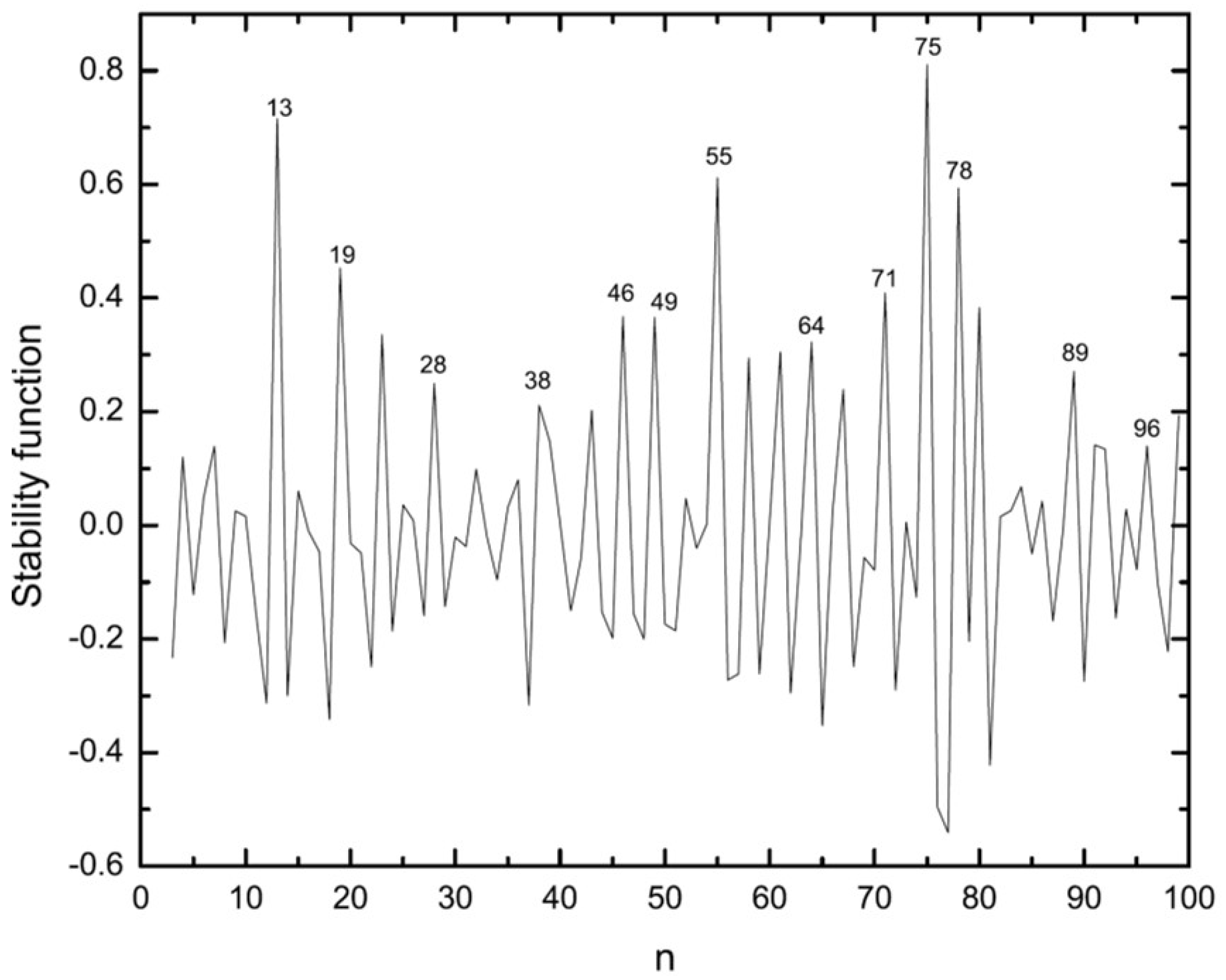
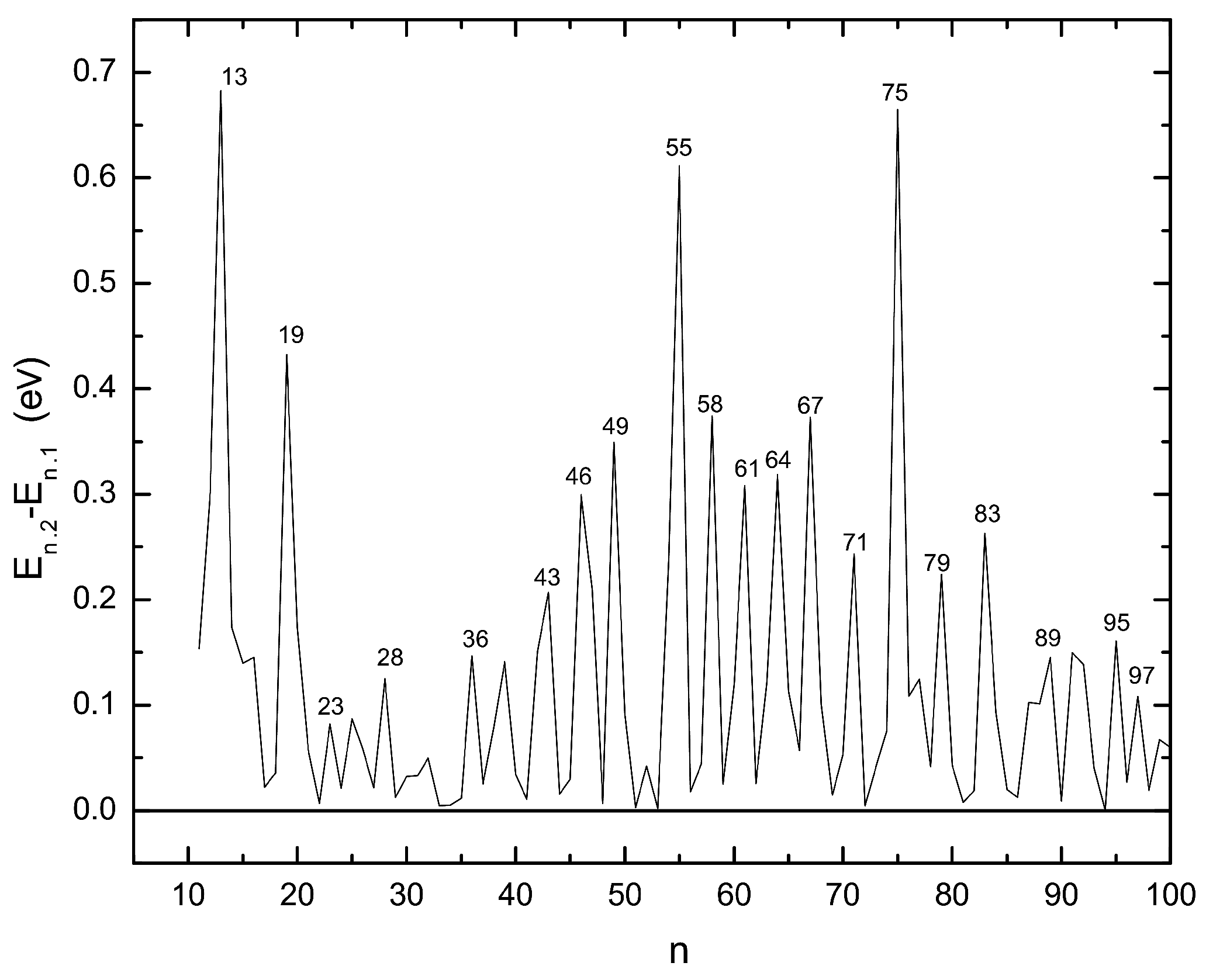
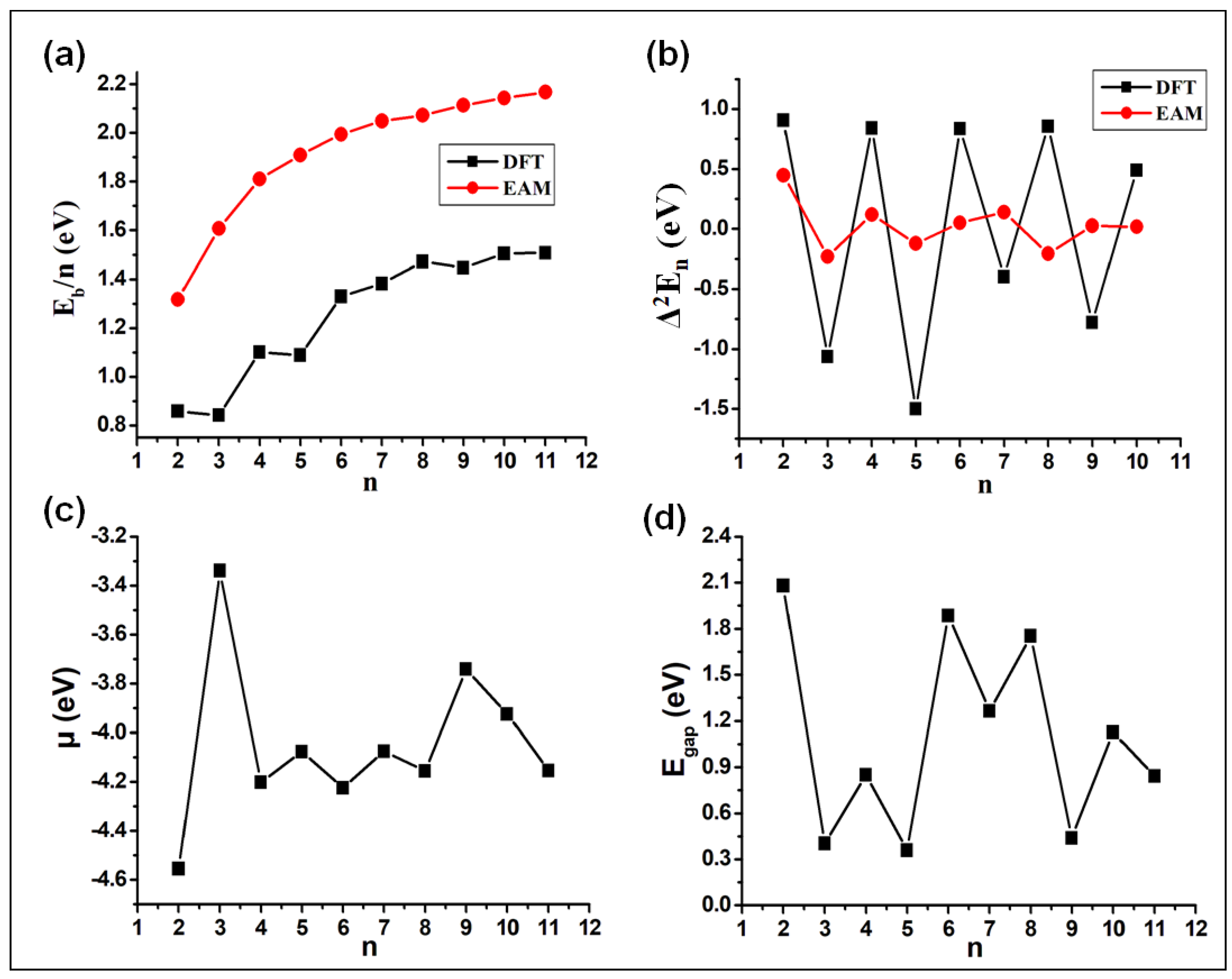
3.2. Energetic Properties
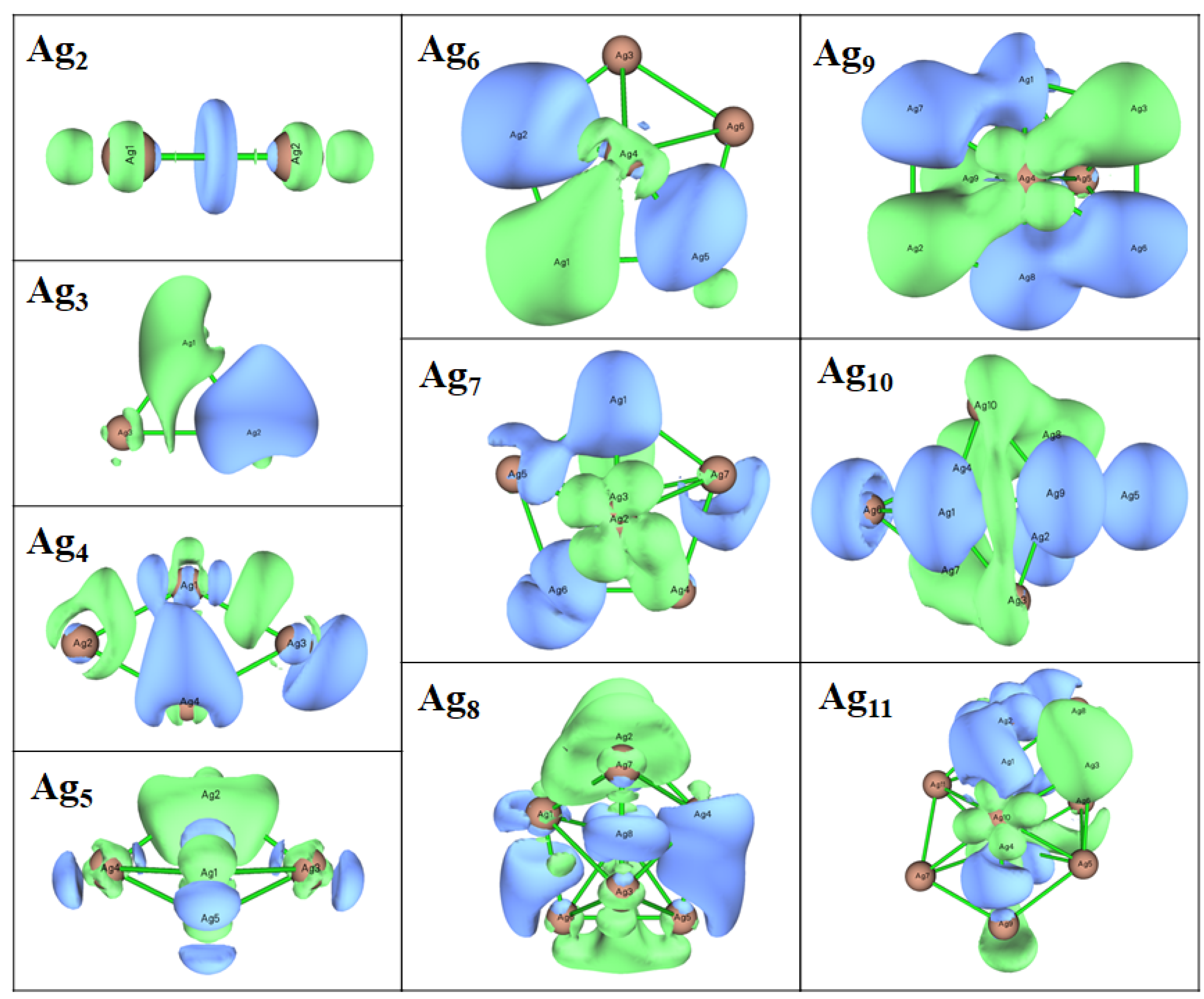
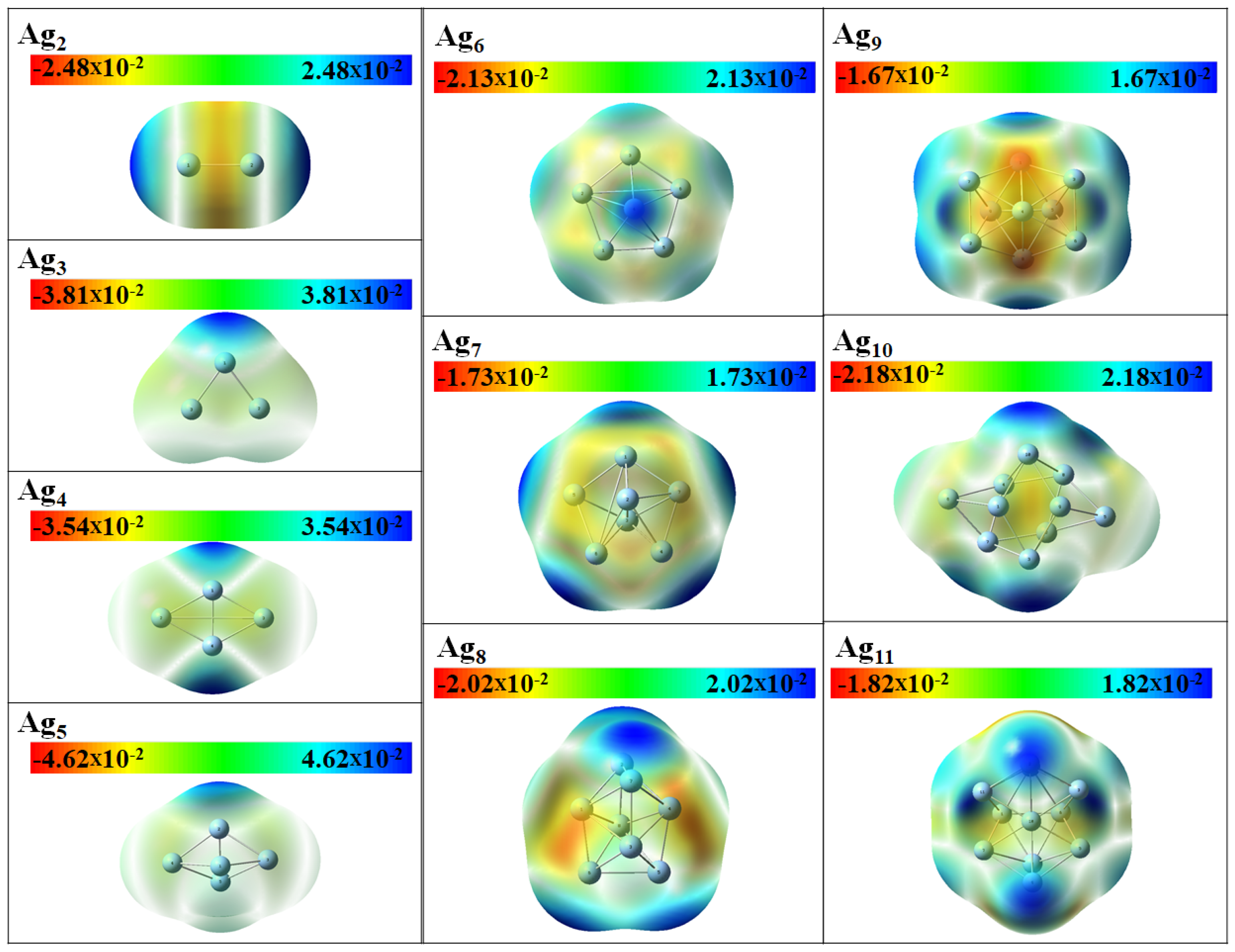
3.3. Electronic Properties
3.4. Growth Patterns
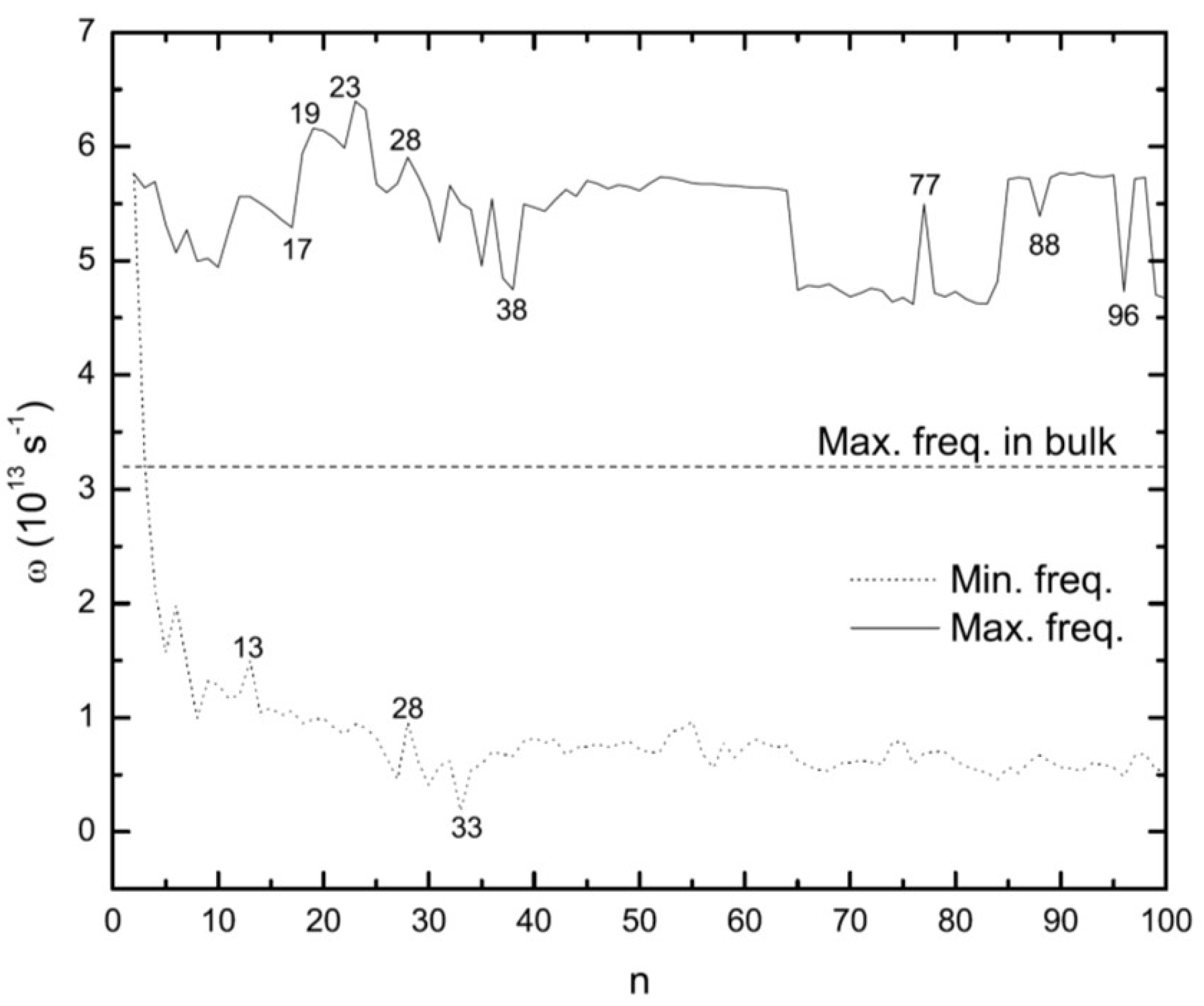
3.5. Vibrational Frequencies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Haslett, T.L.; Bosnick, K.A.; Moskovits, M. Ag5 is a planar trapezoidal molecule. J. Chem. Phys. 1998, 108, 3453–3457. [Google Scholar] [CrossRef]
- Howard, J.A.; Sutcliffe, R.; Mile, B. The geometric and electronic structures of small metal clusters of group 1B metals. Surf. Sci. 1985, 156, 214–227. [Google Scholar] [CrossRef]
- Xing, X.; Danell, R.M.; Garzón, I.L.; Michaelian, K.; Blom, M.N.; Burns, M.M.; Parks, J.H. Size-dependent fivefold and icosahedral symmetry in silver clusters. Phys. Rev. B 2005, 72, 081405. [Google Scholar] [CrossRef]
- Blom, M.N.; Schooss, D.; Stairs, J.; Kappes, M.M. Experimental structure determination of silver cluster ions (Ag, 19 ≤ n ≤ 79). J. Chem. Phys. 2006, 124, 244308. [Google Scholar] [CrossRef]
- Handschuh, H.; Cha, C.Y.; Bechthold, P.S.; Ganteför, G.; Eberhardt, W. Electronic shells or molecular orbitals: Photoelectron spectra of Ag clusters. J. Chem. Phys. 1995, 102, 6406–6422. [Google Scholar] [CrossRef]
- Huda, M.N.; Ray, A.K. Electronic structures and magic numbers of small silver clusters: A many-body perturbation-theoretic study. Phys. Rev. A 2003, 67, 013201. [Google Scholar] [CrossRef]
- Huda, M.; Ray, A. A correlation study of small silver clusters. Eur. Phys. J. D 2003, 22, 217–227. [Google Scholar] [CrossRef]
- Bonačić-Koutecký, V.; Češpiva, L.; Fantucci, P.; Koutecký, J. Effective core potential-configuration interaction study of electronic structure and geometry of small neutral and cationic Agn clusters: Predictions and interpretation of measured properties. J. Chem. Phys. 1993, 98, 7981–7994. [Google Scholar] [CrossRef]
- Bonačić-Koutecký, V.; Pittner, J.; Boiron, M.; Fantucci, P. An accurate relativistic effective core potential for excited states of Ag atom: An application for studying the absorption spectra of Agn and Ag clusters. J. Chem. Phys. 1999, 110, 3876–3886. [Google Scholar] [CrossRef]
- Bonačić-Koutecky, V.; Veyret, V.; Mitrić, R. Ab initio study of the absorption spectra of Agn (n = 5–8) clusters. J. Chem. Phys. 2001, 115, 10450–10460. [Google Scholar] [CrossRef]
- Idrobo, J.C.; Öğüt, S.; Jellinek, J. Size dependence of the static polarizabilities and absorption spectra of Agn (n = 2–8) clusters. Phys. Rev. B 2005, 72, 085445. [Google Scholar] [CrossRef]
- Yang, M.; Jackson, K.A.; Jellinek, J. First-principles study of intermediate size silver clusters: Shape evolution and its impact on cluster properties. J. Chem. Phys. 2006, 125, 144308. [Google Scholar] [CrossRef] [PubMed]
- Michaelian, K.; Rendón, N.; Garzón, I.L. Structure and energetics of Ni, Ag, and Au nanoclusters. Phys. Rev. B 1999, 60, 2000–2010. [Google Scholar] [CrossRef]
- Zhao, J.; Luo, Y.; Wang, G. Tight-binding study of structural and electronic properties of silver clusters. Eur. Phys. J. D 2001, 14, 309–316. [Google Scholar] [CrossRef]
- Shao, X.; Liu, X.; Cai, W. Structural Optimization of Silver Clusters up to 80 Atoms with Gupta and Sutton-Chen Potentials. J. Chem. Theory Comput. 2005, 1, 762–768. [Google Scholar] [CrossRef]
- Alamanova, D.; Grigoryan, V.G.; Springborg, M. Theoretical Study of the Structure and Energetics of Silver Clusters. J. Phys. Chem. C 2007, 111, 12577–12587. [Google Scholar] [CrossRef]
- Baletto, F.; Mottet, C.; Ferrando, R. Reentrant Morphology Transition in the Growth of Free Silver Nanoclusters. Phys. Rev. Lett. 2000, 84, 5544–5547. [Google Scholar] [CrossRef]
- Poteau, R.; Heully, J.L.; Spiegelmann, F. Structure, stability, and vibrational properties of small silver cluster. Z. Phys. At. Mol. Clust. 1997, 40, 479–482. [Google Scholar] [CrossRef]
- Wales, D.J.; Doye, J.P.K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Wales, D.J.; Scheraga, H.A. Global Optimization of Clusters, Crystals, and Biomolecules. Science 1999, 285, 1368–1372. [Google Scholar] [CrossRef]
- Wales, D.J. Energy Landscapes: Applications to Clusters, Biomolecules and Glasses; Cambridge University Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Cleveland, C.L.; Landman, U. The energetics and structure of nickel clusters: Size dependence. J. Chem. Phys. 1991, 94, 7376–7396. [Google Scholar] [CrossRef]
- Vlachos, D.G.; Schmidt, L.D.; Aris, R. Structures of small metal clusters. I. Low temperature behavior. J. Chem. Phys. 1992, 96, 6880–6890. [Google Scholar] [CrossRef]
- Montejano-Carrizales, J.M.; Iñiguez, M.P.; Alonso, J.A.; López, M.J. Theoretical study of icosahedral Ni clusters within the embedded-atom method. Phys. Rev. B 1996, 54, 5961–5969. [Google Scholar] [CrossRef] [PubMed]
- Grigoryan, V.G.; Springborg, M. A theoretical study of the structure of Ni clusters (NiN). Phys. Chem. Chem. Phys. 2001, 3, 5135–5139. [Google Scholar] [CrossRef]
- Grigoryan, V.G.; Springborg, M. Structure and energetics of Ni clusters with up to 150 atoms. Chem. Phys. Lett. 2003, 375, 219–226. [Google Scholar] [CrossRef]
- Rey, C.; Gallego, L.J.; García-Rodeja, J.; Alonso, J.A.; Iñiguez, M.P. Molecular-dynamics study of the binding energy and melting of transition-metal clusters. Phys. Rev. B 1993, 48, 8253–8262. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals. Phys. Rev. Lett. 1983, 50, 1285–1288. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Foiles, S.M.; Baskes, M.I.; Daw, M.S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B 1986, 33, 7983–7991. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.; Baskes, M.I. The embedded-atom method: A review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Clementi, E.; Roetti, C. Roothaan-Hartree-Fock atomic wavefunctions: Basis functions and their coefficients for ground and certain excited states of neutral and ionized atoms, Z ≤ 54. At. Data Nucl. Data Tables 1974, 14, 177–478. [Google Scholar] [CrossRef]
- McLean, A.D.; McLean, R.S. Roothaan-Hartree-Fock atomic wave functions Slater basis-set expansions for Z = 55 − 92. At. Data Nucl. Data Tables 1981, 26, 197–381. [Google Scholar] [CrossRef]
- Daw, M.S. Model of metallic cohesion: The embedded-atom method. Phys. Rev. B 1989, 39, 7441–7452. [Google Scholar] [CrossRef] [PubMed]
- Niesse, J.A.; Mayne, H.R. Global geometry optimization of atomic clusters using a modified genetic algorithm in space-fixed coordinates. J. Chem. Phys. 1996, 105, 4700–4706. [Google Scholar] [CrossRef]
- Johnston, R.L.; Mortimer-Jones, T.V.; Roberts, C.; Darby, S.; Manby, F.R. Applications of Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2279, pp. 25–61. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.J.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Nonlinear optimization simplified by hypersurface deformation. J. Stat. Phys. 1988, 52, 1429–1445. [Google Scholar] [CrossRef]
- Finnila, A.B.; Gomez, M.A.; Sebenik, C.; Stenson, C.; Doll, J.D. Quantum annealing: A new method for minimizing multidimensional functions. Chem. Phys. Lett. 1994, 219, 343–348. [Google Scholar] [CrossRef]
- Doye, J.P.K.; Meyer, L. Mapping the Magic Numbers in Binary Lennard-Jones Clusters. Phys. Rev. Lett. 2005, 95, 063401. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Chiodo, S.; Russo, N.; Sicilia, E. LANL2DZ basis sets recontracted in the framework of density functional theory. J. Chem. Phys. 2006, 125, 104107. [Google Scholar] [CrossRef]
- Al-Odail, F.; Mazher, J.; Abuelela, A.M. A density functional theory study of structural, electronic and magnetic properties of small PdnAg (n = 1–8) clusters. Comput. Theor. Chem. 2018, 1125, 103–111. [Google Scholar] [CrossRef]
- Farshad, M.; Perera, D.C.; Rasaiah, J.C. Theoretical study of the stability, structure, and optical spectra of small silver clusters and their formation using density functional theory. Phys. Chem. Chem. Phys. 2021, 23, 25507–25517. [Google Scholar] [CrossRef] [PubMed]
- Tsuneda, T. Theoretical investigations on geometrical and electronic structures of silver clusters. J. Comput. Chem. 2019, 40, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Kolandaivel, P.; Nirmala, V. Study of proper and improper hydrogen bonding using Bader’s atoms in molecules (AIM) theory and NBO analysis. J. Mol. Struct. 2004, 694, 33–38. [Google Scholar] [CrossRef]
- Beutel, V.; Kramer, H.G.; Bhale, G.L.; Kuhn, M.; Weyers, K.; Demtröder, W. High-resolution isotope selective laser spectroscopy of Ag2 molecules. J. Chem. Phys. 1993, 98, 2699–2708. [Google Scholar] [CrossRef]
- Simard, B.; Hackett, P.A.; James, A.M.; Langridge-Smith, P.R.R. The bond length of silver dimer. Chem. Phys. Lett. 1991, 186, 415–422. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Meng, J.; Wu, Z. Interaction of H2 with transition metal homonuclear dimers Cu2, Ag2, Au2 and heteronuclear dimers PdCu, PdAg and PdAu. J. Mol. Struct. Theochem. 2007, 804, 47–55. [Google Scholar] [CrossRef]
- Häkkinen, H.; Moseler, M.; Kostko, O.; Morgner, N.; Hoffmann, M.A.; Issendorff, B.V. Symmetry and Electronic Structure of Noble-Metal Nanoparticles and the Role of Relativity. Phys. Rev. Lett. 2004, 93, 093401. [Google Scholar] [CrossRef]
- Doye, J.P.K.; Wales, D.J. Global minima for transition metal clusters described by Sutton–Chen potentials. New J. Chem. 1998, 22, 733–744. [Google Scholar] [CrossRef]
- Grigoryan, V.G.; Springborg, M. Structural and energetic properties of nickel clusters: 2 ≤ N ≤ 150. Phys. Rev. B 2004, 70, 205415. [Google Scholar] [CrossRef]
- Grigoryan, V.G.; Alamanova, D.; Springborg, M. Structure and energetics of CuN clusters with 2 ≤ N ≤ 150: An embedded-atom-method study. Phys. Rev. B 2006, 73, 115415. [Google Scholar] [CrossRef]
- Chaves, A.S.; Piotrowski, M.J.; Da Silva, J.L. Evolution of the structural, energetic, and electronic properties of the 3d, 4d, and 5d transition-metal clusters (30 TMn systems for n = 2–15): A density functional theory investigation. Phys. Chem. Chem. Phys. 2017, 19, 15484–15502. [Google Scholar] [CrossRef] [PubMed]
- McKee, M.L.; Samokhvalov, A. Density functional study of neutral and charged silver clusters Agn with n = 2–22. Evolution of properties and structure. J. Phys. Chem. A 2017, 121, 5018–5028. [Google Scholar] [CrossRef] [PubMed]
- Rekha, T.; Rajkumar, B.J. Density functional theory study on silver clusters using dimers, trimers, and tetramers as building units. Can. J. Phys. 2015, 93, 318–325. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Morell, C.; Grand, A.; Toro-Labbé, A. New dual descriptor for chemical reactivity. J. Phys. Chem. A 2005, 109, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Alonso, J.A. Electronic and Atomic Structure, and Magnetism of Transition-Metal Clusters. Chem. Rev. 2000, 100, 637–678. [Google Scholar] [CrossRef]
- Baletto, F.; Ferrando, R. Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects. Rev. Mod. Phys. 2005, 77, 371–423. [Google Scholar] [CrossRef]
- Grigoryan, V.G.; Springborg, M. Vibrational and thermodynamic properties of metal clusters with up to 150 atoms calculated by the embedded-atom method. Phys. Rev. B 2011, 83, 155413. [Google Scholar] [CrossRef]
- Grigoryan, V.G.; Springborg, M. Temperature dependence of stability of copper clusters. Z. Phys. Chem. 2016, 230, 1037–1055. [Google Scholar] [CrossRef]
- Grigoryan, V.G.; Springborg, M. Temperature and isomeric effects in nanoclusters. Phys. Chem. Chem. Phys. 2019, 21, 5646–5654. [Google Scholar] [CrossRef] [PubMed]
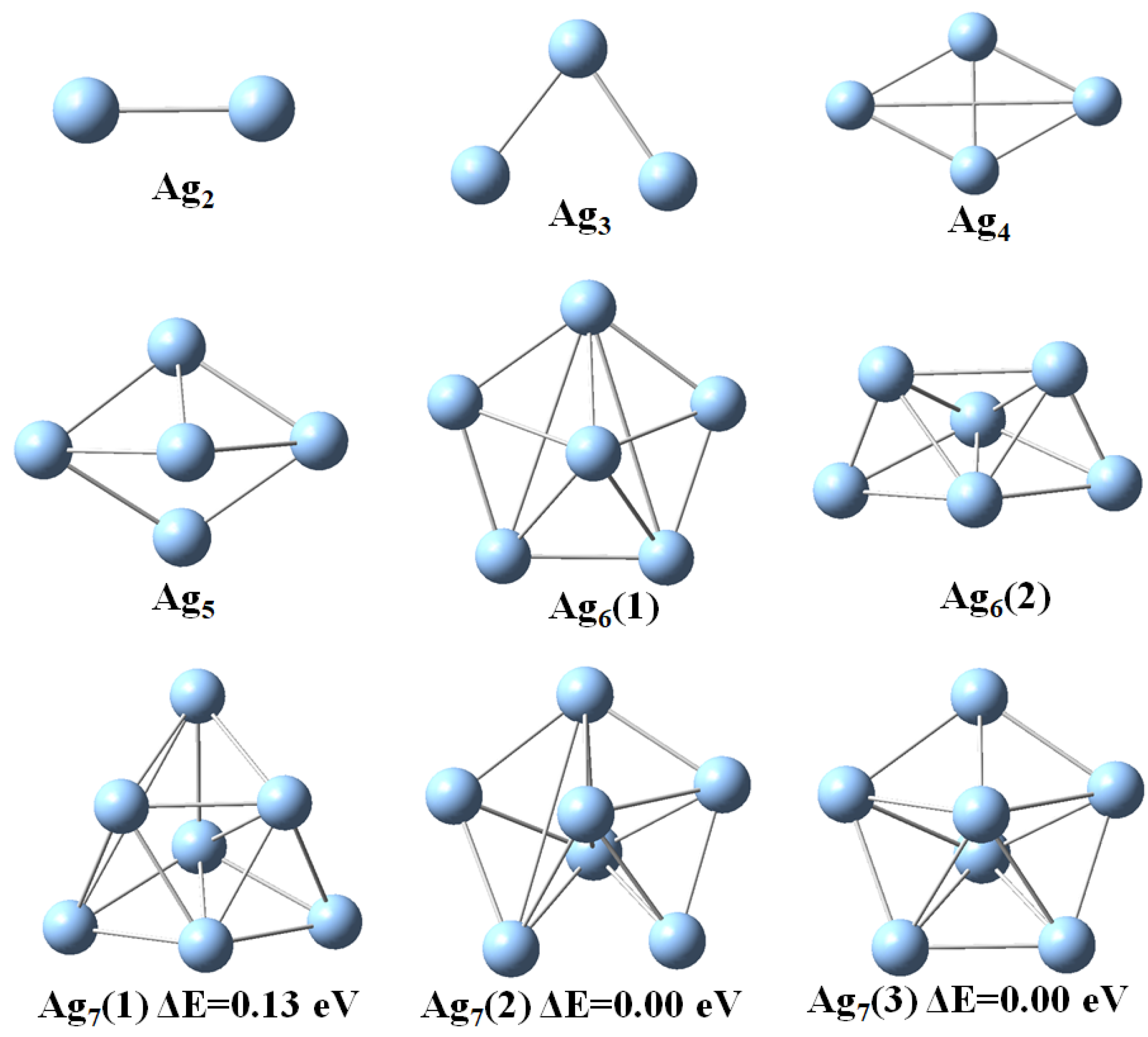
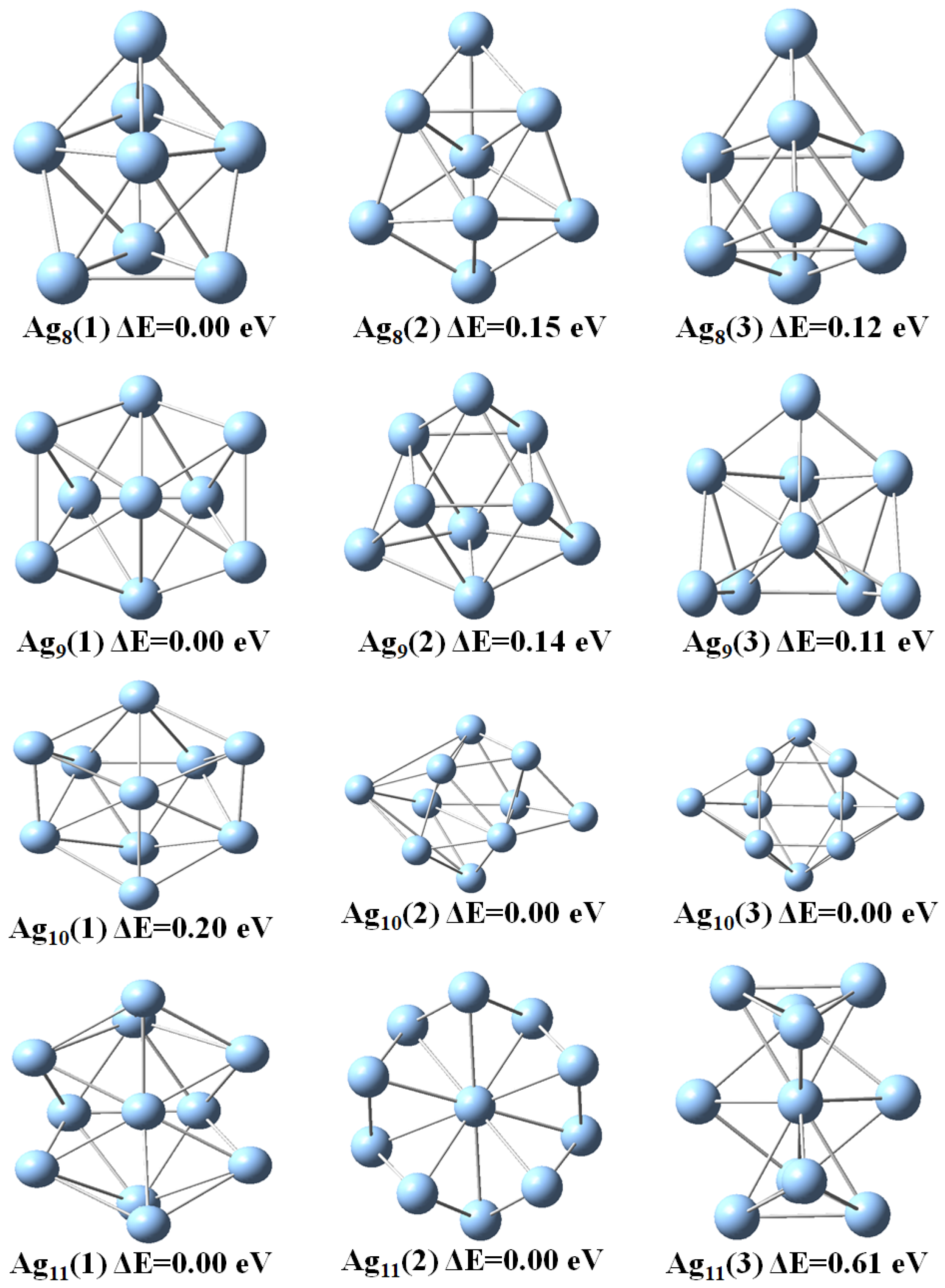

| n | |||
|---|---|---|---|
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 |
| n | n | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 35 | 68 | |||||||||
| 3 | 36 | 69 | |||||||||
| 4 | 37 | 70 | |||||||||
| 5 | 38 | 71 | |||||||||
| 6 | 39 | 72 | |||||||||
| 7 | 40 | 73 | |||||||||
| 8 | 41 | 74 | |||||||||
| 9 | 42 | 75 | |||||||||
| 10 | 43 | 76 | |||||||||
| 11 | 44 | 77 | |||||||||
| 12 | 45 | 78 | |||||||||
| 13 | 46 | 79 | |||||||||
| 14 | 47 | 80 | |||||||||
| 15 | 48 | 81 | |||||||||
| 16 | 49 | 82 | |||||||||
| 17 | 50 | 83 | |||||||||
| 18 | 51 | 84 | |||||||||
| 19 | 52 | 85 | |||||||||
| 20 | 53 | 86 | |||||||||
| 21 | 54 | 87 | |||||||||
| 22 | 55 | 88 | |||||||||
| 23 | 56 | 89 | |||||||||
| 24 | 57 | 90 | |||||||||
| 25 | 58 | 91 | |||||||||
| 26 | 59 | 92 | |||||||||
| 27 | 60 | 93 | |||||||||
| 28 | T | 61 | 94 | ||||||||
| 29 | 62 | 95 | |||||||||
| 30 | 63 | 96 | |||||||||
| 31 | 64 | 97 | |||||||||
| 32 | 65 | 98 | |||||||||
| 33 | 66 | 99 | |||||||||
| 34 | 67 | 100 |
| Cluster Size | VIE | VEA | ||||
|---|---|---|---|---|---|---|
| 2 | 8.02 | 1.08 | −4.55 | −5.26 | −3.18 | 2.08 |
| 3 | 6.11 | 0.56 | −3.34 | −3.90 | −3.49 | 0.40 |
| 4 | 6.67 | 1.73 | −4.20 | −4.51 | −3.66 | 0.85 |
| 5 | 6.30 | 1.86 | −4.08 | −4.23 | −3.87 | 0.36 |
| 6 | 7.01 | 1.44 | −4.23 | −5.01 | −3.13 | 1.89 |
| 7 | 6.15 | 2.00 | −4.08 | −4.22 | −2.95 | 1.26 |
| 8 | 6.80 | 1.51 | −4.16 | −4.90 | −3.14 | 1.75 |
| 9 | 5.57 | 1.91 | −3.74 | −3.86 | −3.42 | 0.44 |
| 10 | 6.13 | 1.72 | −3.93 | −4.41 | −3.29 | 1.13 |
| 11 | 5.92 | 2.38 | −4.15 | −4.26 | −3.42 | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garg, S.; Kaur, N.; Goel, N.; Molayem, M.; Grigoryan, V.G.; Springborg, M. Properties of Naked Silver Clusters with Up to 100 Atoms as Found with Embedded-Atom and Density-Functional Calculations. Molecules 2023, 28, 3266. https://doi.org/10.3390/molecules28073266
Garg S, Kaur N, Goel N, Molayem M, Grigoryan VG, Springborg M. Properties of Naked Silver Clusters with Up to 100 Atoms as Found with Embedded-Atom and Density-Functional Calculations. Molecules. 2023; 28(7):3266. https://doi.org/10.3390/molecules28073266
Chicago/Turabian StyleGarg, Shivangi, Navjot Kaur, Neetu Goel, Mohammad Molayem, Valeri G. Grigoryan, and Michael Springborg. 2023. "Properties of Naked Silver Clusters with Up to 100 Atoms as Found with Embedded-Atom and Density-Functional Calculations" Molecules 28, no. 7: 3266. https://doi.org/10.3390/molecules28073266
APA StyleGarg, S., Kaur, N., Goel, N., Molayem, M., Grigoryan, V. G., & Springborg, M. (2023). Properties of Naked Silver Clusters with Up to 100 Atoms as Found with Embedded-Atom and Density-Functional Calculations. Molecules, 28(7), 3266. https://doi.org/10.3390/molecules28073266





