Impact of Static-Oriented Electric Fields on the Kinetics of Some Representative Suzuki–Miyaura and Metal-Cluster Mediated Reactions
Abstract
:1. Introduction
2. Results and Discussion
2.1. Effect of OEFs on the Free Energy of Activation (Suzuki–Miyaura Coupling Reactions)
2.2. Can OEFs Change the Reaction Mechanism?
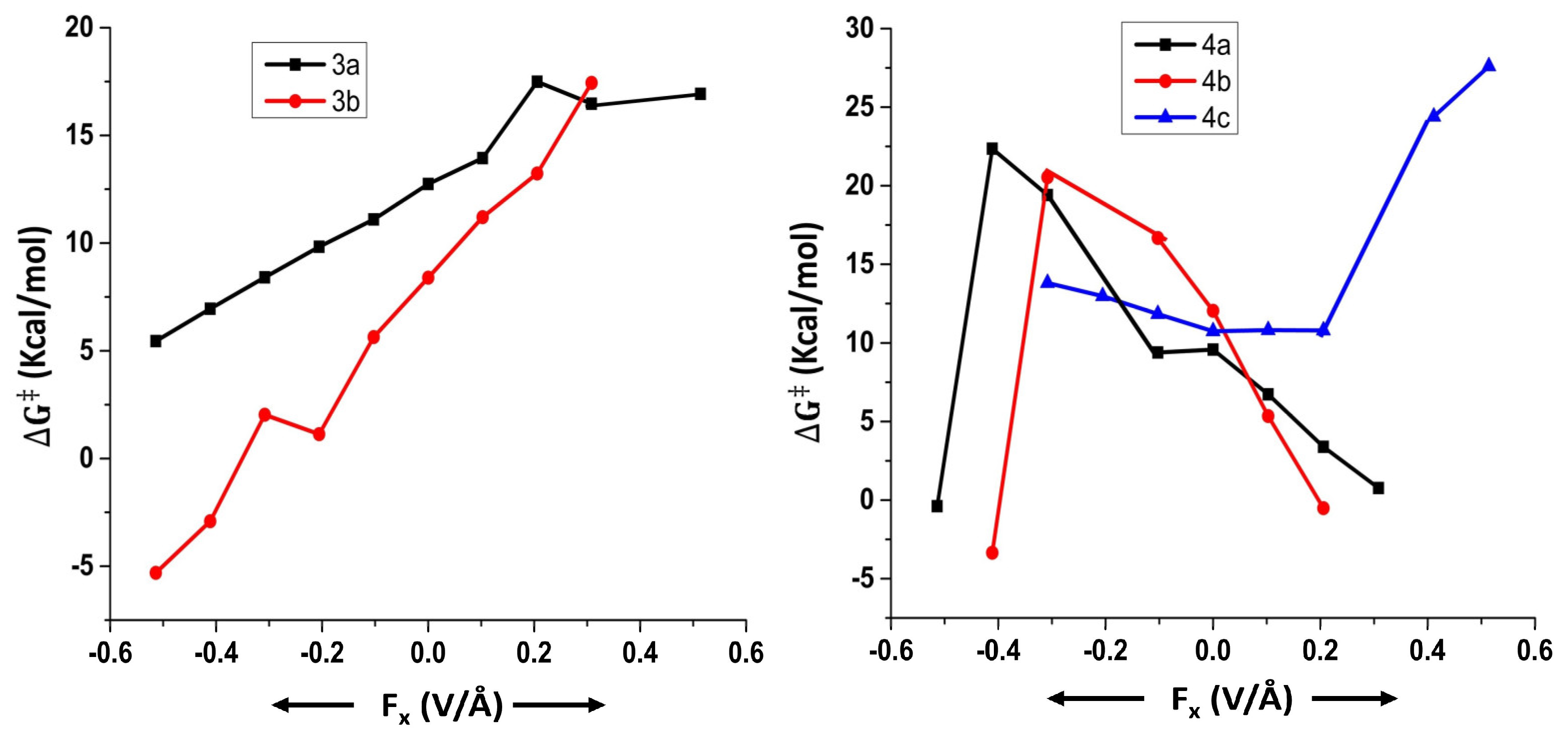
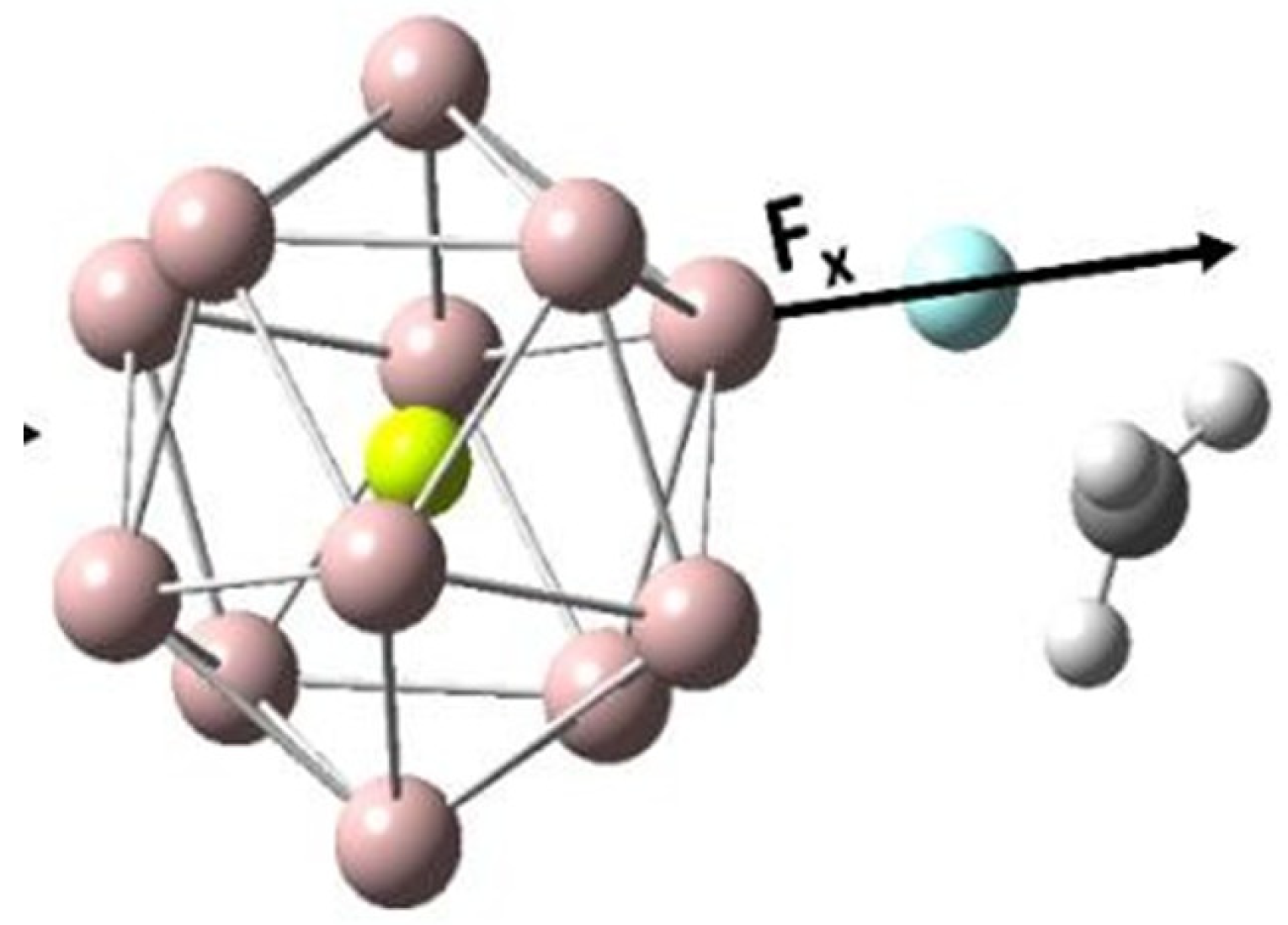
2.3. Effect of OEFs on Free Energy of Activation (Metal Cluster-Mediated Reactions)
2.4. Results Obtained from EDA
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Meir, R.; Chen, H.; Lai, W.; Shaik, S. Oriented Electric Fields Accelerate Diels–Alder Reactions and Control the endo/exo Selectivity. ChemPhysChem 2010, 11, 301–310. [Google Scholar] [CrossRef]
- Timerghazin, Q.K.; Talipov, M.R. Unprecedented External Electric Field Effects on S-Nitrosothiols: Possible Mechanism of Biological Regulation? J. Phys. Chem. Lett. 2013, 4, 1034–1038. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; de Visser, S.P.; Kumar, D. External Electric Field Will Control the Selectivity of Enzymatic-Like Bond Activations. J. Am. Chem. Soc. 2004, 126, 11746–11749. [Google Scholar] [CrossRef]
- Shaik, S.; Ramanan, R.; Danovich, D.; Mandal, D. Structure and reactivity/selectivity control by oriented-external electric fields. Chem. Soc. Rev. 2018, 47, 5125–5145. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, K.; Karmakar, S.; Datta, A. External electric field control: Driving the reactivity of metal-free azide–alkyne click reactions. Phys. Chem. Chem. Phys. 2017, 19, 22482–22486. [Google Scholar] [CrossRef] [PubMed]
- Aragones, A.C.; Haworth, N.L.; Darwish, N.; Ciampi, S.; Bloomfield, N.J.; Wallace, G.G.; Diez-Perez, I.; Coote, M.L. Electrostatic catalysis of a Diels–Alder reaction. Nature 2016, 531, 88–91. [Google Scholar] [CrossRef]
- Dittner, M.; Hartke, B. Globally optimal catalytic fields for a Diels–Alder reaction. J. Chem. Phys. 2020, 152, 114106. [Google Scholar] [CrossRef]
- Gao, Q.F.; Han, Y.; Liang, P.Y.; Meng, J. Influence of an external electric field on the deprotonation reactions of an Fe3+-solvated molecule: A reactive molecular dynamics study. Phys. Chem. Chem. Phys. 2020, 22, 6291–6299. [Google Scholar] [CrossRef] [PubMed]
- English, N.J.; Waldron, C.J. Perspectives on external electric fields in molecular simulation: Progress, prospects and challenges. Phys. Chem. Chem. Phys. 2015, 17, 12407–12440. [Google Scholar] [CrossRef]
- Blyth, M.T.; Noble, B.B.; Russell, I.C.; Coote, M.L. Oriented Internal Electrostatic Fields Cooperatively Promote Ground- and Excited-State Reactivity: A Case Study in Photochemical CO2 Capture. J. Am. Chem. Soc. 2020, 142, 606–613. [Google Scholar] [CrossRef]
- Raynal, M.; Ballester, P.; Vidal-Ferran, A.; van Leeuwen, P.W.N.M. Supramolecular catalysis. Part 1: Non-covalent interactions as a tool for building and modifying homogeneous catalysts. Chem. Soc. Rev. 2014, 43, 1660–1733. [Google Scholar] [CrossRef] [PubMed]
- Ballester, P.; Fujita, M.; Rebek, J. Molecular containers. Chem. Soc. Rev. 2015, 44, 392–393. [Google Scholar] [CrossRef] [PubMed]
- Vallavoju, N.; Sivaguru, J. Supramolecular photocatalysis: Combining confinement and non-covalent interactions to control light initiated reactions. Chem. Soc. Rev. 2014, 43, 4084–4101. [Google Scholar] [CrossRef]
- Mock, W.L.; Irra, T.A.; Wepsiec, J.P.; Manimaran, T.L. Cycloaddition induced by cucurbituril. A case of Pauling principle catalysis. J. Org. Chem. 1983, 48, 3619–3620. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chattaraj, P.K. Bonding, Reactivity, and Dynamics in Confined Systems. J. Phys. Chem. A 2019, 123, 4513–4531. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chattaraj, P.K. Confinement Induced Thermodynamic and Kinetic Facilitation of Some Diels-Alder Reactions Inside a CB [7] Cavitand. J. Comput. Chem. 2018, 39, 151–160. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Hase, W.L.; Hynes, J.T. Current status of transition-state theory. J. Phys. Chem. 1983, 87, 2664–2682. [Google Scholar] [CrossRef]
- Bear, T.; Hase, W.L. Unimolecular Reaction Dynamics–Theory and Experiments; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Pemerantz, A.E.; Camden, J.P.; Chiou, A.S.; Ausfelder, F.; Chawla, N.; Hase, W.L.; Zare, R.N. Reaction products with internal energy beyond the kinematic limit result from trajectories far from the minimum energy path: An example from H + HBr → H2 + Br. J. Am. Chem. Soc. 2005, 127, 16368–16369. [Google Scholar] [CrossRef]
- López, J.G.; Vayner, G.; Lourderaj, U.; Addepalli, S.V.; Kato, S.; DeJong, W.A.; Windus, T.L.; Hase, W.L. A Direct Dynamics Trajectory Study of F− + CH3COOH Reactive Collisions Reveals a Major Non-IRC Reaction Path. J. Am. Chem. Soc. 2007, 129, 9976–9985. [Google Scholar] [CrossRef]
- Ess, D.H. Quasiclassical Direct Dynamics Trajectory Simulations of Organometallic Reactions. Acc. Chem. Res. 2021, 54, 4410–4422. [Google Scholar] [CrossRef]
- Tantillo, D.J. Chapter One—Beyond transition state theory—Non-statistical dynamic effects for organic reactions. Adv. Phys. Org. Chem. 2021, 55, 1–16. [Google Scholar]
- Chakraborty, D.; Hase, W.L. Direct dynamics simulation of the thermal O(3P) + dimethylamine reaction in the triplet surface. I. Rate constant and product branching. J. Phys. Org. Chem. 2022, e4339. [Google Scholar] [CrossRef]
- Tannor, D.J.; Rice, S.A. Control of selectivity of chemical reaction via control of wave packet evolution. J. Chem. Phys. 1985, 83, 5013–5018. [Google Scholar] [CrossRef]
- Judson, R.S.; Rabitz, H. Teaching lasers to control molecules. Phys. Rev. Lett. 1992, 68, 1500–1503. [Google Scholar] [CrossRef]
- Zewail, A.H. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar] [CrossRef]
- Wyatt, R.E. Quantum Dynamics with Trajectories: Introduction to Quantum Hydrodynamics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Chattaraj, P.K.; Maiti, B. Reactivity Dynamics in Atom−Field Interactions: A Quantum Fluid Density Functional Study. J. Phys. Chem. A 2001, 105, 169–183. [Google Scholar] [CrossRef]
- Sarkar, U.; Khatua, M.; Chattaraj, P.K. A Tug-of-war between Electronic Excitation and Confinement in a Dynamical Context. Phys. Chem. Chem. Phys. 2012, 14, 1716–1727. [Google Scholar] [CrossRef] [PubMed]
- Miyaura, N.; Suzuki, A. Palladium-Catalyzed Cross-Coupling Reactions of Organoboron Compounds. Chem. Rev. 1995, 95, 2457–2483. [Google Scholar] [CrossRef]
- Barder, T.E.; Walker, S.D.; Martinelli, J.R.; Buchwald, S.L. Catalysts for Suzuki—Miyaura Coupling Processes: Scope and Studies of the Effect of Ligand Structure. J. Am. Chem. Soc. 2005, 127, 4685–4696. [Google Scholar] [CrossRef]
- Lu, J.; Donnecke, S.; Paci, I.; Leitch, D.C. A Reactivity Model for Oxidative Addition to Palladium Enables Quantitative Predictions for Catalytic Cross-Coupling Reactions. Chem. Sci. 2022, 13, 3477–3488. [Google Scholar] [CrossRef]
- Norman, J.P.; Larson, N.G.; Neufeldt, S.R. Different Oxidative Addition Mechanisms for 12- and 14-Electron Palladium(0) Explain Ligand-Controlled Divergent Site Selectivity. ACS Catal. 2022, 12, 8822–8828. [Google Scholar] [CrossRef]
- Besora, M.; Maseras, F. The Diverse Mechanisms for the Oxidative Addition of C−Br Bonds to Pd(PR3) and Pd(PR3)2 Complexes. Dalton Trans. 2019, 48, 16242–16248. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Chattaraj, P.K. Reactions Involving Some Gas Molecules through Sequestration on Al12Be Cluster: An Electron Density Based Study. J. Comput. Chem. 2018, 39, 535–545. [Google Scholar] [CrossRef] [PubMed]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016.
- Yu, H.S.; He, X.; Truhlar, D.G. MN15-L: A New Local Exchange-Correlation Functional for Kohn–Sham Density Functional Theory with Broad Accuracy for Atoms, Molecules, and Solids. J. Chem. Theory Comput. 2016, 12, 1280–1293. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Long-range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016.
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]

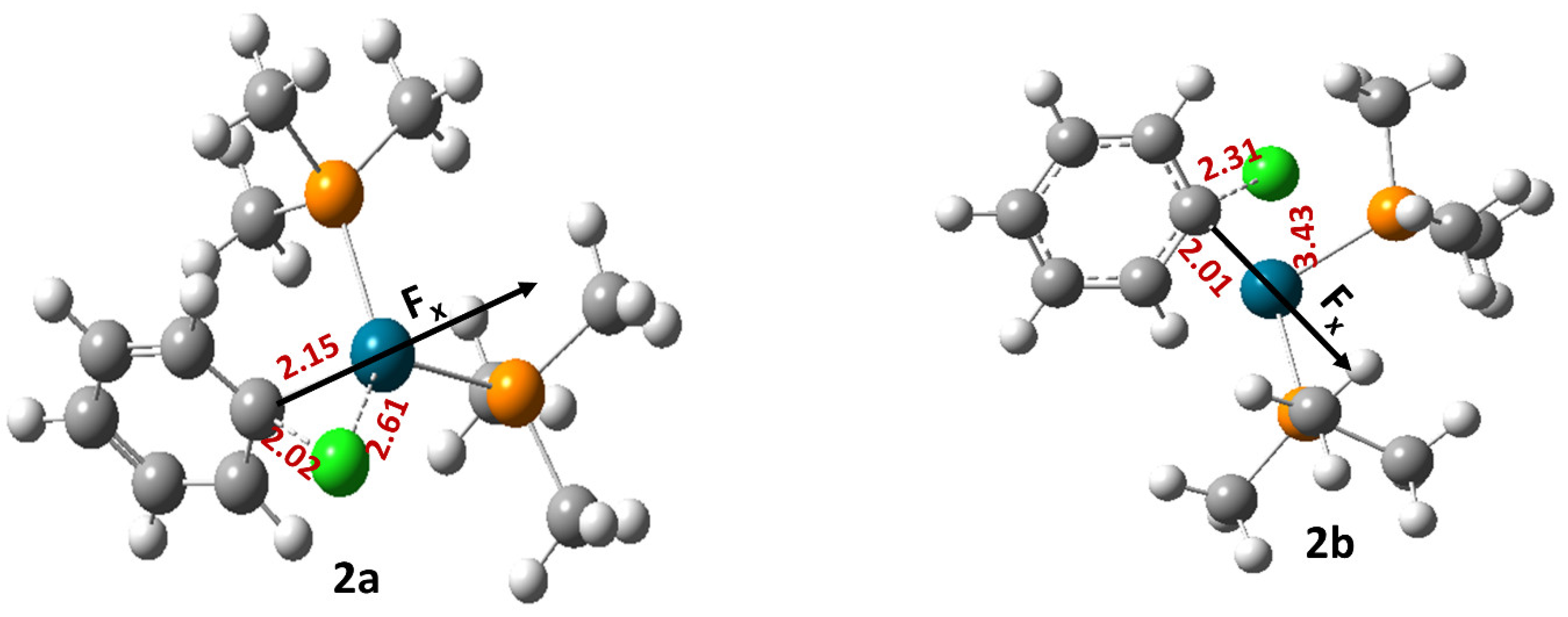
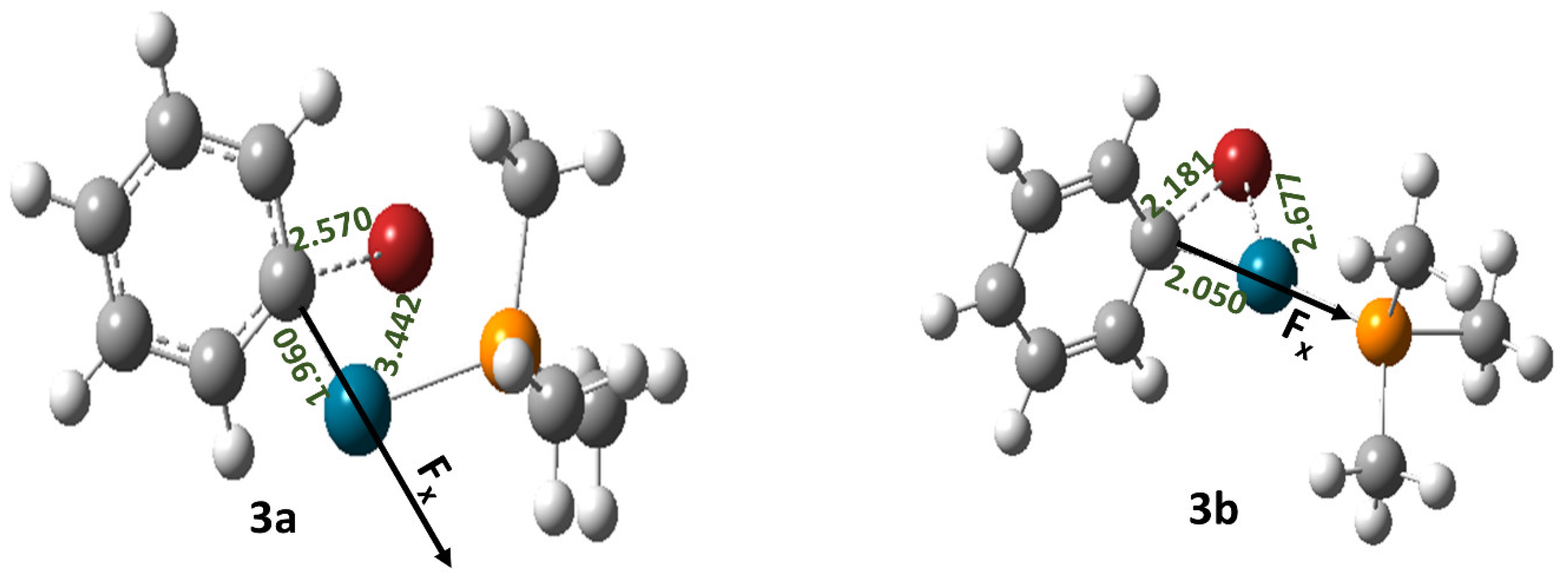
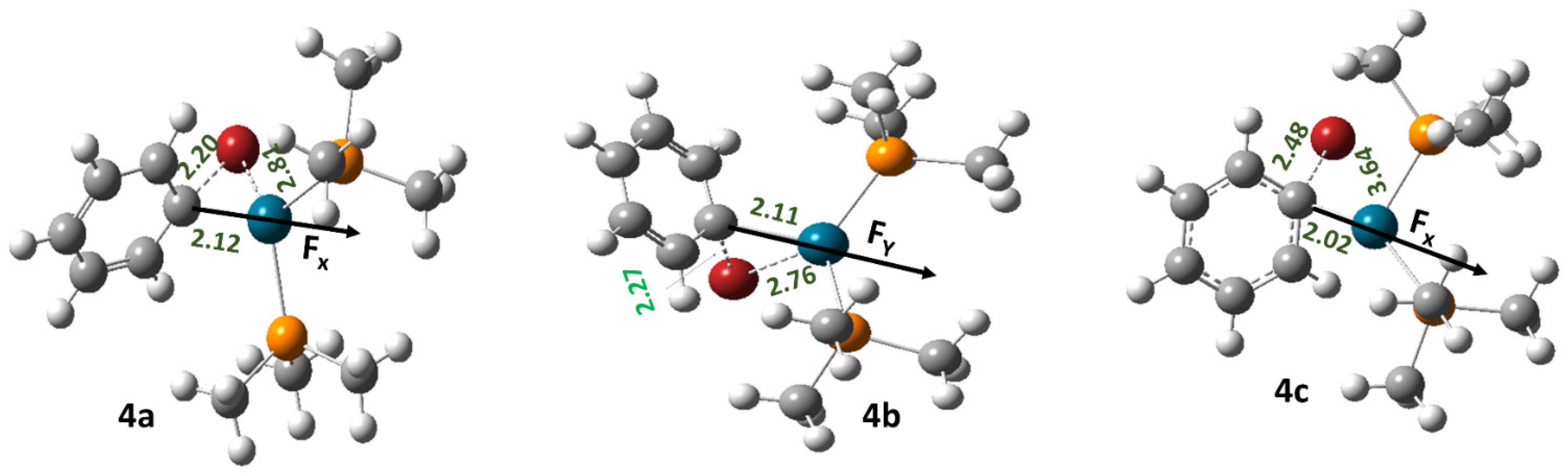
| Field Strength (Fx) (V/Å) | Dipole Moment (μx) (D) (1a) | Free Energy of Activation (∆G‡) (kcal/mol) (1a) | Rate Constant (k, s−1) (1a) | Dipole Moment (μx) (D) (1b) | Free Energy of Activation (∆G‡) (kcal/mol) (1b) | Rate Constant (k, s−1) (1b) | Dipole Moment (μx) (D) (1c) | Free Energy of Activation (∆G‡) (kcal/mol) (1c) | Rate Constant (k, s−1) (1c) |
|---|---|---|---|---|---|---|---|---|---|
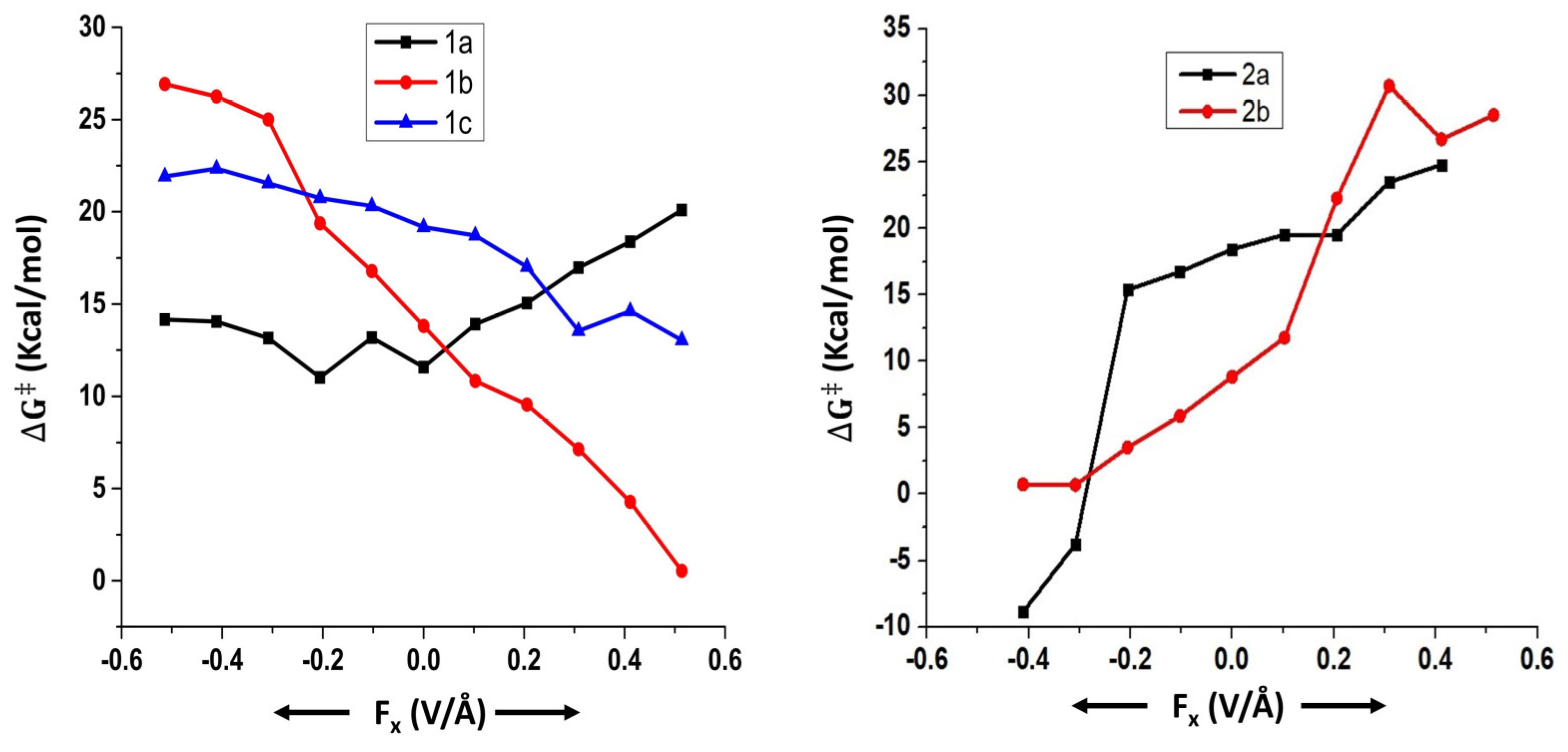
| −0.5140 | 9.90 | 14.2 | 2.6 × 102 | 8.02 | 26.9 | 1.1 × 10−7 | 5.91 | 21.9 | 5.4 × 10−4 |
| −0.4112 | 8.03 | 14.0 | 3.1 × 102 | 5.16 | 26.3 | 3.5 × 10−7 | 3.62 | 22.3 | 2.6 × 10−4 |
| −0.3084 | 6.39 | 13.2 | 1.4 × 103 | 2.98 | 25.0 | 2.9 × 10−6 | 1.43 | 21.5 | 1.0 × 10−3 |
| −0.2056 | 5.12 | 11.0 | 5.2 × 104 | 0.71 | 19.4 | 3.9 × 10−2 | −0.66 | 20.7 | 3.9 × 10−3 |
| −0.1028 | 4.05 | 13.2 | 1.4 × 103 | −1.34 | 16.8 | 3.1 | −2.07 | 20.3 | 8.1 × 10−3 |
| 0 | 3.20 | 11.6 | 2.0 × 104 | −3.55 | 13.8 | 4.7 × 102 | −4.72 | 19.2 | 5.5 × 10−2 |
| 0.1028 | 2.25 | 13.9 | 3.9 × 102 | −5.10 | 10.8 | 7.1 × 104 | −6.75 | 18.7 | 1.2 × 10−1 |
| 0.2056 | 1.13 | 15.1 | 5.7 × 101 | −6.90 | 9.6 | 6.2 × 105 | −8.77 | 17.0 | 2.1 |
| 0.3084 | −0.08 | 17.0 | 2.2 | −8.70 | 7.1 | 3.7 × 107 | −10.86 | 13.5 | 7.3 × 102 |
| 0.4112 | −1.36 | 18.4 | 2.1 × 10−1 | −10.63 | 4.3 | 4.6 × 109 | −12.96 | 14.6 | 1.2 × 102 |
| 0.5140 | −2.70 | 20.1 | 1.2 × 10−2 | −12.77 | 0.5 | 2.5 × 1012 | −15.03 | 13.0 | 1.7 × 103 |
| Field Strength (Fx) (V/Å) | Dipole Moment (μx) (D) (2a) | Free Energy of Activation (∆G‡) (kcal/mol) (2a) | Rate Constant (k, s−1) (2a) | Dipole Moment (μx) (D) (2b) | Free Energy of Activation (∆G‡) (kcal/mol) (2b) | Rate Constant (k, s−1) (2b) |
|---|---|---|---|---|---|---|
| −0.5140 | - | *** | - | - | *** | - |
| −0.4112 | 16.57 | −8.9 | 2.0 × 1019 | 18.12 | 0.7 | 1.8 × 1012 |
| −0.3084 | 16.22 | −3.8 | 3.5 × 1015 | 16.92 | 0.7 | 1.9 × 1012 |
| −0.2056 | 8.53 | 15.4 | 3.3 × 101 | 15.30 | 3.5 | 1.6 × 1010 |
| −0.1028 | 6.00 | 16.7 | 3.3 | 13.28 | 5.9 | 3.0 × 108 |
| 0 | 3.50 | 18.4 | 1.9 × 10−1 | 11.03 | 8.8 | 2.1 × 106 |
| 0.1028 | 1.05 | 19.5 | 3.0 × 10−2 | 8.38 | 11.8 | 1.5 × 104 |
| 0.2056 | −2.33 | 19.5 | 3.1 × 10−2 | 5.61 | 22.3 | 3.0 × 10−4 |
| 0.3084 | −4.99 | 23.5 | 3.8 × 10−5 | 2.30 | 30.7 | 1.8 × 10−10 |
| 0.4112 | −7.51 | 24.8 | 4.2 × 10−6 | −7.56 | 26.7 | 1.6 × 10−7 |
| 0.5140 | - | *** | - | −10.20 | 28.5 | 7.5 × 10−9 |
| Field Strength (Fx) (V/Å) | Dipole Moment (μx) (D) (3a) | Free Energy of Activation (∆G‡) (kcal/mol) (3a) | Rate Constant (k, s−1) (3a) | Dipole Moment (μx) (D) (3b) | Free Energy of Activation (∆G‡) (kcal/mol) (3b) | Rate Constant (k, s−1) (3b) |
|---|---|---|---|---|---|---|
| −0.5140 | 15.04 | 5.4 | 6.3 × 108 | 11.98 | −5.3 | 4.8 × 1016 |
| −0.4112 | 12.90 | 6.9 | 5.0 × 107 | 10.22 | −2.9 | 8.4 × 1014 |
| −0.3084 | 10.78 | 8.4 | 4.2 × 106 | 8.47 | 2.0 | 2.0 × 1011 |
| −0.2056 | 8.64 | 9.8 | 3.9 × 105 | 6.84 | 1.1 | 9.2 × 1011 |
| −0.1028 | 6.50 | 11.1 | 4.6 × 104 | 5.20 | 5.6 | 4.6 × 108 |
| 0 | 4.37 | 12.7 | 2.8 × 103 | 2.85 | 8.4 | 4.4 × 106 |
| 0.1028 | 2.21 | 13.9 | 3.7 × 102 | 0.89 | 11.2 | 3.8 × 104 |
| 0.2056 | 0.07 | 17.5 | 9.3 × 10−1 | −1.27 | 13.2 | 1.2 × 103 |
| 0.3084 | −2.10 | 16.5 | 5.3 | −3.52 | 17.4 | 1.0 |
| 0.4112 | - | # | # | −5.72 | # | - |
| 0.5140 | −6.65 | 16.9 | 2.4 | - | # | - |
| Field Strength (Fx) (V/Å) | Dipole Moment (μx) (D) (4a) | Free Energy of Activation (∆G‡) (kcal/mol) (4a) | Rate Constant (k, s−1) (4a) | Dipole Moment (μy) (D) (4b) | Free Energy of Activation (∆G‡) (kcal/mol) (4b) | Rate Constant (k, s−1) (4b) | Dipole Moment (μx) (D) (4c) | Free Energy of Activation (∆G‡) (kcal/mol) (4c) | Rate Constant (k, s−1) (4c) |
|---|---|---|---|---|---|---|---|---|---|
| −0.5140 | 12.36 | −0.4 | 1.2 × 1013 | 15.57 | *** | - | *** | *** | - |
| −0.4112 | 6.23 | 22.4 | 2.5 × 10−4 | 13.42 | −3.3 | 1.8 × 1015 | *** | *** | - |
| −0.3084 | 4.52 | 19.4 | 3.7 × 10−2 | 11.11 | 20.5 | 5.4 × 10−3 | 3.62 | 13.8 | 4.6 × 102 |
| −0.2056 | - | *** | - | - | *** | - | −5.49 | 13.0 | 1.9 × 103 |
| −0.1028 | −0.28 | 9.4 | 8.1 × 105 | 6.31 | 16.7 | 3.7 | −9.18 | 11.8 | 1.3 × 104 |
| 0 | −10.72 | 9.6 | 6.0 × 105 | 3.88 | 12.0 | 9.2 × 103 | −11.80 | 10.7 | 8.2 × 104 |
| 0.1028 | −15.53 | 6.7 | 7.2 × 107 | 1.58 | 5.3 | 7.5 × 108 | −13.93 | 10.8 | 7.3 × 104 |
| 0.2056 | −15.93 | 3.4 | 2.0 × 1010 | −0.73 | −0.5 | 1.5 × 1013 | −15.33 | 10.8 | 7.7 × 104 |
| 0.3084 | −15.50 | 0.8 | 1.7 × 1012 | −3.11 | *** | - | - | *** | - |
| 0.4112 | *** | - | - | −5.56 | *** | - | -5.5 | 24.4 | 7.5 × 10−6 |
| 0.5140 | *** | - | - | −8.06 | *** | - | -8.05 | 27.6 | 3.5 × 10−6 |
| Field Strength (Fx) (V/Å) | Dipole Moment (μx) (D) | Free Energy of Activation (∆G‡) (kcal/mol) | Rate Constant (k, s−1) |
|---|---|---|---|
| −0.5140 | 10.42 | 43.8 | 5.2 × 10−20 |
| −0.4112 | 7.68 | 38.9 | 1.8 × 10−16 |
| −0.3084 | 4.97 | 34.5 | 3.5 × 10−13 |
| −0.2056 | 2.25 | 29.7 | 9.7 × 10−10 |
| −0.1028 | −0.48 | 25.4 | 1.4 × 10−6 |
| 0 | −3.26 | 20.6 | 4.7 × 10−3 |
| 0.1028 | −6.06 | 16.2 | 8.6 |
| 0.2056 | −8.90 | 11.7 | 1.6 × 104 |
| 0.3084 | −11.20 | 8.8 | 2.2 × 106 |
| 0.4112 | −14.81 | 3.8 | 1.0 × 1010 |
| 0.5140 | −17.97 | −0.9 | 3.0 × 1013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arepalli, N.; Mondal, S.; Chakraborty, D.; Chattaraj, P.K. Impact of Static-Oriented Electric Fields on the Kinetics of Some Representative Suzuki–Miyaura and Metal-Cluster Mediated Reactions. Molecules 2023, 28, 6169. https://doi.org/10.3390/molecules28166169
Arepalli N, Mondal S, Chakraborty D, Chattaraj PK. Impact of Static-Oriented Electric Fields on the Kinetics of Some Representative Suzuki–Miyaura and Metal-Cluster Mediated Reactions. Molecules. 2023; 28(16):6169. https://doi.org/10.3390/molecules28166169
Chicago/Turabian StyleArepalli, Navya, Sukanta Mondal, Debdutta Chakraborty, and Pratim Kumar Chattaraj. 2023. "Impact of Static-Oriented Electric Fields on the Kinetics of Some Representative Suzuki–Miyaura and Metal-Cluster Mediated Reactions" Molecules 28, no. 16: 6169. https://doi.org/10.3390/molecules28166169
APA StyleArepalli, N., Mondal, S., Chakraborty, D., & Chattaraj, P. K. (2023). Impact of Static-Oriented Electric Fields on the Kinetics of Some Representative Suzuki–Miyaura and Metal-Cluster Mediated Reactions. Molecules, 28(16), 6169. https://doi.org/10.3390/molecules28166169






