Exploring the Relationship between Reactivity and Electronic Structure in Isorhodanine Derivatives Using Computer Simulations
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
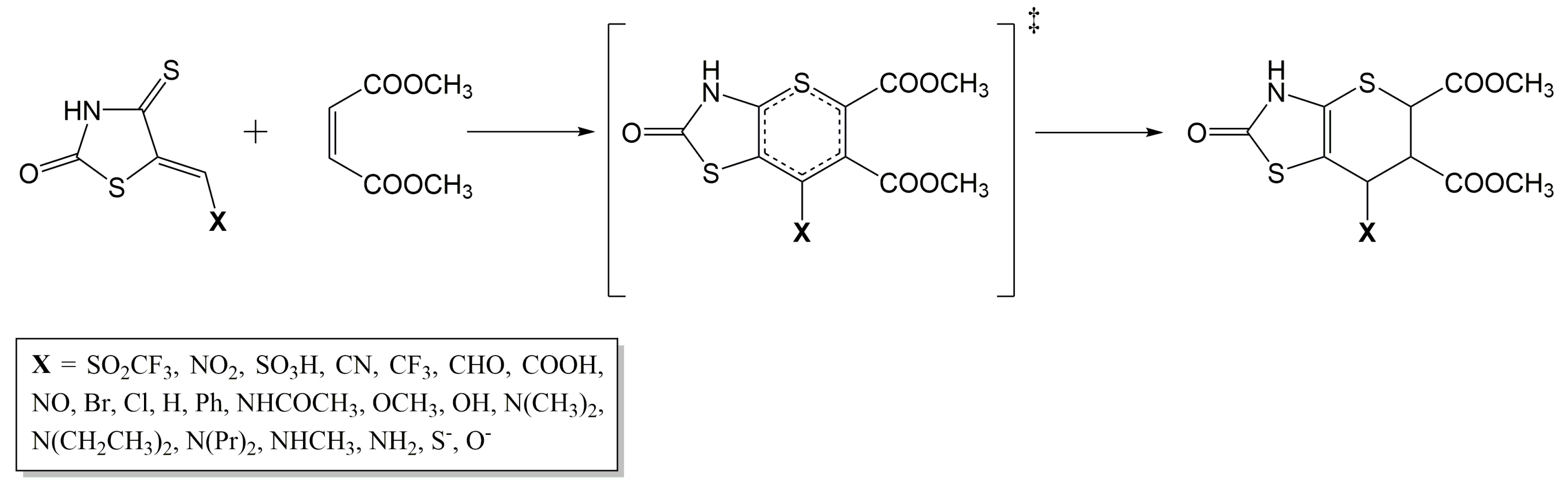
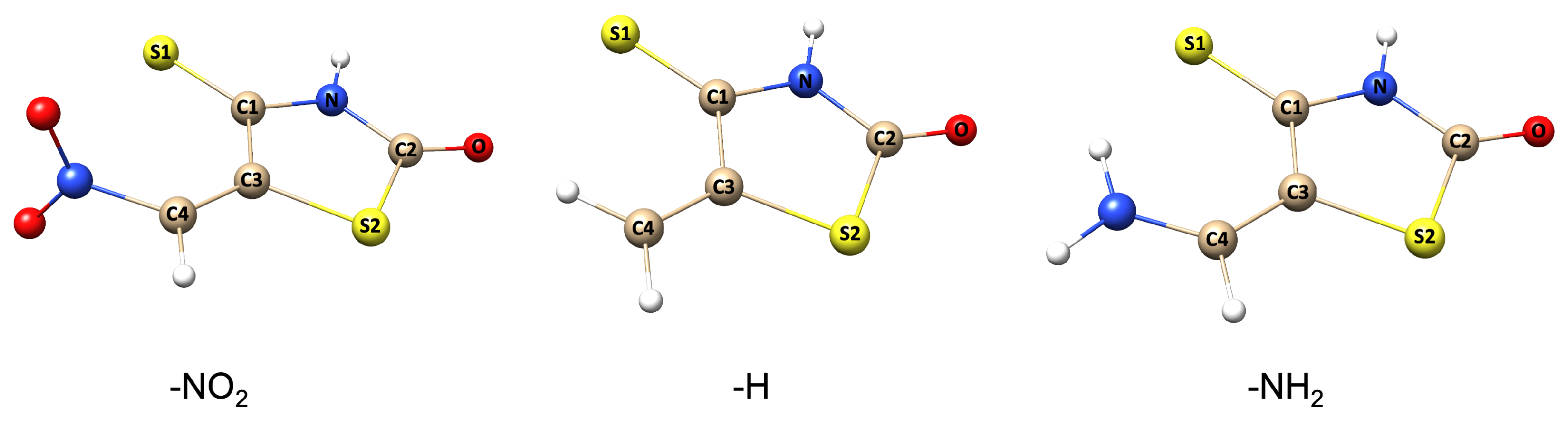
3.1. Geometrical Structures and Energetics
3.2. The Electronic Properties of Isorhodanine Derivatives
4. Conclusions
- The withdrawing and donating substituents produce similar values, and one may assume similar reactivity. However, different conclusions were reached by analyzing values. The free Gibbs reaction energy depends heavily on the chemical group next to the C=C bond. Smaller values were obtained for reactions with EWGs, indicating that the cycloaddition of IsRd with DMm is more favored for derivatives with withdrawing groups. Only for the derivative in the gas phase and PCM model, is positive, making the cycloaddition an endothermic process. Comparison of and in acetic acid and in the gas phase shows that acetic acid has a minimal impact on the energetics of the reaction between IsRd and DMm.
- The analysis of frontier DFT orbitals performed on molecules with EWGs shows a decrease in the electronic energy of HOMO and LUMO orbitals, indicating that a NED character of DA reaction is expected. For EDGs, the energy of frontier MOs increases, resulting in an IED type of cycloaddition reaction.
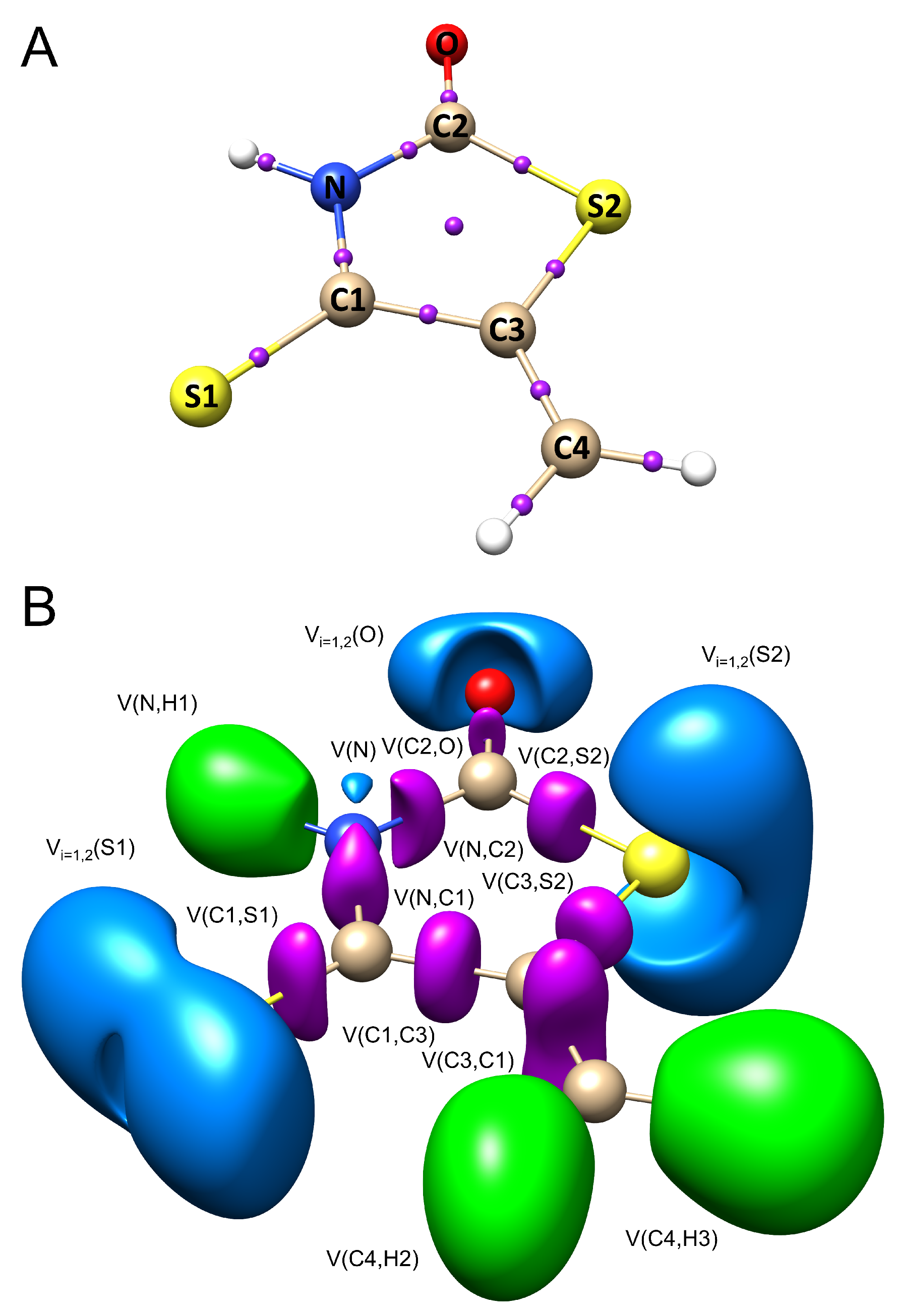
- Topological analysis of shows positive values of the Laplacian for BCPs only for the C1–S1 and C2–O bonds, indicating a depletion of electron density around BCP. The Laplacian values for other bonds are negative, indicating a concentration of electron density around BCP. Thus, C1–S1 and C2–O bonds exhibit a different nature than observed for other covalent bonds where both atoms share electron density. The DI values suggest a single bond type for N–H1, C4–H2, N–C2, N–C1, C1–C3, C2–S2, C3–S2 and a double type for C1–S1 and C3–C4 bonds. The bonding type for C2–O cannot be interpreted by means of DI.
- Topological analysis of ELF partly confirms the results based on electron density. The topological bond orders for C1–S1 and C2–O are 1.28 and 1.23, respectively, thus one may consider these interactions to be of a single nature. Analysis of suggests that the , and , representations for the carbon–oxygen and carbon–sulphur interactions, instead of the classical C=O and S=O formulas, provide a better description of the bond nature.
- The most intriguing discovery was obtained by analyzing the relationship between and the basin populations for the C=S and C=C bonds in the IsRd molecule. The analysis of ELF was performed on isolated molecules. According to the proposed DA reaction mechanism, the electron density from these bonds is distributed to the regions of the two new C–S and C–C bonds that are formed between the IsRd and DMm molecules. The regression analysis applied to this relationship shows that the values of the sum of the populations for the V(C1,S1) and basins, ∑[V(C3, C4), V(C1, S1)], correlates with the value of the free Gibbs reaction energy. Large negative values of correspond to large values of the sum of basin populations. The favorability of the studied DA reaction, which is associated with a rearrangement of chemical bonds and electron density, is high when the C=S and C=C bonds are better saturated with electron density.
- The HOMA values indicate low aromaticity of the IsRd ring.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Komarista, I. Synthesis, Transformations and Biological Activity of Some Azolidones and Their Condensed Derivatives. Ph.D. Thesis, I.M. Sechenov First State Medical Institute, Moscow, Russia, 1989. [Google Scholar]
- Kassab, N.A.E.L.; Allah, S.O.A.; Messeha, N.A. Reactions with 5-Substituted 2-Thiazolidinone-4-thiones. Part IV. J. Prakt. Chem. 1974, 316, 209–214. [Google Scholar] [CrossRef]
- Kassab, N.A.; Abd-Allah, S.O.; Abd-El-Razik, F.M. ChemInform Abstract: Reactions of 5-Substituted 2-Thiazolidinone-4-Thiones with Dienophiles, Acrylonitrile, Ethyl Acrylate, Styryl Ethyl Ketone, Ω-Nitrostyrene, N-Arylmaleimides and Maleic Anhydride. Chem. Inf. 1977, 8, 24. [Google Scholar] [CrossRef]
- Komaritsa, I.D.; Baranov, S.N.; Grishuk, A.P. 4-Thiazolidines, derivatives and analogs. Chem. Heterocycl. Compd. 1967, 3, 533–534. [Google Scholar] [CrossRef]
- Omar, M.T.; El-Khamry, A.; Youssef, A.M.; Ramadan, S. Synthesis and Stereochemistry of Thiapyranothiazoles as Diels-Alder Adducts Obtained from Spirodimers of 1,3-Thiazolidines with Cinnamic Acid and its Ester. Phosphorus Sulfur Silicon Relat. Elem. 2003, 178, 721–735. [Google Scholar] [CrossRef]
- Plevachuk, N.E.; Komaritsa, I.D. A study of azolidones and their derivatives. Chem. Heterocycl. Compd. 1970, 6, 144–145. [Google Scholar] [CrossRef]
- Grischuk, A.P.; Komaritsa, I.D.; Baranov, S.N. 4-Thionazolidones, derivatives and analogs. Chem. Heterocycl. Compd. 1966, 2, 541–543. [Google Scholar] [CrossRef]
- Metwally, N.H. A simple green synthesis of (Z)-5-arylmethylene-4-thioxothiazolidines and thiopyrano[2,3-d]thiazolidine-2-thiones in PEG-400 under catalyst-free conditions. J. Sulfur Chem. 2014, 35, 528–537. [Google Scholar] [CrossRef]
- Lozynskyi, A.; Zimenkovsky, B.; Lesyk, R. Synthesis and Anticancer Activity of New Thiopyrano[2,3-d]thiazoles Based on Cinnamic Acid Amides. Sci. Pharm. 2014, 82, 723–734. [Google Scholar] [CrossRef]
- Lozynskyi, A.; Zasidko, V.; Atamanyuk, D.; Kaminskyy, D.; Derkach, H.; Karpenko, O.; Ogurtsov, V.; Kutsyk, R.; Lesyk, R. Synthesis, antioxidant and antimicrobial activities of novel thiopyrano[2,3-d]thiazoles based on aroylacrylic acids. Mol. Divers. 2017, 21, 427–436. [Google Scholar] [CrossRef]
- Lozynskyi, A.; Zimenkovsky, B.; Nektegayev, I.; Lesyk, R. Arylidene pyruvic acids motif in the synthesis of new thiopyrano[2,3-d]thiazoles as potential biologically active compounds. Heterocycl. Commun. 2015, 21, 55–59. [Google Scholar] [CrossRef]
- Zelisko, N.; Atamanyuk, D.; Ostapiuk, Y.; Bryhas, A.; Matiychuk, V.; Gzella, A.; Lesyk, R. Synthesis of fused thiopyrano[2,3-d][1,3]thiazoles via hetero-Diels–Alder reaction related tandem and domino processes. Tetrahedron 2015, 71, 9501–9508. [Google Scholar] [CrossRef]
- Zelisko, N.; Atamanyuk, D.; Vasylenko, O.; Bryhas, A.; Matiychuk, V.; Gzella, A.; Lesyk, R. Crotonic, cynnamic, and propiolic acids motifs in the synthesis of thiopyrano[2,3-d][1,3]thiazoles via hetero-Diels–Alder reaction and related tandem processes. Tetrahedron 2014, 70, 720–729. [Google Scholar] [CrossRef]
- Lozynskyi, A.; Golota, S.; Zimenkovsky, B.; Atamanyuk, D.; Gzella, A.; Lesyk, R. Synthesis, anticancer and antiviral activities of novel thiopyrano[2,3-d]thiazole-6-carbaldehydes. Phosphorus Sulfur Silicon Relat. Elem. 2016, 191, 1245–1249. [Google Scholar] [CrossRef]
- Kryshchyshyn, A.P.; Atamanyuk, D.V.; Kaminskyy, D.V.; Grellier, P.; Lesyk, R.B. Investigation of anticancer and anti-parasitic activity of thiopyrano[2,3-d]thiazoles bearing norbornane moiety. Biopolym. Cell 2017, 33, 183–205. [Google Scholar] [CrossRef]
- Lesyk, R.; Zimenkovsky, B.; Atamanyuk, D.; Jensen, F.; Kieć-Kononowicz, K.; Gzella, A. Anticancer thiopyrano[2,3-d][1,3]thiazol-2-ones with norbornane moiety. Synthesis, cytotoxicity, physico-chemical properties, and computational studies. Bioorganic Med. Chem. 2006, 14, 5230–5240. [Google Scholar] [CrossRef]
- Atamanyuk, D.; Zimenkovsky, B.; Lesyk, R. Synthesis and anticancer activity of novel thiopyrano[2,3-d]thiazole-based compounds containing norbornane moiety. J. Sulfur Chem. 2008, 29, 151–162. [Google Scholar] [CrossRef]
- Lesyk, R. Drug design: 4-thiazolidinones applications. Part 1. Synthetic routes to the drug-like molecules. J. Med Sci. 2020, 89, e406. [Google Scholar] [CrossRef]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The density functional viewpoint. J. Chem. Phys. 1978, 68, 3801–3807. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc. 1984, 106, 4049–4050. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A molecular electron density theory study of the participation of tetrazines in aza-Diels–Alder reactions. RSC Adv. 2020, 10, 15394–15405. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A molecular electron density theory study of the enhanced reactivity of aza aromatic compounds participating in Diels–Alder reactions. Org. Biomol. Chem. 2020, 18, 292–304. [Google Scholar] [CrossRef] [PubMed]
- Usharani, D.; Lai, W.; Li, C.; Chen, H.; Danovich, D.; Shaik, S. A tutorial for understanding chemical reactivity through the valence bond approach. Chem. Soc. Rev. 2014, 43, 4968–4988. [Google Scholar] [CrossRef] [PubMed]
- Bickelhaupt, F.M.; Houk, K.N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef] [PubMed]
- Polo, V.; Andres, J.; Berski, S.; Domingo, L.R.; Silvi, B. Understanding Reaction Mechanisms in Organic Chemistry from Catastrophe Theory Applied to the Electron Localization Function Topology. J. Phys. Chem. A 2008, 112, 7128–7136. [Google Scholar] [CrossRef]
- Sengupta, A.; Li, B.; Svatunek, D.; Liu, F.; Houk, K.N. Cycloaddition Reactivities Analyzed by Energy Decomposition Analyses and the Frontier Molecular Orbital Model. Accounts Chem. Res. 2022, 55, 2467–2479. [Google Scholar] [CrossRef]
- Tejchman, W.; Michalski, M.; Zborowski, K.K.; Berski, S. Why are rhodanines less efficient reagents in Diels–Alder reactions than isorhodanines? A quantum chemical study. J. Mol. Model. 2019, 25, 190. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in molecules. Accounts Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Accounts 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Wu, Z.H.; Fang, D.C. DFT study on ruthenium-catalyzed N-methylbenzamide-directed 1,4-addition of the ortho C–H bond to maleimide via C–H/C–C activation. Org. Chem. Front. 2022, 9, 6808–6816. [Google Scholar] [CrossRef]
- Nazarski, R.B.; Justyna, K.; Leśniak, S.; Chrostowska, A. A Benefit of Using the IDSCRF- over UFF-Radii Cavities and Why Joint Correlations of NMR Chemical Shifts Can Be Advantageous: Condensed Pyridines as an IEF-PCM/GIAO/DFT Case Study. J. Phys. Chem. A 2016, 120, 9519–9528. [Google Scholar] [CrossRef]
- Nazarski, R.B.; Wałejko, P.; Witkowski, S. Multi-conformer molecules in solutions: An NMR-based DFT/MP2 conformational study of two glucopyranosides of a vitamin E model compound. Org. Biomol. Chem. 2016, 14, 3142–3158. [Google Scholar] [CrossRef]
- Mu, W.H.; Chasse, G.A.; Fang, D.C. Test and modification of the van der Waals’ radii employed in the default PCM model. Int. J. Quantum Chem. 2008, 108, 1422–1434. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. TopMoD Package; Universite Pierre et Marie Curie: Paris, France, 1997. [Google Scholar]
- Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of .pi.-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- Bruno, I.J.; Cole, J.C.; Edgington, P.R.; Kessler, M.; Macrae, C.F.; McCabe, P.; Pearson, J.; Taylor, R. New software for searching the Cambridge Structural Database and visualizing crystal structures. Acta Crystallogr. Sect. B 2002, 58, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Houk, K.N. Frontier molecular orbital theory of cycloaddition reactions. Accounts Chem. Res. 1975, 8, 361–369. [Google Scholar] [CrossRef]
- Malcolm, N.O.J.; Popelier, P.L.A. The full topology of the Laplacian of the electron density: Scrutinising a physical basis for the VSEPR model. Faraday Discuss. 2003, 124, 353–363. [Google Scholar] [CrossRef]
- Silvi, B. The synaptic order: A key concept to understand multicenter bonding. J. Mol. Struct. 2002, 614, 3–10. [Google Scholar] [CrossRef]
- Fradera, X.; Austen, M.A.; Bader, R.F.W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. [Google Scholar] [CrossRef]
- Berski, S.; Gajewski, G.; Latajka, Z. Electron localization function (ELF) study on intramolecular delocalization of the electron density in the H2X, H2CX and XO2 (X=O, S, Se, Te) molecules: Role of the atomic core and lone pair. J. Mol. Struct. 2007, 844–845, 278–285. [Google Scholar] [CrossRef]


| R | Gas Phase | Solvent (Acetic Acid) | ||||||
|---|---|---|---|---|---|---|---|---|
| (C,C) | (C,S) | (C,C) | (C,S) | |||||
| 2.284 | 2.527 | 18.47 | −32.66 | 2.291 | 2.520 | 18.28 | −34.02 | |
| 2.259 | 2.545 | 19.17 | −34.09 | 2.264 | 2.543 | 19.73 | −34.24 | |
| 2.293 | 2.530 | 22.72 | −32.37 | 2.296 | 2.528 | 18.99 | −37.07 | |
| 2.258 | 2.437 | 22.34 | −22.08 | 2.263 | 2.442 | 22.76 | −22.23 | |
| 2.279 | 2.503 | 20.97 | −32.25 | 2.287 | 2.503 | 21.60 | −32.63 | |
| 2.210 | 2.506 | 19.47 | −24.07 | 2.218 | 2.499 | 19.17 | −25.49 | |
| 2.236 | 2.526 | 19.52 | −27.48 | 2.243 | 2.525 | 19.71 | −27.97 | |
| 2.232 | 2.463 | 21.05 | −25.35 | 2.245 | 2.458 | 19.62 | −27.16 | |
| 2.255 | 2.499 | 23.04 | −28.85 | 2.263 | 2.497 | 23.36 | −29.19 | |
| 2.244 | 2.494 | 22.84 | −28.34 | 2.252 | 2.492 | 23.05 | −28.71 | |
| 2.216 | 2.458 | 24.78 | −18.67 | 2.213 | 2.473 | 20.48 | −23.14 | |
| 2.283 | 2.451 | 20.27 | −25.07 | 2.292 | 2.448 | 20.49 | −25.49 | |
| 2.220 | 2.377 | 26.49 | −13.35 | 2.241 | 2.364 | 26.94 | −14.12 | |
| 2.245 | 2.416 | 22.40 | −21.89 | 2.257 | 2.396 | 23.28 | −20.00 | |
| 2.239 | 2.421 | 22.49 | −22.75 | 2.246 | 2.401 | 23.44 | −20.50 | |
| 2.271 | 2.254 | 20.52 | −15.09 | 2.334 | 2.175 | 21.42 | −11.35 | |
| 2.284 | 2.247 | 19.76 | −15.94 | 2.346 | 2.176 | 20.86 | −12.82 | |
| 2.279 | 2.248 | 19.88 | −15.57 | 2.341 | 2.179 | 20.59 | −12.65 | |
| 2.208 | 2.314 | 27.95 | −4.99 | 2.250 | 2.252 | 28.26 | −3.90 | |
| 2.205 | 2.338 | 28.67 | −6.72 | 2.236 | 2.281 | 28.79 | −6.02 | |
| 2.293 | 2.132 | 26.91 | 1.61 | 2.326 | 2.192 | 26.50 | −6.71 | |
| 2.064 | 1.951 | 28.37 | 23.39 | 2.181 | 1.974 | 27.13 | 16.52 | |
| R | HOMO | LUMO | - | - | ||||
|---|---|---|---|---|---|---|---|---|
| −12.36 | 3.18 | 0.76 | −8.42 | −8.875 | −3.081 | 8.026 | 6.433 | |
| −11.44 | 2.65 | 1.00 | −7.79 | −8.792 | −2.743 | 7.943 | 6.771 | |
| −18.32 | 2.80 | 0.70 | −14.82 | −8.648 | −2.939 | 7.799 | 6.575 | |
| −14.47 | 2.17 | 0.96 | −11.34 | −8.628 | −2.948 | 7.779 | 6.566 | |
| −9.88 | 2.50 | 0.79 | −6.59 | −8.626 | −2.746 | 7.777 | 6.768 | |
| −11.63 | 2.42 | 0.81 | −8.40 | −8.639 | −3.028 | 7.790 | 6.486 | |
| −11.64 | 2.45 | 0.94 | −8.25 | −8.520 | −2.417 | 7.671 | 7.097 | |
| −14.42 | 2.35 | 4.59 | −7.48 | −8.267 | −3.205 | 7.418 | 6.309 | |
| −10.05 | 2.27 | 0.81 | −6.97 | −8.156 | −2.352 | 7.307 | 7.162 | |
| −10.23 | 2.45 | 0.81 | −6.97 | −8.222 | −2.322 | 7.373 | 7.192 | |
| −14.87 | 1.87 | 1.04 | −11.96 | −8.339 | −2.175 | 7.490 | 7.339 | |
| −11.19 | 2.33 | 0.93 | −7.93 | −7.696 | −2.243 | 6.847 | 7.271 | |
| −10.34 | 2.57 | 0.80 | −6.97 | −7.794 | −2.141 | 6.945 | 7.373 | |
| −9.58 | 2.34 | −5.72 | −12.96 | −7.615 | −1.686 | 6.766 | 7.828 | |
| −9.53 | 2.30 | 0.82 | −6.41 | −7.765 | −1.724 | 6.916 | 7.790 | |
| −9.32 | 2.16 | 0.53 | −6.63 | −6.943 | −1.429 | 6.094 | 8.085 | |
| −9.62 | 2.17 | 0.62 | −6.83 | −6.865 | −1.410 | 6.016 | 8.104 | |
| −9.69 | 2.19 | 0.63 | −6.87 | −6.828 | −1.373 | 5.979 | 8.141 | |
| −9.72 | 2.39 | 0.72 | −6.61 | −7.112 | −1.379 | 6.263 | 8.135 | |
| −9.64 | 2.33 | 0.75 | −6.56 | −7.339 | −1.501 | 6.490 | 8.013 | |
| −15.74 | 2.24 | 0.74 | −12.76 | −2.833 | 2.359 | 1.984 | 11.873 | |
| −16.23 | 2.24 | 0.73 | −13.26 | −2.698 | 3.168 | 1.849 | 12.682 |
| Bond | Electron Density | Electron Localization Function | |||||||
|---|---|---|---|---|---|---|---|---|---|
| () | () | DI | Basin | (e) | |||||
| Range | Median | Range | Median | Range | Median | Range | Median | ||
| N–H1 | 0.332–0.336 | 0.333 | −1.735–−1.695 | −1.729 | 0.716–0.750 | 0.728 | V(N,H1) | 2.04–2.06 | 2.06 |
| C4–H2 | 0.268–0.286 | 0.282 | −1.007–−0.888 | −0.974 | 0.880–0.953 | 0.911 | V(C4,H2) | 2.12–2.22 | 2.17 |
| N–C2 | 0.298–0.315 | 0.302 | −0.881–−0.839 | −0.851 | 0.937–1.012 | 0.951 | V(N,C2) | 1.97–2.10 | 2.08 |
| N–C1 | 0.282–0.308 | 0.304 | −0.776–−0.672 | −0.765 | 0.987–1.076 | 1.060 | V(N,C1) | 2.08–2.22 | 2.11 |
| C1–C3 | 0.258–0.304 | 0.264 | −0.803–−0.615 | −0.640 | 1.005–1.336 | 1.040 | V(C1,C3) | 2.23–3.37 | 2.28 |
| C1–S1 | 0.206–0.228 | 0.223 | −0.151–0.156 | 0.086 | 1.491–1.784 | 1.723 | V(C1,S1) | 2.26–2.68 | 2.55 |
| C2–O | 0.407–0.428 | 0.425 | −0.117–0.092 | 0.054 | 1.273–1.362 | 1.340 | V(C2,O) | 2.25–2.49 | 2.46 |
| C2–S2 | 0.189–0.197 | 0.193 | −0.341–−0.308 | −0.323 | 1.014–1.083 | 1.045 | V(C2,S2) | 1.90–1.98 | 1.93 |
| C3–S2 | 0.184–0.198 | 0.190 | −0.351–−0.281 | −0.317 | 1.086–1.164 | 1.116 | V(C3,S2) | 1.66–1.85 | 1.77 |
| C3–C4 | 0.286–0.339 | 0.331 | −0.998–−0.747 | −0.947 | 1.157–1.736 | 1.615 | V(C3,C4) | 2.59–3.63 | 3.48 |
| R | HOMA |
|---|---|
| −0.079 | |
| −0.047 | |
| −0.092 | |
| −0.003 | |
| −0.086 | |
| −0.051 | |
| −0.008 | |
| −0.058 | |
| 0.049 | |
| 0.066 | |
| −0.009 | |
| 0.026 | |
| 0.306 | |
| 0.220 | |
| 0.197 | |
| 0.368 | |
| 0.371 | |
| 0.373 | |
| 0.434 | |
| 0.403 | |
| 0.421 | |
| 0.467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalski, M.; Berski, S. Exploring the Relationship between Reactivity and Electronic Structure in Isorhodanine Derivatives Using Computer Simulations. Molecules 2023, 28, 2360. https://doi.org/10.3390/molecules28052360
Michalski M, Berski S. Exploring the Relationship between Reactivity and Electronic Structure in Isorhodanine Derivatives Using Computer Simulations. Molecules. 2023; 28(5):2360. https://doi.org/10.3390/molecules28052360
Chicago/Turabian StyleMichalski, Michal, and Slawomir Berski. 2023. "Exploring the Relationship between Reactivity and Electronic Structure in Isorhodanine Derivatives Using Computer Simulations" Molecules 28, no. 5: 2360. https://doi.org/10.3390/molecules28052360
APA StyleMichalski, M., & Berski, S. (2023). Exploring the Relationship between Reactivity and Electronic Structure in Isorhodanine Derivatives Using Computer Simulations. Molecules, 28(5), 2360. https://doi.org/10.3390/molecules28052360






