A DFT Investigation of the Reactivity of Guanidinium Salts in Tandem aza-Michael Addition/Intramolecular Cyclization
Abstract
1. Introduction
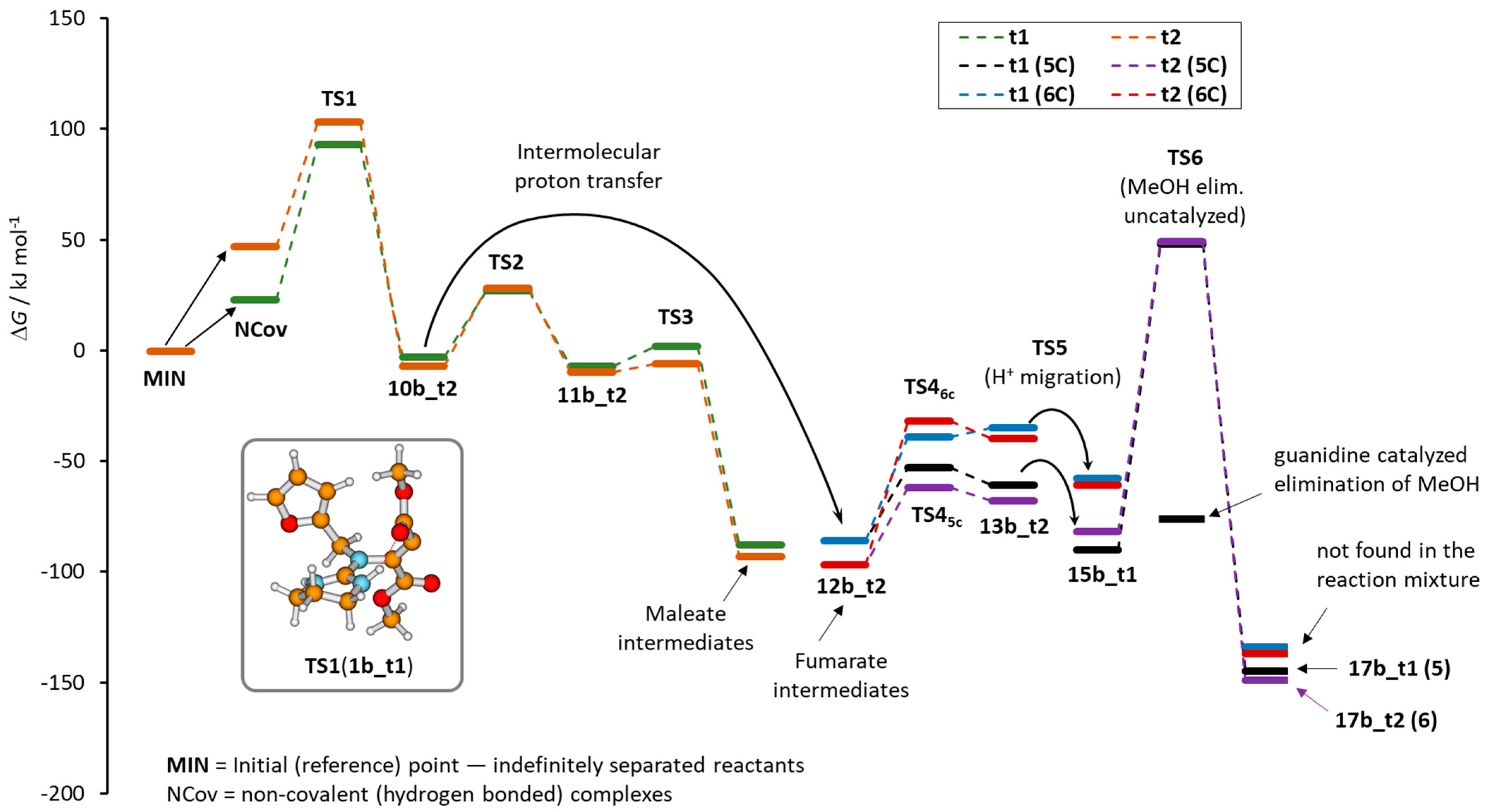
2. Results
Addition of Neutral Guanidines to DMAD
3. Discussion and Conclusions
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Vazdar, K.; Margetić, D.; Kovačević, B.; Sundermeyer, J.; Leito, I.; Jahn, U. Design of novel uncharged organic superbases: Merging basicity and functionality. Acc. Chem. Res. 2021, 54, 3108–3123. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Decouzon, M.; Gal, J.-F.; Maria, P.-C.; Woźniak, K.; Kurg, R.; Cairns, S.N. Superbases and superacids in the gas phase. Trends Org. Chem. 1998, 7, 95–103. [Google Scholar]
- Schug, K.A.; Lindner, W. Noncovalent binding between guanidinium and anionic groups: Focus on biological- and synthetic-based arginine/guanidinium interactions with phosph[on]ate and sulf[on]ate residues. Chem. Rev. 2005, 105, 67–113. [Google Scholar] [CrossRef]
- Maji, B.; Stephenson, D.S.; Mayr, H. Guanidines: Highly nucleophilic organocatalysts. ChemCatChem 2012, 4, 993–999. [Google Scholar] [CrossRef]
- Drozdov, F.V.; Kotov, V.M. Guanidine: A simple molecule with great potential: From catalysts to biocides and molecular glues. INEOS OPEN 2020, 3, 200–213. [Google Scholar] [CrossRef]
- Dale, J.; Eriksen, O.I. Tripple–branched cyanine dyes. Acta Chem. Scand. B 1988, 42, 242–246. [Google Scholar] [CrossRef]
- Powell, D.A.; Ramsden, P.D.; Batey, R.A. Phase-transfer-catalyzed alkylation of guanidines by alkyl halides under biphasic conditions: A convenient protocol for the synthesis of highly functionalized guanidines. J. Org. Chem. 2003, 68, 2300–2309. [Google Scholar] [CrossRef]
- Mao, F.-F.; Zhou, Y.; Zhu, W.; Sang, X.-Y.; Li, Z.-M.; Tao, D.-J. Synthesis of guanidinium-based poly(ionic liquids) with nonporosity for highly efficient SO2 capture from flue gas. Ind. Eng. Chem. Res. 2021, 60, 5984–5991. [Google Scholar] [CrossRef]
- Dodd, D.S.; Kozikowski, A.P. Conversion of alcohols to protected guanidines using the Mitsunobu protocol. Tetrahedron Lett. 1994, 35, 971–980. [Google Scholar] [CrossRef]
- Adachi, M.; Miyasaka, T.; Kudo, Y.; Sugimoto, K.; Yamashita, M.Y.; Nishikawa, T. Total syntheses and determination of absolute configurations of Cep-212 and Cep-210, predicted biosynthetic intermediates of tetrodotoxin isolated from toxic newt. Org. Lett. 2019, 21, 780–784. [Google Scholar] [CrossRef]
- Maji, M.; Borthakur, I.; Guria, S.; Singha, S.; Kundu, S. Direct access to 2-(N-alkylamino)pyrimidines via ruthenium catalyzed tandem multicomponent annulation/N-alkylation. J. Catal. 2021, 402, 37–51. [Google Scholar] [CrossRef]
- Genski, T.; Macdonald, G.; Wei, X.; Lewis, N.; Taylor, R.J.K. Synthesis and application of novel bicyclic guanidines: N-alkylation of 1,5,7-triazabicyclo[4.4.0]dec-5-ene. ARKIVOC 2000, 2000, 266–273. [Google Scholar] [CrossRef]
- Vaidyanathan, G.; Zalutsky, M.R. A new route to guanidines from bromoalkanes. J. Org. Chem. 1997, 62, 4867–4869. [Google Scholar] [CrossRef]
- Rulev, A.Y.; Tyumentsev, I.A. Pull-pull alkenes in the aza-Michael reaction. Adv. Synth. Catal. 2022, 364, 1622–1642. [Google Scholar] [CrossRef]
- Freeeman, C.G.; Turner, J.V.; Ward, A.D. The synthesis and preliminary biological testing of some bicyclic guanidine derivatives. Aust. J. Chem. 1978, 31, 179–186. [Google Scholar] [CrossRef]
- Baum, J.; Scholz, D.; Tataruch, F.; Viehe, H.G. New synthesis of amino–substituted 2-azabutadienes. Chimia 1975, 29, 514–515. [Google Scholar]
- Yavari, I.; Amirahmadia, A.; Halvagar, M.R. A synthesis of functionalized thiazoles and pyrimidine-4(3H)-thiones from 1,1,3,3-tetramethylguanidine, acetylenic Esters, and aryl isothiocyanates. Synlett 2017, 28, 2629–2632. [Google Scholar] [CrossRef]
- Acheson, R.M.; Wallis, J.D. Addition reactions of heterocyclic compounds. Part 74. Products frorn dimethyl acetylenedicarboxylate with thiourea, thioamide, and guanidine derivatives. J. Chem. Soc. Perkin Trans. 1981, 1, 415–422. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Yamazaki, C. Synthesis of nitrogen-containing heterocycles 6. Formation and structures of imidazolinones and related compounds through cyclization of diaminomethylenehydrazones with dimethyl acetylenedicarboxylate. J. Heterocyc. Chem. 1994, 31, 1445–1448. [Google Scholar] [CrossRef]
- Shestakov, A.S.; Sidorenko, O.E.; Shikhaliev, K.H.S. Synthesis of 2-iminoimidazolidin-4-one derivatives by cyclization of 2-aryl-1-(4,6-dimethylpyrimidin-2-yl)guanidines with ethyl bromoacetate, dimethyl acetylenedicarboxylate, and maleic anhydride. Russ. Chem. Bull. Int. Ed. 2007, 56, 1423–1430. [Google Scholar] [CrossRef]
- Erden, I.; Ozer, G.; Hoarau, C.; Cao, W. Cyclocondensation of amidines with dimethyl acetylenedicarboxylate: A convenient entry into tetramic acids. J. Het. Chem. 2006, 43, 395–399. [Google Scholar] [CrossRef]
- Neochoritis, C.G.; Zarganes-Tzitzikas, T.; Stephanidou-Stephanatou, J. Dimethyl acetylenedicarboxylate: A versatile tool in organic synthesis. Synthesis 2014, 46, 537–585. [Google Scholar] [CrossRef]
- Barešić, L.; Margetić, D.; Glasovac, Z. Anion-controlled synthesis of novel guanidine-substituted oxanorbornanes. Int. J. Mol. Sci. 2022, 23, 16036. [Google Scholar] [CrossRef]
- Caine, B.A.; Dardonville, C.; Popelier, P.L.A. Prediction of aqueous pKa values for guanidine-containing compounds using ab initio gas-phase equilibrium bond lengths. ACS Omega 2018, 3, 3835–3850. [Google Scholar] [CrossRef]
- Barešić, L.; Margetić, D.; Glasovac, Z. Cycloaddition of thiourea- and guanidine-substituted furans to dienophiles: A comparison of the environmentally-friendly methods. Chem. Proc. 2021, 3, 57. [Google Scholar] [CrossRef]
- Martin, J.D.D.; Hepburn, J.W. Determination of bond dissociation energies by threshold ion-pair production spectroscopy: An improved D-0(HCl). J. Chem. Phys. 1998, 109, 8139–8142. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density functional theory for reaction energies: Test of meta and hybrid meta functionals, range-separated functionals, and other high-performance functionals. J. Chem. Theory Comput. 2011, 7, 669–676. [Google Scholar] [CrossRef]
- Mezei, P.D.; Csonka, G.L.; Kallay, M. Accurate Diels–Alder reaction energies from efficient density functional calculations. J. Chem. Theory Comput. 2015, 11, 2879–2888. [Google Scholar] [CrossRef]
- Yepes, D.; Valenzuela, J.; Martínez-Araya, J.I.; Pérez, P.; Jaque, P. Effect of exchange-correlation functional on the synchronicity/nonsynchronicity in bond formation in Diels-Alder reactions: A reaction force constant analysis. Phys. Chem. Chem. Phys. 2019, 21, 7412–7428. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Improving the accuracy of hybrid meta-GGA density functionals by range separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef]
- Molteni, G.; Ponti, A. The azide-allene dipolar cycloaddition: Is DFT able to predict site- and regio-selectivity? Molecules 2021, 26, 928. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, L.A.; Raghavachari, K. Gaussian-3 and related methods for accurate thermochemistry. Theor. Chem. Acc. 2002, 108, 61–70. [Google Scholar] [CrossRef]
- Briš, A.; Glasovac, Z.; Margetić, D. Gas-phase basicity of cyclic guanidine derivatives—A DFT study. New J. Chem. 2021, 45, 2384–2392. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Decouzon, M.; Gal, J.-F.; Maria, P.-C.; Gelbard, G.; Vielfaure-Joly, F. Gas-phase structural (internal) effects in strong organic nitrogen bases. J. Phys. Org. Chem. 2001, 14, 25–34. [Google Scholar] [CrossRef]
- Kunetskiy, R.A.; Polyakova, S.M.; Vavřík, J.; Císařová, I.; Saame, J.; Roos Nerut, E.; Koppel, I.; Koppel, I.A.; Kütt, A.; Leito, I.; et al. A New class of organosuperbases, N-alkyl- and N-aryl-1,3-dialkyl-4,5-dimethylimidazol-2-ylidene amines: Synthesis, structure, pKBH+ measurements, and properties. Chem. Eur. J. 2012, 18, 3621–3630. [Google Scholar] [CrossRef]
- Ribeiro, R.F.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation. J. Phys. Chem. B 2011, 115, 14556–14562. [Google Scholar] [CrossRef]
- Antol, I.; Glasovac, Z.; Murata, Y.; Hashikawa, Y.; Margetić, D. Consecutive utilization of mechanochemical and microwave methods for the synthesis of Boc-2-amino-quinazolin-4(3H)-ones and DFT study of mechanism 6π-diazaelectrocyclization process. ChemistrySelect 2022, 7, e202200633. [Google Scholar] [CrossRef]
- Horvath, A. Catalysis and regioselectivity in the Michael addition of azoles. Kinetic vs. thermodynamic control. Tetrahedron Lett. 1996, 37, 4423–4426. [Google Scholar] [CrossRef]
- Shen, J.; Nguyen, T.T.; Goh, Y.-P.; Ye, W.; Fu, X.; Xu, J.; Tan, C.-H. Chiral bicyclic guanidine-catalyzed enantioselective reactions of anthrones. J. Am. Chem. Soc. 2006, 128, 13692–13693. [Google Scholar] [CrossRef] [PubMed]
- Truong, V.X.; Dove, A.P. Organocatalytic, regioselective nucleophilic “click” addition of thiols to propiolic acid esters for polymer–polymer coupling. Angew. Chem. Int. Ed. 2013, 52, 4132–4136. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.-J.; Li, G.-Q.; Liang, Y.-M. DABCO catalyzed reaction of various nucleophiles with activated alkynes leading to the formation of alkenoic acid esters, 1,4-dioxane, morpholine, and piperazinone derivatives. Tetrahedron 2006, 62, 6782–6791. [Google Scholar] [CrossRef]
- Kiesewetter, M.K.; Scholten, M.D.; Kirn, N.; Weber, R.L.; Hedrick, J.L.; Waymouth, R.M. Cyclic guanidine organic catalysts: What is magic about triazabicyclodecene? J. Org. Chem. 2009, 74, 9490–9496. [Google Scholar] [CrossRef] [PubMed]
- Kanzian, T.; Nigst, T.A.; Maier, A.; Pichl, S.; Mayr, H. Nucleophilic reactivities of primary and secondary amines in acetonitrile. Eur. J. Org. Chem. 2009, 2009, 6379–6385. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Jensen, F. Unifying general and segmented contracted basis sets. Segmented polarization consistent basis sets. J. Chem. Theory Comput. 2014, 10, 1074–1085. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis set exchange: A community database for computational sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16. Rev C. 01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Schaftenaar, G.; Vlieg, E.; Vriend, G. Molden 2.0: Quantum chemistry meets proteins. J. Comput.-Aided. Mol. Des. 2017, 31, 789–800. [Google Scholar] [CrossRef] [PubMed]
- Schaftenaar, G.; Noordik, J.H. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput.-Aided. Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef] [PubMed]



| Guandines | Method | ΔG≠ (TS1) | ΔrG (10a–10c) | ΔrG (12a–12c) | ΔG≠ (TS45C) | ΔG≠ (TS46C) | ΔrG (Prod) 2 (17a–17c) | ΔrG (Prod) (18a–18c) |
|---|---|---|---|---|---|---|---|---|
| B3LYP | ||||||||
| 1a_t1 | 117 | 54 | −34 | 37 | 32 | −87 (−83) | −100 | |
| 1a_t2 | 122 | 45 | −56 | −3 | 14 | −102 (−89) | −107 | |
| 1b_t1 | 119 | 53 | −40 | −1 | (27) 3 | −114 (−114) | −92 | |
| 1b_t2 | 122 | 38 | −44 | −3 | 36 | −120 (−114) | −96 | |
| 1c_t1 | 132 | 86 | 8 | 50 | i.p. 3 | −80 (−72) | −23 | |
| 1c_t2 | 146 | 94 | 7 | 42 | r.o. 4 | −75 (−66) | −26 | |
| M06-2X | ||||||||
| 1a_t1 | 94 | 7 | −84 | −19 | −30 | −112 (−107) | −137 | |
| 1a_t2 | 100 | 5 | −99 | −53 | −43 | −126 (−110) | −141 | |
| 1b_t1 | 92 | −3 | −93 | −53 | (−39) 3 | −145 (−144) | −134 | |
| 1b_t2 | 103 | −7 | −94 | −59 | −32 | −149 (−143) | −137 | |
| 1c_t1 | 99 | 22 | −64 | −19 | i.p. 3 | −114 (−112) | −73 | |
| 1c_t2 | 108 | 29 | −57 | −23 | r.o. 4 | −107 (−99) | −78 |
| Guan. | ΔGrel 1 | Product | Ratios | Guan. | ΔGrel 1 | Product | Ratios | Guan. | ΔGrel 1 | Product | Ratios |
|---|---|---|---|---|---|---|---|---|---|---|---|
| calc. | exp. | calc. | exp. | calc. | exp. | ||||||
| 17a_t1 | 21.7 | 0.00 | - | 17b_t1 | 2.1 | 0.44 | 0.50 | 17b_t1 | 0.0 | 1.00 | 1.00 |
| E-17a_t1 | 33.3 | 0.00 | - | E-17b_t1 | 10.2 | 0.02 | - | E-17b_t1 | 2.7 | 0.34 | 0.23 |
| 17a_t2 | 4.3 | 0.18 | 1.00 | 17b_t2 | 0.0 | 1.00 | 1.0 | 17b_t2 | 9.0 | 0.03 | - |
| E-17a_t2 | 25.9 | 0.00 | - | E-17b_t2 | 8.5 | 0.03 | - | E-17b_t2 | 11.6 | 0.01 | - |
| 18a_t1 | 0.9 | 0.69 | 0.33 | 18b_t1 | 14.6 | 0.00 | - | 18b_t1 | 48.3 | 0.00 | - |
| 18a_t2 | 0.0 | 1.00 | 0.39 | 18b_t2 | 18.1 | 0.00 | - | 18b_t2 | 43.5 | 0.00 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glasovac, Z.; Barešić, L.; Margetić, D. A DFT Investigation of the Reactivity of Guanidinium Salts in Tandem aza-Michael Addition/Intramolecular Cyclization. Molecules 2023, 28, 2218. https://doi.org/10.3390/molecules28052218
Glasovac Z, Barešić L, Margetić D. A DFT Investigation of the Reactivity of Guanidinium Salts in Tandem aza-Michael Addition/Intramolecular Cyclization. Molecules. 2023; 28(5):2218. https://doi.org/10.3390/molecules28052218
Chicago/Turabian StyleGlasovac, Zoran, Luka Barešić, and Davor Margetić. 2023. "A DFT Investigation of the Reactivity of Guanidinium Salts in Tandem aza-Michael Addition/Intramolecular Cyclization" Molecules 28, no. 5: 2218. https://doi.org/10.3390/molecules28052218
APA StyleGlasovac, Z., Barešić, L., & Margetić, D. (2023). A DFT Investigation of the Reactivity of Guanidinium Salts in Tandem aza-Michael Addition/Intramolecular Cyclization. Molecules, 28(5), 2218. https://doi.org/10.3390/molecules28052218





