Semi-Polycrystalline Polyaniline-Activated Carbon Composite for Supercapacitor Application
Abstract
1. Introduction
2. Results
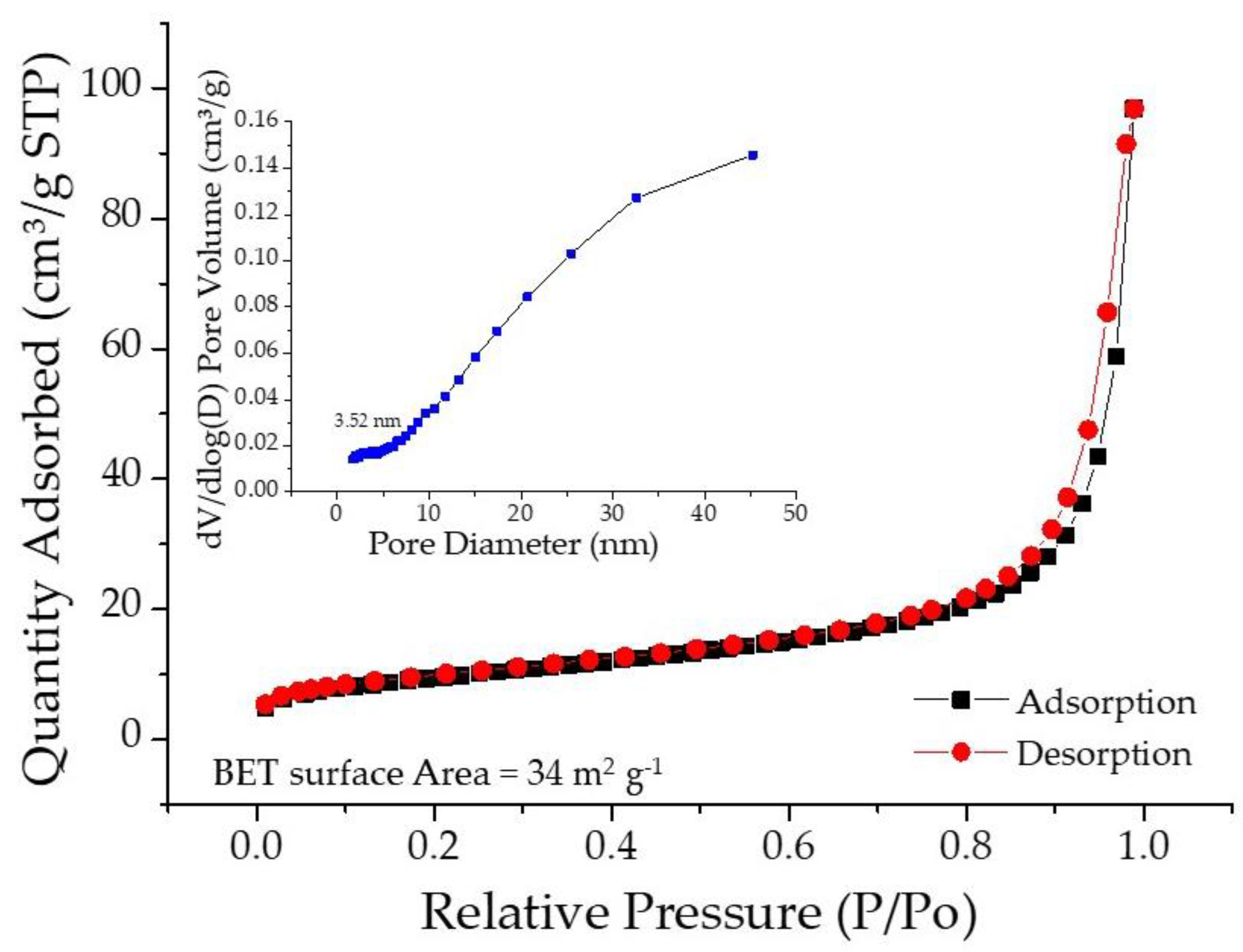
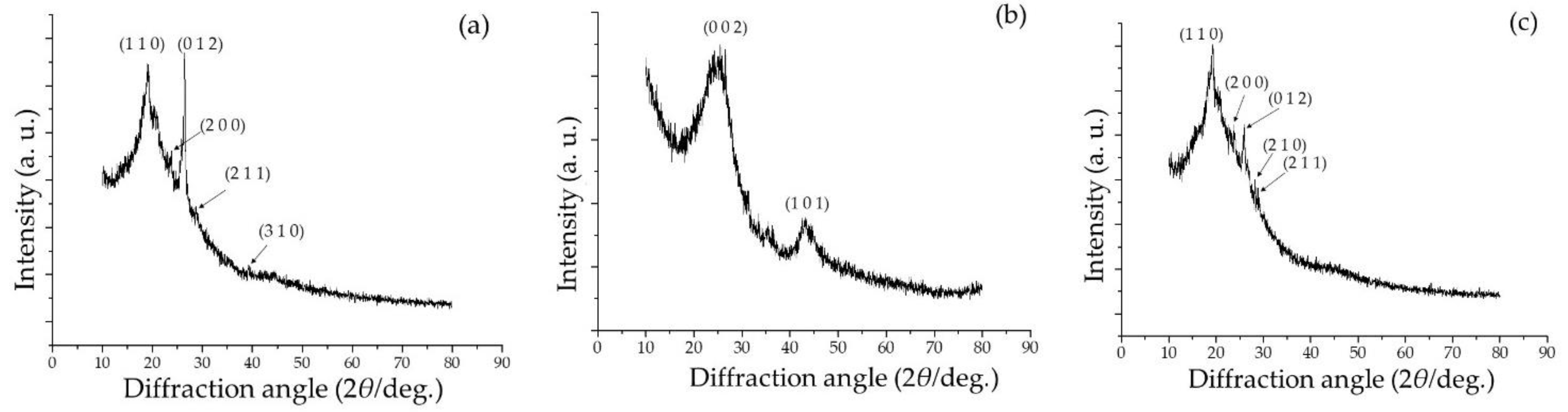
2.1. Microstructure, Phase, and Chemical Properties of SPani-AC
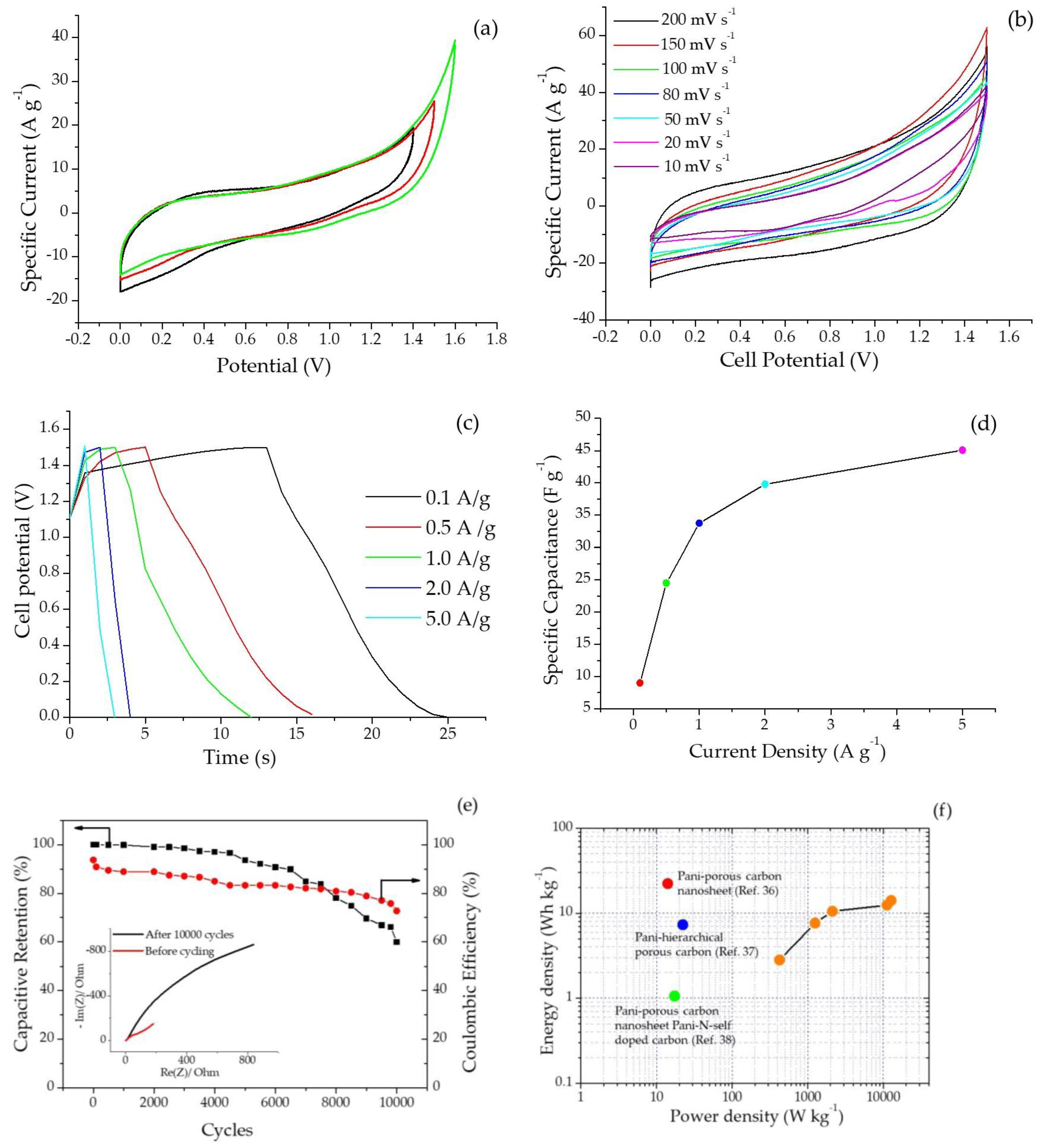
2.2. Electrochemical Capacitor Investigation
2.2.1. Cyclic Voltammetry
2.2.2. Determination of ‘b’ Values
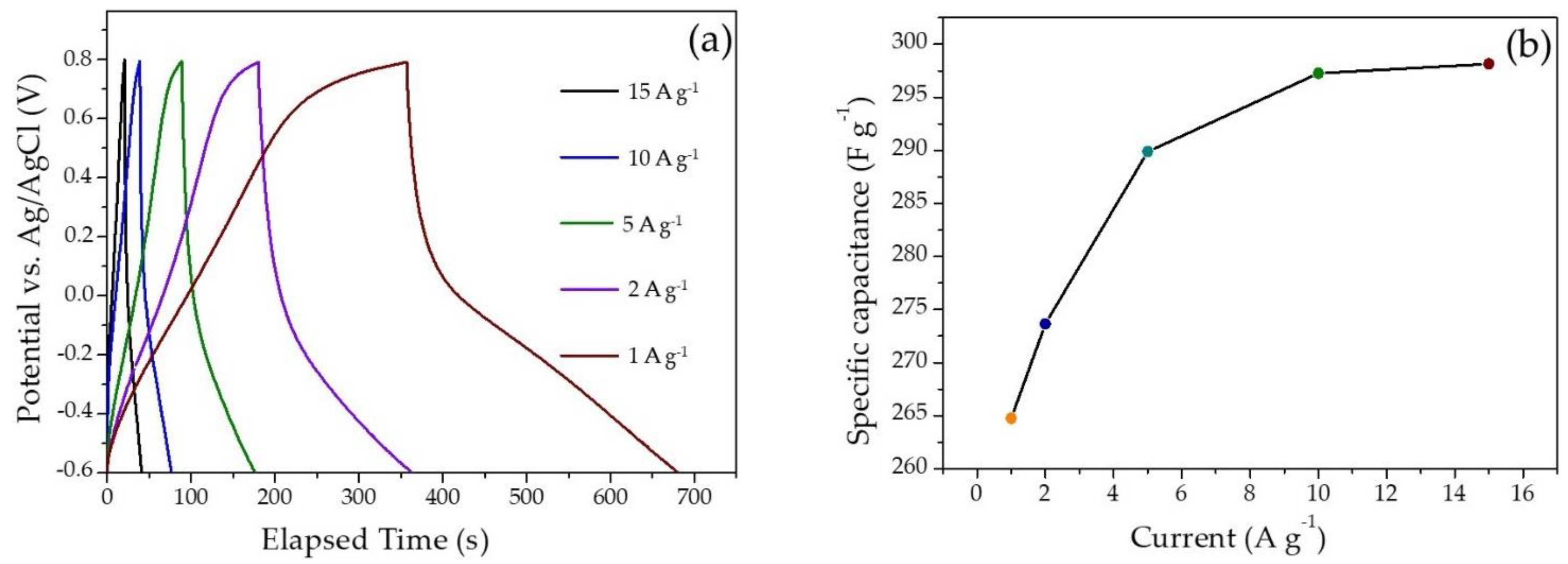
2.2.3. Gravimetric Charge–Discharge
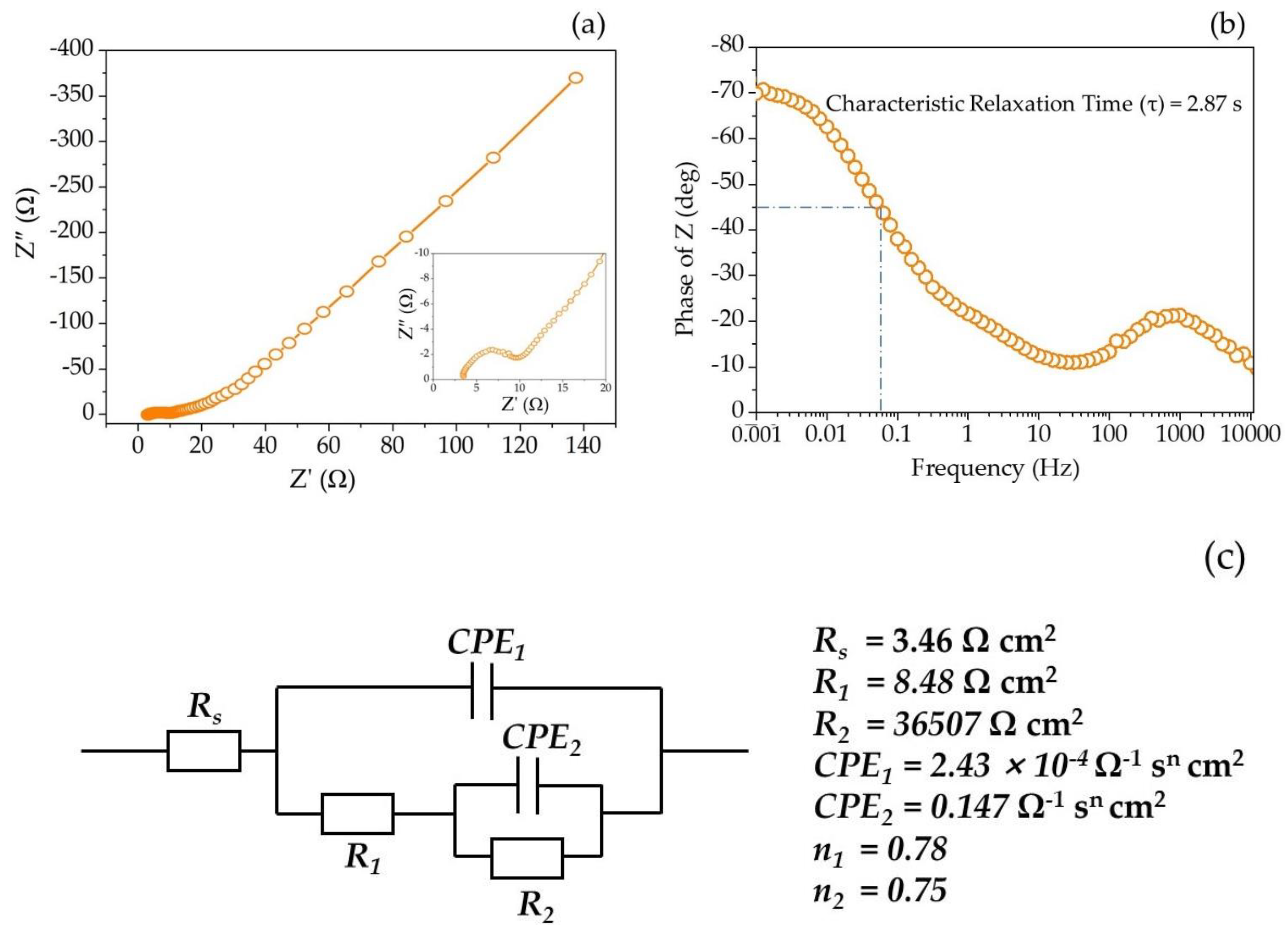
2.2.4. Electrochemical Impedance Spectroscopy
2.2.5. Electrochemical Performance of Symmetric Device made of SPani-AC in Agar- Na2SO4 Polymer Gel Electrolyte
3. Discussion
3.1. Electrochemical Behavior of SPani-AC
3.2. Formation of SPani-AC and Role of Molecular Structure and Morphological Properties on Its Electrochemical Behavior
3.3. Electrochemical Impedance Spectrum Analysis
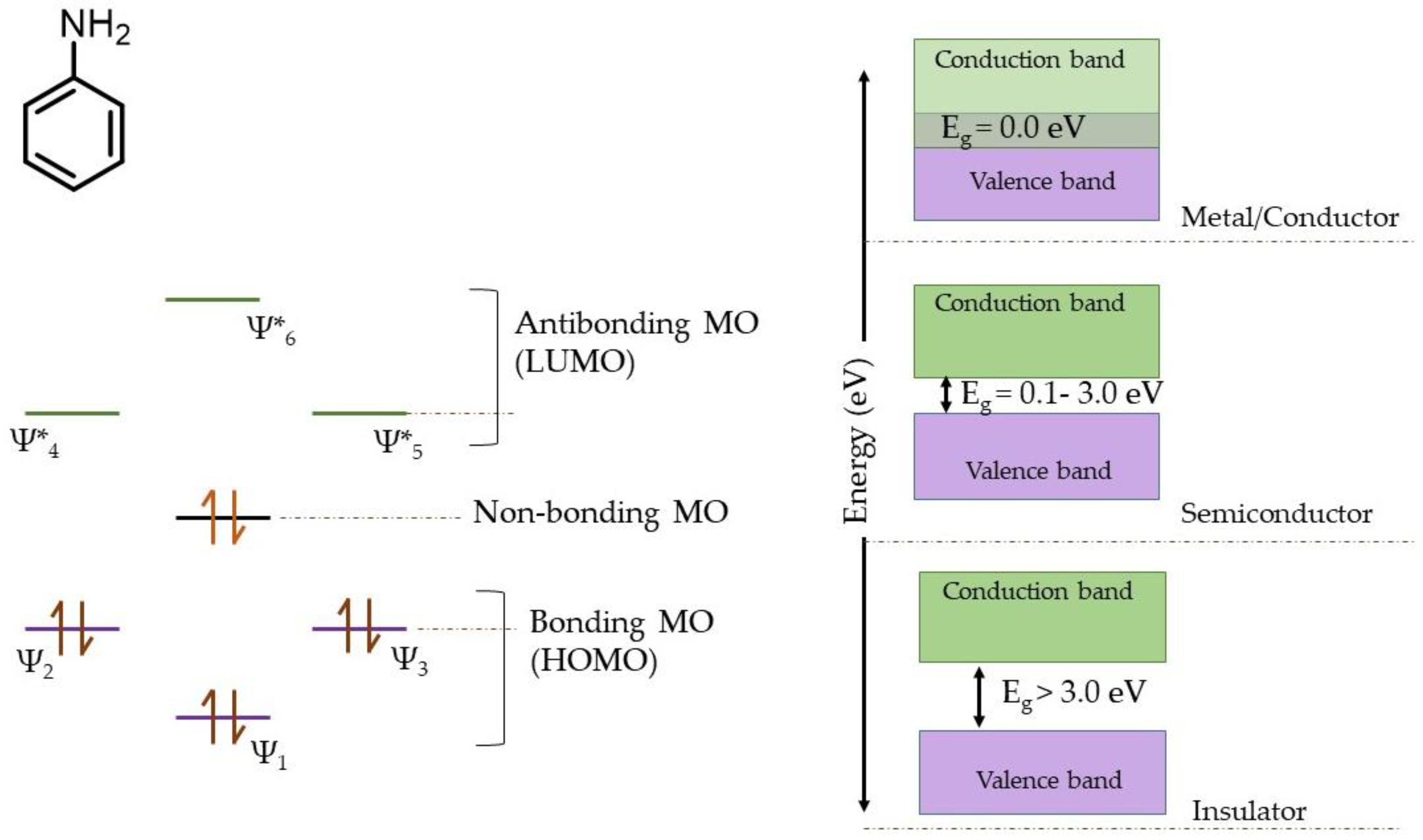
3.4. Application of Molecular Orbital (MO) Theory for Explaining the Charge Storage Mechanism in SPani-AC Composite Electroactive Material
3.5. Mechanism of Charge Storage in SPani-AC
4. Experimental
4.1. Materials
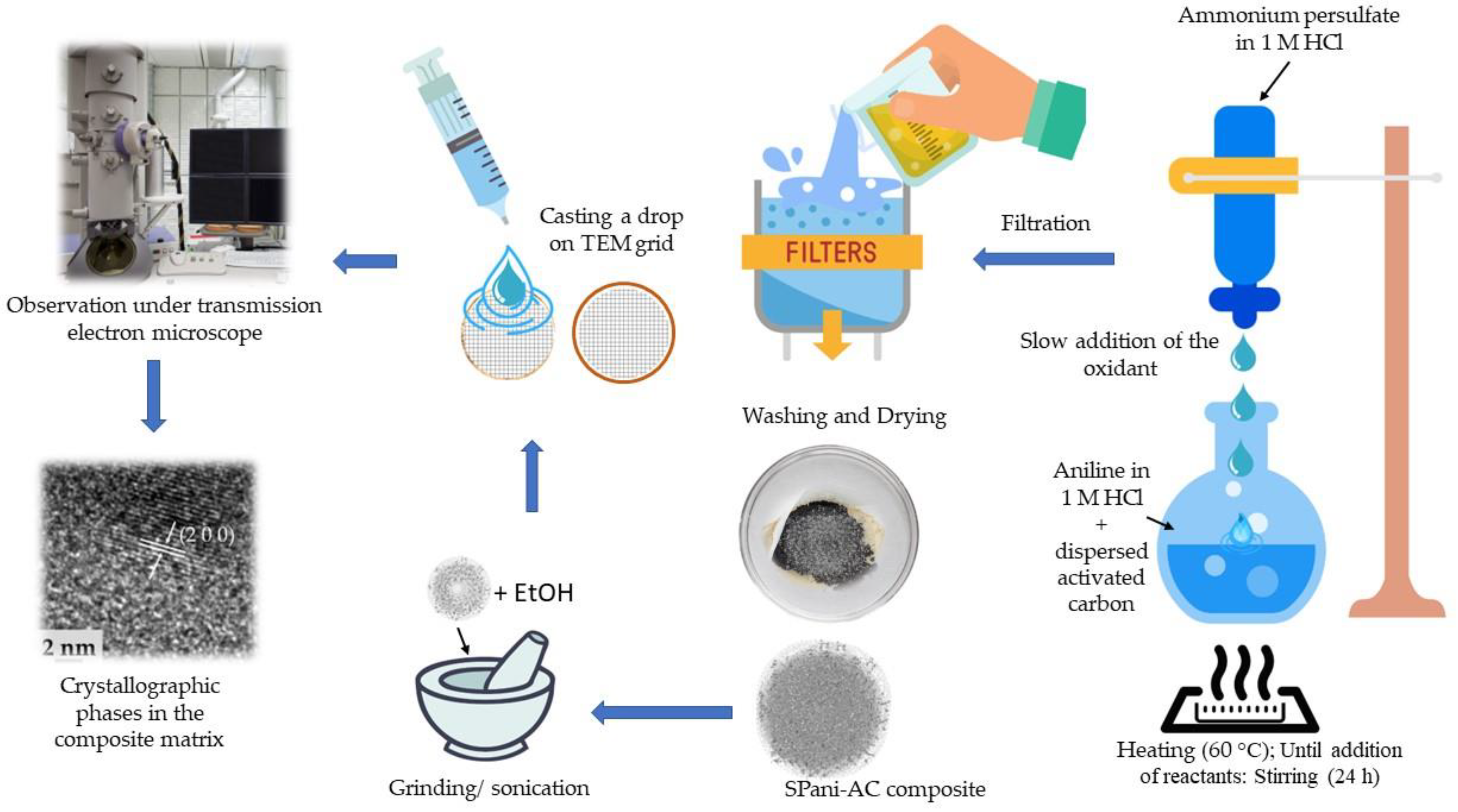
4.2. Synthesis of Semi-Polycrystalline Polyaniline-Activated Carbon Composite
4.3. Material Characterization
4.4. Electrochemical Characterization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Conway, B.E. Transition from “supercapacitor” to “Battery” Behavior in Electrochemical Energy Storage. Proc. Int. Power Sources Symp. 1991, 319–327. [Google Scholar] [CrossRef]
- Oh, M.; Kim, S. Preparation and Electrochemical Characterization of Polyaniline/Activated Carbon Composites as an Electrode Material for Supercapacitors. J. Nanosci. Nanotechnol. 2012, 12, 519–524. [Google Scholar] [CrossRef]
- Kötz, R.; Carlen, M.J.E.A. Principles and Applications of Electrochemical Capacitors. Electrochim. Acta 2000, 45, 2483–2498. [Google Scholar] [CrossRef]
- Jang, W.-K.; Yun, J.-M.; Kim, H.-I.; Lee, Y.-S. Preparation and Characteristics of Conducting Polymer-Coated Multiwalled Carbon Nanotubes for a Gas Sensor. Carbon Lett. 2011, 12, 162–166. [Google Scholar] [CrossRef]
- Conway, B.E.; Birss, V.; Wojtowicz, J. The Role and Utilization of Pseudocapacitance for Energy Storage by Supercapacitors. J. Power Sources 1997, 66, 1–14. [Google Scholar] [CrossRef]
- Atkins, P.W.; Paula, J. De Atkins’ Physical Chemistry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 1475730586. [Google Scholar]
- Choi, C.; Ashby, D.S.; Butts, D.M.; DeBlock, R.H.; Wei, Q.; Lau, J.; Dunn, B. Achieving High Energy Density and High Power Density with Pseudocapacitive Materials. Nat. Rev. Mater. 2020, 5, 5–19. [Google Scholar] [CrossRef]
- González, A.; Goikolea, E.; Barrena, J.A.; Mysyk, R. Review on Supercapacitors: Technologies and Materials. Renew. Sustain. Energy Rev. 2016, 58, 1189–1206. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Xia, Y. Electrochemical Capacitors: Mechanism, Materials, Systems, Characterization and Applications. Chem. Soc. Rev. 2016, 45, 5925–5950. [Google Scholar] [CrossRef]
- Wang, J.; Polleux, J.; Lim, J.; Dunn, B. Pseudocapacitive Contributions to Electrochemical Energy Storage in TiO2 (Anatase) Nanoparticles. J. Phys. Chem. C 2007, 111, 14925–14931. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, Z.; Guo, Y.; Guo, D.; Liu, G. Block Copolymer Derived Uniform Mesopores Enable Ultrafast Electron and Ion Transport at High Mass Loadings. Nat. Commun. 2019, 10, 675. [Google Scholar] [CrossRef]
- Yao, B.; Chandrasekaran, S.; Zhang, H.; Ma, A.; Kang, J.; Zhang, L.; Lu, X.; Qian, F.; Zhu, C.; Duoss, E.B.; et al. 3D-Printed Structure Boosts the Kinetics and Intrinsic Capacitance of Pseudocapacitive Graphene Aerogels. Adv. Mater. 2020, 32, e1906652. [Google Scholar] [CrossRef]
- Chodankar, N.R.; Pham, H.D.; Nanjundan, A.K.; Fernando, J.F.S.; Jayaramulu, K.; Golberg, D.; Han, Y.K.; Dubal, D.P. True Meaning of Pseudocapacitors and Their Performance Metrics: Asymmetric versus Hybrid Supercapacitors. Small 2020, 16, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Mathis, T.S.; Kurra, N.; Wang, X.; Pinto, D.; Simon, P.; Gogotsi, Y. Energy Storage Data Reporting in Perspective—Guidelines for Interpreting the Performance of Electrochemical Energy Storage Systems. Adv. Energy Mater. 2019, 9, 1902007. [Google Scholar] [CrossRef]
- Mahato, N.; Mohapatra, D.; Cho, M.H.; Ahn, K.S. Semi-Polycrystalline–Polyaniline Empowered Electrochemical Capacitor. Energies 2022, 15, 2001. [Google Scholar]
- Gerard, M.; Chaubey, A.; Malhotra, B.D. Application of Conducting Polymers to Biosensors. Biosens. Bioelectron. 2002, 17, 345–359. [Google Scholar] [CrossRef]
- Jugović, B.; Gvozdenović, M.; Stevanović, J.; Trišović, T.; Grgur, B. Characterization of Electrochemically Synthesized PANI on Graphite Electrode for Potential Use in Electrochemical Power Sources. Mater. Chem. Phys. 2009, 114, 939–942. [Google Scholar] [CrossRef]
- Mahato, N.; Cho, M.H. Graphene Integrated Polyaniline Nanostructured Composite Coating for Protecting Steels from Corrosion: Synthesis, Characterization, and Protection Mechanism of the Coating Material in Acidic Environment. Constr. Build. Mater. 2016, 115, 618–633. [Google Scholar] [CrossRef]
- Mahato, N.; Parveen, N.; Cho, M.H. Synthesis of Highly Crystalline Polyaniline Nanoparticles by Simple Chemical Route. Mater. Lett. 2015, 161. [Google Scholar] [CrossRef]
- Parveen, N.; Mahato, N.; Ansari, M.O.; Cho, M.H. Enhanced Electrochemical Behavior and Hydrophobicity of Crystalline Polyaniline@graphene Nanocomposite Synthesized at Elevated Temperature. Compos. Part B Eng. 2016, 87, 281–290. [Google Scholar] [CrossRef]
- Sowmya; Selvakumar, M. Multilayered Electrode Materials Based on Polyaniline/Activated Carbon Composites for Supercapacitor Applications. Int. J. Hydrog. Energy 2018, 43, 4067–4080. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.L.; Gao, F.; Li, W.S.; Wu, K.Z.; Wang, X.D. Activated Carbon Coated with Polyaniline as an Electrode Material in Supercapacitors. Xinxing Tan Cailiao/ New Carbon Mater. 2008, 23, 275–280. [Google Scholar] [CrossRef]
- Eftekhari, A.; Jafarkhani, P. Polymerization of Aniline through Simultaneous Chemical and Electrochemical Routes. Polym. J. 2006, 38, 651–658. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Q.; Zhou, S.; Liu, N.; Wang, X.; Li, J.; Wang, F. Aqueous Dispersed Conducting Polyaniline Nanofibers: Promising High Specific Capacity Electrode Materials for Supercapacitor. J. Power Sources 2011, 196, 10484–10489. [Google Scholar] [CrossRef]
- Park, D.-Y.; Lim, Y.-S.; Kim, M.-S. Performance of Expanded Graphite as Anode Materials for High Power Li-Ion Secondary Batteries. Carbon Lett. 2010, 11, 343–346. [Google Scholar] [CrossRef]
- Liu, X.Y.; Huang, M.; Ma, H.L.; Zhang, Z.Q.; Gao, J.M.; Zhu, Y.L.; Han, X.J.; Guo, X.Y. Preparation of a Carbon-Based Solid Acid Catalyst by Sulfonating Activated Carbon in a Chemical Reduction Process. Molecules 2010, 15, 7188–7196. [Google Scholar] [CrossRef]
- Goswami, S.; Maiti, U.N.; Maiti, S.; Nandy, S.; Mitra, M.K.; Chattopadhyay, K.K. Preparation of Graphene-Polyaniline Composites by Simple Chemical Procedure and Its Improved Field Emission Properties. Carbon N. Y. 2011, 49, 2245–2252. [Google Scholar] [CrossRef]
- Lapin, E.; Jureviit, I.; Maeikien, R.; Niaura, G.; Malinauskas, A. A Study of Electropolymerization of N,N-Dimethylaniline. Synth. Met. 2010, 160, 1843–1847. [Google Scholar] [CrossRef]
- Abdullah, H.S. Electrochemical Polymerization and Raman Study of Polypyrrole and Polyaniline Thin Films. Int. J. Phys. Sci. 2012, 7, 5468–5476. [Google Scholar] [CrossRef]
- Mažeikienė, R.; Niaura, G.; Malinauskas, A. A Comparative Raman Spectroelectrochemical Study of Selected Polyaniline Derivatives in a PH-Neutral Solution. Synth. Met. 2010, 160, 1060–1064. [Google Scholar] [CrossRef]
- Rozlivkova, Z.; Trchova, M.; Exnerova, M.; Stejskal, J. The Carbonization of Granular Polyaniline to Produce Nitrogen-Containing Carbon. Synth. Met. 2011, 161, 1122–1129. [Google Scholar] [CrossRef]
- Bernard, M.C.; Hugot-Le Goff, A. Raman Spectroscopy for the Study of Polyaniline. Synth. Met. 1997, 85, 1145–1146. [Google Scholar] [CrossRef]
- Hao, Q.; Lei, W.; Xia, X.; Yan, Z.; Yang, X.; Lu, L.; Wang, X. Exchange of Counter Anions in Electropolymerized Polyaniline Films. Electrochim. Acta 2010, 55, 632–640. [Google Scholar] [CrossRef]
- Nekrasov, A.A.; Gribkova, O.; Iakobson, O.D.; Ardabievskii, I.N.; Ivanov, V.F.; Vannikov, A. V Raman Spectroelectrochemical Study of Electrodeposited Polyaniline Doped with Polymeric Sulfonic Acids of Different Structures. Chem. Pap. 2016, 71, 449–458. [Google Scholar] [CrossRef]
- Majumder, M.; Thakur, A.K.; Bhushan, M.; Mohapatra, D. Polyaniline Integration and Interrogation on Carbon Nano-Onions Empowered Supercapacitors. Electrochim. Acta 2021, 370, 137659. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, X.; Chai, H.; Diao, G.; Piao, Y. 3D Hybrids of Interconnected Porous Carbon Nanosheets/Vertically Aligned Polyaniline Nanowires for High-Performance Supercapacitors. Adv. Mater. Interfaces 2018, 5, 1–8. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Z.; Ren, Y.; Ran, W.; Chen, X.; Wu, J.; Gao, F. Vapor Deposition Polymerization of Aniline on 3D Hierarchical Porous Carbon with Enhanced Cycling Stability as Supercapacitor Electrode. J. Power Sources 2015, 286, 1–9. [Google Scholar] [CrossRef]
- Hu, Y.; Tong, X.; Zhuo, H.; Zhong, L.; Peng, X. Biomass-Based Porous N-Self-Doped Carbon Framework/Polyaniline Composite with Outstanding Supercapacitance. ACS Sustain. Chem. Eng. 2017, 5, 8663–8674. [Google Scholar] [CrossRef]
- Eftekhari, A.; Li, L.; Yang, Y. Polyaniline Supercapacitors. J. Power Sources 2017, 347, 86–107. [Google Scholar] [CrossRef]
- Karthikeyan, K.; Amaresh, S.; Lee, S.N.; An, J.Y.; Lee, Y.S. High-Power Lithium-Ion Capacitor Using LiMnBO3-Nanobead Anode and Polyaniline-Nanofiber Cathode with Excellent Cycle Life. ChemSusChem 2014, 7, 2310–2316. [Google Scholar] [CrossRef]
- Heme, H.N.; Alif, M.S.N.; Rahat, S.M.S.M.; Shuchi, S.B. Recent Progress in Polyaniline Composites for High Capacity Energy Storage: A Review. J. Energy Storage 2021, 42, 103018. [Google Scholar] [CrossRef]
- Augustyn, V.; Simon, P.; Dunn, B. Pseudocapacitive Oxide Materials for High-Rate Electrochemical Energy Storage. Energy Environ. Sci. 2014, 7, 1597–1614. [Google Scholar] [CrossRef]
- Ciric-Marjanovic, G.; Trchová, M.; Stejskal, J. MNDO-PM3 Study of the Early Stages of the Chemical Oxidative Polymerization of Aniline. Collect. Czechoslov. Chem. Commun. 2006, 71, 1407–1426. [Google Scholar] [CrossRef]
- Ćirić-Marjanović, G. Recent Advances in Polyaniline Research: Polymerization Mechanisms, Structural Aspects, Properties and Applications. Synth. Met. 2013, 177, 1–47. [Google Scholar] [CrossRef]
- Marjanović, B.; Juranić, I.; Ćirić-Marjanović, G. Revised Mechanism of Boyland−Sims Oxidation. J. Phys. Chem. A 2011, 115, 3536–3550. [Google Scholar] [CrossRef]
- Wawzonek, S.; McIntyre, T.W. Electrolytic Oxidation of Aromatic Amines. J. Electrochem. Soc. 1967, 114, 1025. [Google Scholar] [CrossRef]
- Mohilner, D.M.; Adams, R.N.; Argersinger, W.J. Investigation of the Kinetics and Mechanism of the Anodic Oxidation of Aniline in Aqueous Sulfuric Acid Solution at a Platinum Electrode. J. Am. Chem. Soc. 1962, 84, 3618–3622. [Google Scholar] [CrossRef]
- Manikandan, R.; Raj, C.J.; Rajesh, M.; Kim, B.C.; Sim, J.Y.; Yu, K.H. Electrochemical Behaviour of Lithium, Sodium and Potassium Ion Electrolytes in a Na0.33V2O5 Symmetric Pseudocapacitor with High Performance and High Cyclic Stability. ChemElectroChem 2018, 5, 101–111. [Google Scholar] [CrossRef]
- Mahato, N.; Singh, M.M. Investigation of Passive Film Properties and Pitting Resistance of AISI 316 in Aqueous Ethanoic Acid Containing Chloride Ions Using Electrochemical Impedance Spectroscopy(EIS). Port. Electrochim. Acta 2011, 29, 233–251. [Google Scholar] [CrossRef]
- Molapo, K.M.; Ndangili, P.M.; Ajayi, R.F.; Mbambisa, G.; Mailu, S.M.; Njomo, N.; Masikini, M.; Baker, P.; Iwuoha, E.I. Electronics of Conjugated Polymers (I): Polyaniline. Int. J. Electrochem. Sci. 2012, 7, 11859–11875. [Google Scholar]
- Orton, J. Polycrystalline and Amorphous Semiconductors. In The Story of Semiconductors; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Heeger, A.J.; MacDiarmid, A.G.; Shirakawa, H. Advanced Information—The Nobel Prize in Chemistry 2000. In Nobel Media AB 2019; Vetenskapsakademien: Stockholm, Sweden, 1974; pp. 1–16. [Google Scholar] [CrossRef]
- Conway, B.E. Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications; Springer Science & Business Media, LLC: New York, NY, USA, 2013; ISBN 9781475730586. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahato, N.; Sreekanth, T.V.M.; Yoo, K.; Kim, J. Semi-Polycrystalline Polyaniline-Activated Carbon Composite for Supercapacitor Application. Molecules 2023, 28, 1520. https://doi.org/10.3390/molecules28041520
Mahato N, Sreekanth TVM, Yoo K, Kim J. Semi-Polycrystalline Polyaniline-Activated Carbon Composite for Supercapacitor Application. Molecules. 2023; 28(4):1520. https://doi.org/10.3390/molecules28041520
Chicago/Turabian StyleMahato, Neelima, T. V. M. Sreekanth, Kisoo Yoo, and Jonghoon Kim. 2023. "Semi-Polycrystalline Polyaniline-Activated Carbon Composite for Supercapacitor Application" Molecules 28, no. 4: 1520. https://doi.org/10.3390/molecules28041520
APA StyleMahato, N., Sreekanth, T. V. M., Yoo, K., & Kim, J. (2023). Semi-Polycrystalline Polyaniline-Activated Carbon Composite for Supercapacitor Application. Molecules, 28(4), 1520. https://doi.org/10.3390/molecules28041520








