Abstract
At low temperature, methyl groups act as hindered quantum rotors exhibiting rotational quantum tunneling, which is highly sensitive to a local methyl group environment. Recently, we observed this effect using pulsed electron paramagnetic resonance (EPR) in two dimethylammonium-containing hybrid perovskites doped with paramagnetic Mn2+ ions. Here, we investigate the feasibility of using an alternative fast-relaxing Co2+ paramagnetic center to study the methyl group tunneling, and, as a model compound, we use dimethylammonium zinc formate [(CH3)2NH2][Zn(HCOO)3] hybrid perovskite. Our multifrequency (X-, Q- and W-band) EPR experiments reveal a high-spin state of the incorporated Co2+ center, which exhibits fast spin-lattice relaxation and electron spin decoherence. Our pulsed EPR experiments reveal magnetic field independent electron spin echo envelope modulation (ESEEM) signals, which are assigned to the methyl group tunneling. We use density operator simulations to extract the tunnel frequency of 1.84 MHz from the experimental data, which is then used to calculate the rotational barrier of the methyl groups. We compare our results with the previously reported Mn2+ case showing that our approach can detect very small changes in the local methyl group environment in hybrid perovskites and related materials.
1. Introduction
The methyl group is the most widely spread functional group found in various naturally occurring and synthetic compounds. At temperatures higher than its rotational barrier, this group exhibits classical reorientation dynamics around its three-fold symmetry axis, while at lower temperatures, it acts as a hindered quantum rotor for which only the ro-librational ground state is significantly populated [1,2,3,4]. In this case, stochastic rotation is replaced by rotational quantum tunneling caused by the wavefunction overlap of the three localized states [1,2] (see Figure 1a). The overlap also causes a splitting of the ro-librational ground state into the symmetric ground (A) and two antisymmetric degenerate excited () states. For rotational barriers expected for aliphatic methyl groups, the tunnel frequency that splits these energy states depends approximately exponentially on and thus it can vary in a broad frequency range (GHz-kHz) making it a very sensitive probe to study the local methyl group environment such as chemical bonding, steric effects and defect-induced deformations [4,5,6].
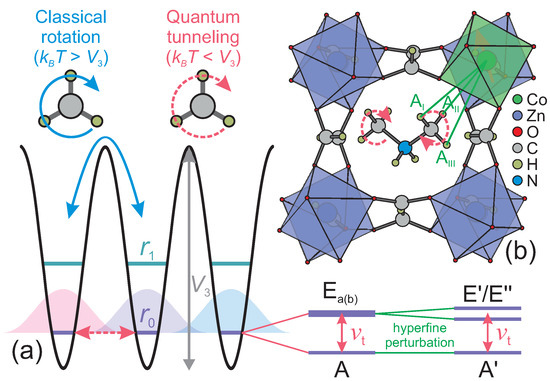
Figure 1.
(a) Schematic energy level diagram of a methyl group rotor with rotational barrier . At temperatures much lower than , the group exhibits quantum tunneling enabled by the wavefunction overlap, which also splits the ro-librational levels into the A and states. The splitting of the lowest level is called the tunnel splitting . In the presence of an unpaired electron spin, the states are further perturbed due to the hyperfine interaction. (b) Low-temperature structure of DMAZn:Co. The hyperfine interactions between the paramagnetic Co2+ ion and protons of the nearest methyl group are indicated by green lines. Structural data taken from Ref. [7].
The tunnel frequency can be obtained using different experimental techniques such as neutron scattering [4], heat capacity measurements [8], vibrational spectroscopy [9], NMR [1,3], continuous wave electron paramagnetic resonance (CW EPR) [10,11] and electron nuclear double resonance (ENDOR) [12,13,14,15]. The latter two techniques require paramagnetic centers to be naturally present or artificially introduced close to the methyl groups in the studied compounds. Recently, we demonstrated that pulsed EPR electron spin echo envelope modulation (ESEEM) experiments can be used to excite and detect the coherence between the tunnel-split states of the methyl groups providing a way to precisely determine in the MHz frequency range [16,17]. In contrast to ordinary ESEEM used to measure small hyperfine interactions with nearby nuclei [18], a distinct signature of the tunneling ESEEM is its independence of the magnetic field.
Our previous measurements of tunneling ESEEM were performed on [(CH3)2NH2] [Zn(HCOO)3] (DMAZn:Mn) and [(CH3)2NH2][Cd(N3)3] (DMACd:Mn) hybrid perovskites containing dimethylammonium (DMA) cations [17]. In these compounds, a tiny amount of diamagnetic metals (Zn2+ and Cd2+) was replaced by paramagnetic Mn2+ impurities [16,17] acting as probes for detection of the tunneling process. For DMAZn:Mn, the main tunneling signals were observed close to 2 MHz and 0.3 MHz, while for DMACd:Mn they appeared at about 0.7 MHz [17]. This allowed us to distinguish small differences in the rotational barriers of the DMA methyl groups in both systems, demonstrating the sensitivity of this method. In addition, we observed splittings of the spectral lines suggesting different methyl group environments were likely due to crystal defects and the soft nature of the hybrid perovskites.
In general, paramagnetic Mn2+ centers are well-suited replacements of divalent diamagnetic ions for detection of tunneling ESEEM due to their relatively slow spin-lattice relaxation and decoherence. In addition, in contrast to some other transition metals such as Cu2+ [19], these ions are not susceptible to Jahn–Teller distortion, which may significantly affect the rotational potential of neighboring methyl groups. On the other hand, tunneling ESEEM may provide information on such local lattice distortions created by various impurities in hybrid perovskites [20,21,22,23] and other materials, which is essential for understanding resilience and stability of different frameworks and the role of the defects on the dynamics and ordering of the molecular cations. This stimulates further studies on the detection of the methyl group tunneling using alternative paramagnetic centers, which exhibit different structural and relaxation properties.
Here, we explore the feasibility of fast-relaxing Co2+ ions to study the methyl group tunneling using DMAZn hybrid perovskite as an exemplary system. DMAZn consists of the ZnO6 octahedra joined by the formate linkers into cuboid cavities containing DMA cations (see Figure 1b), which become ordered in the low-temperature phase (phase transition at about 160 K) [7,19,24,25,26,27]. We use X-, Q- and W-band EPR spectroscopy to show that Co2+ ions replace Zn2+ in DMAZn forming a high-spin state, which exhibits rapid relaxation and decoherence. We obtain the tunneling frequency and the rotational barrier of the methyl groups in DMAZn:Co by simulating the experimental ESEEM spectra using the density operator simulations. The obtained results are compared with the previously reported Mn2+ case revealing sensitivity of this method to resolve minute differences in the range of a couple % of the methyl group rotational barriers perturbed by different paramagnetic centers.
2. Results and Discussion
2.1. Spin Hamiltonian
First, we used CW EPR spectroscopy to characterize the Co2+ centers in DMAZn hybrid perovskite. The measured X-, Q- and W-band CW EPR spectra of DMAZn:Co powder obtained at low temperature are presented in Figure 2, revealing a typical EPR powder pattern of a high-spin Co2+ (electron configuration 3d) having a rhombic tensor [28,29,30,31,32]. The high-spin state of Co2+ is in agreement with the observations in pure DMACo hybrid perovskite [33]. The observed EPR lines are further split by the hyperfine interaction between the unpaired electrons and nucleus of the 59Co isotope (100% natural abundance). Note that we also observed traces of unintentionally incorporated Mn2+ impurities (see Figure S2), which were analyzed in detail in previous studies where they had been introduced intentionally [16,21,25,26,34,35].
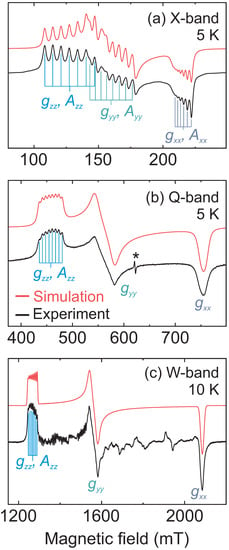
Figure 2.
Measured (black) and simulated (red) CW EPR spectrum of DMAZn:Co obtained at (a) X- (5 K), (b) Q- (5 K) and (c) W-band (10 K). Asterisk in (b) marks unassigned impurity signal at . Signals unaccounted by the simulation in (c) originate from a non-ideal powder average caused by a limited number of crystallites.
The high-spin Co2+ center has three unpaired electrons, and hence the total electron spin is . In addition, the orbital angular momentum of this ion is not quenched () leading to a strong spin-orbit coupling [28,30,36,37]. This interaction causes a very high zero-field splitting between the two lowest Kramers doublets, and thus the paramagnetic center can be effectively described using the effective electron spin-1/2 formalism [28,32,37].
We simulated the observed Co2+ spectra of DMAZn:Co using the effective spin Hamiltonian [28,32,37]:
where the first term describes the electron Zeeman interaction characterized by the effective electron spin and the effective tensor of the Co2+ center. The second term takes into account the hyperfine interaction between the electron spin and the nuclear spin of 59Co. This interaction is described by the effective hyperfine tensor . and denote the external magnetic field and Bohr magneton, respectively.
The simulated spectra, presented in Figure 2, reveal a very good agreement with the experiments for all three frequency bands. Note that the same set of the spin Hamiltonian parameters was used for the three simulations. The determined principal components of are , , and with a mean value of 4.28(1), which is typical for high-spin Co2+ [29,30,31,36,38], supporting our assignment of the spin state. The effective 59Co hyperfine tensor obtained from the simulations has the following principal components: MHz, MHz and MHz, which also fall within the expected range of values for high-spin Co2+ in an octahedral environment [30,31].
The effective components can be used to calculate the real and tensors of the full spin Hamiltonian () [28,32,37,38] yielding and MHz. The rhombic tensor indicates that Co2+ centers in DMAZn occupy a low-symmetry environment, which is in agreement with the low-temperature structures of both DMAZn and DMACo which show distorted metal-oxygen octahedra [7,39]. The spectral simulations obtained using the model with real and tensors reproduce the results of the spin-1/2 approach for a very high value of the splitting between the two lowest Kramers doublets ( GHz). A very high value of is in agreement with our simulations of the W-band CW EPR spectrum, where we did not observe any deviations from the effective spin-1/2 model, indicating GHz.
To assess the value of , we performed temperature-dependent X-band CW EPR experiments of DMAZn:Co (see Figure S3). We observed that with increasing temperature, the signal intensity starts to decrease, and the spectrum completely disappears at about 75 K indicating fast relaxation of the Co2+ centers. The temperature at which the signal vanishes can be used to estimate [30] providing THz, which is much higher than our measurement frequencies.
We also recorded the spectrum of DMAZn:Co using pulsed EPR at different frequency bands and low temperature. The obtained EDFS spectra (see Figure S4) show both Co2+ and Mn2+ impurities, allowing us to perform further characterization using more advanced pulsed EPR experiments.
2.2. Relaxation Properties
We used pulsed EPR to study the relaxation properties of the Co2+ centers in DMAZn:Co, which are important for a subsequent investigation of the methyl group tunneling. The spin-lattice relaxation time was obtained by fitting a stretched exponential function to the experimental data using the same stretching factor for both frequency bands (see Figure S5), indicating a nearly-Gaussian distribution [40] of in DMAZn:Co. Note that a similar type of distribution was also observed in other hybrid perovskites [16,41]. The obtained temperature dependence of the relaxation rate is presented in Figure 3a, exhibiting a fast increase with increasing temperature in the range from 5 K to 12 K. Such a rapid relaxation is typical for high-spin Co2+ and is mainly governed by the Orbach (two phonon) process [42,43]. This process involves a high-lying excited spin state, and thus it can be used to determine the splitting between the two lowest Kramers doublets.
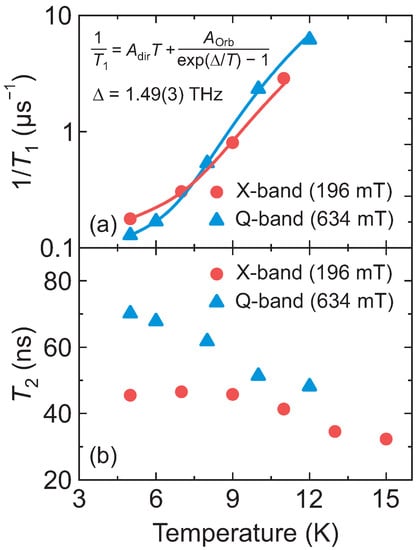
Figure 3.
Temperature dependence of the (a) spin-lattice relaxation rate and (b) electron spin coherence time of DMAZn:Co obtained at X- (196 mT) and Q-band (634 mT) frequencies. Error bars are smaller than data points. Solid curves in (a) represent the best fit to the combination of the direct and Orbach relaxation model.
We approximated the obtained temperature dependence of the relaxation rate using a combination of the Orbach and direct (single phonon) processes [36]:
Here, and correspond to the contributions of both processes. A global fit, with respect to the splitting , was performed for both frequency data sets revealing a perfect agreement with the experimental data (see Figure 3a). The obtained value of of 1.49(3) THz perfectly agrees with the value determined from the temperature-dependent CW EPR experiments (Figure S3), further supporting our interpretation. Other fit parameters are , (X-band), and , (Q-band).
The temperature dependence of the electron spin coherence time of DMAZn:Co obtained at X- and Q-band frequencies is presented in Figure 3b (see Figure S6 for the Hahn echo decays). The value of measured at X-band decreases from about 45 ns at 5 K to about 30 ns at 15 K, which is the detection limit of our spectrometer, while the Q-band is slightly longer in the whole temperature range. Note that the times at both frequency bands are significantly shorter than indicating a different cause of the decoherence such as the zero-field splitting. We also performed measurements of the instantaneous diffusion suppression [44], which revealed no changes in the time indicating that it is not limited by the interactions between the Co2+ ions.
We note that the observed and values of Co2+ in DMAZn are significantly shorter compared with the slow-relaxing transition metal ions such as Mn2+ (e.g., s and s in DMAZn:Mn at 10 K [16]). Such short relaxation times may pose problems for detection of the methyl group tunneling using ESEEM, which is tested in the following.
2.3. Methyl Group Tunneling
We performed X-, Q- and W-band 3p ESEEM experiments of DMAZn:Co to investigate the feasibility of Co2+ centers to detect the methyl group tunneling. The obtained 3p ESEEM time-domain traces are presented in Figure 4a (also see Figure S7) revealing pronounced ESEEM oscillations. The corresponding frequency-domain spectra (Figure 4b) show a peak at 1.71 MHz, which is not affected by the magnetic field. Such a field independent ESEEM is a distinct signature of the methyl group tunneling, as revealed in our previous study [17]. This is further supported by the 3p ESEEM experiments performed at different values showing a buildup of the ESEEM modulation [17], as revealed in the amplitude of the frequency-domain spectra (Figure 4c).
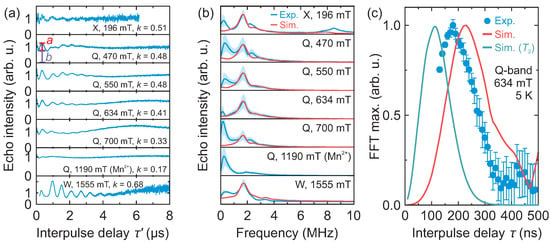
Figure 4.
(a) Background corrected 3p ESEEM time-domain traces of DMAZn:Co obtained at 5 K and at different microwave frequencies and magnetic fields. The interpulse delay was 130 ns (X- and Q-band) and 200 ns (W-band). Parameters a and b indicated on the second trace are used to define the modulation depth as . (b) Corresponding experimental and simulated frequency-domain spectra. The shaded regions mark the uncertainty obtained using different levels of apodization. (c) -dependence of the frequency-domain signal obtained at 643 mT (Q-band) and 5 K. Solid curves show simulation obtained using MHz and the effective , with and without the relaxation taken into account.
In addition to the tunneling signals around 1.7 MHz, we also detected a low-frequency line in the frequency range of 0.15–0.3 MHz (see Figure 4b). The amplitude of this signal is sensitive to the background correction and apodization level suggesting that it may be an artefact due to non-ideal data processing. To investigate this further, we performed analysis of the time-domain data with varying apodization to obtain the confidence region of the frequency-domain signals (Figure 4b). Our results show that this signal can be partially suppressed, but not fully removed using different background functions. An alternative explanation for this low-frequency line may be the transition between the hyperfine-perturbed and states (see Figure 1a), although its intensity is expected to be much lower [17]. Note that similar 3p ESEEM signals in the low-frequency part of the spectrum were also observed for the DMAZn:Mn case [17].
We used density operator calculations to simulate the tunneling ESEEM of DMAZn:Co. In the simulations, we assumed the effective spin-1/2 model, while the hyperfine couplings between the Co2+ center and protons of the 16 nearest methyl groups were calculated using the recently reported low-temperature structure of DMAZn [7] (see Simulation details). The tunnel frequency was the only free parameter in the simulations. The simulated ESEEM spectra (see Figure S8 for the time-domain data) obtained using MHz are presented in Figure 4b, revealing a very good agreement with the experimental data for all measured field and frequency values. Figure S9 shows the individual time-domain contribution for each of the 16 methyl groups used in the simulations, indicating that only the eight nearest groups have a noticeable effect, while the dominant contribution arises from the two closest groups that point to the Co2+ ion.
We also investigated how well our simulations reproduce the modulation depth parameter (see Figure 4a for the definition of a and b) of the time-domain signals. Depending on the frequency and magnetic field, the measured value of k ranges from 0.33 to 0.68, with a mean value of 0.48 (Figure 4a). The simulated modulation depth varies from 0.42 to 0.86 (mean 0.64) (see Figure S8), which is in satisfactory agreement with the experiment. In both cases, the highest modulation depth is observed at W-band frequency. Slightly lower measured values point to a distribution of the tunneling frequency caused by different methyl group environments, which may originate from the structural defects [45] and local deformations due to the soft nature of the hybrid perovskite [46].
Our simulations rather well reproduced the experimentally observed buildup of the modulation (Figure 4c). By taking into account the relaxation, which occurs when the interpulse delay is incremented, the simulated FFT maximum appears at about 120 ns, which is 60 ns lower compared with the experiment. This discrepancy may indicate that a full spin Hamiltonian approach is needed to fully reproduce all aspects of the experimental results. However, determination of this Hamiltonian requires either EPR experiments at very high frequency [32] or sophisticated calculations, both of which are beyond the scope of this work. Note that the ESEEM spectra simulated using the effective and real g-factors are very similar (see Figure S10), indicating that the spin-1/2 formalism is sufficient to extract the tunnel frequency .
The tunnel frequency can be used to calculate the rotational barrier of the methyl groups [2]. The obtained value of 1.84(2) MHz for DMAZn:Co translates to kJ/mol, which is in a reasonable agreement with the density functional theory (DFT) prediction of 12.3 kJ/mol reported in our previous work [17]. We aimed to compare this result with the rotational barrier determined using the unintentionally doped traces of Mn2+ in DMAZn:Co. However, we observed that the tunneling ESEEM signal probed by Mn2+ impurities in DMAZn:Co is significantly broader compared to our previous study [17], where Mn2+ ions were intentionally doped into the structure of DMAZn (see Figure S11 for comparison). We assume that this additional broadening occurs due to faster relaxation of Mn2+ centers induced by Co2+ ions that are simultaneously present within the crystal structure.
Thus, for a better comparison of both paramagnetic centers, we decided to use the ESEEM data of the previously reported DMAZn:Mn system [17]. The experimental ESEEM spectra of DMAZn:Co and DMAZn:Mn are presented in Figure 5 revealing that the main tunneling signal obtained using the Mn2+ centers occurs at about 120 kHz higher frequency. We also used the same procedure as for the DMAZn:Co case to simulate the Mn2+ spectrum, which provided a tunnel frequency of MHz. Note that this value is slightly higher than reported in our previous work ( MHz) [17], where the simulations were performed using a less sophisticated structural model based on the crystal structure of the related DMAMn hybrid perovskite.
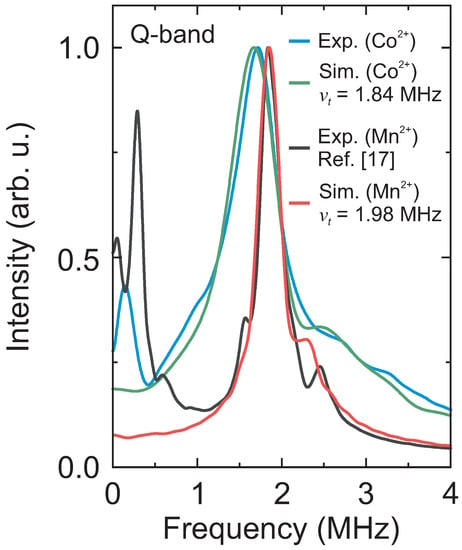
Figure 5.
Comparison of the Q-band ESEEM spectra of DMAZn:Co (634 mT, 5 K) and DMAZn:Mn (1194 mT, 10 K, see also Ref. [17]) and their corresponding simulations. The same data analysis routine was employed in both cases. Simulation parameters: MHz, (DMAZn:Co), and MHz, [26] (DMAZn:Mn).
The obtained MHz translates to the methyl group rotational barrier of 10.50(1) kJ/mol, which is only slightly lower compared to the Co2+ case (10.60(1) kJ/mol). Such a difference may originate from a higher degree of lattice distortion caused by the high-spin Co2+ ions, which, in contrast to the high-spin Mn2+, can exhibit a pseudo Jahn–Teller effect. The ability to reliably resolve minute changes (of the order of 1%) in introduced by different paramagnetic centers demonstrates an incredible sensitivity of the tunneling ESEEM recorded with the 3p ESEEM pulse sequence to probe the local methyl group environment.
3. Experimental and Simulation Details
3.1. Sample Synthesis and Characterization
ZnCl2 (99.999%, Sigma-Aldrich, St. Louis, MO, USA), CoCl2·xH2O (99.999%, Sigma-Aldrich), a 2.0 M solution of (CH3)2NH in methanol (Sigma-Aldrich), methanol (99.8%, Sigma-Aldrich) and formic acid (98%, Fluka, Switzerland) were commercially available and used without further purification. Crystals of DMAZn: 1 Co2+ mol% were grown by a slow diffusion method. In a typical experiment, 2.5 mL of 2.0 M solution of (CH3)2NH in methanol and 0.5 mL of formic acid were added to 10 mL of methanol. This solution was placed at the bottom of a glass tube (20 mm inner diameter). To this solution, 2 mL of methanol was layered, followed by 20 mL of methanol solution containing 0.99 mmol of ZnCl2 and 0.01 mmol of CoCl2·xH2O. The tube was sealed and kept undisturbed. The pink crystals were harvested after 4 days, washed three times with methanol, and dried at room temperature.
The preservation of the perovskite phase after doping with Co was confirmed by the Raman spectroscopy (see Figure S1) [47]. Raman spectra were measured using a Bruker FT 100/S spectrometer with Nd:YAG laser excitation (1064 nm). The spectral resolution was 2 cm.
3.2. EPR Spectroscopy
The synthesized DMAZn:Co crystals were ground into a fine powder, which was placed into 4, 1.6 and 0.9 mm outer diameter EPR tubes for measurements at X- (9.5 GHz), Q- (34 GHz) and W-band (94 GHz) frequencies, respectively. For X- and Q-band EPR experiments, we used a Bruker ELEXSYS E580/IF-Q EPR spectrometer equipped with Bruker ER4118X-MD5 (pulsed X-band), high-Q ER4102ST (CW X-band) and EN5107D2 (pulsed/CW Q-band) microwave resonators. High-power pulses were obtained using 1 kW TWT (X-band) and 10 W solid-state (Q-band) microwave amplifiers. The EPR experiments at W-band were carried out using a Bruker ELEXSYS E680 X-/W-band spectrometer equipped with an EN 680-1021H resonator and a 2 W solid-state amplifier. The helium flow cryostats were used to stabilize the temperature.
For the CW EPR experiments, we used the following amplitude and frequency of the modulation field: 100 kHz and 1 G (X-band), 50 kHz and 1 G (Q-band), and 100 kHz and 4 G (W-band). The microwave power was adjusted to avoid saturation of the EPR signal.
The pulsed EPR experiments of DMAZn:Co were performed using 16 ns - and 32 ns -pulses. The echo-detected field sweep (EDFS) spectra were recorded using a Hahn echo pulse sequence () with an interpulse delay of 130 ns (X- and Q-band) and 200 ns (W-band). The three-pulse (3p) ESEEM was recorded by integrating the stimulated echo obtained using the pulse sequence, where the interpulse delay was incremented by a time step of 6 ns (X- and Q-band) and 4 ns (W-band). The spin-lattice relaxation time was obtained using the inversion recovery pulse sequence (), while the spin decoherence time was measured using the Hahn echo experiment. Four-step phase cycling was used to cancel unwanted echoes except for the two-pulse experiments, where two-step phase cycling was employed.
For the data analysis, the experimental 3p ESEEM time-domain traces were divided by bi-exponential decay functions followed by Hamming apodization, zero-filling and fast Fourier transform with cross-term averaging [48] to yield the frequency-domain spectra. The values of relaxation time were obtained by fitting a stretched exponential function () to the inversion recovery data, which provided a significantly better agreement compared to the single and bi-exponential recovery functions. The times were extracted from the Hahn echo decay experiments using a single exponential decay (). All steps were carried out using home-written MATLAB R2021b (The MathWorks Inc., Natick, MA, USA) scripts.
3.3. Simulation Details
We used EasySpin 5.2.33 [49] running on MATLAB R2021b (The MathWorks Inc.) to simulate the CW EPR spectra.
The 3p ESEEM signals of the methyl group tunneling were simulated using density operator formalism in home-written MATLAB scripts [17,50]. Spin-operator matrices and orientation grids were generated using EasySpin sop and sphgrid functions. The hyperfine interactions between the Co2+ center and methyl protons were calculated using the point-dipole approximation from the low-temperature structure of DMAZn [7]. The eight nearest DMA cations (16 methyl groups) were considered during the simulations. For each orientation, a product of the simulated time-domain traces of all 16 groups was obtained as for ordinary 3p ESEEM. The resulting time-domain signal was obtained by calculating a weighted average of the traces obtained at different orientations. The baseline was removed by normalizing the signal to its average value.
The rotational barrier was calculated from the tunnel frequency by diagonalizing the rotational Hamiltonian in a basis of the free quantum rotor [2]. The tunnel frequency was taken as the energy difference between the two lowest-energy states.
4. Summary and Conclusions
In this work, we used EPR spectroscopy to study the methyl group tunneling in DMAZn hybrid perovskite doped with a small amount of paramagnetic Co2+ impurities. Our CW EPR experiments revealed that Co2+ centers occupy a low-symmetry site in the DMAZn structure forming a high-spin state, the lowest lying doublet of which can be well described using the effective spin-1/2 formalism. We observed a fast decrease of with increasing temperature, which was explained by the Orbach relaxation process with a 1.5 THz splitting between the two lowest Kramers doublets. The obtained time of DMAZn:Co also proved to be very short, of the order of tens of nanoseconds.
We used 3p ESEEM spectroscopy to study the feasibility of these fast-relaxing Co2+ ions to facilitate detection of the methyl group tunneling in DMAZn. A pronounced field-independent tunneling signal was observed at about 1.7 MHz, which we reproduced using simulations based on density operator formalism with a tunnel frequency of 1.84(2) MHz. This value translates to a rotational barrier of 10.60(2) kJ/mol. A comparison with the DMAZn:Mn case allowed us to resolve very small differences (in the range of a couple %) of the methyl group rotational barriers in the presence of Co2+ and Mn2+ paramagnetic centers in DMAZn.
In general, our results show that ESEEM of Co2+ centers can be successfully employed to study tunneling of the neighboring methyl groups in hybrid perovskites and other materials. In addition, we demonstrated that this spectroscopic approach is highly effective in determining minute differences in the rotational potentials of the methyl groups, providing a sensitive handle to probe their local environment. In terms of hybrid perovskites, this method could be used to investigate small structural distortions caused by different framework impurities, which otherwise are difficult to study.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28030979/s1, Figure S1: Raman spectra of DMAZn:Co and DMAZn, Figure S2: Additional Q-band CW EPR spectrum, Figure S3: Additional X-band CW EPR spectra, Figure S4: EDFS spectra of DMAZn:Co, Figure S5: Inversion recovery data of DMAZn:Co, Figure S6: Hahn echo decays of DMAZn:Co, Figure S7: Experimental 3p ESEEM time-domain traces of DMAZn:Co, Figure S8: Simulated 3p ESEEM time-domain traces of DMAZn:Co, Figure S9: Simulated 3p ESEEM time-domain traces of the nearest 16 methyl groups, Figure S10: Additional simulations of the frequency-domain spectrum, Figure S11: Additional 3p ESEEM spectrum.
Author Contributions
Conceptualization: G.U., D.K., A.P., G.J., M.Š.; data curation: G.U., A.E., D.K., G.J., M.Š.; formal analysis: G.U., A.E.; funding acquisition: M.M., J.B., G.J., M.Š.; investigation: G.U., A.E., I.P., V.K., D.K., M.Š.; methodology: G.U., A.E., D.K., A.P., G.J., M.Š.; project administration: M.Š.; resources: M.M., J.B., G.J., M.Š.; software: G.U., A.E., D.K., G.J.; supervision: D.K., A.P., J.B., G.J., M.Š.; validation: D.K., G.J., M.Š.; visualization: G.U., M.Š.; writing—original draft: G.U., M.Š; writing—review and editing: All authors. All authors have read and agreed to the published version of the manuscript.
Funding
This project has been funded by the Research Council of Lithuania (LMTLT) (agreement No. S-MIP-22-73).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DMAZn | Dimethylammonium zinc formate |
| DMACo | Dimethylammonium cobalt formate |
| DMAMn | Dimethylammonium manganese formate |
| 3p ESEEM | Three pulse electron spin echo envelope modulation |
| EPR | Electron paramagnetic resonance |
| CW | Continuous wave |
| ENDOR | Electron nuclear double resonance |
| NMR | Nuclear magnetic resonance |
| DFT | Density functional theory |
References
- Horsewill, A. Quantum tunnelling aspects of methyl group rotation studied by NMR. Prog. Nucl. Magn. Reson. Spectrosc. 1999, 35, 359–389. [Google Scholar] [CrossRef]
- Dimeo, R.M. Visualization and measurement of quantum rotational dynamics. Am. J. Phys. 2003, 71, 885–893. [Google Scholar] [CrossRef]
- Latanowicz, L. NMR relaxation study of methyl groups in solids from low to high temperatures. Concepts Magn. Reson. Part A 2005, 27A, 38–53. [Google Scholar] [CrossRef]
- Prager, M.; Heidemann, A. Rotational Tunneling and Neutron Spectroscopy: A Compilation. Chem. Rev. 1997, 97, 2933–2966. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.; Johnson, M.R. Methyl group tunneling - A quantitative probe of atom-atom potentials. J. Chem. Phys. 1997, 107, 1725–1731. [Google Scholar] [CrossRef]
- Spangler, L.H. Structural information from methyl internal rotation spectroscopy. Annu. Rev. Phys. Chem. 1997, 48, 481–510. [Google Scholar] [CrossRef] [PubMed]
- Peksa, P.; Nowok, A.; Formalik, F.; Zaręba, J.K.; Trzmiel, J.; Gągor, A.; Mączka, M.; Sieradzki, A. More complex than originally thought: Revisiting the origins of the relaxation processes in dimethylammonium zinc formate. J. Mater. Chem. C 2022, 10, 6866–6877. [Google Scholar] [CrossRef]
- Inaba, A. Calorimetric studies of tunneling phenomena. Phys. B 1994, 202, 325–331. [Google Scholar] [CrossRef]
- Trapani, A.P.; Strauss, H.L. Infrared structural holeburning and orientational tunneling of NH3D+ ions in ammonium cobalt sulfate. J. Chem. Phys. 1987, 87, 1899–1900. [Google Scholar] [CrossRef]
- Clough, S.; Hill, J.; Poldy, F. Tunnelling sidebands of methyl group hyperfine structure. J. Phys. C Solid State Phys. 1972, 5, 1739. [Google Scholar] [CrossRef]
- Geoffroy, M.; Kispert, L.D.; Hwang, J.S. An ESR, ENDOR, and ELDOR study of tunneling rotation of a hindered methyl group in x-irradiated 2,2,5-trimethyl-1,3-dioxane-4,6-dione crystals. J. Chem. Phys. 1979, 70, 4238–4242. [Google Scholar] [CrossRef]
- Clough, S.; Poldy, F. Study of Tunneling Rotation of Methyl Groups by Electron Spin Resonance and Electron Nuclear Double Resonance. J. Chem. Phys. 1969, 51, 2076–2084. [Google Scholar] [CrossRef]
- Clough, S.; Hill, J.; Poldy, F. Methyl group tunnelling rotation frequency in γ-irradiated methyl malonic acid crystals. J. Phys. C Solid State Phys. 1972, 5, 518. [Google Scholar] [CrossRef]
- Bonon, F.; Brustolon, M.; Maniero, A.; Segre, U. An ENDOR study of the temperature dependence of methyl tunnelling. Chem. Phys. 1992, 161, 257–263. [Google Scholar] [CrossRef]
- Martínez, J.I.; Alonso, P.J.; García-Rubio, I.; Medina, M. Methyl rotors in flavoproteins. Phys. Chem. Chem. Phys. 2014, 16, 26203–26212. [Google Scholar] [CrossRef]
- Šimėnas, M.; Macalik, L.; Aidas, K.; Kalendra, V.; Klose, D.; Jeschke, G.; Mączka, M.; Völkel, G.; Banys, J.; Pöppl, A. Pulse EPR and ENDOR Study of Manganese Doped [(CH3)2NH2][Zn(HCOO)3] Hybrid Perovskite Framework. J. Phys. Chem. C 2017, 121, 27225–27232. [Google Scholar] [CrossRef]
- Šimėnas, M.; Klose, D.; Ptak, M.; Aidas, K.; Mączka, M.; Banys, J.; Pöppl, A.; Jeschke, G. Magnetic excitation and readout of methyl group tunnel coherence. Sci. Adv. 2020, 6, eaba1517. [Google Scholar] [CrossRef] [PubMed]
- Deligiannakis, Y.; Louloudi, M.; Hadjiliadis, N. Electron spin echo envelope modulation (ESEEM) spectroscopy as a tool to investigate the coordination environment of metal centers. Coord. Chem. Rev. 2000, 204, 1–112. [Google Scholar] [CrossRef]
- Šimėnas, M.; Ciupa, A.; Usevičius, G.; Aidas, K.; Klose, D.; Jeschke, G.; Mączka, M.; Völkel, G.; Pöppl, A.; Banys, J. Electron paramagnetic resonance of a copper doped [(CH3)2NH2][Zn(HCOO)3] hybrid perovskite framework. Phys. Chem. Chem. Phys. 2018, 20, 12097–12105. [Google Scholar] [CrossRef]
- Lien, S.Y.; Wang, C.W.; Chen, W.R.; Liu, C.H.; Kang, C.C.; Huang, C.J. The Influence of Oxygen Plasma on Methylammonium Lead Iodide (MAPbI3) Film Doped with Lead Cesium Triiodide (CsPbI3). Molecules 2021, 26, 5133. [Google Scholar] [CrossRef] [PubMed]
- Ptak, M.; Sieradzki, A.; Šimėnas, M.; Maczka, M. Molecular Spectroscopy of Hybrid Organic-Inorganic Perovskites and Related Compounds. Coord. Chem. Rev. 2021, 448, 214180. [Google Scholar] [CrossRef]
- Šimėnas, M.; Balciunas, S.; Wilson, J.N.; Svirskas, S.; Kinka, M.; Garbaras, A.; Kalendra, V.; Gagor, A.; Szewczyk, D.; Sieradzki, A.; et al. Suppression of Phase Transitions and Glass Phase Signatures in Mixed Cation Halide Perovskites. Nat. Commun. 2020, 11, 5103. [Google Scholar] [CrossRef]
- Šimėnas, M.; Balčiūnas, S.; Gągor, A.; Pieniążek, A.; Tolborg, K.; Kinka, M.; Klimavicius, V.; Svirskas, S.; Kalendra, V.; Ptak, M.; et al. Mixology of MA1-xEAxPbI3 Hybrid Perovskites: Phase Transitions, Cation Dynamics, and Photoluminescence. Chem. Mat. 2022, 34, 10104–10112. [Google Scholar] [CrossRef]
- Jain, P.; Dalal, N.S.; Toby, B.H.; Kroto, H.W.; Cheetham, A.K. Order-Disorder Antiferroelectric Phase Transition in a Hybrid Inorganic-Organic Framework with the Perovskite Architecture. J. Am. Chem. Soc. 2008, 130, 10450–10451. [Google Scholar] [CrossRef]
- Šimėnas, M.; Ciupa, A.; Mączka, M.; Pöppl, A.; Banys, J. EPR Study of Structural Phase Transition in Manganese-Doped [(CH3)2NH2][Zn(HCOO)3] Metal-Organic Framework. J. Phys. Chem. C 2015, 119, 24522–24528. [Google Scholar] [CrossRef]
- Šimėnas, M.; Kultaeva, A.; Balčiūnas, S.; Trzebiatowska, M.; Klose, D.; Jeschke, G.; Mączka, M.; Banys, J.; Pöppl, A. Single Crystal Electron Paramagnetic Resonance of Dimethylammonium and Ammonium Hybrid Formate Frameworks: Influence of External Electric Field. J. Phys. Chem. C 2017, 121, 16533–16540. [Google Scholar] [CrossRef]
- Šimėnas, M.; Balčiūnas, S.; Ciupa, A.; Vilčiauskas, L.; Jablonskas, D.; Kinka, M.; Sieradzki, A.; Samulionis, V.; Mączka, M.; Banys, J. Elucidation of Dipolar Dynamics and the Nature of Structural Phases in the [(CH3)2NH2][Zn(HCOO)3] Hybrid Perovskite Framework. J. Mater. Chem. C 2019, 7, 6779–6785. [Google Scholar] [CrossRef]
- Banci, L.; Bencini, A.; Benelli, C.; Gatteschi, D.; Zanchini, C. Spectral-Structural Correlations in High-Spin Cobalt(II) Complexes; Springer: Berlin/Heidelberg, Germany, 1982; pp. 37–86. [Google Scholar]
- Makinen, M.W.; Kuo, L.C.; Yim, M.B.; Wells, G.B.; Fukuyama, J.M.; Kim, J.E. Ground term splitting of high-spin cobalt(2+) ion as a probe of coordination structure. 1. Dependence of the splitting on coordination geometry. J. Am. Chem. Soc. 1985, 107, 5245–5255. [Google Scholar] [CrossRef]
- Pilbrow, J. Transition Ion Electron Paramagnetic Resonance; Oxford Science Publications, Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Lässig, D.; Lincke, J.; Griebel, J.; Kirmse, R.; Krautscheid, H. Synthesis, Crystal Structure, and Electron Paramagnetic Resonance Investigations of Heteronuclear CoII/ZnII and CoII/CdII Coordination Polymers. Inorg. Chem. 2011, 50, 213–219. [Google Scholar] [CrossRef]
- Misochko, E.Y.; Akimov, A.V.; Korchagin, D.V.; Nehrkorn, J.; Ozerov, M.; Palii, A.V.; Clemente-Juan, J.M.; Aldoshin, S.M. Purely Spectroscopic Determination of the Spin Hamiltonian Parameters in High-Spin Six-Coordinated Cobalt(II) Complexes with Large Zero-Field Splitting. Inorg. Chem. 2019, 58, 16434–16444. [Google Scholar] [CrossRef]
- Hughey, K.D.; Clune, A.J.; Yokosuk, M.O.; Li, J.; Abhyankar, N.; Ding, X.; Dalal, N.S.; Xiang, H.; Smirnov, D.; Singleton, J.; et al. Structure-Property Relations in Multiferroic [(CH3)2NH2]M(HCOO)3 (M = Mn, Co, Ni). Inorg. Chem. 2018, 57, 11569–11577. [Google Scholar] [CrossRef]
- Šimėnas, M.; Ptak, M.; Khan, A.H.; Dagys, L.; Balevičius, V.; Bertmer, M.; Völkel, G.; Mączka, M.; Pöppl, A.; Banys, J. Spectroscopic Study of [(CH3)2NH2][Zn(HCOO)3] Hybrid Perovskite Containing Different Nitrogen Isotopes. J. Phys. Chem. C 2018, 122, 10284–10292. [Google Scholar] [CrossRef]
- Orio, M.; Bindra, J.K.; van Tol, J.; Giorgi, M.; Dalal, N.S.; Bertaina, S. Quantum dynamics of Mn2+ in dimethylammonium magnesium formate. J. Chem. Phys. 2021, 154, 154201. [Google Scholar] [CrossRef]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Mabbs, F.E.; Collison, D. (Eds.) Electron Paramagnetic Resonance of d Transition Metal Compounds; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Pilbrow, J. Effective g values for S = 3/2 and S = 5/2. J. Magn. Reson. (1969) 1978, 31, 479–490. [Google Scholar] [CrossRef]
- Fu, D.W.; Zhang, W.; Cai, H.L.; Zhang, Y.; Ge, J.Z.; Xiong, R.G.; Huang, S.D.; Nakamura, T. A Multiferroic Perdeutero Metal-Organic Framework. Angew. Chem. Int. Ed. 2011, 50, 11947–11951. [Google Scholar] [CrossRef]
- Völkel, G.; Müller, H.E.; Flohrer, W. Critical Anomaly of the Electron Spin-Lattice Relaxation in X-Irradiated Rochelle Salt. Phys. Status Solidi B 1981, 108, 501–506. [Google Scholar] [CrossRef]
- Šimėnas, M.; Balčiūnas, S.; Trzebiatowska, M.; Ptak, M.; Mączka, M.; Völkel, G.; Pöppl, A.; Banys, J. Electron paramagnetic resonance and electric characterization of a [CH3NH2NH2][Zn(HCOO)3] perovskite metal formate framework. J. Mater. Chem. C 2017, 5, 4526–4536. [Google Scholar] [CrossRef]
- Orbach, R. Spin-lattice relaxation in rare-earth salts. Proc. R. Soc. Lond. Ser. A 1961, 264, 458–484. [Google Scholar]
- Finn, C.B.P.; Orbach, R.; Wolf, W.P. Spin-Lattice Relaxation in Cerium Magnesium Nitrate at Liquid Helium Temperature: A New Process. Proc. Phys. Soc. Lond. 1961, 77, 261. [Google Scholar] [CrossRef]
- Tyryshkin, A.M.; Tojo, S.; Morton, J.J.L.; Riemann, H.; Abrosimov, N.V.; Becker, P.; Pohl, H.J.; Schenkel, T.; Thewalt, M.L.W.; Itoh, K.M.; et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 2012, 11, 143–147. [Google Scholar] [CrossRef]
- Boström, H.L.B.; Kieslich, G. Influence of Metal Defects on the Mechanical Properties of ABX3 Perovskite-Type Metal-formate Frameworks. J. Phys. Chem. C 2021, 125, 1467–1471. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, J.; Yin, W.J. Atomistic origin of lattice softness and its impact on structural and carrier dynamics in three dimensional perovskites. Energy Environ. Sci. 2022, 15, 660–671. [Google Scholar] [CrossRef]
- Mączka, M.; Ptak, M.; Macalik, L. Infrared and Raman Studies of Phase Transitions in Metal-Organic Frameworks of [(CH3)2NH2][M(HCOO)3] with M=Zn, Fe. Vib. Spectrosc. 2014, 71, 98–104. [Google Scholar] [CrossRef]
- Van Doorslaer, S.; Sierra, G.; Schweiger, A. Dead Time-Dependent Line Distortions in Absolute-Value Electron Spin Echo Envelope Modulation Spectra. J. Magn. Reson. 1999, 136, 152–158. [Google Scholar] [CrossRef] [PubMed]
- Stoll, S.; Schweiger, A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Jeschke, G. Rotational Coupling in Methyl-Tunneling Electron Spin Echo Envelope Modulation. Appl. Magn. Reson. 2022, 53, 635–651. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).