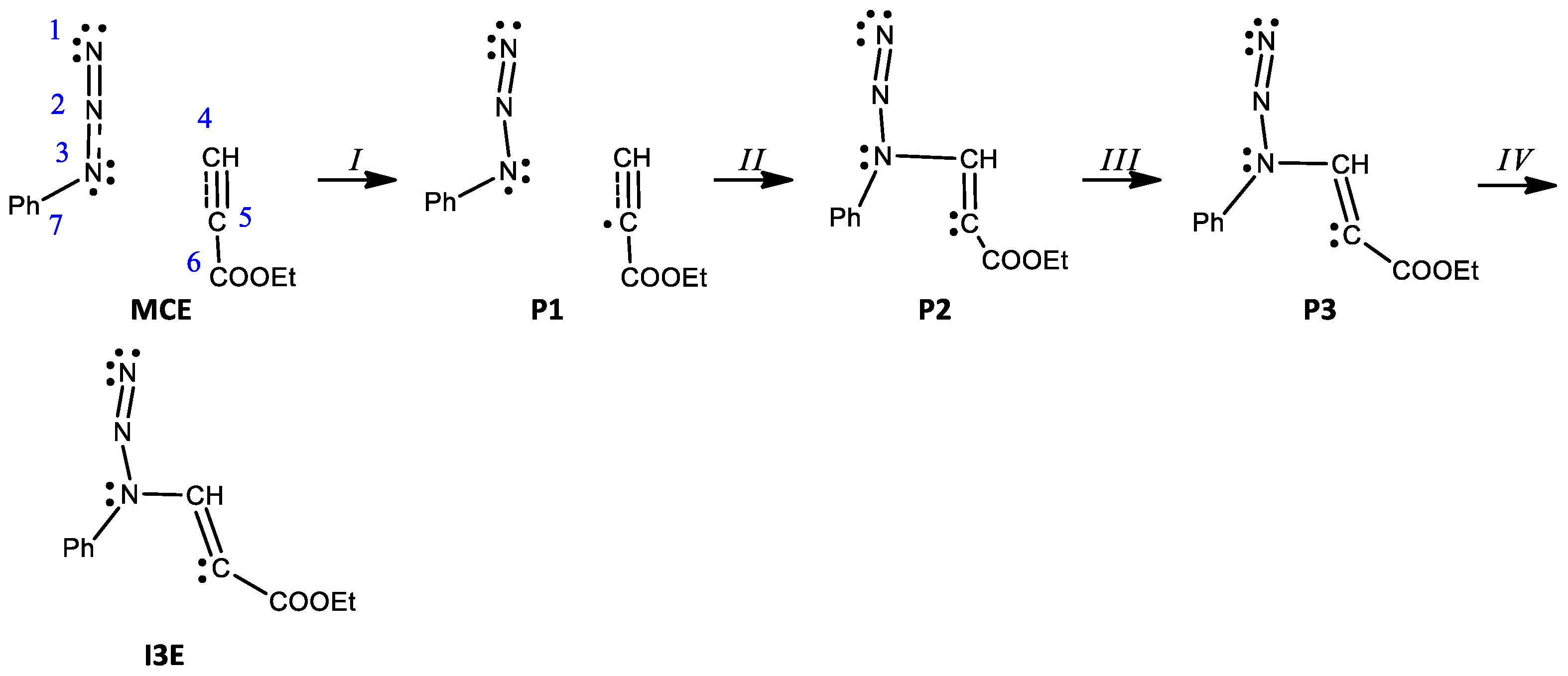
On the Question of Zwitterionic Intermediates in the [3+2] Cycloaddition Reactions between Aryl Azides and Ethyl Propiolate
Abstract
:1. Introduction
2. Results and Discussion
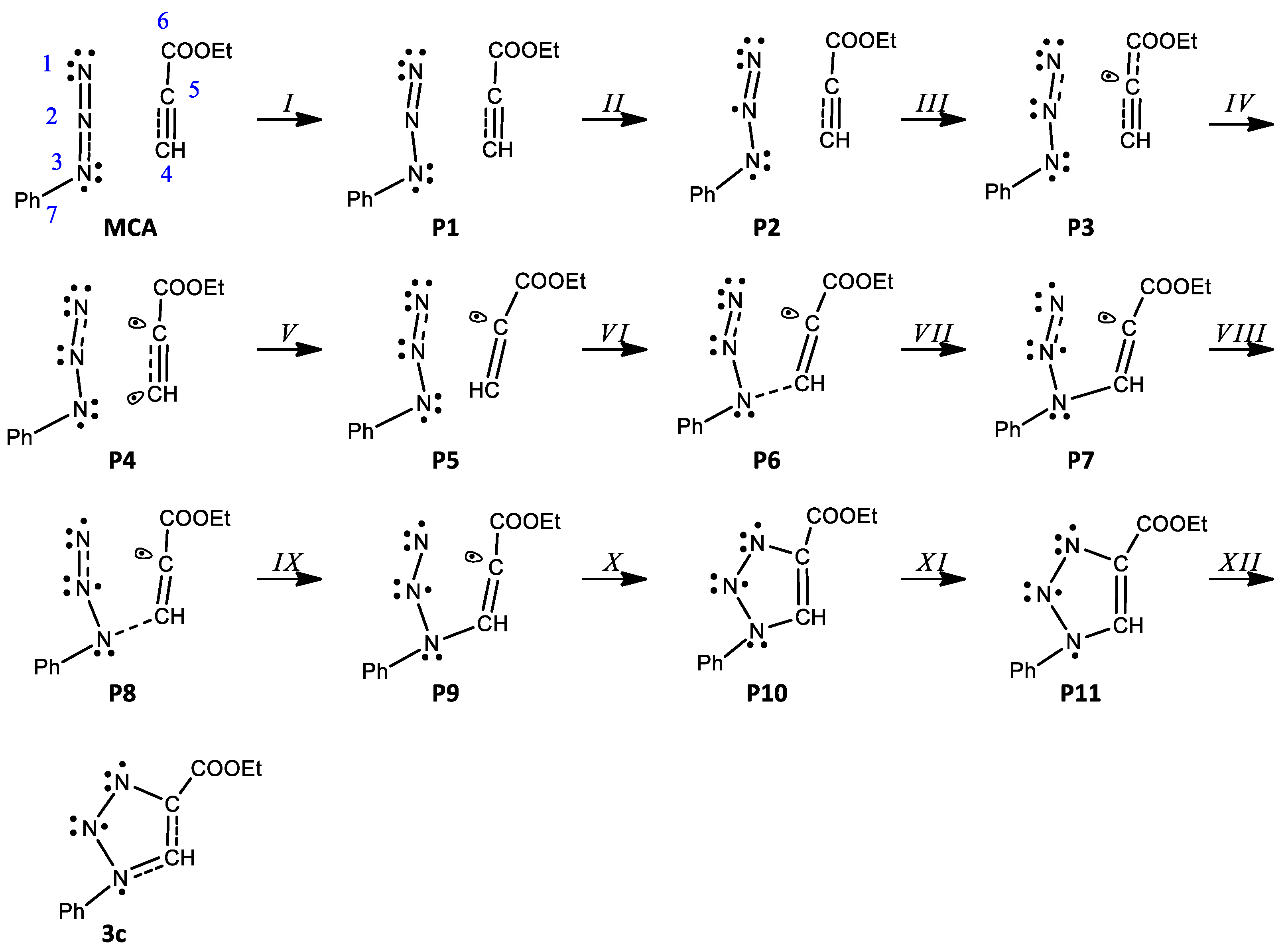
- (1)
- In phases I–II, disynaptic basins V(N1,N2) and V′(N1,N2) go through topological changes leading to the creation of a new monosynaptic basin V(N2). First, in P1, disynaptic basin V′(N1,N2) disappears, transferring its electron density into V(N1,N2) and integrating 4.20e. Next, in P2, monosynaptic basin V(N2) representing nonbonding electron density is created with a population of 0.62e originating from V(N1,N2). The energy increases by 9.4 kcal/mol.
- (2)
- In phases III–VI, events leading to the creation of the first new single bond can be observed. During phase III, the integration of disynaptic basins V(N1,N2) and V(N1,N2) decreases by 0.81e and 0.42e, respectively, increasing the population of monosynaptic basin V(N2). In P3, a pseudoradical center is created on C5 represented by the V(C5) monosynaptic basin, integrating 0.14e. An increase of 9.9 kcal/mol in energy can be observed, and the GEDT is −0.08e. Next, a short-phase V starts with the creation of a pseudoradical center on C4 integrating 0.05e; at the same time, an increase in the population in basins V(C5) and V(N2) can be seen. In P5, monosynaptic basin V(C4) disappears, with its electron density being transferred to the monosynaptic basin V(N3) and integrating 3.48e.
- (3)
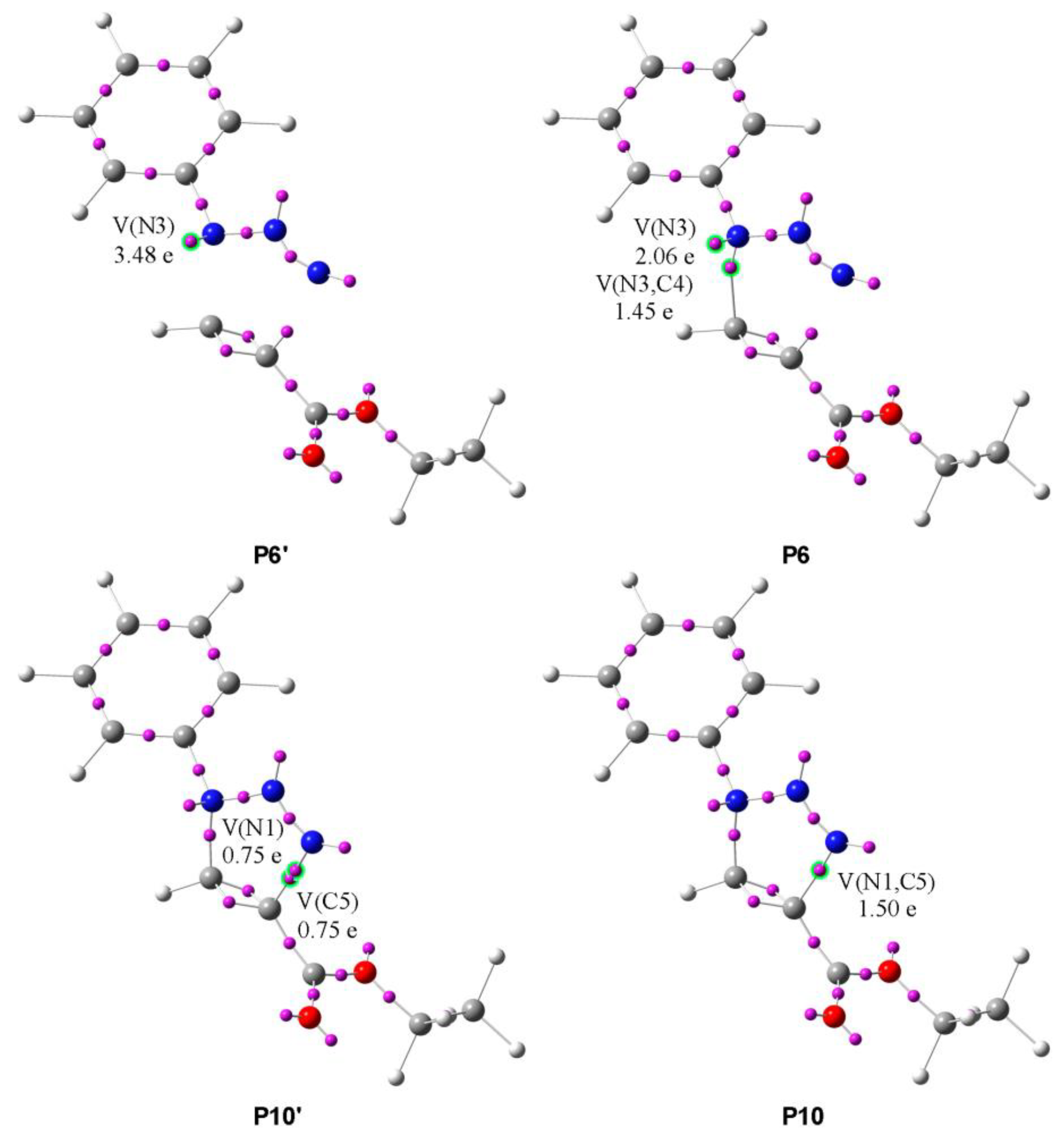
- Phase VII, d(N1-C5) = 2.104 Å and d(N3-C4) = 1.878 Å, starts with the creation of the first new C-N bond by donation of the nonbonding electron density of N3 to C4. The disynaptic basin V(N3,C4) is created with an initial population of 1.45e, while the V(N3) monosynaptic basin’s integration decreases to 2.06e, as shown by structures P6′ and P6 in Figure 6.
- (4)
- In P7, a new monosynaptic basin V′(N1) integrating 0.38e is created with its population originating from V(N1) now integrating 3.45e. Meanwhile, a transfer of population from disynaptic basins V(C4,C5) and V′(C4,C5) of the C4-C5 double bond to V(N3,C4) and V(C5) can be observed. The GEDT is 0.14e, and the energy decreases by 15.3 kcal/mol.
- (5)
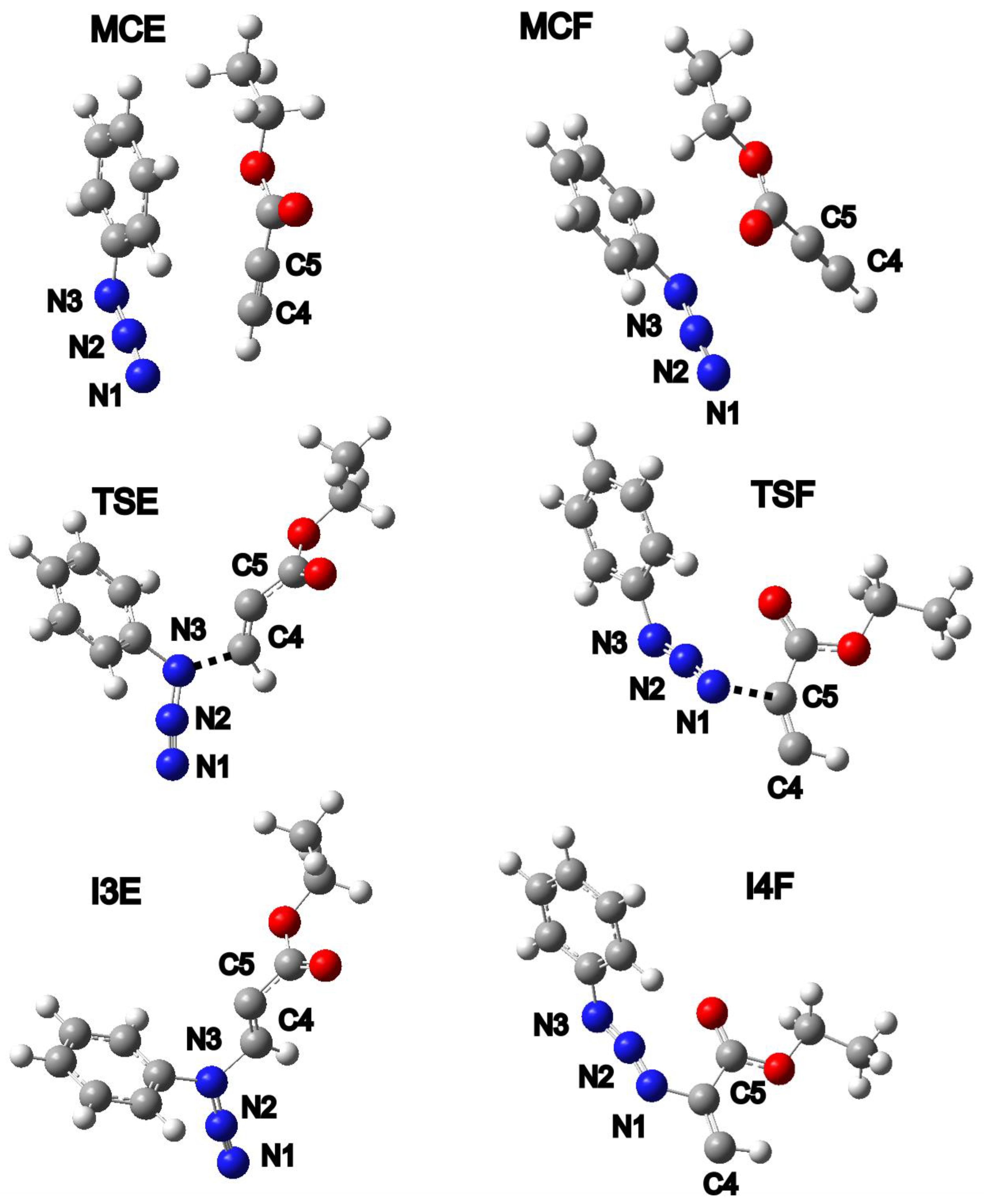
- Phase IX starts with the creation of a monosynaptic basin V′(N3), integrating 0.50e, and at the same time the population of the disynaptic basin V(N3,C4) decreases to 1.33e. Next, at P9, basin V′(N3) disappears transferring its population back to V(N3,C4), integrating now 2.02e. Additionally, an increase in population of the monosynaptic basin V′(N1) of 0.30e originating from V(N1) can be seen. The energy decreases by 20.2 kcal/mol and the GEDT increases to 0.24e.
- (6)
- The second new C-N bond is created at P10, d(N1-C5) = 1.720 Å and d(N3-C4) = 1.561 Å, by shearing of the pseudoradical center C5 and nonbonding electron density of N1. The monosynaptic basin V(C5) and V′(N1), both integrating 0.75e, merge to create the new disynaptic basin V(N1,C5) with a population of 1.50e, as shown by structures P10′ and P10 in Figure 6.
- (7)
- Phase XII starts with the disappearance of V′(C4,C5) with the transfer of its population to V(C4,C5), now integrating 3.67e. A decrease in energy of 27.3 kcal/mol and a GEDT of 0.29e can be observed.
- (8)
- The 32CA of phenylazide 1c with alkyne 2 takes place via a two-stage one-step mechanism of the attack of nucleophilic N3 of the azide on the most electrophilic carbon C4 of the alkyne.
- (1)
- In P1, a monosynaptic basin V(C5) integrating 0.24e is created with its population originating from two disynaptic basins V(C4,C5) and V′(C4,C5), as shown by P1′ and P1 in Figure 7. The energy increases by 17.0 kcal/mol and the GEDT is −0.03e.
- (2)
- At P2, the most significant topological change can be observed, and a new bond is created by sharing the N3 nonbonding electron density with C4. The monosynaptic basin V(N3) is depopulated and a new disynaptic basin V(N3,C4) is created, integrating 1.68e, as shown by structures P2′ and P2 in Figure 7. The GEDT increases to −0.31e, and another significant rise in energy of 17.7 kcal/mol can be seen.
- (3)
- The last phase IV starts with the creation of monosynaptic basin V′(N3) integrating 0.69e. The energy decreases by 0.9 kcal/mol, while the GEDT increases to −0.51e. The energy of the final structure of the zwitterion I3E is 0.5 kcal/mol lower and the GEDT reaches −0.53e.

| Structures | 1c | 2 | MCE | P1 | P2 | TSE | P3 | I3E | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Phases | I | II | III | IV | |||||||
| d1(N3-C4) | 3.460 | 2.474 | 1.798 | 1.710 | 1.532 | 1.518 | |||||
| GEDT | 0.00 | −0.03 | −0.31 | −0.38 | −0.51 | −0.53 | |||||
| dE | −6.2 | 10.8 | 28.5 | 28.8 | 27.6 | 27.1 | |||||
| V(N1) | 3.76 | 3.77 | 3.80 | 3.67 | 3.64 | 3.59 | 3.59 | ||||
| V(N1.N2) | 2.34 | 2.32 | 2.50 | 2.67 | 2.65 | 2.37 | 2.32 | ||||
| V′(N1.N2) | 1.80 | 1.81 | 1.67 | 1.70 | 1.75 | 2.02 | 2.06 | ||||
| V(N2.N3) | 2.50 | 2.51 | 2.47 | 2.28 | 2.25 | 2.27 | 2.28 | ||||
| V(N3) | 3.37 | 3.37 | 3.28 | 1.70 | 1.54 | 1.25 | 1.10 | ||||
| V(N3.C7) | 1.83 | 1.84 | 1.88 | 1.81 | 1.80 | 1.80 | 1.79 | ||||
| V(C4.C5) | 2.56 | 2.56 | 2.49 | 2.06 | 2.00 | 1.83 | 1.81 | ||||
| V′(C4.C5) | 2.73 | 2.72 | 2.59 | 2.10 | 2.04 | 1.88 | 1.85 | ||||
| V(C5.C6) | 2.40 | 2.40 | 2.41 | 2.31 | 2.32 | 2.32 | 2.29 | ||||
| V′(N3) | 0.69 | 0.84 | |||||||||
| V(N3.C4) | 1.68 | 1.90 | 1.59 | 1.61 | |||||||
| V(C4) | 0.24 | 1.35 | 1.47 | 1.81 | 1.90 |
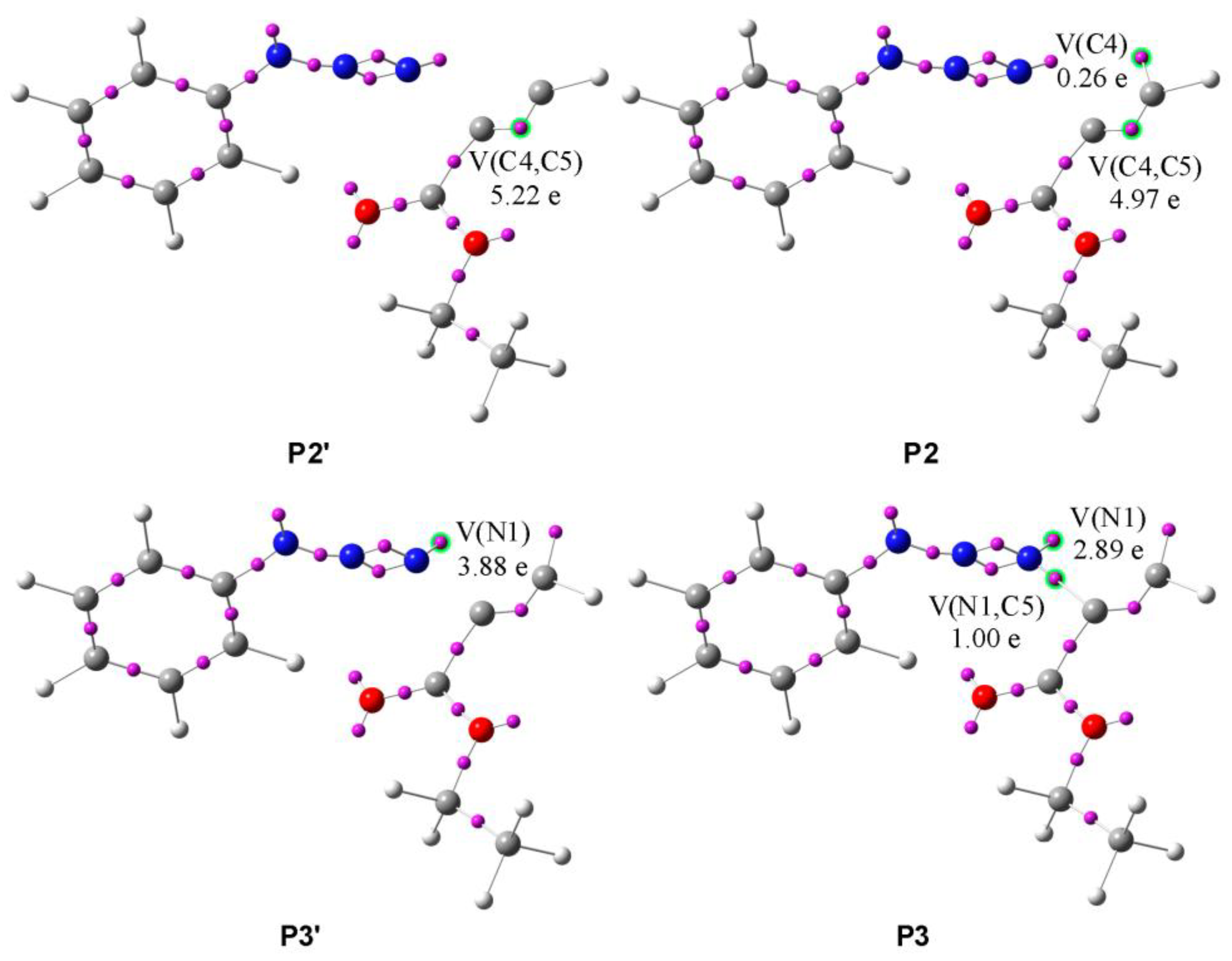
- (1)
- The first topological change takes place in P1 where disynaptic basin V′(C4,C5) merges with V(C4,C5), now integrating 5.19e, and an increase in energy of 27.8 kcal/mol can be observed. Next, phase III starts with the creation of a monosynaptic basin V(C4), with an initial population of 0.26e, which represents the developing negative charge of the zwitterion, as shown in Figure 8 by P2′ and P2. The energy increases by 8.0 kcal/mol and the GEDT is −0.06e.
- (2)
- With the start of phase IV, another mayor jump in energy can be seen; it rises by 17.4 kcal/mol. The new bond between C5 and N1 is created by shearing the nonbonding electron density of N1 with C5. The disynaptic basin V(N1,C5) is created with the initial population of 1.00e coming from the monosynaptic basin V(N1), as shown in Figure 8 by P3′ and P3. The GEDT increases to −0.26e.
- (3)
- In phases V-X, further reorganization of the electron density can be observed. The disynaptic basin V(C4,C5) and monosynaptic basins V(N1) and V(N3) gradually depopulate while the disynaptic basins V(N1,C5), V(N2,N3), and V′(N2,N3) and monosynaptic basin V(C4) increase in population. The final structure of the zwitterion I4F possesses 5.1 kcal/mol lower energy than the transition state.

| Structures | 1c | 2 | MCF | P1 | P2 | P3 | P4 | P5 | TSF | P6 | P7 | P8 | P9 | I4F | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Phases | I | II | III | IV | V | VI | VII | VIII | IX | X | |||||||||||||
| d1(N1-C5) | 3.740 | 2.189 | 2.075 | 1.817 | 1.778 | 1.722 | 1.700 | 1.558 | 1.492 | 1.446 | 1.443 | 1.428 | |||||||||||
| GEDT | 0.00 | −0.03 | −0.06 | −0.26 | −0.30 | −0.36 | −0.38 | −0.49 | −0.51 | −0.50 | −0.50 | −0.48 | |||||||||||
| dE | −6.6 | 21.2 | 29.2 | 46.6 | 47.7 | 48.4 | 48.5 | 47.1 | 46.1 | 44.8 | 44.5 | 43.4 | |||||||||||
| V(N1) | 3.76 | 3.74 | 3.74 | 3.74 | 2.89 | 2.78 | 2.68 | 2.65 | 2.53 | 2.49 | 2.46 | 2.45 | 2.41 | ||||||||||
| V(N1.N2) | 1.80 | 1.81 | 1.90 | 1.90 | 1.79 | 1.77 | 1.74 | 1.73 | 1.70 | 3.71 | 2.90 | 3.79 | 3.84 | ||||||||||
| V′(N1.N2) | 2.34 | 2.37 | 2.24 | 2.23 | 2.10 | 2.08 | 2.05 | 2.04 | 2.01 | ||||||||||||||
| V(N2.N3) | 2.50 | 2.47 | 2.54 | 2.57 | 2.80 | 2.84 | 2.90 | 2.92 | 1.53 | 1.50 | 1.49 | 1.51 | 2.85 | ||||||||||
| V(N3) | 3.37 | 3.39 | 3.34 | 3.29 | 3.07 | 3.03 | 2.98 | 2.95 | 2.83 | 2.79 | 2.78 | 2.78 | 2.82 | ||||||||||
| V(N3.C7) | 1.83 | 1.83 | 1.84 | 1.86 | 1.89 | 1.90 | 1.91 | 1.91 | 1.94 | 1.95 | 1.97 | 1.97 | 1.95 | ||||||||||
| V(C4.C5) | 2.73 | 2.78 | 5.19 | 4.97 | 4.07 | 1.95 | 3.90 | 3.86 | 3.63 | 3.53 | 3.42 | 3.41 | 3.37 | ||||||||||
| V′(C4.C5) | 2.56 | 2.56 | 2.06 | ||||||||||||||||||||
| V(C5.C6) | 2.40 | 2.41 | 2.47 | 2.49 | 2.46 | 2.43 | 2.41 | 2.40 | 2.37 | 2.36 | 2.36 | 2.36 | 2.36 | ||||||||||
| V(N1.C5) | 1.00 | 1.17 | 1.35 | 1.40 | 1.68 | 1.80 | 1.92 | 1.93 | 2.01 | ||||||||||||||
| V(N2) | 0.90 | ||||||||||||||||||||||
| V′(N2.N3) | 1.47 | 1.49 | 1.41 | 1.39 | 1.39 | ||||||||||||||||||
| V(C4) | 0.26 | 1.62 | 1.73 | 1.87 | 1.91 | 2.11 | 2.16 | 2.19 | 2.19 | 2.20 |
3. Computational Details
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katritzky, A.R. Introduction: Heterocycles. Chem. Rev. 2004, 104, 2125–2126. [Google Scholar] [CrossRef]
- Kerru, N.; Gummidi, L.; Maddila, S.; Gangu, K.K.; Jonnalagadda, S.B. A Review on Recent Advances in Nitrogen-Containing Molecules and Their Biological Applications. Molecules 2020, 25, 1909. [Google Scholar] [CrossRef] [PubMed]
- Saliyeva, L.M.; Dyachenko, I.V.; Danyliuk, I.Y.; Vovk, M.V. Di-, tetra-, and perhydropyrrolo[1,2-a]imidazoles: The Methods of Synthesis and Some Aspects of Application. Chem. Heterocycl. Compd. 2022, 58, 661–680. [Google Scholar] [CrossRef]
- Hyjek, K.; Jodłowski, P. Metal-organic frameworks for efficient drug adsorption and delivery. Sci. Rad. 2023, 2, 118–189. [Google Scholar] [CrossRef]
- Komkov, A.V.; Sukhanova, A.А.; Menchikov, L.G.; Zavarzin, I.V. o-Aminopyrimidine Aldehydes and Ketones: Synthesis and use as Precursors to Fused Pyrimidines. Chem. Heterocycl. Compd. 2022, 58, 547–566. [Google Scholar] [CrossRef]
- Danyliuk, I.Y.; Vovk, M.V. Tetrahydroazepines with an annulated five-membered heteroaromatic ring. Chem. Heterocycl. Compd. 2022, 58, 567–581. [Google Scholar] [CrossRef]
- Obernikhina, N.V.; Kachaeva, M.V.; Kachkovsky, O.D.; Brovarets, V.S. In silico Study of Conjugated Nitrogen Heterocycles Affinity in their Biological Complexes. Chem. Heterocycl. Compd. 2022, 58, 412–420. [Google Scholar] [CrossRef]
- Khomenko, D.M.; Doroshchuk, R.O.; Ohorodnik, Y.M.; Ivanova, H.V.; Zakharchenko, B.V.; Raspertova, I.V.; Vaschenko, O.V.; Dobrydnev, A.V.; Grygorenko, O.O.; Lampeka, R.D. Expanding the chemical space of 3(5)-functionalized 1,2,4-triazoles. Chem. Heterocycl. Compd. 2022, 58, 116–128. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Z.; Gao, C.; Ren, Q.-C.; Chang, L.; Lv, Z.-S.; Feng, L.-S. Triazole derivatives and their anti-tubercular activity. Eur. J. Med. Chem. 2017, 138, 501–513. [Google Scholar] [CrossRef]
- Keri, R.S.; Patil, S.A.; Budagumpi, S.; Nagaraja, B.M. Triazole: A Promising Antitubercular Agent. Chem. Biol. Drug. Des. 2015, 86, 410–423. [Google Scholar] [CrossRef]
- Chu, X.M.; Wang, C.; Wang, W.L.; Liang, L.L.; Liu, W.; Gong, K.K.; Sun, K.L. Triazole derivatives and their antiplasmodial and antimalarial activities. Eur. J. Med. Chem. 2019, 15, 206–223. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Liu, Y.; Wan, J.; Wang, M.; Rocchi, P.; Qu, F.; Iovanna, J.L.; Peng, L. Novel Triazole Ribonucleoside Down-Regulates Heat Shock Protein 27 and Induces Potent Anticancer Activity on Drug-Resistant Pancreatic Cancer. J. Med. Chem. 2009, 52, 6083–6096. [Google Scholar] [CrossRef] [PubMed]
- Groll, A.H.; Townsend, R.; Desai, A.; Azie, N.; Jones, M.; Engelhardt, M.; Schmitt-Hoffman, A.; Brüggemann, R.J.M. Drug-drug interactions between triazole antifungal agents used to treat invasive aspergillosis and immunosuppressants metabolized by cytochrome P450 3A4. Transpl. Infect. Dis. 2017, 19, e12751. [Google Scholar] [CrossRef] [PubMed]
- Lass-Flörl, C. Triazole Antifungal Agents in Invasive Fungal Infections. Drugs 2011, 71, 2405–2419. [Google Scholar] [CrossRef] [PubMed]
- Groll, A.H.; Townsend, R.; Desai, A.; Azie, N.; Jones, M.; Engelhardt, M.; Schmitt-Hoffman, A.; Brüggemann, R.J.M. The Enzymatic Basis of Drug-Drug Interactions with Systemic Triazole Antifungals. Clin. Pharmacokinet. 2008, 47, 779–792. [Google Scholar]
- Ayati, A.; Emami, S.; Foroumadi, A. The importance of triazole scaffold in the development of anticonvulsant agents. Eur. J. Med. Chem. 2016, 109, 380–392. [Google Scholar] [CrossRef]
- Kharb, R.; Sharma, P.C.; Yar, M.S. Pharmacological significance of triazole scaffold. J. Enzyme Inhib. Med. Chem. 2011, 26, 1–21. [Google Scholar] [CrossRef]
- Kras, J.; Sadowski, M.; Zawadzińska, K.; Nagatsky, R.; Woliński, P.; Kula, K.; Łapczuk, A. Thermal [3+2] cycloaddition reactions as most universal way for the effective preparation of five-membered nitrogen containing heterocycles. Sci. Rad. 2023, 2, 247–267. [Google Scholar] [CrossRef]
- Tiwari, G.; Khanna, A.; Mishra, V.K.; Sagar, R. Recent developments on microwave-assisted organic synthesis of nitrogen- and oxygen-containing preferred heterocyclic scaffolds. RSC Adv. 2023, 13, 32858–32892. [Google Scholar] [CrossRef]
- Appukkuttan, P.; Mehta, V.P.; Van der Eycken, E.V. Microwave-assisted cycloaddition reactions. Chem. Soc. Rev. 2009, 39, 1467–1477. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Why is phenyl azide so unreactive in [3+2] cycloaddition reactions? Demystifying Sustmann’s paradigmatic parabola. Org. Chem. Front. 2023, 10, 5579–5591. [Google Scholar] [CrossRef]
- Gomonov, K.A.; Pilipenko, I.A. Formation of Five- and Six-membered Oxygen-containing Heterocycles on the Basis of 1-halo-1-nitroalkenes. Chem. Heterocycl. Compd. 2023, 59, 1–4. [Google Scholar] [CrossRef]
- Milišiūnaitė, V.; Plytninkienė, E.; Bakšienė, R.; Bieliauskas, A.; Krikštolaitytė, S.; Račkauskienė, G.; Arbačiauskienė, E.; Šačkus, A. Convenient Synthesis of Pyrazolo[4′,3′:5,6]pyrano[4,3-c][1,2]oxazoles via Intramolecular Nitrile Oxide Cycloaddition. Molecules 2021, 26, 5604. [Google Scholar] [CrossRef] [PubMed]
- Zawadzińska, K.; Ríos-Gutiérrez, M.; Kula, K.; Woliński, P.; Mirosław, B.; Krawczyk, T.; Jasiński, R. The Participation of 3,3,3-Trichloro-1-nitroprop-1-ene in the [3+2] Cycloaddition Reaction with Selected Nitrile N-Oxides in the Light of the Experimental and MEDT Quantum Chemical Study. Molecules 2021, 26, 6774. [Google Scholar] [CrossRef]
- Sadowski, S.; Mudyna, A.; Knap, K.; Demchuk, O.M.; Łapczuk, A. Synthesis of (Z)-N-aryl-C-(pyrid-3-yl)-nitrones. Sci. Rad. 2023, 2, 319–324. [Google Scholar] [CrossRef]
- Jasiński, E.; Żmigrodzka, M.; Dresler, E.; Kula, K. A Full Regioselective and Stereoselective Synthesis of 4-Nitroisoxazolidines via Stepwise [3+2] Cycloaddition Reactions between (Z)-C-(9-Anthryl)-N-arylnitrones and (E)-3,3,3-Trichloro-1-nitroprop-1-ene: Comprehensive Experimental and Theoretical Study. J. Heterocycl. Chem. 2017, 54, 3314–3320. [Google Scholar] [CrossRef]
- Woliński, P.; Kącka-Zych, A.; Dziuk, B.; Ejsmont, K.; Łapczuk-Krygier, A.; Dresler, E. The structural aspects of the transformation of 3-nitroisoxazoline-2-oxide to 1-aza-2,8-dioxabicyclo[3.3.0]octane derivatives: Experimental and MEDT theoretical study. J. Mol. Struct. 2019, 1192, 27–34. [Google Scholar] [CrossRef]
- Żmigrodzka, M.; Sadowski, M.; Kras, J.; Desler, E.; Demchuk, O.M.; Kula, K. Polar [3+2] cycloaddition between N-methyl azomethine ylide and trans-3,3,3-trichloro-1-nitroprop-1-ene. Sci. Rad. 2022, 1, 26–35. [Google Scholar] [CrossRef]
- Rostovtsev, V.V.; Green, L.G.; Fokin, V.V.; Sharpless, K.B. A stepwise huisgen cycloaddition process: Copper(I)-catalyzed regioselective “ligation” of azides and terminal alkynes. Angew. Chem. Int. Ed. Engl. 2002, 41, 2596–2599. [Google Scholar] [CrossRef]
- Levandowski, B.J.; Gamache, R.F.; Murphy, J.M.; Houk, K.N. Readily Accessible Ambiphilic Cyclopentadienes for Bioorthogonal Labeling. J. Am. Chem. Soc. 2018, 140, 6426–6431. [Google Scholar] [CrossRef]
- Yoshida, S.; Kuribara, T.; Ito, H.; Meguro, T.; Nishiyama, Y.; Karaki, F.; Hatakeyama, Y.; Koike, Y.; Kii, I.; Hosoya, T. A facile preparation of functional cycloalkynes via an azide-to-cycloalkyne switching approach. Chem. Commun. 2019, 19, 3556–3559. [Google Scholar] [CrossRef] [PubMed]
- Siadati, S.A.; Rezazadeh, S. The extraordinary gravity of three atom 4π-components and 1,3-dienes to C20-nXn fullerenes; a new gate to the future of Nano technology. Sci. Rad. 2022, 1, 46–68. [Google Scholar] [CrossRef]
- Boren, B.C.; Narayan, S.; Rasmussen, L.K.; Zhang, L.; Zhao, H.; Lin, Z.; Jia, G.; Fokin, V.V. Ruthenium-Catalyzed Azide−Alkyne Cycloaddition: Scope and Mechanism. J. Am. Chem. Soc. 2008, 130, 8923–8930. [Google Scholar] [CrossRef] [PubMed]
- Abu-Orabi, S.T.; Atfah, M.A.; Jibril, I.; Mari’i, F.M.; Ali, A.A.-S. Dipolar cycloaddition reactions of organic azides with some acetylenic compounds. J. Heterocycl. Chem. 1989, 26, 1461–1468. [Google Scholar] [CrossRef]
- Kula, K.; Kącka-Zych, A.; Łapczuk-Krygier, A.; Wzorek, Z.; Nowak, A.K.; Jasiński, R. Experimental and Theoretical Mechanistic Study on the Thermal Decomposition of 3,3-diphenyl-4-(trichloromethyl)-5-nitropyrazoline. Molecules 2021, 26, 1364. [Google Scholar] [CrossRef] [PubMed]
- Jasiński, R. A stepwise, zwitterionic mechanism for the 1,3-dipolar cycloaddition between (Z)-C-4-methoxyphenyl-N-phenylnitrone and gem-chloronitroethene catalysed by 1-butyl-3-methylimidazolium ionic liquid cations. Tetrahedron Lett. 2015, 56, 532–535. [Google Scholar] [CrossRef]
- Jasiński, R. A new insight on the molecular mechanism of the reaction between (Z)-C,N-diphenylnitrone and 1,2-bismethylene-3,3,4,4,5,5-hexamethylcyclopentane. J. Mol. Graph. Model. 2020, 94, 107461. [Google Scholar] [CrossRef]
- Domingo, L.R.; Saéz, J.A.; Zaragozá, R.J.; Arnó, M. Understanding the Participation of Quadricyclane as Nucleophile in Polar [2σ + 2σ + 2π] Cycloadditions toward Electrophilic π Molecules. J. Org. Chem. 2008, 73, 8791–8799. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M. A Useful Classification of Organic Reactions Based on the Flux of the Electron Density. Sci. Rad. 2023, 2, 1–24. [Google Scholar] [CrossRef]
- Mondal, A.; Mohammad-Salim, H.A.; Acharjee, N. Unveiling substituent effects in [3+2] cycloaddition reactions of benzonitrile N-oxide and benzylideneanilines from the molecular electron density theory perspective. Sci. Rad. 2023, 2, 75–92. [Google Scholar] [CrossRef]
- Ríos-Gutiérrez, M.; Domingo, L.R. Unravelling the Mysteries of the [3+2] Cycloaddition Reactions. Eur. J. Org. Chem. 2019, 2019, 267–282. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Unveiling the Chemistry of Higher-Order Cycloaddition Reactions within the Molecular Electron Density Theory. Chemistry 2022, 4, 735–752. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef]
- Domingo, L.R. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef] [PubMed]
- Tolstikov, G.A.; Shults, E.E.; Malikova, T.S.; Spirikhin, L.V. The Importance of Preliminary Orientation in [4+2]-Cycloadditions of Dienes and Dienophiles with Complex Structures. Mendeleev Commun. 1994, 4, 60–62. [Google Scholar] [CrossRef]
- Aitouna, A.O.; Barhoumi, A.; Zeroual, A. A Mechanism Study and an Investigation of the Reason for the Stereoselectivity in the [4+2] Cycloaddition Reaction between Cyclopentadiene and Gem-substituted Ethylene Electrophiles. Sci. Rad. 2023, 2, 217–228. [Google Scholar] [CrossRef]
- Mondal, A.; Acharjee, N. Unveiling the exclusive stereo and site selectivity in [3+2] cycloaddition reactions of a tricyclic strained alkene with nitrile oxides from the molecular electron density theory perspective. Chem. Heterocycl. Comp. 2023, 59, 145–154. [Google Scholar] [CrossRef]
- Kula, K.; Sadowski, M. Regio- and stereoselectivity of [3+2] cycloaddition reactions between (Z)-1-(anthracen-9-yl)-N-methyl nitrone and analogs of trans-β-nitrostyrene on the basis of MEDT computational study. Chem. Heterocycl. Comp. 2023, 59, 138–144. [Google Scholar] [CrossRef]
- Gillies, C.W.; Gillies, J.Z.; Suenram, D.R.; Lovas, F.J.; Kraka, E.; Cremer, D. Van der Waals complexes in 1,3-dipolar cycloaddition reactions: Ozone-ethylene. J. Am. Chem. Soc. 1991, 113, 2412–2421. [Google Scholar] [CrossRef]
- Gillies, J.Z.; Gillies, C.W.; Lovas, F.J.; Matsumura, K.; Suenram, R.D.; Kraka, E.; Cremer, D. Van der Waals complexes of chemically reactive gases: Ozone-acetylene. J. Am. Chem. Soc. 1991, 113, 6408–6415. [Google Scholar] [CrossRef]
- Lupinski, J.H. The chargé transfer complex between β-carotene and iodine. II. Characterization of complex. J. Phys. Chem. 1963, 67, 2725–2728. [Google Scholar] [CrossRef]
- Bahnick, D.A.; Person, W.B. Raman Intensity Study of Charge-Transfer Complexes of ICN. J. Chem. Phys. 1968, 48, 5637–5645. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
- Woliński, P.; Kącka-Zych, A.; Wróblewska, A.; Wielgus, E.; Dolot, R.; Jasiński, R. Fully Selective Synthesis of Spirocyclic-1,2-oxazine N-Oxides via Non-Catalysed Hetero Diels-Alder Reactions with the Participation of Cyanofunctionalysed Conjugated Nitroalkenes. Molecules 2023, 28, 4586. [Google Scholar] [CrossRef] [PubMed]
- Kula, K.; Łapczuk, A.; Sadowski, M.; Kras, J.; Zawadzińska, K.; Demchuk, O.M.; Gaurav, G.K.; Wróblewska, A.; Jasiński, R. On the Question of the Formation of Nitro-Functionalized 2,4-Pyrazole Analogs on the Basis of Nitrylimine Molecular Systems and 3,3,3-Trichloro-1-Nitroprop-1-Ene. Molecules 2022, 27, 8409. [Google Scholar] [CrossRef] [PubMed]
- Woliński, P.; Kącka-Zych, A.; Demchuk, O.M.; Łapczuk-Krygier, A.; Mirosław, B.; Jasiński, R. Clean and molecularly programmable protocol for preparation of bis-heterobiarylic systems via a domino pseudocyclic reaction as a valuable alternative for TM-catalyzed cross-couplings. J. Clean. Prod. 2020, 275, 122086. [Google Scholar] [CrossRef]
- Jasiński, R. β-Trifluoromethylated nitroethenes in Diels-Alder reaction with cyclopentadiene: A DFT computational study. J. Fluor. Chem. 2018, 206, 1–7. [Google Scholar] [CrossRef]
- Jasiński, R. Searching for zwitterionic intermediates in Hetero Diels–Alder reactions between methyl α,p-dinitrocinnamate and vinyl-alkyl ethers. Comput. Theor. Chem. 2014, 1046, 93–98. [Google Scholar] [CrossRef]
- Krokidis, K.; Noury, S.; Silvi, B. Characterization of Elementary Chemical Processes by Catastrophe Theory. J. Phys. Chem. A. 1997, 101, 7277–7282. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Kącka-Zych, A. The Molecular Mechanism of the Formation of Four-Membered Cyclic Nitronates and Their Retro (3 + 2) Cycloaddition: A DFT Mechanistic Study. Molecules 2021, 26, 4786. [Google Scholar] [CrossRef] [PubMed]
- Fryźlewicz, A.; Kącka-Zych, A.; Demchuk, O.M.; Mirosław, B.; Woliński, P.; Jasiński, R. Green synthesis of nitrocyclopropane-type precursors of inhibitors for the maturation of fruits and vegetables via domino reactions of diazoalkanes with 2-nitroprop-1-ene. J. Clean. Prod. 2021, 292, 126079. [Google Scholar] [CrossRef]
- Pérez, P.; Domingo, L.R.; Aizman, A.; Contreras, R. The electrophilicity index in organic chemistry. Theor. Aspects Chem. React. 2008, 19, 139–201. [Google Scholar]
- Perez, P.; Domingo, L.R.; Aurell, M.J.; Contreras, R. Quantitative characterization of the global electrophilicity patternof some reagents involved in 1,3-dipolar cycloaddition reactions. Tetrahedron 2003, 59, 3117–3125. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the Reactivity of Captodative Ethylenes in Polar Cycloaddition Reactions. A Theoretical Study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comp. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Kącka-Zych, A. Understanding the uniqueness of the stepwise [4 + 1] cycloaddition reaction between conjugated nitroalkenes and electrophilic carbene systems with a molecular electron density theory perspective. Int. J. Quant. Chem. 2021, 121, e26440. [Google Scholar] [CrossRef]
- Jasiński, R. Stepwise, zwitterionic course of hetero-Diels–Alder reaction between 1,2,4-triazine molecular systems and 2-cyclopropylidene-1,3-dimethylimidazoline. Chem. Heterocycl. Comp. 2022, 58, 260–262. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational Tools for the Electron Localization Function Topological Analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]



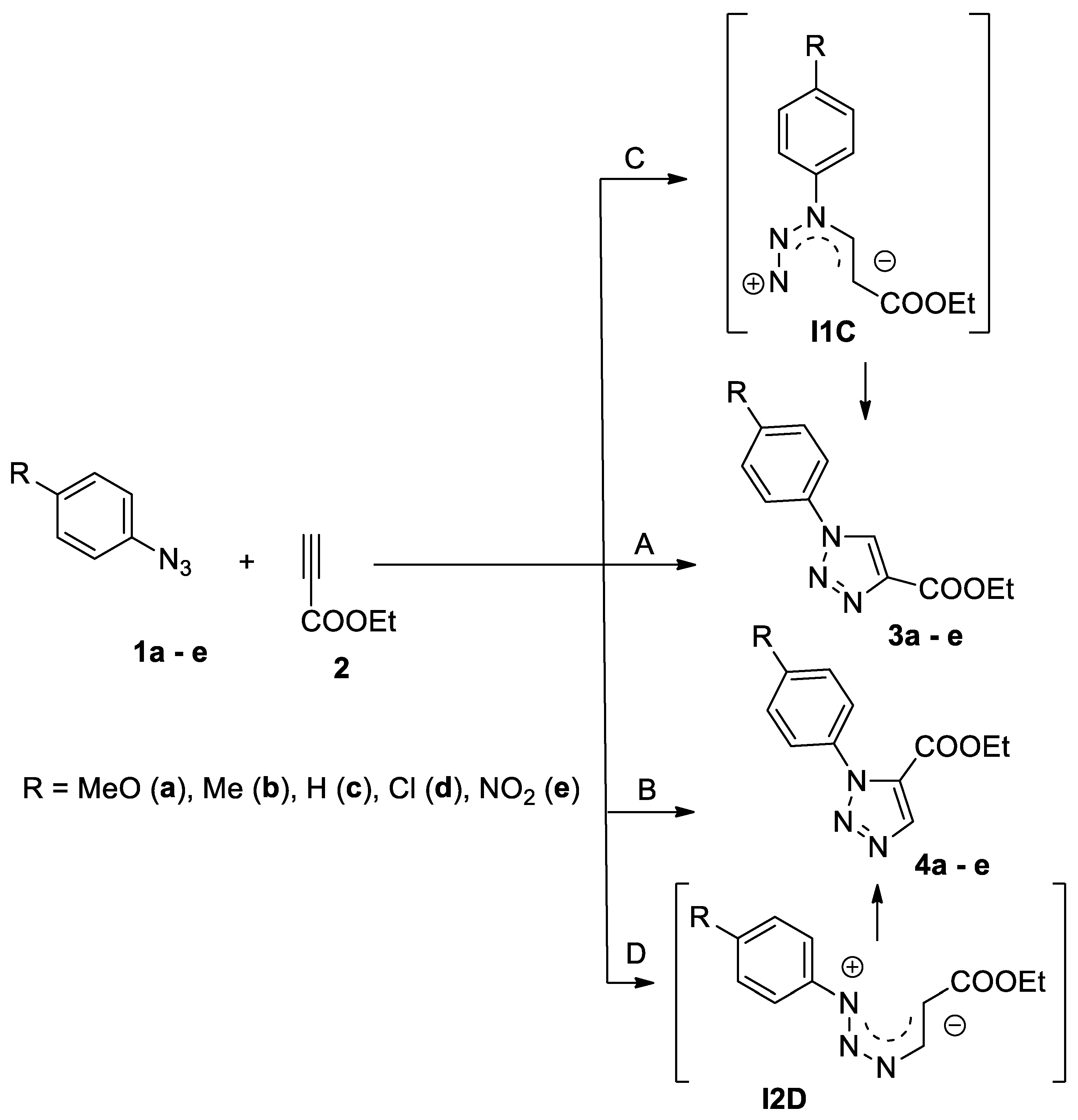
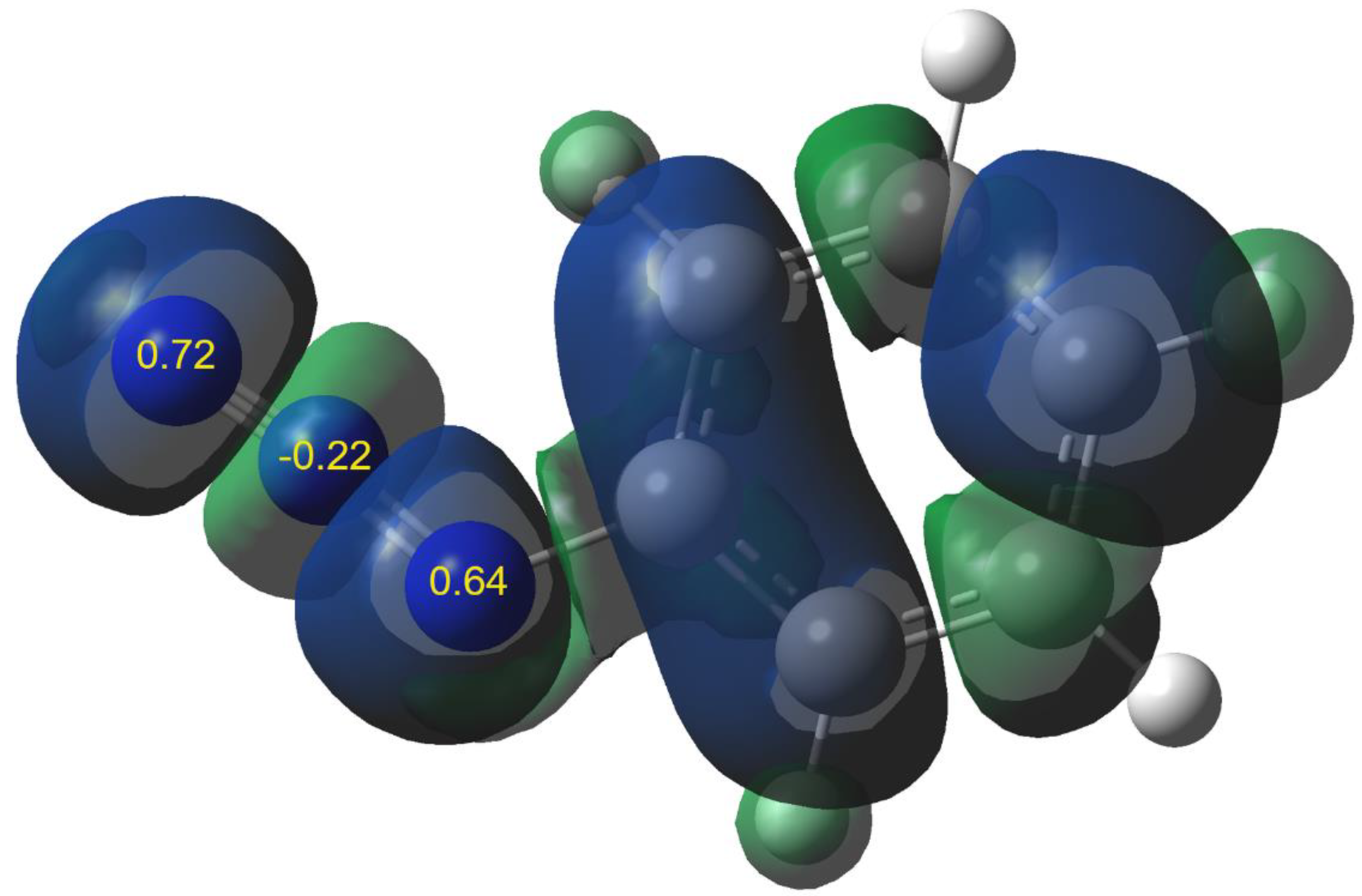
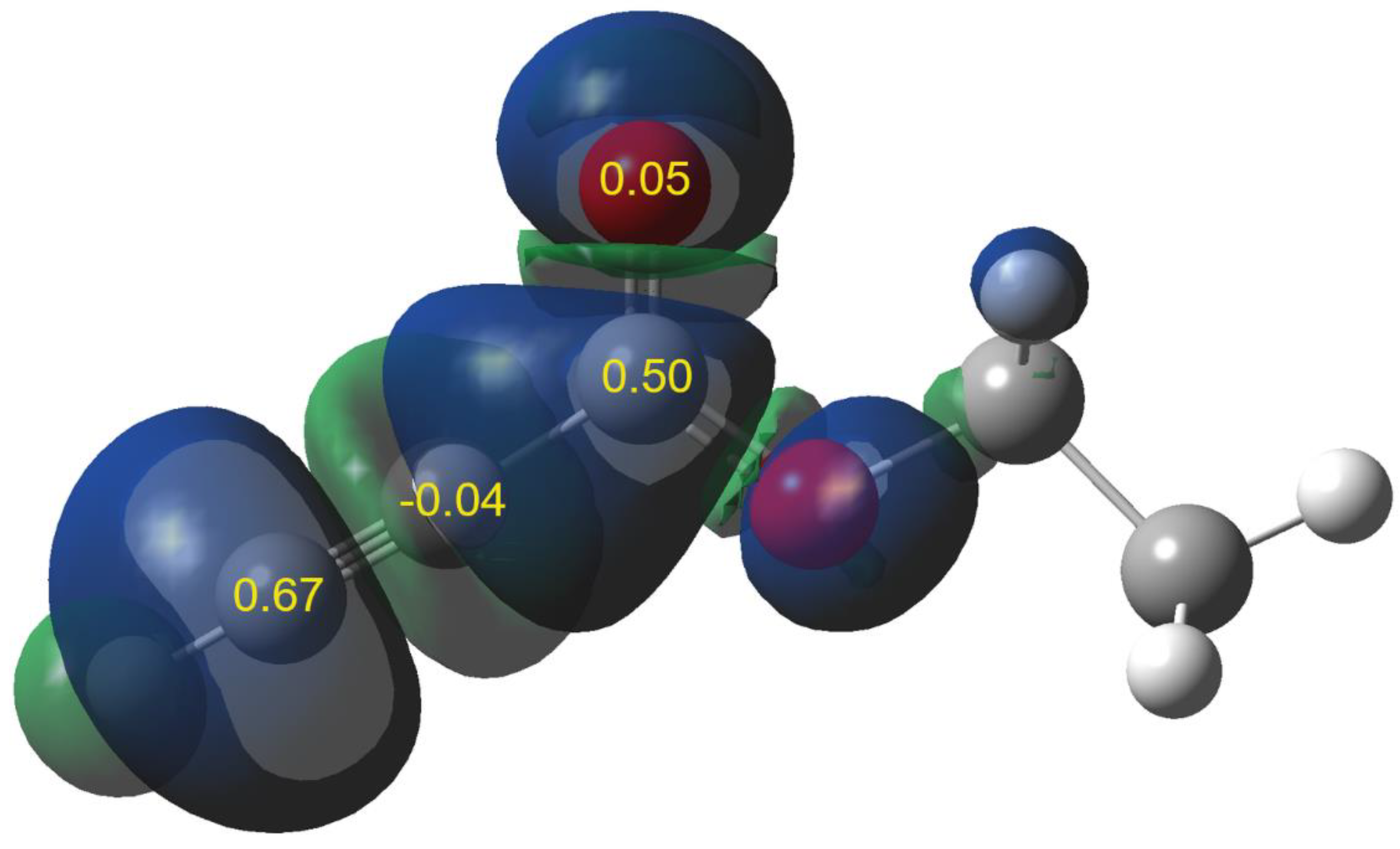


 | ||||
|---|---|---|---|---|
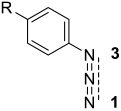
| No | R | N | N1 | N3 |
| 1a | MeO | 3.45 | 0.65 | 0.47 |
| 1b | Me | 3.11 | 0.71 | 0.57 |
| 1c | H | 2.92 | 0.72 | 0.64 |
| 1d | Cl | 2.80 | 0.60 | 0.51 |
| 1e | NO2 | 2.12 | 0.53 | 0.52 |
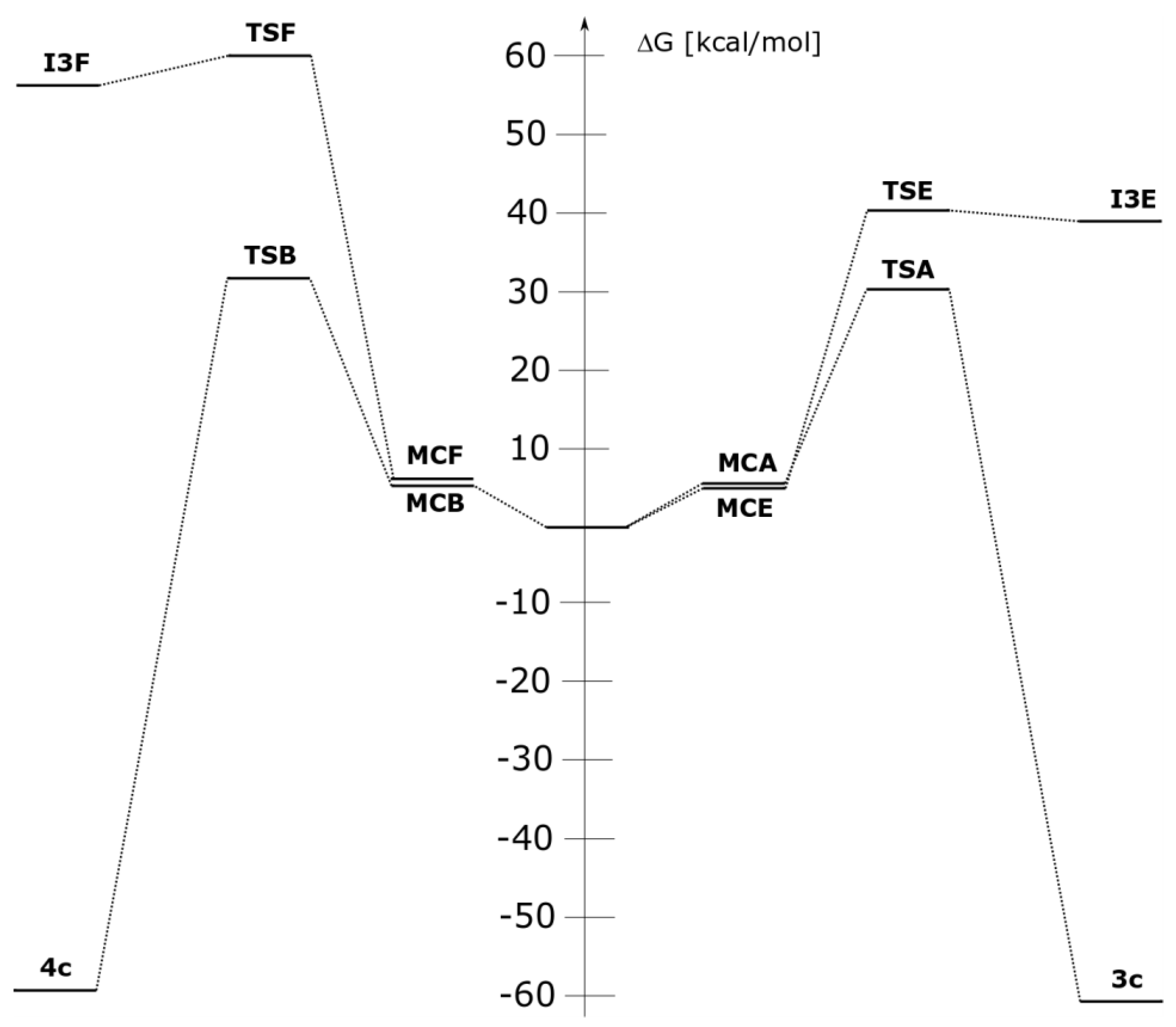
| Reaction | Path | Transition | ΔH | ΔS | ΔG |
|---|---|---|---|---|---|
| 1a+2 | A | 1a+2→MCA | −3.3 | −25.5 | 4.3 |
| 1a+2→TSA | 17.4 | −40.7 | 29.6 | ||
| 1a+2→3a | −76.6 | −48.6 | −62.1 | ||
| B | 1a+2→MCB | −3.7 | −39.3 | 8.0 | |
| 1a+2→TSB | 17.1 | −44.3 | 30.3 | ||
| 1a+2→4a | −74.4 | −45.4 | −60.9 | ||
| E | 1a+2→MCE | −5.9 | −37.3 | 5.2 | |
| 1a+2→TSE | 28.3 | −35.3 | 38.8 | ||
| 1a+2→I3E | 27.2 | −39.0 | 38.8 | ||
| F | 1a+2→MCF | −5.7 | −35.3 | 4.9 | |
| 1a+2→TSF | 46.8 | −41.7 | 59.3 | ||
| 1a+2→I4F | 42.6 | −43.6 | 55.6 | ||
| 1b+2 | A | 1b+2→MCA | −5.7 | −34.1 | 4.4 |
| 1b+2→TSA | 17.8 | −42.4 | 30.4 | ||
| 1b+2→3b | −76.1 | −49.2 | −61.5 | ||
| B | 1b+2→MCB | −6.0 | −39.1 | 5.7 | |
| 1b+2→TSB | 17.0 | −49.2 | 31.7 | ||
| 1b+2→4b | −74.3 | −53.5 | −58.4 | ||
| E | 1b+2→MCE | −6.0 | −39.1 | 5.7 | |
| 1b+2→TSE | 28.3 | −43.9 | 41.3 | ||
| 1b+2→I3E | 28.1 | −36.8 | 39.0 | ||
| F | 1b+2→MCF | −5.7 | −34.1 | 4.4 | |
| 1b+2→TSF | 47.6 | −39.7 | 59.5 | ||
| 1b+2→I4F | 43.8 | −41.6 | 56.2 | ||
| 1c+2 | A | 1c+2→MCA | −3.2 | −29.0 | 5.4 |
| 1c+2→TSA | 18.0 | −41.0 | 30.2 | ||
| 1c+2→3c | −75.7 | −48.6 | −61.3 | ||
| B | 1c+2→MCB | −5.0 | −32.6 | 4.7 | |
| 1c+2→TSB | 18.0 | −44.8 | 31.3 | ||
| 1c+2→4c | −73.2 | −45.1 | −59.7 | ||
| E | 1c+2→MCE | −4.9 | −34.4 | 5.3 | |
| 1c+2→TSE | 29.4 | −37.5 | 40.5 | ||
| 1c+2→I3E | 28.7 | −35.9 | 39.4 | ||
| F | 1c+2→MCF | −5.3 | −34.7 | 5.0 | |
| 1c+2→TSF | 48.3 | −40.5 | 60.4 | ||
| 1c+2→I4F | 44.6 | −42.8 | 57.4 | ||
| 1d+2 | A | 1d+2→MCA | −3.4 | −30.4 | 5.7 |
| 1d+2→TSA | 18.2 | −41.7 | 30.6 | ||
| 1d+2→3d | −75.3 | −48.7 | −60.8 | ||
| B | 1d+2→MCB | −5.9 | −36.6 | 5.0 | |
| 1d+2→TSB | 18.1 | −44.1 | 31.2 | ||
| 1d+2→4d | −73.1 | −47.1 | −59.0 | ||
| E | 1d+2→MCE | −5.9 | −36.3 | 4.9 | |
| 1d+2→TSE | 29.8 | −37.4 | 41.0 | ||
| 1d+2→I3E | 29.4 | −38.0 | 40.7 | ||
| F | 1d+2→MCF | −5.6 | −34.5 | 4.7 | |
| 1d+2→TSF | 48.8 | −41.3 | 61.1 | ||
| 1d+2→I4F | 45.3 | −41.7 | 57.7 | ||
| 1e+2 | A | 1e+2→MCA | −4.2 | −35.4 | 6.3 |
| 1e+2→TSA | 18.7 | −38.9 | 30.2 | ||
| 1e+2→3e | −73.5 | −48.7 | −58.9 | ||
| B | 1e+2→MCB | −5.2 | −35.0 | 5.2 | |
| 1e+2→TSB | 18.9 | −42.6 | 31.6 | ||
| 1e+2→4e | −71.0 | −46.7 | −57.1 | ||
| E | 1e+2→MCE | −5.6 | −36.8 | 5.4 | |
| 1e+2→TSE | 31.9 | −38.9 | 43.4 | ||
| 1e+2→I3E | 32.0 | −33.9 | 42.1 | ||
| F | 1e+2→MCF | −5.3 | −34.8 | 5.0 | |
| 1e+2→TSF | 51.0 | −40.9 | 63.2 | ||
| 1e+2→I4F | 48.0 | −40.7 | 60.2 |
| Reaction | Path | Structure | Interatomic Distances r [Å] | GEDT | ||||
|---|---|---|---|---|---|---|---|---|
| N1-N2 | N2-N3 | N3-C4 | C4-C5 | C5-N1 | [e] | |||
| 1a+2 | A | 1a | 1.127 | 1.226 | ||||
| 2 | 1.200 | |||||||
| MCA | 1.127 | 1.226 | 3.447 | 1.199 | 3.403 | |||
| TSA | 1.149 | 1.254 | 2.031 | 1.232 | 2.279 | 0.30 | ||
| 3a | 1.290 | 1.349 | 1.343 | 1.375 | 1.359 | |||
| B | MCB | 1.125 | 1.227 | 3.655 | 1.200 | 3.798 | ||
| TSB | 1.160 | 1.251 | 2.191 | 1.231 | 2.075 | 0.25 | ||
| 4a | 1.302 | 1.332 | 1.361 | 1.374 | 1.350 | |||
| E | MCE | 1.127 | 1.226 | 3.523 | 1.199 | 4.030 | ||
| TSE | 1.119 | 1.246 | 1.720 | 1.260 | 4.561 | 0.75 | ||
| I3E | 1.114 | 1.257 | 1.515 | 1.303 | 4.548 | 0.89 | ||
| F | MCF | 1.126 | 1.227 | 3.907 | 1.199 | 3.893 | ||
| TSF | 1.156 | 1.195 | 4.459 | 1.284 | 1.707 | 0.55 | ||
| I4F | 1.177 | 1.192 | 4.661 | 1.355 | 1.428 | 0.70 | ||
| 1b+2 | A | 1b | 1.126 | 1.227 | ||||
| MCA | 1.126 | 1.227 | 3.461 | 1.199 | 3.416 | |||
| TSA | 1.149 | 1.253 | 2.033 | 1.232 | 2.272 | 0.31 | ||
| 3b | 1.289 | 1.349 | 1.343 | 1.375 | 1.359 | |||
| MCB | 1.126 | 1.227 | 3.649 | 1.199 | 3.534 | |||
| B | TSB | 1.159 | 1.250 | 2.193 | 1.231 | 2.066 | 0.26 | |
| 4b | 1.302 | 1.332 | 1.361 | 1.374 | 1.349 | |||
| MCE | 1.126 | 1.227 | 3.491 | 1.199 | 4.047 | |||
| E | TSE | 1.119 | 1.246 | 1.717 | 1.261 | 4.547 | 0.74 | |
| I3E | 1.114 | 1.256 | 1.516 | 1.303 | 4.550 | 0.90 | ||
| MCF | 1.125 | 1.228 | 3.949 | 1.199 | 4.052 | |||
| F | TSF | 1.154 | 1.195 | 4.502 | 1.285 | 1.702 | 0.55 | |
| I4F | 1.175 | 1.192 | 4.663 | 1.354 | 1.428 | 0.68 | ||
| 1c+2 | A | 1c | 1.125 | 1.228 | ||||
| MCA | 1.125 | 1.228 | 3.430 | 1.199 | 3.412 | |||
| TSA | 1.149 | 1.254 | 2.038 | 1.232 | 2.264 | 0.31 | ||
| 3c | 1.289 | 1.349 | 1.344 | 1.374 | 1.360 | |||
| MCB | 1.125 | 1.228 | 3.684 | 1.200 | 3.326 | |||
| H | B | TSB | 1.159 | 1.251 | 2.195 | 1.231 | 2.061 | 0.27 |
| 4c | 1.302 | 1.332 | 1.361 | 1.374 | 1.349 | |||
| MCE | 1.125 | 1.228 | 3.459 | 1.199 | 4.056 | |||
| E | TSE | 1.118 | 1.247 | 1.710 | 1.263 | 4.525 | 0.76 | |
| I3E | 1.114 | 1.256 | 1.518 | 1.303 | 4.537 | 0.87 | ||
| MCF | 1.125 | 1.229 | 3.886 | 1.199 | 3.740 | |||
| F | TSF | 1.153 | 1.196 | 4.538 | 1.286 | 1.700 | 0.55 | |
| I4F | 1.173 | 1.193 | 4.665 | 1.354 | 1.428 | 0.68 | ||
| 1d+2 | A | 1d | 1.124 | 1.229 | ||||
| MCA | 1.125 | 1.229 | 3.445 | 1.199 | 3.426 | |||
| TSA | 1.149 | 1.255 | 2.046 | 1.232 | 2.253 | 0.29 | ||
| 3d | 1.288 | 1.350 | 1.344 | 1.374 | 1.360 | |||
| MCB | 1.124 | 1.229 | 3.598 | 1.199 | 3.568 | |||
| B | TSB | 1.159 | 1.252 | 2.197 | 1.231 | 2.060 | 0.24 | |
| 4d | 1.301 | 1.333 | 1.361 | 1.374 | 1.350 | |||
| MCE | 1.124 | 1.229 | 3.433 | 1.199 | 4.036 | |||
| E | TSE | 1.118 | 1.248 | 1.706 | 1.264 | 4.517 | 0.75 | |
| I3E | 1.114 | 1.257 | 1.521 | 1.302 | 4.526 | 0.89 | ||
| MCF | 1.124 | 1.230 | 3.949 | 1.199 | 4.079 | |||
| F | TSF | 1.152 | 1.196 | 4.548 | 1.287 | 1.695 | 0.55 | |
| I4F | 1.173 | 1.194 | 4.663 | 1.355 | 1.426 | 0.68 | ||
| 1e+2 | A | 1e | 1.122 | 1.234 | ||||
| MCA | 1.122 | 1.234 | 3.419 | 1.200 | 3.464 | |||
| TSA | 1.149 | 1.258 | 2.073 | 1.231 | 2.217 | 0.27 | ||
| 3e | 1.286 | 1.352 | 1.346 | 1.372 | 1.361 | |||
| MCB | 1.122 | 1.234 | 3.741 | 1.200 | 3.416 | |||
| B | TSB | 1.157 | 1.256 | 2.209 | 1.231 | 2.041 | 0.22 | |
| 4e | 1.299 | 1.335 | 1.362 | 1.373 | 1.351 | |||
| MCE | 1.121 | 1.235 | 3.388 | 1.199 | 4.099 | |||
| E | TSE | 1.116 | 1.252 | 1.690 | 1.268 | 4.454 | 0.75 | |
| I3E | 1.113 | 1.261 | 1.530 | 1.303 | 4.339 | 0.87 | ||
| MCF | 1.121 | 1.235 | 3.978 | 1.199 | 4.218 | |||
| F | TSF | 1.149 | 1.199 | 4.615 | 1.289 | 1.681 | 0.55 | |
| I4F | 1.169 | 1.197 | 4.665 | 1.355 | 1.424 | 0.65 | ||
| Structures | 1c | 2 | MCA | P1 | P2 | P3 | TSA | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | 3c | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Phases | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |||||||||||||||
| d2(N1-C5) | 3.431 | 3.024 | 2.693 | 2.335 | 2.263 | 2.179 | 2.108 | 2.104 | 1.931 | 1.910 | 1.743 | 1.720 | 1.477 | 1.360 | |||||||||||||
| d1(N3-C4) | 3.137 | 2.717 | 2.433 | 2.105 | 2.037 | 1.953 | 1.883 | 1.878 | 1.718 | 1.701 | 1.575 | 1.561 | 1.435 | 1.344 | |||||||||||||
| GEDT | 0.00 | −0.03 | −0.06 | −0.08 | −0.07 | −0.03 | 0.01 | 0.02 | 0.14 | 0.15 | 0.24 | 0.24 | 0.29 | 0.25 | |||||||||||||
| dE | −4.5 | 0.7 | 6.9 | 16.8 | 17.5 | 16.3 | 13.2 | 12.9 | −2.4 | −4.8 | −25.0 | −28.6 | −55.9 | −73.1 | |||||||||||||
| V(N1) | 3.76 | 3.77 | 3.76 | 3.74 | 3.70 | 3.70 | 3.72 | 3.75 | 3.75 | 3.45 | 3.42 | 3.20 | 3.19 | 3.00 | 2.89 | ||||||||||||
| V(N1.N2) | 2.34 | 2.32 | 4.20 | 3.77 | 2.96 | 2.87 | 2.79 | 2.72 | 2.72 | 2.56 | 2.54 | 2.41 | 2.39 | 2.18 | 2.04 | ||||||||||||
| V′(N1.N2) | 1.80 | 1.82 | |||||||||||||||||||||||||
| V(N2.N3) | 2.50 | 2.51 | 2.46 | 2.31 | 1.89 | 1.83 | 1.77 | 1.74 | 1.73 | 1.70 | 1.69 | 1.70 | 1.70 | 1.72 | 1.71 | ||||||||||||
| V(N3) | 3.37 | 3.37 | 3.31 | 3.26 | 3.25 | 3.27 | 3.30 | 3.48 | 2.06 | 1.89 | 1.87 | 1.73 | 1.72 | 1.43 | 0.59 | ||||||||||||
| V(N3.C7) | 1.83 | 1.84 | 1.87 | 1.9 | 1.91 | 1.89 | 1.88 | 1.86 | 1.85 | 1.83 | 1.82 | 1.82 | 1.82 | 1.86 | 2.02 | ||||||||||||
| V(C4.C5) | 2.56 | 2.52 | 2.48 | 2.38 | 2.43 | 2.39 | 2.31 | 2.20 | 2.19 | 2.04 | 2.02 | 1.93 | 1.92 | 3.67 | 3.36 | ||||||||||||
| V′(C4.C5) | 2.73 | 2.75 | 2.78 | 2.87 | 2.56 | 2.42 | 2.32 | 2.21 | 2.21 | 2.05 | 2.04 | 1.98 | 1.97 | ||||||||||||||
| V(C5.C6) | 2.4 | 2.40 | 2.43 | 2.46 | 2.51 | 2.45 | 2.42 | 2.4 | 2.4 | 2.35 | 2.35 | 2.31 | 2.3 | 2.25 | 2.38 | ||||||||||||
| V(N1.C5) | 1.50 | 1.93 | 2.23 | ||||||||||||||||||||||||
| V(N3.C4) | 1.45 | 1.78 | 1.33 | 2.02 | 2.04 | 2.29 | 3.00 | ||||||||||||||||||||
| V′(N1) | 0.38 | 0.43 | 0.73 | ||||||||||||||||||||||||
| V(N2) | 0.62 | 1.88 | 2.06 | 2.22 | 2.35 | 2.35 | 2.59 | 2.62 | 2.77 | 2.79 | 3.00 | 3.16 | |||||||||||||||
| V′(N3) | 0.50 | ||||||||||||||||||||||||||
| V(C4) | 0.05 | ||||||||||||||||||||||||||
| V(C5) | 0.14 | 0.36 | 0.49 | 0.58 | 0.59 | 0.71 | 0.72 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dresler, E.; Woliński, P.; Wróblewska, A.; Jasiński, R. On the Question of Zwitterionic Intermediates in the [3+2] Cycloaddition Reactions between Aryl Azides and Ethyl Propiolate. Molecules 2023, 28, 8152. https://doi.org/10.3390/molecules28248152
Dresler E, Woliński P, Wróblewska A, Jasiński R. On the Question of Zwitterionic Intermediates in the [3+2] Cycloaddition Reactions between Aryl Azides and Ethyl Propiolate. Molecules. 2023; 28(24):8152. https://doi.org/10.3390/molecules28248152
Chicago/Turabian StyleDresler, Ewa, Przemysław Woliński, Aneta Wróblewska, and Radomir Jasiński. 2023. "On the Question of Zwitterionic Intermediates in the [3+2] Cycloaddition Reactions between Aryl Azides and Ethyl Propiolate" Molecules 28, no. 24: 8152. https://doi.org/10.3390/molecules28248152
APA StyleDresler, E., Woliński, P., Wróblewska, A., & Jasiński, R. (2023). On the Question of Zwitterionic Intermediates in the [3+2] Cycloaddition Reactions between Aryl Azides and Ethyl Propiolate. Molecules, 28(24), 8152. https://doi.org/10.3390/molecules28248152







