Confining He Atoms in Diverse Ice-Phases: Examining the Stability of He Hydrate Crystals through DFT Approaches
Abstract
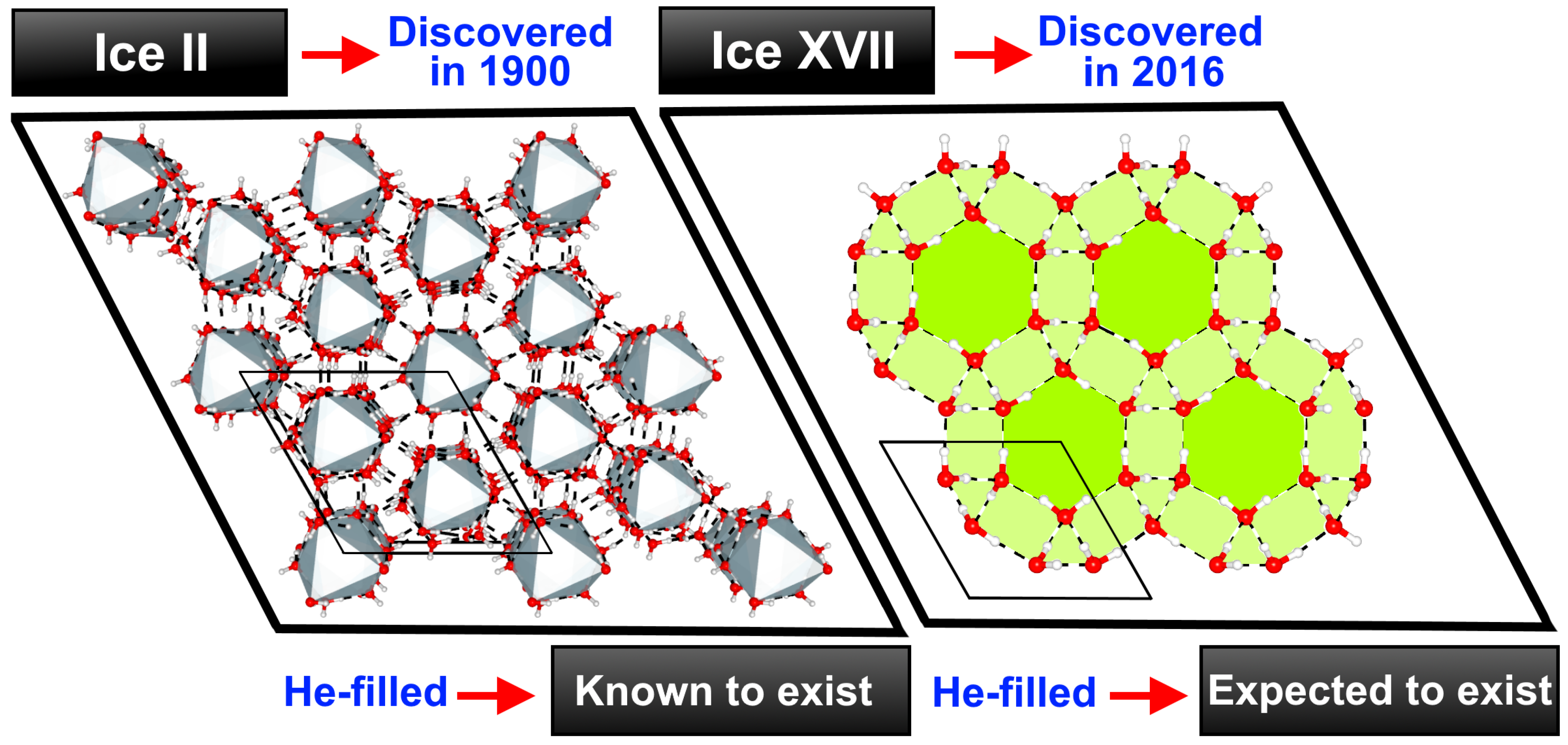
:1. Introduction
2. Results and Discussion
2.1. Simulation Cells, Computational Details and Lattice Energies
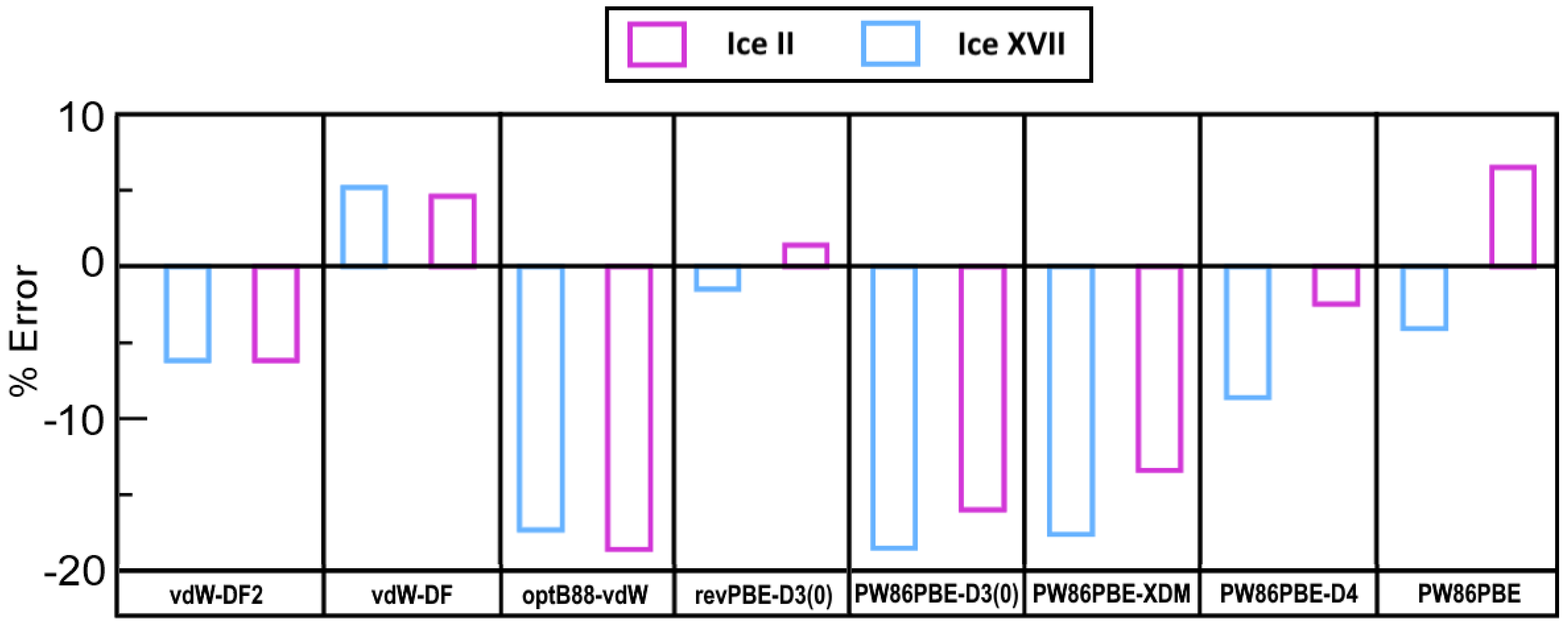
2.2. Benchmarking DFT-D Calculations
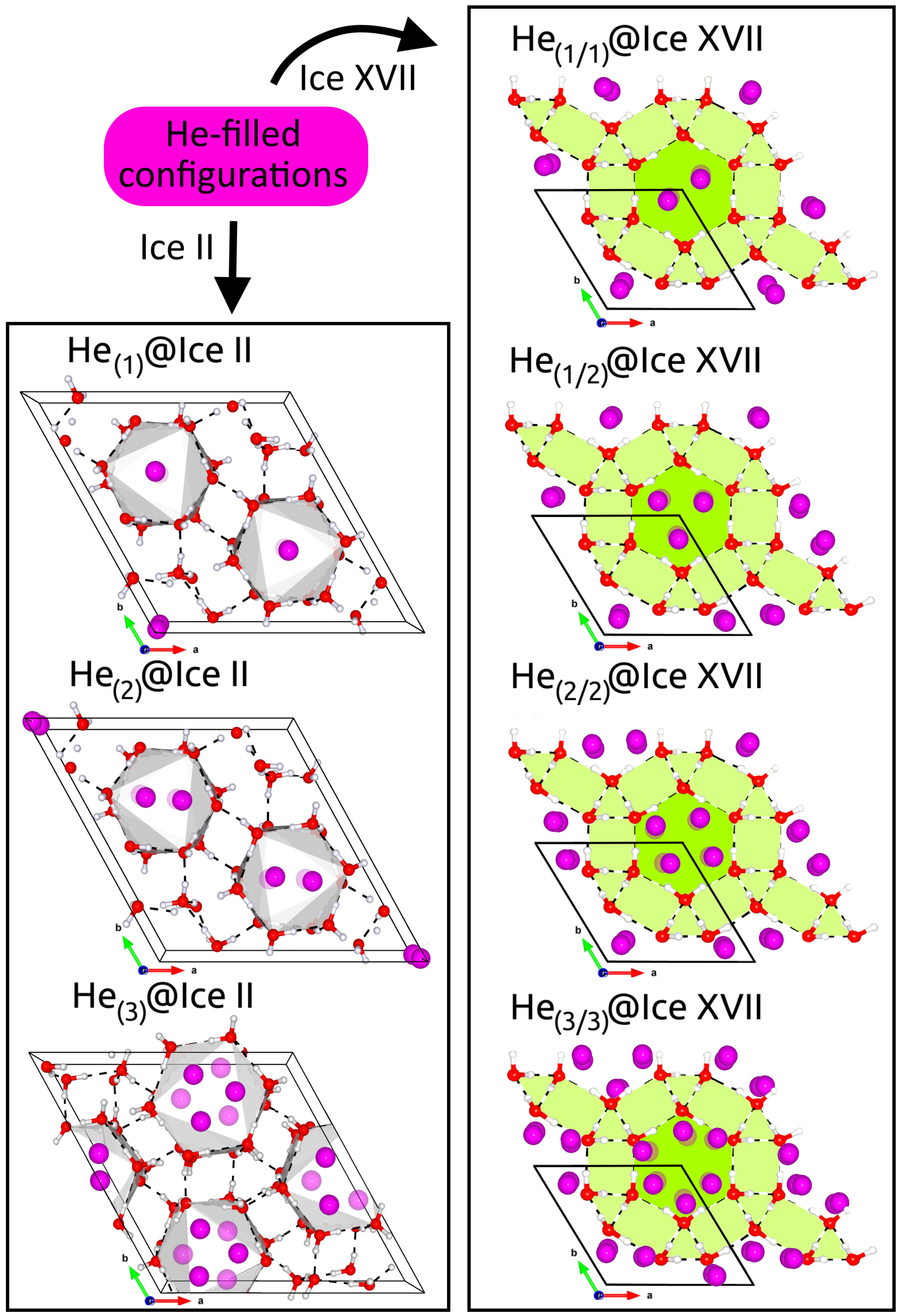
2.3. Influence of Increasing Number of He Atoms on Ice Crystal Properties
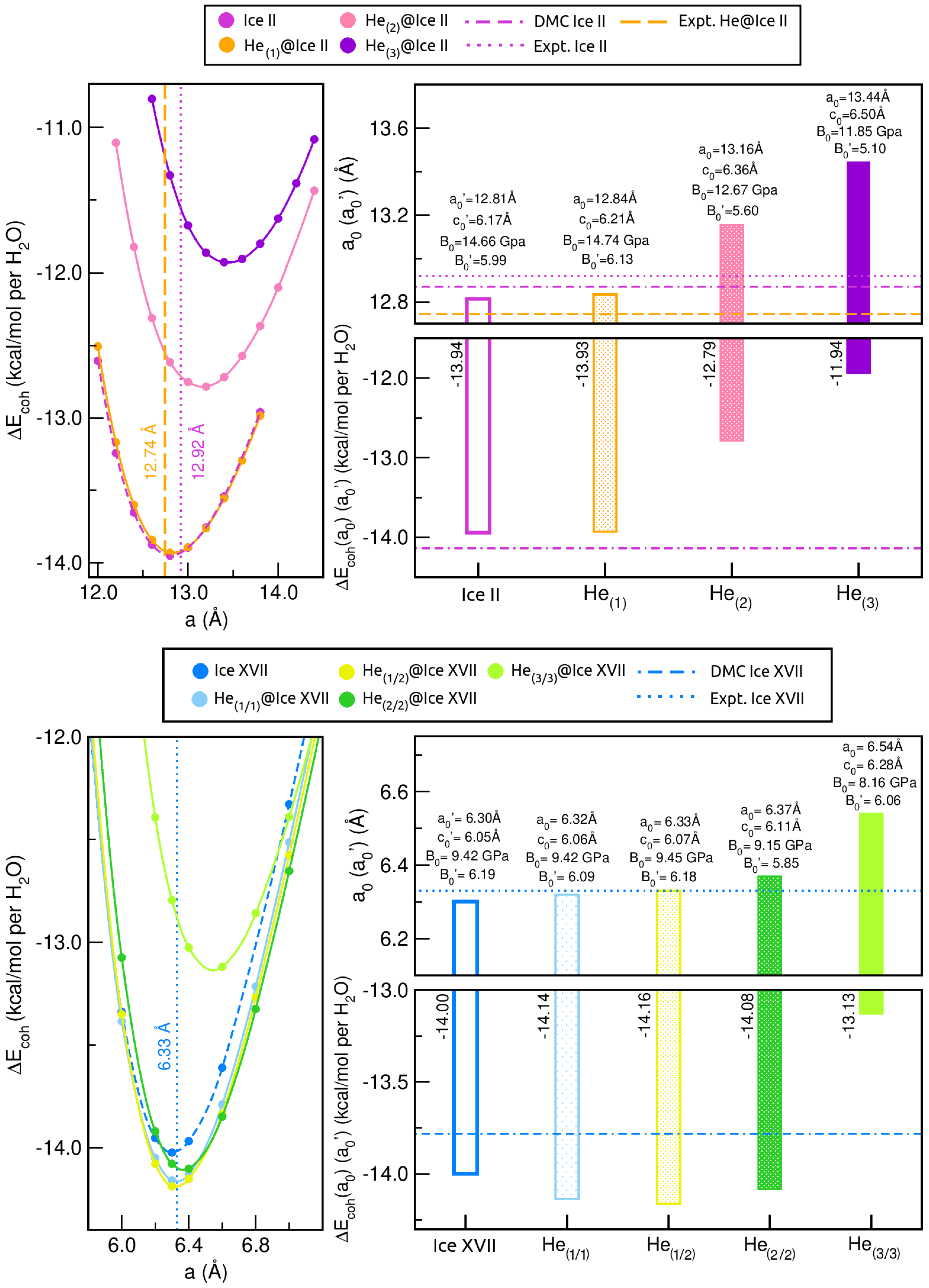
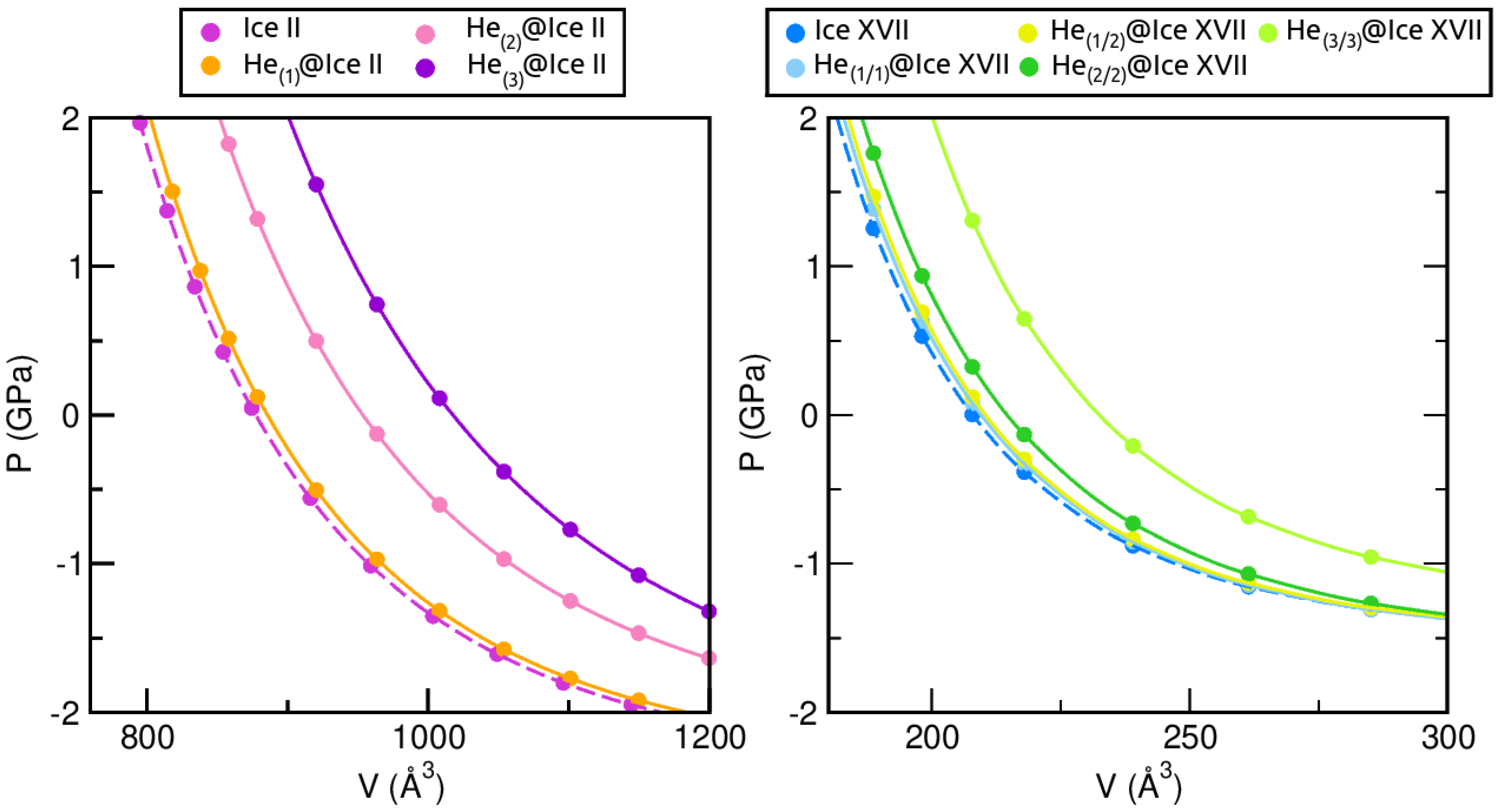
2.3.1. Structural and Mechanical Analysis
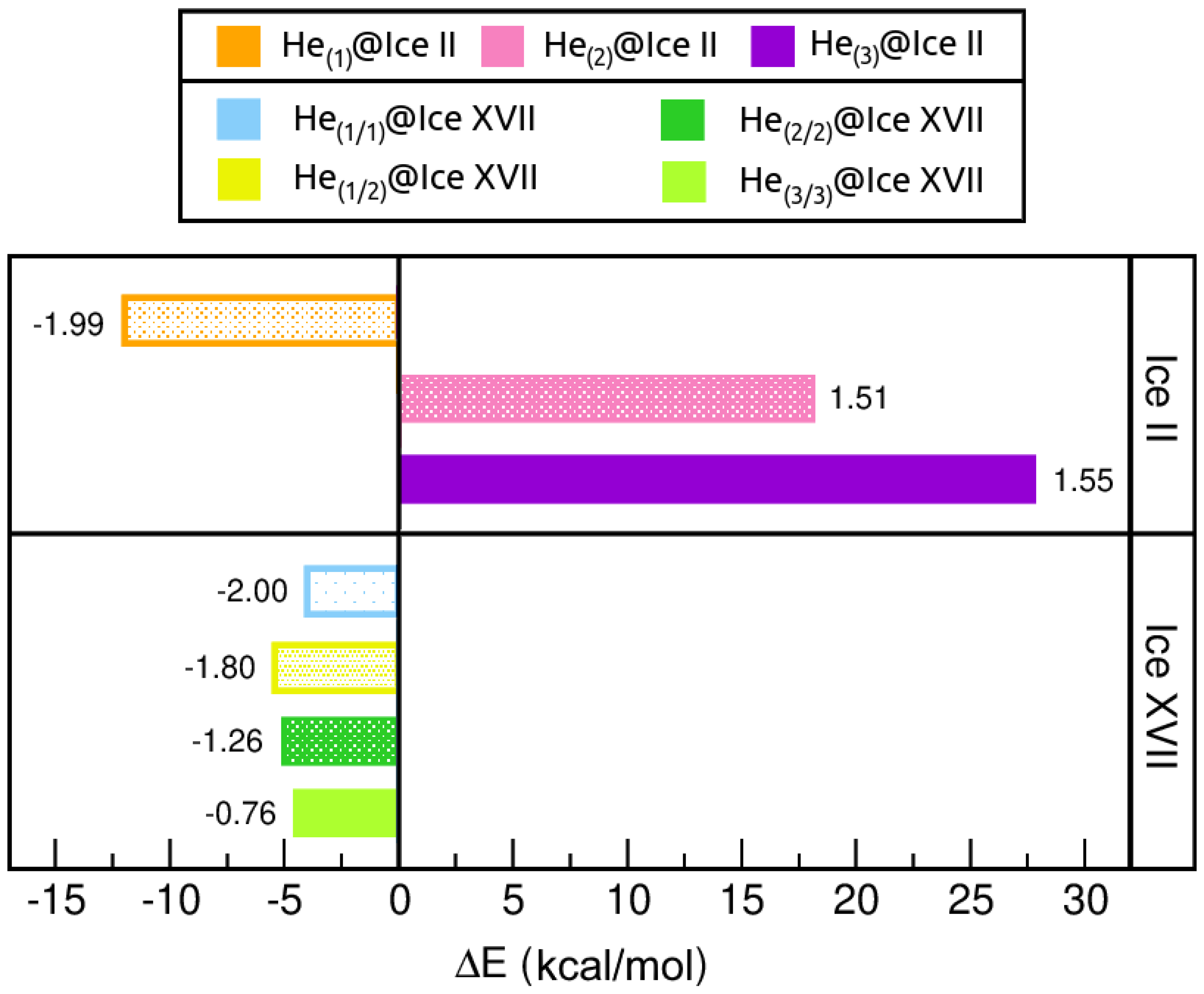
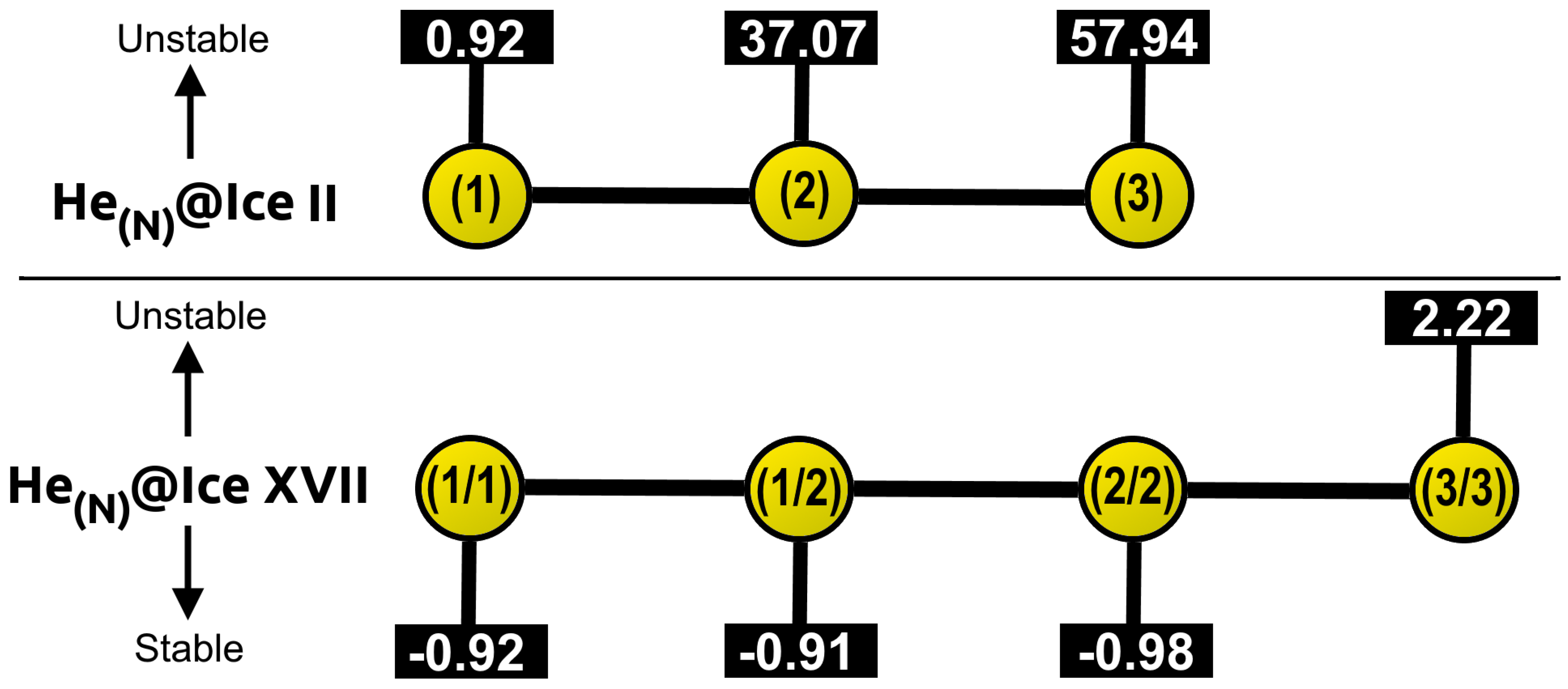
2.3.2. Energetic Analysis
3. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Londono, D.; Kuhs, W.F.; Finney, J.L. Enclathration of Helium in Ice II: The First Helium Hydrate. Nature 1988, 332, 141–142. [Google Scholar] [CrossRef]
- Londono, D.; Kuhs, W.F.; Finney, J.L. Formation, Stability and Structure of Helium Hydrate at High Pressure. J. Chem. Phys. 1992, 97, 547–552. [Google Scholar] [CrossRef]
- Loveday, J.S.; Nelmes, R.J. High-Pressure Gas Hydrates. Phys. Chem. Chem. Phys. 2008, 10, 913–1068. [Google Scholar] [CrossRef] [PubMed]
- Kuhs, W.F.; Hansen, T.C.; Falenty, A. Filling Ices with Helium and the Formation of Helium Clathrate Hydrate. J. Phys. Chem. Lett. 2018, 9, 3194–3198. [Google Scholar] [CrossRef] [PubMed]
- Arnold, G.P.; Wenzel, R.G.; Rabideau, S.W.; Nereson, N.G.; Bowman, A.L. Neutron Diffraction Study of Ice Polymorphs under Helium Pressure. J. Chem. Phys. 1971, 55, 589–595. [Google Scholar] [CrossRef]
- Namiot, A.Y.; Bukhgalter, E.B. Clathrates formed by gases in ice. J. Struct. Chem. 1965, 6, 873–874. [Google Scholar] [CrossRef]
- Kahane, A.; Klinger, J.; Philippe, M. Dopage Selectif De La Glace Monocristalline Avec De L’Helium Et Du Neon. Solid State Commun. 1969, 7, 1055–1056. [Google Scholar] [CrossRef]
- Haas, J.; Bullemer, B.; Kahane, A. Diffusion de l’helium dans la glace monocristalline. Solid State Commun. 1971, 9, 2033–2035. [Google Scholar] [CrossRef]
- Klinger, J. Thermal conductivity of ice doped with helium. Solid State Commun. 1975, 16, 961–963. [Google Scholar] [CrossRef]
- Satoh, K.; Uchida, T.; Hondoh, T.; Mae, S. Diffusion coefficient and solubility measurements of noble gases in ice crystals. Proc. NIPR Symp. Polar Meteorol. Glaciol. 1996, 10, 73–81. [Google Scholar]
- Lobban, C.; Finney, J.L.; Kuhs, W.F. The p-T Dependency of the Ice II Crystal Structure and the Effect of Helium Inclusion. J. Chem. Phys. 2002, 117, 3928–3934. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.C. Diffuse neutron-scattering studies of ice Ih under high pressures. Can. J. Phys. 2003, 81, 409–413. [Google Scholar] [CrossRef]
- Ildyakov, A.V.; Manakov, A.Y.; Aladko, E.Y.; Kosyakov, V.I.; Shestakov, V.A. Solubility of Helium in Ice Ih at Pressures up to 2000 bar: Experiment and Calculations. J. Phys. Chem. B 2013, 117, 7756–7762. [Google Scholar] [CrossRef] [PubMed]
- Malenkov, G.; Zheligovskaya, E. Dynamics of Some He and Ar Clathrate Hydrates. Computer Simulation Study. J. Incl. Phenom. Macrocycl. Chem. 2004, 48, 45–54. [Google Scholar] [CrossRef]
- Belosludov, V.; Subbotin, O.; Bozhko, Y.; Belosludov, R.; Mizuseki, H.; Kawazoe, Y.; Fomin, V. Prediction of Structure, Composition and Phase Behavior of Helium Hydrates. In Proceedings of the 7th International Conference on Gas Hydrates (ICGH 2011), Edinburgh, UK, 17–21 July 2011; pp. 1–9. [Google Scholar] [CrossRef]
- Belosludov, R.V.; Bozhko, Y.Y.; Subbotin, O.S.; Belosludov, V.R.; Mizuseki, H.; Kawazoe, Y.; Fomin, V.M. Stability and Composition of Helium Hydrates Based on Ices Ih and II at Low Temperatures. J. Phys. Chem. C 2014, 118, 2587–2593. [Google Scholar] [CrossRef]
- Teeratchanan, P.; Hermann, A. Computational phase diagrams of noble gas hydrates under pressure. J. Chem. Phys. 2015, 143, 154507. [Google Scholar] [CrossRef]
- Kaur, S.P.; Ramachandran, C.N. Host-guest and guest-guest interactions in noble gas hydrates. Mol. Phys. 2018, 116, 54–63. [Google Scholar] [CrossRef]
- Papadimitriou, N.I.; Tsimpanogiannis, I.N.; Stubos, A.K.; Martin, A.; Rovetto, L.J.; Peters, C.J. Unexpected Behavior of Helium as Guest Gas in sII Binary Hydrates. J. Phys. Chem. Lett. 2010, 1, 1014–1017. [Google Scholar] [CrossRef]
- Papadimitriou, N.I.; Tsimpanogiannis, I.N.; Stubos, A.K.; Martín, A.; Rovetto, L.J.; Florusse, L.J.; Peters, C.J. Experimental and Computational Investigation of the sII Binary He-THF Hydrate. J. Phys. Chem. B 2011, 115, 1411–1415. [Google Scholar] [CrossRef]
- Ildyakov, A.V.; Manakov, A.Y.; Zavjalov, A.P.; Bardakhanov, S.P. Gas Hydrate Formation by Methane-Helium Mixtures. Chem. Eng. Technol. 2011, 34, 1733–1738. [Google Scholar] [CrossRef]
- Mondal, S.; Chattaraj, P.K. Noble gas encapsulation: Clathrate hydrates and their HF doped analogues. Phys. Chem. Chem. Phys. 2014, 16, 17943–17954. [Google Scholar] [CrossRef] [PubMed]
- Salzmann, C.G. Advances in the experimental exploration of water’s phase diagram. J. Chem. Phys. 2019, 150, 060901. [Google Scholar] [CrossRef] [PubMed]
- Falenty, A.; Hansen, T.C.; Kuhs, W.F. Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate. Nature 2014, 516, 231–233. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Szczypiński, F.T.; Bennett, S.; Jelfs, K.E. Can we predict materials that can be synthesised? Chem. Sci. 2021, 12, 830–840. [Google Scholar] [CrossRef] [PubMed]
- Mroz, A.M.; Posligua, V.; Tarzia, A.; Wolpert, E.H.; Jelfs, K.E. Into the Unknown: How Computation Can Help Explore Uncharted Material Space. J. Am. Chem. Soc. 2022, 144, 18730–18743. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J.; Zurek, E. Computational materials discovery. J. Chem. Phys. 2022, 156, 210401. [Google Scholar] [CrossRef]
- Chang, C.; Deringer, V.L.; Katti, K.S.; Van Speybroeck, V.; Wolverton, C.M. Simulations in the era of exascale computing. Nat. Rev. Mater. 2023, 8, 309–313. [Google Scholar] [CrossRef]
- Liu, T.; Lu, D.; Zhang, H.; Zheng, M.; Yang, H.; Xu, Y.; Luo, C.; Zhu, W.; Yu, K.; Jiang, H. Applying high-performance computing in drug discovery and molecular simulation. Natl. Sci. Rev. 2016, 3, 49–63. [Google Scholar] [CrossRef]
- Penchoff, D.A.; Valeev, E.; Jagode, H.; Luszczek, P.; Danalis, A.; Bosilca, G.; Harrison, R.J.; Dongarra, J.; Windus, T.L. An Introduction to High Performance Computing and Its Intersection with Advances in Modeling Rare Earth Elements and Actinides. In Rare Earth Elements and Actinides: Progress in Computational Science Applications; ACS Publications: Washington, DC, USA, 2021; Chapter 1; pp. 3–53. [Google Scholar] [CrossRef]
- Malyshkina, M.V.; Novikov, A.S. Modern Software for Computer Modeling in Quantum Chemistry and Molecular Dynamics. Compounds 2021, 1, 134–144. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Xia, Y.; Huang, Y.P.; Lin, X.; Han, X.; Ni, N.; Wang, Z.; Yu, F.; Yang, L.; et al. Artificial Intelligence Enhanced Molecular Simulations. J. Chem. Theory Comput. 2023, 19, 4338–4350. [Google Scholar] [CrossRef] [PubMed]
- Bogojeski, M.; Vogt-Maranto, L.; Tuckerman, M.E.; Müller, K.R.; Burke, K. Quantum chemical accuracy from density functional approximations via machine learning. Nat. Commun. 2020, 11, 5223. [Google Scholar] [CrossRef]
- Keith, J.A.; Vassilev-Galindo, V.; Cheng, B.; Chmiela, S.; Gastegger, M.; Müller, K.R.; Tkatchenko, A. Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems. Chem. Rev. 2021, 121, 9816–9872. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Ma, H.; Li, S.; Ma, J. Computational and data driven molecular material design assisted by low scaling quantum mechanics calculations and machine learning. Chem. Sci. 2021, 12, 14987–15006. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Chen, M. Editorial: Advances in Density Functional Theory and beyond for Computational Chemistry. Front. Chem. 2021, 9, 705762. [Google Scholar] [CrossRef] [PubMed]
- Yanes-Rodríguez, R.; Cabrera-Ramírez, A.; Prosmiti, R. Delving into guest-free and He-filled sI and sII clathrate hydrates: A first-principles computational study. Phys. Chem. Chem. Phys. 2022, 24, 13119–13129. [Google Scholar] [CrossRef] [PubMed]
- Yanes-Rodríguez, R.; Prosmiti, R. Computational investigations of stable multiple cage occupancy He clathrate-like hydrostructures. Phys. Chem. Chem. Phys. 2023, 25, 16844–16855. [Google Scholar] [CrossRef]
- Yanes-Rodríguez, R.; Prosmiti, R. Analysing the stability of He-filled hydrates: How many He atoms fit in the sII crystal? Phys. Chem. Chem. Phys. 2023. [Google Scholar]
- del Rosso, L.; Celli, M.; Ulivi, L. New porous water ice metastable at atmospheric pressure obtained by emptying a hydrogen-filled ice. Nat. Commun. 2016, 7, 13394. [Google Scholar] [CrossRef]
- Catti, M.; del Rosso, L.; Ulivi, L.; Celli, M.; Grazzi, F.; Hansen, T.C. Ne- and O2-filled ice XVII: A neutron diffraction study. Phys. Chem. Chem. Phys. 2019, 21, 14671–14677. [Google Scholar] [CrossRef]
- del Rosso, L.; Grazzi, F.; Celli, M.; Colognesi, D.; Garcia-Sakai, V.; Ulivi, L. Refined Structure of Metastable Ice XVII from Neutron Diffraction Measurements. J. Phys. Chem. C 2016, 120, 26955–26959. [Google Scholar] [CrossRef]
- del Rosso, L.; Celli, M.; Colognesi, D.; Rudić, S.; English, N.J.; Burnham, C.J.; Ulivi, L. Dynamics of hydrogen guests in ice XVII nanopores. Phys. Rev. Mater. 2017, 1, 065602. [Google Scholar] [CrossRef]
- Amos, D.M.; Donnelly, M.E.; Teeratchanan, P.; Bull, C.L.; Falenty, A.; Kuhs, W.F.; Hermann, A.; Loveday, J.S. A Chiral Gas–Hydrate Structure Common to the Carbon Dioxide-Water and Hydrogen-Water Systems. J. Phys. Chem. Lett. 2017, 8, 4295–4299. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.L.; Yuan, Z.Y.; Jiang, L.; Zhang, K.; Wang, Z.R.; Luo, H.W.; Gu, Y.; Cao, J.W.; Qin, X.L.; Zhang, P. Computational analysis of vibrational spectrum and hydrogen bonds of ice XVII. New. J. Phys. 2019, 21, 043054. [Google Scholar] [CrossRef]
- Pradana, I.P.; Mardiana, D.; Hakim, L. Carbon dioxide occupancies inside ice XVII structure from grand-canonical Monte Carlo simulation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 833, 012035. [Google Scholar] [CrossRef]
- Yanes-Rodríguez, R.; Arismendi-Arrieta, D.; Prosmiti, R. He inclusion in ice-like and clathrate-like frameworks: A benchmark quantum chemistry study of guest-host interactions. J. Chem. Inf. Model. 2020, 60, 3043–3056. [Google Scholar] [CrossRef]
- Cabrera-Ramírez, A.; Yanes-Rodríguez, R.; Prosmiti, R. Computational density-functional approaches on finite-size and guest-lattice effects in CO2@sII clathrate hydrate. J. Chem. Phys. 2021, 154, 044301. [Google Scholar] [CrossRef]
- Kapil, V.; Schran, C.; Zen, A.; Chen, J.; Pickard, C.J.; Michaelides, A. The first-principles phase diagram of monolayer nanoconfined water. Nature 2022, 609, 512–516. [Google Scholar] [CrossRef]
- Yanes-Rodríguez, R.; Prosmiti, R. Assessment of DFT approaches in noble gas clathrate-like clusters: Stability and thermodynamics. Phys. Chem. Chem. Phys. 2022, 24, 1475–1485. [Google Scholar] [CrossRef]
- Cabrera-Ramírez, A.; Prosmiti, R. Modeling of Structure H Carbon Dioxide Clathrate Hydrates: Guest-Lattice Energies, Crystal Structure, and Pressure Dependencies. J. Phys. Chem. C 2022, 126, 14832–14842. [Google Scholar] [CrossRef]
- Della Pia, F.; Zen, A.; Alfè, D.; Michaelides, A. DMC-ICE13: Ambient and high pressure polymorphs of ice from diffusion Monte Carlo and density functional theory. J. Chem. Phys. 2022, 157, 134701. [Google Scholar] [CrossRef] [PubMed]
- Valdés, A.; Cabrera-Ramírez, A.; Prosmiti, R. Confining CO2 inside sI clathrate-hydrates: The impact of the CO2-water interaction on quantized dynamics. J. Comput. Chem. 2023, 44, 1587–1598. [Google Scholar] [CrossRef]
- Chaplin, M. Water Structure and Science. Available online: https://water.lsbu.ac.uk/water/water_structure_science.html (accessed on 29 Septembre 2023).
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric ans morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baseggio, O.; Bonfá, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A post-Hartree-Fock model of intermolecular interactions. J. Chem. Phys. 2005, 123, 024101. [Google Scholar] [CrossRef]
- Becke, A.D.; Johnson, E.R. Exchange-hole dipole moment and the dispersion interaction. J. Chem. Phys. 2005, 122, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Jens, A.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Universität-Bonn. D4—A Generally Applicable Atomic-Charge Dependent London Dispersion Correction. Available online: https://github.com/dftd4/dftd4 (accessed on 20 July 2023).
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef] [PubMed]
- Caldeweyher, E.; Mewes, J.M.; Ehlert, S.; Grimme, S. Extension and evaluation of the D4 London-dispersion model for periodic systems. Phys. Chem. Chem. Phys. 2020, 22, 8499–8512. [Google Scholar] [CrossRef]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2009, 22, 022201. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef]
- Lee, K.; Murray, E.D.; Kong, L.; Lundqvist, B.I.; Langreth, D.C. Higher-accuracy van der Waals density functional. Phys. Rev. B 2010, 82, 081101. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Makov, G.; Payne, M.C. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 1995, 51, 4014–4022. [Google Scholar] [CrossRef]
- Santra, B.; Klimeš, J.; Tkatchenko, A.; Alfè, D.; Slater, B.; Michaelides, A.; Car, R.; Scheffler, M. On the accuracy of van der Waals inclusive density-functional theory exchange-correlation functionals for ice at ambient and high pressures. J. Chem. Phys. 2013, 139, 154702. [Google Scholar] [CrossRef] [PubMed]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Fortes, A.D.; Wood, I.G.; Brodholt, J.P.; Vočadlo, L. Ab initio simulation of the ice II structure. J. Chem. Phys. 2003, 119, 4567–4572. [Google Scholar] [CrossRef]
- Gagnon, R.E.; Kiefte, H.; Clouter, M.J.; Whalley, E. Acoustic velocities and densities of polycrystalline ice Ih, II, III, V, and VI by Brillouin spectroscopy. J. Chem. Phys. 1990, 92, 1909–1914. [Google Scholar] [CrossRef]
- Fortes, A.D.; Wood, I.G.; Alfredsson, M.; Vočadlo, L.; Knight, K.S. The incompressibility and thermal expansivity of D2O ice II determined by powder neutron diffraction. J. Appl. Crystallogr. 2005, 38, 612–618. [Google Scholar] [CrossRef]
- Ohto, T.; Dodia, M.; Xu, J.; Imoto, S.; Tang, F.; Zysk, F.; Kühne, T.D.; Shigeta, Y.; Bonn, M.; Wu, X.; et al. Accessing the Accuracy of Density Functional Theory through Structure and Dynamics of the Water–Air Interface. J. Phys. Chem. Lett. 2019, 10, 4914–4919. [Google Scholar] [CrossRef]
- Yu, X.; Zhu, J.; Du, S.; Xu, H.; Vogel, S.C.; Han, J.; Germann, T.C.; Zhang, J.; Jin, C.; Francisco, J.S.; et al. Crystal structure and encapsulation dynamics of ice II-structured neon hydrate. Proc. Natl. Acad. Sci. USA 2014, 111, 10456–10461. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanes-Rodríguez, R.; Prosmiti, R. Confining He Atoms in Diverse Ice-Phases: Examining the Stability of He Hydrate Crystals through DFT Approaches. Molecules 2023, 28, 7893. https://doi.org/10.3390/molecules28237893
Yanes-Rodríguez R, Prosmiti R. Confining He Atoms in Diverse Ice-Phases: Examining the Stability of He Hydrate Crystals through DFT Approaches. Molecules. 2023; 28(23):7893. https://doi.org/10.3390/molecules28237893
Chicago/Turabian StyleYanes-Rodríguez, Raquel, and Rita Prosmiti. 2023. "Confining He Atoms in Diverse Ice-Phases: Examining the Stability of He Hydrate Crystals through DFT Approaches" Molecules 28, no. 23: 7893. https://doi.org/10.3390/molecules28237893
APA StyleYanes-Rodríguez, R., & Prosmiti, R. (2023). Confining He Atoms in Diverse Ice-Phases: Examining the Stability of He Hydrate Crystals through DFT Approaches. Molecules, 28(23), 7893. https://doi.org/10.3390/molecules28237893