Calculation of Mechanical Properties, Electronic Structure and Optical Properties of CsPbX3 (X = F, Cl, Br, I)
Abstract
:1. Introduction
2. Results and Discussion
2.1. Mechanical Properties
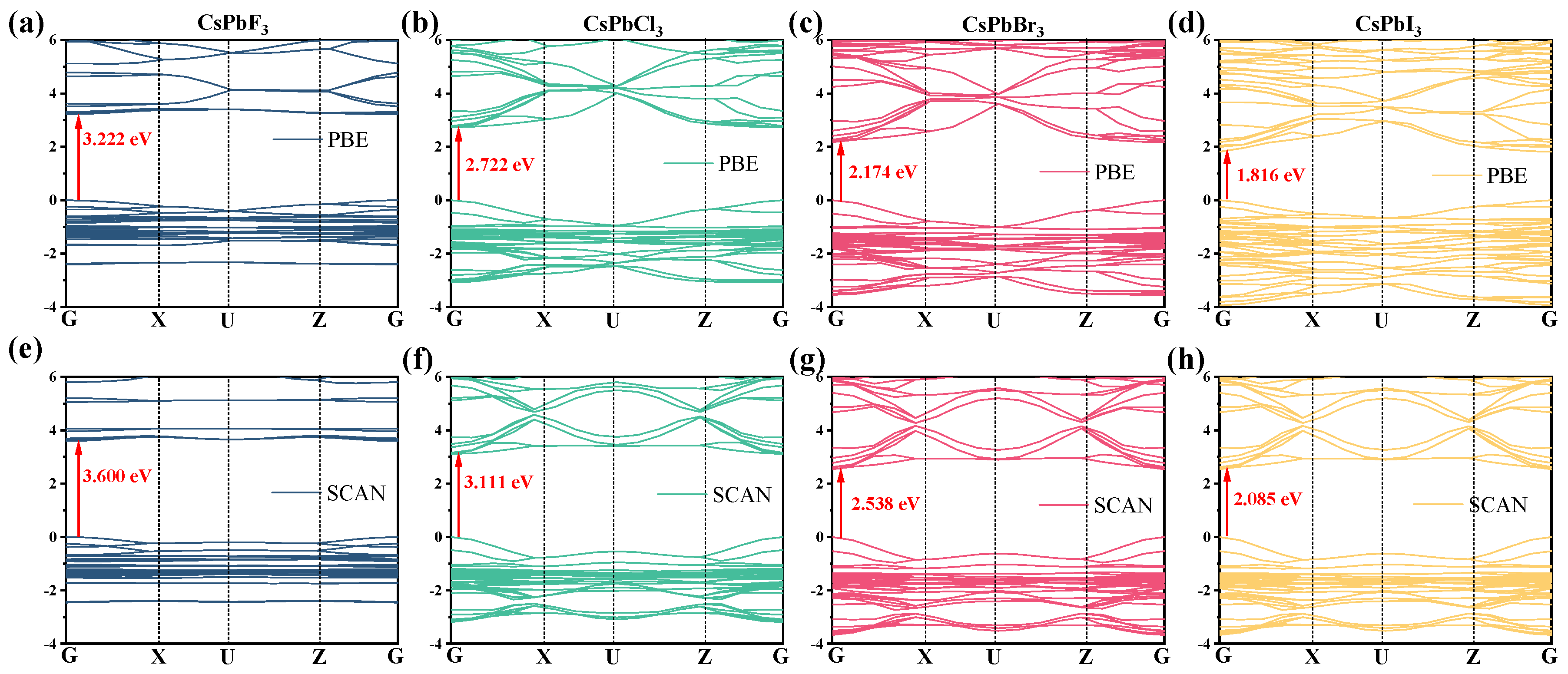
2.2. Electronic Properties
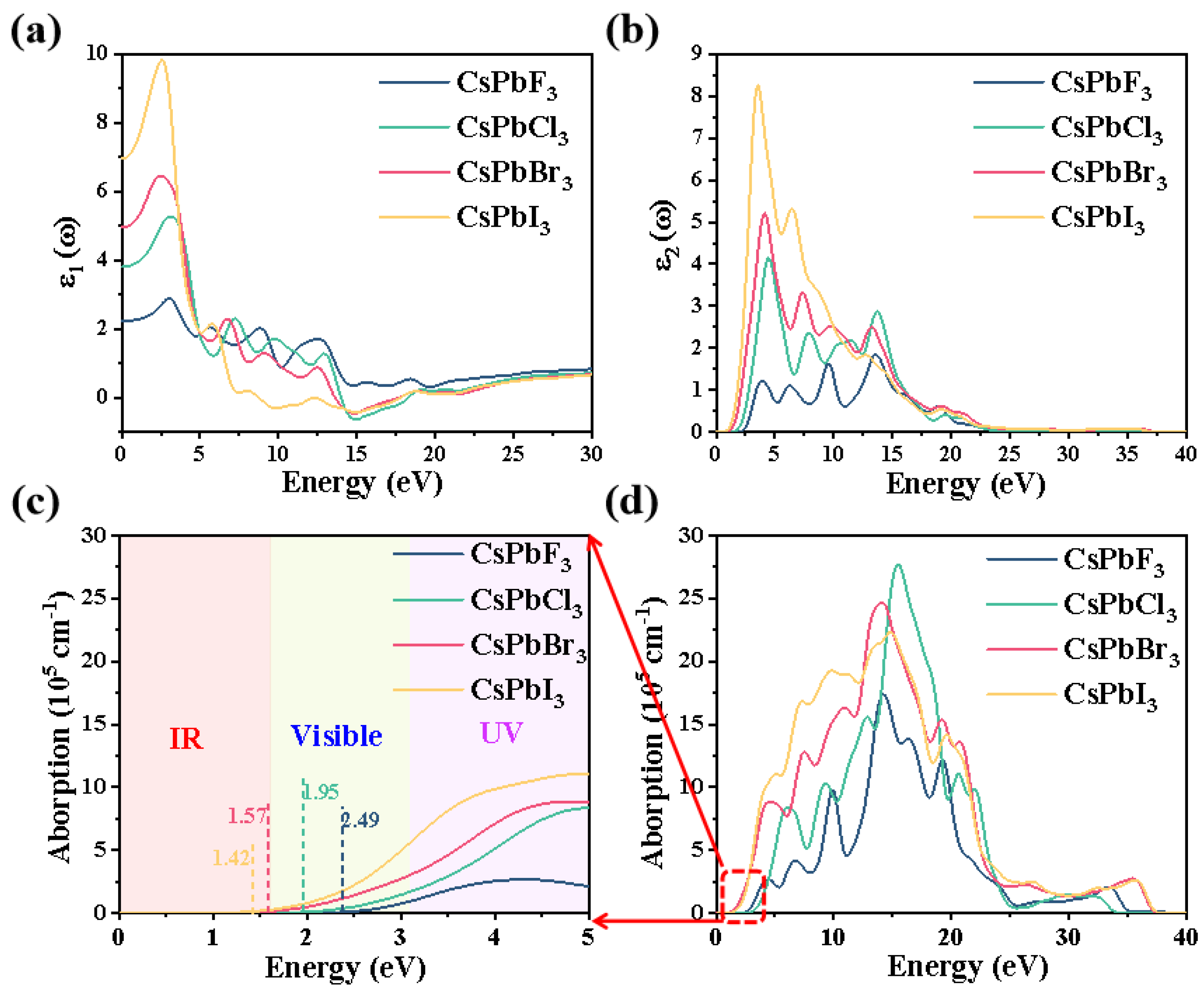
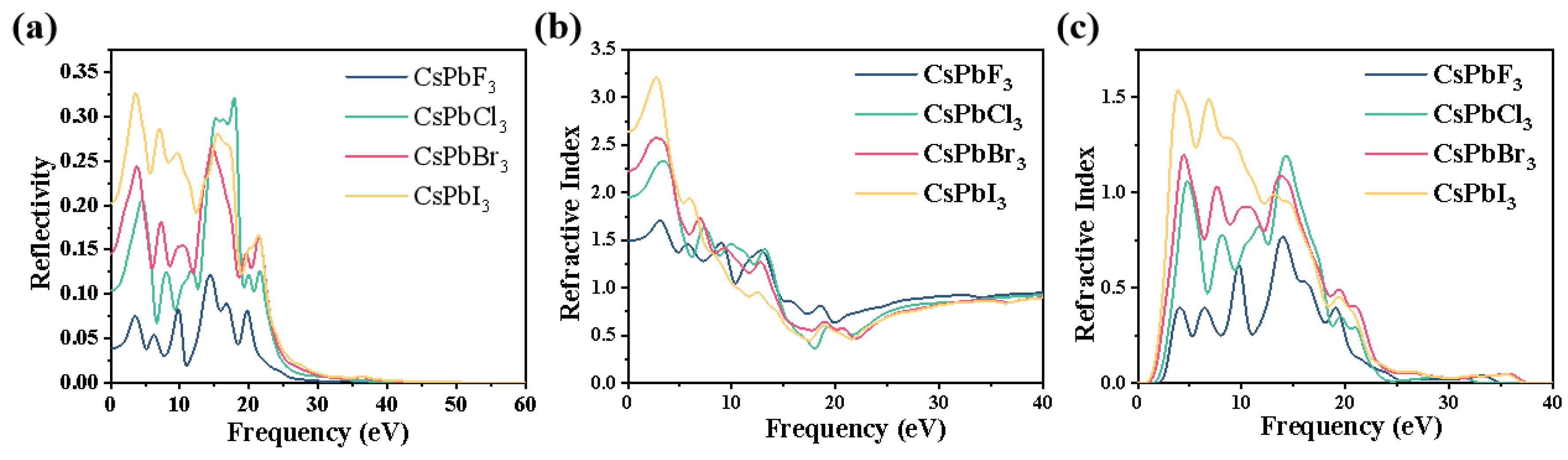
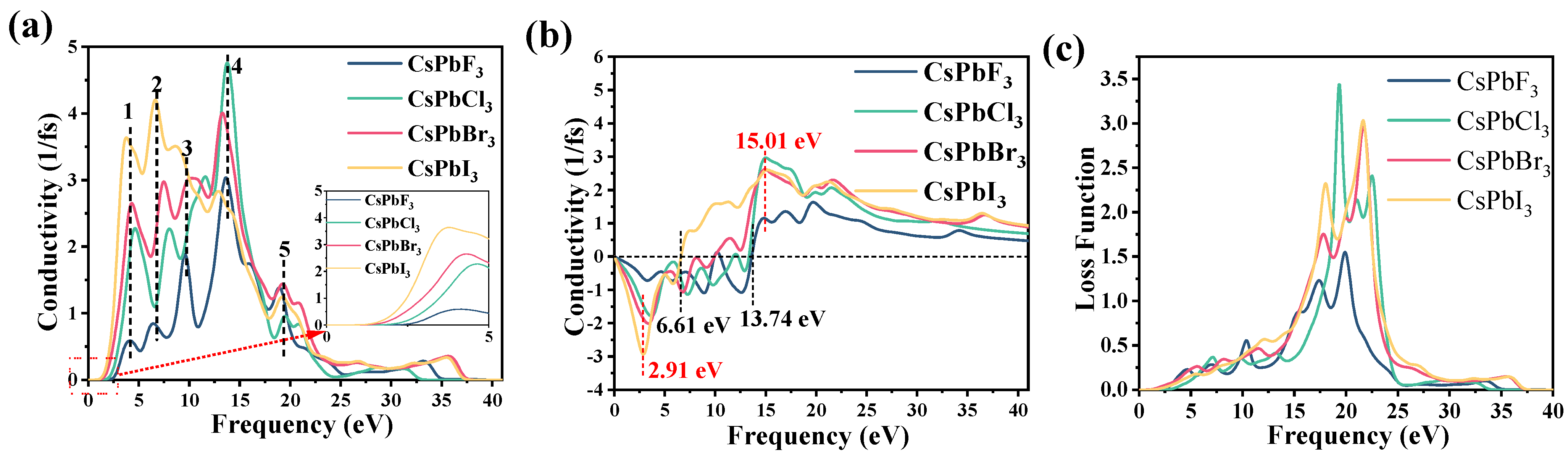
2.3. Optical Properties
3. Computation Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chakhmouradian, A.R.; Woodward, P.M. Celebrating 175 years of perovskite research: A tribute to Roger H. Mitchell. Phys. Chem. Miner. 2014, 41, 387–391. [Google Scholar] [CrossRef]
- Tanaka, H.; Misono, M. Advances in designing perovskite catalysts. Curr. Opin. Solid State Mater. Sci. 2001, 5, 381–387. [Google Scholar] [CrossRef]
- Dong, H.; Ran, C.; Gao, W.; Li, M.; Xia, Y.; Huang, W. Metal Halide Perovskite for next-generation optoelectronics: Progresses and prospects. eLight 2023, 3, 3. [Google Scholar] [CrossRef]
- Babu, R.; Giribabu, L.; Singh, S.P. Recent Advances in Halide-Based Perovskite Crystals and Their Optoelectronic Applications. Cryst. Growth Des. 2018, 18, 2645–2664. [Google Scholar] [CrossRef]
- Protesescu, L.; Yakunin, S.; Bodnarchuk, M.I.; Krieg, F.; Caputo, R.; Hendon, C.H.; Yang, R.X.; Walsh, A.; Kovalenko, M.V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. [Google Scholar] [CrossRef]
- Usman, M.; Balsalobre-Lorente, D. Environmental concern in the era of industrialization: Can financial development, renewable energy and natural resources alleviate some load? Energy Policy 2022, 162, 112780. [Google Scholar] [CrossRef]
- Zheng, Y.; Pan, Z.; Wang, X. Advances in photocatalysis in China. Chin. J. Catal. 2013, 34, 524–535. [Google Scholar] [CrossRef]
- Schanze, K.S.; Kamat, P.V.; Yang, P.; Bisquert, J. Progress in Perovskite Photocatalysis. ACS Energy Lett. 2020, 5, 2602–2604. [Google Scholar] [CrossRef]
- Lin, C.-C.; Liu, T.-R.; Lin, S.-R.; Boopathi, K.M.; Chiang, C.-H.; Tzeng, W.-Y.; Chien, W.-H.C.; Hsu, H.-S.; Luo, C.-W.; Tsai, H.-Y.; et al. Spin-Polarized Photocatalytic CO2 Reduction of Mn-Doped Perovskite Nanoplates. J. Am. Chem. Soc. 2022, 144, 15718–15726. [Google Scholar] [CrossRef]
- Ali, S.A.; Ahmad, T. Treasure trove for efficient hydrogen evolution through water splitting using diverse perovskite photocatalysts. Mater. Today Chem. 2023, 29, 101387. [Google Scholar] [CrossRef]
- Park, S.; Chang, W.J.; Lee, C.W.; Park, S.; Ahn, H.-Y.; Nam, K.T. Photocatalytic hydrogen generation from hydriodic acid using methylammonium lead iodide in dynamic equilibrium with aqueous solution. Nat. Energy 2016, 2, 16185. [Google Scholar] [CrossRef]
- Liu, D.; Shao, Z.; Li, C.; Pang, S.; Yan, Y.; Cui, G. Structural Properties and Stability of Inorganic CsPbI3 Perovskites. Small Struct. 2021, 2, 2000089. [Google Scholar] [CrossRef]
- Zhang, J.; Hodes, G.; Jin, Z.; Liu, S. All-Inorganic CsPbX3 Perovskite Solar Cells: Progress and Prospects. Angew. Chem. Int. Ed. 2019, 58, 15596–15618. [Google Scholar] [CrossRef] [PubMed]
- Xiang, W.; Tress, W. Review on Recent Progress of All-Inorganic Metal Halide Perovskites and Solar Cells. Adv. Mater. 2019, 31, 1902851. [Google Scholar] [CrossRef]
- Shamsi, J.; Urban, A.S.; Imran, M.; De Trizio, L.; Manna, L. Metal Halide Perovskite Nanocrystals: Synthesis, Post-Synthesis Modifications, and Their Optical Properties. Chem. Rev. 2019, 119, 3296–3348. [Google Scholar] [CrossRef]
- Xu, Y.-F.; Yang, M.-Z.; Chen, B.-X.; Wang, X.-D.; Chen, H.-Y.; Kuang, D.-B.; Su, C.-Y. A CsPbBr3 Perovskite Quantum Dot/Graphene Oxide Composite for Photocatalytic CO2 Reduction. J. Am. Chem. Soc. 2017, 139, 5660–5663. [Google Scholar] [CrossRef]
- Sebastian, M.; Peters, J.A.; Stoumpos, C.C.; Im, J.; Kostina, S.S.; Liu, Z.; Kanatzidis, M.G.; Freeman, A.J.; Wessels, B.W. Excitonic emissions and above-band-gap luminescence in the single-crystal perovskite semiconductors CsPbBr3 and CsPbCl3. Phys. Rev. B 2015, 92, 235210. [Google Scholar] [CrossRef]
- Heidrich, K.; Schäfer, W.; Schreiber, M.; Söchtig, J.; Trendel, G.; Treusch, J.; Grandke, T.; Stolz, H.J. Electronic structure, photoemission spectra, and vacuum-ultraviolet optical spectra of CsPbCl3 and CsPbBr3. Phys. Rev. B 1981, 24, 5642–5649. [Google Scholar] [CrossRef]
- Heidrich, K.; Künzel, H.; Treusch, J. Optical properties and electronic structure of CsPbCl3 and CsPbBr3. Solid State Commun. 1978, 25, 887–889. [Google Scholar] [CrossRef]
- Trots, D.M.; Myagkota, S.V. High-temperature structural evolution of caesium and rubidium triiodoplumbates. J. Phys. Chem. Solids 2008, 69, 2520–2526. [Google Scholar] [CrossRef]
- Rohrer, G.S. Structure and Bonding in Crystalline Materials; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Berastegui, P.; Hull, S.; Eriksson, S.G. A low-temperature structural phase transition in CsPbF3. J. Phys. Condens. Matter 2001, 13, 5077. [Google Scholar] [CrossRef]
- Murtaza, G.; Ahmad, I. First principle study of the structural and optoelectronic properties of cubic perovskites CsPbM3 (M = Cl, Br, I). Phys. B Condens. Matter 2011, 406, 3222–3229. [Google Scholar] [CrossRef]
- Qian, J.; Xu, B.; Tian, W. A comprehensive theoretical study of halide perovskites ABX3. Org. Electron. 2016, 37, 61–73. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Lond. Sect. A 1952, 65, 349–355. [Google Scholar] [CrossRef]
- Tian, Y.J.; Xu, B.; Zhao, Z.S. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Peng, C.; Liu, Y.; Cui, J.; Luo, K.; Shen, Y.; Li, X. First-principle calculation of the electronic structure of α-Ag3VO4 using two different exchange correlation functionals. Mater. Chem. Phys. 2021, 262, 124307. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, K.; Guo, C.; Lu, Y.; Du, K.; Peng, C.; Hu, X.; Jia, Y.; Xu, B.; Wang, R.; et al. Growth and Characterization of All-Inorganic Halide Perovskite CsPbF3 Single Crystals. Crystals 2023, 13, 765. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Deng, W.; Li, W.; Chun, F.J.; Luo, C.; Xie, M.L.; Pu, B.; Lin, N.; Gao, B.; Yang, W.Q. Antisolvent-Induced Fastly Grown All-Inorganic Perovskite CsPbCl3 Microcrystal Films for High-Sensitive UV Photodetectors. Adv. Mater. Interfaces 2021, 8, 2001812. [Google Scholar] [CrossRef]
- Yuan, H.W.; Zhao, Y.Y.; Duan, J.L.; Wang, Y.D.; Yang, X.Y.; Tang, Q.W. All-inorganic CsPbBr3 perovskite solar cell with 10.26% efficiency by spectra engineering. J. Mater. Chem. A 2018, 6, 24324–24329. [Google Scholar] [CrossRef]
- Tan, S.; Yu, B.C.; Cui, Y.Q.; Meng, F.Q.; Huang, C.J.; Li, Y.M.; Chen, Z.J.; Wu, H.J.; Shi, J.J.; Luo, Y.H.; et al. Temperature-Reliable Low-Dimensional Perovskites Passivated Black-Phase CsPbI3 toward Stable and Efficient Photovoltaics. Angew. Chem.-Int. Ed. 2022, 61, e202201300. [Google Scholar] [CrossRef] [PubMed]
- Yonghua, D.; Lishi, M.; Ping, L.; Yong, C. First-principles calculations of electronic structures and optical, phononic, and thermodynamic properties of monoclinic α-spodumene. Ceram. Int. 2017, 43, 6312–6321. [Google Scholar] [CrossRef]
- Sifi, C.; Meradji, H.; Slimani, M.; Labidi, S.; Ghemid, S.; Hanneche, E.B.; El Haj Hassan, F. First principle calculations of structural, electronic, thermodynamic and optical properties of Pb1−xCaxS, Pb1−xCaxSe and Pb1−xCaxTe ternary alloys. J. Phys. Condens. Matter 2009, 21, 195401. [Google Scholar] [CrossRef] [PubMed]
- Drief, F.; Tadjer, A.; Mesri, D.; Aourag, H. First principles study of structural, electronic, elastic and optical properties of MgS, MgSe and MgTe. Catal. Today 2004, 89, 343–355. [Google Scholar] [CrossRef]
- Gous, M.H.; Meddour, A.; Bourouis, C. First principles study of structural, electronic, magnetic and elastic properties of Mg0.75TM0.25S (TM = Mn, Fe, Co, Ni). J. Magn. Magn. Mater. 2017, 422, 271–279. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, A.; Duan, Y.; Peng, M. Structural stability, electronic and optical properties of MAX-phase ternary nitrides β-TM4AlN3 (TM = V, Nb, and Ta) using the first-principles explorations. Vacuum 2021, 193, 110529. [Google Scholar] [CrossRef]
- Yaseen, M.; Ambreen, H.; Sufyan, A.; Butt, M.K.; UrRehman, S.; Iqbal, J.; Misbah Bibi, S.; Murtaza, A.; Ramay, S.M. Optical and magnetic properties of manganese doped zinc sulphide: Density functional theory approach. Ferroelectrics 2020, 557, 112–122. [Google Scholar]
- Vu, T.V.; Tong, H.D.; Tran, D.P.; Binh, N.T.T.; Nguyen, C.V.; Phuc, H.V.; Do, H.M.; Hieu, N.N. Electronic and optical properties of Janus ZrSSe by density functional theory. RSC Adv. 2019, 9, 41058–41065. [Google Scholar] [CrossRef]
- Behzad, S. Electronic structure, optical absorption and energy loss spectra of GaN graphitic sheet. J. Mater. Sci. Mater. Electron. 2015, 26, 9898–9906. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Fur Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Saputro, D.R.S.; Widyaningsih, P. Limited Memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) Method for The Parameter Estimation on Geographically Weighted Ordinal Logistic Regression Model (GWOLR). In Proceedings of the 4th International Conference on Research, Implementation, and Education of Mathematics and Sciences (ICRIEMS), Yogyakarta, Indonesia, 15–16 May 2017; Yogyakarta State University: Yogyakarta, Indonesia, 2017. [Google Scholar]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Rodova, M.; Brozek, J.; Knizek, K.; Nitsch, K. Phase transitions in ternary caesium lead bromide. J. Therm. Anal. Calorim. 2003, 71, 667–673. [Google Scholar] [CrossRef]


| System | C11 | C12 | C13 | C23 | C22 | C33 | C44 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|
| CsPbF3 | 26.944 | 10.646 | 3.018 | 1.472 | 31.857 | 30.189 | 10.787 | 10.463 | 19.287 |
| CsPbCl3 | 27.868 | 16.536 | 9.232 | 7.208 | 28.541 | 24.298 | 6.298 | 4.122 | 11.598 |
| CsPbBr3 | 23.542 | 14.357 | 7.679 | 6.120 | 24.981 | 18.857 | 5.313 | 3.298 | 10.711 |
| CsPbI3 | 16.193 | 10.061 | 4.949 | 5.355 | 18.191 | 15.175 | 4.266 | 2.126 | 7.425 |
| System | Bulk Modulus (B) | Shear Modulus (G) | Young’s Modulus (E) | Poisson’s Ratio (ν) | Hardness (H) | B/G | H/E |
|---|---|---|---|---|---|---|---|
| CsPbF3 | 13.170 | 12.542 | 28.560 | 0.138 | 5.215 | 1.050 | 0.183 |
| CsPbCl3 | 16.008 | 7.064 | 18.474 | 0.307 | 1.448 | 2.266 | 0.078 |
| CsPbBr3 | 13.361 | 5.954 | 15.553 | 0.306 | 1.298 | 2.244 | 0.083 |
| CsPbI3 | 9.870 | 4.295 | 11.253 | 0.309 | 1.002 | 2.298 | 0.089 |
| System | Lattice Constant/Å | Unit Cell Volume V/Å3 | Band Gap/eV | Pb-X Bond Length/Å | Pb-X-Pb Bond Angle/° | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | PBE | SCAN | Exp. | I | II | I | II | ||
| CsPbF3 | 6.950 | 7.030 | 10.095 | 493.149 | 3.222 | 3.600 | 3.68 [30] | 2.494/2.493 | 2.550 | 164.758 | 163.341 |
| CsPbCl3 | 8.030 | 8.112 | 11.389 | 741.918 | 2.722 | 3.111 | 2.90 [31] | 2.918/2.915 | 2.951 | 156.167 | 149.494 |
| CsPbBr3 | 8.388 | 8.504 | 11.869 | 846.726 | 2.174 | 2.538 | 2.30 [32] | 3.060/3.056 | 3.097 | 155.108 | 146.726 |
| CsPbI3 | 8.894 | 9.087 | 12.587 | 1017.39 | 1.816 | 2.085 | ~1.70 [33] | 3.273/3.271 | 3.307 | 152.672 | 144.151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Fang, C.; Lin, S.; Liu, G.; Zhang, B.; Shi, H.; Dong, N.; Yang, N.; Zhang, F.; Guo, X.; et al. Calculation of Mechanical Properties, Electronic Structure and Optical Properties of CsPbX3 (X = F, Cl, Br, I). Molecules 2023, 28, 7643. https://doi.org/10.3390/molecules28227643
Liu Y, Fang C, Lin S, Liu G, Zhang B, Shi H, Dong N, Yang N, Zhang F, Guo X, et al. Calculation of Mechanical Properties, Electronic Structure and Optical Properties of CsPbX3 (X = F, Cl, Br, I). Molecules. 2023; 28(22):7643. https://doi.org/10.3390/molecules28227643
Chicago/Turabian StyleLiu, Yang, Canxiang Fang, Shihe Lin, Gaihui Liu, Bohang Zhang, Huihui Shi, Nan Dong, Nengxun Yang, Fuchun Zhang, Xiang Guo, and et al. 2023. "Calculation of Mechanical Properties, Electronic Structure and Optical Properties of CsPbX3 (X = F, Cl, Br, I)" Molecules 28, no. 22: 7643. https://doi.org/10.3390/molecules28227643
APA StyleLiu, Y., Fang, C., Lin, S., Liu, G., Zhang, B., Shi, H., Dong, N., Yang, N., Zhang, F., Guo, X., & Liu, X. (2023). Calculation of Mechanical Properties, Electronic Structure and Optical Properties of CsPbX3 (X = F, Cl, Br, I). Molecules, 28(22), 7643. https://doi.org/10.3390/molecules28227643







