Next Article in Journal
IGF2 Peptide-Based LYTACs for Targeted Degradation of Extracellular and Transmembrane Proteins
Next Article in Special Issue
Comparative Study of Two Spectral Methods for Estimating the Excited State Dipole Moment of Non-Fluorescent Molecules
Previous Article in Journal
Feature Papers in Food Chemistry—2nd Edition
Previous Article in Special Issue
Interaction of Vinyl-Type Carbocations, C3H5+ and C4H7+ with Molecules of Water, Alcohols, and Acetone
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 22
10.3390/molecules28227520
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

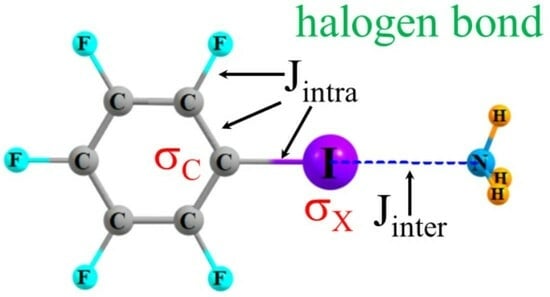
Relation between Halogen Bond Strength and IR and NMR Spectroscopic Markers

by
Akhtam Amonov
1 and
Steve Scheiner
2,*
1
Department of Optics and Spectroscopy, Engineering Physics Institute, Samarkand State University, University blv. 15, Samarkand 140104, Uzbekistan
2
Department of Chemistry and Biochemistry, Utah State University, Logan, UT 84322-0300, USA
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(22), 7520; https://doi.org/10.3390/molecules28227520
Submission received: 23 October 2023 / Revised: 4 November 2023 / Accepted: 8 November 2023 / Published: 10 November 2023
(This article belongs to the Special Issue Chemical Bond and Intermolecular Interactions, 2nd Edition)
Browse Figures
Versions Notes

Abstract

:
The relationship between the strength of a halogen bond (XB) and various IR and NMR spectroscopic quantities is assessed through DFT calculations. Three different Lewis acids place a Br or I atom on a phenyl ring; each is paired with a collection of N and O bases of varying electron donor power. The weakest of the XBs display a C–X bond contraction coupled with a blue shift in the associated frequency, whereas the reverse trends occur for the stronger bonds. The best correlations with the XB interaction energy are observed with the NMR shielding of the C atom directly bonded to X and the coupling constants involving the C–X bond and the C–H/F bond that lies ortho to the X substituent, but these correlations are not accurate enough for the quantitative assessment of energy. These correlations tend to improve as the Lewis acid becomes more potent, which makes for a wider range of XB strengths.

Graphical Abstract

1. Introduction

Of all the noncovalent interactions that have been probed over the years, it is the H-bond (HB) that has fostered the largest body of research, stretching back more than a century [1,2,3,4,5,6,7,8,9]. One of the offshoots of this extensive body of work has been the recently developing interest in a set of noncovalent bonds where the bridging proton of the HB is replaced by any of a broad spectrum of other atoms, most commonly from the right side of the periodic table [10,11,12,13,14,15,16]. Some of these analogous interactions are known as chalcogen, pnicogen, and tetrel bonds, depending of course on the particular family from which the bridging atom is drawn [17,18,19,20,21,22,23,24,25,26].
Within this grouping of interactions, it is the halogen bond (XB) that has captured the lion’s share of attention. The analogue of the H-bonding A–H··B configuration is altered to A–X··B, where X represents any of the halogen atoms, usually Cl, Br, or I. Although the electronegativity of X works against an overall partial positive atomic charge as is present on H, the molecular electrostatic potential (MEP) surrounding the X is characterized by a positive region directed along the extension of the A–H bond, complemented by a negative equatorial ring. The former is commonly referred to as a σ-hole, which is capable of electrostatically attracting a nucleophile in much the same way as does the bridging proton of an HB [25,27,28,29,30,31,32,33,34]. This coulombic component is supplemented by a stabilizing charge transfer from the nucleophile to the σ*(AX) antibonding orbital, in full analogy to the transfer to the σ*(AH) of the HB, to which is attributed the well-known red shift in the A–H vibrational stretching frequency.
Again, with reference to the HB, there are a set of spectroscopic indicators of the presence of such a bond, which can be used in some cases to assess the strength of the bond. The aforementioned red shift in ν(AH) is a prime example, where larger shifts are taken as evidence of more powerful HBs [35,36,37,38]. Along with its displacement to lower frequencies, this IR band is typically intensified, the degree of which serves as another indicator of a stronger bond. NMR spectroscopy provides alternative measures of HB strength, particularly through the downfield shift in the signal of the bridging proton.
Because of the high degree of similarity between the HB and XB, one would expect that spectroscopic features ought to serve as useful measures of the strength of the latter bond as well. However, examination of this question has been fragmentary, with little in the way of general trends emerging from past work. A large fraction of the past work concentrated on the effects of the XB upon the electron donor unit [39,40,41,42], meaning it ignored issues arising within the acid. A few cases have been identified where XB formation leads to a red shift in the internal stretching frequency within the halogen donor, usually in small molecules such as a dihalogen [43,44], FX [45,46], CH3X [47], or CF3X [48], and there are cases where a blue shift has been observed [49], but little systematic work has addressed this issue in larger systems.
There have been solid state NMR measurements [50] that delved into the effects of the angular characteristics of XB formation upon the NMR spectrum. A number of works have considered very small Lewis acids such as dihalogens [45,46,51,52,53]. NMR coupling constants have been computed for the specific pair of atoms involved directly in the bond [39,54,55,56] but little attention has been paid to the more peripheral nuclei or to the coupling constants within the Lewis acid unit. In connection with larger systems, a certain amount of attention has been drawn toward halobenzenes [57,58,59,60,61,62] where the X atom is connected to a simple phenyl ring. As electron-withdrawing substituents on the ring amplify the X σ-hole, haloperfluorobenzenes have also been the subject of scrutiny [61,63,64,65,66,67].
One concept emanating from this work [68,69,70,71] has been that the shielding of the C atom directly attached to I tends to diminish as the XB strengthens and the internal C–I bond grows longer. Indeed, it has been suggested [72] that shielding of this C nucleus might serve as a sort of reporter or measure of XB strength. Some recent calculations echo this idea [73,74] for certain other halogenated systems. A recent paper [75] raised another intriguing proposal that the internal coupling constants within Lewis acids have potential as a monitor of XB strength, at least in the context of fluorinated iodobenzene, where the measurements were made.
The goal of the present work is a systematic evaluation of the ability of various spectroscopic markers to predict and correlate with XB strengths of halobenzene derivatives. To this end, bromobenzene is considered first. The replacement of Br by I is expected to strengthen the XB, which will be further amplified by the perfluorination of the phenyl ring, thus providing a wide range of halogen donor strengths. A variety of bases are considered of both N and O types. The N bases encompass all sp, sp2, and sp3 hybridizations. H2O and OMe2 are taken as O bases, followed by the carbonyl O of OCH2, OCHNH2, and N-methylacetamide, so as to monitor the effects of certain functional groups.

2. Results

The optimized geometries of several representative halogen-bonded complexes are displayed in Figure 1, where R refers to the distance from X, either Br or I, to the electron-donating N or O atom of the base. The principal properties of the various complexes are assembled in Table 1 and are organized as follows. The first section refers to Lewis acid bromobenzene PhBr, followed by iodobenzene PhI, and then perfluorinated iodobenzene PhF5I in the lowermost section. The internal C–X bond length of each Lewis acid monomer is reported, as well as its vibrational stretching frequency. Within each section, a series of bases are listed, first N-bases, followed by a variety of O-bases, where NMA refers to N-methylacetamide OCMeNHMe. For each acid–base pair, its interaction energy is displayed, along with the intermolecular distance and the AIM bond critical point density of the XB. The next two columns of Table 1 contain the change caused by the complexation in both the C–X bond length and its vibrational frequency. The final column reports the NMR intermolecular coupling constant between the halogen nucleus and the N or O electron donor atom.

2.1. Measures of Halogen Bond Strength

Bromobenzene engages in fairly weak XBs, with interaction energies all less than 3 kcal/mol. The sp-hybridization of the N in NCH provides the weakest bonding, less than 1 kcal/mol, which is enhanced in the sp2 hybridization of HN=NH and pyridine. The sp3 hybridization of NH3 and NMe3 leads to the strongest bonding, particularly in the latter, with its three electron-releasing methyl groups. This same electron donating property makes dimethylether a stronger base than water, and the O-bases collectively lead to XB energies between 1.3 and 2.6 kcal/mol. All of the XB energies rise as the Br atom of PhBr is replaced by the more polarizable and electropositive I atom, and a further boost is provided by adding five F substituents to the phenyl ring. The interaction energy range involving PhF5I is between 3.6 and 8.7 kcal/mol.
The intermolecular distances generally reflect the energetic trends. As the XBs strengthen, one sees a shortening of R(X··N/O). The shortest XB of all pairs is PhF5I with NMe3, with R(I··N) equal to 2.82 Å and an interaction energy of 8.7 kcal/mol. Given their usual tight correspondence with interatomic distance, it is not surprising that the intermolecular AIM bond critical point densities track closely with R. The smallest ρBCP of 0.0076 au refers to the weak PhBr··NCH complex with R(Br··N) = 3.26 Å, whereas the much shorter 2.82 Å XB in PhF5I··NMe3 rises up to 0.0199 au. It should be noted parenthetically that several of the complexes bear a second intermolecular bond path. Their densities which are contained in parentheses in Table 1 are fairly small, but not negligible, and they refer to weak H··X H-bonding interactions. Despite these secondary bond paths, the density of the primary X··N/O bond correlates modestly well with the overall interaction energy, as illustrated by the correlation diagram of Figure 2.
The next two columns of Table 1 are suggestive of the perturbing effect of each XB upon the internal C–X covalent bond of the Lewis acid. The weaker XBs tend to induce a small contraction in each such bond and a blue shift in its stretching frequency, i.e., positive Δν. As the bonds strengthen toward the bottom of the table, the pattern shifts toward stretches that are accompanied by red shifts. This reversal of bond characteristics has been explained recently [76] in similar systems in terms of the competition between two effects. While density shifts into the σ*(CX) antibonding orbital tend to weaken and elongate this bond, a contraction which deepens the σ-hole on X would be favored on energetic grounds. The former bond weakening wins this competition when there is a large charge transfer as occurs with the stronger XBs, while the smaller transfers in the weaker XBs allows the C–X contraction to gain the advantage. Other computations [48] have demonstrated there may be a close connection between the C–X bond length in small Lewis acid units such as F3CX and the amount by which its stretching frequency changes. Specifically regarding the frequencies, the reader is cautioned that the normal modes in these aromatic systems are not pure C–X stretching motions, but include varying amounts of other nuclear displacement, such as ring distortions. This contamination inhibits the close correspondence between internal bond length and stretching frequency. Indeed, other computations [77] have documented that a blue shift in certain small halogen-bonded complexes such as FCl··CH3 can result from a mixing of modes in the two molecules, rather than from electron density shifts.
The 4–6 cm−1 red shifts of the C–I stretch are consistent with prior calculations [73] and experimental measurements of the complexes between PhF5I and various N bases in solution [66] in the 7–14 cm−1 range. Another set of measurements considered the related C–I bond in heptafluoro-2-iodopropane [60] and observed red shifts between 4 and 7 cm−1 with aromatic N-bases, closely matching the range observed here for PhF5I. A frequency reduction of 19 cm−1 was measured when PhF5I was paired with a quinuclidine N base [78].
A number of other parameters related to the intermolecular bond strengths are collected in Table 2. The first four columns relate the total energy density, H, the potential energy density, V, the Laplacian of the density, and the ellipticity at the intermolecular bond critical point. The next column contains the density at the ring critical point at the approximate center of the ring, which provides a measure of the aromaticity. Another means of assessing this property is Egap, the difference in energy between the HOMO and LUMO, both of which are represented by the phenyl π-system. The final column lists E2, the NBO energetic measure of the charge transfer from the lone pair(s) of the electron donor O or N atom into the antibonding σ*(CX) orbital.
The total energy density is rather flat, being mostly positive but only slightly so. V is, of course, negative throughout but does not appear to be closely related to the interaction energy. The density Laplacian is fully positive, suggestive of a closed shell noncovalent interaction. The ellipticity seems to bounce around with no clear pattern. The density of the ring critical point of the phenyl ring shows little variation, around 0.024 for the phenyl system and somewhat lower, at 0.022, for the perfluorinated system. The HOMO–LUMO separation varies slightly more but with no clear association with halogen bond strength. E2, on the other hand, does appear to be closely connected to bond strength. In general, these quantities are poorly correlated with the interaction energy, with correlation coefficients less than 0.4. V and ∇2ρ are somewhat better, with R2 = 0.87 and 0.78, respectively. The parameter that shows a much stronger linear relationship with the interaction energy is E2, with a correlation coefficient of 0.90.

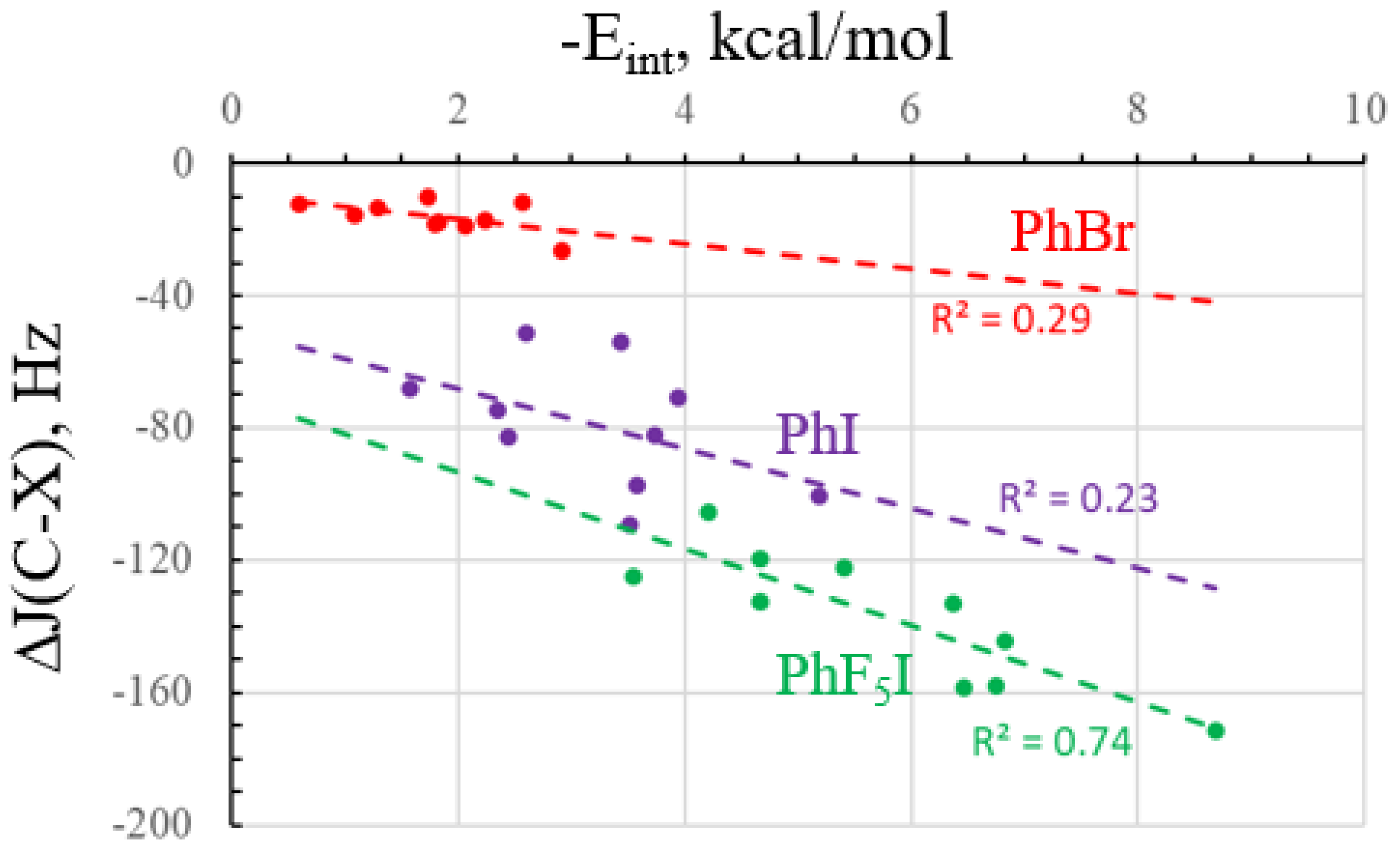
2.2. NMR Data

The last column of Table 1 lists the intermolecular coupling constant between the halogen nucleus and the N or O electron donor of the base. These quantities are positive and negative for N and O, respectively. Although there are indications in the literature [54] that these intermolecular coupling constants tend to correlate with bond strength for various sorts of noncovalent bonds, their magnitudes are only very broadly indicative of Eint. For example, J(I··N) drops from 278 to 218 Hz when the base coupled with PhI is switched out from NH3 to NMe3, despite the rise in interaction energy. This moderate to poor correlation has been observed previously for other CI XBs [79] and for the related pnicogen bonds [80].
The remaining NMR data for these monomers and their complexes are organized in Table 3 in much the same way as in Table 1. The first two columns contain the isotropic shielding of the halogen and the C atom to which it is attached within the Lewis acid. As may be seen in the first row of Table 3, this shielding is 2085.9 ppm for the Br of the PhBr monomer, which rises to 3103.7 and 3517.6 ppm for the I atom of PhI and PhF5I, respectively. The shielding of the neighboring C also rises in this same progression from 26.2 ppm in PhBr up to 73.3 ppm for PhF5I. Also presented in the last three columns are the coupling constants between the pertinent atoms of the acid. The coupling constant for the C–Br bond in PhBr is −67.0 Hz, rising in magnitude for the other two acids up to −270.7 Hz for PhF5I. J for the adjacent C–C pair that includes the C to which X is bonded is positive, between 80 and 105 Hz. That for the C–H/C–F bond that is ortho to the halogen atom is quite variable in sign. While J(CH) is positive at 170 Hz, the C–F coupling constant is quite negative at −300 Hz for the same ortho bond in PhF5I.
Of particular interest are the perturbations in these NMR spectroscopic quantities upon forming a XB with a base. These changes are listed in the ensuing rows of Table 3 and follow several interesting patterns. Both the X and its neighboring C are deshielded by the interaction to varying degrees. In the case of the X nucleus, Δσ does not strictly adhere to a close relationship with XB strength. The I nucleus of PhI, for example, experiences its smallest change for the very strong bond with NMe3, while its largest deshielding occurs for the strong XB with OCHNH2 and NMA. In contrast to the behavior of PhI, when in the context of the perfluorinated PhF5I acid, the strong bond with NMe3 results in a large deshielding of I.
The deshielding of the C atom conforms more closely to the trends of the XB strength, even if imperfectly. Taking PhI as an example, the C nucleus is deshielded by 4.3 ppm in the context of a weak bond with NCH, which builds as the N-base becomes more potent, up to 7.3 ppm with NMe3. The relationship with Eint is tighter for the perfluorinated acid, for which the C deshielding seems to represent a good indicator of bond strength. A similar sort of correlation was noted previously [74] for a host of substituents other than F when placed on the phenyl ring. It should be noted as well that this enhanced deshielding of the C nucleus conforms to a previous study [81] where a di-iodo perfluorinated benzene was complexed to several anions. The 7 ppm deshielding observed in these strong XBs lies sensibly on the upper range of those computed here for neutral pairs. A similar sort of deshielding accompanies the XB formation of perfluorohalobenzene [82] as well as in iodoalkynes [83]. The chemical shift in C atoms attached to I atoms has been catalogued [68], and the shielding drops as the XB strengthens and the internal C–I bond grows longer, with Δσ varying over a 20 ppm range, easily encompassing the changes of 10 ppm computed above. Another work [72] noted this C is deshielded by 6–7 ppm upon forming a CI··N XB, quite in line with the values computed here. Deshielding of the same magnitude occurs [81,84,85] with other fluorinated iodobenzenes. Deshielding of some 12 ppm has been noted in the acetylenic C≡C-I 13C spectrum [70,86], with even larger changes occasioned by the binding to anions [87].
The extent of this relationship is visualized in Figure 3, where a separate line is drawn for each of the three Lewis acids. The red points corresponding to PhBr, with its weak XBs, are rather scattered. The correlation coefficient is quite small, so this NMR parameter would be of little use as a yardstick of XB strength. The stronger XBs containing PhI cover a wider spread, up to 5.2 kcal/mol. The correlation of the purple points in Figure 3 is only marginally better, with R2 = 0.39, so the C chemical shift has only limited potential as a gauge of XB strength. The PhF5I acid spans an even wider range of energies, and the correlation coefficient is improved to 0.81. It would appear, therefore, that the ability of the C chemical shift to predict the XB energy is best for more potent Lewis acids that cover a wider range of bond strengths.
The coupling constants in the next three columns conform to their own patterns. The largest changes occur within the C–X bonds that interact directly with the base. These quantities are negative and become larger in magnitude as the interaction grows stronger, with certain exceptions. Taking the PhF5I acid as an example, the J(CI) coupling constant is −271 Hz. As each N base becomes a more potent nucleophile and yields a stronger XB, this quantity becomes larger in magnitude, swelling by 172 Hz up to −442 Hz for PhF5I··NMe3. These patterns are evident in Figure 4, which compares ΔJ(CX) with the interaction energy of each dyad. As for Δσ(C), the data for PhBr extends only over a limited range, so the correlation coefficient is poor, at only 0.29. There remains quite a bit of scatter for PhI and no improvement in R2. The best correlation is again found in the PhF5I systems, where R2 climbs to 0.74.
The changes in the other coupling constants are much less dramatic. J(CC) is in the neighborhood of 80–105 Hz and drops a small amount as the XB is formed, less than 2 Hz. There does appear to be a certain correlation, albeit a weak one, between this decrease in J and the XB strength. The coupling constant of the ortho CH/CF bond is about 170 Hz for PhBr and PhI, but a strongly negative −300 Hz for perfluorosubstituted PhF5I. In each case, the formation of the XB reduces the magnitude of J. This drop is roughly 1–2 Hz for the first two acids but enlarges to 3–7 Hz for PhF5I.
Like the other coupling constants, J(CH/CF) bears a relation to XB bond strength, but not a highly quantitative one. As is evident in Figure 5, the correlation coefficients range from 0.31 for PhBr up to a maximum of 0.67 for PhI. In the case of this particular parameter, its association with Eint is poorer for the stronger PhF5I acid. The values of these changes in J(CF) are right in line with changes of 2–4 Hz measured in an earlier study [75].
An earlier examination of the correlations between noncovalent bond strength and spectroscopic features [53] was limited to very small Lewis acids, such as the diatomic FX in the case of halogen bonds. Without the complication of impurity of the F–X stretching frequency arising in a larger molecule such as PhX, linear relationships were found between Eint and Δν(FX) with correlation coefficients exceeding 0.9. As noted here, for the larger acids, the relationship with the change in shielding on the X atom was much poorer, at less than 0.7. This work also considered σ-hole bonds other than XBs, but again with small acids such as FHSe and FH2As, with similar findings. Other calculations [45] focused on the changes in the IR and NMR spectra resulting from modifications within the acid, keeping the base fixed, and again with small acid molecules. The shift in the X–F bond stretching vibrational frequency diminished as the X atom grew heavier, attributed to this increased mass. In the case of these small FX diatomics, the formation of the XB induced a rise in the X chemical shielding as compared to the reductions observed here for the much larger aromatic systems, with their CX bonds. The replacement of the NH3 base by the larger O-base NMA [46] left many of these patterns intact, again limited to the small FX diatomics.

3. Methods

Quantum chemical calculations were performed via the density functional approach (DFT) within the context of the M06-2X functional [88], which has been shown to be an accurate means of treating noncovalent bonds of the sort of interest here [89,90,91,92,93,94,95,96,97,98,99]. A polarized triple-ζ def2-TZVP basis set was chosen so as to afford a large and flexible set. Geometries were fully optimized and verified as true minima by the absence of imaginary vibrational frequencies. The Gaussian 16 [100] program was chosen as the specific means to conduct these computations.
The interaction energy Eint of each dyad was calculated as the difference between the energy of the complex and the sum of the energies of the two constituent subunits, each in the geometry they adopt within the dimer. The counterpoise procedure [101] was applied to correct the basis set superposition error of Eint. Atoms in molecules (AIM) bond paths and their associated critical points were located and their densities evaluated with the aid of the AIMAll program [102]. NMR properties were assessed by the application of the GIAO approach [103,104,105]. In order to allow adjustment of core orbitals to complexation, the def2-TZVP pseudopotential of I was bypassed in the associated NMR calculations, applying instead the all-electron Sapporo-DKH3-TZP-2012-diffuse set [106,107], designed to include certain relativistic effects.

4. Conclusions

As has been noted on multiple occasions in the past, the AIM bond critical point density scales closely with halogen bond strength, as well as the intermolecular distance. Analysis of the vibrational normal modes shows a significant mixing of the C–X stretching motion with other nuclear displacements such as phenyl ring distortion. The weakest of the halogen bonds display a C–X bond contraction coupled with a blue shift in the associated frequency, whereas the reverse trends occur for the stronger bonds. The intermolecular X··N/O NMR coupling constant is only partially related to XB strength, with numerous disagreements from one complex to the next. There is better agreement arising from certain internal NMR quantities. The correlation between Eint and the shielding change occurring on the C atom bonded to X is poor for the weaker XBs involving PhBr but improves considerably for the stronger XBs involving I, particularly PhF5I. The internal C–X coupling constant is likewise best for the most potent Lewis acid, forming the strongest XBs. The coupling constant between the C lying ortho to X and its substituent, whether H or F, also correlates with the XB energy, although not with quantitative accuracy.

Author Contributions

Conceptualization, S.S.; methodology, S.S. and A.A.; validation, S.S.; formal analysis, A.A.; data curation, A.A.; writing-original draft preparation, A.A.; writing-review and editing, S.S. supervision, S.S.; funding acquisition, S.S.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the U.S. National Science Foundation, grant number No. 1954310.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pimentel, G.C.; McClellan, A.L. The Hydrogen Bond; Freeman: San Francisco, CA, USA, 1960. [Google Scholar]
  2. Hamilton, W.C.; Ibers, J.A. Hydrogen Bonding in Solids; W. A. Benjamin: New York, NY, USA, 1968; p. 284. [Google Scholar]
  3. Latajka, Z.; Bouteiller, Y.; Scheiner, S. Critical assessment of density functional methods for study of proton transfer processes. (FHF)−. Chem. Phys. Lett. 1995, 234, 159–164. [Google Scholar] [CrossRef]
  4. Joesten, M.D.; Schaad, L.J. Hydrogen Bonding; Marcel Dekker: New York, NY, USA, 1974; p. 622. [Google Scholar]
  5. Latajka, Z.; Scheiner, S. Ab initio comparison of H bonds and Li bonds. Complexes of LiF, LiCl, HF, and HCl with NH3. J. Chem. Phys. 1984, 81, 4014–4017. [Google Scholar] [CrossRef]
  6. Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond in Structural Chemistry and Biology; Oxford: New York, NY, USA, 1999; p. 507. [Google Scholar]
  7. Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond; Oxford University Press: Oxford, UK, 2009; p. 313. [Google Scholar]
  8. Luth, K.; Scheiner, S. Excited-state energetics and proton-transfer barriers in malonaldehyde. J. Phys. Chem. 1994, 98, 3582–3587. [Google Scholar] [CrossRef]
  9. Scheiner, S. Hydrogen Bonding: A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997; p. 375. [Google Scholar]
  10. Gleiter, R.; Werz, D.B.; Rausch, B.J. A World Beyond Hydrogen Bonds?—Chalcogen–Chalcogen Interactions Yielding Tubular Structures. Chem. Eur. J. 2003, 9, 2676–2683. [Google Scholar] [CrossRef] [PubMed]
  11. Bleiholder, C.; Werz, D.B.; Koppel, H.; Gleiter, R. Theoretical investigations on chalcogen-chalcogen interactions: What makes these nonbonded interactions bonding? J. Am. Chem. Soc. 2006, 128, 2666–2674. [Google Scholar] [CrossRef] [PubMed]
  12. Bauzá, A.; Quiñonero, D.; Deyà, P.M.; Frontera, A. Halogen bonding versus chalcogen and pnicogen bonding: A combined Cambridge structural database and theoretical study. CrystEngComm 2013, 15, 3137–3144. [Google Scholar] [CrossRef]
  13. Fanfrlík, J.; Přáda, A.; Padělková, Z.; Pecina, A.; Macháček, J.; Lepšík, M.; Holub, J.; Růžička, A.; Hnyk, D.; Hobza, P. The Dominant Role of Chalcogen Bonding in the Crystal Packing of 2D/3D Aromatics. Angew. Chem. Int. Ed. 2014, 53, 10139–10142. [Google Scholar] [CrossRef]
  14. Alikhani, E.; Fuster, F.; Madebene, B.; Grabowski, S.J. Topological reaction sites—Very strong chalcogen bonds. Phys. Chem. Chem. Phys. 2014, 16, 2430–2442. [Google Scholar] [CrossRef]
  15. Trujillo, C.; Sanchez-Sanz, G.; Alkorta, I.; Elguero, J. Halogen, chalcogen and pnictogen interactions in (XNO2)2 homodimers (X = F, Cl, Br, I). New J. Chem. 2015, 39, 6791–6802. [Google Scholar] [CrossRef]
  16. Galmés, B.; Juan-Bals, A.; Frontera, A.; Resnati, G. Charge-Assisted Chalcogen Bonds: CSD and DFT Analyses and Biological Implication in Glucosidase Inhibitors. Chem. Eur. J. 2020, 26, 4599–4606. [Google Scholar] [CrossRef]
  17. Jungbauer, S.H.; Huber, S.M. Cationic Multidentate Halogen-Bond Donors in Halide Abstraction Organocatalysis: Catalyst Optimization by Preorganization. J. Am. Chem. Soc. 2015, 137, 12110–12120. [Google Scholar] [CrossRef] [PubMed]
  18. Chakraborty, S.; Maji, S.; Ghosh, R.; Jana, R.; Datta, A.; Ghosh, P. Aryl-platform-based tetrapodal 2-iodo-imidazolium as an excellent halogen bond receptor in aqueous medium. Chem. Commun. 2019, 55, 1506–1509. [Google Scholar] [CrossRef]
  19. Scheiner, S. Comparison of halide receptors based on H, halogen, chalcogen, pnicogen, and tetrel bonds. Faraday Disc. 2017, 203, 213–226. [Google Scholar] [CrossRef]
  20. Bauzá, A.; Mooibroek, T.J.; Frontera, A. σ-Hole Opposite to a Lone Pair: Unconventional Pnicogen Bonding Interactions between ZF3 (Z=N, P, As, and Sb) Compounds and Several Donors. ChemPhysChem 2016, 17, 1608–1614. [Google Scholar] [CrossRef]
  21. Bauzá, A.; Quiñonero, D.; Deyà, P.M.; Frontera, A. Pnicogen–π complexes: Theoretical study and biological implications. Phys. Chem. Chem. Phys. 2012, 14, 14061–14066. [Google Scholar] [CrossRef]
  22. Grabowski, S.J. Pnicogen and tetrel bonds—Tetrahedral Lewis acid centres. Struct. Chem. 2019, 30, 1141–1152. [Google Scholar]
  23. Alkorta, I.; Elguero, J.; Grabowski, S.J. Pnicogen and hydrogen bonds: Complexes between PH3X+ and PH2X systems. Phys. Chem. Chem. Phys. 2015, 17, 3261–3272. [Google Scholar] [CrossRef] [PubMed]
  24. Moaven, S.; Andrews, M.C.; Polaske, T.J.; Karl, B.M.; Unruh, D.K.; Bosch, E.; Bowling, N.P.; Cozzolino, A.F. Triple-Pnictogen Bonding as a Tool for Supramolecular Assembly. Inorg. Chem. 2019, 58, 16227–16235. [Google Scholar] [CrossRef]
  25. Scheiner, S. Origins and properties of the tetrel bond. Phys. Chem. Chem. Phys. 2021, 23, 5702–5717. [Google Scholar] [CrossRef]
  26. Adhikari, U.; Scheiner, S. Effects of carbon chain substituent on the P···N noncovalent bond. Chem. Phys. Lett. 2012, 536, 30–33. [Google Scholar] [CrossRef]
  27. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
  28. Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. σ-Holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef]
  29. Mertsalov, D.F.; Gomila, R.M.; Zaytsev, V.P.; Grigoriev, M.S.; Nikitina, E.V.; Zubkov, F.I.; Frontera, A. On the Importance of Halogen Bonding Interactions in Two X-ray Structures Containing All Four (F, Cl, Br, I) Halogen Atoms. Crystals 2021, 11, 1406. [Google Scholar] [CrossRef]
  30. Palusiak, M.; Grabowski, S.J. Do intramolecular halogen bonds exist? Ab initio calculations and crystal structures’ evidences. Struct. Chem. 2008, 19, 5–11. [Google Scholar] [CrossRef]
  31. Kolár, M.; Hostaš, J.; Hobza, P. The strength and directionality of a halogen bond are co-determined by the magnitude and size of the σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 9987–9996. [Google Scholar] [CrossRef]
  32. Cunha, A.V.; Havenith, R.W.A.; van Gog, J.; De Vleeschouwer, F.; De Proft, F.; Herrebout, W. The Halogen Bond in Weakly Bonded Complexes and the Consequences for Aromaticity and Spin-Orbit Coupling. Molecules 2023, 28, 772. [Google Scholar] [CrossRef] [PubMed]
  33. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
  34. Scheiner, S. Sensitivity of Noncovalent Bonds to Intermolecular Separation: Hydrogen, Halogen, Chalcogen, and Pnicogen Bonds. CrystEngComm 2013, 15, 3119–3124. [Google Scholar] [CrossRef]
  35. Joesten, M.D.; Drago, R.S. The Validity of Frequency Shift-Enthalpy Correlations. I. Adducts of Phenol with Nitrogen and Oxygen Donors. J. Am. Chem. Soc. 1962, 84, 3817–3821. [Google Scholar] [CrossRef]
  36. Drago, R.S.; Epley, T.D. Enthalpies of hydrogen bonding and changes in hydroxy frequency shifts for a series of adducts with substituted phenols. J. Am. Chem. Soc. 1969, 91, 2883–2890. [Google Scholar] [CrossRef]
  37. Rozenberg, M.; Loewenschuss, A.; Marcus, Y. An empirical correlation between stretching vibration redshift and hydrogen bond length. Phys. Chem. Chem. Phys. 2000, 2, 2699–2702. [Google Scholar] [CrossRef]
  38. Rao, C.N.R.; Dwivedi, P.C.; Ratajczak, H.; Orville-Thomas, W.J. Relation between O–H stretching frequency and hydrogen bond energy: Re-examination of the Badger–Bauer rule. J. Chem. Soc. Faraday Trans. 2 1975, 71, 955–966. [Google Scholar] [CrossRef]
  39. Ellington, T.L.; Reves, P.L.; Simms, B.L.; Wilson, J.L.; Watkins, D.L.; Tschumper, G.S.; Hammer, N.I. Quantifying the Effects of Halogen Bonding by Haloaromatic Donors on the Acceptor Pyrimidine. ChemPhysChem 2017, 18, 1267–1273. [Google Scholar] [CrossRef] [PubMed]
  40. Attrell, R.J.; Widdifield, C.M.; Korobkov, I.; Bryce, D.L. Weak Halogen Bonding in Solid Haloanilinium Halides Probed Directly via Chlorine-35, Bromine-81, and Iodine-127 NMR Spectroscopy. Cryst. Growth Des. 2012, 12, 1641–1653. [Google Scholar] [CrossRef]
  41. Amonov, A.; Scheiner, S. Heavy pnicogen atoms as electron donors in sigma-hole bonds. Phys. Chem. Chem. Phys. 2023, 25, 23530–23537. [Google Scholar] [CrossRef]
  42. Amonov, A.; Scheiner, S. Competition between Binding to Various Sites of Substituted Imidazoliums. J. Phys. Chem. A 2023, 127, 6292–6299. [Google Scholar] [CrossRef]
  43. Alkorta, I.; Rozas, S.; Elguero, J. Charge-transfer complexes between dihalogen compounds and electron donors. J. Phys. Chem. A 1998, 102, 9278–9285. [Google Scholar] [CrossRef]
  44. Ford, T.A. An ab initio study of some halogen-bonded complexes containing cyclic ethers. Mol. Phys. 2021, 119, e1919326. [Google Scholar] [CrossRef]
  45. Lu, J.; Scheiner, S. Effects of Halogen, Chalcogen, Pnicogen, and Tetrel Bonds on IR and NMR Spectra. Molecules 2019, 24, 2822. [Google Scholar] [CrossRef]
  46. Michalczyk, M.; Zierkiewicz, W.; Wysokiński, R.; Scheiner, S. Theoretical Studies of IR and NMR Spectral Changes Induced by Sigma-Hole Hydrogen, Halogen, Chalcogen, Pnicogen, and Tetrel Bonds in a Model Protein Environment. Molecules 2019, 24, 3329. [Google Scholar] [CrossRef]
  47. Parra, R.D.; Grabowski, S.J. Enhancing Effects of the Cyano Group on the C-X…N Hydrogen or Halogen Bond in Complexes of X-Cyanomethanes with Trimethyl Amine: CH3−n(CN)nX…NMe3, (n = 0–3; X = H, Cl, Br, I). Int. J. Mol. Sci. 2022, 23, 11289. [Google Scholar] [CrossRef]
  48. Wang, W.; Zhang, Y.; Ji, B.; Tian, A. On the correlation between bond-length change and vibrational frequency shift in halogen-bonded complexes. J. Chem. Phys. 2011, 134, 224303. [Google Scholar] [CrossRef] [PubMed]
  49. Zhou, Z.-J.; Liu, H.-L.; Huang, X.-R.; Li, Q.-Z.; Sun, C.-C. Effect of substitution and cooperativity on the Cl–F blue shift in single-electron halogen-bonded H3C ··· ClF complex. Mol. Phys. 2010, 108, 2021–2026. [Google Scholar] [CrossRef]
  50. Xu, Y.; Gabidullin, B.; Bryce, D.L. Single-Crystal NMR Characterization of Halogen Bonds. J. Phys. Chem. A 2019, 123, 6194–6209. [Google Scholar] [CrossRef] [PubMed]
  51. Alkorta, I.; Elguero, J.; Yáñez, M.; Mó, O.; Montero-Campillo, M.M. Relativistic Effects on NMR Parameters of Halogen-Bonded Complexes. Molecules 2019, 24, 4399. [Google Scholar] [CrossRef]
  52. Karpfen, A. Charge-transfer complexes between NH3 and the halogens F2, ClF, and Cl2: An ab initio study on the intermolecular interaction. J. Phys. Chem. A 2000, 104, 6871–6879. [Google Scholar] [CrossRef]
  53. Lu, J.; Scheiner, S. Relationships between Bond Strength and Spectroscopic Quantities in H-Bonds and Related Halogen, Chalcogen, and Pnicogen Bonds. J. Phys. Chem. A 2020, 124, 7716–7725. [Google Scholar] [CrossRef]
  54. Jaźwiński, J. Chapter One—Indirect spin-spin coupling constants across noncovalent bonds. In Annual Reports on NMR Spectroscopy; Webb, G.A., Ed.; Academic Press: Cambridge, MA, USA, 2021; Volume 104, pp. 1–73. [Google Scholar]
  55. Del Bene, J.E.; Alkorta, I.; Elguero, J. Probing the structures, binding energies, and spin-spin coupling constants of halogen-bonded Azine:ClF complexes. Chem. Phys. Lett. 2020, 761, 137916. [Google Scholar] [CrossRef]
  56. Scheiner, S. Characterization of Type I and II Interactions between Halogen Atoms. Cryst. Growth Des. 2022, 22, 2692–2702. [Google Scholar] [CrossRef]
  57. Alkorta, I.; Sanchez-Sanz, G.; Elguero, J. Linear free energy relationships in halogen bonds. CrystEngComm 2013, 15, 3178–3186. [Google Scholar] [CrossRef]
  58. Tang, Q.; Li, Q. Non-additivity of F substituent in enhancing the halogen bond in C6H5I…NCH. Comput. Theor. Chem. 2015, 1070, 21–26. [Google Scholar] [CrossRef]
  59. Margiotta, E.; van der Lubbe, S.C.C.; de Azevedo Santos, L.; Paragi, G.; Moro, S.; Bickelhaupt, F.M.; Fonseca Guerra, C. Halogen Bonds in Ligand–Protein Systems: Molecular Orbital Theory for Drug Design. J. Chem. Infor. Model. 2020, 60, 1317–1328. [Google Scholar] [CrossRef] [PubMed]
  60. Lambert, E.C.; Williams, A.E.; Fortenberry, R.C.; Hammer, N.I. Probing halogen bonding interactions between heptafluoro-2-iodopropane and three azabenzenes with Raman spectroscopy and density functional theory. Phys. Chem. Chem. Phys. 2022, 24, 11713–11720. [Google Scholar] [CrossRef] [PubMed]
  61. Côté, M.; Ovens, J.S.; Bryce, D.L. Anticooperativity and Competition in Some Cocrystals Featuring Iodine-Nitrogen Halogen Bonds. Chem. Asian J. 2023, 18, e202201221. [Google Scholar] [CrossRef]
  62. Toikka, Y.N.; Starova, G.L.; Suslonov, V.V.; Gomila, R.M.; Frontera, A.; Kukushkin, V.Y.; Bokach, N.A. Combined σ- and π-Hole Donor Properties of Perfluorinated Iodo(or bromo)benzenes: Halogen Bonding and π-Hole Interactions in Cocrystals Including Cu4I4 Clusters. Cryst. Growth Des. 2023, 23, 5194–5203. [Google Scholar] [CrossRef]
  63. Tsuzuki, S.; Uchimaru, T.; Wakisaka, A.; Ono, T. Magnitude and Directionality of Halogen Bond of Benzene with C6F5X, C6H5X, and CF3X (X = I, Br, Cl, and F). J. Phys. Chem. A 2016, 120, 7020–7029. [Google Scholar] [CrossRef]
  64. Stoesser, J.; Rojas, G.; Bulfield, D.; Hidalgo, P.I.; Pasan, J.; Ruiz-Perez, C.; Jimenez, C.A.; Huber, S.M. Halogen bonding two-point recognition with terphenyl derivatives. New J. Chem. 2018, 42, 10476–10480. [Google Scholar] [CrossRef]
  65. Dang, Q.M.; Simpson, J.H.; Parish, C.A.; Leopold, M.C. Evaluating Halogen-Bond Strength as a Function of Molecular Structure Using Nuclear Magnetic Resonance Spectroscopy and Computational Analysis. J. Phys. Chem. A 2021, 125, 9377–9393. [Google Scholar] [CrossRef]
  66. Bramlett, T.A.; Matzger, A.J. Halogen Bonding Propensity in Solution: Direct Observation and Computational Prediction. Chem. Eur. J. 2021, 27, 15472–15478. [Google Scholar] [CrossRef]
  67. Grabowski, S.J. Halogen Bonds between Diiodotetrafluorobenzenes and Halide Anions: Theoretical Analysis. Cryst. Growth Des. 2023, 23, 489–500. [Google Scholar] [CrossRef]
  68. Vioglio, P.C.; Chierotti, M.R.; Gobetto, R. Solid-state nuclear magnetic resonance as a tool for investigating the halogen bond. CrystEngComm 2016, 18, 9173–9184. [Google Scholar] [CrossRef]
  69. Gao, K.; Goroff, N.S. Two New Iodine-Capped Carbon Rods. J. Am. Chem. Soc. 2000, 122, 9320–9321. [Google Scholar] [CrossRef]
  70. Rege, P.D.; Malkina, O.L.; Goroff, N.S. The Effect of Lewis Bases on the 13C NMR of Iodoalkynes. J. Am. Chem. Soc. 2002, 124, 370–371. [Google Scholar] [CrossRef] [PubMed]
  71. Webb, J.A.; Klijn, J.E.; Hill, P.A.; Bennett, J.L.; Goroff, N.S. Experimental Studies of the 13C NMR of Iodoalkynes in Lewis-Basic Solvents. J. Org. Chem. 2004, 69, 660–664. [Google Scholar] [CrossRef]
  72. Popa, M.M.; Man, I.C.; Draghici, C.; Shova, S.; Caira, M.R.; Dumitrascu, F.; Dumitrescu, D. Halogen bonding in 5-iodo-1-arylpyrazoles investigated in the solid state and predicted by solution 13C-NMR spectroscopy. CrystEngComm 2019, 21, 7085–7093. [Google Scholar] [CrossRef]
  73. Lapp, J.; Scheiner, S. Proximity Effects of Substituents on Halogen Bond Strength. J. Phys. Chem. A 2021, 125, 5069–5077. [Google Scholar] [CrossRef]
  74. Scheiner, S.; Hunter, S. Influence of Substituents in the Benzene Ring on the Halogen Bond of Iodobenzene with Ammonia. ChemPhysChem 2022, 23, e202200011. [Google Scholar] [CrossRef] [PubMed]
  75. Jimmink, B.; Sethio, D.; Turunen, L.; von der Heiden, D.; Erdélyi, M. Probing Halogen Bonds by Scalar Couplings. J. Am. Chem. Soc. 2021, 143, 10695–10699. [Google Scholar] [CrossRef] [PubMed]
  76. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  77. Kříž, K.; Řezáč, J. Non-covalent interactions atlas benchmark data sets 4: σ-hole interactions. Phys. Chem. Chem. Phys. 2022, 24, 14794–14804. [Google Scholar] [CrossRef]
  78. Boese, A.D. Density Functional Theory and Hydrogen Bonds: Are We There Yet? ChemPhysChem. 2015, 16, 978–985. [Google Scholar] [CrossRef] [PubMed]
  79. Kozuch, S.; Martin, J.M.L. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef] [PubMed]
  80. Walker, M.; Harvey, A.J.A.; Sen, A.; Dessent, C.E.H. Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. J. Phys. Chem. A 2013, 117, 12590–12600. [Google Scholar] [CrossRef]
  81. Thanthiriwatte, K.S.; Hohenstein, E.G.; Burns, L.A.; Sherrill, C.D. Assessment of the performance of DFT and DFT-D methods for describing distance dependence of hydrogen-bonded interactions. J. Chem. Theory Comput. 2011, 7, 88–96. [Google Scholar] [CrossRef]
  82. Liao, M.S.; Lu, Y.; Scheiner, S. Performance assessment of density-functional methods for study of charge-transfer complexes. J. Comput. Chem. 2003, 24, 623–631. [Google Scholar] [CrossRef] [PubMed]
  83. Deible, M.J.; Tuguldur, O.; Jordan, K.D. Theoretical Study of the Binding Energy of a Methane Molecule in a (H2O)20 Dodecahedral Cage. J. Phys. Chem. B 2014, 118, 8257–8263. [Google Scholar] [CrossRef]
  84. Li, A.; Muddana, H.S.; Gilson, M.K. Quantum Mechanical Calculation of Noncovalent Interactions: A Large-Scale Evaluation of PMx, DFT, and SAPT Approaches. J. Chem. Theory Comput. 2014, 10, 1563–1575. [Google Scholar] [CrossRef]
  85. Mardirossian, N.; Head-Gordon, M. Characterizing and Understanding the Remarkably Slow Basis Set Convergence of Several Minnesota Density Functionals for Intermolecular Interaction Energies. J. Chem. Theory Comput. 2013, 9, 4453–4461. [Google Scholar] [CrossRef]
  86. Elm, J.; Bildeb, M.; Mikkelsena, K.V. Assessment of binding energies of atmospherically relevant clusters. Phys. Chem. Chem. Phys. 2013, 15, 16442–16445. [Google Scholar] [CrossRef]
  87. Bhattacharyya, S.; Bhattacherjee, A.; Shirhatti, P.R.; Wategaonkar, S. O–H···S Hydrogen Bonds Conform to the Acid–Base Formalism. J. Phys. Chem. A 2013, 117, 8238–8250. [Google Scholar] [CrossRef]
  88. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  89. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  90. Keith, T.A. AIMAll; TK Gristmill Software: Overland Park, KS, USA, 2013. [Google Scholar]
  91. Ditchfield, R. GIAO studies of magnetic shielding in FHF− and HF. Chem. Phys. Lett. 1976, 40, 53–56. [Google Scholar] [CrossRef]
  92. Hinton, J.F.; Wolinski, K. Ab initio GIAO magnetic shielding tensor for hydrogen-bonded systems. In Theoretical Treatments of Hydrogen Bonding; Hadzi, D., Ed.; John Wiley: Chichester, UK, 1997; pp. 75–93. [Google Scholar]
  93. Alkorta, I.; Elguero, J. Ab initio (GIAO) calculations of absolute nuclear shieldings for representative compounds containing 1(2)H, 6(7)Li, 11B, 13C, 14(15)N, 17O, 19F, 29Si, 31P, 33S, and 35Cl nuclei. Struct. Chem. 1998, 9, 187–202. [Google Scholar] [CrossRef]
  94. Noro, T.; Sekiya, M.; Koga, T. Segmented contracted basis sets for atoms H through Xe: Sapporo-(DK)-nZP sets (n = D, T, Q). Theor. Chem. Acc. 2012, 131, 1124. [Google Scholar] [CrossRef]
  95. Noro, T.; Sekiya, M.; Koga, T. Sapporo-(DKH3)-nZP (n = D, T, Q) sets for the sixth period s-, d-, and p-block atoms. Theor. Chem. Acc. 2013, 132, 1363. [Google Scholar] [CrossRef]
  96. Michalczyk, M.; Kizior, B.; Zierkiewicz, W.; Scheiner, S. Factors contributing to halogen bond strength and stretch or contraction of internal covalent bond. Phys. Chem. Chem. Phys. 2023, 25, 2907–2915. [Google Scholar] [CrossRef]
  97. Raghavendra, B.; Arunan, E. Unpaired and bond electrons as H, Cl, and Li bond acceptors: An anomalous one-electron blue-shifting chlorine. J. Phys. Chem. A 2007, 111, 9699–9706. [Google Scholar] [CrossRef]
  98. Otte, F.; Kleinheider, J.; Grabe, B.; Hiller, W.; Busse, F.; Wang, R.; Kreienborg, N.M.; Merten, C.; Englert, U.; Strohmann, C. Gauging the Strength of the Molecular Halogen Bond via Experimental Electron Density and Spectroscopy. ACS Omega 2023, 8, 21531–21539. [Google Scholar] [CrossRef]
  99. Zhang, Y.; Ji, B.; Tian, A.; Wang, W. Competition between π…π interaction and halogen bond in solution: A combined 13C NMR and density functional theory study. J. Chem. Phys. 2012, 136, 141101. [Google Scholar] [CrossRef]
  100. Del Bene, J.E.; Alkorta, I.; Sanchez-Sanz, G.; Elguero, J. Structures, energies, bonding, and NMR properties of pnicogen complexes H2XP:NXH2 (X = H, CH3, NH2, OH, F, Cl). J. Phys. Chem. A 2011, 115, 13724–13731. [Google Scholar] [CrossRef]
  101. Viger-Gravel, J.; Leclerc, S.; Korobkov, I.; Bryce, D.L. Correlation between 13C chemical shifts and the halogen bonding environment in a series of solid para-diiodotetrafluorobenzene complexes. CrystEngComm 2013, 15, 3168–3177. [Google Scholar] [CrossRef]
  102. Ma, N.; Zhang, Y.; Ji, B.; Tian, A.; Wang, W. Structural competition between halogen bonds and lone-pair..π interactions in solution. ChemPhysChem 2012, 13, 1411–1414. [Google Scholar] [CrossRef]
  103. Moss, W.N.; Goroff, N.S. Theoretical Analysis of the 13C NMR of Iodoalkynes upon Complexation with Lewis Bases. J. Org. Chem. 2005, 70, 802–808. [Google Scholar] [CrossRef] [PubMed]
  104. Widdifield, C.M.; Cavallo, G.; Facey, G.A.; Pilati, T.; Lin, J.; Metrangolo, P.; Resnati, G.; Bryce, D.L. Multinuclear Solid-State Magnetic Resonance as a Sensitive Probe of Structural Changes upon the Occurrence of Halogen Bonding in Co-crystals. Chem. Eur. J. 2013, 19, 11949–11962. [Google Scholar] [CrossRef] [PubMed]
  105. Cerreia Vioglio, P.; Catalano, L.; Vasylyeva, V.; Nervi, C.; Chierotti, M.R.; Resnati, G.; Gobetto, R.; Metrangolo, P. Natural Abundance 15N and 13C Solid-State NMR Chemical Shifts: High Sensitivity Probes of the Halogen Bond Geometry. Chem. Eur. J. 2016, 22, 16819–16828. [Google Scholar] [CrossRef] [PubMed]
  106. Morin, V.M.; Szell, P.M.J.; Caron-Poulin, E.; Gabidullin, B.; Bryce, D.L. Mechanochemical Preparations of Anion Coordinated Architectures Based on 3-Iodoethynylpyridine and 3-Iodoethynylbenzoic Acid. ChemistryOpen 2019, 8, 1328–1336. [Google Scholar] [CrossRef]
  107. Szell, P.M.J.; Cavallo, G.; Terraneo, G.; Metrangolo, P.; Gabidullin, B.; Bryce, D.L. Comparing the Halogen Bond to the Hydrogen Bond by Solid-State NMR Spectroscopy: Anion Coordinated Dimers from 2- and 3-Iodoethynylpyridine Salts. Chem. Eur. J. 2018, 24, 11364–11376. [Google Scholar] [CrossRef]
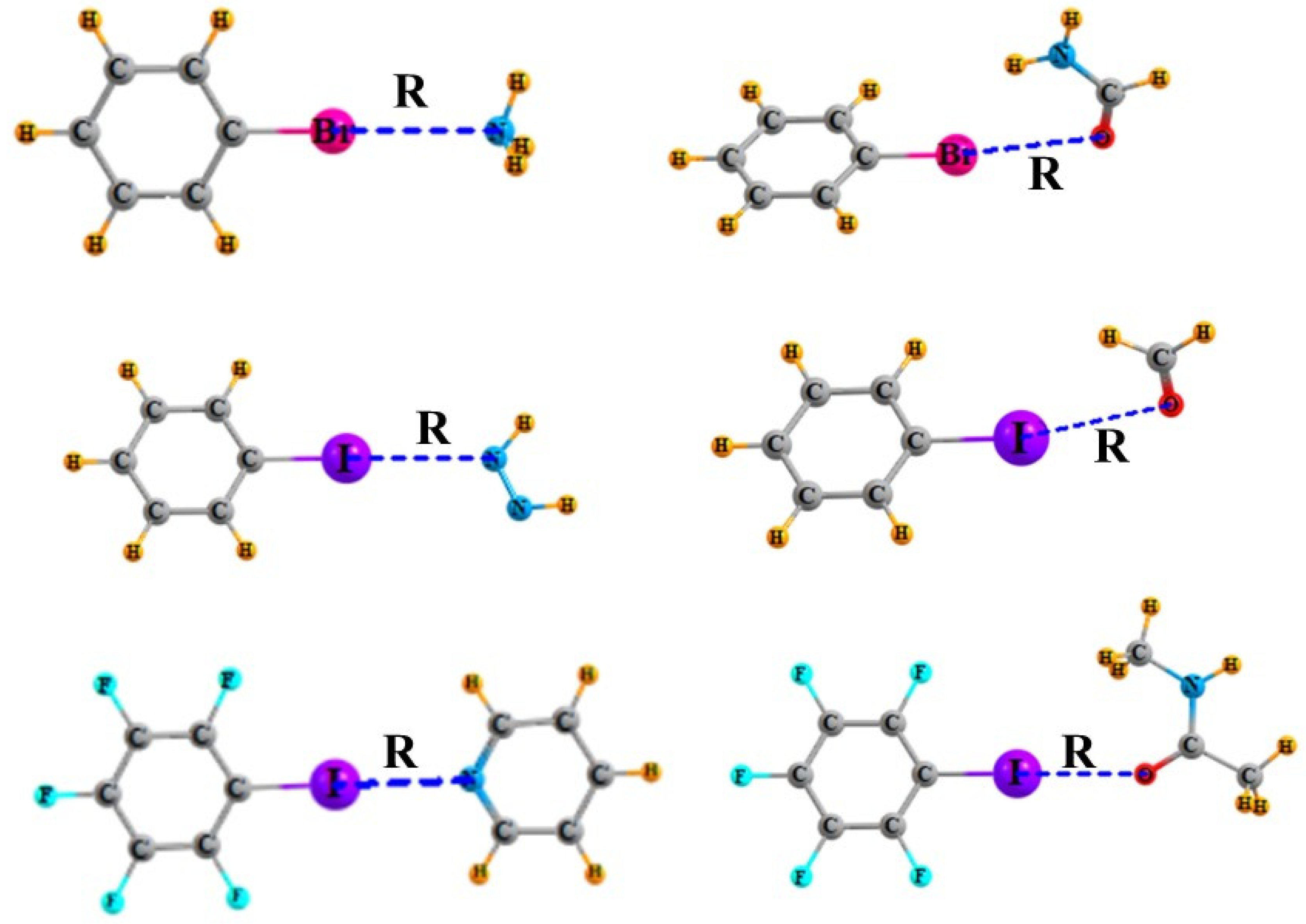
Molecules 28 07520 g001
Figure 1. Optimized geometries of several representative complexes. R refers to halogen bond length R(N/O···X).
Figure 1. Optimized geometries of several representative complexes. R refers to halogen bond length R(N/O···X).
Molecules 28 07520 g001
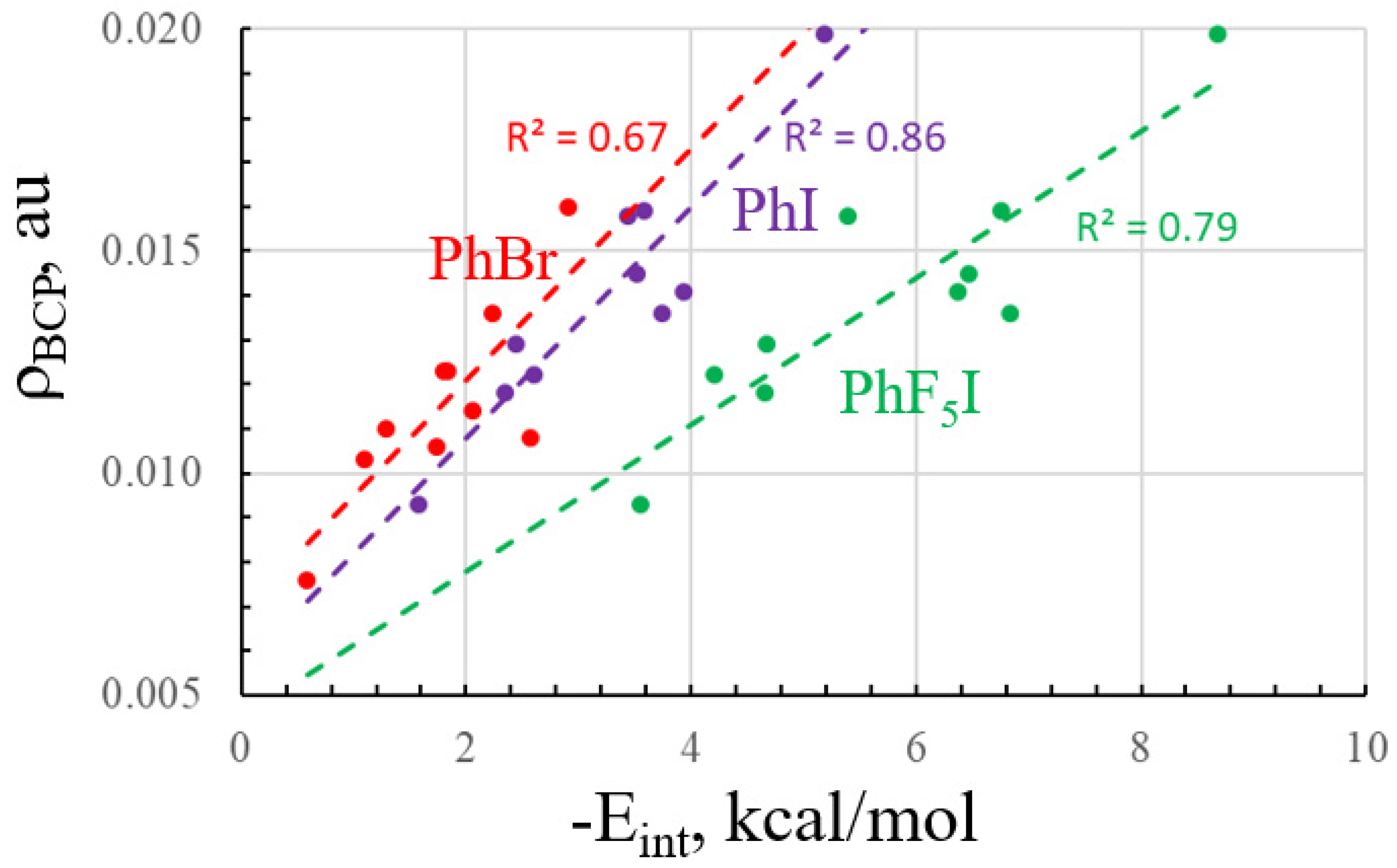
Molecules 28 07520 g002
Figure 2. Relationship between interaction energy and X··N/O BCP density.
Figure 2. Relationship between interaction energy and X··N/O BCP density.
Molecules 28 07520 g002
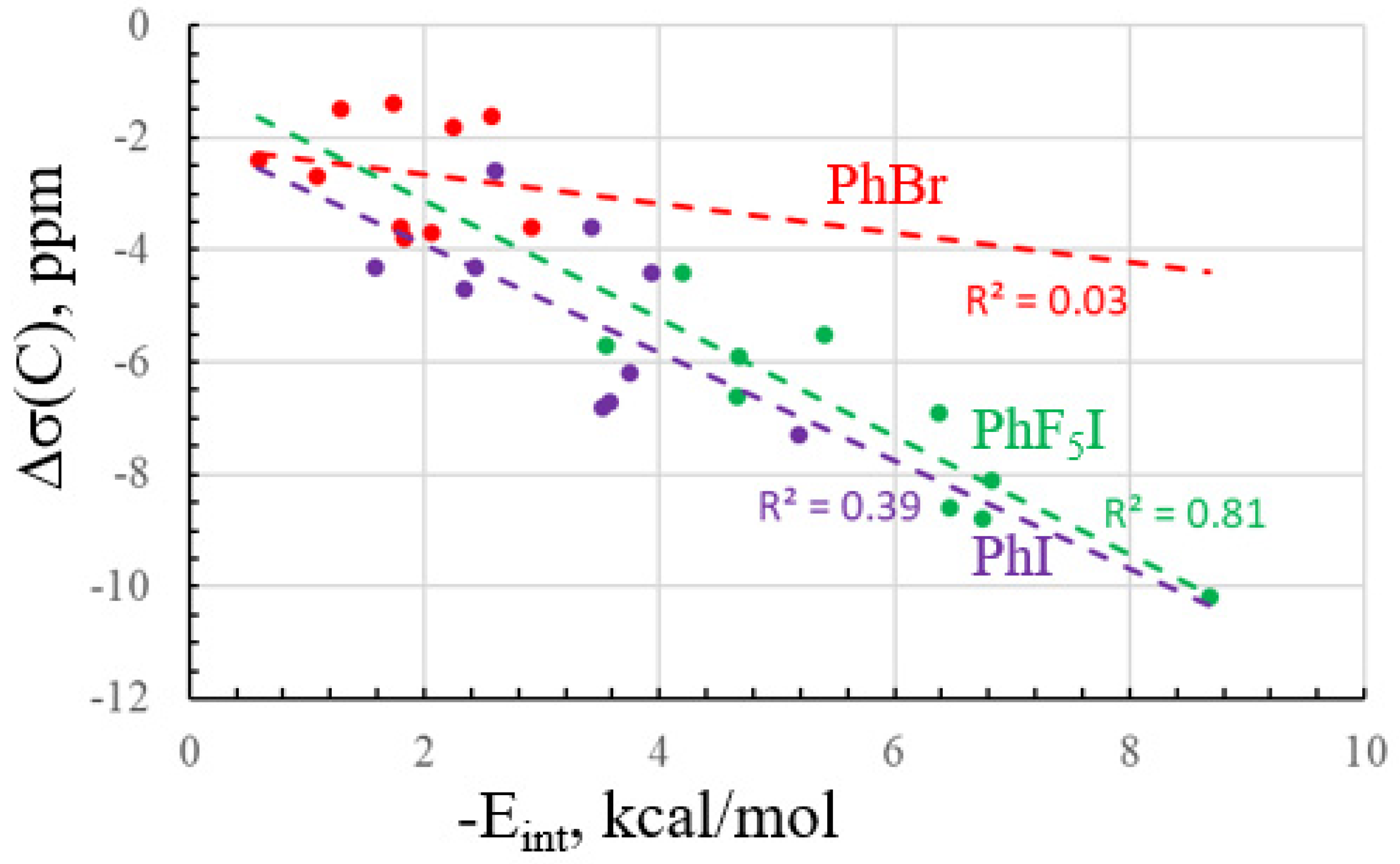
Molecules 28 07520 g003
Figure 3. The relationship between interaction energy and change in the isotropic shielding of the C atom bonded to X caused by complexation.
Figure 3. The relationship between interaction energy and change in the isotropic shielding of the C atom bonded to X caused by complexation.
Molecules 28 07520 g003
Molecules 28 07520 g004
Figure 4. The relationship between the interaction energy and change in the C–X coupling constant caused by complexation.
Figure 4. The relationship between the interaction energy and change in the C–X coupling constant caused by complexation.
Molecules 28 07520 g004
Molecules 28 07520 g005
Figure 5. The relationship between the interaction energy and change in the C–H/F coupling constant, ortho to X, caused by complexation.
Figure 5. The relationship between the interaction energy and change in the C–H/F coupling constant, ortho to X, caused by complexation.
Molecules 28 07520 g005
Table 1. The interaction energies (kcal/mol), intermolecular distance, bond critical point density (au), and intermolecular coupling constant (Hz) within dyads, and the change in C–X bond length (Å) and vibrational stretching frequency (cm−1) upon complexation with base.
Table 1. The interaction energies (kcal/mol), intermolecular distance, bond critical point density (au), and intermolecular coupling constant (Hz) within dyads, and the change in C–X bond length (Å) and vibrational stretching frequency (cm−1) upon complexation with base.
Base−EintR(X··N/O)ρBCP aΔr(C-X)Δν(CX)J(X··N/O)
PhBr·· 1.89571109.7
N≡CH0.593.2600.0076−0.00225.242.1
HN=NH1.093.1800.0103−0.00145.753.0
PyrN1.803.1030.01230.00011.357.3
NH31.833.1240.0123−0.00032.857.3
NMe32.913.0080.01600.00302.455.3
OH21.293.0890.0110−0.00010.6−58.3
OMe22.242.9820.01360.00117.7−69.7
OCH21.733.1010.0106
(0.0071)		0.00020.8−43.8
OCHNH22.573.0910.0108
(0.0086)		0.00160.6−58.5
NMA2.063.0070.0114
(0.0053)		−0.00196.1−103.6
PhI·· 2.09391100.5
N≡CH1.58 3.2840.0093−0.00042.4227.3
HN=NH2.343.2210.0118−0.00022.2244.1
PyrN3.583.0800.01590.00263.3267.1
NH33.523.1460.01450.00373.6277.8
NMe35.183.0010.01990.00813.9217.8
OH22.443.1000.01290.00053.0−409.2
OMe23.433.0130.0158−0.00023.0−343.8
OCH22.603.1430.0122−0.00114.4−256.7
OCHNH23.943.0550.0141
(0.0079)		0.00193.4−357.2
NMA3.743.0220.0136
(0.0054)		−0.00054.7−491.2
PhF5I·· 2.0688828.3
NCH3.553.1010.00930.0072−1.0334.9
HN=NH4.663.0240.01180.01094.7354.6
Pyr-N6.752.9220.01590.0195−3.9354.6
NH36.472.9760.01450.0186−3.6377.9
NMe38.682.8230.01990.0303−6.4308.9
OH24.672.9370.01290.00816.3−692.9
OMe25.402.8900.01580.01035.0−510.5
OCH24.202.9670.01220.00745.7−406.5
OCHNH26.372.8950.0141
(0.0079)		0.0126−1.3−524.4
NMA6.832.8740.0136
(0.0054)		0.01070.8−702.5
a (H··X) in parentheses.
Table 2. AIM values of the intermolecular bond critical point, density of the ring critical point at the center of an aromatic ring, the LUMO–HOMO energy gap, and NBO E2 for the N/O lone pair → σ*(CX) charge transfer. All values are measured in au except E2, which is measured in kcal/mol.
Table 2. AIM values of the intermolecular bond critical point, density of the ring critical point at the center of an aromatic ring, the LUMO–HOMO energy gap, and NBO E2 for the N/O lone pair → σ*(CX) charge transfer. All values are measured in au except E2, which is measured in kcal/mol.
BaseHV∇2ρEllipticityρrcpEgapE2
PhBr··
N≡CH0.0016−0.00440.03020.00170.02450.3061.15
HN=NH0.0015−0.00610.03640.06520.02450.2771.99
PyrN0.0015−0.00760.04250.06120.02680.2882.70
NH30.0014−0.00760.04140.00190.02450.3053.48
NMe30.0012−0.01030.05070.00420.02450.2943.38
OH20.0018−0.00710.04270.05690.02450.3072.45
OMe20.0020−0.00940.05320.00680.02450.3072.16
OCH20.0019−0.00680.04220.00070.02450.2961.62
OCHNH20.0018−0.00670.04160.01150.02450.3082.29
NMA0.0021−0.00780.04810.02080.02450.3042.30
PhI··
N≡CH0.0016−0.00540.03420.00070.02460.2951.97
HN=NH0.0011−0.01110.05360.07640.02210.2613.00
PyrN0.0011−0.01020.04990.05690.02680.2724.74
NH30.0011−0.00900.04460.00010.02460.2965.12
NMe30.0004−0.01310.0557 0.00270.02460.2975.43
OH20.0017−0.00860.04790.07460.02460.2963.61
OMe20.0016−0.01100.05680.02550.02460.2973.33
OCH20.0017−0.00770.04470.02480.02460.2792.47
OCHNH20.0017−0.00940.05140.00820.02460.2984.12
NMA0.0020−0.00950.05380.02960.02450.2943.52
PhF5I··
NCH0.0017−0.00840.04730.00650.02200.2993.83
HN=NH0.0011−0.01110.05370.07640.02210.2705.87
Pyr-N0.0006−0.01460.06320.05000.02220.2838.46
NH30.0007−0.01310.05780.00720.02210.3009.01
NMe3−0.0012−0.01970.06930.00490.02790.30210.58
OH20.0018−0.01220.06340.10570.02200.2965.39
OMe20.0014−0.01460.06920.03990.02210.3005.69
OCH20.0017−0.01170.06030.02670.02200.2874.83
OCHNH20.0016−0.01370.06750.00490.02210.3007.26
NMA0.0019−0.01360.06990.03440.02210.2976.17
Table 3. Values of isotropic shielding (σ, ppm) and coupling constants (J, Hz) in monomers and changes caused by complexation.
Table 3. Values of isotropic shielding (σ, ppm) and coupling constants (J, Hz) in monomers and changes caused by complexation.
BaseΔσ(X)Δσ(C)ΔJ(C-X)ΔJ(C-C)ΔJ(C-H/F)
PhBr··2085.926.2−67.083.7170.3
N≡CH−35.3−2.4−12.5−0.6−0.2
HN=NH−43.3−2.7−15.6−0.7−0.8
PyrN−44.1−3.6−18.2−1.1−1.0
NH3−47.0−3.8−18.0−1.3−1.2
NMe3−52.6−3.6−26.7−1.3−1.2
OH2−20.8−1.5−13.4−0.7−0.3
OMe2−44.8−1.8−17.2−0.6−0.4
OCH2−31.3−1.4−10.0−0.3−0.7
OCHNH2−34.8−1.6−11.7−0.5−0.7
NMA−61.1−3.7−19.0−1.1−1.1
PhI··3103.739.1−172.680.8170.7
N≡CH−77.9−4.3−68.2−1.1−1.1
HN=NH−67.6−4.7−74.8−1.3−1.4
PyrN−80.8−6.7−97.6−1.6−1.9
NH3−49.6−6.8−109.5−1.7−1.9
NMe3−15.4−7.3−100.5−1.9−2.1
OH2−64.6−4.3−83.0−1.2−1.2
OMe2−48.5−3.6−54.2−1.1−1.4
OCH2−77.8−2.6−51.6−0.7−1.4
OCHNH2−118.1−4.4−71.0−1.1−1.6
NMA−120.5−6.2−82.4−1.3−2.2
PhF5I··3517.673.3−270.7105.0−299.5
NCH−79.8−5.7−125.0−1.22.8
HN=NH−88.8−6.6−132.7−1.33.2
Pyr-N−52.2−8.8−157.9−1.64.8
NH3−10.4−8.6−158.5−1.64.4
NMe3−82.0−10.2−171.6−1.55.2
OH2−75.9−5.9−119.7−1.03.0
OMe2−56.5−5.5−122.1−1.23.2
OCH2 a−36.4−4.4−105.2−0.84.2
OCHNH2 a+0.9−6.9−132.9−1.07.3
NMA−77.5−8.1−144.2−1.26.0
a J(CF) for F syn to base.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Amonov, A.; Scheiner, S. Relation between Halogen Bond Strength and IR and NMR Spectroscopic Markers. Molecules 2023, 28, 7520. https://doi.org/10.3390/molecules28227520

AMA Style

Amonov A, Scheiner S. Relation between Halogen Bond Strength and IR and NMR Spectroscopic Markers. Molecules. 2023; 28(22):7520. https://doi.org/10.3390/molecules28227520

Chicago/Turabian Style

Amonov, Akhtam, and Steve Scheiner. 2023. "Relation between Halogen Bond Strength and IR and NMR Spectroscopic Markers" Molecules 28, no. 22: 7520. https://doi.org/10.3390/molecules28227520

APA Style

Amonov, A., & Scheiner, S. (2023). Relation between Halogen Bond Strength and IR and NMR Spectroscopic Markers. Molecules, 28(22), 7520. https://doi.org/10.3390/molecules28227520

Article Metrics

Back to TopTop