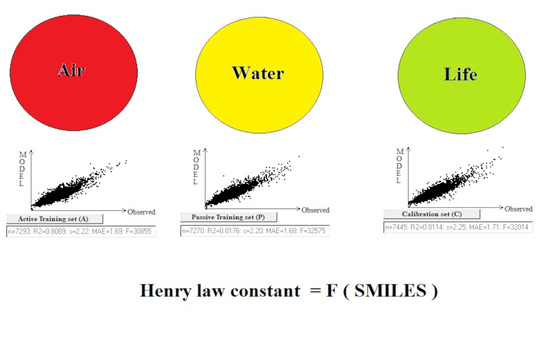
The System of Self-Consistent Models: The Case of Henry’s Law Constants
Abstract
:1. Introduction
2. Results and Discussion
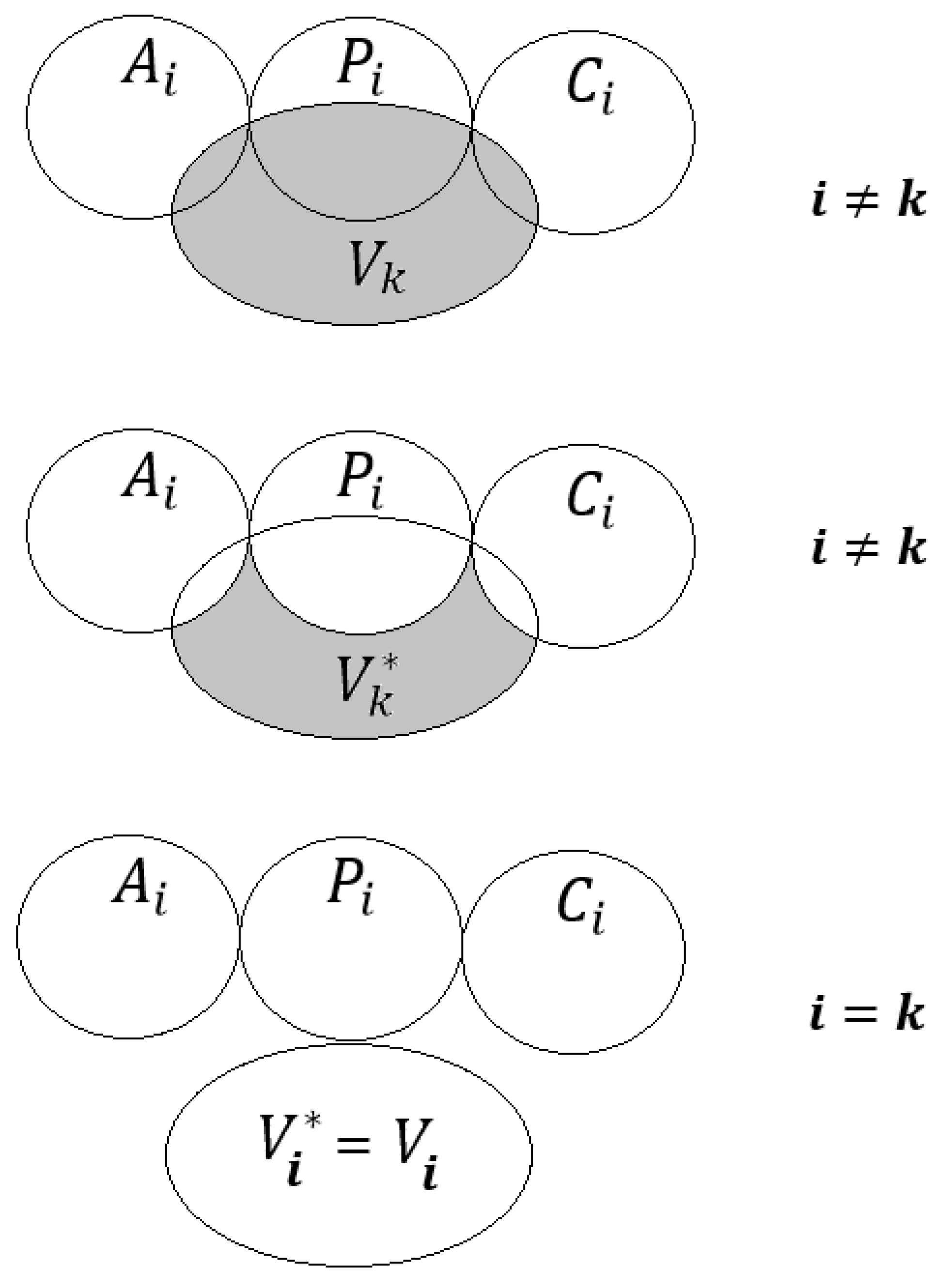
2.1. The System of Self-Consistent Models
2.2. The Statistical Quality of Models
2.3. Why Are Models Needed?
2.4. Model as a Hired Worker in a Workshop
2.5. A Model Is Either Knowledge or Delusion
3. Method
3.1. Data
3.2. Model
3.3. Optimal Descriptor
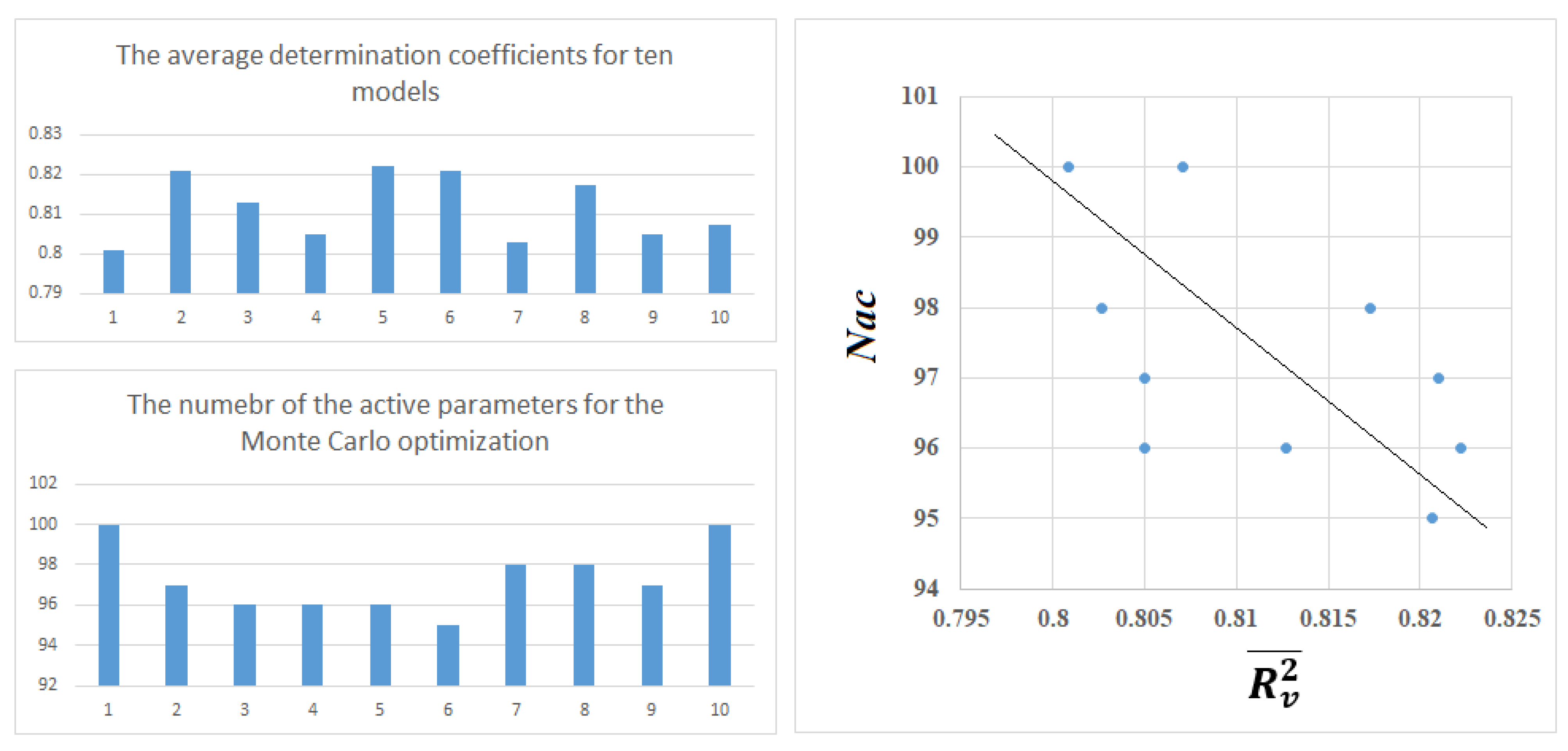
3.4. The Monte Carlo Optimization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, Y.; Cao, T.; Thompson, J.E. The chemical evolution & physical properties of organic aerosol: A molecular structure based approach. Atmos. Environ. 2012, 62, 199–207. [Google Scholar] [CrossRef]
- Kuosmanen, T.; Zhou, X.; Dai, S. How much climate policy has cost for OECD countries? World Dev. 2020, 125, 104681. [Google Scholar] [CrossRef]
- Duchowicz, P.R.; Aranda, J.F.; Bacelo, D.E.; Fioressi, S.E. QSPR study of the Henry’s law constant for heterogeneous compounds. Chem. Eng. Res. Des. 2020, 154, 115–121. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Roncaglioni, A.; Benfenati, E. Does the accounting of the local symmetry fragments in SMILES improve the predictive potential of the QSPR-model for Henry’s law constants? Environ. Sci. Adv. 2023, 2, 916–921. [Google Scholar] [CrossRef]
- Kang, X.; Lv, Z.; Zhao, Y.; Chen, Z. A QSPR model for estimating Henry’s law constant of H2S in ionic liquids by ELM algorithm. Chemosphere 2021, 269, 128743. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A. The system of self-consistent of models: A new approach to build up and validation of predictive models of the octanol/water partition coefficient for gold nanoparticles. Int. J. Environ. Res. 2021, 15, 709–722. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. The system of self-consistent models for the uptake of nanoparticles in PaCa2 cancer cells. Nanotoxicology 2021, 15, 995–1004. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, S.; Basak, S.C. Beware of naïve q2, use true q2: Some comments on QSAR model building and cross validation. Curr. Comput. Aided Drug Des. 2018, 14, 5–6. [Google Scholar] [CrossRef] [PubMed]
- Kuei Lin, L. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Consonni, V.; Ballabio, D.; Todeschini, R. Comments on the definition of the Q2 parameter for QSAR validation. J. Chem. Inf. Model. 2009, 49, 1669–1678. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Kar, S. The rm2 metrics and regression through origin approach: Reliable and useful validation tools for predictive QSAR models (Commentary on ‘Is regression through origin useful in external validation of QSAR models?’). Eur. J. Pharm. Sci. 2014, 62, 111–114. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. QSPR/QSAR: State-of-art, weirdness, the future. Molecules 2020, 25, 1292. [Google Scholar] [CrossRef]
- Box, G.E.P. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. QSAR as a random event: Criteria of predictive potential for a chance model. Struct. Chem. 2019, 30, 1677–1683. [Google Scholar] [CrossRef]
- Rakhimbekova, A.; Akhmetshin, T.N.; Minibaeva, G.I.; Nugmanov, R.I.; Gimadiev, T.R.; Madzhidov, T.I.; Baskin, I.I.; Varnek, A. Cross-validation strategies in QSPR modelling of chemical reactions. SAR QSAR Environ. Res. 2021, 32, 207–219. [Google Scholar] [CrossRef] [PubMed]
- Varnek, A.; Kireeva, N.; Tetko, I.V.; Baskin, I.I.; Solov’ev, V.P. Exhaustive QSPR studies of a large diverse set of ionic liquids: How accurately can we predict melting points? J. Chem. Inf. Model. 2007, 47, 1111–1122. [Google Scholar] [CrossRef] [PubMed]
- Ghaedi, A. Predicting the cytotoxicity of ionic liquids using QSAR model based on SMILES optimal descriptors. J. Mol. Liq. 2015, 208, 269–279. [Google Scholar] [CrossRef]
- Worachartcheewan, A.; Nantasenamat, C.; Isarankura-Na-Ayudhya, C.; Prachayasittikul, V. QSAR study of H1N1 neuraminidase inhibitors from influenza a virus. Lett. Drug Des. Discov. 2014, 11, 420–427. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, A.; Lal, S.; Singh, D.; Lotfi, S.; Ahmadi, S. CORAL: Quantitative Structure Retention Relationship (QSRR) of flavors and fragrances compounds studied on the stationary phase methyl silicone OV-101 column in gas chromatography using correlation intensity index and consensus modelling. J. Mol. Struct. 2022, 1265, 133437. [Google Scholar] [CrossRef]
- Jain, S.; Bhardwaj, B.; Amin, S.A.; Adhikari, N.; Jha, T.; Gayen, S. Exploration of good and bad structural fingerprints for inhibition of indoleamine-2,3-dioxygenase enzyme in cancer immunotherapy using Monte Carlo optimization and Bayesian classification QSAR modeling. J. Biomol. Struct. Dyn. 2020, 38, 1683–1696. [Google Scholar] [CrossRef]
- Begum, S.; Achary, P.G.R. Simplified molecular input line entry system-based: QSAR modelling for MAP kinase-interacting protein kinase (MNK1). SAR QSAR Environ. Res. 2015, 26, 343–361. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.; Aghabeygi, S.; Farahmandjou, M.; Azimi, N. The predictive model for band gap prediction of metal oxide nanoparticles based on quasi-SMILES. Struct. Chem. 2021, 32, 1893–1905. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, A.; Sindhu, J.; Lal, S. Quasi-SMILES as a basis for the development of QSPR models to predict the CO2 capture capacity of deep eutectic solvents using correlation intensity index and consensus modelling. Fuel 2023, 345, 128237. [Google Scholar] [CrossRef]
- Tajiani, F.; Ahmadi, S.; Lotfi, S.; Kumar, P.; Almasirad, A. In-silico activity prediction and docking studies of some flavonol derivatives as anti-prostate cancer agents based on Monte Carlo optimization. BMC Chem. 2023, 17, 87. [Google Scholar] [CrossRef] [PubMed]
- Weininger, D. SMILES, a Chemical Language and Information System: 1: Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
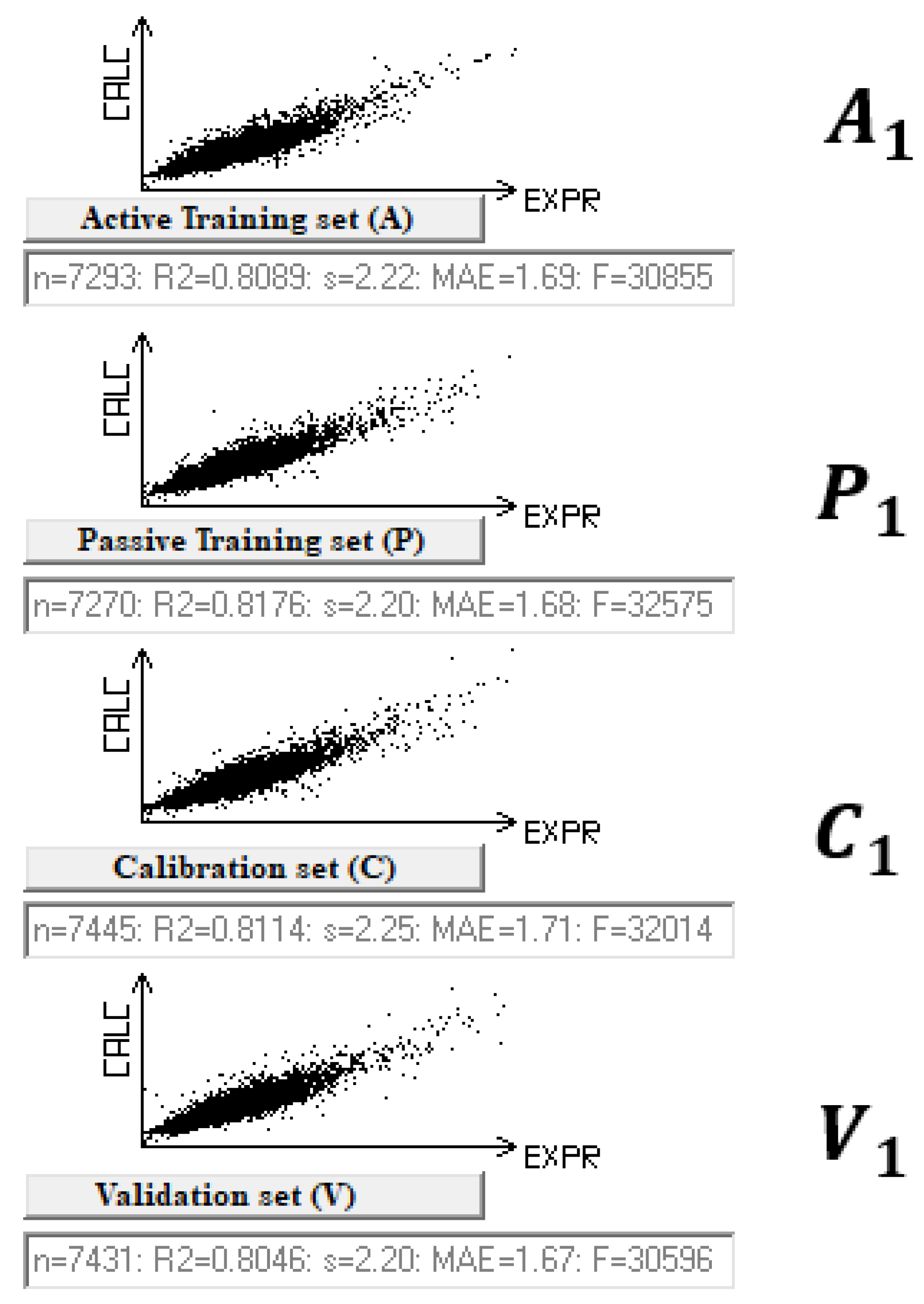
| Split | Set | n* | R2 | CCC | Q2F1 | Q2F2 | Q2F3 | <Rm2> | RMSE | MAE | F | Nac |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 7293 | 0.8089 | 0.8943 | 2.22 | 1.69 | 30,855 | |||||
| P | 7270 | 0.8176 | 0.8980 | 2.20 | 1.68 | 32,575 | ||||||
| C | 7445 | 0.8114 | 0.8957 | 0.8114 | 0.8114 | 0.8060 | 0.7341 | 2.25 | 1.71 | 32,014 | ||
| V | 7431 | 0.8046 | - | - | - | - | - | 2.20 | 1.67 | - | 100 | |
| 2 | A | 7374 | 0.8288 | 0.9064 | 2.10 | 1.59 | 35,690 | |||||
| P | 7156 | 0.8223 | 0.9019 | 2.14 | 1.61 | 33,112 | ||||||
| C | 7410 | 0.8226 | 0.9023 | 0.8226 | 0.8225 | 0.8173 | 0.7502 | 2.17 | 1.61 | 34,345 | ||
| V | 7499 | 0.8239 | - | - | - | - | - | 2.15 | 1.62 | - | 97 | |
| 3 | A | 7258 | 0.8160 | 0.8987 | 2.14 | 1.62 | 32,179 | |||||
| P | 7371 | 0.8187 | 0.9006 | 2.19 | 1.66 | 33,278 | ||||||
| C | 7473 | 0.8217 | 0.9015 | 0.8217 | 0.8217 | 0.8140 | 0.7425 | 2.18 | 1.65 | 34,436 | ||
| V | 7337 | 0.8157 | - | - | - | - | - | 2.19 | 1.64 | - | 96 | |
| 4 | A | 7335 | 0.8174 | 0.8995 | 2.18 | 1.65 | 32,824 | |||||
| P | 7364 | 0.8174 | 0.8987 | 2.18 | 1.65 | 32,955 | ||||||
| C | 7336 | 0.8293 | 0.9065 | 0.8293 | 0.8293 | 0.8243 | 0.7589 | 2.14 | 1.63 | 35,629 | ||
| V | 7404 | 0.8002 | - | - | - | - | - | 2.25 | 1.71 | - | 96 | |
| 5 | A | 7431 | 0.8248 | 0.9040 | 2.13 | 1.61 | 34,978 | |||||
| P | 7369 | 0.8187 | 0.9001 | 2.13 | 1.62 | 33,268 | ||||||
| C | 7313 | 0.8305 | 0.9078 | 0.8305 | 0.8305 | 0.8221 | 0.7617 | 2.13 | 1.60 | 35,828 | ||
| V | 7326 | 0.8239 | - | - | - | - | - | 2.15 | 1.63 | - | 95 | |
| 6 | A | 7348 | 0.8130 | 0.8968 | 2.16 | 1.63 | 31,931 | |||||
| P | 7413 | 0.8227 | 0.9028 | 2.16 | 1.65 | 34,391 | ||||||
| C | 7346 | 0.8149 | 0.8968 | 0.8148 | 0.8148 | 0.8065 | 0.7291 | 2.23 | 1.66 | 32,334 | ||
| V | 7332 | 0.8240 | - | - | - | - | - | 2.14 | 1.62 | - | 98 | |
| 7 | A | 7264 | 0.8068 | 0.8931 | 2.23 | 1.70 | 30,321 | |||||
| P | 7338 | 0.8068 | 0.8935 | 2.26 | 1.73 | 30,627 | ||||||
| C | 7453 | 0.8021 | 0.8911 | 0.8019 | 0.8019 | 0.8036 | 0.7230 | 2.26 | 1.73 | 30,191 | ||
| V | 7384 | 0.8030 | - | - | - | - | - | 2.26 | 1.74 | - | 98 | |
| 8 | A | 7184 | 0.8232 | 0.9030 | 2.16 | 1.63 | 33,431 | |||||
| P | 7413 | 0.8262 | 0.9039 | 2.14 | 1.61 | 35,239 | ||||||
| C | 7284 | 0.8335 | 0.9083 | 0.8334 | 0.8334 | 0.8293 | 0.7595 | 2.12 | 1.60 | 36,444 | ||
| V | 7558 | 0.8132 | - | - | - | - | - | 2.14 | 1.62 | - | 97 | |
| 9 | A | 7470 | 0.8064 | 0.8928 | 2.27 | 1.73 | 31,109 | |||||
| P | 7312 | 0.8002 | 0.8898 | 2.26 | 1.72 | 29,275 | ||||||
| C | 7389 | 0.7884 | 0.8823 | 0.7885 | 0.7884 | 0.7966 | 0.7043 | 2.31 | 1.75 | 27,523 | ||
| V | 7268 | 0.8067 | - | - | - | - | - | 2.27 | 1.74 | - | 100 | |
| 10 | A | 7344 | 0.8092 | 0.8946 | 2.24 | 1.70 | 31,144 | |||||
| P | 7360 | 0.8044 | 0.8930 | 2.28 | 1.73 | 30,254 | ||||||
| C | 7358 | 0.7973 | 0.8887 | 0.7971 | 0.7971 | 0.8023 | 0.7171 | 2.28 | 1.74 | 28,937 | ||
| V | 7377 | 0.8073 | - | - | - | - | - | 2.22 | 1.69 | - | 103 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 7431 | 1896 | 1809 | 1861 | 1891 | 1797 | 1846 | 1938 | 1642 | 1823 |
| M2 | 1896 | 7499 | 1853 | 1926 | 1952 | 1872 | 1940 | 1916 | 1822 | 1931 |
| M3 | 1809 | 1853 | 7337 | 1891 | 1790 | 1863 | 1846 | 1837 | 1817 | 1824 |
| M4 | 1861 | 1926 | 1891 | 7404 | 1877 | 1797 | 1886 | 1873 | 1775 | 1872 |
| M5 | 1891 | 1952 | 1790 | 1877 | 7326 | 1801 | 1805 | 1853 | 1857 | 1842 |
| M6 | 1797 | 1872 | 1863 | 1797 | 1801 | 7332 | 1885 | 1835 | 1844 | 1826 |
| M7 | 1846 | 1940 | 1846 | 1886 | 1805 | 1885 | 7384 | 1907 | 1855 | 1848 |
| M8 | 1938 | 1916 | 1837 | 1873 | 1853 | 1835 | 1907 | 7558 | 1835 | 1919 |
| M9 | 1842 | 1822 | 1817 | 1775 | 1857 | 1844 | 1855 | 1835 | 7268 | 1808 |
| M10 | 1823 | 1931 | 1824 | 1872 | 1842 | 1826 | 1848 | 1919 | 1808 | 7377 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 0.8046 | 0.8191 | 0.8045 | 0.7898 | 0.7918 | 0.8105 | 0.8072 | 0.7958 | 0.7984 | 0.7873 | 0.8009 ± 0.0095 |
| M2 | 0.8280 | 0.8239 | 0.8132 | 0.8040 | 0.8221 | 0.8283 | 0.8147 | 0.8265 | 0.8222 | 0.8271 | 0.8210 ± 0.0075 |
| M3 | 0.8098 | 0.8048 | 0.8157 | 0.7895 | 0.8161 | 0.8194 | 0.8175 | 0.8107 | 0.8233 | 0.8206 | 0.8127 ± 0.0094 |
| M4 | 0.7970 | 0.7901 | 0.7844 | 0.8002 | 0.8020 | 0.8065 | 0.8035 | 0.7924 | 0.8149 | 0.8146 | 0.8050 ± 0.0095 |
| M5 | 0.8093 | 0.8226 | 0.8278 | 0.8099 | 0.8239 | 0.8233 | 0.8353 | 0.8180 | 0.8116 | 0.8406 | 0.8222 ± 0.0100 |
| M6 | 0.8196 | 0.8227 | 0.8216 | 0.8083 | 0.8197 | 0.8240 | 0.8121 | 0.8184 | 0.8400 | 0.8204 | 0.8207 ± 0.0101 |
| M7 | 0.7986 | 0.7932 | 0.8078 | 0.7931 | 0.8154 | 0.7982 | 0.8030 | 0.7861 | 0.8147 | 0.8166 | 0.8027 ± 0.0101 |
| M8 | 0.8125 | 0.8227 | 0.8193 | 0.7985 | 0.8179 | 0.8240 | 0.8106 | 0.8132 | 0.8268 | 0.8282 | 0.8173 ± 0.0085 |
| M9 | 0.7881 | 0.7970 | 0.8100 | 0.8003 | 0.7933 | 0.8262 | 0.8110 | 0.8100 | 0.8067 | 0.8177 | 0.8050 ± 0.0109 |
| M10 | 0.7789 | 0.8005 | 0.8043 | 0.8059 | 0.8241 | 0.8053 | 0.8162 | 0.8083 | 0.8202 | 0.8073 | 0.8071 ± 0.0118 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 1.67 | 1.66 | 1.67 | 1.71 | 1.71 | 1.64 | 1.65 | 1.69 | 1.67 | 1.63 |
| M2 | 1.57 | 1.62 | 1.62 | 1.66 | 1.62 | 1.58 | 1.62 | 1.59 | 1.61 | 1.61 |
| M3 | 1.63 | 1.66 | 1.64 | 1.70 | 1.64 | 1.60 | 1.67 | 1.63 | 1.66 | 1.58 |
| M4 | 1.67 | 1.72 | 1.73 | 1.71 | 1.72 | 1.71 | 1.68 | 1.71 | 1.71 | 1.66 |
| M5 | 1.63 | 1.61 | 1.60 | 1.67 | 1.62 | 1.60 | 1.61 | 1.66 | 1.67 | 1.56 |
| M6 | 1.59 | 1.61 | 1.60 | 1.69 | 1.61 | 1.62 | 1.63 | 1.60 | 1.63 | 1.57 |
| M7 | 1.70 | 1.77 | 1.76 | 1.75 | 1.73 | 1.73 | 1.74 | 1.76 | 1.73 | 1.68 |
| M8 | 1.60 | 1.60 | 1.59 | 1.68 | 1.65 | 1.58 | 1.63 | 1.62 | 1.61 | 1.64 |
| M9 | 1.73 | 1.73 | 1.76 | 1.78 | 1.78 | 1.72 | 1.73 | 1.70 | 1.74 | 1.67 |
| M10 | 1.68 | 1.74 | 1.68 | 1.70 | 1.66 | 1.65 | 1.68 | 1.75 | 1.65 | 1.69 |
| SMILES Attribute | Correlation Weight |
|---|---|
| Sk | CW (Sk) |
| N........... | 0.9532 |
| C........... | −0.0412 |
| #........... | 0.2896 |
| N........... | 0.9532 |
| SSk | CW (SSk) |
| N...C....... | 0.9275 |
| C...#....... | 0.0088 |
| N...#....... | 0.6083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toropov, A.A.; Toropova, A.P.; Roncaglioni, A.; Benfenati, E.; Leszczynska, D.; Leszczynski, J. The System of Self-Consistent Models: The Case of Henry’s Law Constants. Molecules 2023, 28, 7231. https://doi.org/10.3390/molecules28207231
Toropov AA, Toropova AP, Roncaglioni A, Benfenati E, Leszczynska D, Leszczynski J. The System of Self-Consistent Models: The Case of Henry’s Law Constants. Molecules. 2023; 28(20):7231. https://doi.org/10.3390/molecules28207231
Chicago/Turabian StyleToropov, Andrey A., Alla P. Toropova, Alessandra Roncaglioni, Emilio Benfenati, Danuta Leszczynska, and Jerzy Leszczynski. 2023. "The System of Self-Consistent Models: The Case of Henry’s Law Constants" Molecules 28, no. 20: 7231. https://doi.org/10.3390/molecules28207231
APA StyleToropov, A. A., Toropova, A. P., Roncaglioni, A., Benfenati, E., Leszczynska, D., & Leszczynski, J. (2023). The System of Self-Consistent Models: The Case of Henry’s Law Constants. Molecules, 28(20), 7231. https://doi.org/10.3390/molecules28207231