Modus Operandi of a Pedalo-Type Molecular Switch: Insight from Dynamics and Theoretical Spectroscopy
Abstract
1. Introduction
2. Results and Discussion
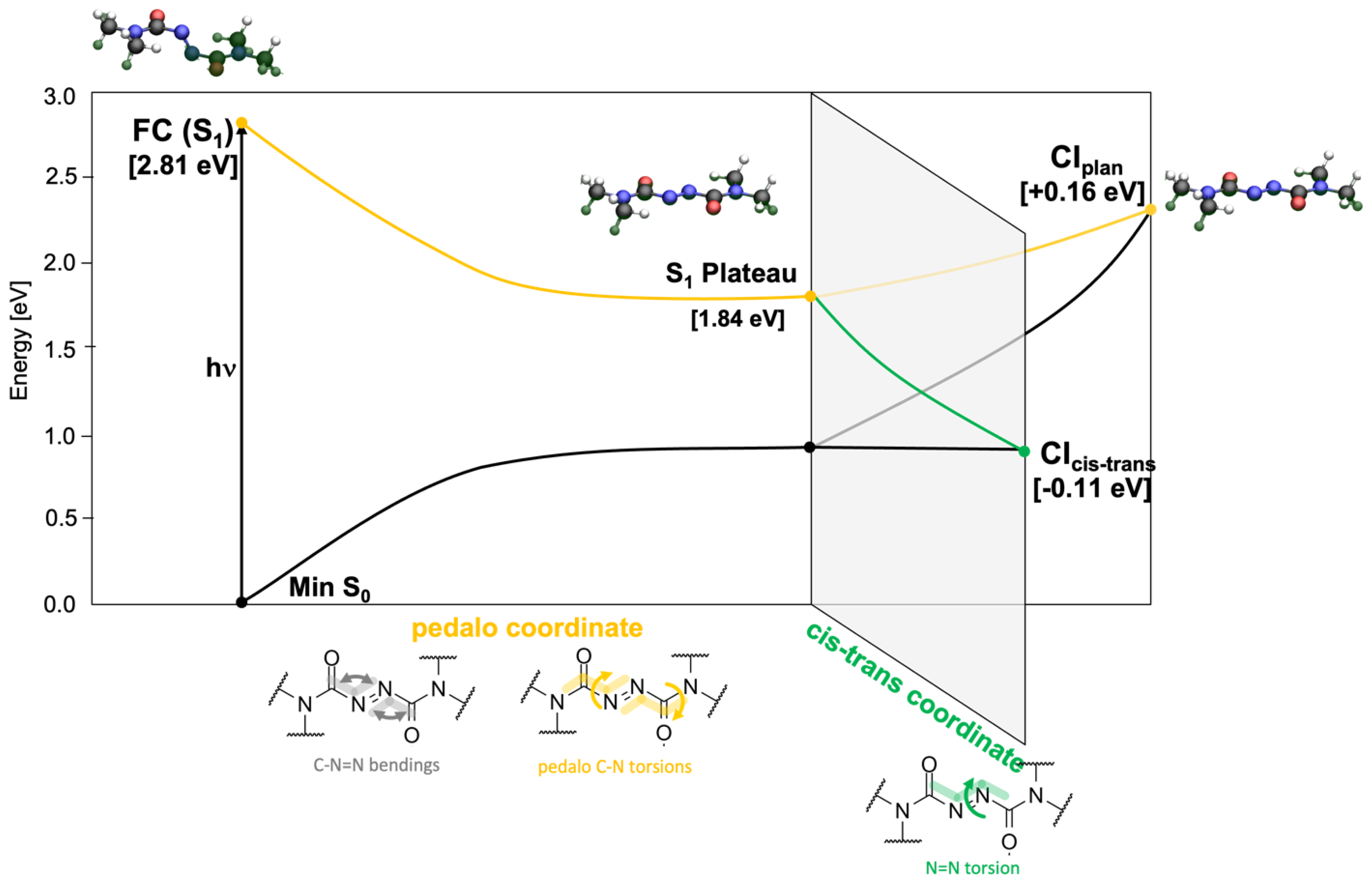
2.1. Static Calculation: Critical Points and MEPs
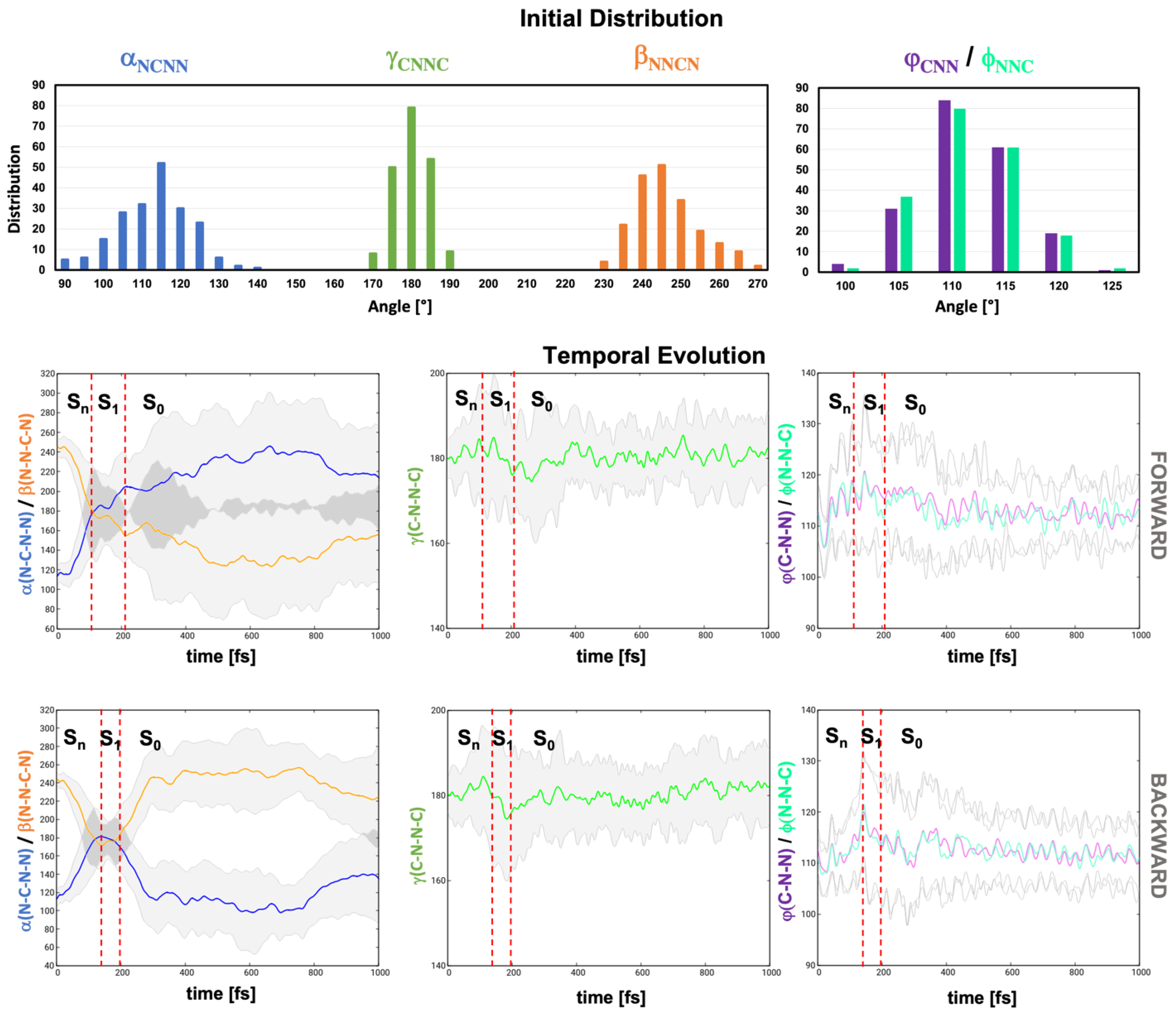
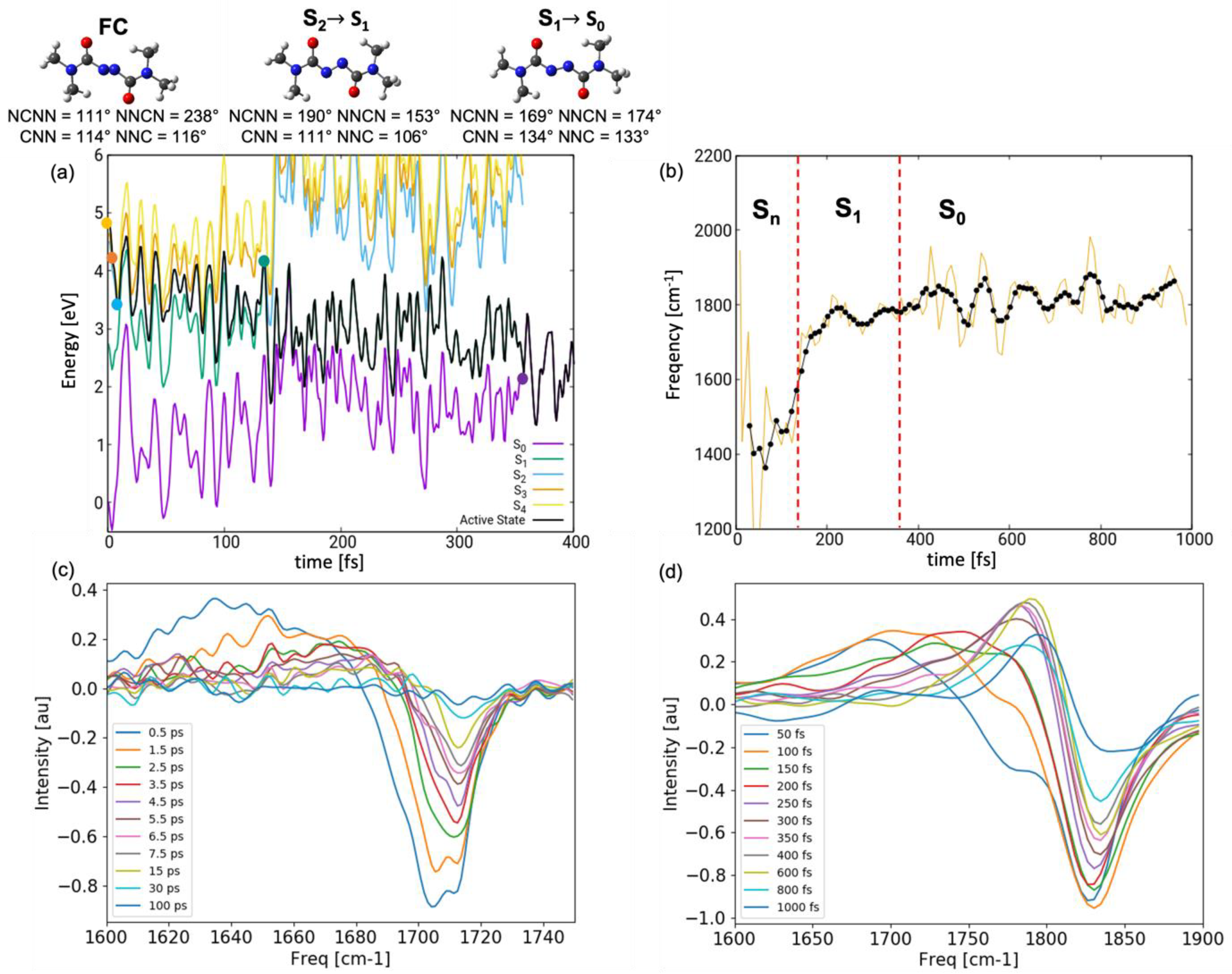
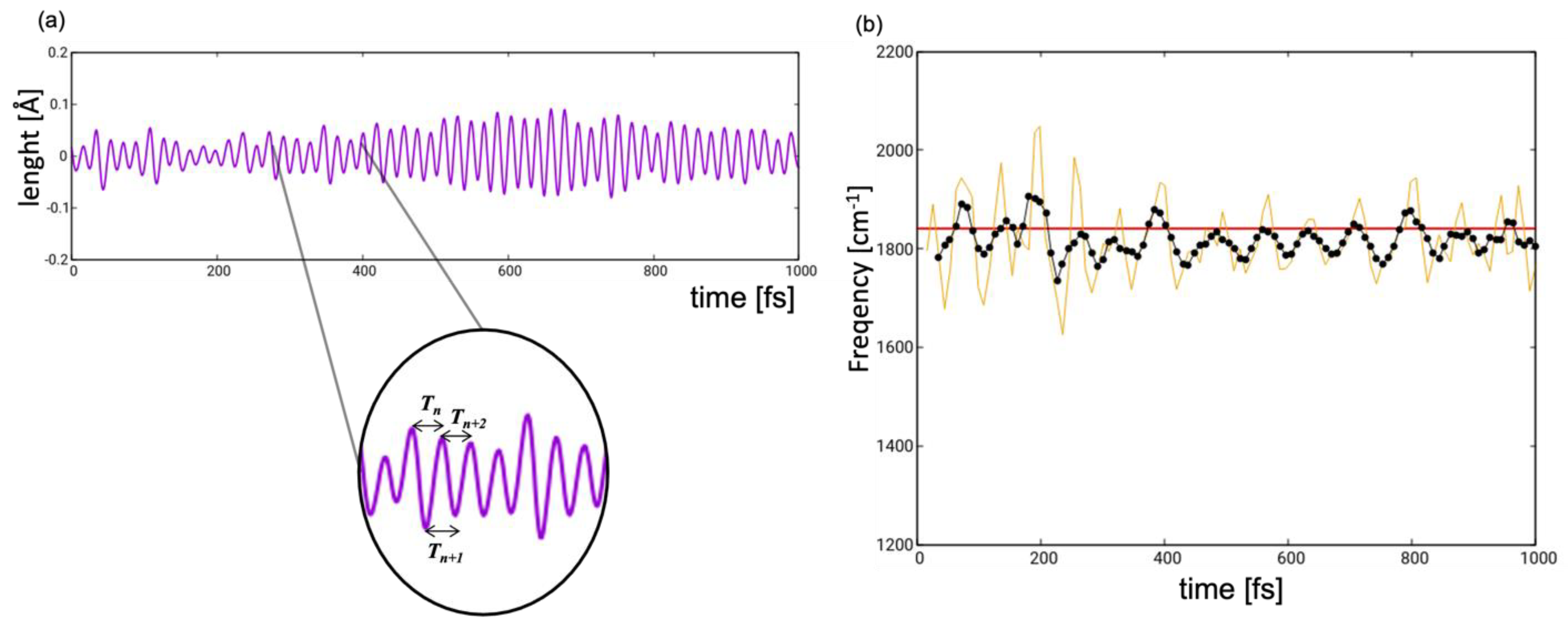
2.2. Dynamics
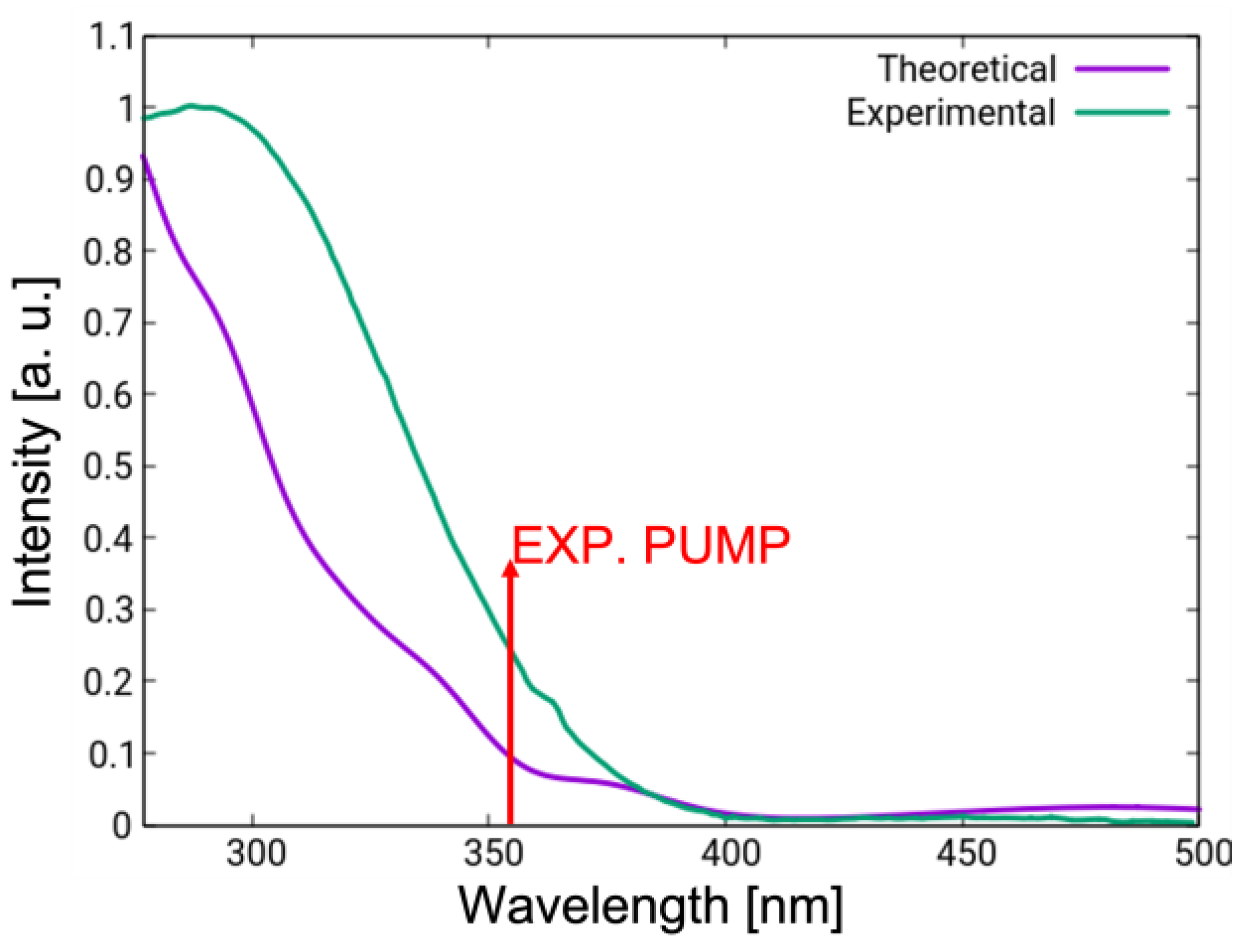
2.3. Spectroscopy
3. Methods
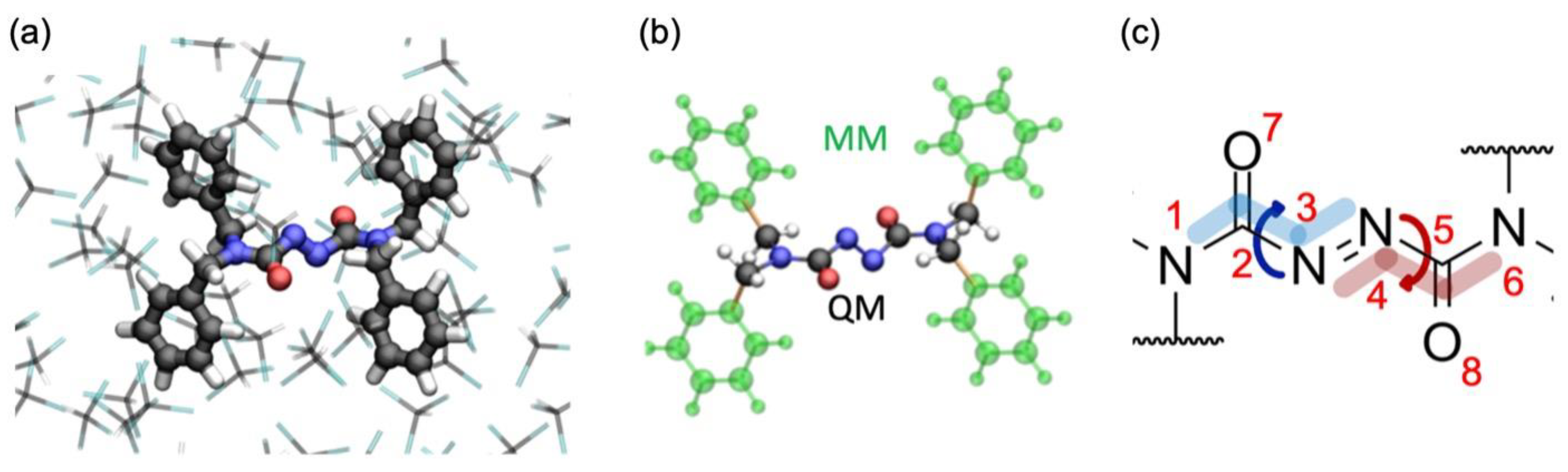
3.1. QM/MM Setup
3.2. Electronic Structure Calculation
3.3. Linear Absorption Spectra in Chloroform
3.4. Mixed Quantum Classical Dynamics Gas-Phase
3.5. Theory and Implementation of the Time-Resolved IR Spectroscopy Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Polli, D.; Altoè, P.; Weingart, O.; Spillane, K.M.; Manzoni, C.; Brida, D.; Tomasello, G.; Orlandi, G.; Kukura, P.; Mathies, R.A.; et al. Conical Intersection Dynamics of the Primary Photoisomerization Event in Vision. Nature 2010, 467, 440–443. [Google Scholar] [CrossRef]
- Wang, Z.; Müller, K.; Valášek, M.; Grosjean, S.; Bräse, S.; Wöll, C.; Mayor, M.; Heinke, L. Series of Photoswitchable Azobenzene-Containing Metal–Organic Frameworks with Variable Adsorption Switching Effect. J. Phys. Chem. C 2018, 122, 19044–19050. [Google Scholar] [CrossRef]
- Mutruc, D.; Goulet-Hanssens, A.; Fairman, S.; Wahl, S.; Zimathies, A.; Knie, C.; Hecht, S. Modulating Guest Uptake in Core–Shell MOFs with Visible Light. Angew. Chem. Int. Ed. 2019, 58, 12862–12867. [Google Scholar] [CrossRef]
- Danowski, W.; van Leeuwen, T.; Abdolahzadeh, S.; Roke, D.; Browne, W.R.; Wezenberg, S.J.; Feringa, B.L. Unidirectional Rotary Motion in a Metal–Organic Framework. Nat. Nanotechnol. 2019, 14, 488–494. [Google Scholar] [CrossRef]
- Kolodzeiski, E.; Amirjalayer, S. Atomistic Insight Into the Host–Guest Interaction of a Photoresponsive Metal–Organic Framework. Chem. A Eur. J. 2020, 26, 1263–1268. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.D.; Moran, M.J.; Aprahamian, I. New Molecular Switch Architectures. Proc. Natl. Acad. Sci. USA 2016, 115, 9414–9422. [Google Scholar] [CrossRef] [PubMed]
- Dattler, D.; Fuks, G.; Heiser, J.; Moulin, E.; Perrot, A.; Yao, X.; Giuseppone, N. Design of Collective Motions from Synthetic Molecular Switches, Rotors, and Motors. Chem. Rev. 2020, 120, 310–433. [Google Scholar] [CrossRef] [PubMed]
- Kassem, S.; van Leeuwen, T.; Lubbe, A.S.; Wilson, M.R.; Feringa, B.L.; Leigh, D.A. Artificial Molecular Motors. Chem. Soc. Rev. 2017, 46, 2592–2621. [Google Scholar] [CrossRef] [PubMed]
- Pianowski, Z.L. Recent Implementations of Molecular Photoswitches into Smart Materials and Biological Systems. Chem. A Eur. J. 2019, 25, 5128–5144. [Google Scholar] [CrossRef]
- Fitzmaurice, O.; Bartkowski, M.; Giordani, S. Molecular Switches—Tools for Imparting Control in Drug Delivery Systems. Front. Chem. 2022, 10, 859450. [Google Scholar] [CrossRef]
- Amirjalayer, S. Photonic Materials: On the Molecular Mechanism of a Photo-Responsive Phase Change Memory (Adv. Theory Simul. 5/2021). Adv. Theory Simul. 2021, 4, 2170009. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q. Light-Driven Chiral Molecular Switches or Motors in Liquid Crystals. Adv. Mater. 2012, 24, 1926–1945. [Google Scholar] [CrossRef]
- Tsivgoulis, G.M.; Lehn, J.-M. Photonic Molecular Devices: Reversibly Photoswitchable Fluorophores for Nondestructive Readout for Optical Memory. Angew. Chem. Int. Ed. Engl. 1995, 34, 1119–1122. [Google Scholar] [CrossRef]
- Amirjalayer, S.; Martinez-Cuezva, A.; Berna, J.; Woutersen, S.; Buma, W.J. Photoinduced Pedalo-Type Motion in an Azodicarboxamide-Based Molecular Switch. Angew. Chem. 2018, 130, 1810–1814. [Google Scholar] [CrossRef]
- Conti, I.; Buma, W.J.; Buma, W.J.; Garavelli, M.; Amirjalayer, S.; Amirjalayer, S.; Amirjalayer, S. Photoinduced Forward and Backward Pedalo-Type Motion of a Molecular Switch. J. Phys. Chem. Lett. 2020, 11, 4741–4746. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Garibay, M.A. Nanoscale Gadgets. Nat. Mater 2008, 7, 431–432. [Google Scholar] [CrossRef]
- Davis, J.J.; Orlowski, G.A.; Rahman, H.; Beer, P.D. Mechanically Interlocked and Switchable Molecules at Surfaces. Chem. Commun. 2010, 46, 54–63. [Google Scholar] [CrossRef]
- Fahrenbach, A.C.; Warren, S.C.; Incorvati, J.T.; Avestro, A.-J.; Barnes, J.C.; Stoddart, J.F.; Grzybowski, B.A. Organic Switches for Surfaces and Devices. Adv. Mater. 2013, 25, 331–348. [Google Scholar] [CrossRef]
- Xu, G.; Li, S.; Liu, C.; Wu, S. Photoswitchable Adhesives Using Azobenzene-Containing Materials. Chem. Asian. J. 2020, 15, 547–554. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Luo, J. Nonadiabatic Dynamics Simulation of Photoisomerization Mechanism of Photoswitch Azodicarboxamide: Hydrogen Bonding Effects. J. Photochem. Photobiol. A Chem. 2018, 367, 236–239. [Google Scholar] [CrossRef]
- Conti, I.; Garavelli, M.; Orlandi, G. The Different Photoisomerization Efficiency of Azobenzene in the Lowest Nπ* and Ππ* Singlets: The Role of a Phantom State. J. Am. Chem. Soc. 2008, 130, 5216–5230. [Google Scholar] [CrossRef] [PubMed]
- Aleotti, F.; Nenov, A.; Salvigni, L.; Bonfanti, M.; El-Tahawy, M.M.; Giunchi, A.; Gentile, M.; Spallacci, C.; Ventimiglia, A.; Cirillo, G.; et al. Spectral Tuning and Photoisomerization Efficiency in Push–Pull Azobenzenes: Designing Principles. J. Phys. Chem. A 2020, 124, 9513–9523. [Google Scholar] [CrossRef] [PubMed]
- Weingart, O.; Nenov, A.; Altoè, P.; Rivalta, I.; Segarra-Martí, J.; Dokukina, I.; Garavelli, M. COBRAMM 2.0—A Software Interface for Tailoring Molecular Electronic Structure Calculations and Running Nanoscale (QM/MM) Simulations. J. Mol. Model. 2018, 24, 271. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.; et al. Gaussian 09 (Revision A02); Gaussian Inc.: Wallingford CT, USA, 2009. [Google Scholar]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; de Vico, L.; Fdez Galván, I.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations across the Periodic Table. J. Comput. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef]
- Case, D.; Ben-Shalom, I.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.; Cruzeiro, V.W.D.; Darden, T.; Duke, R.; Ghoreishi, D.; Gilson, M.; et al. Amber 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Cieplak, P.; Caldwell, J.; Kollman, P. Molecular Mechanical Models for Organic and Biological Systems Going beyond the Atom Centered Two Body Additive Approximation: Aqueous Solution Free Energies of Methanol and N-Methyl Acetamide, Nucleic Acid Base, and Amide Hydrogen Bonding and Chloroform/Water Partition Coefficients of the Nucleic Acid Bases. J. Comput. Chem. 2001, 22, 1048–1057. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Bearpark, M.J.; Robb, M.A.; Bernhard Schlegel, H. A Direct Method for the Location of the Lowest Energy Point on a Potential Surface Crossing. Chem. Phys. Lett. 1994, 223, 269–274. [Google Scholar] [CrossRef]
- Du, L.; Lan, Z. An On-the-Fly Surface-Hopping Program JADE for Nonadiabatic Molecular Dynamics of Polyatomic Systems: Implementation and Applications. J. Chem. Theory Comput. 2015, 11, 1360–1374. [Google Scholar] [CrossRef]
- Kobus, M.; Lieder, M.; Nguyen, P.H.; Stock, G. Simulation of Transient Infrared Spectra of a Photoswitchable Peptide. J. Chem. Phys. 2011, 135, 225102. [Google Scholar] [CrossRef] [PubMed]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford Univ. Press: New York, NY, USA, 1995. [Google Scholar]
- Pollard, W.T.; Lee, S.; Mathies, R.A. Wave Packet Theory of Dynamic Absorption Spectra in Femtosecond Pump–Probe Experiments. J. Chem. Phys. 1990, 92, 4012–4029. [Google Scholar] [CrossRef]
- Kubo, R. A Stochastic Theory of Line Shape. In Advances in Chemical Physics; Advances in Chemical Physics: Hoboken, NJ, USA, 1969; pp. 101–127. ISBN 9780470143605. [Google Scholar]
- Tanimura, Y. Stochastic Liouville, Langevin, Fokker–Planck, and Master Equation Approaches to Quantum Dissipative Systems. J. Physical. Soc. Jpn. 2006, 75, 082001. [Google Scholar] [CrossRef]
- Reiher, M.; Neugebauer, J. A Mode-Selective Quantum Chemical Method for Tracking Molecular Vibrations Applied to Functionalized Carbon Nanotubes. J. Chem. Phys. 2003, 118, 1634–1641. [Google Scholar] [CrossRef]


| MIN S0 | Min S1 | CIcis-trans | CIplan | |||||
|---|---|---|---|---|---|---|---|---|
| Parameters | Gas | CHCl3 | Gas | CHCl3 | Gas | CHCl3 | Gas | CHCl3 |
| α(N-C-N-N) | 106.4° | 103.1° | 175.8° | 178.8° | −179° | 170° | 178° | 176° |
| β(N-N-C-N) | −107.4° | −115° | 178.1° | 176.1° | 179° | 170° | 179° | 178° |
| γ(C-N-N-C) | 179.9° | 175.9° | −174° | 177.7° | −112° | 125° | −160° | 176° |
| CNN | 109.7° | 110° | 125.2° | 125.8° | 123° | 130° | 135° | 138° |
| NNC | 109.8° | 109.7° | 123.6° | 122.5° | 124° | 124° | 136° | 133° |
| CASPT2(18,12) | CAM-B3LYP | |||||
|---|---|---|---|---|---|---|
| Electronic Transition (Weight) | Energy (eV/nm) | o.s. | Electronic Transition (Weight) | Energy (eV/nm) | o.s. | |
| S1 | nN → π*N (0.85) | 2.64/470 | 0.00 | nN → π*N (0.66) | 2.79/444 | 0.00 |
| S2 | nO2 → π*N (0.47) π3 → π*N (0.28) | 4.48/277 | 0.02 | π3 → π*N (0.67) | 4.74/262 | 0.00 |
| S3 | π3 → π*N (0.33) π4 → π*N (0.31) | 4.54/273 | 0.01 | π4 → π*N (0.69) | 4.75/261 | 0.01 |
| S4 | π4 → π*N (0.51) π3 → π*N (0.19) | 4.54/273 | 0.01 | nO2 → π*N (0.68) | 5.02/247 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taddei, M.; Garavelli, M.; Amirjalayer, S.; Conti, I.; Nenov, A. Modus Operandi of a Pedalo-Type Molecular Switch: Insight from Dynamics and Theoretical Spectroscopy. Molecules 2023, 28, 816. https://doi.org/10.3390/molecules28020816
Taddei M, Garavelli M, Amirjalayer S, Conti I, Nenov A. Modus Operandi of a Pedalo-Type Molecular Switch: Insight from Dynamics and Theoretical Spectroscopy. Molecules. 2023; 28(2):816. https://doi.org/10.3390/molecules28020816
Chicago/Turabian StyleTaddei, Mario, Marco Garavelli, Saeed Amirjalayer, Irene Conti, and Artur Nenov. 2023. "Modus Operandi of a Pedalo-Type Molecular Switch: Insight from Dynamics and Theoretical Spectroscopy" Molecules 28, no. 2: 816. https://doi.org/10.3390/molecules28020816
APA StyleTaddei, M., Garavelli, M., Amirjalayer, S., Conti, I., & Nenov, A. (2023). Modus Operandi of a Pedalo-Type Molecular Switch: Insight from Dynamics and Theoretical Spectroscopy. Molecules, 28(2), 816. https://doi.org/10.3390/molecules28020816







