Incorporation of a Boron–Nitrogen Covalent Bond Improves the Charge-Transport and Charge-Transfer Characteristics of Organoboron Small-Molecule Acceptors for Organic Solar Cells
Abstract
1. Introduction
2. Results and Discussion
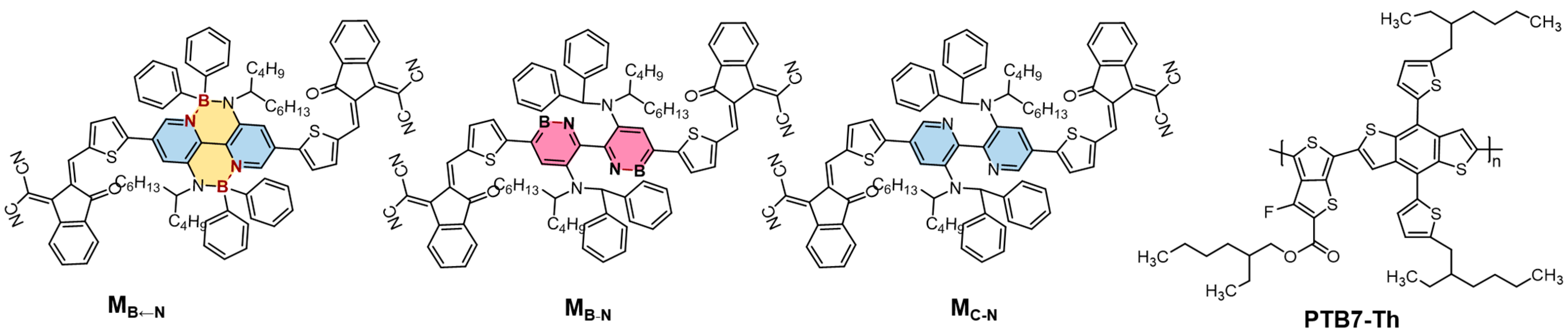
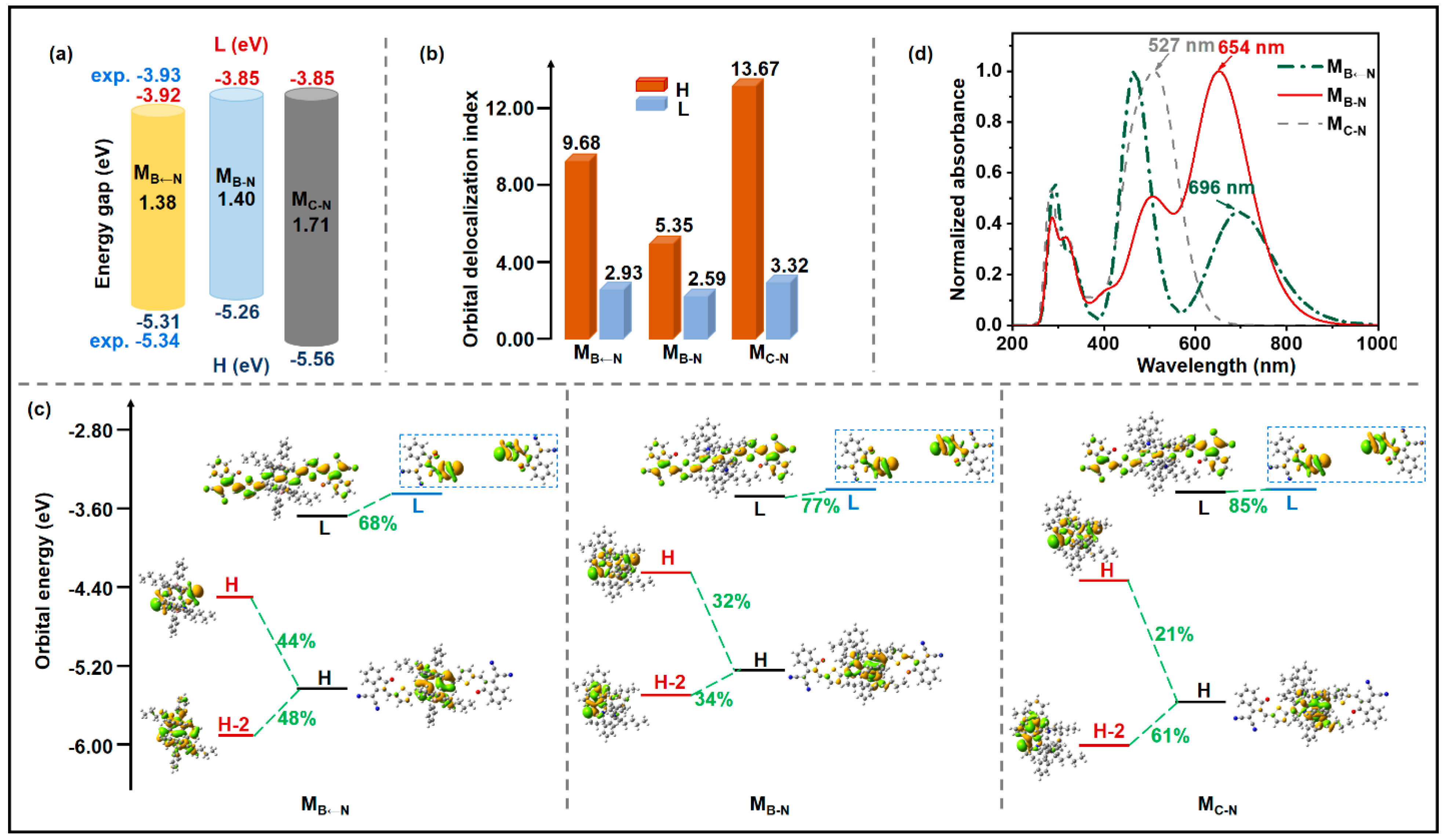
2.1. Monomolecular Characteristics
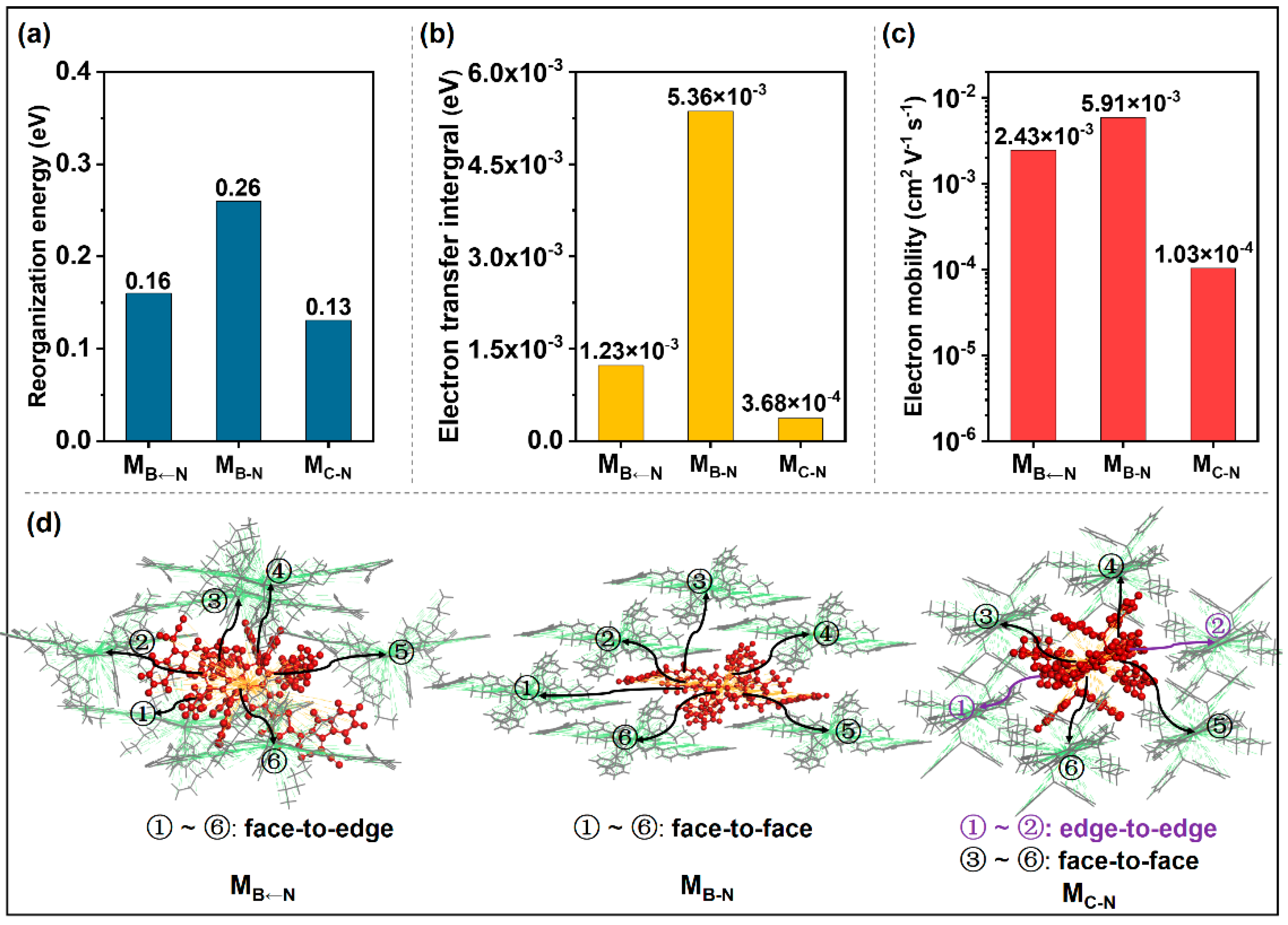
2.2. Acceptor/Acceptor Charge Transport Properties
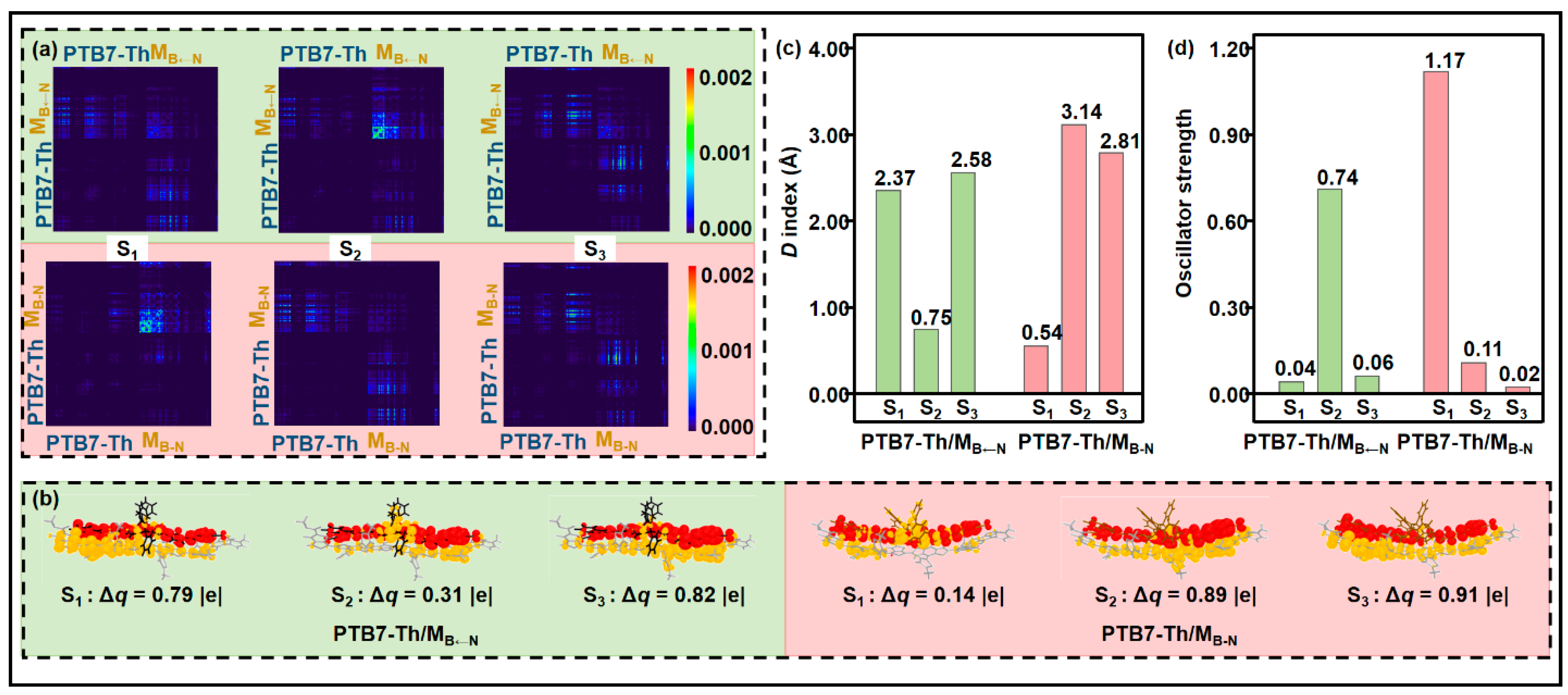
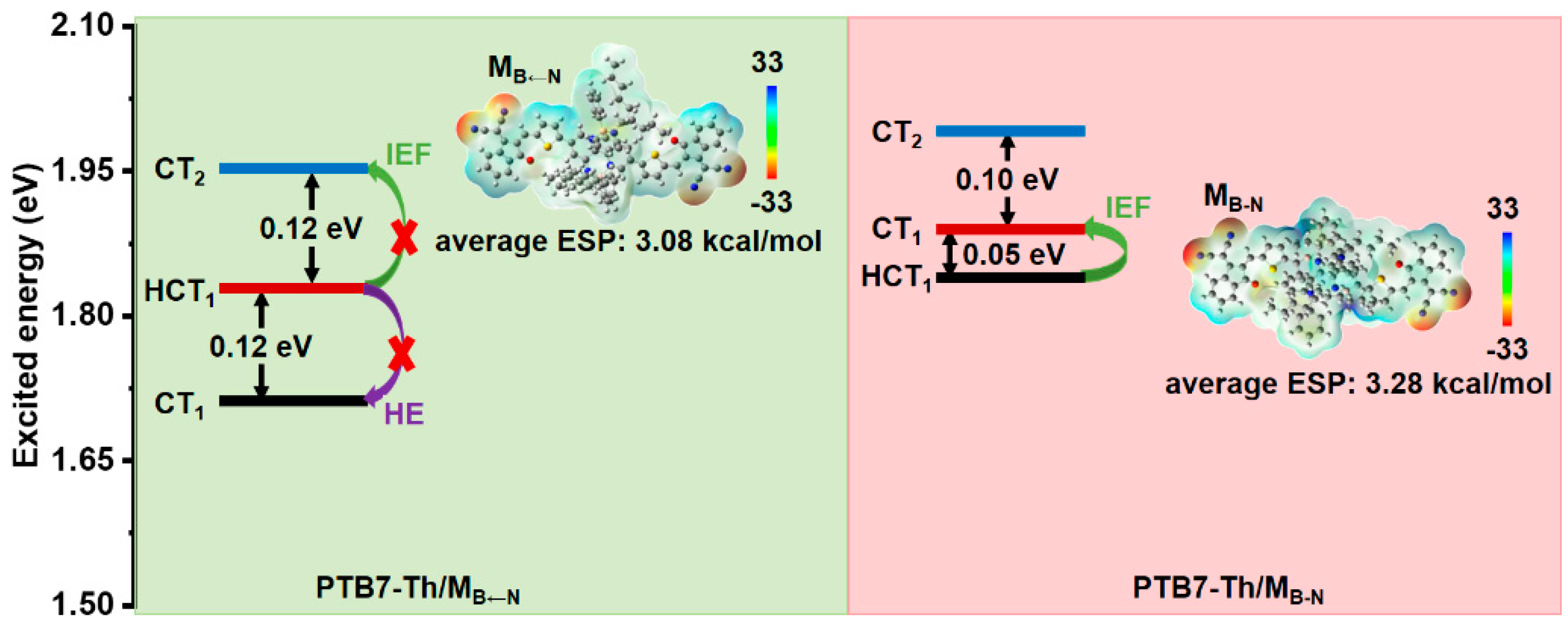
2.3. Donor/Acceptor Interfacial Charge Transfer Performance
3. Computational Methods
3.1. Computational Details
3.2. Orbital Delocalization Index
3.3. Electron Mobility
3.4. Net Transferred Charge
3.5. D Index
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Kim, H.J.; Godumala, M.; Kim, S.K.; Yoon, J.; Kim, C.Y.; Park, H.; Kwon, J.H.; Cho, M.J.; Choi, D.H. Color-Tunable Boron-Based Emitters Exhibiting Aggregation-Induced Emission and Thermally Activated Delayed Fluorescence for Efficient Solution-Processable Nondoped Deep-Blue to Sky-Blue OLEDs. Adv. Opt. Mater. 2020, 8, 1902175. [Google Scholar] [CrossRef]
- Lu, L.; He, J.; Wu, P.; Wu, Y.; Chao, Y.; Li, H.; Tao, D.; Fan, L.; Li, H.; Zhu, W. Taming electronic properties of boron nitride nanosheets as metal-free catalysts for aerobic oxidative desulfurization of fuels. Green Chem. 2018, 20, 4453–4460. [Google Scholar] [CrossRef]
- Lu, H.; Chen, K.; Bobba, R.S.; Shi, J.; Li, M.; Wang, Y.; Xue, J.; Xue, P.; Zheng, X.; Thorn, K.E.; et al. Simultaneously Enhancing Exciton/Charge Transport in Organic Solar Cells by an Organoboron Additive. Adv. Mater. 2022, 34, 2205926. [Google Scholar] [CrossRef] [PubMed]
- Kothavale, S.S.; Lee, J.Y. Three- and Four-Coordinate, Boron-Based, Thermally Activated Delayed Fluorescent Emitters. Adv. Opt. Mater. 2020, 8, 2000922. [Google Scholar] [CrossRef]
- Ma, X.D.; Tian, Z.W.; Jia, R.; Bai, F.Q. B–N counterpart of biphenylene network: A theoretical investigation. Appl. Surf. Sci. 2022, 598, 153674. [Google Scholar] [CrossRef]
- Hatakeyama, T.; Hashimoto, S.; Seki, S.; Nakamura, M. Synthesis of BN-fused polycyclic aromatics via tandem intramolecular electrophilic arene borylation. J. Am. Chem. Soc. 2011, 133, 18614–18617. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Lin, H.R.; Lei, T.; Yang, D.C.; Zhuang, F.D.; Wang, J.Y.; Yuan, S.C.; Pei, J. Azaborine compounds for organic field-effect transistors: Efficient synthesis, remarkable stability, and BN dipole interactions. Angew. Chem. Int. Ed. 2013, 52, 3117–3120. [Google Scholar] [CrossRef]
- Wang, J.Y.; Pei, J. BN-embedded aromatics for optoelectronic applications. Chin. Chem. Lett. 2016, 27, 1139–1146. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhuang, F.D.; Zhou, X.; Yang, D.C.; Wang, J.Y.; Pei, J. Influence of alkyl chain length on the solid-state properties and transistor performance of BN-substituted tetrathienonaphthalenes. J. Mater. Chem. C 2014, 2, 8152–8161. [Google Scholar] [CrossRef]
- Dou, C.; Ding, Z.; Zhang, Z.; Xie, Z.; Liu, J.; Wang, L. Developing conjugated polymers with high electron affinity by replacing a C-C unit with a B←N unit. Angew. Chem. Int. Ed. 2015, 54, 3648–3652. [Google Scholar] [CrossRef]
- Shao, X.; Liu, M.; Liu, J.; Wang, L. A Resonating B, N Covalent Bond and Coordination Bond in Aromatic Compounds and Conjugated Polymers. Angew. Chem. Int. Ed. 2022, 61, e202205893. [Google Scholar] [CrossRef]
- Grandl, M.; Schepper, J.; Maity, S.; Peukert, A.; von Hauff, E.; Pammer, F. N→B Ladder Polymers Prepared by Postfunctionalization: Tuning of Electron Affinity and Evaluation as Acceptors in All-Polymer Solar Cells. Macromolecules 2019, 52, 1013–1024. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Wang, L. Polymer Acceptors Containing B←N Units for Organic Photovoltaics. Acc. Chem. Res. 2020, 53, 1557–1567. [Google Scholar] [CrossRef]
- de la Torre, G.; Bottari, G.; Torres, T. Phthalocyanines and Subphthalocyanines: Perfect Partners for Fullerenes and Carbon Nanotubes in Molecular Photovoltaics. Adv. Energy Mater. 2017, 7, 1601700. [Google Scholar] [CrossRef]
- Miao, J.; Wang, Y.; Liu, J.; Wang, L. Organoboron molecules and polymers for organic solar cell applications. Chem. Soc. Rev. 2022, 51, 153–187. [Google Scholar] [CrossRef]
- Ikeda, N.; Oda, S.; Matsumoto, R.; Yoshioka, M.; Fukushima, D.; Yoshiura, K.; Yasuda, N.; Hatakeyama, T. Solution-Processable Pure Green Thermally Activated Delayed Fluorescence Emitter Based on the Multiple Resonance Effect. Adv. Mater. 2020, 32, 2004072. [Google Scholar] [CrossRef] [PubMed]
- Park, I.S.; Min, H.; Yasuda, T. Ultrafast Triplet-Singlet Exciton Interconversion in Narrowband Blue Organoboron Emitters Doped with Heavy Chalcogens. Angew. Chem. Int. Ed. 2022, 61, e202205684. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, Y.; Dai, H.; Li, G.; Liu, M.; Meng, G.; Zeng, X.; Huang, T.; Wang, L.; Peng, Q.; et al. Mesityl-Functionalized Multi-Resonance Organoboron Delayed Fluorescent Frameworks with Wide-Range Color Tunability for Narrowband OLEDs. Angew. Chem. Int. Ed. 2022, 61, e202206916. [Google Scholar]
- Yan, Z.P.; Yuan, L.; Zhang, Y.; Mao, M.X.; Liao, X.J.; Ni, H.X.; Wang, Z.H.; An, Z.; Zheng, Y.X.; Zuo, J.L. A Chiral Dual-Core Organoboron Structure Realizes Dual-Channel Enhanced Ultrapure Blue Emission and Highly Efficient Circularly Polarized Electroluminescence. Adv. Mater. 2022, 34, 2204253. [Google Scholar] [CrossRef]
- Cheon, H.J.; Woo, S.J.; Baek, S.H.; Lee, J.H.; Kim, Y.H. Dense Local Triplet States and Steric Shielding of Multi-Resonance TADF Emitter Enables High-Performance Deep Blue OLEDs. Adv. Mater. 2022, 34, 2207416. [Google Scholar] [CrossRef]
- Gurubasavaraj, P.M.; Sajjan, V.P.; Munoz-Flores, B.M.; Jimenez Perez, V.M.; Hosmane, N.S. Recent Advances in BODIPY Compounds: Synthetic Methods, Optical and Nonlinear Optical Properties, and Their Medical Applications. Molecules 2022, 27, 1877. [Google Scholar] [CrossRef]
- Nowicki, K.; Pacholak, P.; Lulinski, S. Heteroelement Analogues of Benzoxaborole and Related Ring Expanded Systems. Molecules 2021, 26, 5464. [Google Scholar] [CrossRef]
- Dou, C.; Long, X.; Ding, Z.; Xie, Z.; Liu, J.; Wang, L. An Electron-Deficient Building Block Based on the B←N Unit: An Electron Acceptor for All-Polymer Solar Cells. Angew. Chem. Int. Ed. 2016, 55, 1436–1440. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Wang, N.; Yu, Y.; Liu, J. Organoboron Polymer for 10% Efficiency All-Polymer Solar Cells. Chem. Mater. 2020, 32, 1308–1314. [Google Scholar] [CrossRef]
- Liu, F.; Ding, Z.; Liu, J.; Wang, L. An organoboron compound with a wide absorption spectrum for solar cell applications. Chem. Commun. 2017, 53, 12213–12216. [Google Scholar] [CrossRef]
- Liu, F.; Liu, J.; Wang, L. Effect of fluorine substitution in organoboron electron acceptors for photovoltaic application. Org. Chem. Front. 2019, 6, 1996–2003. [Google Scholar] [CrossRef]
- Morgan, M.M.; Patrick, E.A.; Rautiainen, J.M.; Tuononen, H.M.; Piers, W.E.; Spasyuk, D.M. Zirconocene-Based Methods for the Preparation of BN-Indenes: Application to the Synthesis of 1,5-Dibora-4a,8a-diaza-1,2,3,5,6,7-hexaaryl-4,8-dimethyl-s-indacenes. Organometallics 2017, 36, 2541–2551. [Google Scholar] [CrossRef]
- Morgan, M.M.; Nazari, M.; Pickl, T.; Rautiainen, J.M.; Tuononen, H.M.; Piers, W.E.; Welch, G.C.; Gelfand, B.S. Boron-nitrogen substituted dihydroindeno[1,2-b]fluorene derivatives as acceptors in organic solar cells. Chem. Commun. 2019, 55, 11095–11098. [Google Scholar] [CrossRef]
- Liu, X.; Pang, S.; Zeng, L.; Deng, W.; Yang, M.; Yuan, X.; Li, J.; Duan, C.; Huang, F.; Cao, Y. An electron acceptor featuring a B-N covalent bond and small singlet-triplet gap for organic solar cells. Chem. Commun. 2022, 58, 8686–8689. [Google Scholar] [CrossRef]
- Blom, P.W.M.; Mihailetchi, V.D.; Koster, L.J.A.; Markov, D.E. Device Physics of Polymer:Fullerene Bulk Heterojunction Solar Cells. Adv. Mater. 2007, 19, 1551–1566. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, N. Enhanced Performance and Stability of Ternary Organic Solar Cells Utilizing Two Similar Structure Blend Fullerene-Free Molecules as Electron Acceptor. Adv. Opt. Mater. 2019, 7, 1901241. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Q.; Guo, X.; Li, W.; Guo, B.; Su, W.; Ou, X.; Zhang, M. High-performance nonfullerene polymer solar cells based on a fluorinated wide bandgap copolymer with a high open-circuit voltage of 1.04 V. J. Mater. Chem. A 2017, 5, 22180–22185. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J.; Jakle, F. Electron-Deficient Conjugated Materials via p-π* Conjugation with Boron: Extending Monomers to Oligomers, Macrocycles, and Polymers. Chem. Eur. J. 2021, 27, 2973–2986. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, N. Small Energy Loss and Broad Energy Levels Offsets Lead to Efficient Ternary Polymer Solar Cells from a Blend of Two Fullerene-Free Small Molecules as Electron Acceptors. Adv. Opt. Mater. 2019, 7, 1900913. [Google Scholar] [CrossRef]
- Li, S.Y.; Sun, Z.B.; Zhao, C.H. Charge-Transfer Emitting Triarylborane pi-Electron Systems. Inorg. Chem. 2017, 56, 8705–8717. [Google Scholar] [CrossRef]
- Li, C.; Song, J.; Cai, Y.; Han, G.; Zheng, W.; Yi, Y.; Ryu, H.S.; Woo, H.Y.; Sun, Y. Heteroatom substitution-induced asymmetric A–D–A type non-fullerene acceptor for efficient organic solar cells. J. Energy Chem. 2020, 40, 144–150. [Google Scholar] [CrossRef]
- Jeon, S.J.; Kim, Y.H.; Kim, I.N.; Yang, N.G.; Yun, J.H.; Moon, D.K. Utilizing 3,4-ethylenedioxythiophene (EDOT)-bridged non-fullerene acceptors for efficient organic solar cells. J. Energy Chem. 2022, 65, 194–204. [Google Scholar] [CrossRef]
- Wu, J.; Liao, Y.; Wu, S.X.; Li, H.B.; Su, Z.M. Phenylcarbazole and phosphine oxide/sulfide hybrids as host materials for blue phosphors: Effectively tuning the charge injection property without influencing the triplet energy. Phys. Chem. Chem. Phys. 2012, 14, 1685–1693. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Yan, X.; Lu, T.; Zheng, W.; Xiong, W. Bonding Character, Electron Delocalization, and Aromaticity of Cyclo[18]Carbon (C18) Precursors, C18-(CO)n (n = 6, 4, and 2): Focusing on the Effect of Carbonyl (-CO) Groups. Chem. Eur. J. 2022, 28, e202103815. [Google Scholar]
- Wu, J.; Wu, S.; Geng, Y.; Yang, G.; Muhammad, S.; Jin, J.; Liao, Y.; Su, Z. Theoretical study on dithieno[3,2-b:2’,3’-d]phosphole derivatives: High-efficiency blue-emitting materials with ambipolar semiconductor behavior. Theor. Chem. Acc. 2010, 127, 419–427. [Google Scholar] [CrossRef]
- Lin, H.; Wang, Q. Non-fullerene small molecule electron acceptors for high-performance organic solar cells. J. Energy Chem. 2018, 27, 990–1016. [Google Scholar] [CrossRef]
- Aldrich, T.J.; Matta, M.; Zhu, W.; Swick, S.M.; Stern, C.L.; Schatz, G.C.; Facchetti, A.; Melkonyan, F.S.; Marks, T.J. Fluorination Effects on Indacenodithienothiophene Acceptor Packing and Electronic Structure, End-Group Redistribution, and Solar Cell Photovoltaic Response. J. Am. Chem. Soc. 2019, 141, 3274–3287. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.J.; Zhao, Z.W.; Geng, Y.; Pan, Q.Q.; Gu, H.Y.; Zhao, L.; Zhang, M.; Wu, S.X.; Su, Z.M. Can we utilize the higher Frenkel exciton state in biazulene diimides-based non-fullerene acceptors to promote charge separation at the donor/acceptor interface? New J. Chem. 2020, 44, 9767–9774. [Google Scholar] [CrossRef]
- Xia, K.; Li, Y.; Wang, Y.; Portilla, L.; Pecunia, V. Narrowband-Absorption-Type Organic Photodetectors for the Far-Red Range Based on Fullerene-Free Bulk Heterojunctions. Adv. Opt. Mater. 2020, 8, 1902056. [Google Scholar] [CrossRef]
- Jia, Z.; Qin, S.; Meng, L.; Ma, Q.; Angunawela, I.; Zhang, J.; Li, X.; He, Y.; Lai, W.; Li, N.; et al. High performance tandem organic solar cells via a strongly infrared-absorbing narrow bandgap acceptor. Nat. Commun. 2021, 12, 178. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, C.; Yuan, J.; Zhou, L.; Liu, W.; Xia, X.; Hong, J.; Chen, H.; Wei, Q.; Lu, X.; et al. Optimizing side chains on different nitrogen aromatic rings achieving 17% efficiency for organic photovoltaics. J. Energy Chem. 2022, 65, 173–178. [Google Scholar] [CrossRef]
- Guo, Y.; Han, G.; Duan, R.; Geng, H.; Yi, Y. Boosting the electron mobilities of dimeric perylenediimides by simultaneously enhancing intermolecular and intramolecular electronic interactions. J. Mater. Chem. A 2018, 6, 14224–14230. [Google Scholar] [CrossRef]
- Koh, S.E.; Risko, C.; da Silva Filho, D.A.; Kwon, O.; Facchetti, A.; Brédas, J.L.; Marks, T.J.; Ratner, M.A. Modeling Electron and Hole Transport in Fluoroarene-Oligothiopene Semiconductors: Investigation of Geometric and Electronic Structure Properties. Adv. Funct. Mater. 2008, 18, 332–340. [Google Scholar] [CrossRef]
- Kupgan, G.; Chen, X.K.; Brédas, J.L. Molecular packing of non-fullerene acceptors for organic solar cells: Distinctive local morphology in Y6 vs. ITIC derivatives. Mater. Today Adv. 2021, 11, 100154. [Google Scholar] [CrossRef]
- Dassault Systemes. One Molecular Simulation Software. Available online: https://www.accelrys.com (accessed on 28 October 2017).
- Shuai, Z.; Wang, L.; Li, Q. Evaluation of charge mobility in organic materials: From localized to delocalized descriptions at a first-principles level. Adv. Mater. 2011, 23, 1145–1153. [Google Scholar] [CrossRef]
- Li, G.; Feng, L.W.; Mukherjee, S.; Jones, L.; Jacobberger, R.; Huang, W.; Young, R.M.; Pankow, R.M.; Zhu, W.; Lu, N.; et al. Non-Fullerene Acceptors with Direct and Indirect Hexa-fluorination Afford >17% Efficiency in Polymer Solar Cells. Energy Environ. Sci. 2022, 15, 645–659. [Google Scholar] [CrossRef]
- Wang, L.; Nan, G.; Yang, X.; Peng, Q.; Li, Q.; Shuai, Z. Computational methods for design of organic materials with high charge mobility. Chem. Soc. Rev. 2010, 39, 423–434. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.F.; Zeng, J.C.; Zhuang, F.D.; Zhao, K.X.; Sun, Z.H.; Yao, Z.F.; Lu, Y.; Wang, X.Y.; Wang, J.Y.; Pei, J. Parent B2N2-Perylenes with Different BN Orientations. Angew. Chem. Int. Ed. 2021, 60, 23313–23319. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Yao, Z.F.; Wang, Z.Y.; Zeng, J.C.; Ding, L.; Xiong, M.; Wang, J.Y.; Pei, J. “Spine Surgery” of Perylene Diimides with Covalent B-N Bonds toward Electron-Deficient BN-Embedded Polycyclic Aromatic Hydrocarbons. J. Am. Chem. Soc. 2022, 144, 3091–3098. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Du, C.Z.; Chen, X.Y.; Fu, L.; Gao, R.R.; Yao, Z.F.; Wang, J.Y.; Hu, W.; Pei, J.; Wang, X.Y. BN-Anthracene for High-Mobility Organic Optoelectronic Materials through Periphery Engineering. Angew. Chem. Int. Ed. 2022, 61, e202201464. [Google Scholar]
- Oh, C.M.; Jang, S.; Lee, J.; Park, S.H.; Hwang, I.W. Versatile control of concentration gradients in non-fullerene acceptor-based bulk heterojunction films using solvent rinse treatments. Green Energy Environ. 2022, 7, 1102–1110. [Google Scholar] [CrossRef]
- Cao, Z.; Yang, S.; Wang, B.; Shen, X.; Han, G.; Yi, Y. Multi-channel exciton dissociation in D18/Y6 complexes for high-efficiency organic photovoltaics. J. Mater. Chem. A 2020, 8, 20408–20413. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, X.; Wu, H.; Feng, G.; Wu, H.; Li, J.; Yi, Y.; Feng, X.; Ma, Z.; Li, W.; et al. Increasing donor-acceptor spacing for reduced voltage loss in organic solar cells. Nat. Commun. 2021, 12, 6679. [Google Scholar] [CrossRef]
- Rahmanudin, A.; Yao, L.; Jeanbourquin, X.A.; Liu, Y.; Sekar, A.; Ripaud, E.; Sivula, K. Melt-processing of small molecule organic photovoltaics via bulk heterojunction compatibilization. Green Chem. 2018, 20, 2218–2224. [Google Scholar] [CrossRef]
- Holmes, N.P.; Munday, H.; Barr, M.G.; Thomsen, L.; Marcus, M.A.; Kilcoyne, A.L.D.; Fahy, A.; van Stam, J.; Dastoor, P.C.; Moons, E. Unravelling donor–acceptor film morphology formation for environmentally-friendly OPV ink formulations. Green Chem. 2019, 21, 5090–5103. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Pan, Q.Q.; Geng, Y.; Wu, Y.; Zhao, L.; Zhang, M.; Su, Z.M. Theoretical Insight into Multiple Charge-Transfer Mechanisms at the P3HT/Nonfullerenes Interface in Organic Solar Cells. ACS Sustain. Chem. Eng. 2019, 7, 19699–19707. [Google Scholar] [CrossRef]
- Zarrabi, N.; Sandberg, O.J.; Zeiske, S.; Li, W.; Riley, D.B.; Meredith, P.; Armin, A. Charge-generating mid-gap trap states define the thermodynamic limit of organic photovoltaic devices. Nat. Commun. 2020, 11, 5567. [Google Scholar] [CrossRef]
- Gao, F.; Inganas, O. Charge generation in polymer-fullerene bulk-heterojunction solar cells. Phys. Chem. Chem. Phys. 2014, 16, 20291–20304. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Li, Q.S.; Li, Z.S. End-capped group manipulation of indacenodithienothiophene-based non-fullerene small molecule acceptors for efficient organic solar cells. Nanoscale 2020, 12, 17795–17804. [Google Scholar] [CrossRef] [PubMed]
- Vandewal, K.; Albrecht, S.; Hoke, E.T.; Graham, K.R.; Widmer, J.; Douglas, J.D.; Schubert, M.; Mateker, W.R.; Bloking, J.T.; Burkhard, G.F.; et al. Efficient charge generation by relaxed charge-transfer states at organic interfaces. Nat. Mater. 2013, 13, 63–68. [Google Scholar] [CrossRef]
- Shi, X.; Yang, Y.; Wang, L.; Li, Y. Introducing Asymmetry Induced by Benzene Substitution in a Rigid Fused π Spacer of D−π–A-Type Solar Cells: A Computational Investigation. J. Phys. Chem. C 2019, 123, 4007–4021. [Google Scholar] [CrossRef]
- Yao, C.; Yang, Y.; Li, L.; Bo, M.; Zhang, J.; Peng, C.; Huang, Z.; Wang, J. Elucidating the Key Role of the Cyano (−C≡N) Group to Construct Environmentally Friendly Fused-Ring Electron Acceptors. J. Phys. Chem. C 2020, 124, 23059–23068. [Google Scholar] [CrossRef]
- Sobolewski, A.L. Organic photovoltaics without p-n junctions: A computational study of ferroelectric columnar molecular clusters. Phys. Chem. Chem. Phys. 2015, 17, 20580–20587. [Google Scholar] [CrossRef]
- Schwarz, C.; Bassler, H.; Bauer, I.; Koenen, J.M.; Preis, E.; Scherf, U.; Kohler, A. Does conjugation help exciton dissociation? a study on poly(p-phenylene)s in planar heterojunctions with C60 or TNF. Adv. Mater. 2012, 24, 922–925. [Google Scholar] [CrossRef]
- Yao, H.; Cui, Y.; Qian, D.; Ponseca, C.S., Jr.; Honarfar, A.; Xu, Y.; Xin, J.; Chen, Z.; Hong, L.; Gao, B.; et al. 14.7% Efficiency Organic Photovoltaic Cells Enabled by Active Materials with a Large Electrostatic Potential Difference. J. Am. Chem. Soc. 2019, 141, 7743–7750. [Google Scholar] [CrossRef]
- Yao, H.; Qian, D.; Zhang, H.; Qin, Y.; Xu, B.; Cui, Y.; Yu, R.; Gao, F.; Hou, J. Critical Role of Molecular Electrostatic Potential on Charge Generation in Organic Solar Cells. Chin. J. Chem. 2018, 36, 491–494. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Yang, Q.; Muntwiler, M. Charge-transfer excitons at organic semiconductor surfaces and interfaces. Acc. Chem. Res. 2009, 42, 1779–1787. [Google Scholar] [CrossRef]
- Grancini, G.; Maiuri, M.; Fazzi, D.; Petrozza, A.; Egelhaaf, H.J.; Brida, D.; Cerullo, G.; Lanzani, G. Hot exciton dissociation in polymer solar cells. Nat. Mater. 2013, 12, 29–33. [Google Scholar] [CrossRef] [PubMed]
- Iizuka, H.; Nakayama, T. Quantum process of exciton dissociation at organic semiconductor interfaces: Effects of interface roughness and hot exciton. Jpn. J. Appl. Phys. 2016, 55, 021601. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Musgrave, C.B. Comparison of DFT methods for molecular orbital eigenvalue calculations. J. Phys. Chem. A 2007, 111, 1554–1561. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Chem. Phys. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Sokolov, A.N.; Atahan-Evrenk, S.; Mondal, R.; Akkerman, H.B.; Sánchez-Carrera, R.S.; Granados-Focil, S.; Schrier, J.; Mannsfeld, S.C.B.; Zoombelt, A.P.; Bao, Z.; et al. From computational discovery to experimental characterization of a high hole mobility organic crystal. Nat. Commun. 2011, 2, 437. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Geng, Y.; Wu, S.X.; Li, H.B.; Tang, X.D.; Wu, Y.; Su, Z.M.; Liao, Y. A theoretical discussion on the relationships among molecular packings, intermolecular interactions, and electron transport properties for naphthalene tetracarboxylic diimide derivatives. J. Mater. Chem. 2011, 21, 15558–15566. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005, 123, 154101. [Google Scholar] [CrossRef]
- Mennucci, B. Polarizable continuum model. WIREs Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016; Volume 3. [Google Scholar]
- Mahmood, A.; Irfan, A.; Wang, J.L. Molecular level understanding of the chalcogen atom effect on chalcogen-based polymers through electrostatic potential, non-covalent interactions, excited state behaviour, and radial distribution function. Polym. Chem. 2022, 13, 5993–6001. [Google Scholar] [CrossRef]
- Pan, Q.Q.; Li, S.B.; Duan, Y.C.; Wu, Y.; Zhang, J.; Geng, Y.; Zhao, L.; Su, Z.M. Exploring what prompts ITIC to become a superior acceptor in organic solar cell by combining molecular dynamics simulation with quantum chemistry calculation. Phys. Chem. Chem. Phys. 2017, 19, 31227–31235. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Li, P.; Song, C.; Zhang, H. Terminal Modulation of D−π–A Small Molecule for Organic Photovoltaic Materials: A Theoretical Molecular Design. J. Phys. Chem. C 2016, 120, 28939–28950. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 2002, 114, 10024–10035. [Google Scholar] [CrossRef]
- Casewit, C.J.; Colwell, K.S.; Rappe, A.K. Application of a universal force field to organic molecules. J. Am. Chem. Soc. 2002, 114, 10035–10046. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.J. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Tender, L.; Carter, M.T.; Murray, R.W. Cyclic Voltammetric Analysis of Ferrocene Alkanethiol Monolayer Electrode Kinetics Based on Marcus Theory. Anal. Chem. 1994, 66, 3173–3181. [Google Scholar] [CrossRef]
- Mayer, J.M. Understanding Hydrogen Atom Transfer: From Bond Strengths to Marcus Theory. Acc. Chem. Res. 2011, 44, 36–46. [Google Scholar] [CrossRef]
- Cornil, J.; Brédas, J.L.; Zaumseil, J.; Sirringhaus, H. Ambipolar Transport in Organic Conjugated Materials. Adv. Mater. 2007, 19, 1791–1799. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599–610. [Google Scholar] [CrossRef]
- Chen, H.Y.; Chao, I. Effect of perfluorination on the charge-transport properties of organic semiconductors: Density functional theory study of perfluorinated pentacene and sexithiophene. Chem. Phys. Lett. 2005, 401, 539–545. [Google Scholar] [CrossRef]
- Yang, X.; Li, Q.; Shuai, Z. Theoretical modelling of carrier transports in molecular semiconductors: Molecular design of triphenylamine dimer systems. Nanotechnology 2007, 18, 424029. [Google Scholar] [CrossRef]
- Coropceanu, V.; Cornil, J.; da Silva Filho, D.A.; Olivier, Y.; Silbey, R.; Brédas, J.L. Charge Transport in Organic Semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Ding, W.-L.; Li, Q.-S.; Li, Z.-S. Incorporation of a Boron–Nitrogen Covalent Bond Improves the Charge-Transport and Charge-Transfer Characteristics of Organoboron Small-Molecule Acceptors for Organic Solar Cells. Molecules 2023, 28, 811. https://doi.org/10.3390/molecules28020811
Yang J, Ding W-L, Li Q-S, Li Z-S. Incorporation of a Boron–Nitrogen Covalent Bond Improves the Charge-Transport and Charge-Transfer Characteristics of Organoboron Small-Molecule Acceptors for Organic Solar Cells. Molecules. 2023; 28(2):811. https://doi.org/10.3390/molecules28020811
Chicago/Turabian StyleYang, Jie, Wei-Lu Ding, Quan-Song Li, and Ze-Sheng Li. 2023. "Incorporation of a Boron–Nitrogen Covalent Bond Improves the Charge-Transport and Charge-Transfer Characteristics of Organoboron Small-Molecule Acceptors for Organic Solar Cells" Molecules 28, no. 2: 811. https://doi.org/10.3390/molecules28020811
APA StyleYang, J., Ding, W.-L., Li, Q.-S., & Li, Z.-S. (2023). Incorporation of a Boron–Nitrogen Covalent Bond Improves the Charge-Transport and Charge-Transfer Characteristics of Organoboron Small-Molecule Acceptors for Organic Solar Cells. Molecules, 28(2), 811. https://doi.org/10.3390/molecules28020811