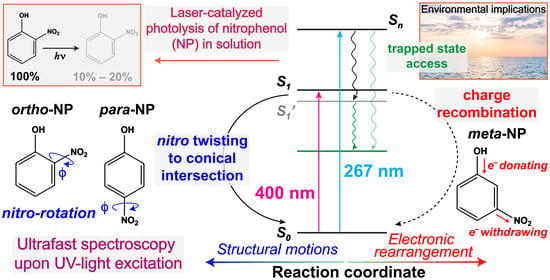
Ultrafast Spectroscopies of Nitrophenols and Nitrophenolates in Solution: From Electronic Dynamics and Vibrational Structures to Photochemical and Environmental Implications
Abstract
1. Introduction
2. Results
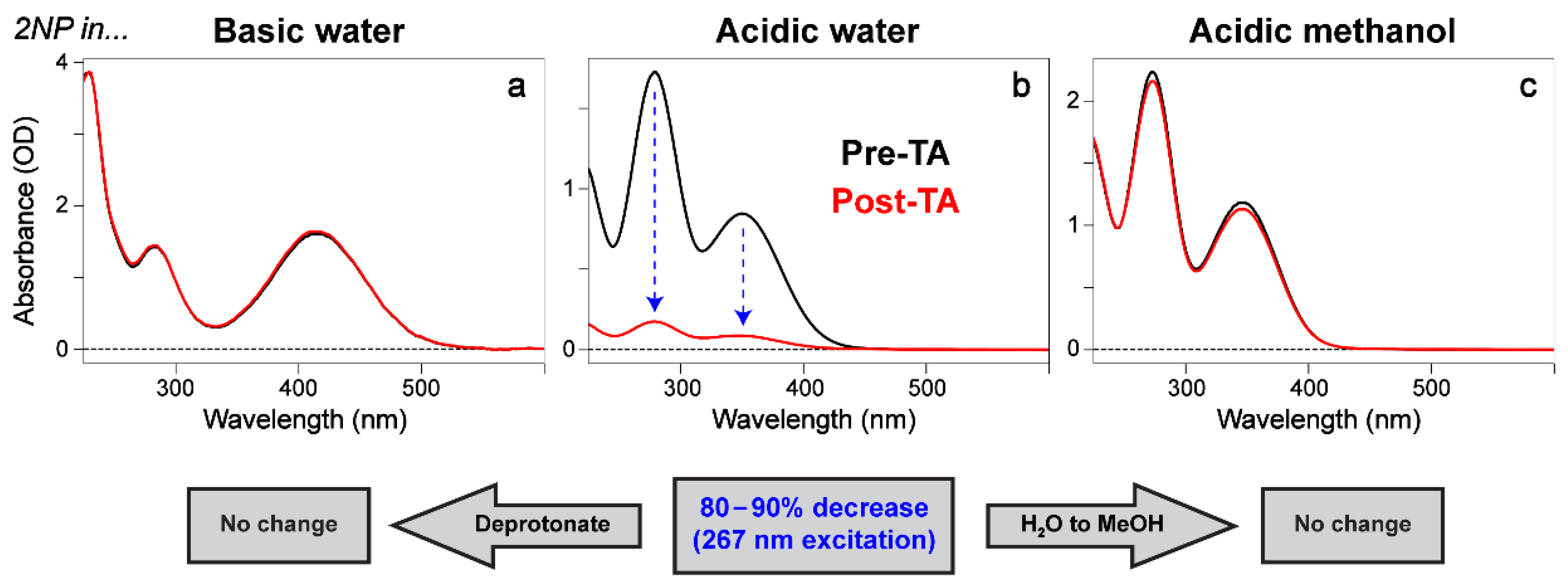
2.1. Steady-State Electronic Spectroscopy of a Series of Nitrophenols and Nitrophenolates in Solution
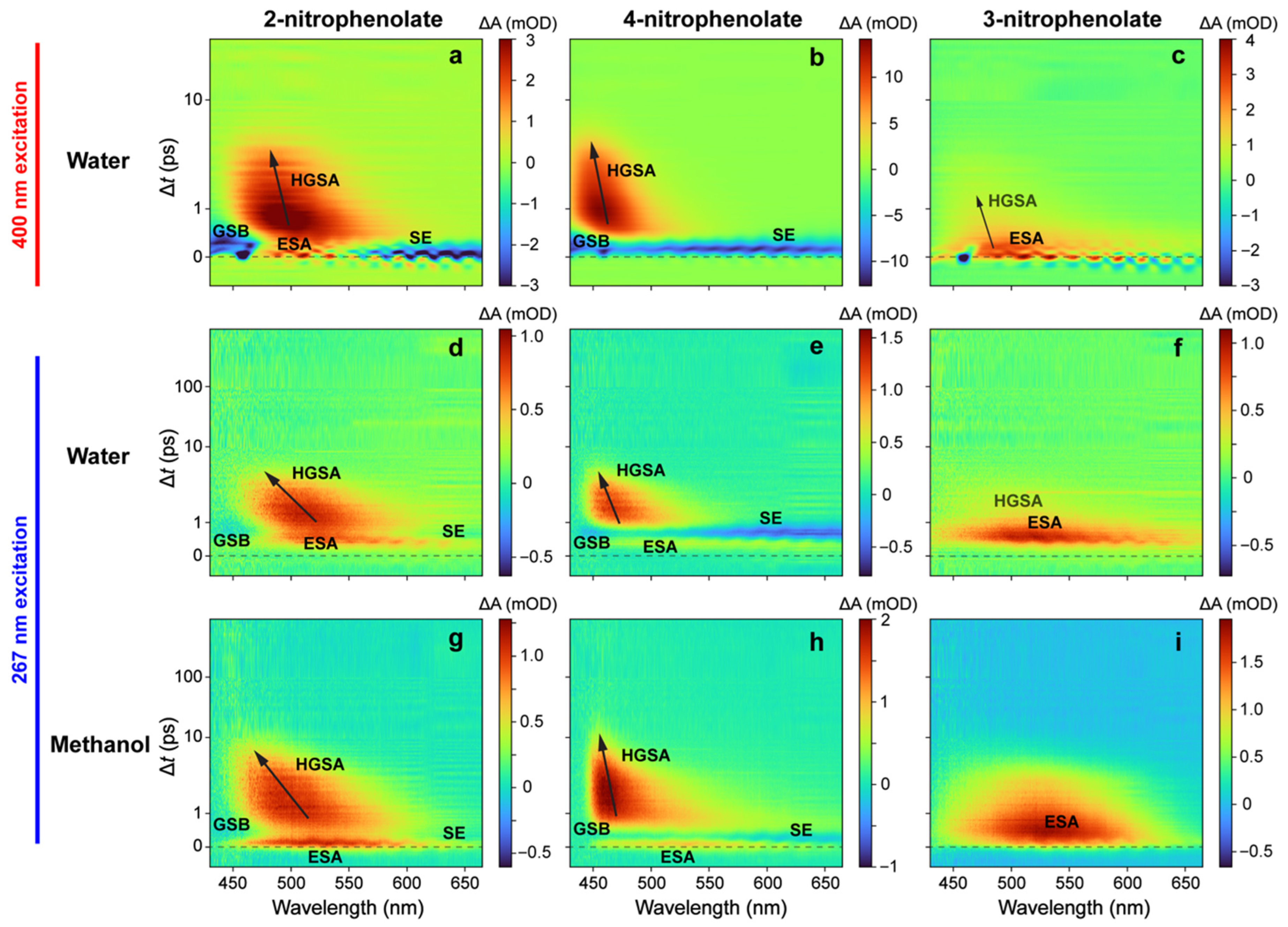
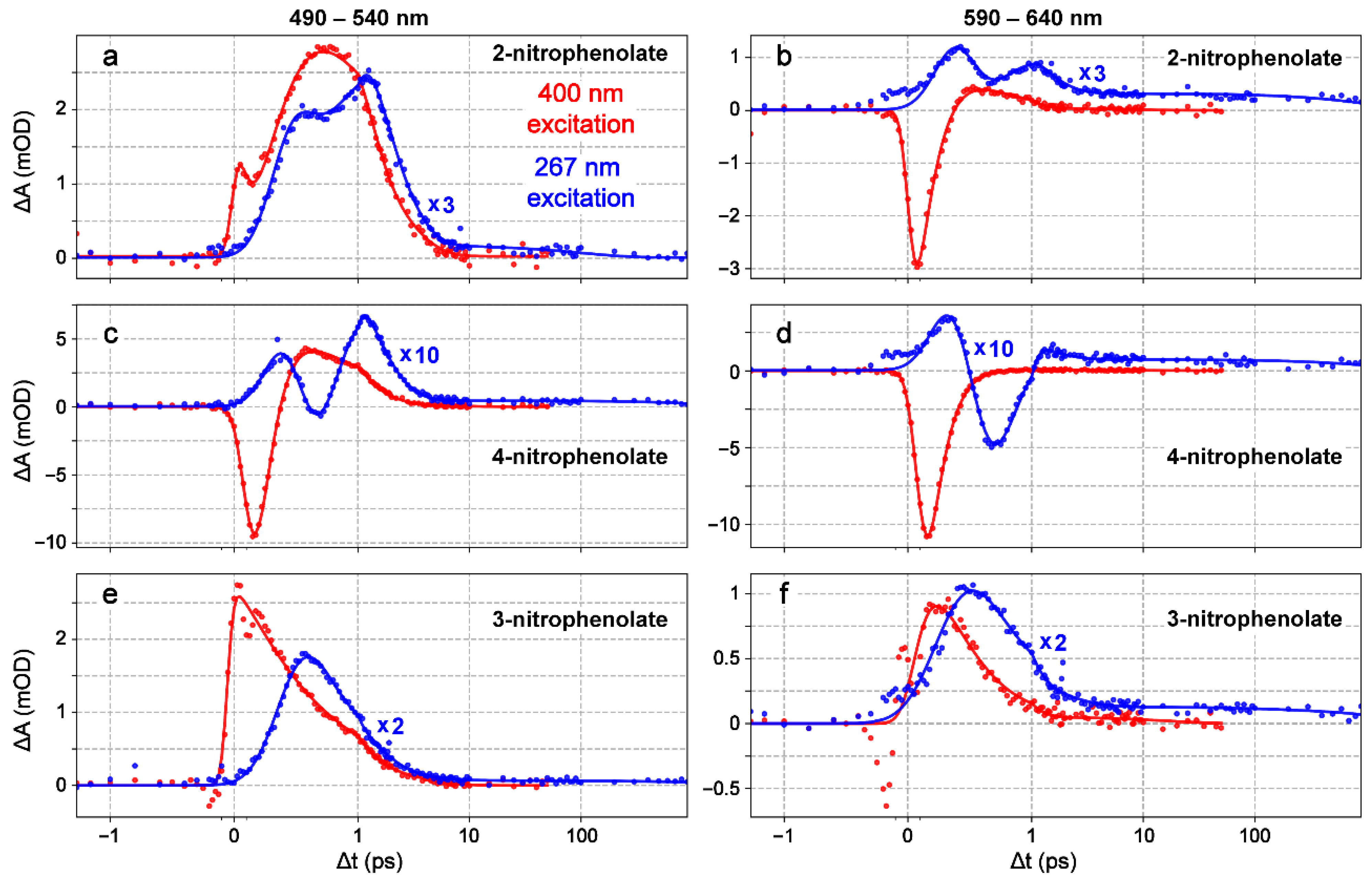
2.2. Ultrafast Electronic Spectroscopy of Nitrophenolates in Water
2.3. Ultrafast Electronic Spectroscopy of Nitrophenolates in Methanol
2.4. Excited-State Quantum Calculations of Nitrophenolates in Water

2.5. Potential Energy Surfaces (PESs) of Nitrophenolates in Water after Photoexcitation
2.6. Fs-TA Spectroscopy of Nitrophenols in Water after 267 nm Excitation
2.7. Fs-TA Spectroscopy of Nitrophenols in Methanol after 267 nm Excitation
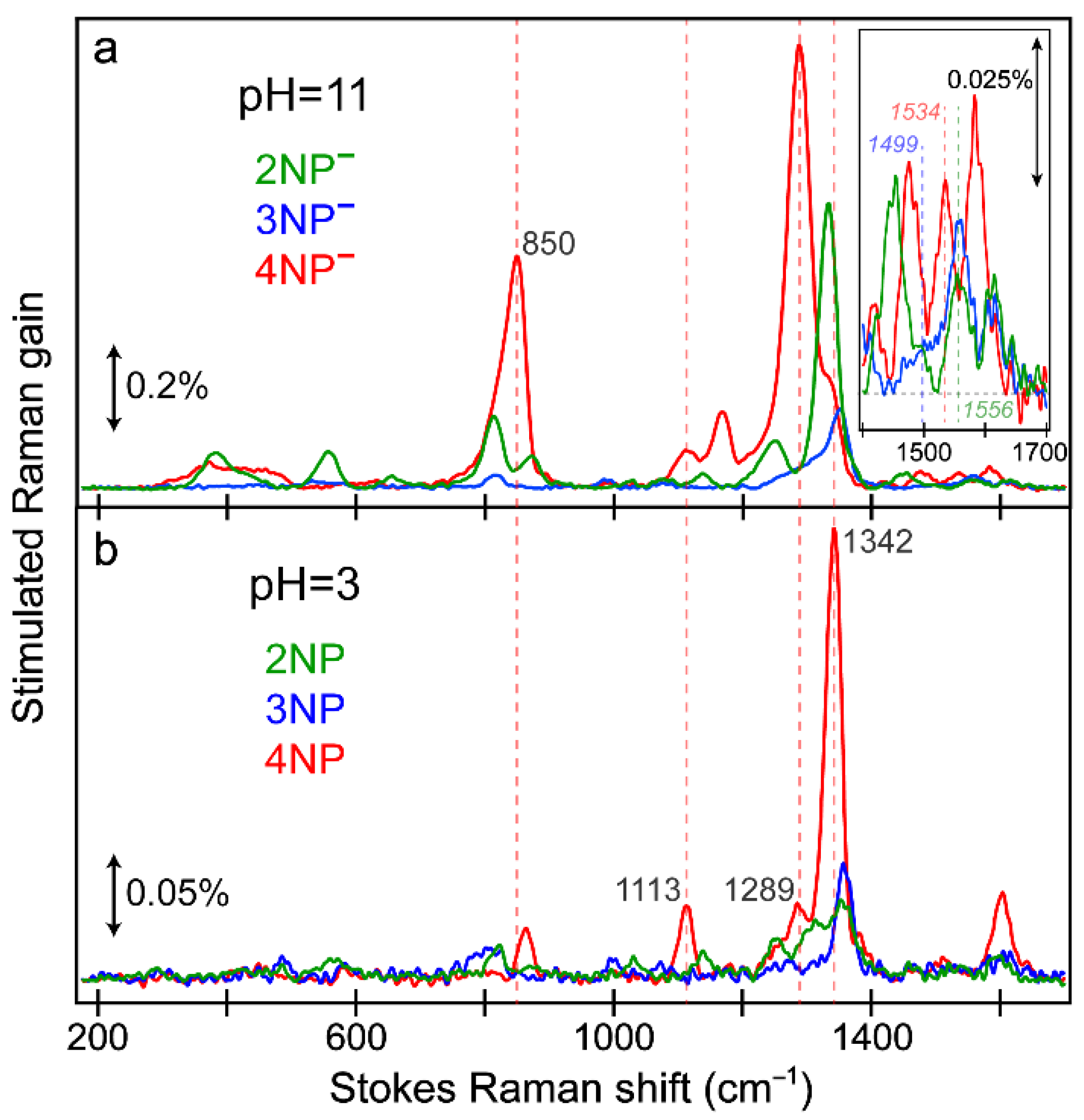
2.8. FSRS Signatures of Nitrophenols and Nitrophenolates in Water
3. Discussion
4. Materials and Methods
4.1. Sample Preparation
4.2. Steady-State Electronic Absorption Measurements
4.3. Femtosecond Stimulated Raman Spectroscopy (FSRS) and Femtosecond Transient Absorption (fs-TA) Spectroscopy
4.4. Quantum Calculations
4.5. Probe-Dependent Spectral Analysis
4.6. Global Analysis
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Schwarzenbach, R.P.; Stierli, R.; Folsom, B.R.; Zeyer, J. Compound properties relevant for assessing the environmental partitioning of nitrophenols. Environ. Sci. Technol. 1988, 22, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Koubaissy, B.; Joly, G.; Magnoux, P. Adsorption and competitive adsorption on zeolites of nitrophenol compounds present in wastewater. Ind. Eng. Chem. Res. 2008, 47, 9558–9565. [Google Scholar] [CrossRef]
- Vione, D.; Maurino, V.; Minero, C.; Duncianu, M.; Olariu, R.-I.; Arsene, C.; Sarakha, M.; Mailhot, G. Assessing the transformation kinetics of 2- and 4-nitrophenol in the atmospheric aqueous phase. Implications for the distribution of both nitroisomers in the atmosphere. Atmos. Environ. 2009, 43, 2321–2327. [Google Scholar] [CrossRef]
- Uberoi, V.; Bhattacharya, S.K. Toxicity and degradability of nitrophenols in anaerobic systems. Water Environ. Res. 1997, 69, 146–156. [Google Scholar] [CrossRef]
- Kovacic, P.; Somanathan, R. Nitroaromatic compounds: Environmental toxicity, carcinogenicity, mutagenicity, therapy and mechanism. J. Appl. Toxicol. 2014, 34, 810–824. [Google Scholar] [CrossRef]
- Majewska, M.; Khan, F.; Pieta, I.S.; Wróblewska, A.; Szmigielski, R.; Pieta, P. Toxicity of selected airborne nitrophenols on eukaryotic cell membrane models. Chemosphere 2021, 266, 128996. [Google Scholar] [CrossRef]
- Atkinson, R. Atmospheric chemistry of VOCs and NOx. Atmos. Environ. 2000, 34, 2063–2101. [Google Scholar] [CrossRef]
- Harrison, M.A.J.; Barra, S.; Borghesi, D.; Vione, D.; Arsene, C.; Iulian Olariu, R. Nitrated phenols in the atmosphere: A review. Atmos. Environ. 2005, 39, 231–248. [Google Scholar] [CrossRef]
- Bejan, I.; Abd El Aal, Y.; Barnes, I.; Benter, T.; Bohn, B.; Wiesen, P.; Kleffmann, J. The photolysis of ortho-nitrophenols: A new gas phase source of HONO. Phys. Chem. Chem. Phys. 2006, 8, 2028–2035. [Google Scholar] [CrossRef]
- Sangwan, M.; Zhu, L. Absorption cross sections of 2-nitrophenol in the 295–400 nm region and photolysis of 2-nitrophenol at 308 and 351 nm. J. Phys. Chem. A 2016, 120, 9958–9967. [Google Scholar] [CrossRef]
- Xu, J.; Wang, B.; Zhang, W.-h.; Zhang, F.-J.; Deng, Y.-d.; Wang, Y.; Gao, J.-J.; Tian, Y.-S.; Peng, R.-H.; Yao, Q.-H. Biodegradation of p-nitrophenol by engineered strain. AMB Expr. 2021, 11, 124. [Google Scholar] [CrossRef] [PubMed]
- Wanko, M.; Houmøller, J.; Støchkel, K.; Suhr Kirketerp, M.-B.; Petersen, M.Å.; Nielsen, M.B.; Nielsen, S.B.; Rubio, A. Substitution effects on the absorption spectra of nitrophenolate isomers. Phys. Chem. Chem. Phys. 2012, 14, 12905–12911. [Google Scholar] [CrossRef] [PubMed]
- Vereecken, L.; Chakravarty, H.K.; Bohn, B.; Lelieveld, J. Theoretical study on the formation of H- and O-atoms, HONO, OH, NO, and NO2 from the lowest lying singlet and triplet states in ortho-nitrophenol photolysis. Int. J. Chem. Kinet. 2016, 48, 785–795. [Google Scholar] [CrossRef]
- Xu, C.; Yu, L.; Zhu, C.; Yu, J.; Cao, Z. Intersystem crossing-branched excited-state intramolecular proton transfer for o-nitrophenol: An ab initio on-the-fly nonadiabatic molecular dynamic simulation. Sci. Rep. 2016, 6, 26768. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Yin, H.-M.; Sun, J.-L.; Yue, X.-F.; Han, K.-L. The dynamics of OH channel in the 266 and 355 nm photodissociation of 2-nitrophenol. Chem. Phys. Lett. 2008, 463, 340–344. [Google Scholar] [CrossRef]
- Ernst, H.A.; Wolf, T.J.A.; Schalk, O.; González-García, N.; Boguslavskiy, A.E.; Stolow, A.; Olzmann, M.; Unterreiner, A.-N. Ultrafast dynamics of o-nitrophenol: An experimental and theoretical study. J. Phys. Chem. A 2015, 119, 9225–9235. [Google Scholar] [CrossRef]
- Michenfelder, N.C.; Ernst, H.A.; Schweigert, C.; Olzmann, M.; Unterreiner, A.N. Ultrafast stimulated emission of nitrophenolates in organic and aqueous solutions. Phys. Chem. Chem. Phys. 2018, 20, 10713–10720. [Google Scholar] [CrossRef]
- Nitta, Y.; Schalk, O.; Kaneshima, K.; Sekikawa, T. Ultrafast photolysis of o-nitrophenol studied by time-resolved photoelectron spectroscopy. EPJ Web Conf. 2019, 205, 09022. [Google Scholar] [CrossRef]
- Kleffmann, J. Daytime sources of nitrous acid (HONO) in the atmospheric boundary layer. ChemPhysChem 2007, 8, 1137–1144. [Google Scholar] [CrossRef]
- Nitta, Y.; Schalk, O.; Igarashi, H.; Wada, S.; Tsutsumi, T.; Saita, K.; Taketsugu, T.; Sekikawa, T. Real-time probing of an atmospheric photochemical reaction by ultrashort extreme ultraviolet pulses: Nitrous acid release from o-nitrophenol. J. Phys. Chem. Lett. 2021, 12, 674–679. [Google Scholar] [CrossRef]
- Gligorovski, S.; Strekowski, R.; Barbati, S.; Vione, D. Environmental implications of hydroxyl radicals (•OH). Chem. Rev. 2015, 115, 13051–13092. [Google Scholar] [CrossRef] [PubMed]
- Lyngsie, G.; Krumina, L.; Tunlid, A.; Persson, P. Generation of hydroxyl radicals from reactions between a dimethoxyhydroquinone and iron oxide nanoparticles. Sci. Rep. 2018, 8, 10834. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Fang, C. Nitration of tyrosine channels photoenergy through a conical intersection in water. J. Phys. Chem. B 2019, 123, 4915–4928. [Google Scholar] [CrossRef] [PubMed]
- Takezaki, M.; Hirota, N.; Terazima, M. Nonradiative relaxation processes and electronically excited states of nitrobenzene studied by picosecond time-resolved transient grating method. J. Phys. Chem. A 1997, 101, 3443–3448. [Google Scholar] [CrossRef]
- Ciavardini, A.; Coreno, M.; Callegari, C.; Spezzani, C.; De Ninno, G.; Ressel, B.; Grazioli, C.; de Simone, M.; Kivimäki, A.; Miotti, P.; et al. Ultra-fast-VUV photoemission study of UV excited 2-nitrophenol. J. Phys. Chem. A 2019, 123, 1295–1302. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, M.A. Spin—Orbit coupling and the radiationless processes in nitrogen heterocyclics. J. Chem. Phys. 1963, 38, 2834–2838. [Google Scholar] [CrossRef]
- Baba, M. Intersystem crossing in the 1nπ* and 1ππ* states. J. Phys. Chem. A 2011, 115, 9514–9519. [Google Scholar] [CrossRef]
- Szatylowicz, H.; Jezuita, A.; Ejsmont, K.; Krygowski, T.M. Classical and reverse substituent effects in meta- and para-substituted nitrobenzene derivatives. Struct. Chem. 2017, 28, 1125–1132. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Abboud, J.-L.M.; Abraham, M.H.; Taft, R.W. Linear solvation energy relationships. 23. A comprehensive collection of the solvatochromic parameters, π*, α, and β, and some methods for simplifying the generalized solvatochromic equation. J. Org. Chem. 1983, 48, 2877–2887. [Google Scholar] [CrossRef]
- Reichardt, C. Solvatochromic dyes as solvent polarity indicators. Chem. Rev. 1994, 94, 2319–2358. [Google Scholar] [CrossRef]
- Sasaki, S.; Drummen, G.P.C.; Konishi, G.-i. Recent advances in twisted intramolecular charge transfer (TICT) fluorescence and related phenomena in materials chemistry. J. Mater. Chem. C 2016, 4, 2731–2743. [Google Scholar] [CrossRef]
- Kumpulainen, T.; Lang, B.; Rosspeintner, A.; Vauthey, E. Ultrafast elementary photochemical processes of organic molecules in liquid solution. Chem. Rev. 2017, 117, 10826–10939. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Tutol, J.N.; Tang, L.; Zhu, L.; Ong, W.S.Y.; Dodani, S.; Fang, C. Excitation ratiometric chloride sensing in a standalone yellow fluorescent protein is powered by the interplay between proton transfer and conformational reorganization. Chem. Sci. 2021, 12, 11382–11393. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chi, W.; Qiao, Q.; Tan, D.; Xu, Z.; Liu, X. Twisted intramolecular charge transfer (TICT) and twists beyond TICT: From mechanisms to rational designs of bright and sensitive fluorophores. Chem. Soc. Rev. 2021, 50, 12656–12678. [Google Scholar] [CrossRef]
- Agmon, N.; Huppert, D.; Masad, A.; Pines, E. Excited-state proton-transfer to methanol water mixtures. J. Phys. Chem. 1991, 95, 10407–10413. [Google Scholar] [CrossRef]
- Fang, C.; Tang, L.; Chen, C. Unveiling coupled electronic and vibrational motions of chromophores in condensed phases. J. Chem. Phys. 2019, 151, 200901. [Google Scholar] [CrossRef]
- Tang, L.; Wang, Y.; Zhu, L.; Lee, C.; Fang, C. Correlated molecular structural motions for photoprotection after deep-UV irradiation. J. Phys. Chem. Lett. 2018, 9, 2311–2319. [Google Scholar] [CrossRef]
- Krueger, T.D.; Tang, L.; Giesbers, G.; Van Court, R.C.; Zhu, L.; Robinson, S.C.; Ostroverkhova, O.; Fang, C. Ultrafast triplet state formation in a methylated fungi-derived pigment: Toward rational molecular design for sustainable optoelectronics. J. Phys. Chem. C 2021, 125, 17565–17572. [Google Scholar] [CrossRef]
- Ghosh, R.; Palit, D.K. Ultrafast dynamics of the excited states of 1-(p-nitrophenyl)-2-(hydroxymethyl)pyrrolidine. J. Phys. Chem. A 2012, 116, 1993–2005. [Google Scholar] [CrossRef]
- Tilley, A.J.; Pensack, R.D.; Lee, T.S.; Djukic, B.; Scholes, G.D.; Seferos, D.S. Ultrafast triplet formation in thionated perylene diimides. J. Phys. Chem. C 2014, 118, 9996–10004. [Google Scholar] [CrossRef]
- Ostroverkhova, O. Organic optoelectronic materials: Mechanisms and applications. Chem. Rev. 2016, 116, 13279–13412. [Google Scholar] [CrossRef] [PubMed]
- Horng, M.L.; Gardecki, J.A.; Papazyan, A.; Maroncelli, M. Subpicosecond measurements of polar solvation dynamics: Coumarin 153 revisited. J. Phys. Chem. 1995, 99, 17311–17337. [Google Scholar] [CrossRef]
- Oscar, B.G.; Chen, C.; Liu, W.; Zhu, L.; Fang, C. Dynamic Raman line shapes on an evolving excited-state landscape: Insights from tunable femtosecond stimulated Raman spectroscopy. J. Phys. Chem. A 2017, 121, 5428–5441. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Krueger, T.D.; Giesbers, G.; Van Court, R.C.; Zhu, L.; Kim, R.; Beaudry, C.M.; Robinson, S.C.; Ostroverkhova, O.; Fang, C. Ultrafast dynamics and photoresponse of a fungi-derived pigment xylindein from solution to thin films. Chem. Eur. J. 2021, 27, 5627–5631. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.; Tang, L.; Oscar, B.G.; Zhu, L.; Fang, C. Panoramic portrait of primary molecular events preceding excited state proton transfer in water. Chem. Sci. 2016, 7, 5484–5494. [Google Scholar] [CrossRef]
- Stephansen, A.B.; Sølling, T.I. Distortion dependent intersystem crossing: A femtosecond time-resolved photoelectron spectroscopy study of benzene, toluene, and p-xylene. Struct. Dyn. 2017, 4, 044008. [Google Scholar] [CrossRef]
- Isukapalli, S.V.K.; Lekshmi, R.S.; Samanta, P.K.; Vennapusa, S.R. Formation of excited triplet states in naphthalene diimide and perylene diimide derivatives: A detailed theoretical study. J. Chem. Phys. 2020, 153, 124301. [Google Scholar] [CrossRef]
- Tominaga, K.; Walker, G.C.; Jarzeba, W.; Barbara, P.F. Ultrafast charge separation in adma: Experiment, simulation, and theoretical issues. J. Phys. Chem. 1991, 95, 10475–10485. [Google Scholar] [CrossRef]
- Liu, S. Where does the electron go? The nature of ortho/para and meta group directing in electrophilic aromatic substitution. J. Chem. Phys. 2014, 141, 194109. [Google Scholar] [CrossRef]
- Krueger, T.D.; Fang, C. Elucidating inner workings of naturally sourced organic optoelectronic materials with ultrafast spectroscopy. Chem. Eur. J. 2021, 27, 17736–17750. [Google Scholar] [CrossRef]
- Zhao, J.; Ji, S.; Chen, Y.; Guo, H.; Yang, P. Excited state intramolecular proton transfer (ESIPT): From principal photophysics to the development of new chromophores and applications in fluorescent molecular probes and luminescent materials. Phys. Chem. Chem. Phys. 2012, 14, 8803–8817. [Google Scholar] [CrossRef] [PubMed]
- Sedgwick, A.C.; Wu, L.; Han, H.-H.; Bull, S.D.; He, X.-P.; James, T.D.; Sessler, J.L.; Tang, B.Z.; Tian, H.; Yoon, J. Excited-state intramolecular proton-transfer (ESIPT) based fluorescence sensors and imaging agents. Chem. Soc. Rev. 2018, 47, 8842–8880. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Tang, L.; Oscar, B.G.; Chen, C. Capturing structural snapshots during photochemical reactions with ultrafast Raman spectroscopy: From materials transformation to biosensor responses. J. Phys. Chem. Lett. 2018, 9, 3253–3263. [Google Scholar] [CrossRef] [PubMed]
- Krueger, T.D.; Boulanger, S.A.; Zhu, L.; Tang, L.; Fang, C. Discovering a rotational barrier within a charge-transfer state of a photoexcited chromophore in solution. Struct. Dyn. 2020, 7, 024901. [Google Scholar] [CrossRef] [PubMed]
- Ishag, M.I.O.; Moseley, P.G.N. Effects of UV light on dilute aqueous solutions of m- and p-nitrophenol. Tetrahedron 1977, 33, 3141–3144. [Google Scholar] [CrossRef]
- Alif, A.; Pilichowski, J.-F.; Boule, P. Photochemistry and environment XIII: Phototransformation of 2-nitrophenol in aqueous solution. J. Photochem. Photobiol. A 1991, 59, 209–219. [Google Scholar] [CrossRef]
- Rabbani, M.; Bathaee, H.; Rahimi, R.; Maleki, A. Photocatalytic degradation of p-nitrophenol and methylene blue using Zn-TCPP/Ag doped mesoporous TiO2 under UV and visible light irradiation. Desalin. Water Treat. 2016, 57, 25848–25856. [Google Scholar] [CrossRef]
- Tang, K.-C.; Chang, M.-J.; Lin, T.-Y.; Pan, H.-A.; Fang, T.-C.; Chen, K.-Y.; Hung, W.-Y.; Hsu, Y.-H.; Chou, P.-T. Fine tuning the energetics of excited-state intramolecular proton transfer (ESIPT): White light generation in a single ESIPT system. J. Am. Chem. Soc. 2011, 133, 17738–17745. [Google Scholar] [CrossRef]
- Xia, S.-H.; Xie, B.-B.; Fang, Q.; Cui, G.; Thiel, W. Excited-state intramolecular proton transfer to carbon atoms: Nonadiabatic surface-hopping dynamics simulations. Phys. Chem. Chem. Phys. 2015, 17, 9687–9697. [Google Scholar] [CrossRef]
- Jankowska, J.; Sobolewski, A.L. Modern theoretical approaches to modeling the excited-state intramolecular proton transfer: An overview. Molecules 2021, 26, 5140. [Google Scholar] [CrossRef]
- Boulanger, S.A.; Chen, C.; Myasnyanko, I.N.; Baranov, M.S.; Fang, C. Fluorescence modulation of ortho-green fluorescent protein chromophores following ultrafast proton transfer in solution. J. Phys. Chem. B 2022, 126, 5081–5093. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Tang, L.; Oscar, B.G.; Wang, Y.; Chen, C.; Fang, C. Tracking ultrafast vibrational cooling during excited state proton transfer reaction with anti-Stokes and Stokes femtosecond stimulated Raman spectroscopy. J. Phys. Chem. Lett. 2017, 8, 997–1003. [Google Scholar] [CrossRef] [PubMed]
- Ferrante, C.; Batignani, G.; Pontecorvo, E.; Montemiglio, L.C.; Vos, M.H.; Scopigno, T. Ultrafast dynamics and vibrational relaxation in six-coordinate heme proteins revealed by femtosecond stimulated Raman spectroscopy. J. Am. Chem. Soc. 2020, 142, 2285–2292. [Google Scholar] [CrossRef] [PubMed]
- Shenje, L.; Qu, Y.; Popik, V.; Ullrich, S. Femtosecond photodecarbonylation of photo-ODIBO studied by stimulated Raman spectroscopy and density functional theory. Phys. Chem. Chem. Phys. 2021, 23, 25637–25648. [Google Scholar] [CrossRef]
- Myers, A.B.; Mathies, R.A. Resonance Raman intensities: A probe of excited-state structure and dynamics. In Biological Applications of Raman Spectroscopy; Spiro, T.G., Ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1987; Volume 2, pp. 1–58. [Google Scholar]
- Hoffman, D.P.; Mathies, R.A. Femtosecond stimulated Raman exposes the role of vibrational coherence in condensed-phase photoreactivity. Acc. Chem. Res. 2016, 49, 616–625. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Romei, M.G.; Boxer, S.G. Structural evidence of photoisomerization pathways in fluorescent proteins. J. Am. Chem. Soc. 2019, 141, 15504–15508. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-i.; Tang, L.; Mirabedini, P.; Yokoi, A.; Muratli, J.M.; Guo, Q.; Lerner, M.M.; Gotoh, K.; Greaney, P.A.; Fang, C.; et al. [LiCl2]− superhalide: A new charge carrier for graphite cathode of dual-ion batteries. Adv. Funct. Mater. 2022, 32, 2112709. [Google Scholar] [CrossRef]
- McCamant, D.W.; Kukura, P.; Yoon, S.; Mathies, R.A. Femtosecond broadband stimulated Raman spectroscopy: Apparatus and methods. Rev. Sci. Instrum. 2004, 75, 4971–4980. [Google Scholar] [CrossRef]
- Kukura, P.; McCamant, D.W.; Mathies, R.A. Femtosecond stimulated Raman spectroscopy. Annu. Rev. Phys. Chem. 2007, 58, 461–488. [Google Scholar] [CrossRef]
- Fang, C.; Frontiera, R.R.; Tran, R.; Mathies, R.A. Mapping GFP structure evolution during proton transfer with femtosecond Raman spectroscopy. Nature 2009, 462, 200–204. [Google Scholar] [CrossRef]
- Mallick, B.; Lakhsmanna, A.; Umapathy, S. Ultrafast Raman loss spectroscopy (URLS): Instrumentation and principle. J. Raman Spectrosc. 2011, 42, 1883–1890. [Google Scholar] [CrossRef]
- Pontecorvo, E.; Ferrante, C.; Elles, C.G.; Scopigno, T. Spectrally tailored narrowband pulses for femtosecond stimulated Raman spectroscopy in the range 330–750 nm. Opt. Express 2013, 21, 6866–6872. [Google Scholar] [CrossRef] [PubMed]
- Dietze, D.R.; Mathies, R.A. Femtosecond stimulated Raman spectroscopy. ChemPhysChem 2016, 17, 1224–1251. [Google Scholar] [CrossRef] [PubMed]
- Hall, C.R.; Conyard, J.; Heisler, I.A.; Jones, G.; Frost, J.; Browne, W.R.; Feringa, B.L.; Meech, S.R. Ultrafast dynamics in light-driven molecular rotary motors probed by femtosecond stimulated Raman spectroscopy. J. Am. Chem. Soc. 2017, 139, 7408–7414. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, R.K.; Kayal, S.; Barak, A.; Orr-Ewing, A.J.; Umapathy, S. Intermolecular hydrogen bonding controlled intersystem crossing rates of benzophenone. J. Phys. Chem. Lett. 2018, 9, 1642–1648. [Google Scholar] [CrossRef]
- Batignani, G.; Ferrante, C.; Scopigno, T. Accessing excited state molecular vibrations by femtosecond stimulated Raman spectroscopy. J. Phys. Chem. Lett. 2020, 11, 7805–7813. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, L.; Fang, C. Femtosecond stimulated Raman line shapes: Dependence on resonance conditions of pump and probe pulses. Chin. J. Chem. Phys. 2018, 31, 492–502. [Google Scholar] [CrossRef]
- Quick, M.; Dobryakov, A.L.; Kovalenko, S.A.; Ernsting, N.P. Resonance femtosecond-stimulated Raman spectroscopy without actinic excitation showing low-frequency vibrational activity in the S2 state of all-trans β-carotene. J. Phys. Chem. Lett. 2015, 6, 1216–1220. [Google Scholar] [CrossRef]
- Ni, F.; Thomas, L.; Cotton, T.M. Surface-enhanced resonance Raman spectroscopy as an ancillary high-performance liquid chromatography dectector for nitrophenol compounds. Anal. Chem. 1989, 61, 888–894. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Wang, H.-G.; Zhang, S.-Q.; Pei, K.-M.; Zheng, X.; Lee Phillips, D. Resonance Raman intensity analysis of the excited state proton transfer dynamics of 2-nitrophenol in the charge-transfer band absorption. J. Chem. Phys. 2006, 125, 214506. [Google Scholar] [CrossRef]
- Oscar, B.G.; Zhu, L.; Wolfendeen, H.; Rozanov, N.D.; Chang, A.; Stout, K.T.; Sandwisch, J.W.; Porter, J.J.; Mehl, R.A.; Fang, C. Dissecting optical response and molecular structure of fluorescent proteins with non-canonical chromophores. Front. Mol. Biosci. 2020, 7, 131. [Google Scholar] [CrossRef] [PubMed]
- Dreuw, A.; Head-Gordon, M. Failure of time-dependent density functional theory for long-range charge-transfer excited states: The zincbacteriochlorin−bacteriochlorin and bacteriochlorophyll−spheroidene complexes. J. Am. Chem. Soc. 2004, 126, 4007–4016. [Google Scholar] [CrossRef] [PubMed]
- Mester, D.; Kállay, M. Charge-transfer excitations within density functional theory: How accurate are the most recommended approaches? J. Chem. Theory Comput. 2022, 18, 1646–1662. [Google Scholar] [CrossRef] [PubMed]
- Jen, M.; Lee, S.; Jeon, K.; Hussain, S.; Pang, Y. Ultrafast intramolecular proton transfer of alizarin investigated by femtosecond stimulated Raman spectroscopy. J. Phys. Chem. B 2017, 121, 4129–4136. [Google Scholar] [CrossRef]
- Simkovitch, R.; Shomer, S.; Gepshtein, R.; Huppert, D. How fast can a proton-transfer reaction be beyond the solvent-control limit? J. Phys. Chem. B 2015, 119, 2253–2262. [Google Scholar] [CrossRef]
- Lee, S.; Jen, M.; Jang, T.; Lee, G.; Pang, Y. Twisted intramolecular charge transfer of nitroaromatic push–pull chromophores. Sci. Rep. 2022, 12, 6557. [Google Scholar] [CrossRef]
- Liebel, M.; Schnedermann, C.; Wende, T.; Kukura, P. Principles and applications of broadband impulsive vibrational spectroscopy. J. Phys. Chem. A 2015, 119, 9506–9517. [Google Scholar] [CrossRef]
- Kuramochi, H.; Takeuchi, S.; Tahara, T. Femtosecond time-resolved impulsive stimulated Raman spectroscopy using sub-7-fs pulses: Apparatus and applications. Rev. Sci. Instrum. 2016, 87, 043107. [Google Scholar]
- Batignani, G.; Sansone, C.; Ferrante, C.; Fumero, G.; Mukamel, S.; Scopigno, T. Excited-state energy surfaces in molecules revealed by impulsive stimulated Raman excitation profiles. J. Phys. Chem. Lett. 2021, 12, 9239–9247. [Google Scholar] [CrossRef]
- Martínez, C.H.R.; Dardonville, C. Rapid determination of ionization constants (pKa) by UV spectroscopy using 96-well microtiter plates. ACS Med. Chem. Lett. 2013, 4, 142–145. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, W.; Fang, C. A versatile femtosecond stimulated Raman spectroscopy setup with tunable pulses in the visible to near infrared. Appl. Phys. Lett. 2014, 105, 041106. [Google Scholar]
- Tang, L.; Zhu, L.; Taylor, M.A.; Wang, Y.; Remington, S.J.; Fang, C. Excited state structural evolution of a GFP single-site mutant tracked by tunable femtosecond-stimulated Raman spectroscopy. Molecules 2018, 23, 2226. [Google Scholar] [CrossRef] [PubMed]
- Hong, M.J.; Zhu, L.; Chen, C.; Tang, L.; Lin, Y.-H.; Li, W.; Johnson, R.; Chattopadhyay, S.; Snaith, H.J.; Fang, C.; et al. Time-resolved changes in dielectric constant of metal halide perovskites under illumination. J. Am. Chem. Soc. 2020, 142, 19799–19803. [Google Scholar] [CrossRef] [PubMed]
- Tachibana, S.R.; Tang, L.; Chen, C.; Zhu, L.; Takeda, Y.; Fushimi, K.; Seevers, T.K.; Narikawa, R.; Sato, M.; Fang, C. Transient electronic and vibrational signatures during reversible photoswitching of a cyanobacteriochrome photoreceptor. Spectrochim. Acta A 2021, 250, 119379. [Google Scholar] [CrossRef]
- Chiu, N.-C.; Nord, M.T.; Tang, L.; Lancaster, L.S.; Hirschi, J.S.; Wolff, S.K.; Hutchinson, E.M.; Goulas, K.A.; Stickle, W.F.; Zuehlsdorff, T.J.; et al. Designing dual-functional metal–organic frameworks for photocatalysis. Chem. Mater. 2022, 34, 8798–8807. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, L.; Baranov, M.S.; Tang, L.; Baleeva, N.S.; Smirnov, A.Y.; Yampolsky, I.V.; Solntsev, K.M.; Fang, C. Photoinduced proton transfer of GFP-inspired fluorescent superphotoacids: Principles and design. J. Phys. Chem. B 2019, 123, 3804–3821. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Van Stokkum, I.H.M.; Larsen, D.S.; van Grondelle, R. Global and target analysis of time-resolved spectra. Biochim. Biophys. Acta 2004, 1657, 82–104. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liu, W.; Baranov, M.S.; Baleeva, N.S.; Yampolsky, I.V.; Zhu, L.; Wang, Y.; Shamir, A.; Solntsev, K.M.; Fang, C. Unveiling structural motions of a highly fluorescent superphotoacid by locking and fluorinating the GFP chromophore in solution. J. Phys. Chem. Lett. 2017, 8, 5921–5928. [Google Scholar] [CrossRef] [PubMed]
- Snellenburg, J.J.; Laptenok, S.P.; Seger, R.; Mullen, K.M.; van Stokkum, I.H.M. Glotaran: A Java-based graphical user interface for the R-package TIMP. J. Stat. Softw. 2012, 49, 1–22. [Google Scholar] [CrossRef]
- Snellenburg, J.J.; Laptenok, S.P.; DeSa, R.J.; Naumov, P.; Solntsev, K.M. Excited-state dynamics of oxyluciferin in firefly luciferase. J. Am. Chem. Soc. 2016, 138, 16252–16258. [Google Scholar] [CrossRef]
- Schweigert, N.; Zehnder, A.J.B.; Eggen, R.I.L. Chemical properties of catechols and their molecular modes of toxic action in cells, from microorganisms to mammals. Environ. Microbiol. 2001, 3, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Romero, R.; Salgado, P.R.; Soto, C.; Contreras, D.; Melin, V. An experimental validated computational method for pKa determination of substituted 1,2-dihydroxybenzenes. Front. Chem. 2018, 6, 208. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.A.P.; Turner, R.J.; Horbury, M.D.; Hine, N.D.M.; Stavros, V.G. Examining solvent effects on the ultrafast dynamics of catechol. J. Chem. Phys. 2019, 151, 084305. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, W.; Tang, L.; Oscar, B.G.; Han, F.; Fang, C. Early time excited-state structural evolution of pyranine in methanol revealed by femtosecond stimulated Raman spectroscopy. J. Phys. Chem. A 2013, 117, 6024–6042. [Google Scholar] [CrossRef]
- He, X.; Bell, A.F.; Tonge, P.J. Ground state isomerization of a model green fluorescent protein chromophore. FEBS Lett. 2003, 549, 35–38. [Google Scholar] [CrossRef]
- Nibbering, E.T.J.; Fidder, H.; Pines, E. Ultrafast chemistry: Using time-resolved vibrational spectroscopy for interrogation of structural dynamics. Annu. Rev. Phys. Chem. 2005, 56, 337–367. [Google Scholar] [CrossRef]
- Maillard, J.; Klehs, K.; Rumble, C.; Vauthey, E.; Heilemann, M.; Fürstenberg, A. Universal quenching of common fluorescent probes by water and alcohols. Chem. Sci. 2021, 12, 1352–1362. [Google Scholar] [CrossRef] [PubMed]



| Molecule | Exc. (nm) | Solvent | (ps) | (ps) | (ps) | (ps) | (ps) | (ns) |
|---|---|---|---|---|---|---|---|---|
| 2NP− | 400 | Water | 0.23 | 0.21 | 1.2 | |||
| 267 | <0.3 | 0.5 | 1.1 | 1.6 | ||||
| Methanol | <0.3 | 0.7 | 1.2 | 9.6 | ||||
| 4NP− | 400 | Water | 0.21 | 0.21 | 1.4 | |||
| 267 | <0.3 | <0.3 | 0.5 | 1.4 | 1.3 | |||
| Methanol | <0.3 | <0.3 | 0.5 | 1.5 | 8.1 | |||
| 3NP− | 400 | Water | 0.5 | 1.4 | ||||
| 267 | 0.6 | 0.89 | ||||||
| Methanol | <0.3 | 1.3 | 5.7 |
| Molecule | Exc. (nm) | Region Center (nm) | (ps) | FWHM (ps) | (ps) | (ps) | (ps) | (ps) |
|---|---|---|---|---|---|---|---|---|
| 2NP− | 400 | 515 | –0.01 | 0.11 | 0.3 | 0.3 | 0.3 | 1.7 |
| 615 | 0.01 | 0.13 | 0.1 | 0.2 | 0.3 | 7.4 | ||
| 267 | 515 | 0.41 † | 0.41 † | 0.1 | 0.2 | 1.3 | 100 | |
| 615 | 0.37 † | 0.41 † | <0.1 | 0.1 | 0.7 | 1000 | ||
| 4NP− | 400 | 515 | 0.07 | 0.17 | <0.1 | <0.1 | 0.7 | 5.2 |
| 615 | 0.08 | 0.17 | 0.1 | 0.2 | 0.1 | 22 | ||
| 267 | 515 | 0.44 † | 0.39 † | <0.1 | 0.1 | 0.9 | 1400 | |
| 615 | 0.40 † | 0.43 † | <0.1 | 0.1 | 0.8 | 1300 | ||
| 3NP− | 400 | 515 | –0.05 | 0.10 | 0.3 | 0.3 | 2.5 | |
| 615 | 0.02 | 0.20 | 0.2 | 0.2 | 16 | |||
| 267 | 515 | 0.46 † | 0.48 † | <0.1 | 0.9 | 3.5 | 2000 | |
| 615 | 0.31 † | 0.55 † | 0.3 | 1.4 | 85 | 1700 |
| Molecule | Solvent | (ps) | (ps) | (ps) | (ps) | (ps) a | (ps) |
|---|---|---|---|---|---|---|---|
| 2NP | Water | <0.3 | <0.3 | 1.1 | 900 | ||
| Methanol | 0.3 | 5.5 | 390 | ||||
| 4NP | Water | <0.3 | <0.3 | 2.1 | 36 | 4300 | |
| Methanol | 0.3 | 12 | 37 | 1300 | |||
| 3NP | Water | <0.3 | 0.8 | 140 | |||
| Methanol | <0.3 | 4.3 | 5.0 | 810 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bailey-Darland, S.; Krueger, T.D.; Fang, C. Ultrafast Spectroscopies of Nitrophenols and Nitrophenolates in Solution: From Electronic Dynamics and Vibrational Structures to Photochemical and Environmental Implications. Molecules 2023, 28, 601. https://doi.org/10.3390/molecules28020601
Bailey-Darland S, Krueger TD, Fang C. Ultrafast Spectroscopies of Nitrophenols and Nitrophenolates in Solution: From Electronic Dynamics and Vibrational Structures to Photochemical and Environmental Implications. Molecules. 2023; 28(2):601. https://doi.org/10.3390/molecules28020601
Chicago/Turabian StyleBailey-Darland, Sullivan, Taylor D. Krueger, and Chong Fang. 2023. "Ultrafast Spectroscopies of Nitrophenols and Nitrophenolates in Solution: From Electronic Dynamics and Vibrational Structures to Photochemical and Environmental Implications" Molecules 28, no. 2: 601. https://doi.org/10.3390/molecules28020601
APA StyleBailey-Darland, S., Krueger, T. D., & Fang, C. (2023). Ultrafast Spectroscopies of Nitrophenols and Nitrophenolates in Solution: From Electronic Dynamics and Vibrational Structures to Photochemical and Environmental Implications. Molecules, 28(2), 601. https://doi.org/10.3390/molecules28020601