Trivalent Polyhedra as Duals of Borane Deltahedra: From Molecular Endohedral Germanium Clusters to the Smallest Fullerenes
Abstract
:1. Introduction
- (1)
- All faces are triangles—hence their designation as deltahedra relating to the shape of the Greek letter delta (∆). This feature maximizes the number of edges for a given number of vertices and thus maximizes the connectivity between the vertices.
- (2)
- The vertices are as nearly similar as possible thereby providing the best approximation to a sphere rather than a prolate or oblate ellipsoid.
- (3)
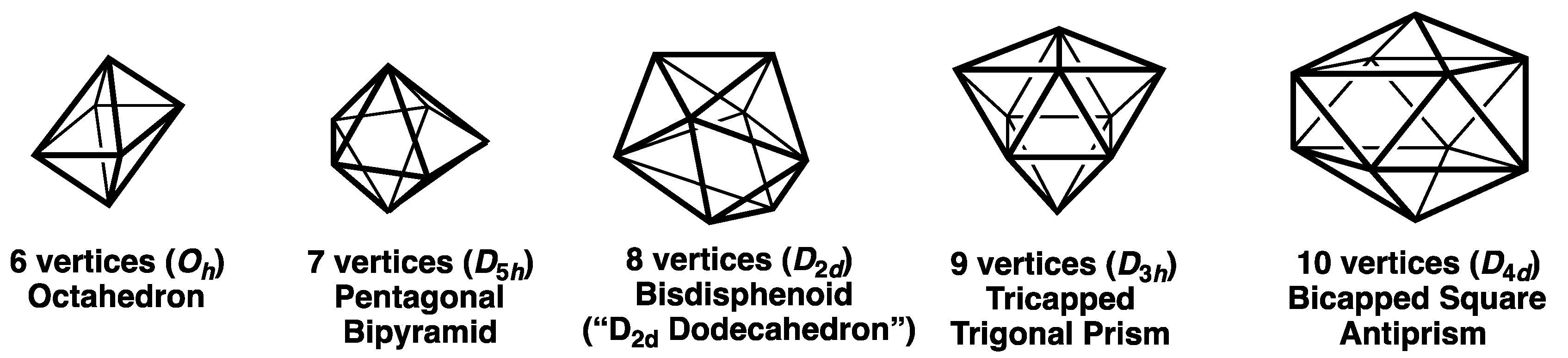
- Deltahedra with exclusively degree 4 and 5 vertices where the degree of a given vertex is the number of edges meeting at that vertex (Figure 1). These start with the highly symmetrical (Oh) 6-vertex regular octahedron with exclusively degree 4 vertices and go as far as the D4d 10-vertex bicapped square antiprism with two degree 4 vertices and eight degree 5 vertices. These deltahedra are found in the borane dianions BnHn2− and the isoelectronic carboranes CBn−1Hn− and C2Bn−2Hn [1,2,3].
- (4)
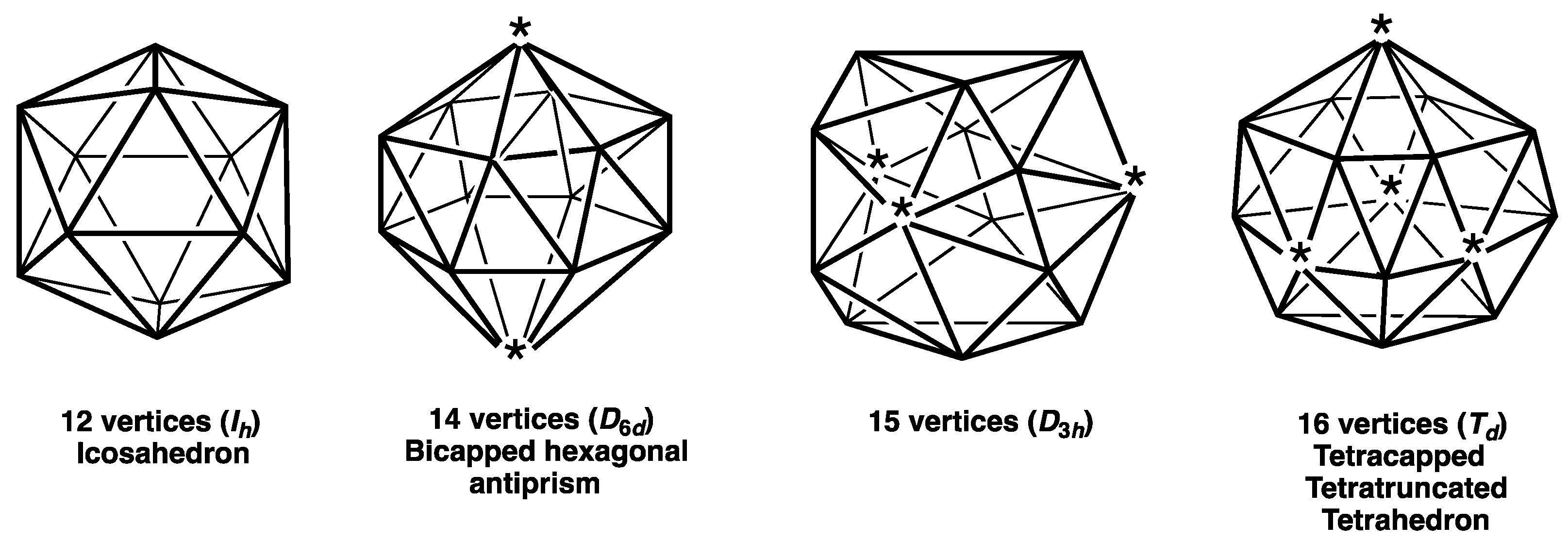
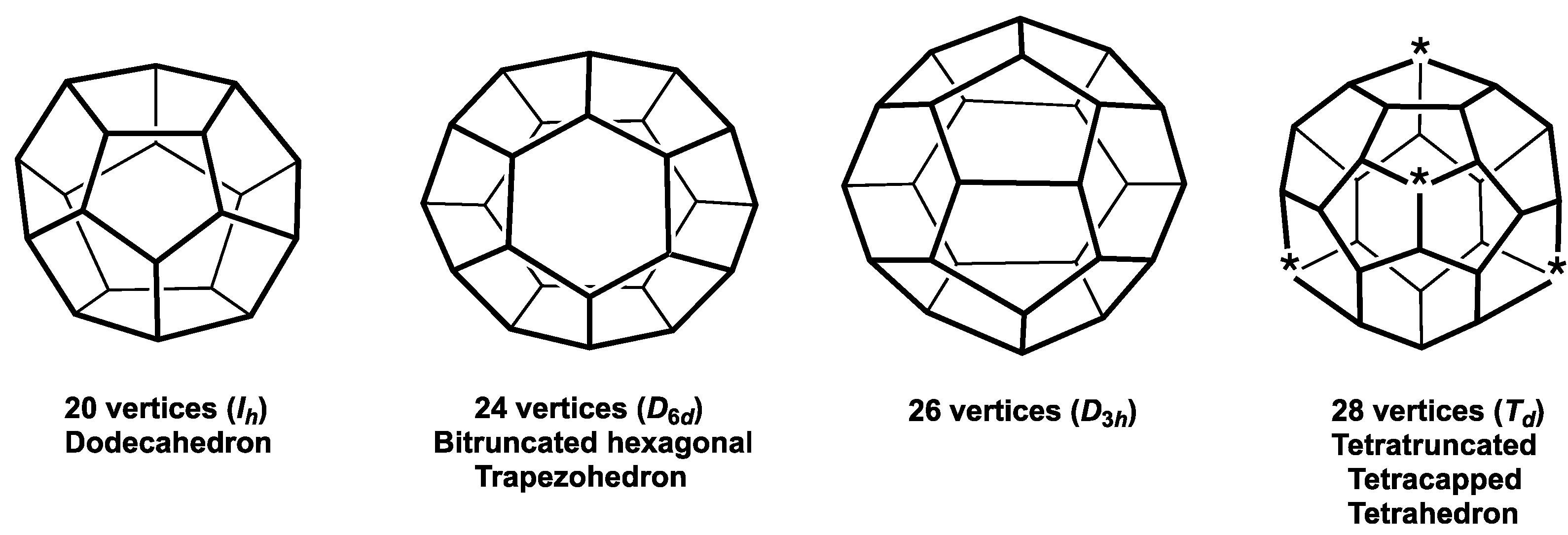
- The four Frank-Kasper deltahedra [4] with exclusively degree 5 and degree 6 vertices with no pair of degree 6 vertices sharing an edge (Figure 2). These start with the highly symmetrical (Ih) 12-vertex regular icosahedron and also include the 14-vertex D6d bicapped hexagonal antiprism with antipodal degree 6 vertices, a 15-vertex D3h deltahedron with its three degree 6 vertices forming an equilateral macrotriangle, and the 16-vertex Td tetracapped tetratruncated tetrahedron with its four degree 6 vertices forming a regular macrotetrahedron. The icosahedral structure is found in the borane dianion B12H122− as well as the isoelectronic carboranes CB11H12− and C2B10H12 [1,2,3]. The 14-vertex bicapped hexagonal antiprism is found in (µ-CH2)3C2B12H12 in which the two carbon vertices are bridged by a trimethylene unit [5]. The 16-vertex tetracapped tetratruncated tetrahedron is found in the unusual pentarhodium complex (Cp*Rh)3B12H12Rh(B4H9 RhCp*) (Cp* = η5-Me5C5) [6].
- (5)
- For the 11- and 13-vertex systems the closo deltahedra are less symmetrical and necessarily contain vertices of three different degrees, namely 4, 5, and 6 (Figure 3).
2. Dualization of Polyhedra
3. The Most Spherical Trivalent Polyhedra in Chemistry
| Vertices/ | Faces/ | Closo Deltahedron | Dual Trivalent | Chemical Example | |
|---|---|---|---|---|---|
| Faces (Dual) | Edges | Vertices (Dual) | (Symmetry) | Polyhedron | of Dual a [lit. ref.] |
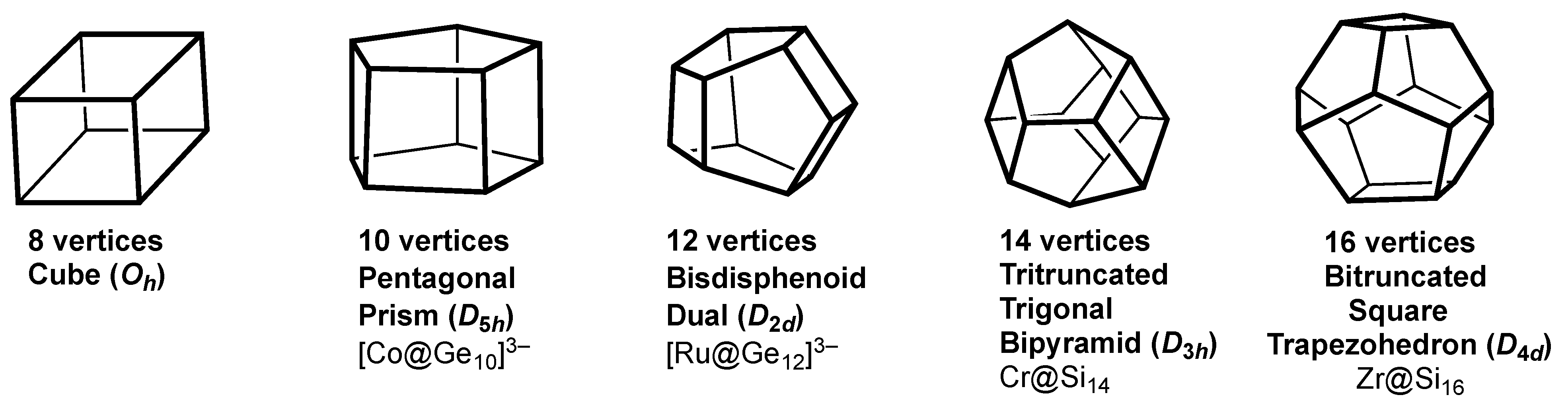
| 6 | 12 | 8 | Octahedron (Oh) | Cube | |
| 7 | 15 | 10 | Pentag bipyramid (D5h) | Pentag prism | [Co@Ge10]3− [14] |
| 8 | 18 | 12 | Bisdisphenoid (D2d) | [Ru@Ge12]3− [15] | |
| 9 | 21 | 14 | Tricap trig prism (D3h) | Tritrunc trig bipyramid | Cr@Si14 [28] |
| 10 | 24 | 16 | Bicap sq antiprism (D4d) | Bitrunc sq trapezohedron | Zr@Si16 [29,30,31] |
| 11 | 27 | 18 | (C2v) | ||
| 12 | 30 | 20 | Icosahedron (Ih) | Dodecahedron | {[U@Si20]6−} [34] |
| 13 | 33 | 22 | |||
| 14 | 36 | 24 | Bicap hex antiprism (D6d) | Bitrunc hex trapezohedron | {Pu@C24} [33] |
| 15 | 39 | 26 | 15v Frank Kasper (D3h) | {U@C26} [32] | |
| 16 | 42 | 28 | Tetracap tetratrunc tet (Td) | Tetratrunc tetracap tet | Th@C28 [16] |
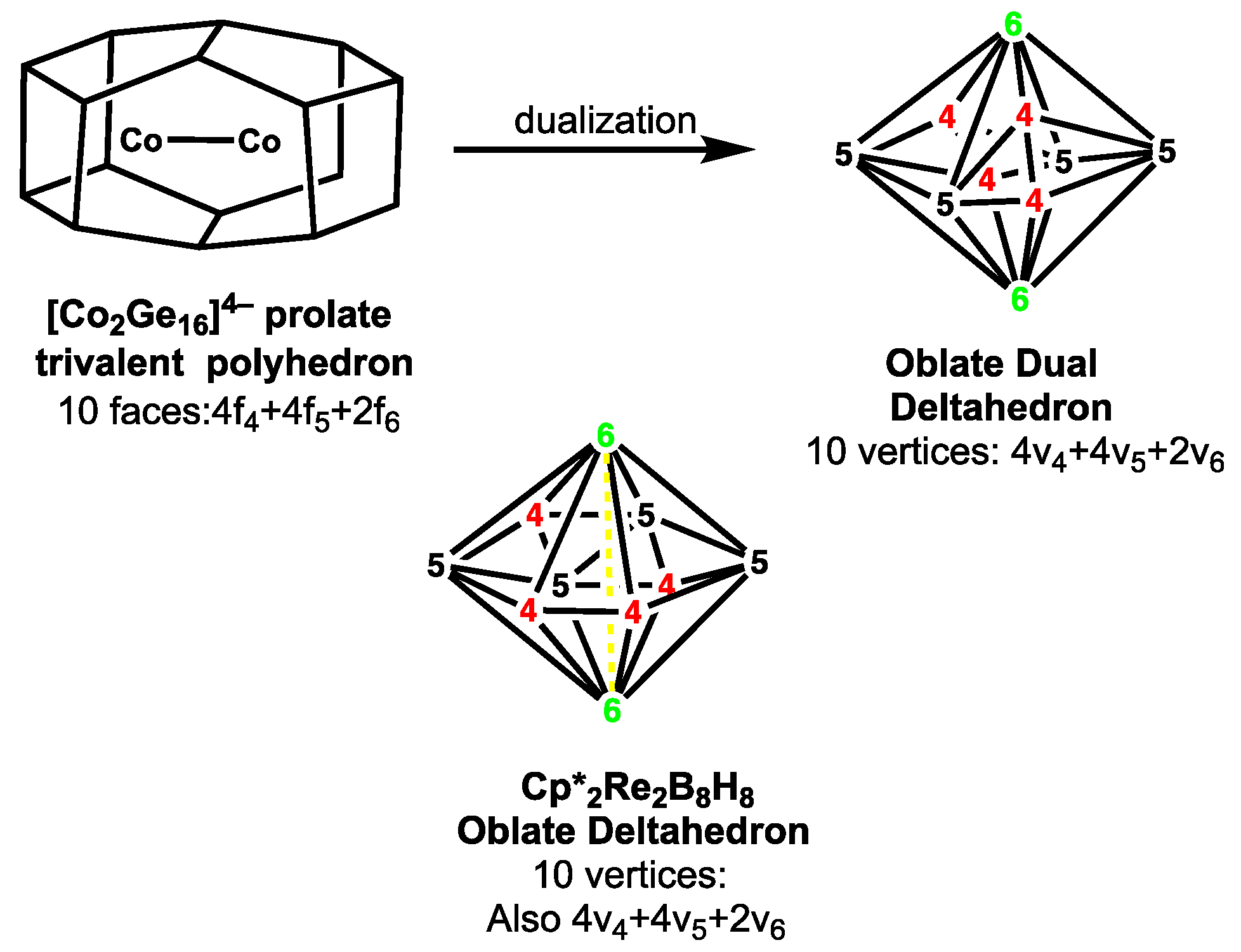
4. Prolate Elongated Ellipsoidal Trivalent Polyhedra as Duals of Oblate Flattened Ellipsoidal Deltahedra
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williams, R.E. Carboranes and boranes; polyhedral and polyhedral fragments. Inorg. Chem. 1971, 10, 210–214. [Google Scholar] [CrossRef]
- Williams, R.E. The polyborane, carborane, carbocation continuum: Architectural patterns. Chem. Rev. 1992, 92, 177–207. [Google Scholar] [CrossRef]
- King, R.B. Three-dimensional aromaticity in polyhedral boranes and related molecules. Chem. Rev. 2001, 101, 1119–1152. [Google Scholar] [CrossRef]
- Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. 1. Definitions and basic principles. Acta Cryst. 1958, 11, 184–190. [Google Scholar] [CrossRef]
- Dong, L.; Chen, H.S.; Xie, Z. Synthesis, reactivity, and structural characterization of a 14-vertex carborane. Angew. Chem. Int. Ed. Engl. 2005, 44, 2128–2131. [Google Scholar] [CrossRef]
- Roy, S.K.; Mondal, B.; Shankhari, P.; Anju, R.S.; Geetharani, K.; Mobin, S.M.; Ghosh, S. Supraicosahedral polyhedra in metallaboranes: Synthesis and structural characterization of 12-, 15-, and 16-vertex rhodaboranes. Inorg. Chem. 2013, 52, 6705–6712. [Google Scholar] [CrossRef]
- Scharfe, S.; Fässler, T.F.; Stegmaier, S.; Hoffmann, S.D.; Klaus, R. [Cu@Sn9]3− and [Cu@Pb9]3−: Intermetalloid clusters with endohedral Cu atoms in spherical environments. Chem. Eur. J. 2008, 14, 4479–4483. [Google Scholar] [CrossRef]
- Sevov, S.C.; Corbett, J.C. K8In10Zn—Interstitially stabilized analogs of early-transition metal halide clusters. Inorg. Chem. 1993, 32, 1059–1061. [Google Scholar] [CrossRef]
- Esenturk, E.N.; Fettinger, J.; Eichhorn, B. The closo-Pb102− Zintl ion in the [Ni@Pb10]2− cluster. Chem. Commun. 2005, 247–249. [Google Scholar] [CrossRef]
- Esenturk, E.N.; Fettinger, J.; Eichhorn, B. The Pb122− and Pb102− Zintl ions and the M@Pb122− and M@Pb102− cluster series where M = Ni, Pd, Pt. J. Am. Chem. Soc. 2006, 128, 9178–9186. [Google Scholar] [CrossRef]
- Henning, R.W.; Corbett, J.D. Formation of isolated nickel-centered gallium clusters in Na10Ga10Ni and a 2-D network of gallium octahedra in K2Ga3. Inorg. Chem. 1999, 38, 3883–3888. [Google Scholar] [CrossRef]
- Ruck, M.; Dubenskyy, V.; Söhnel, T. Structure and bonding of [Pd@Bi10]4+ in the subbromide Bi14PdBr16. Angew. Chem. Int. Ed. 2003, 45, 2978–2982. [Google Scholar] [CrossRef]
- Esenturk, E.N.; Fettinger, J.; Lam, Y.-F.; Eichhorn, B. [Pt@Pb12]2−. Angew. Chem. Int. Ed. 2004, 43, 2132–2134. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Stegmaier, S.; Fässler, T.F. [Co@Ge10]3−: An intermetalloid cluster with Archimedean pentagonal prismatic structure. Angew. Chem. Int. Ed. 2009, 48, 1998–2002. [Google Scholar] [CrossRef]
- Zhou, B.; Denning, M.S.; Kays, D.L.; Goicoechea, J.M. Synthesis and isolation of [Fe@Ge10]3−: A pentagonal prismatic Zintl ion cage encapsulating an interstitial iron atom. J. Am. Chem.Soc. 2009, 132, 2802–2803. [Google Scholar] [CrossRef]
- Dunk, P.W.; Kaiser, N.K.; Mulet-Gas, M.; Rodriguez-Fortea, A.; Poblet, J.M.; Shinohara, H.; Hendrickson, C.L.; Marshall, A.G.; Kroto, H.W. The smallest stable fullerene, M@C28 (M = Ti, Zr, U): Stabilization and growth from carbon vapor. J. Am. Chem. Soc. 2012, 134, 9308–9389. [Google Scholar] [CrossRef]
- For a review of much of the relevant chemistry from Fehlner’s group see Fehlner, T. P. In Group 13 Chemistry: From Fundamentals to Applications; Shapiro, P.J.; Atwood, D.A. (Eds.) American Chemical Society: Washington, DC, USA, 2002; pp. 49–67. [Google Scholar]
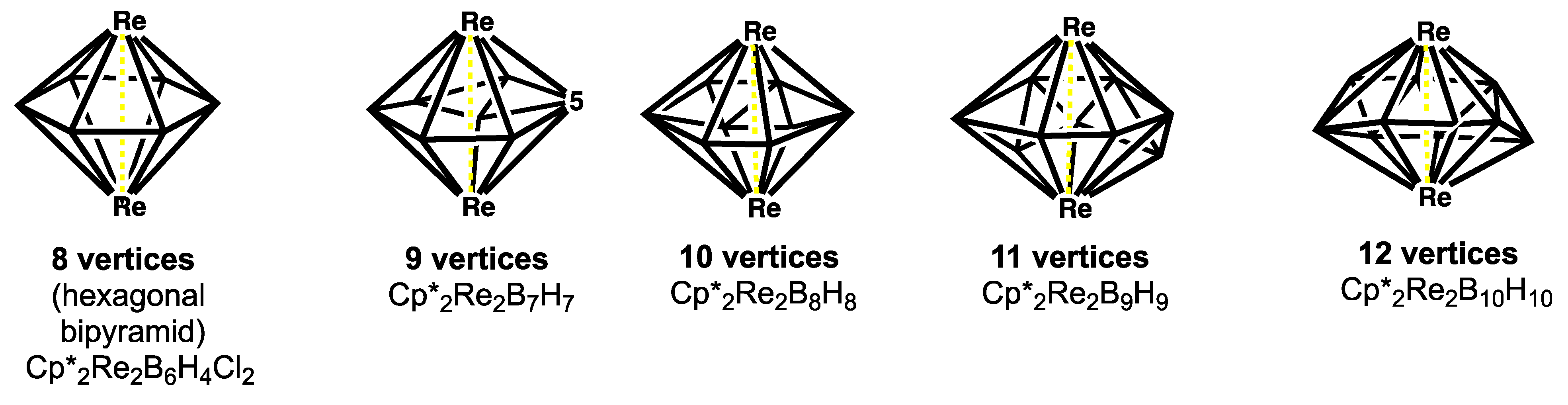
- Ghosh, S.; Shang, M.; Li, Y.; Fehlner, T.P. Synthesis of [(Cp*Re)2BnHn] (n = 8–10): Metal boride particles that stretch the cluster structure paradigms. Angew. Chem. Int. Ed. 2001, 40, 1125–1128. [Google Scholar] [CrossRef]
- Wadepohl, H. Hypoelectronic dimetallaboranes. Angew. Chem. Int. Ed. 2002, 41, 4220. [Google Scholar] [CrossRef]
- Le Guennic, B.; Jiao, H.; Kahlal, S.; Saillard, J.-Y.; Halet, J.-F.; Ghosh, S.; Shang, M.; Beatty, A.M.; Rheingold, A.L.; Fehlner, T.P. Synthesis and characterization of hypoelectronic rhenaboranes. analysis of the geometric and electronic structures of species following neither borane nor metal cluster electron-counting paradigms. J. Am. Chem. Soc. 2004, 126, 3203–3217. [Google Scholar] [CrossRef] [PubMed]
- King, R.B. The oblate deltahedra in dimetallaboranes: Geometry and chemical bonding. Inorg. Chem. 2006, 45, 8211–8216. [Google Scholar] [CrossRef]
- Jin, X.; Espionoza-Quintero, G.; Below, B.; Arcisauskaite, V.; Goicoechea, J.M.; McGrady, J.E. Structure and bonding in a bimetallic endohedral cage, [Co2@Ge16]2−. J. Organometal. Chem. 2015, 792, 149–153. [Google Scholar] [CrossRef]
- Liu, C.; Popov, I.A.; Li, L.-J.; Li, N.; Boldyrev, A.I.; Sun, Z.-M. [Co2@Ge16]4−: Localized versus delocalized bonding in two isomeric intermetalloid clusters. Chem. Eur. J. 2018, 24, 699–705. [Google Scholar] [CrossRef]
- Espinoza-Qunitero, G.; Duckworth, J.C.A.; Myers, W.K.; McGrady, J.E.; Goicoechea, J.M. Synthesis and characterization of [Ru@Ge12]3−: An endohedral 3-connected cluster. J. Am. Chem. Soc. 2014, 136, 1210–1213. [Google Scholar] [CrossRef]
- Goicoechea, J.M.; McGrady, J.E. On the structural landscape in endohedral silicon and germanium clusters, M@Si12 and M@Ge12. Dalton Trans. 2015, 44, 6755–6766. [Google Scholar] [CrossRef]
- Mitzinger, S.; Broeckaert, L.; Massa, W.; Wiegend, F.; Dehnen, S. Understanding of multimetallic cluster growth. Nat. Commun. 2016, 7, 10480. [Google Scholar] [CrossRef]
- Lips, F.; Holyńska, M.; Clérac, R.; Linne, U.; Schellenberg, I.; Pöttgen, R.; Weigend, F. Dehnen, S. Doped semimetal clusters: Ternary intermetalloid anions [Ln@Sn7Bi7]4− and [Ln@Sn4Bi9]4− (Ln = La, Ce) with adjustable magnetic properties. J. Am. Chem. Soc. 2012, 134, 1181–1191. [Google Scholar] [CrossRef]
- Jin, X.; Arcisauskaite, V.; McGrady, J. The structural landscape in 14-vertex clusters of silicon, M@Si14: When two bonding paradigms collide. Dalton Trans. 2017, 46, 11636–11644. [Google Scholar] [CrossRef]
- Kumar, V. Novel metal-encapsulated caged clusters of silicon and germanium. Eur. Phys. J. D 2003, 24, 227–232. [Google Scholar] [CrossRef]
- Kumar, V. Recent theoretical progress on electronic and structural properties of clusters: Permanent electric dipoles, magnetism, novel caged structures, and their assemblies. Comput. Mater. Sci. 2006, 35, 375–381. [Google Scholar] [CrossRef]
- Kumar, V.; Majumder, C.; Kawazoe, Y. M@Si16, M = Ti, Zr, Hf: π conjugation, ionization potentials and electron affinities. Chem. Phys. Lett. 2002, 363, 319–322. [Google Scholar] [CrossRef]
- Manna, D.; Ghanty, T.K. Prediction of a new series of thermodynamically stable actinide encapsulated fullerene systems fulfilling the 32-electron principle. J. Phys. Chem. C 2012, 116, 25630–25641. [Google Scholar] [CrossRef]
- Manna, D.; Sirohiwal, A.; Ghanty, T.K. Pu@C24: A new example satisfying the 32-electron principle. J. Phys. Chem. C 2014, 118, 7211–7221. [Google Scholar] [CrossRef]
- Dognon, J.-P.; Clavaguéra, C.; Pyykkö, P. A new, centered 32-electron system: The predicted [U@Si20]6−-like isoelectronic series. Chem. Sci. 2012, 3, 2843–2848. [Google Scholar] [CrossRef]
- Bühl, M.; Hirsch, A. Spherical aromaticity of fullerenes. Chem. Rev. 2001, 101, 1153–1184. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
King, R.B. Trivalent Polyhedra as Duals of Borane Deltahedra: From Molecular Endohedral Germanium Clusters to the Smallest Fullerenes. Molecules 2023, 28, 496. https://doi.org/10.3390/molecules28020496
King RB. Trivalent Polyhedra as Duals of Borane Deltahedra: From Molecular Endohedral Germanium Clusters to the Smallest Fullerenes. Molecules. 2023; 28(2):496. https://doi.org/10.3390/molecules28020496
Chicago/Turabian StyleKing, R. Bruce. 2023. "Trivalent Polyhedra as Duals of Borane Deltahedra: From Molecular Endohedral Germanium Clusters to the Smallest Fullerenes" Molecules 28, no. 2: 496. https://doi.org/10.3390/molecules28020496
APA StyleKing, R. B. (2023). Trivalent Polyhedra as Duals of Borane Deltahedra: From Molecular Endohedral Germanium Clusters to the Smallest Fullerenes. Molecules, 28(2), 496. https://doi.org/10.3390/molecules28020496





