Unicorns, Rhinoceroses and Chemical Bonds
Abstract
:1. Introduction: History of the Chemical Bond
2. Bond Properties
QTAIM and Kinetic Energy Ambiguity
The Space of All ZFS and Condensed Properties
3. Computational Details
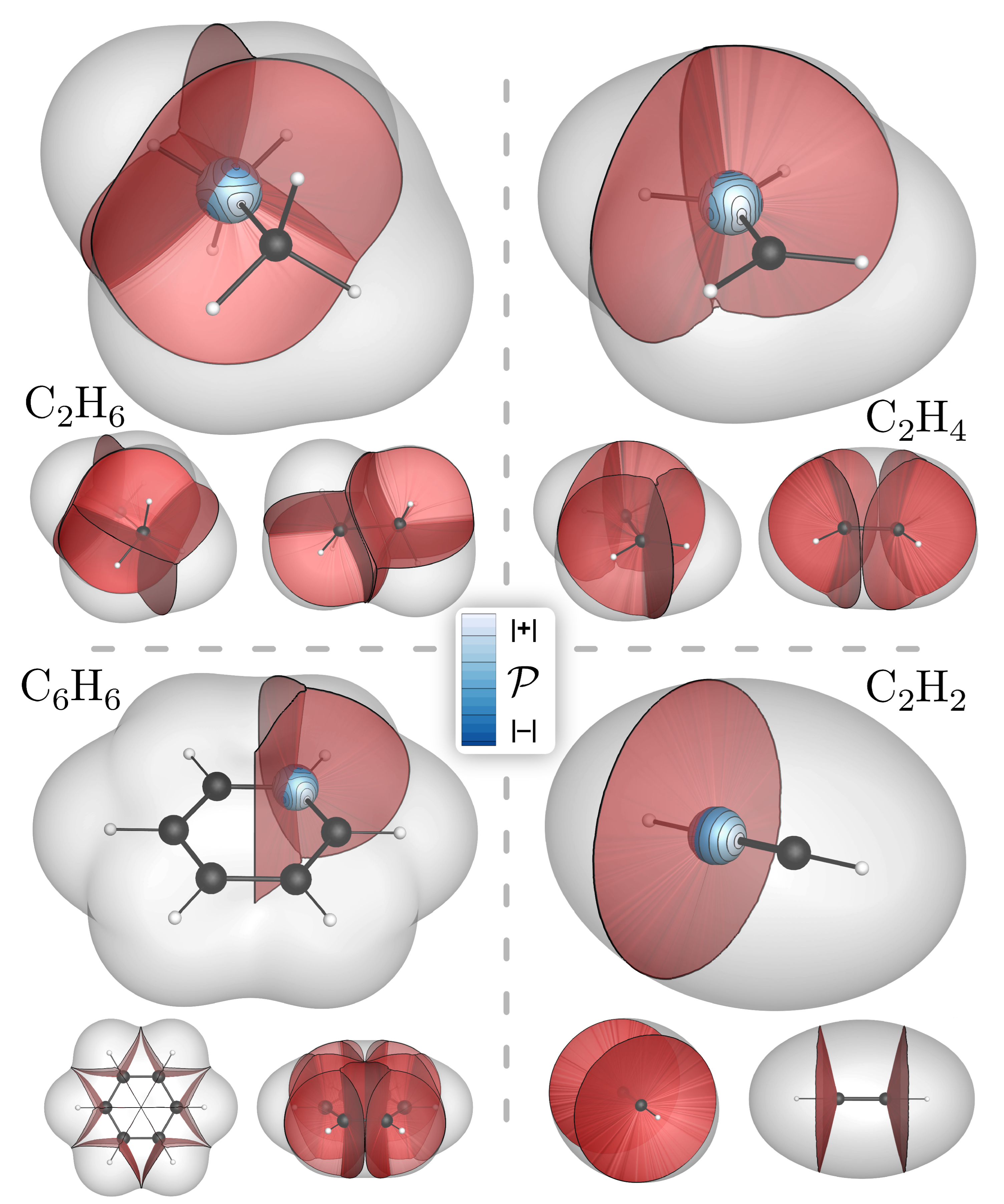
4. Bond-Wedges and Bond Bundles
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. System Coordinates [Å]
| D | X | Y | Z | D | X | Y | Z |
|---|---|---|---|---|---|---|---|
| C | 0.7163 | 0.7163 | 0 | C | −0.7817 | −0.6652 | 0 |
| C | −0.7163 | 0.7163 | 0 | C | 0.7817 | −0.6652 | 0 |
| C | 0.7163 | −0.7163 | 0 | C | −0.7817 | 0.6652 | 0 |
| C | −0.7163 | −0.7163 | 0 | C | 0.7817 | 0.6652 | 0 |
| H | 1.4873 | 1.4873 | 0 | H | −1.5570 | −1.4341 | 0 |
| H | 1.4873 | −1.4873 | 0 | H | −1.5570 | 1.4341 | 0 |
| H | −1.4873 | 1.4873 | 0 | H | 1.5570 | −1.4341 | 0 |
| H | −1.4873 | −1.4873 | 0 | H | 1.5570 | 1.4341 | 0 |
| X | Y | Z |
|---|---|---|
| 0 | 2.04 | 2.04 |
| 2.04 | 0 | 2.04 |
| 2.04 | 2.04 | 0 |
References
- Matta, C.F.; Boyd, R.J. (Eds.) The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007. [Google Scholar]
- Jones, T.E.; Eberhart, M.E.; Imlay, S.; Mackey, C.; Olson, G.B. Better Alloys with Quantum Design. Phys. Rev. Lett. 2012, 109, 125506. [Google Scholar] [CrossRef] [PubMed]
- Counts, W.A.; Friák, M.; Raabe, D.; Neugebauer, J. Using Ab Initio Calculations in Designing BCC MgLi-X Alloys for Ultra-Lightweight Applications. Adv. Eng. Mater. 2010, 12, 1198–1205. [Google Scholar] [CrossRef]
- Datta, A.; Ramamurty, U.; Ranganathan, S.; Waghmare, U. Crystal structures of a Mg-Zn-Y alloy: A first principles study. Comput. Mater. Sci. 2006, 37, 69–73. [Google Scholar] [CrossRef]
- Levy, O.; Jahnátek, M.; Chepulskii, R.V.; Hart, G.L.W.; Curtarolo, S. Ordered Structures in Rhenium Binary Alloys from First-Principles Calculations. J. Am. Chem. Soc. 2011, 133, 158–163. [Google Scholar] [CrossRef]
- Constable, E.C.; Housecroft, C.E. Chemical Bonding: The Journey from Miniature Hooks to Density Functional Theory. Molecules 2020, 25, 2623. [Google Scholar] [CrossRef]
- Ball, P. Beyond the bond. Nature 2011, 469, 26–28. [Google Scholar] [CrossRef]
- Frenking, G.; Krapp, A. Unicorns in the world of chemical bonding models. J. Comput. Chem. 2007, 28, 15–24. [Google Scholar] [CrossRef]
- Bader, R.F.W. Bond Paths Are Not Chemical Bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef]
- Coulson, C.A. The contributions of wave mechanics to chemistry. J. Chem. Soc. 1955, 2069–2084. [Google Scholar] [CrossRef]
- Vargas, S.; Hennefarth, M.R.; Liu, Z.; Alexandrova, A.N. Machine Learning to Predict Diels–Alder Reaction Barriers from the Reactant State Electron Density. J. Chem. Theory Comput. 2021, 17, 6203–6213. [Google Scholar] [CrossRef]
- Wilson, T.R.; Morgenstern, A.; Alexandrova, A.N.; Eberhart, M. Bond Bundle Analysis of Ketosteroid Isomerase. J. Phys. Chem. B 2022, 126, 46. [Google Scholar] [CrossRef] [PubMed]
- Westermayr, J.; Gastegger, M.; Schütt, K.T.; Maurer, R.J. Perspective on Integrating Machine Learning into Computational Chemistry and Materials Science. J. Chem. Phys. 2021, 154, 230903. [Google Scholar] [CrossRef] [PubMed]
- Noé, F.; Tkatchenko, A.; Müller, K.R.; Clementi, C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020, 71, 361–390. [Google Scholar] [CrossRef]
- Mazurenko, S.; Prokop, Z.; Damborsky, J. Machine Learning in Enzyme Engineering. ACS Catal. 2020, 10, 1210–1223. [Google Scholar] [CrossRef]
- Chen, C.T.; Gu, G.X. Machine Learning for Composite Materials. MRS Commun. 2019, 9, 556–566. [Google Scholar] [CrossRef]
- Brockherde, F.; Vogt, L.; Li, L.; Tuckerman, M.E.; Burke, K.; Müller, K.R. Bypassing the Kohn-Sham Equations with Machine Learning. Nat. Commun. 2017, 8, 872. [Google Scholar] [CrossRef]
- Kermack, W.O.; Robinson, R. LI.—An explanation of the property of induced polarity of atoms and an interpretation of the theory of partial valencies on an electronic basis. J. Chem. Soc. Trans. 1922, 121, 427–440. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Feinberg, M.; Ruedenberg, K.; Mehler, E.L. The Origin of Binding and Antibinding in the Hydrogen Molecule-Lon. In Advances in Quantum Chemistry; Löwdin, P.O., Ed.; Academic Press: Cambridge, MA, USA, 1970; Volume 5, pp. 27–98. [Google Scholar]
- Feinberg, M.J.; Ruedenberg, K. Paradoxical Role of the Kinetic-Energy Operator in the Formation of the Covalent Bond. J. Chem. Phys. 1971, 54, 1495–1511. [Google Scholar] [CrossRef]
- Feinberg, M.J.; Ruedenberg, K. Heteropolar One-Electron Bond. J. Chem. Phys. 1971, 55, 5804–5818. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Preston, H.J.T. The kinetic energy of molecular charge distributions and molecular stability. Int. J. Quantum Chem. 1969, 3, 327–347. [Google Scholar] [CrossRef]
- Heidarzadeh, F.; Shahbazian, S. The Quantum Divided Basins: A New Class of Quantum Subsystems. Int. J. Quantum Chem. 2011, 111, 2788–2801. [Google Scholar] [CrossRef]
- Anderson, J.S.M.; Ayers, P.W.; Hernandez, J.I.R. How Ambiguous Is the Local Kinetic Energy? J. Phys. Chem. A 2010, 114, 8884–8895. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, M.E. A quantum description of the chemical bond. Philos. Mag. B 2001, 81, 721. [Google Scholar] [CrossRef]
- Jones, T.E.; Eberhart, M.E. The bond bundle in open systems. Int. J. Quantum Chem. 2010, 110, 1500–1505. [Google Scholar] [CrossRef]
- Jones, T.E.; Eberhart, M.E. The irreducible bundle: Further structure in the kinetic energy distribution. J. Chem. Phys. 2009, 130, 204108. [Google Scholar] [CrossRef]
- Morgenstern, A.; Morgenstern, C.; Miorelli, J.; Wilson, T.; Eberhart, M. The influence of zero-flux surface motion on chemical reactivity. Phys. Chem. Chem. Phys. 2016, 18, 5638–5646. [Google Scholar] [CrossRef]
- Morgenstern, A.; Wilson, T.; Miorelli, J.; Jones, T.; Eberhart, M. In Search of an Intrinsic Chemical Bond. Comput. Theor. Chem. 2015, 1053, 31–37. [Google Scholar] [CrossRef]
- Morgenstern, A.; Eberhart, M. Bond Dissociation Energies from the Topology of the Charge Density Using Gradient Bundle Analysis. Phys. Scr. 2016, 91, 023012. [Google Scholar] [CrossRef]
- Goss, J.; Wilson, T.; Morgenstern, A.; Eberhart, M. Charge Density Analysis Attending Bond Torsion: A Bond Bundle Case Study. Int. J. Quantum Chem. 2018, 118, e25783. [Google Scholar] [CrossRef]
- Wilson, T.R.; Rajivmoorthy, M.; Goss, J.; Riddle, S.; Eberhart, M.E. Observing the 3D Chemical Bond and Its Energy Distribution in a Projected Space. ChemPhysChem 2019, 20, 3289–3305. [Google Scholar] [CrossRef]
- Te Velde, G.; Baerends, E.J. Precise density-functional method for periodic structures. Phys. Rev. B 1991, 44, 7888. [Google Scholar] [CrossRef]
- Wiesenekker, G.; Baerends, E.J. Quadratic integration over the three-dimensional Brillouin zone. J. Phys. Condens. Matter 1991, 3, 6721. [Google Scholar] [CrossRef]
- BAND2019. SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 20 April 2020).
- te Velde, G.; Bickelhaupt, F.; van Gisbergen, S.; Guerra, C.F.; Baerends, E.; Snijders, J.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Bashford, D.; Baseggio, O.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerritger, P.M.; et al. ADF2019, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. ADF. Available online: http://www.scm.com (accessed on 20 April 2020).
- Wilson, T.R.; Eberhart, M.E. Bondalyzer. 2022. Available online: https://github.com/moltheorygroup/BondalyzerTecplotAddon (accessed on 20 April 2020).
- Morgenstern, A. Gradient Bundles. In Advances in Quantum Chemical Topology Beyond Qtaim, 1st ed.; Rodriguez, J.I., Cortés-Guzmán, F., Anderson, J.S.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 359–373. [Google Scholar]
- Wilson, T.R.; Eberhart, M.E. A Bond Bundle Case Study of Diels-Alder Catalysis Using Oriented Electric Fields. In Advances in Quantum Chemical Topology Beyond Qtaim, 1st ed.; Rodriguez, J.I., Cortés-Guzmán, F., Anderson, J.S.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 407–430. [Google Scholar]
- Inc., T. Tecplot 360 2013R1, 2013. Available online: https://www.tecplot.com (accessed on 1 January 2017).
- Slater, J.C. The Virial and Molecular Structure. J. Chem. Phys. 1933, 1, 687–691. [Google Scholar] [CrossRef]
- Rodríguez, J.I.; Ayers, P.W.; Götz, A.W.; Castillo-Alvarado, F.L. Virial theorem in the Kohn–Sham density-functional theory formalism: Accurate calculation of the atomic quantum theory of atoms in molecules energies. J. Chem. Phys. 2009, 131, 021101. [Google Scholar] [CrossRef] [PubMed]
- Snyder, L.C. Jahn-Teller Distortions in Cyclobutadiene, Cyclopentadienyl Radical, and Benzene Positive and Negative Ions. J. Chem. Phys. 1960, 33, 619–621. [Google Scholar] [CrossRef]
- Cram, D.J.; Tanner, M.E.; Thomas, R. The Taming of Cyclobutadiene. Angew. Chem. Int. Ed. Engl. 1991, 30, 1024–1027. [Google Scholar] [CrossRef]
- Kollmar, H.; Staemmler, V. A theoretical study of the structure of cyclobutadiene. J. Am. Chem. Soc. 1977, 99, 3583–3587. [Google Scholar] [CrossRef]
- Polo, M.; Ricci, A.; Benedetto, L. The Travels of Marco Polo: Translated Into English from the Text of L.F. Benedetto; Broadway travelers, Asian Educational Services: New Delhi, India, 2001. [Google Scholar]



| [e] | [Ha] | |||||
|---|---|---|---|---|---|---|
| D D | D D | D D | ||||
| C of C=C | 1.991 | 2.521 | 12.474 | 15.506 | 0.329 | 0.407 |
| C of C–C | 1.991 | 1.546 | 12.474 | 10.043 | 0.329 | 0.267 |
| C of C–H | 2.053 | 1.968 | 12.916 | 12.325 | 0.343 | 0.327 |
| H of C–H | 0.924 | 0.922 | 0.553 | 0.552 | 1 | 1 |
| Valence | Bond Energy | |||
|---|---|---|---|---|
| Electrons | [kJ/mol] | |||
| D D | D D | |||
| C=C | 2.668 | 3.416 | 597.9 | 1074.9 |
| C–C | 2.668 | 2.027 | 597.9 | 98.3 |
| C–H | 2.291 | 2.237 | 305.8 | 331.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gribben, J.; Wilson, T.R.; Eberhart, M.E. Unicorns, Rhinoceroses and Chemical Bonds. Molecules 2023, 28, 1746. https://doi.org/10.3390/molecules28041746
Gribben J, Wilson TR, Eberhart ME. Unicorns, Rhinoceroses and Chemical Bonds. Molecules. 2023; 28(4):1746. https://doi.org/10.3390/molecules28041746
Chicago/Turabian StyleGribben, Jordan, Timothy R. Wilson, and Mark E. Eberhart. 2023. "Unicorns, Rhinoceroses and Chemical Bonds" Molecules 28, no. 4: 1746. https://doi.org/10.3390/molecules28041746
APA StyleGribben, J., Wilson, T. R., & Eberhart, M. E. (2023). Unicorns, Rhinoceroses and Chemical Bonds. Molecules, 28(4), 1746. https://doi.org/10.3390/molecules28041746






