Exploring the Steps of Infrared (IR) Spectral Analysis: Pre-Processing, (Classical) Data Modelling, and Deep Learning
Abstract
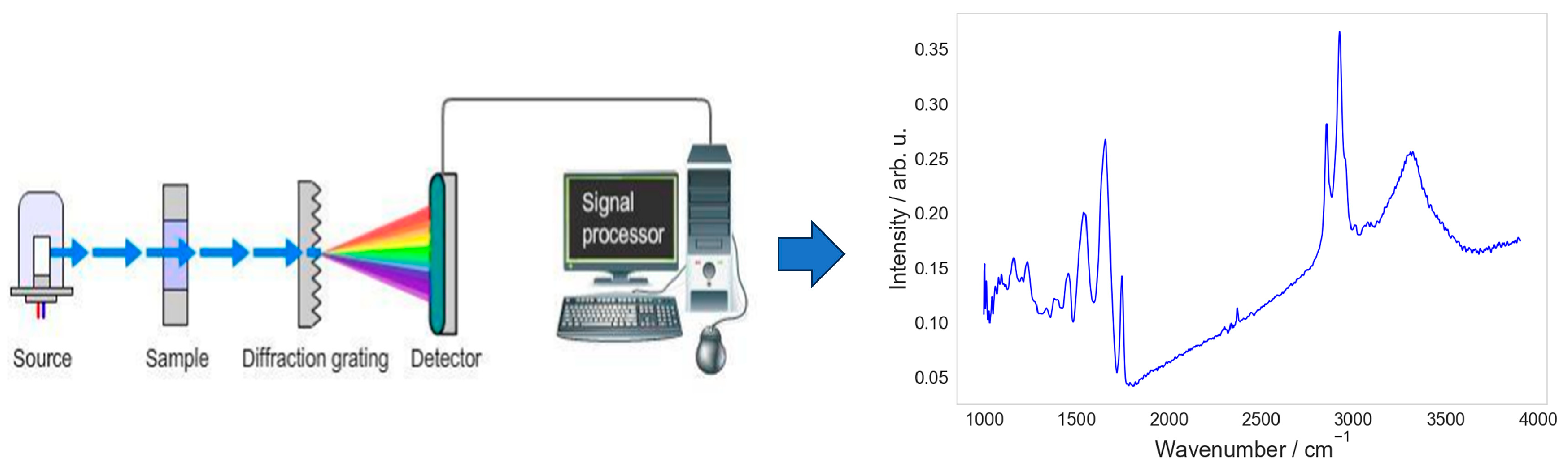
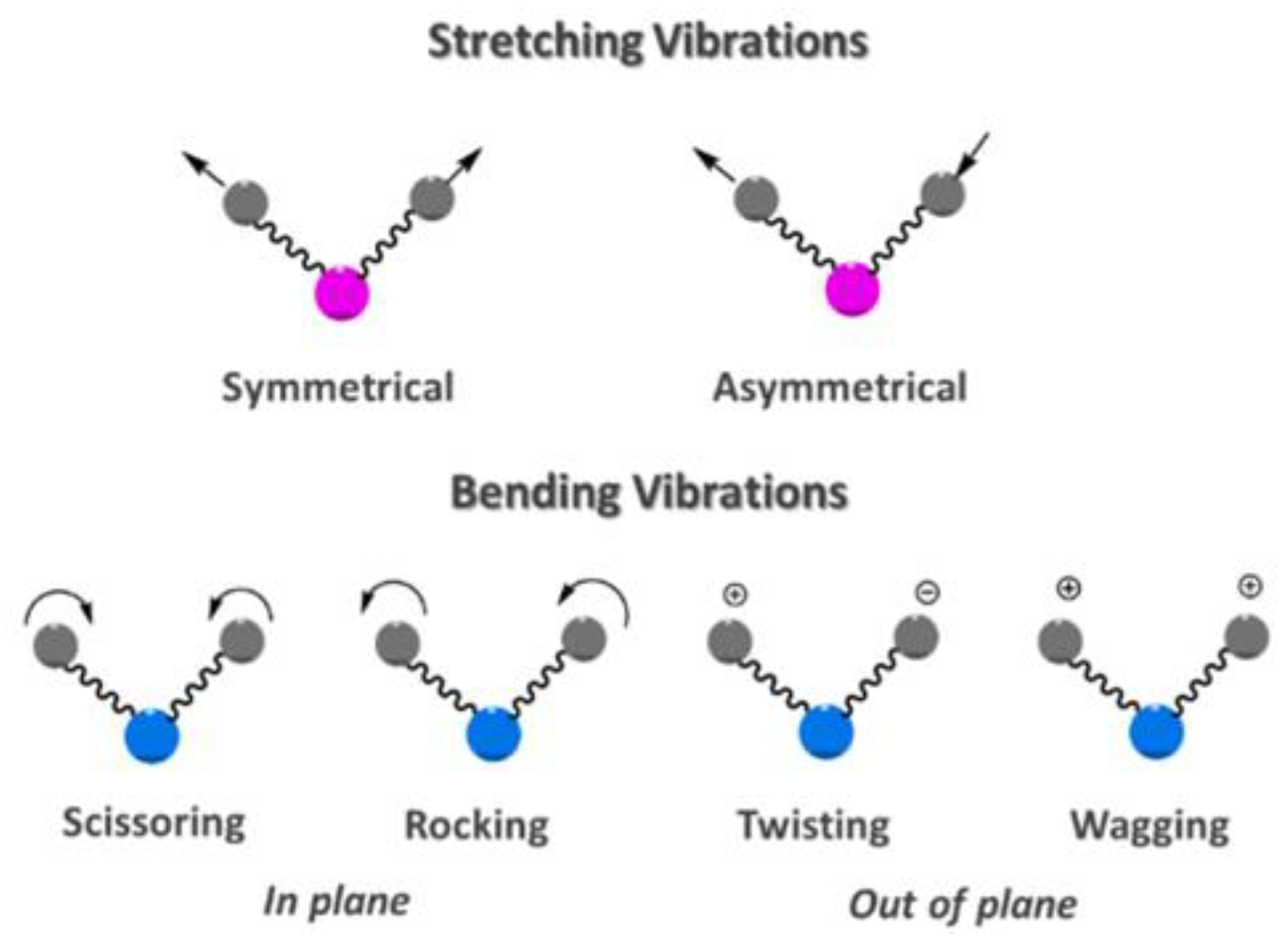
:1. Introduction
2. Pre-Processing
2.1. Exclusion (Cleaning)
2.2. Filtering
2.2.1. Derivative Filters
2.2.2. Savitzky–Golay (SG) Filtering
2.2.3. Other Filtering Methods
2.2.4. Fourier Self-Deconvolution
2.3. Baseline Correction
2.4. Normalization
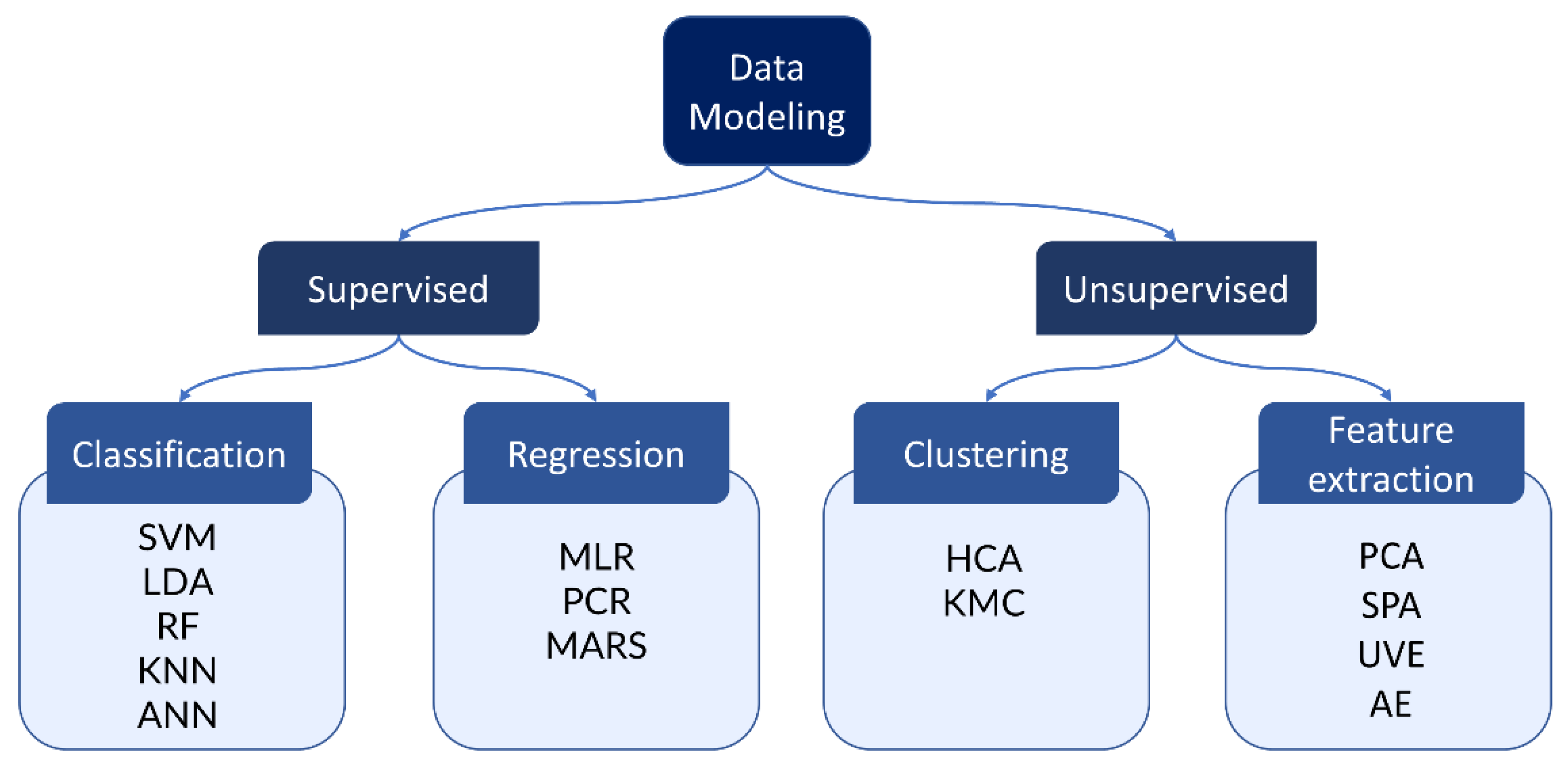
3. Data Modelling and Data Analysis
3.1. Classification
3.1.1. Support Vector Machine (SVM)
3.1.2. Linear Discriminant Analysis (LDA)
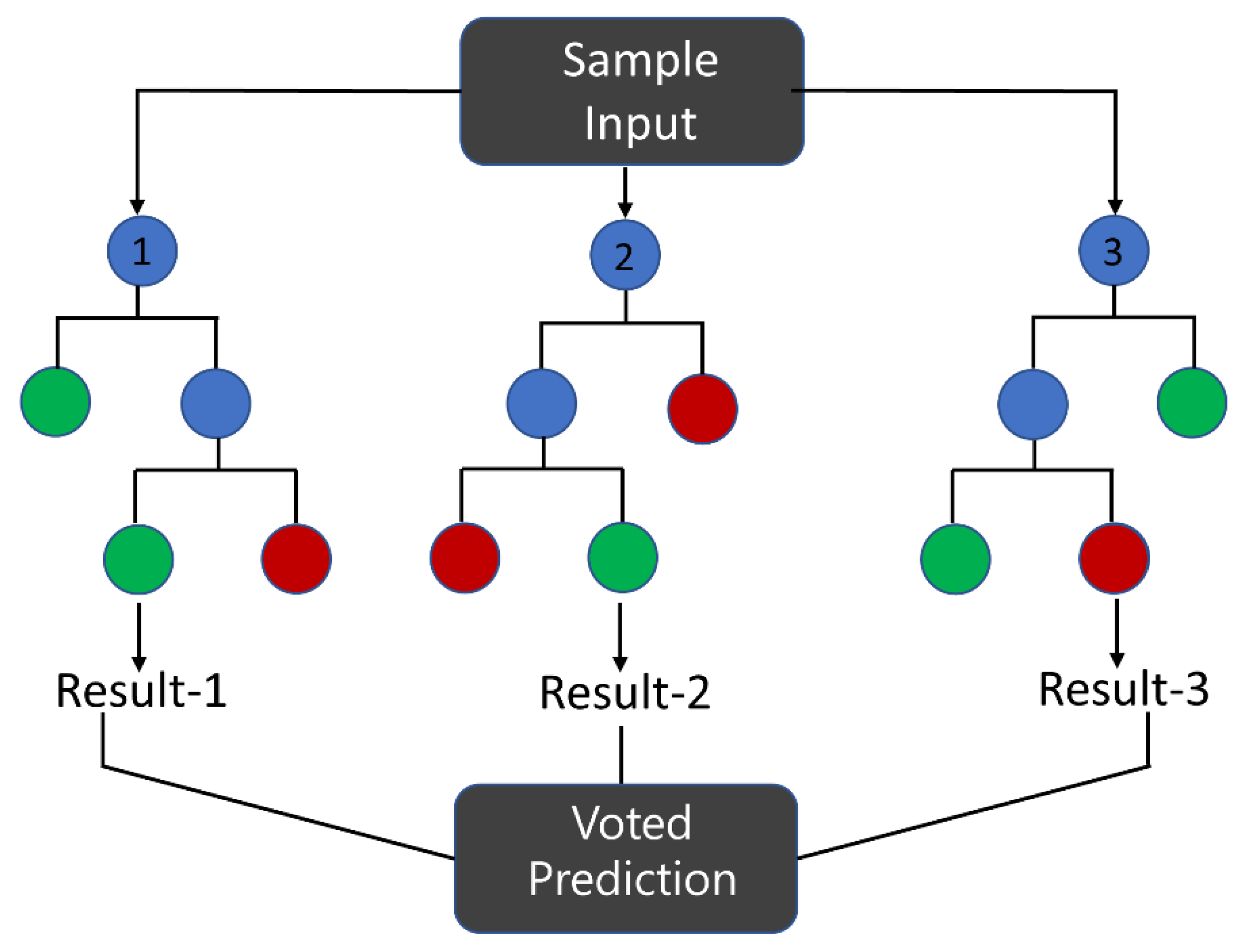
3.1.3. Random Forest (RF)
3.1.4. K-Nearest Neighbor (KNN)
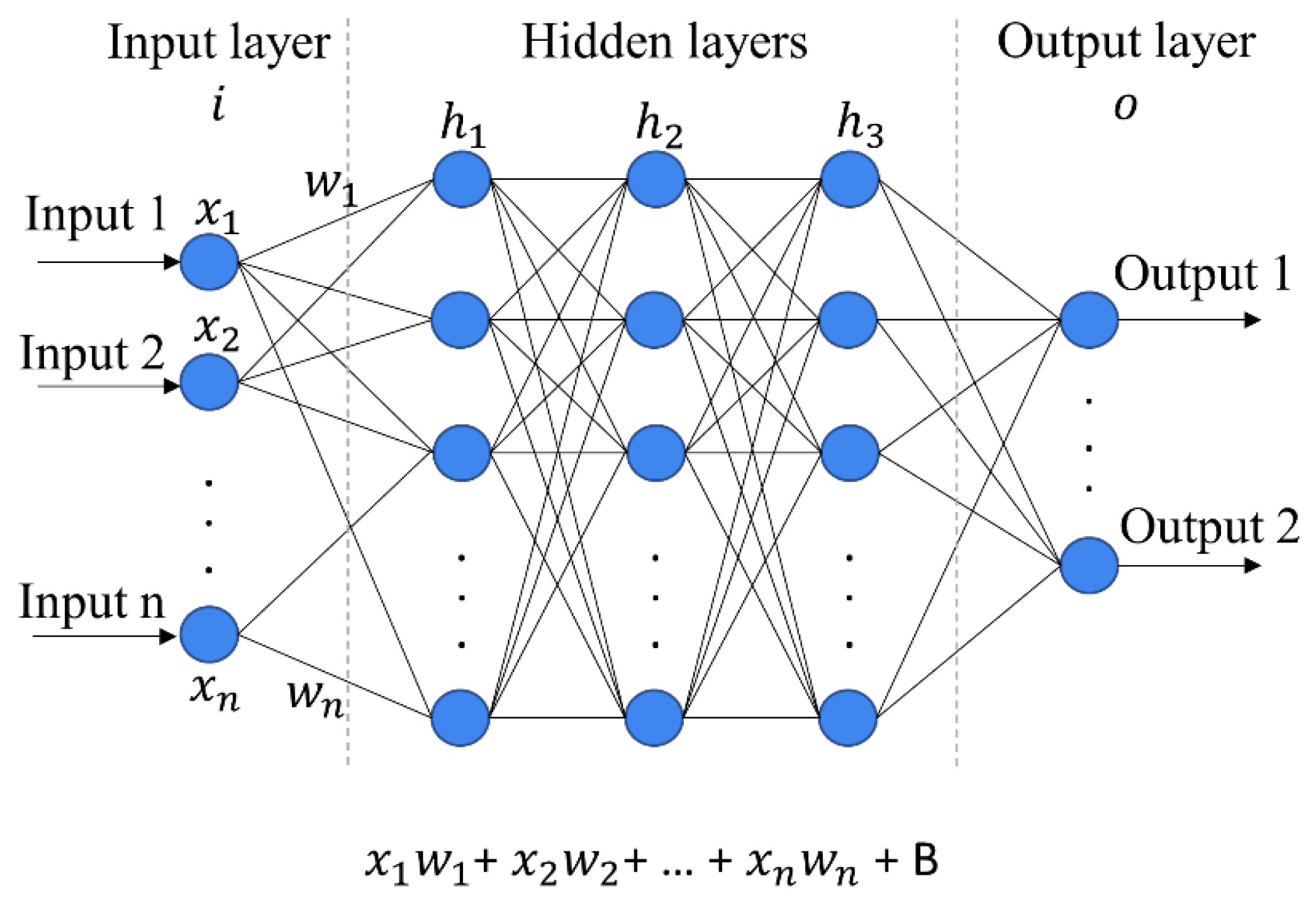
3.1.5. Artificial Neural Network (ANN)
3.2. Regression
3.3. Clustering
3.4. Feature Extraction
3.5. Evaluation Metrics for Classification and Regression Models
4. Deep Learning in the Analysis and Pre-Processing of IR Spectroscopy
4.1. Deep Learning in Pre-Processing
4.2. Deep Learning for Data Modeling
5. Feasibility of Machine Learning Approaches for High-Resolution Spectroscopy
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozaki, Y. Near-infrared spectroscopy—Its versatility in analytical chemistry. Anal. Sci. 2012, 28, 545–563. [Google Scholar] [CrossRef] [PubMed]
- Siesler, H.W.; Ozaki, Y.; Kawata, S.; Heise, H.M. Near-Infrared Spectroscopy: Principles, Instruments, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- McClure, W. Near-Infrared Spectroscopy in Food Science and Technology; Ozaki, Y., McClure, W.F., Christy, A.A., Eds.; Wiley-Interscience: Hoboken, NJ, USA, 2007; Chapter 1. [Google Scholar]
- Lau, W.S. Introduction to Infrared Spectroscopy. In Infrared Characterization For Microelectronics; World Scientific: Singapore, 1999. [Google Scholar]
- Mendes, E.; Duarte, N. Mid-infrared spectroscopy as a valuable tool to tackle food analysis: A literature review on coffee, dairies, honey, olive oil and wine. Foods 2021, 10, 477. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, A.; Beltran, V.; Nuyts, G.; Borondics, F.; De Meyer, S.; Van Bos, M.; Jaroszewicz, J.; Otten, E.; Debulpaep, M.; De Wael, K. Novel optical photothermal infrared (O-PTIR) spectroscopy for the noninvasive characterization of heritage glass-metal objects. Sci. Adv. 2022, 8, eabl6769. [Google Scholar] [CrossRef] [PubMed]
- Baker, M.J.; Trevisan, J.; Bassan, P.; Bhargava, R.; Butler, H.J.; Dorling, K.M.; Fielden, P.R.; Fogarty, S.W.; Fullwood, N.J.; Heys, K.A. Using Fourier transform IR spectroscopy to analyze biological materials. Nat. Protoc. 2014, 9, 1771–1791. [Google Scholar] [CrossRef]
- Baker, M.J.; Hussain, S.R.; Lovergne, L.; Untereiner, V.; Hughes, C.; Lukaszewski, R.A.; Thiéfin, G.; Sockalingum, G.D. Developing and understanding biofluid vibrational spectroscopy: A critical review. Chem. Soc. Rev. 2016, 45, 1803–1818. [Google Scholar] [CrossRef]
- Haka, A.S.; Shafer-Peltier, K.E.; Fitzmaurice, M.; Crowe, J.; Dasari, R.R.; Feld, M.S. Diagnosing breast cancer by using Raman spectroscopy. Proc. Natl. Acad. Sci. USA 2005, 102, 12371–12376. [Google Scholar] [CrossRef]
- Kondepati, V.R.; Heise, H.M.; Backhaus, J. Recent applications of near-infrared spectroscopy in cancer diagnosis and therapy. Anal. Bioanal. Chem. 2008, 390, 125–139. [Google Scholar] [CrossRef]
- Petrich, W.; Lewandrowski, K.; Muhlestein, J.; Hammond, M.; Januzzi, J.; Lewandrowski, E.; Pearson, R.; Dolenko, B.; Früh, J.; Haass, M. Potential of mid-infrared spectroscopy to aid the triage of patients with acute chest pain. Analyst 2009, 134, 1092–1098. [Google Scholar] [CrossRef]
- Roy, S.; Perez-Guaita, D.; Andrew, D.W.; Richards, J.S.; McNaughton, D.; Heraud, P.; Wood, B.R. Simultaneous ATR-FTIR based determination of malaria parasitemia, glucose and urea in whole blood dried onto a glass slide. Anal. Chem. 2017, 89, 5238–5245. [Google Scholar] [CrossRef]
- Spalding, K.; Bonnier, F.; Bruno, C.; Blasco, H.; Board, R.; Benz-de Bretagne, I.; Byrne, H.J.; Butler, H.J.; Chourpa, I.; Radhakrishnan, P. Enabling quantification of protein concentration in human serum biopsies using attenuated total reflectance–Fourier transform infrared (ATR-FTIR) spectroscopy. Vib. Spectrosc. 2018, 99, 50–58. [Google Scholar] [CrossRef]
- Gajjar, K.; Trevisan, J.; Owens, G.; Keating, P.J.; Wood, N.J.; Stringfellow, H.F.; Martin-Hirsch, P.L.; Martin, F.L. Fourier-transform infrared spectroscopy coupled with a classification machine for the analysis of blood plasma or serum: A novel diagnostic approach for ovarian cancer. Analyst 2013, 138, 3917–3926. [Google Scholar] [CrossRef] [PubMed]
- Ritz, M.; Vaculíková, L.; Plevová, E. Application of Infrared Spectroscopy and Chemometrics Methods to Identification of Selected Minerals. Acta Geodyn. Geomater. 2011, 8, 47–58. [Google Scholar]
- Gautam, R.; Vanga, S.; Ariese, F.; Umapathy, S. Review of multidimensional data processing approaches for Raman and infrared spectroscopy. EPJ Tech. Instrum. 2015, 2, 1–38. [Google Scholar] [CrossRef]
- Faria-bill, E.C.; Harvey, T.; Hughes, C.G.E.; Ward, A.; Correia, F.E.; Snook, R.; Clarke, N.B.M.; Gardner, P. Classification of fixed urological cells using Raman Tweezers. In Proceedings of the DASIM 2008, Dublin, Ireland, 2008. [Google Scholar]
- Bocklitz, T.; Walter, A.; Hartmann, K.; Rösch, P.; Popp, J. How to pre-process Raman spectra for reliable and stable models? Anal. Chim. Acta 2011, 704, 47–56. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Tooke, P. Fourier self-deconvolution in IR spectroscopy. TrAC Trends Anal. Chem. 1988, 7, 130–136. [Google Scholar] [CrossRef]
- Krafft, C.; Sobottka, S.B.; Geiger, K.D.; Schackert, G.; Salzer, R. Classification of malignant gliomas by infrared spectroscopic imaging and linear discriminant analysis. Anal. Bioanal. Chem. 2007, 387, 1669–1677. [Google Scholar] [CrossRef]
- Martens, H.; Jensen, S.; Geladi, P. Multivariate linearity transformation for near-infrared reflectance spectrometry. In Proceedings of the Nordic Symposium on Applied Statistics; Stokkand Forlag Publishers: Stavanger, Norway, 1983; pp. 205–234. [Google Scholar]
- Geladi, P.; MacDougall, D.; Martens, H. Linearization and scatter-correction for near-infrared reflectance spectra of meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Decker, M.; Nielsen, P.V.; Martens, H. Near-infrared spectra of Penicillium camemberti strains separated by extended multiplicative signal correction improved prediction of physical and chemical variations. Appl. Spectrosc. 2005, 59, 56–68. [Google Scholar] [CrossRef]
- Thennadil, S.; Martin, E. Empirical preprocessing methods and their impact on NIR calibrations: A simulation study. J. Chemom. A J. Chemom. Soc. 2005, 19, 77–89. [Google Scholar] [CrossRef]
- Martens, H.; Nielsen, J.P.; Engelsen, S.B. Light scattering and light absorbance separated by extended multiplicative signal correction. Application to near-infrared transmission analysis of powder mixtures. Anal. Chem. 2003, 75, 394–404. [Google Scholar]
- Kohler, A.; Afseth, N.K.; Martens, H. Chemometrics in biospectroscopy. Appl. Vib. Spectrosc. Food Sci. 2010, 1, 89–106. [Google Scholar]
- Liu, K.-Z.; Tsang, K.S.; Li, C.K.; Shaw, R.A.; Mantsch, H.H. Infrared spectroscopic identification of β-thalassemia. Clin. Chem. 2003, 49, 1125–1132. [Google Scholar] [CrossRef] [PubMed]
- Randolph, T.W. Scale-based normalization of spectral data. Cancer Biomark. 2006, 2, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Barnes, R.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Lasch, P. Spectral pre-processing for biomedical vibrational spectroscopy and microspectroscopic imaging. Chemom. Intell. Lab. Syst. 2012, 117, 100–114. [Google Scholar] [CrossRef]
- Revelle, W. Hierarchical cluster analysis and the internal structure of tests. Multivar. Behav. Res. 1979, 14, 57–74. [Google Scholar] [CrossRef]
- Romesburg, C. Cluster Analysis for Researchers; Lulu Press: Morrisville, NC, USA, 2004. [Google Scholar]
- Lever, J.; Krzywinski, M.; Altman, N. Points of significance: Principal component analysis. Nat. Methods 2017, 14, 641–643. [Google Scholar] [CrossRef]
- Soares, S.F.C.; Gomes, A.A.; Araujo, M.C.U.; Galvão Filho, A.R.; Galvão, R.K.H. The successive projections algorithm. TrAC Trends Anal. Chem. 2013, 42, 84–98. [Google Scholar] [CrossRef]
- Ye, S.; Wang, D.; Min, S. Successive projections algorithm combined with uninformative variable elimination for spectral variable selection. Chemom. Intell. Lab. Syst. 2008, 91, 194–199. [Google Scholar] [CrossRef]
- Liu, T.; Li, Z.; Yu, C.; Qin, Y. NIRS feature extraction based on deep auto-encoder neural network. Infrared Phys. Technol. 2017, 87, 124–128. [Google Scholar] [CrossRef]
- Xu, Y.; Zomer, S.; Brereton, R.G. Support vector machines: A recent method for classification in chemometrics. Crit. Rev. Anal. Chem. 2006, 36, 177–188. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Partial least squares discriminant analysis: Taking the magic away. J. Chemom. 2014, 28, 213–225. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.; Stevens, J. Random forests. Ensemble machine learning. In Ensemble Machine Learning; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Ding, X.; Ni, Y.; Kokot, S. NIR spectroscopy and chemometrics for the discrimination of pure, powdered, purple sweet potatoes and their samples adulterated with the white sweet potato flour. Chemom. Intell. Lab. Syst. 2015, 144, 17–23. [Google Scholar] [CrossRef]
- Backhaus, J.; Mueller, R.; Formanski, N.; Szlama, N.; Meerpohl, H.-G.; Eidt, M.; Bugert, P. Diagnosis of breast cancer with infrared spectroscopy from serum samples. Vib. Spectrosc. 2010, 52, 173–177. [Google Scholar] [CrossRef]
- Choi, Y.; Hong, J.; Kim, B.H.; Ahn, S. Determination of seed content in red pepper powders by 1H NMR and second-derivative FT-IR spectroscopy combined with statistical analyses. Bull. Korean Chem. Soc. 2022, 43, 450–459. [Google Scholar] [CrossRef]
- Shepherd, K.D.; Walsh, M.G. Development of reflectance spectral libraries for characterization of soil properties. Soil Sci. Soc. Am. J. 2002, 66, 988–998. [Google Scholar] [CrossRef]
- Belousov, A.; Verzakov, S.; Von Frese, J. Applicational aspects of support vector machines. J. Chemom. A J. Chemom. Soc. 2002, 16, 482–489. [Google Scholar] [CrossRef]
- Langeron, Y.; Doussot, M.; Hewson, D.J.; Duchêne, J. Classifying NIR spectra of textile products with kernel methods. Eng. Appl. Artif. Intell. 2007, 20, 415–427. [Google Scholar] [CrossRef]
- Caetano, S.; Üstün, B.; Hennessy, S.; Smeyers-Verbeke, J.; Melssen, W.; Downey, G.; Buydens, L.; Heyden, Y.V. Geographical classification of olive oils by the application of CART and SVM to their FT-IR. J. Chemom. A J. Chemom. Soc. 2007, 21, 324–334. [Google Scholar] [CrossRef]
- Wei, C.; Lei, F.; Ai, W.; Feng, J.; Zheng, H.; Ma, D.; Shi, X. Rapid identification of 6 kinds of traditional Chinese medicines containing resins and other components based on near infrared refectance spectroscopy and PCA-SVM algorithm. Chin. J. Exp. Tradit. Med. Formulae 2017, 23, 25–31. [Google Scholar]
- Butler, H.J.; Brennan, P.M.; Cameron, J.M.; Finlayson, D.; Hegarty, M.G.; Jenkinson, M.D.; Palmer, D.S.; Smith, B.R.; Baker, M.J. Development of high-throughput ATR-FTIR technology for rapid triage of brain cancer. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Devos, O.; Ruckebusch, C.; Durand, A.; Duponchel, L.; Huvenne, J.-P. Support vector machines (SVM) in near infrared (NIR) spectroscopy: Focus on parameters optimization and model interpretation. Chemom. Intell. Lab. Syst. 2009, 96, 27–33. [Google Scholar] [CrossRef]
- Hands, J.R.; Dorling, K.M.; Abel, P.; Ashton, K.M.; Brodbelt, A.; Davis, C.; Dawson, T.; Jenkinson, M.D.; Lea, R.W.; Walker, C. Attenuated total reflection Fourier transform infrared (ATR-FTIR) spectral discrimination of brain tumour severity from serum samples. J. Biophotonics 2014, 7, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.C.; Liong, C.-Y.; Jemain, A.A. Partial least squares-discriminant analysis (PLS-DA) for classification of high-dimensional (HD) data: A review of contemporary practice strategies and knowledge gaps. Analyst 2018, 143, 3526–3539. [Google Scholar] [CrossRef]
- Medipally, D.K.; Nguyen, T.N.Q.; Bryant, J.; Untereiner, V.; Sockalingum, G.D.; Cullen, D.; Noone, E.; Bradshaw, S.; Finn, M.; Dunne, M. Monitoring radiotherapeutic response in prostate cancer patients using high throughput FTIR spectroscopy of liquid biopsies. Cancers 2019, 11, 925. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Sun, M.; Wang, Z.; Li, H.; Li, Y.; Li, G.; Lin, L. Blood species identification using Near-Infrared diffuse transmitted spectra and PLS-DA method. Infrared Phys. Technol. 2016, 76, 587–591. [Google Scholar] [CrossRef]
- Ogruc Ildiz, G.; Bayari, S.; Karadag, A.; Kaygisiz, E.; Fausto, R. Fourier Transform Infrared spectroscopy based complementary diagnosis tool for autism spectrum disorder in children and adolescents. Molecules 2020, 25, 2079. [Google Scholar] [CrossRef]
- Ruiz-Perez, D.; Guan, H.; Madhivanan, P.; Mathee, K.; Narasimhan, G. So you think you can PLS-DA? BMC Bioinform. 2020, 21, 1–10. [Google Scholar] [CrossRef]
- Cameron, J.M.; Rinaldi, C.; Butler, H.J.; Hegarty, M.G.; Brennan, P.M.; Jenkinson, M.D.; Syed, K.; Ashton, K.M.; Dawson, T.P.; Palmer, D.S. Stratifying brain tumour histological sub-types: The application of ATR-FTIR serum spectroscopy in secondary care. Cancers 2020, 12, 1710. [Google Scholar] [CrossRef]
- Zhang, S.; Tan, Z.; Liu, J.; Xu, Z.; Du, Z. Determination of the food dye indigotine in cream by near-infrared spectroscopy technology combined with random forest model. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 227, 117551. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.R.; Ashton, K.M.; Brodbelt, A.; Dawson, T.; Jenkinson, M.D.; Hunt, N.T.; Palmer, D.S.; Baker, M.J. Combining random forest and 2D correlation analysis to identify serum spectral signatures for neuro-oncology. Analyst 2016, 141, 3668–3678. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zuo, Z.; Xu, F.; Wang, Y. Origin identification of Panax notoginseng by multi-sensor information fusion strategy of infrared spectra combined with random forest. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 226, 117619. [Google Scholar] [CrossRef]
- Sala, A.; Spalding, K.E.; Ashton, K.M.; Board, R.; Butler, H.J.; Dawson, T.P.; Harris, D.A.; Hughes, C.S.; Jenkins, C.A.; Jenkinson, M.D. Rapid analysis of disease state in liquid human serum combining infrared spectroscopy and “digital drying”. J. Biophotonics 2020, 13, e202000118. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.R.; Baker, M.J.; Palmer, D.S. PRFFECT: A versatile tool for spectroscopists. Chemom. Intell. Lab. Syst. 2018, 172, 33–42. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Lechowicz, L.; Chrapek, M.; Gaweda, J.; Urbaniak, M.; Konieczna, I. Use of Fourier-transform infrared spectroscopy in the diagnosis of rheumatoid arthritis: A pilot study. Mol. Biol. Rep. 2016, 43, 1321–1326. [Google Scholar] [CrossRef]
- Sánchez-Brito, M.; Luna-Rosas, F.J.; Mendoza-González, R.; Mata-Miranda, M.M.; Martínez-Romo, J.C.; Vázquez-Zapién, G.J. A machine-learning strategy to evaluate the use of FTIR spectra of saliva for a good control of type 2 diabetes. Talanta 2021, 221, 121650. [Google Scholar] [CrossRef]
- Shahid, N.; Rappon, T.; Berta, W. Applications of artificial neural networks in health care organizational decision-making: A scoping review. PLoS ONE 2019, 14, e0212356. [Google Scholar] [CrossRef]
- Almeida, J.S. Predictive non-linear modeling of complex data by artificial neural networks. Curr. Opin. Biotechnol. 2002, 13, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Lux, A.; Müller, R.; Tulk, M.; Olivieri, C.; Zarrabeita, R.; Salonikios, T.; Wirnitzer, B. HHT diagnosis by Mid-infrared spectroscopy and artificial neural network analysis. Orphanet J. Rare Dis. 2013, 8, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.S.; Santosh, W.; Kumar, S.; Christlet, T.H.T. Neural network algorithm for the early detection of Parkinson’s disease from blood plasma by FTIR micro-spectroscopy. Vib. Spectrosc. 2010, 53, 181–188. [Google Scholar] [CrossRef]
- Ma, Y.-K.; Rigolet, S.; Michelin, L.; Paillaud, J.-L.; Mintova, S.; Khoerunnisa, F.; Daou, T.J.; Ng, E.-P. Facile and fast determination of Si/Al ratio of zeolites using FTIR spectroscopy technique. Microporous Mesoporous Mater. 2021, 311, 110683. [Google Scholar] [CrossRef]
- Venkatesan, P.; Dharuman, C.; Gunasekaran, S. A comparative study of principal component regression and partial least squares regression with application to FTIR diabetes data. Indian J. Sci. Technol. 2011, 4, 740–746. [Google Scholar] [CrossRef]
- Dalal, R.; Henry, R. Simultaneous determination of moisture, organic carbon, and total nitrogen by near infrared reflectance spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 344. [Google Scholar]
- Bair, E. Semi-supervised clustering methods. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 349–361. [Google Scholar] [CrossRef]
- Zheng, L.; Li, T. Semi-supervised hierarchical clustering. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, Canada, 11 December 2011; pp. 982–991. [Google Scholar]
- Caixeta, D.C.; Aguiar, E.M.; Cardoso-Sousa, L.; Coelho, L.M.; Oliveira, S.W.; Espindola, F.S.; Raniero, L.; Crosara, K.T.; Baker, M.J.; Siqueira, W.L. Salivary molecular spectroscopy: A sustainable, rapid and non-invasive monitoring tool for diabetes mellitus during insulin treatment. PLoS ONE 2020, 15, e0223461. [Google Scholar] [CrossRef]
- Takamura, A.; Watanabe, K.; Akutsu, T.; Ozawa, T. Soft and robust identification of body fluid using Fourier transform infrared spectroscopy and chemometric strategies for forensic analysis. Sci. Rep. 2018, 8, 8459. [Google Scholar] [CrossRef]
- Gok, S.; Aydin, O.Z.; Sural, Y.S.; Zorlu, F.; Bayol, U.; Severcan, F. Bladder cancer diagnosis from bladder wash by Fourier transform infrared spectroscopy as a novel test for tumor recurrence. J. Biophotonics 2016, 9, 967–975. [Google Scholar] [CrossRef]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst. Appl. 2013, 40, 200–210. [Google Scholar] [CrossRef]
- Murtagh, F. A survey of recent advances in hierarchical clustering algorithms. Comput. J. 1983, 26, 354–359. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A.K. Principal component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef]
- Chaber, R.; Arthur, C.J.; Depciuch, J.; Łach, K.; Raciborska, A.; Michalak, E.; Cebulski, J. Distinguishing Ewing sarcoma and osteomyelitis using FTIR spectroscopy. Sci. Rep. 2018, 8, 15081. [Google Scholar] [CrossRef] [PubMed]
- Medipally, D.K.; Cullen, D.; Untereiner, V.; Sockalingum, G.D.; Maguire, A.; Nguyen, T.N.Q.; Bryant, J.; Noone, E.; Bradshaw, S.; Finn, M. Vibrational spectroscopy of liquid biopsies for prostate cancer diagnosis. Ther. Adv. Med. Oncol. 2020, 12. [Google Scholar] [CrossRef] [PubMed]
- Rashid, N.A.; Hussain, W.S.E.C.; Ahmad, A.R.; Abdullah, F.N. Performance of Classification Analysis: A Comparative Study between PLS-DA and Integrating PCA+LDA. Math. Stat. 2019, 7, 24–28. [Google Scholar] [CrossRef]
- Diem, M. Modern Vibrational Spectroscopy and Micro-Spectroscopy: Theory, Instrumentation and Biomedical Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zlotogorski-Hurvitz, A.; Dekel, B.Z.; Malonek, D.; Yahalom, R.; Vered, M. FTIR-based spectrum of salivary exosomes coupled with computational-aided discriminating analysis in the diagnosis of oral cancer. J. Cancer Res. Clin. Oncol. 2019, 145, 685–694. [Google Scholar] [CrossRef]
- Jo, S.; Sohng, W.; Lee, H.; Chung, H. Evaluation of an autoencoder as a feature extraction tool for near-infrared spectroscopic discriminant analysis. Food Chem. 2020, 331, 127332. [Google Scholar] [CrossRef]
- Cataltas, O.; Tutuncu, K. Detection of protein, starch, oil, and moisture content of corn kernels using one-dimensional convolutional autoencoder and near-infrared spectroscopy. PeerJ Comput. Sci. 2023, 9, e1266. [Google Scholar] [CrossRef]
- Schoot, M.; Kapper, C.; van Kollenburg, G.H.; Postma, G.J.; van Kessel, G.; Buydens, L.M.; Jansen, J.J. Investigating the need for preprocessing of near-infrared spectroscopic data as a function of sample size. Chemom. Intell. Lab. Syst. 2020, 204, 104105. [Google Scholar] [CrossRef]
- Cramer, R.D., III. Partial least squares (PLS): Its strengths and limitations. Perspect. Drug Discov. Des. 1993, 1, 269–278. [Google Scholar] [CrossRef]
- Chatzidakis, M.; Botton, G. Towards calibration-invariant spectroscopy using deep learning. Sci. Rep. 2019, 9, 2126. [Google Scholar] [CrossRef] [PubMed]
- Larsen, J.S.; Clemmensen, L. Deep learning for Chemometric and non-translational data. arXiv 2019, arXiv:1910.00391. [Google Scholar]
- Cui, C.; Fearn, T. Modern practical convolutional neural networks for multivariate regression: Applications to NIR calibration. Chemom. Intell. Lab. Syst. 2018, 182, 9–20. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Raulf, A.P.; Butke, J.; Küpper, C.; Großerueschkamp, F.; Gerwert, K.; Mosig, A. Deep representation learning for domain adaptable classification of infrared spectral imaging data. Bioinformatics 2020, 36, 287–294. [Google Scholar] [CrossRef]
- Guo, S.; Mayerhöfer, T.; Pahlow, S.; Hübner, U.; Popp, J.; Bocklitz, T. Deep learning for ‘artefact’removal in infrared spectroscopy. Analyst 2020, 145, 5213–5220. [Google Scholar] [CrossRef]
- Jian, D.; Bing-liang, H.; Yong-zheng, L.; Cui-yu, W.; Geng, Z.; Xing-jia, T.; Hu, B. Study on Quality Identification of Macadamia Nut Based on Convolutional Neural Networks and Spectral Features. Spectrosc. Spectr. Anal. 2018, 38, 1514–1519. [Google Scholar]
- Chen, X.; Chai, Q.; Lin, N.; Li, X.; Wang, W. 1D convolutional neural network for the discrimination of aristolochic acids and their analogues based on near-infrared spectroscopy. Anal. Methods 2019, 11, 5118–5125. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Hou, R. Classification modeling method for near-infrared spectroscopy of tobacco based on multimodal convolution neural networks. J. Anal. Methods Chem. 2020, 9652470. [Google Scholar] [CrossRef]
- Yue, F.; Chen, C.; Yan, Z.; Chen, C.; Guo, Z.; Zhang, Z.; Chen, Z.; Zhang, F.; Lv, X. Fourier transform infrared spectroscopy combined with deep learning and data enhancement for quick diagnosis of abnormal thyroid function. Photodiagnosis Photodyn. Ther. 2020, 32, 101923. [Google Scholar] [CrossRef] [PubMed]
- Leng, H.; Chen, C.; Chen, C.; Chen, F.; Du, Z.; Chen, J.; Yang, B.; Zuo, E.; Xiao, M.; Lv, X. Raman spectroscopy and FTIR spectroscopy fusion technology combined with deep learning: A novel cancer prediction method. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 285, 121839. [Google Scholar] [CrossRef] [PubMed]
- Tafintseva, V.; Shapaval, V.; Blazhko, U.; Kohler, A. Correcting replicate variation in spectroscopic data by machine learning and model-based pre-processing. Chemom. Intell. Lab. Syst. 2021, 215, 104350. [Google Scholar] [CrossRef]
- Gruszczyński, S.; Gruszczyński, W. Supporting soil and land assessment with machine learning models using the Vis-NIR spectral response. Geoderma 2022, 405, 115451. [Google Scholar] [CrossRef]
- Fu, L.; Sun, J.; Wang, S.; Xu, M.; Yao, K.; Cao, Y.; Tang, N. Identification of maize seed varieties based on stacked sparse autoencoder and near-infrared hyperspectral imaging technology. J. Food Process Eng. 2022, 45, e14120. [Google Scholar] [CrossRef]
- Zuo, E.; Sun, L.; Yan, J.; Chen, C.; Chen, C.; Lv, X. Rapidly detecting fennel origin of the near-infrared spectroscopy based on extreme learning machine. Sci. Rep. 2022, 12, 13593. [Google Scholar] [CrossRef]
- Zheng, A.; Yang, H.; Pan, X.; Yin, L.; Feng, Y. Identification of multi-class drugs based on near infrared spectroscopy and bidirectional generative adversarial networks. Sensors 2021, 21, 1088. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Meng, Q.; Liu, S.; Zhang, Y.; Wang, J. Infrared image super resolution by combining compressive sensing and deep learning. Sensors 2018, 18, 2587. [Google Scholar] [CrossRef]
- Liu, F.; Han, P.; Wang, Y.; Li, X.; Bai, L.; Shao, X. Super resolution reconstruction of infrared images based on classified dictionary learning. Infrared Phys. Technol. 2018, 90, 146–155. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokari, A.; Guo, S.; Bocklitz, T. Exploring the Steps of Infrared (IR) Spectral Analysis: Pre-Processing, (Classical) Data Modelling, and Deep Learning. Molecules 2023, 28, 6886. https://doi.org/10.3390/molecules28196886
Mokari A, Guo S, Bocklitz T. Exploring the Steps of Infrared (IR) Spectral Analysis: Pre-Processing, (Classical) Data Modelling, and Deep Learning. Molecules. 2023; 28(19):6886. https://doi.org/10.3390/molecules28196886
Chicago/Turabian StyleMokari, Azadeh, Shuxia Guo, and Thomas Bocklitz. 2023. "Exploring the Steps of Infrared (IR) Spectral Analysis: Pre-Processing, (Classical) Data Modelling, and Deep Learning" Molecules 28, no. 19: 6886. https://doi.org/10.3390/molecules28196886
APA StyleMokari, A., Guo, S., & Bocklitz, T. (2023). Exploring the Steps of Infrared (IR) Spectral Analysis: Pre-Processing, (Classical) Data Modelling, and Deep Learning. Molecules, 28(19), 6886. https://doi.org/10.3390/molecules28196886






