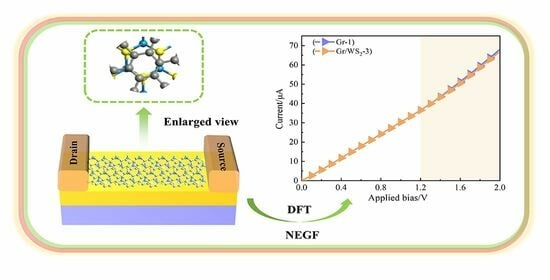
Electron Transport Properties of Graphene/WS2 Van Der Waals Heterojunctions
Abstract
:1. Introduction
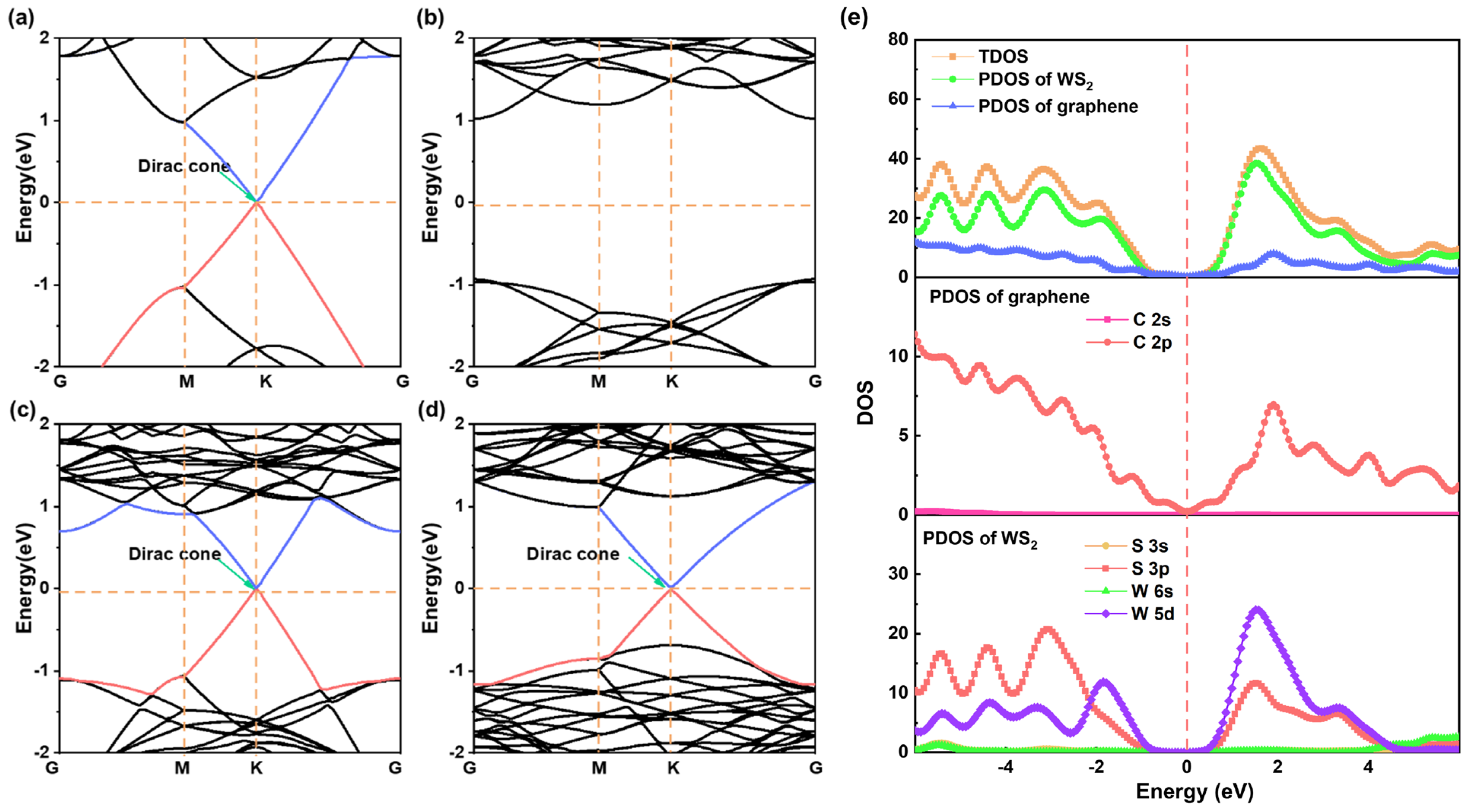
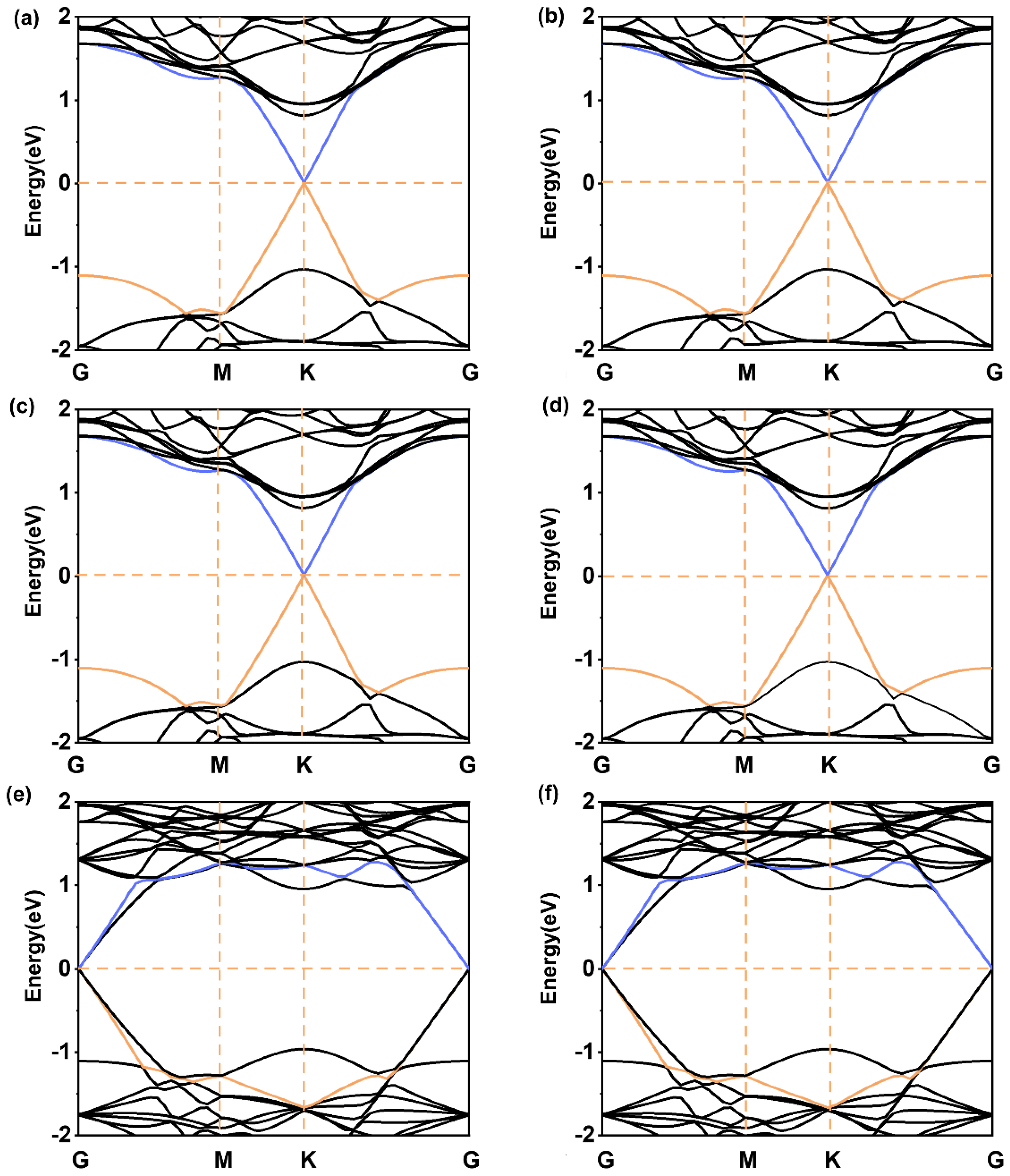
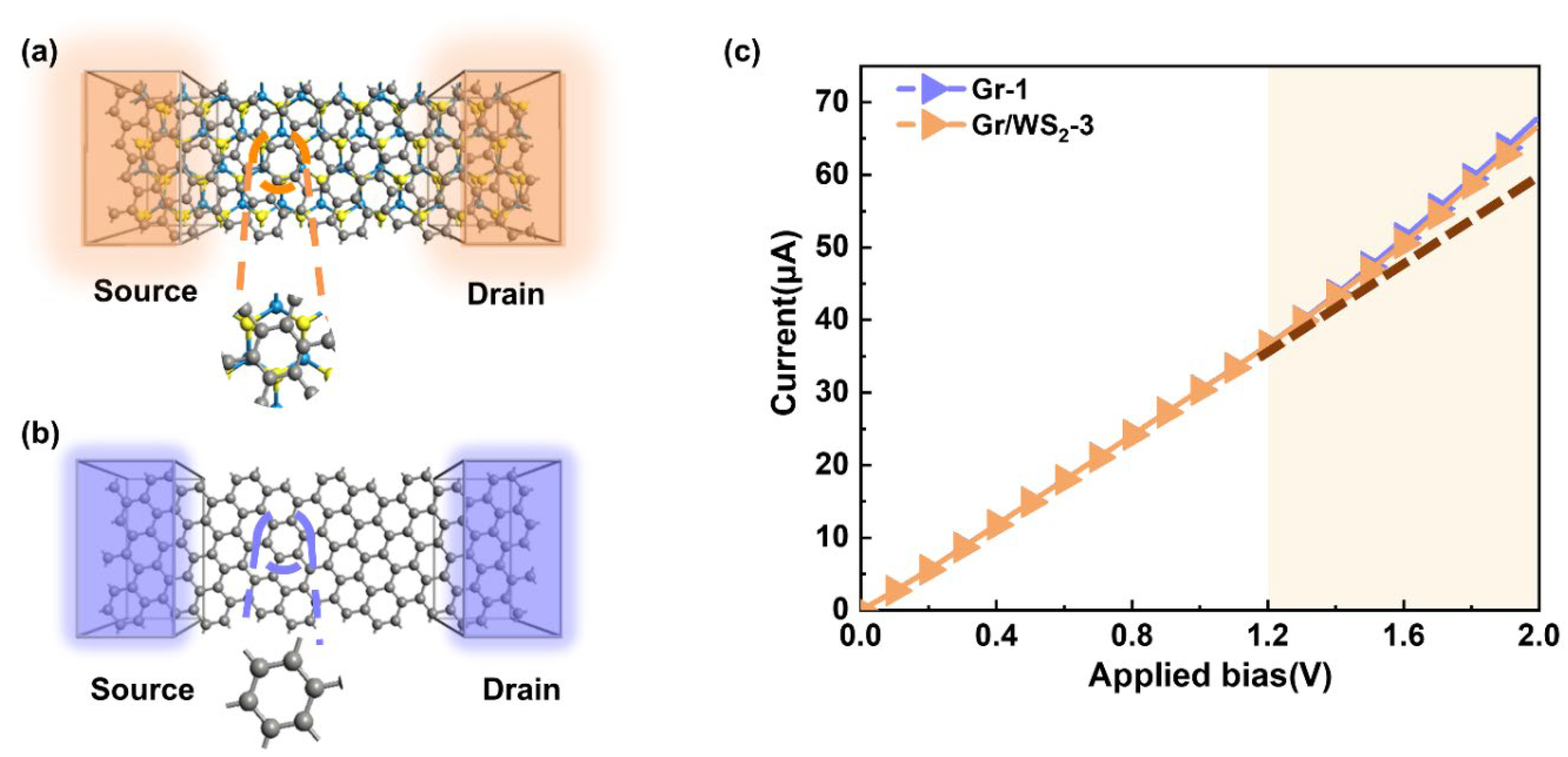
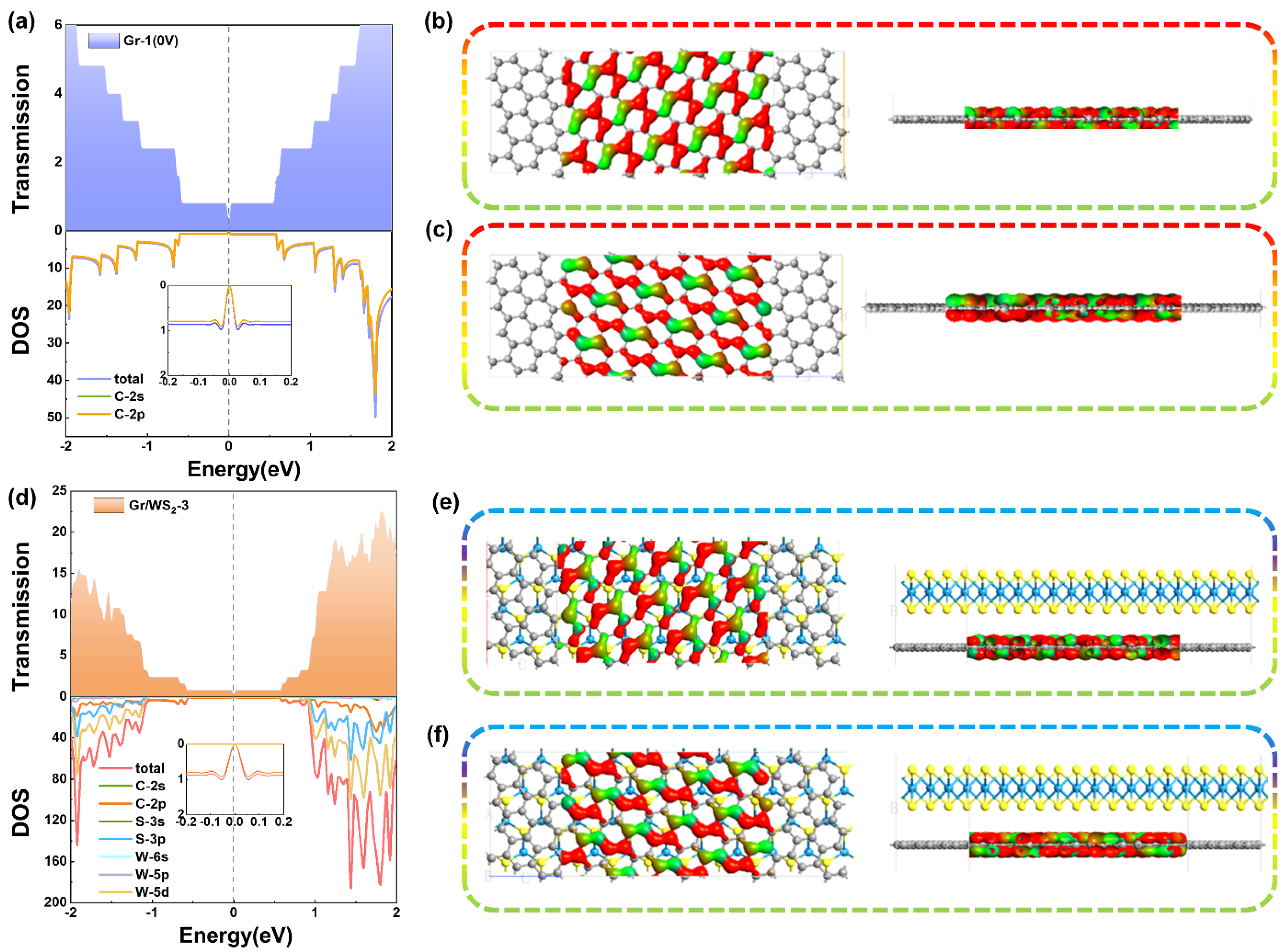
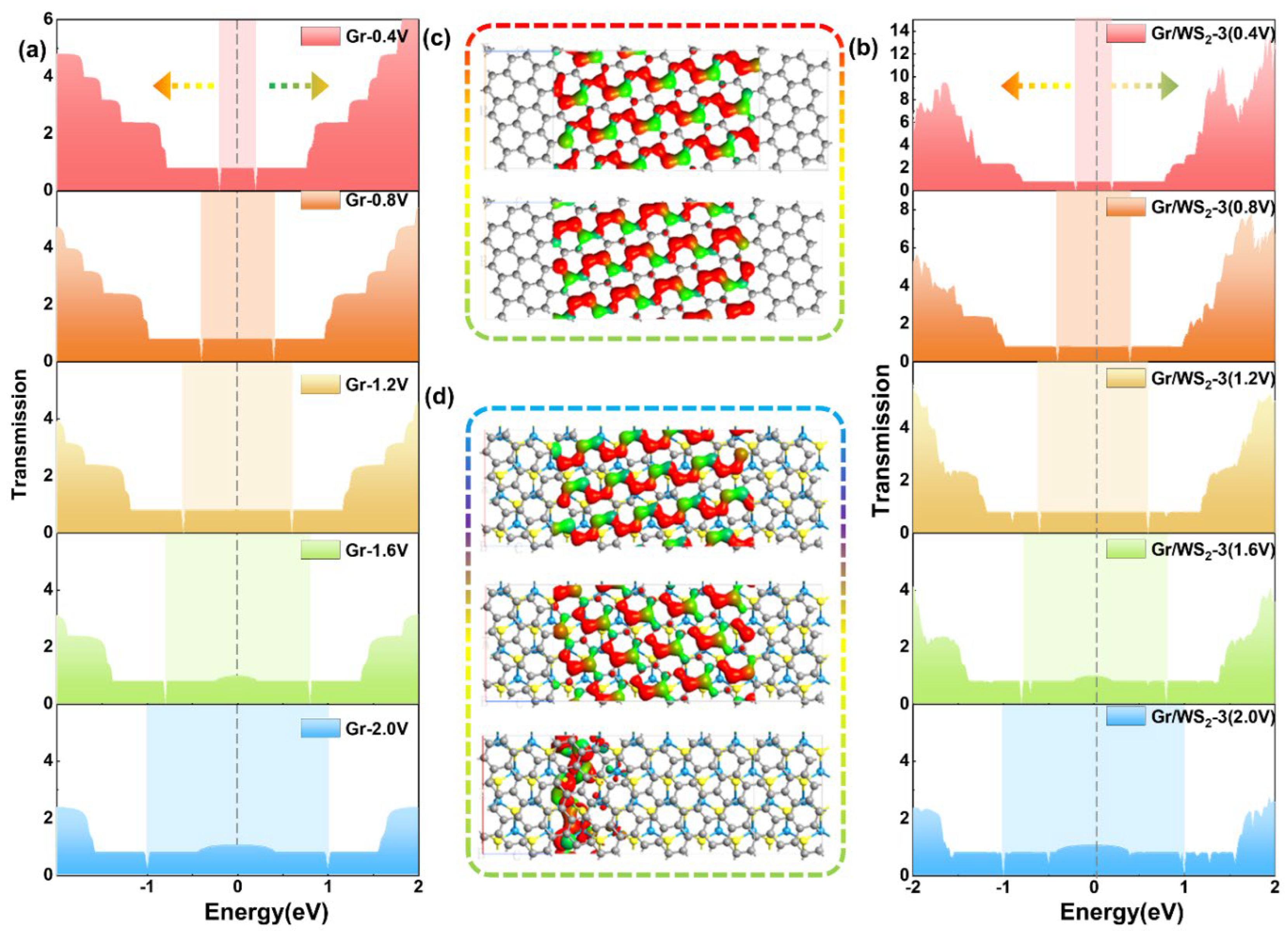
2. Results and Discussions
3. Computational Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coleman, J.N.; Lotya, M.; O’Neill, A.; Bergin, S.D.; King, P.J.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R.J. Two-dimensional nanosheets produced by liquid exfoliation of layered materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef] [PubMed]
- Britnell, L.; Ribeiro, R.M.; Eckmann, A.; Jalil, R.; Belle, B.D.; Mishchenko, A.; Kim, Y.-J.; Gorbachev, R.V.; Georgiou, T.; Morozov, S.V. Strong light-matter interactions in heterostructures of atomically thin films. Science 2013, 340, 1311–1314. [Google Scholar] [CrossRef]
- Yu, W.J.; Liu, Y.; Zhou, H.; Yin, A.; Li, Z.; Huang, Y.; Duan, X. Highly efficient gate-tunable photocurrent generation in vertical heterostructures of layered materials. Nat. Nanotechnol. 2013, 8, 952–958. [Google Scholar] [CrossRef] [PubMed]
- Chhowalla, M.; Jena, D.; Zhang, H. Two-dimensional semiconductors for transistors. Nat. Rev. Mater. 2016, 1, 16052. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Colombo, L.; Gellert, P.; Schwab, M.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Sun, Z.; Chang, H. Graphene and graphene-like two-dimensional materials in photodetection: Mechanisms and methodology. ACS Nano 2014, 8, 4133–4156. [Google Scholar] [CrossRef]
- Kandpal, H.; Anand, S.; Vaishya, J. Experimental observation of the phenomenon of spectral switching for a class of partially coherent light. IEEE J. Quantum Electron. 2002, 38, 336–339. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Yang, J.; Tang, L.; Luo, W.; Feng, S.; Leng, C.; Shi, H.; Wei, X. Interface engineering of a silicon/graphene heterojunction photodetector via a diamond-like carbon interlayer. ACS Appl. Mater. Interfaces 2021, 13, 4692–4702. [Google Scholar] [CrossRef]
- Xia, F.; Wang, H.; Jia, Y. Rediscovering black phosphorus as an anisotropic layered material for optoelectronics and electronics. Nat. Commun. 2014, 5, 4458. [Google Scholar] [CrossRef]
- Haberer, D.; Vyalikh, D.; Taioli, S.; Dora, B.; Farjam, M.; Fink, J.; Marchenko, D.; Pichler, T.; Ziegler, K.; Simonucci, S. Tunable band gap in hydrogenated quasi-free-standing graphene. Nano Lett. 2010, 10, 3360–3366. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, D.; Swaminathan, V.; Recine, G.; Balu, R.; Karna, S. Bandgap tuning of mono-and bilayer graphene doped with group IV elements. J. Appl. Phys. 2013, 113, 183701. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Kwon, J.; Jeong, Y.; Watanabe, K.; Taniguchi, T.; Im, S.; Lee, G.H. Graphene Via Contact Architecture for Vertical Integration of vdW Heterostructure Devices. Small 2022, 18, 2200882. [Google Scholar] [CrossRef]
- Lan, J.-C.; Qiao, J.; Sung, W.-H.; Chen, C.-H.; Jhang, R.-H.; Lin, S.-H.; Ng, L.-R.; Liang, G.; Wu, M.-Y.; Tu, L.-W. Role of carrier-transfer in the optical nonlinearity of graphene/Bi2Te3 heterojunctions. Nanoscale 2020, 12, 16956–16966. [Google Scholar] [CrossRef]
- Hu, J.; Li, L.; Wang, R.; Chen, H.; Xu, Y.; Zang, Y.; Li, Z.; Feng, S.; Lei, Q.; Xia, C. Fabrication and photoelectric properties of a graphene-silicon nanowire heterojunction on a flexible polytetrafluoroethylene substrate. Mater. Lett. 2020, 281, 128599. [Google Scholar] [CrossRef]
- Ren, X.; Wang, B.; Huang, Z.; Qiao, H.; Duan, C.; Zhou, Y.; Zhong, J.; Wang, Z.; Qi, X. Flexible self-powered photoelectrochemical-type photodetector based on 2D WS2-graphene heterojunction. FlatChem 2021, 25, 100215. [Google Scholar] [CrossRef]
- Liu, Y.; Weinert, M.; Li, L. Spiral growth without dislocations: Molecular beam epitaxy of the topological insulator Bi2Se3 on epitaxial graphene/SiC (0001). Phys. Rev. Lett. 2012, 108, 115501. [Google Scholar] [CrossRef]
- Vu, Q.A.; Shin, Y.S.; Kim, Y.R.; Nguyen, V.L.; Kang, W.T.; Kim, H.; Luong, D.H.; Lee, I.M.; Lee, K.; Ko, D.-S. Two-terminal floating-gate memory with van der Waals heterostructures for ultrahigh on/off ratio. Nat. Commun. 2016, 7, 12725. [Google Scholar] [CrossRef]
- Liu, X.; Gao, J.; Zhang, G.; Zhang, Y.-W. Design of phosphorene/graphene heterojunctions for high and tunable interfacial thermal conductance. Nanoscale 2018, 10, 19854–19862. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Q.; Xu, B. Lattice mismatch dominant yet mechanically tunable thermal conductivity in bilayer heterostructures. ACS Nano 2016, 10, 5431–5439. [Google Scholar] [CrossRef]
- Sun, X.; Li, X.; Zeng, Y.; Meng, L. Improving the stability of perovskite by covering graphene on FAPbI3 surface. Int. J. Energy Res. 2021, 45, 10808–10820. [Google Scholar] [CrossRef]
- Wang, X.; Long, R. Rapid charge separation boosts solar hydrogen generation at the graphene–MoS2 Junction: Time-domain Ab initio analysis. J. Phys. Chem. Lett. 2021, 12, 2763–2769. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Gao, S.; Zhang, F.; Meng, F.; Guo, Z.; Cao, R.; Zeng, Y.; Zhao, J.; Chen, S.; Hu, H. Repression of interlayer recombination by graphene generates a sensitive nanostructured 2D vdW heterostructure based photodetector. Adv. Sci. 2021, 8, 2100503. [Google Scholar] [CrossRef] [PubMed]
- Cong, C.; Shang, J.; Wang, Y.; Yu, T. Optical properties of 2D semiconductor WS2. Adv. Opt. Mater. 2018, 6, 1700767. [Google Scholar] [CrossRef]
- Yue, Y.; Chen, J.; Zhang, Y.; Ding, S.; Zhao, F.; Wang, Y.; Zhang, D.; Li, R.; Dong, H.; Hu, W. Two-dimensional high-quality monolayered triangular WS2 flakes for field-effect transistors. ACS Appl. Mater. Interfaces 2018, 10, 22435–22444. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.W.; Iqbal, M.Z.; Khan, M.F.; Kamran, M.A.; Majid, A.; Alharbi, T.; Eom, J. Tailoring the electrical and photo-electrical properties of a WS2 field effect transistor by selective n-type chemical doping. RSC Adv. 2016, 6, 24675–24682. [Google Scholar] [CrossRef]
- Brandbyge, M.; Mozos, J.-L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef]
- Jiang, J.-W. Graphene versus MoS2: A short review. Front. Phys. 2015, 10, 287–302. [Google Scholar] [CrossRef]
- Georgiou, T.; Yang, H.; Jalil, R.; Chapman, J.; Novoselov, K.S.; Mishchenko, A. Electrical and optical characterization of atomically thin WS2. Dalton Trans. 2014, 43, 10388–10391. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y.; Ni, J.; Shi, L.; Shi, S.; Tang, W. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M=Mo, Nb, W, Ta; X=S, Se, Te) monolayers. Phys. B Phys. Condens. Matter 2011, 406, 2254–2260. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207, Erratum in J. Chem. Phys. 2006, 124, 219906. [Google Scholar] [CrossRef]
- Li, W.; Wei, J.; Bian, B.; Liao, B.; Wang, G. The effect of different covalent bond connections and doping on transport properties of planar graphene/MoS2/graphene heterojunctions. Phys. Chem. Chem. Phys. 2021, 23, 6871–6879. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yang, Y.; Guo, Y.; Wang, Q.; Yan, X. Influence of length and interface structure on electron transport properties of graphene-MoS_2 in-plane heterojunction. Appl. Surf. Sci. 2019, 497, 143764. [Google Scholar] [CrossRef]
- Dong, J.C.; Li, H. Monoatomic Layer Electronics Constructed by Graphene and Boron Nitride Nanoribbons. J. Phys. Chem. C 2012, 116, 17259–17267. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Uddin, I.; Phan, N.A.N.; Whang, D.; Kim, G.-H. Dual-Channel WS2/WSe2 Heterostructure with Tunable Graphene Electrodes. ACS Appl. Electron. Mater. 2023, 5, 913–919. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, J.C.; Li, H. Electronic transport properties of in-plane heterostructures constructed by MoS2 and WS2 nanoribbons. RSC Adv. 2015, 5, 66852–66860. [Google Scholar] [CrossRef]
- Zheng, J.; Li, E.; Ma, D.; Cui, Z.; Wang, X. Effect on Schottky Barrier of Graphene/WS2 Heterostructure with Vertical Electric Field and Biaxial Strain. Phys. Status Solidi (b) 2019, 256, 1900161. [Google Scholar] [CrossRef]
- Georgiou, T.; Jalil, R.; Belle, B.D.; Britnell, L.; Gorbachev, R.V.; Morozov, S.V.; Kim, Y.J.; Gholinia, A.; Haigh, S.J.; Makarovsky, O. Vertical field-effect transistor based on graphene-WS2 heterostructures for flexible and transparent electronics. Nat. Nanotechnol. 2013, 8, 100–103. [Google Scholar] [CrossRef]
- Bai, Z.; Xiao, Y.; Luo, Q.; Li, M.; Peng, G.; Zhu, Z.; Luo, F.; Zhu, M.; Qin, S.; Novoselov, K. Highly Tunable Carrier Tunneling in Vertical Graphene-WS2-Graphene van der Waals Heterostructures. ACS Nano 2022, 16, 7880–7889. [Google Scholar] [CrossRef]
- Xia, C.; Xiong, W.; Xiao, W.; Du, J.; Jia, Y. Enhanced Carrier Concentration and Electronic Transport by Inserting Graphene into van der Waals Heterostructures of Transition-Metal Dichalcogenides. Phys. Rev. Appl. 2018, 10, 024028. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Pastawski, H.M. Classical and quantum transport from generalized Landauer-Büttiker equations. Phys. Rev. B 1991, 44, 6329. [Google Scholar] [CrossRef] [PubMed]

| Heterojunction | Lattice Parameters of Graphene (Å) | Rotation Angle of Graphene (°) | Lattice Parameters of WS2 (Å) | Rotation Angle of WS2 (°) | Lattice Mismatch (%) |
|---|---|---|---|---|---|
| Gr/WS2-1 | a = b = 9.8 | 0.0 | a = b = 9.5 | 0.0 | 3.1 |
| Gr/WS2-2 | a = b = 12.3 | 0.0 | a = b = 12.6 | 0.0 | 2.4 |
| Gr/WS2-3 | a = b = 6.5 | 21.8 | a = b = 6.3 | 60.0 | 3.1 |
| Gr/WS2-4 | a = b = 6.5 | 141.8 | a = b = 6.3 | 60.0 | 3.1 |
| Gr/WS2-5 | a = b = 6.5 | 21.8 | a = b = 6.3 | 180.0 | 3.1 |
| Gr/WS2-6 | a = b = 6.5 | 141.8 | a = b = 6.3 | 180.0 | 3.1 |
| Gr/WS2-7 | a = b = 8.5 | 0.0 | a = b = 8.3 | 21.8 | 2.1 |
| Gr/WS2-8 | a = b = 8.5 | 120.0 | a = b = 8.3 | 21.8 | 2.1 |
| Heterojunction | Energy of Graphene (eV) | Energy of WS2 (eV) | Energy of Heterojunction (eV) | Binding Energy (eV) |
|---|---|---|---|---|
| Gr/WS2-1 | −5038.3 | −10,206.0 | −15,246.9 | −2.6 |
| Gr/WS2-2 | −7874.7 | −18,145.4 | −26,022.2 | −2.1 |
| Gr/WS2-3 | −2204.4 | −4563.7 | −6741.6 | −0.6 |
| Gr/WS2-4 | −2204.4 | −4563.7 | −6741.6 | −0.6 |
| Gr/WS2-5 | −2204.4 | −4563.7 | −6741.6 | −0.6 |
| Gr/WS2-6 | −2204.4 | −4563.7 | −6741.6 | −0.6 |
| Gr/WS2-7 | −3779.3 | −7939.2 | −11,719.4 | −0.9 |
| Gr/WS2-8 | −3379.3 | −7939.2 | −11,719.4 | −0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Dai, X.; Zhang, L.; Li, H. Electron Transport Properties of Graphene/WS2 Van Der Waals Heterojunctions. Molecules 2023, 28, 6866. https://doi.org/10.3390/molecules28196866
Guo J, Dai X, Zhang L, Li H. Electron Transport Properties of Graphene/WS2 Van Der Waals Heterojunctions. Molecules. 2023; 28(19):6866. https://doi.org/10.3390/molecules28196866
Chicago/Turabian StyleGuo, Junnan, Xinyue Dai, Lishu Zhang, and Hui Li. 2023. "Electron Transport Properties of Graphene/WS2 Van Der Waals Heterojunctions" Molecules 28, no. 19: 6866. https://doi.org/10.3390/molecules28196866
APA StyleGuo, J., Dai, X., Zhang, L., & Li, H. (2023). Electron Transport Properties of Graphene/WS2 Van Der Waals Heterojunctions. Molecules, 28(19), 6866. https://doi.org/10.3390/molecules28196866