Einstein Model of a Graph to Characterize Protein Folded/Unfolded States
Abstract
:1. Introduction
2. Results and Discussion
2.1. Theory
2.1.1. Mechanical Interpretation of a Simple, Connected, and Undirected Graph
2.1.2. Thermostatistical Interpretation of Topological Descriptors of a Simple, Connected, and Undirected Graph
2.1.3. Relation between the Global Force Constant and the Average Shortest Path Length: Analytical Results
2.1.4. Einstein’s Model of a Graph
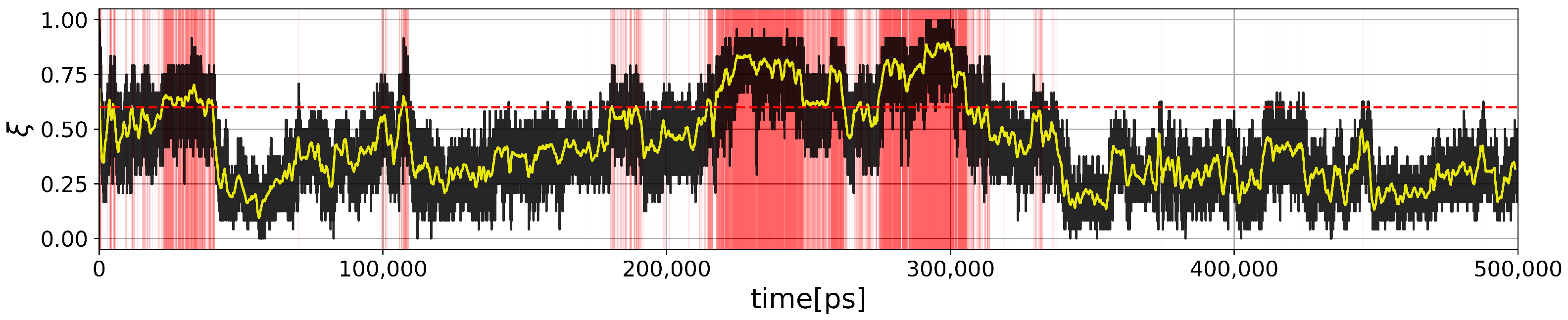
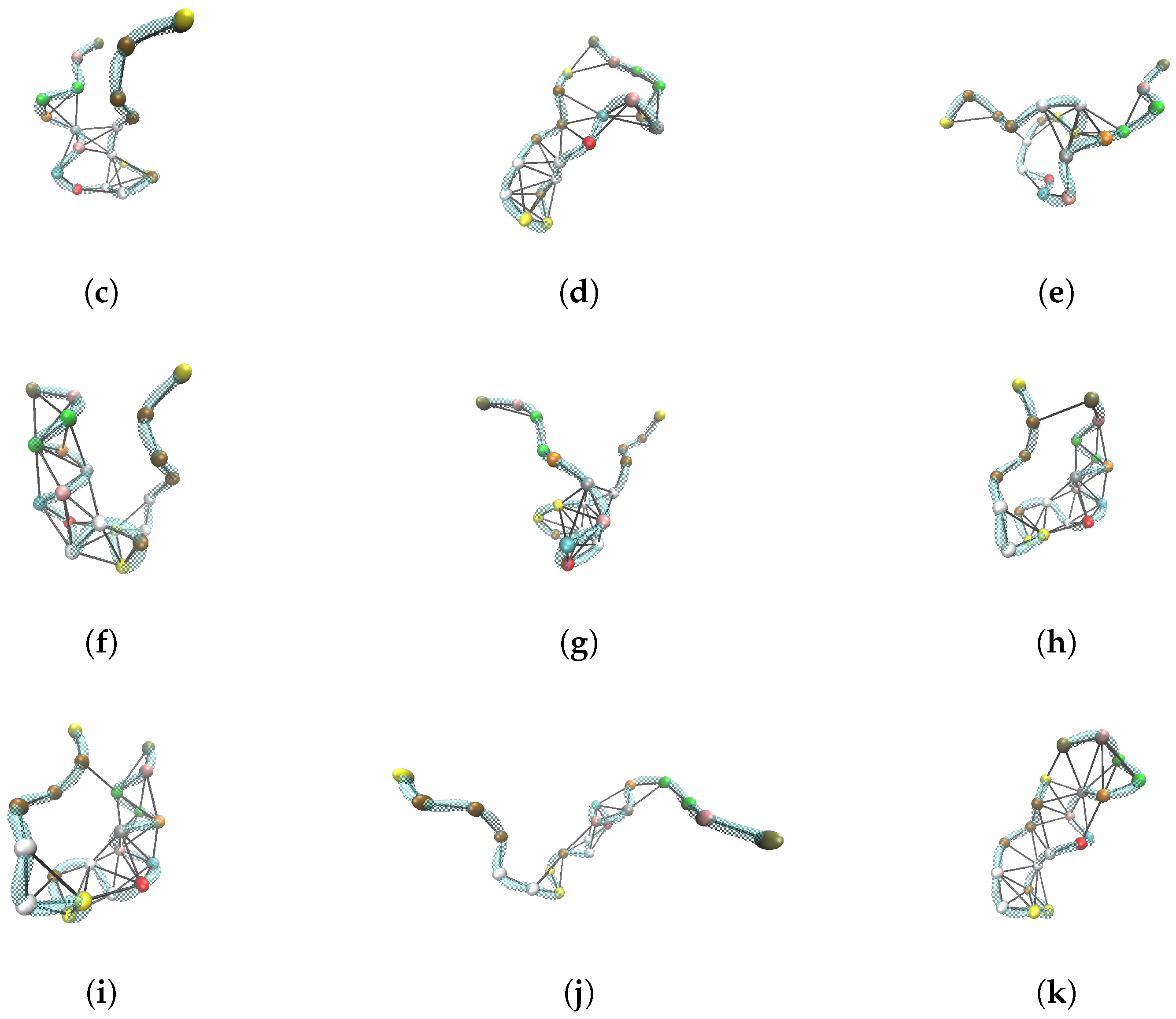
2.2. Topological Analysis of Folding/Unfolding MD Trajectory of Trp-Cage
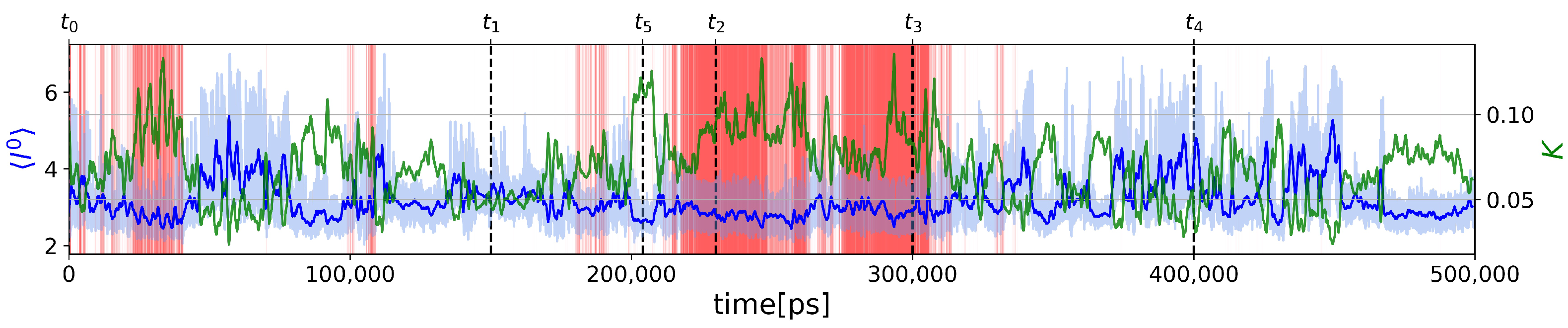
2.2.1. Two-State Definition
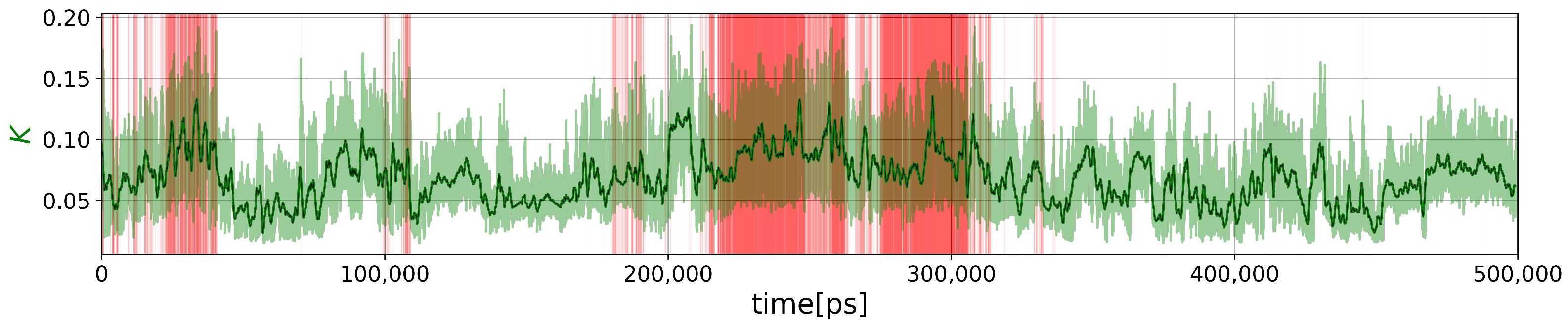
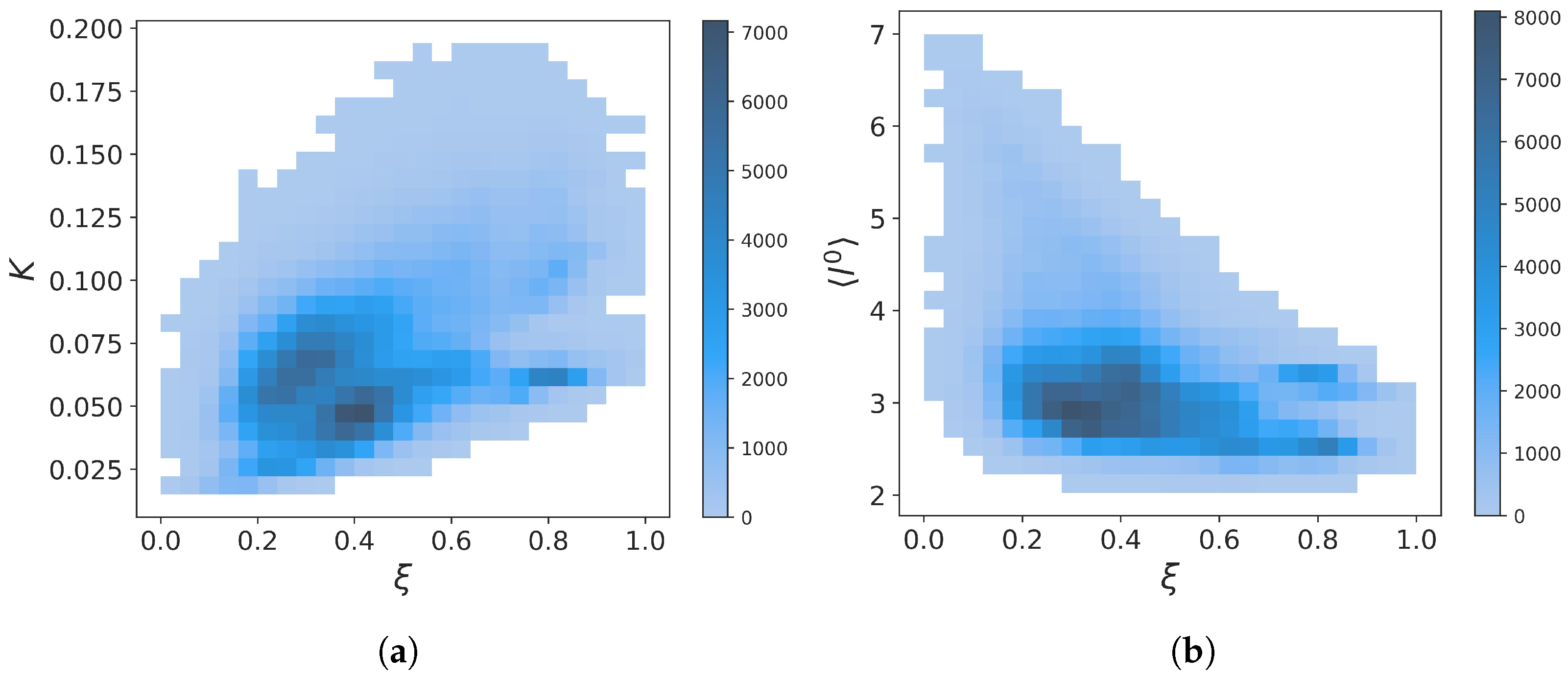
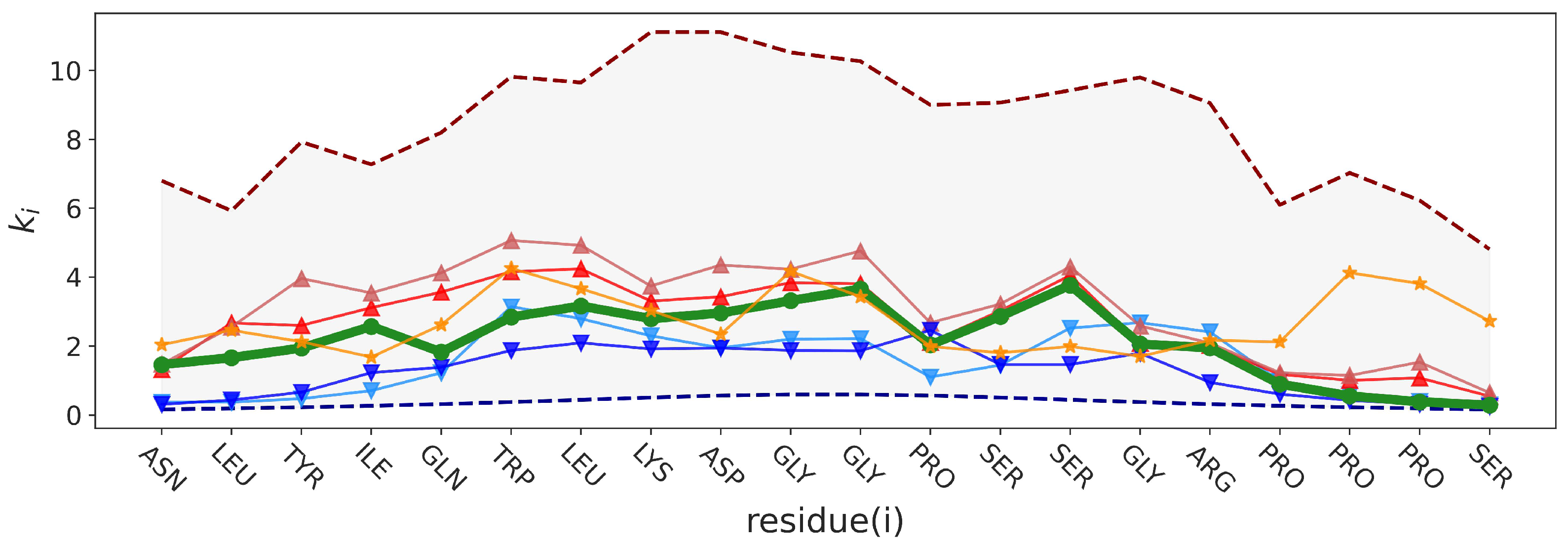
2.2.2. Force Constants and Shortest Path Length
2.2.3. Calculation of Free Energies Using the Einstein Model
3. Materials and Methods
3.1. Contacts and Protein Graph (PG)
3.2. Molecular Dynamics Trajectories
3.3. Statistics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | Molecular Dynamics |
| Probability Density Function |
References
- Dyson, H.J.; Wright, P.E. Unfolded Proteins and Protein Folding Studied by NMR. Chem. Rev. 2004, 104, 3607–3622. [Google Scholar] [CrossRef]
- Schuler, B.; Eaton, W.A. Protein folding studied by single-molecule FRET. Curr. Opin. Struct. Biol. 2008, 18, 16–26. [Google Scholar] [CrossRef]
- Lai, J.K.; Kubelka, G.S.; Kubelka, J. Sequence, structure, and cooperativity in folding of elementary protein structural motifs. Proc. Natl. Acad. Sci. USA 2015, 112, 9890–9895. [Google Scholar] [CrossRef]
- Sukenik, S.; Pogorelov, T.V.; Gruebele, M. Can Local Probes Go Global? A Joint Experiment–Simulation Analysis of λ6–85 Folding. J. Phys. Chem. Lett. 2016, 7, 1960–1965. [Google Scholar] [CrossRef]
- Muñoz, V.; Campos, L.A.; Sadqi, M. Limited cooperativity in protein folding. Curr. Opin. Struct. Biol. 2016, 36, 58–66. [Google Scholar] [CrossRef]
- Muñoz, V.; Cerminara, M. When fast is better: Protein folding fundamentals and mechanisms from ultrafast approaches. Biochem. J. 2016, 473, 2545–2559. [Google Scholar] [CrossRef]
- Zhuravleva, A.; Korzhnev, D.M. Protein folding by NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 100, 52–77. [Google Scholar] [CrossRef]
- Anfinsen, C.B. Principles that Govern the Folding of Protein Chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Anfinsen, C.B.; Scheraga, H.A. Experimental and Theoretical Aspects of Protein Folding. In Advances in Protein Chemistry; Anfinsen, C.B., Edsall, J.T., Richards, F.M., Eds.; Academic Press: Cambridge, MA, USA, 1975; Volume 29, pp. 205–300. [Google Scholar] [CrossRef]
- Dill, K.A.; Bromberg, S.; Yue, K.; Chan, H.S.; Ftebig, K.M.; Yee, D.P.; Thomas, P.D. Principles of protein folding—A perspective from simple exact models. Protein Sci. 1995, 4, 561–602. [Google Scholar] [CrossRef]
- Muñoz, V.; Eaton, W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11311–11316. [Google Scholar] [CrossRef]
- Onuchic, J.N.; Wolynes, P.G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004, 14, 70–75. [Google Scholar] [CrossRef]
- Scheraga, H.A. From helix–coil transitions to protein folding. Biopolymers 2008, 89, 479–485. [Google Scholar] [CrossRef]
- Senet, P.; Maisuradze, G.G.; Foulie, C.; Delarue, P.; Scheraga, H.A. How main-chains of proteins explore the free energy landscape in native states. Proc. Natl. Acad. Sci. USA 2008, 105, 19708–19713. [Google Scholar] [CrossRef]
- Dill, K.A.; Ozkan, S.B.; Shell, M.S.; Weikl, T.R. The Protein Folding Problem. Annu. Rev. Biophys. 2008, 37, 289–316. [Google Scholar] [CrossRef]
- Henry, E.R.; Best, R.B.; Eaton, W.A. Comparing a simple theoretical model for protein folding with all-atom molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17880–17885. [Google Scholar] [CrossRef]
- Grassein, P.; Delarue, P.; Scheraga, H.A.; Maisuradze, G.G.; Senet, P. Statistical Model to Decipher Protein Folding/Unfolding at a Local Scale. J. Phys. Chem. B 2018, 122, 3540–3549. [Google Scholar] [CrossRef]
- Grassein, P.; Delarue, P.; Nicolaï, A.; Neiers, F.; Scheraga, H.A.; Maisuradze, G.G.; Senet, P. Curvature and Torsion of Protein Main Chain as Local Order Parameters of Protein Unfolding. J. Phys. Chem. B 2020, 124, 4391–4398. [Google Scholar] [CrossRef]
- Vila, J.A. Rethinking the protein folding problem from a new perspective. Eur. Biophys. J. 2023, 52, 189–193. [Google Scholar] [CrossRef]
- Kussell, E.; Shimada, J.; Shakhnovich, E.I. A structure-based method for derivation of all-atom potentials for protein folding. Proc. Natl. Acad. Sci. USA 2002, 99, 5343–5348. [Google Scholar] [CrossRef]
- Vila, J.A.; Ripoll, D.R.; Scheraga, H.A. Atomically detailed folding simulation of the B domain of staphylococcal protein A from random structures. Proc. Natl. Acad. Sci. USA 2003, 100, 14812–14816. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How Fast-Folding Proteins Fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef]
- Nguyen, H.; Maier, J.; Huang, H.; Perrone, V.; Simmerling, C. Folding Simulations for Proteins with Diverse Topologies Are Accessible in Days with a Physics-Based Force Field and Implicit Solvent. J. Am. Chem. Soc. 2014, 136, 13959–13962. [Google Scholar] [CrossRef]
- Shao, Q.; Zhu, W. How Well Can Implicit Solvent Simulations Explore Folding Pathways? A Quantitative Analysis of α-Helix Bundle Proteins. J. Chem. Theory Comput. 2017, 13, 6177–6190. [Google Scholar] [CrossRef] [PubMed]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Buel, G.R.; Walters, K.J. Can AlphaFold2 predict the impact of missense mutations on structure? Nat. Struct. Mol. Biol. 2022, 29, 1–2. [Google Scholar] [CrossRef]
- Marx, V. Method of the Year: Protein structure prediction. Nat. Methods 2022, 19, 5–10. [Google Scholar] [CrossRef]
- Callaway, E. AlphaFold’s new rival? Meta AI predicts shape of 600 million proteins. Nature 2022, 611, 211–212. [Google Scholar] [CrossRef]
- Jones, D.T.; Thornton, J.M. The impact of AlphaFold2 one year on. Nat. Methods 2022, 19, 15–20. [Google Scholar] [CrossRef]
- Austin, R.H.; Beeson, K.W.; Eisenstein, L.; Frauenfelder, H.; Gunsalus, I.C. Dynamics of ligand binding to myoglobin. Biochemistry 1975, 14, 5355–5373. [Google Scholar] [CrossRef]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, P.G. The Energy Landscapes and Motions of Proteins. Science 1991, 254, 1598–1603. [Google Scholar] [CrossRef]
- Nicolaï, A.; Petiot, N.; Grassein, P.; Delarue, P.; Neiers, F.; Senet, P. Free-Energy Landscape Analysis of Protein-Ligand Binding: The Case of Human Glutathione Transferase A1. Appl. Sci. 2022, 12, 8196. [Google Scholar] [CrossRef]
- Guzzo, A.; Delarue, P.; Rojas, A.; Nicolaï, A.; Maisuradze, G.G.; Senet, P. Missense Mutations Modify the Conformational Ensemble of the α-Synuclein Monomer Which Exhibits a Two-Phase Characteristic. Front. Mol. Biosci. 2021, 8, 1104. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Das, R.; Soylu, M. A key review on graph data science: The power of graphs in scientific studies. Chemom. Intell. Lab. Syst. 2023, 240, 104896. [Google Scholar] [CrossRef]
- Vishveshwara, S.; Brinda, K.V.; Kannan, N. Protein structure: Insights from graph theory. J. Theor. Comput. Chem. 2002, 1, 187–211. [Google Scholar] [CrossRef]
- Giuliani, A.; Krishnan, A.; Zbilut, J.P.; Tomita, M. Proteins As Networks: Usefulness of Graph Theory in Protein Science. Curr. Protein Pept. Sci. 2008, 9, 28–38. [Google Scholar] [CrossRef]
- Atilgan, C.; Okan, O.B.; Atilgan, A.R. Network-Based Models as Tools Hinting at Nonevident Protein Functionality. Annu. Rev. Biophys. 2012, 41, 205–225. [Google Scholar] [CrossRef]
- Kantelis, K.F.; Asteriou, V.; Papadimitriou-Tsantarliotou, A.; Petrou, A.; Angelis, L.; Nicopolitidis, P.; Papadimitriou, G.; Vizirianakis, I.S. Graph theory-based simulation tools for protein structure networks. Simul. Model. Pract. Theory 2022, 121, 102640. [Google Scholar] [CrossRef]
- Scala, A.; Amaral, L.A.N.; Barthélémy, M. Small-world networks and the conformation space of a short lattice polymer chain. Europhys. Lett. 2001, 55, 594–600. [Google Scholar] [CrossRef]
- Vendruscolo, M.; Dokholyan, N.V.; Paci, E.; Karplus, M. Small-world view of the amino acids that play a key role in protein folding. Phys. Rev. E 2002, 65, 061910. [Google Scholar] [CrossRef]
- Atilgan, A.R.; Akan, P.; Baysal, C. Small-World Communication of Residues and Significance for Protein Dynamics. Biophys. J. 2004, 86, 85–91. [Google Scholar] [CrossRef]
- Bagler, G.; Sinha, S. Network properties of protein structures. Phys. A Stat. Mech. Its Appl. 2005, 346, 27–33. [Google Scholar] [CrossRef]
- Srivastava, D.; Bagler, G.; Kumar, V. Graph Signal Processing on protein residue networks helps in studying its biophysical properties. Phys. A Stat. Mech. Its Appl. 2023, 615, 128603. [Google Scholar] [CrossRef]
- Higman, V.A.; Greene, L.H. Elucidation of conserved long-range interaction networks in proteins and their significance in determining protein topology. Phys. A Stat. Mech. Its Appl. 2006, 368, 595–606. [Google Scholar] [CrossRef]
- Jacobs, D.J.; Rader, A.; Kuhn, L.A.; Thorpe, M. Protein flexibility predictions using graph theory. Proteins Struct. Funct. Bioinform. 2001, 44, 150–165. [Google Scholar] [CrossRef] [PubMed]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of Fluctuation Dynamics of Proteins with an Elastic Network Model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Rader, A.J.; Hespenheide, B.M.; Kuhn, L.A.; Thorpe, M.F. Protein unfolding: Rigidity lost. Proc. Natl. Acad. Sci. USA 2002, 99, 3540–3545. [Google Scholar] [CrossRef] [PubMed]
- Rao, F.; Caflisch, A. The Protein Folding Network. J. Mol. Biol. 2004, 342, 299–306. [Google Scholar] [CrossRef]
- Yin, Y.; Maisuradze, G.G.; Liwo, A.; Scheraga, H.A. Hidden Protein Folding Pathways in Free-Energy Landscapes Uncovered by Network Analysis. J. Chem. Theory Comput. 2012, 8, 1176–1189. [Google Scholar] [CrossRef]
- Jacobs, W.M.; Shakhnovich, E.I. Structure-Based Prediction of Protein-Folding Transition Paths. Biophys. J. 2016, 111, 925–936. [Google Scholar] [CrossRef]
- Zaccai, G. How Soft Is a Protein? A Protein Dynamics Force Constant Measured by Neutron Scattering. Science 2000, 288, 1604–1607. [Google Scholar] [CrossRef] [PubMed]
- Klein, D.J.; Randić, M. Resistance distance. J. Math. Chem. 1993, 12, 81–95. [Google Scholar] [CrossRef]
- Scaramozzino, D.; Khade, P.M.; Jernigan, R.L.; Lacidogna, G.; Carpinteri, A. Structural compliance: A new metric for protein flexibility. Proteins Struct. Funct. Bioinform. 2020, 88, 1482–1492. [Google Scholar] [CrossRef] [PubMed]
- Hill, T. An Introduction to Statistical Thermodynamics; Dover Publications, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Sum of the Reciprocal of Sine Squared. Published: Mathematics Stack Exchange. Available online: https://math.stackexchange.com/q/122933 (accessed on 5 August 2023).
- Handscomb, D.C.; Mason, J.C. Chebyshev Polynomials; Chapman and Hall/CRC: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Dai, X.; Fu, W.; Chi, H.; Mesias, V.S.D.; Zhu, H.; Leung, C.W.; Liu, W.; Huang, J. Optical tweezers-controlled hotspot for sensitive and reproducible surface-enhanced Raman spectroscopy characterization of native protein structures. Nat. Commun. 2021, 12, 1292. [Google Scholar] [CrossRef] [PubMed]
- Neidigh, J.W.; Fesinmeyer, R.M.; Andersen, N.H. Designing a 20-residue protein. Nat. Struct. Biol. 2002, 9, 425–430. [Google Scholar] [CrossRef] [PubMed]
- Ferreiro, D.U.; Komives, E.A.; Wolynes, P.G. Frustration in biomolecules. Q. Rev. Biophys. 2014, 47, 285–363. [Google Scholar] [CrossRef] [PubMed]
- Parra, R.G.; Schafer, N.P.; Radusky, L.G.; Tsai, M.Y.; Guzovsky, A.B.; Wolynes, P.G.; Ferreiro, D.U. Protein Frustratometer 2: A tool to localize energetic frustration in protein molecules, now with electrostatics. Nucleic Acids Res. 2016, 44, W356–W360. [Google Scholar] [CrossRef] [PubMed]
- Nicolaï, A.; Delarue, P.; Senet, P. Intrinsic Localized Modes in Proteins. Sci. Rep. 2015, 5, 18128. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 21 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008; pp. 11–15. [Google Scholar]
- Guzzo, A.; Delarue, P.; Rojas, A.; Nicolaï, A.; Maisuradze, G.G.; Senet, P. Wild-Type α-Synuclein and Variants Occur in Different Disordered Dimers and Pre-Fibrillar Conformations in Early Stage of Aggregation. Front. Mol. Biosci. 2022, 9, 910104. [Google Scholar] [CrossRef]
- Frauenfelder, H.; Fenimore, P.W.; Chen, G.; McMahon, B.H. Protein folding is slaved to solvent motions. Proc. Natl. Acad. Sci. USA 2006, 103, 15469–15472. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyler, S.; Laforge, C.; Guzzo, A.; Nicolaï, A.; Maisuradze, G.G.; Senet, P. Einstein Model of a Graph to Characterize Protein Folded/Unfolded States. Molecules 2023, 28, 6659. https://doi.org/10.3390/molecules28186659
Tyler S, Laforge C, Guzzo A, Nicolaï A, Maisuradze GG, Senet P. Einstein Model of a Graph to Characterize Protein Folded/Unfolded States. Molecules. 2023; 28(18):6659. https://doi.org/10.3390/molecules28186659
Chicago/Turabian StyleTyler, Steve, Christophe Laforge, Adrien Guzzo, Adrien Nicolaï, Gia G. Maisuradze, and Patrick Senet. 2023. "Einstein Model of a Graph to Characterize Protein Folded/Unfolded States" Molecules 28, no. 18: 6659. https://doi.org/10.3390/molecules28186659
APA StyleTyler, S., Laforge, C., Guzzo, A., Nicolaï, A., Maisuradze, G. G., & Senet, P. (2023). Einstein Model of a Graph to Characterize Protein Folded/Unfolded States. Molecules, 28(18), 6659. https://doi.org/10.3390/molecules28186659






