CO2 Capture and Release in Amine Solutions: To What Extent Can Molecular Simulations Help Understand the Trends?
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Systems: Structural Properties
2.1.1. AMP
2.1.2. BZA
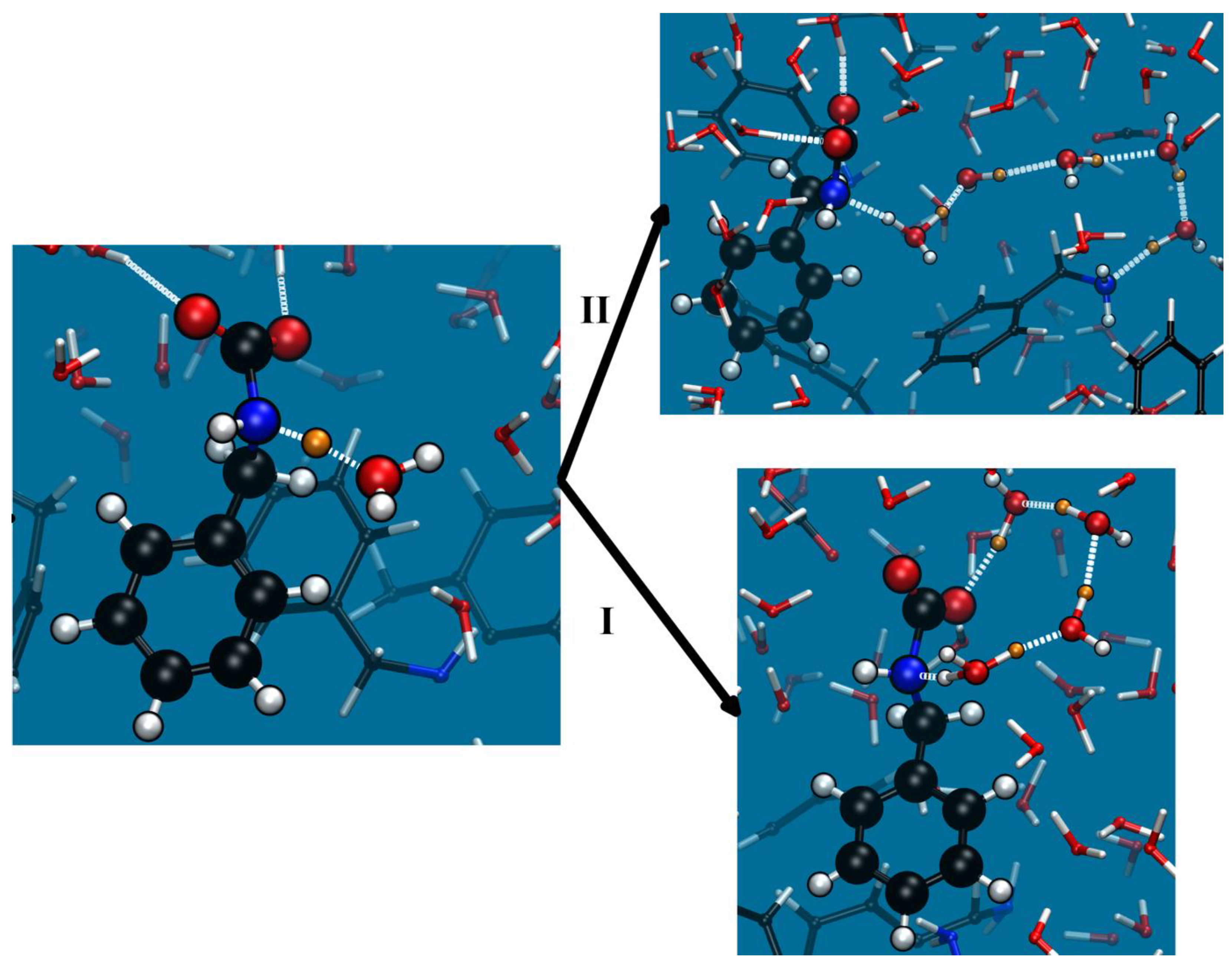
2.2. Reactions: CO2 Uptake and Release via Carbamate
2.2.1. AMP
2.2.2. BZA
2.3. Reactions: CO2 Uptake via Bicarbonate
2.4. What Have We Learned?
3. Methods
3.1. Methods Used in the Present Investigation
3.2. Methods Used by Other Authors
4. Conclusions
- Current molecular simulations necessarily refer to simplified scenarios, thus ignoring the role of several parameters such as the pH of the solution, the CO2 concentration, and the operating conditions, which are bound to influence the “performance” of the real systems.
- So far, most calculations have targeted the absorption of CO2 in the solvent and its release. We believe that, in order to better contribute to the tremendous effort to optimize the capturing agents of CO2, even staying with amine-based solvents, the focus of molecular simulations should move to physico-chemical processes leading to instability of the solvents and their consequences, e.g., thermal and oxidative degradation, precipitation, and corrosion.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zanco, S.E.; Pérez-Calvo, J.-F.; Gasós, A.; Cordiano, B.; Becattini, V.; Mazzotti, M. Postcombution CO2 Capture: A Comparative Techno-Economic Assessment of Three Technologies Using a Solvent, an Adsorbent, and a Membrane. ACS Eng. Au 2021, 1, 50–72. [Google Scholar] [CrossRef]
- Siegel, R.E.; Pattanayak, S.; Berben, L.A. Reactive Capture of CO2: Opportunities and Challenges. ACS Catal. 2023, 13, 766–784. [Google Scholar] [CrossRef]
- Dutcher, B.; Fan, M.; Russell, A.G. Amine-Based CO2 Capture Technology Development from the Beginning of 2013: A Review. ACS Appl. Mater. Interfaces 2015, 7, 2137–2148. [Google Scholar] [CrossRef] [PubMed]
- de Meyer, F.; Bignaud, C. The use of catalysis for faster CO2 absorption and energy-efficient solvent regeneration: An industry-focused critical review. Chem. Eng. J. 2022, 428, 131264. [Google Scholar] [CrossRef]
- Li, T.; Yu, Q.; Barzagli, F.; Li, C.; Che, M.; Zhang, Z.; Zhang, R. Energy efficient catalytic CO2 desorption: Mechanism, technological progress and perspective. Carbon Capture Sci. Technol. 2023, 6, 100099. [Google Scholar] [CrossRef]
- Waseem, M.; Al-Marzouqi, M.; Ghasem, N. A review of catalytically enhanced CO2-rich amine solutions regeneration. Environ. Chem. Eng. 2023, 11, 110188. [Google Scholar] [CrossRef]
- Zhao, S.; Feron, P.H.M.; Deng, L.; Favre, E.; Chabanon, E.; Yan, S.; Hou, J.; Chen, V.; Qi, H. Status and progress of membrane contactors in post-combustion carbon capture: A state-of-the-art review of new developments. J. Membr. Sci. 2016, 511, 180–206. [Google Scholar] [CrossRef]
- Chen, J.; Duan, L.; Ma, Y.; Jiang, Y.; Huang, A.; Zhu, H.; Jiao, H.; Li, M.; Hu, Y.; Zhou, H.; et al. Recent progress in calcium looping integrated with chemical looping combustion (CaL-CLC) using bifunctional CaO/CuO composites for CO2 capture: A state-of-the-art review. Fuel 2023, 334, 126630. [Google Scholar] [CrossRef]
- Li, Y.; Gambelli, A.M.; Rossi, F.; Mei, S. Effect of promoters on CO2 hydrate formation: Thermodynamic assessment and microscale Rama Raman spectroscopy/hydrate crystal morphology characterization analysis. Fluid Phase Equilibria 2021, 550, 113218. [Google Scholar] [CrossRef]
- Beiron, J.; Normann, F.; Johnsson, F. A techno-economic assessment of CO2 capture in biomass and waste-fired combined heat and power plants—A Swedish case study. Int. J. Greenh. Gas Control 2022, 118, 103684. [Google Scholar] [CrossRef]
- Panja, P.; McPherson, B.; Deo, M. Techno-Economic Analysis of Amine-based CO2 Capture Technology: Hunter Plant Case Study. Carbon Capture Sci. Technol. 2022, 3, 100041. [Google Scholar] [CrossRef]
- Meng, F.; Meng, Y.; Ju, T.; Han, S.; Lin, L.; Jiang, J. Research progress of aqueous amine solution for CO2 capture: A review. Renew. Sustain. Energy Rev. 2022, 168, 112902–112917. [Google Scholar] [CrossRef]
- Vevelstad, S.J.; Buvik, V.; Knuutila, H.K.; Grimstvedt, A.; da Silva, E.F. Important Aspects Regarding the Chemical Stability of Aqueous Amine Solvents for CO2 Capture. Ind. Eng. Chem. Res. 2022, 61, 15737–15753. [Google Scholar] [CrossRef]
- Sartori, G.; Savage, D.W. Sterically Hindered Amines for CO2 Removal from Gases. Ind. Eng. Chem. Fundam. 1983, 22, 239–249. [Google Scholar] [CrossRef]
- Zhang, P.; Shi, Y.; Wei, J.; Zhao, W.; Qing, Y.E. Regeneration of 2-amino-2-methyl-1-propanol used for carbon dioxide absorption. J. Environ. Sci. 2008, 20, 39–44. [Google Scholar] [CrossRef]
- Bougie, F.; Iliuta, M.C. Sterically Hindered Amine-Based Absorbents for the Removal of CO2 from Gas Streams. J. Chem. Eng. Data 2012, 57, 635–669. [Google Scholar] [CrossRef]
- da Silva, E.F. Theoretical study of the equilibrium constants for solvents for CO2 capture. Energy Procedia 2011, 4, 164–170. [Google Scholar] [CrossRef]
- Puxty, G.; Rowland, R.; Allport, A.; Yang, Q.; Bown, M.; Burns, R.; Maeder, M.; Attalla, M. Carbon Dioxide Postcombustion Capture: A Novel Screening Study of the Carbon Dioxide Absorption Performance of 76 Amines. Environ. Sci. Technol. 2009, 43, 6427–6433. [Google Scholar] [CrossRef]
- Perinu, C.; Arstad, B.; Bouzga, A.M.; Jens, K.J. 13C and 15N NMR Characterization of Amine Reactivity and Solvent Effects in CO2 Capture. J. Chem. Phys. B 2014, 118, 10167–10174. [Google Scholar] [CrossRef]
- Puxty, G.; Conway, W.; Yang, Q.; Bennett, R.; Fernandes, D.; Pearson, P.; Maher, D.; Feron, P. The evolution of a new class of CO2 absorbents: Aromatic amines. Int. J. Greenh. Gas Control 2019, 83, 11–19. [Google Scholar] [CrossRef]
- Conway, W.; Beyad, Y.; Feron, P.; Richner, G.; Puxty, G. CO2 Absorption into Aqueous Amine Blends containing Benzylamine (BZA), Monoethanolamine (MEA), and Sterically Hindered/Tertiary Amines. Energy Procedia 2014, 63, 1835–1841. [Google Scholar] [CrossRef]
- Richner, G.; Puxty, G.; Carnal, A.; Conway, W.; Maeder, M.; Pearson, P. Thermokinetic properties and performance evaluation of benzylamine-based solvents for CO2 capture. Chem. Eng. J. 2015, 264, 230–240. [Google Scholar] [CrossRef]
- Guido, C.A.; Pietrucci, F.; Andreoni, W. The Fate of a Zwitterion in Water from ab Initio Molecular Dynamics: Monoethanolamine (MEA)-CO2. J. Chem. Theory Comput. 2013, 9, 28–32. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Pietrucci, F.; Andreoni, W. Capture and Release of CO2 in Monoethanolamine Aqueous Solutions: New Insights from First-Principles Reaction Dynamics. J. Chem. Theory Comput. 2015, 11, 3189–3198. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Pietrucci, F.; Andreoni, W. Reaction dynamics of CO2 in aqueous amines from ab initio molecular dynamics: 2-amino-2-methyl-1,3-propanediol (AMPD) compared to monoethanolamine (MEA). Theor. Chem. Acc. 2016, 135, 60. [Google Scholar] [CrossRef]
- Ma, C.; Pietrucci, F.; Andreoni, W. Capturing CO2 in Monoethanolamine (MEA) Aqueous Solutions: Fingerprints of Carbamate Formation Assessed with First-Principles Simulations. J. Phys. Chem. Lett. 2014, 5, 1672–1677. [Google Scholar] [CrossRef]
- Andreoni, W.; Pietrucci, F. CO2 capture in amine solutions: Modelling and simulations with non-empirical methods. J. Phys. Condens. Matter 2016, 28, 503003. [Google Scholar] [CrossRef]
- da Silva, E.F.; Svendsen, H.F. Prediction of the pKa values of amines using ab initio methods and free-energy perturbations. Ind. Eng. Chem. Res. 2003, 42, 4414–4421. [Google Scholar] [CrossRef]
- da Silva, E.F.; Svendsen, H.F. Ab initio study of the reaction of carbamate formation from CO2 and alkanolamine. Ind. Eng. Chem. Res. 2004, 43, 3413–3418. [Google Scholar] [CrossRef]
- da Silva, E.F.; Svendsen, H.F. Study of the Carbamate Stability of Amines Using ab Initio Methods and Free-Energy Perturbations. Ind. Eng. Chem. Res. 2006, 45, 2497–2504. [Google Scholar] [CrossRef]
- da Silva, E.F.; Svendsen, H.F. Computational chemistry study of reactions, equilibrium and kinetics of chemical CO2 absorption. Int. J. Greenh. Gas Control 2007, 1, 151–157. [Google Scholar] [CrossRef]
- Stowe, H.M.; Hwang, G.S. Fundamental Understanding of CO2 Capture and Regeneration in Aqueous Amines from First-Principles Studies: Recent Progress and Remaining Challenges. Ind. Eng. Chem. Res. 2017, 56, 6887–6899. [Google Scholar] [CrossRef]
- Yang, X.; Rees, R.J.; Conway, W.; Puxty, G.; Yang, Q.; Winkler, D.A. Computational Modeling and Simulation of CO2 Capture by Aqueous Amines. Chem. Rev. 2017, 117, 9524–9593. [Google Scholar] [CrossRef] [PubMed]
- Kollias, L.; Zhang, D.; Allec, S.I.; Nguyen, M.-T.; Lee, M.-S.; Cantu, D.C.; Rousseau, R.; Glezakou, V.-A. Advanced Theory and Simulation to Guide the Development of CO2 Capture Solvents. ACS Omega 2022, 7, 12453–12466. [Google Scholar] [CrossRef]
- McCann, N.; Phan, D.; Fernandes, D.; Maeder, M. A systematic investigation of carbamate stability constants by 1H NMR. Int. J. Greenh. Gas Control 2011, 5, 396–400. [Google Scholar] [CrossRef]
- Ciftja, A.F.; Hartono, A.; Svendsen, H.F. Experimental study on carbamate formation in the AMP–CO2–H2O system at different temperatures. Chem. Eng. Sci. 2014, 107, 318–327. [Google Scholar] [CrossRef]
- Ciftja, A.F.; Hartono, A.; da Silva, E.F.; Svendsen, H.F. Study on Carbamate Stability in the AMP/CO2/H2O System from 13C-NMR Spectroscopy. Energy Procedia 2011, 4, 614–620. [Google Scholar] [CrossRef]
- Sherman, B.J.; Rochelle, G.T. Thermodynamic and Mass-Transfer Modeling of Carbon Dioxide Absorption into Aqueous 2-Amino-2-Methyl-1-Propanol. Ind. Eng. Chem. Res. 2017, 56, 319–330. [Google Scholar] [CrossRef]
- Conway, W.; Wang, X.; Fernandes, D.; Burns, R.; Lawrance, G.; Puxty, G.; Maeder, M. Comprehensive Kinetic and Thermodynamic Study of the Reactions of CO2(aq) and HCO3− with Monoethanolamine (MEA) in Aqueous Solution. J. Phys. Chem. A 2011, 115, 14340–14349. [Google Scholar] [CrossRef]
- Matsuzaki, Y.; Yamada, H.; Chowdhury, F.A.; Yamamoto, S.; Goto, K. Ab Initio Study of CO2 Capture Mechanisms in Aqueous 2-Amino-2-methyl-1-propanol: Electronic and Steric Effects of Methyl Substituents on the Stability of Carbamate. Ind. Eng. Chem. Res. 2019, 58, 3549–3554. [Google Scholar] [CrossRef]
- Gangarapu, S.; Marcelis, A.T.M.; Alhamed, Y.A.; Zuilhof, H. The transition states for CO2 capture by substituted ethanolamines. ChemPhysChem 2015, 16, 3000–3006. [Google Scholar] [CrossRef]
- Stowe, H.M.; Vilciauskas, L.; Paek, E.; Hwang, G.S. On the origin of preferred bicarbonate production from carbon dioxide (CO2) capture in aqueous 2-amino-2-methy-1-propanol (AMP). Phys. Chem. Chem. Phys. 2015, 17, 29184–29192. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Conway, W.; Burns, R.; McCann, N.; Maeder, M. Comprehensive Study of the Hydration and Dehydration Reactions of Carbon Dioxide in Aqueous Solution. J. Phys. Chem. A 2010, 114, 1734–1740. [Google Scholar] [CrossRef] [PubMed]
- Matin, N.S.; Remias, J.E.; Neathery, J.K.; Liu, K. Facile Method for Determination of Amine Speciation in CO2 Capture Solutions. Ind. Eng. Chem. Res. 2012, 51, 6613–6618. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A.; Tiwari, P. Metadynamics: A unified framework for accelerating rare events and sampling thermodynamics and kinetics. In Handbook of Materials Modeling—Methods: Theory and Modeling; Andreoni, W., Yip, S., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 565–595. [Google Scholar]
- da Silva, E.F.; Kuznetsova, T.; Kvamme, B.; Merz, K.M. Molecular Dynamics Study of Ethanolamine as a Pure Liquid and in Aqueous Solution. J. Phys. Chem. B 2007, 111, 3695–3703. [Google Scholar] [CrossRef]
- Wang, J.M.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 1988, 27, 1787–1799. [Google Scholar] [CrossRef]
- Price, D.J.; Brooks, C.L. A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Pietrucci, F.; Saitta, A.M. Formamide reaction network in gas phase and solution via a unified theoretical approach: Toward a reconciliation of different prebiotic scenarios. Proc. Natl. Acad. Sci. USA 2015, 112, 15030–15035. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation models based on electron density and on a continuum model of the solvent defined by the bulk dieletric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Pietrucci, F. Strategies for the exploration of free energy landscapes: Unity in diversity and challenges ahead. Rev. Phys. 2017, 2, 32–45. [Google Scholar] [CrossRef]
- Magrino, T.; Huét, L.; Saitta, A.M.; Pietrucci, F. Critical Assessment of Data-Driven versus Heuristic Reaction Coordinates in Solution Chemistry. J. Phys. Chem. A 2022, 126, 8887–8900. [Google Scholar] [CrossRef]
- Mostafavi, E.; Ashrafi, O.; Navarri, P. Assessment of process modifications for amine based post-combustion carbon capture processes. Clean. Eng. Technol. 2021, 4, 100249. [Google Scholar] [CrossRef]
- Helei, L.; Tantikhajorngosol, P.; Chan, C.; Tontiwachwuthikul, P. Technology Development and applications of artificial intelligence for post-combustion carbon dioxide capture: Critical literature review and perspectives. J. Greenh. Gas Control 2021, 108, 103307. [Google Scholar] [CrossRef]
- Yan, Y.; Borhani, T.N.; Subraveti, S.G.; Pai, K.N.; Prasad, V.; Rajendran, A.; Nkulikiyinka, P.; Asibor, J.O.; Zhang, Z.; Shao, D.; et al. Harnessing the power of machine learning for carbon capture, utilisation, and storage (CCUS)—A state-of-the-art review. Energy Environ. Sci. 2021, 14, 6122–6157. [Google Scholar] [CrossRef]
- Chatziasteriou, C.C.; Kikkinides, E.S.; Georgiadis, M.C. Recent advances on the modeling and optimization of CO2 capture processes. Comput. Chem. Eng. 2022, 165, 107938. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- CPMD. IBM Corp 1990–2022 and MPI für Festkörperforschung Stuttgart 1997–2001. Available online: https://www.cpmd.org/ (accessed on 29 December 2021).
- Bonomi, M.; Branduardi, D.D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raitei, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
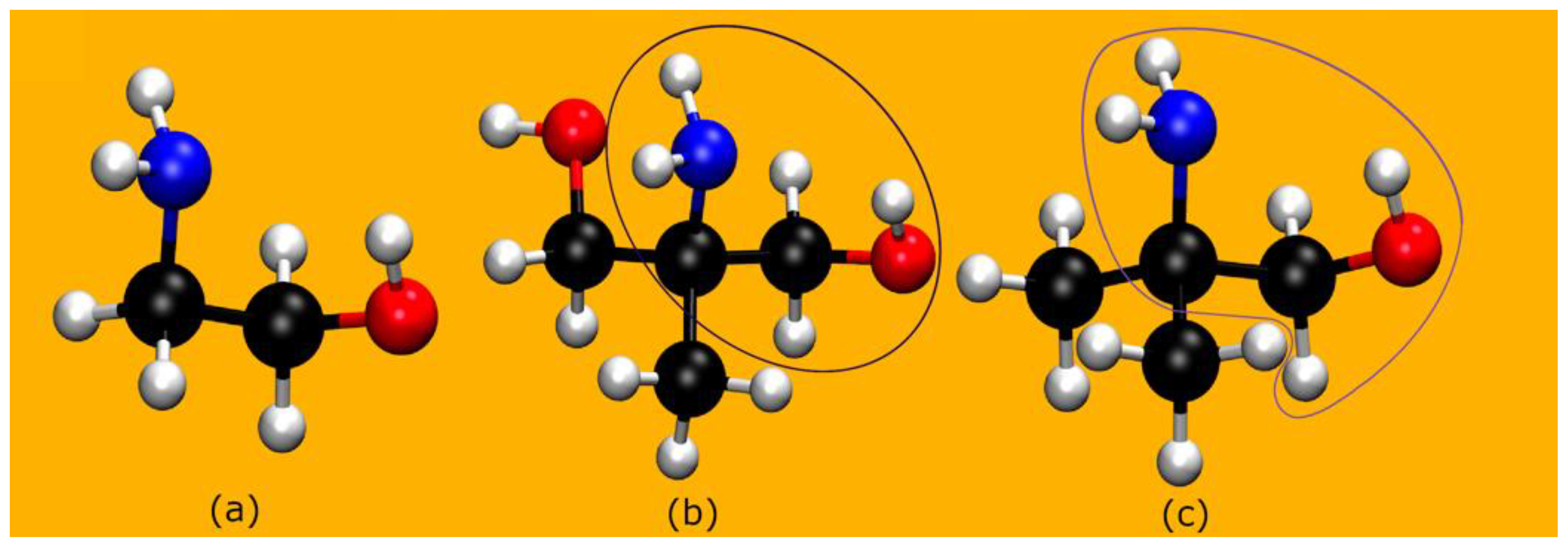
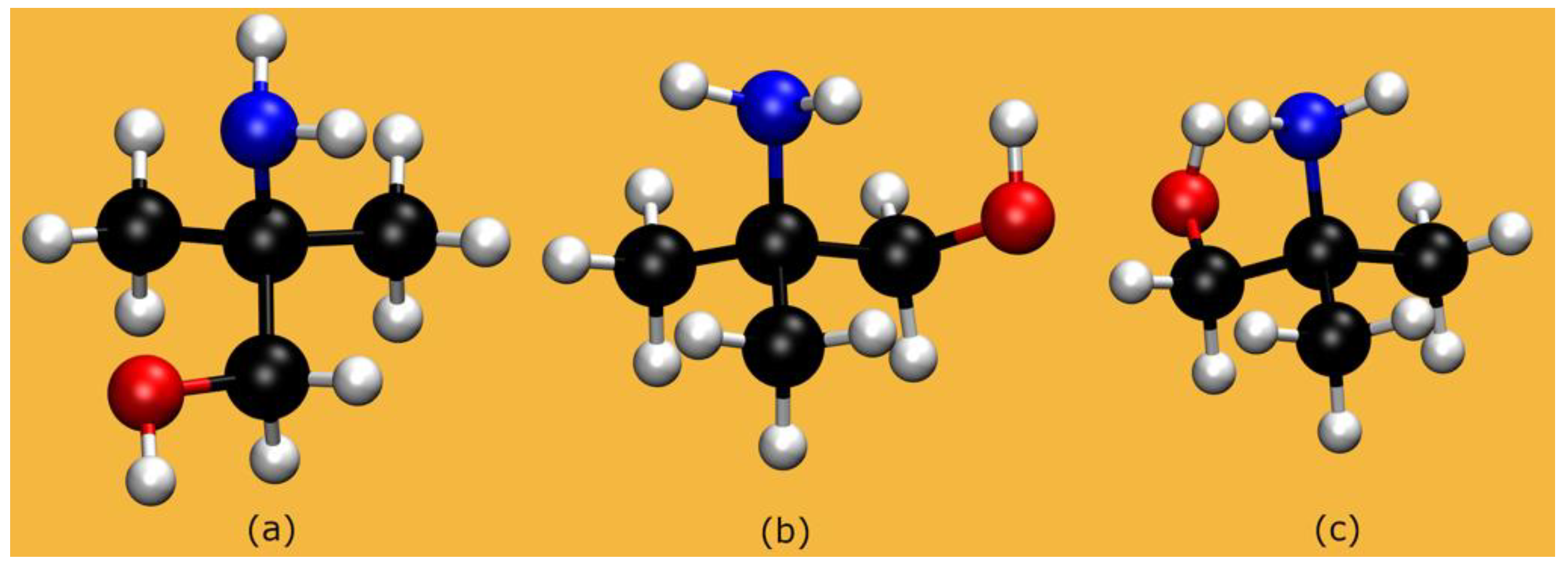
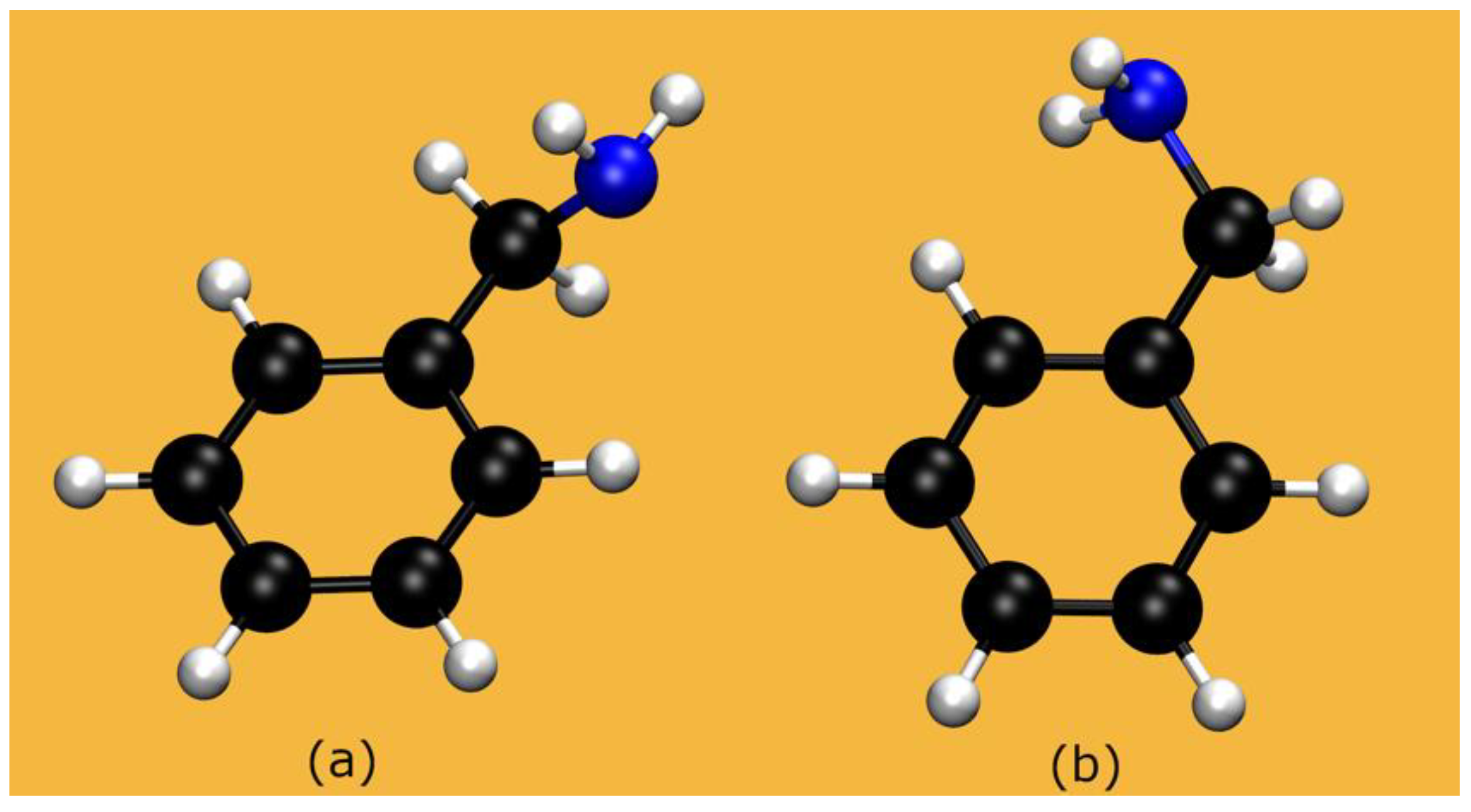

| Dihedral Angle | AMP-a | AMP-b | AMP-c | |||
|---|---|---|---|---|---|---|
| mol | aq | mol | aq | mol | aq | |
| (OCCN) | 61 | 64 [8] | 54 | 62 [9] | 56 | 57 [11] |
| (HOCC) | 179 | 171 [9] | −72 | 65 [15] | 42 | 46 [15] |
| Dihedral Angle | BZA-a | BZA-b | ||
|---|---|---|---|---|
| mol | aq | mol | aq | |
| (H1NCC) | −63 | −63 [17] | −60 | −63 [17] |
| (H2NCC) | 177 | 165 [17] | 59 | 50 [11] |
| (NCCC) | 130 | 138 [9] | 3 | 11 [7] |
| (NCCC) | −50 | −58 [11] | −178 | −169 [10] |
| N | L (Å) | N | L (Å) | ||
|---|---|---|---|---|---|
| AMP-a | 3.0 [0.8] | 1.82 [0.18] | MEA-a | 4.6 [1.2] | 1.76 [0.18] |
| AMP-b | 2.7 [0.7] | 1.88 [0.18] | MEA-b | 4.2 [0.6] | 1.77 [0.20] |
| AMP-c | 2.5 [0.9] | 1.97 [0.15] | |||
| AMPD-a | 4.5 [0.9] | 1.84 [0.20] | AMPD-b | 4.5 [0.9] | 1.84 [0.20] |
| BZA-a | 5.2 [1.1] | 1.86 [0.21] | BZA-b | 4.8 [1.2] | 1.81 [0.19] |
| BZA | MEA | AMPD | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| N (amine) | 4.2 [0.9] | 4.2 [0.7] | 3.3 [0.8] | 3.7 [1.0] | 5.3 [0.7] | 5.6 [1.4] |
| O (COO) | 7.2 [0.8] | 6.5 [0.6] | 5.3 [0.7] | 4.9 [1.0] | 6.6 [1.6] | 6.5 [1.6] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Pietrucci, F.; Andreoni, W. CO2 Capture and Release in Amine Solutions: To What Extent Can Molecular Simulations Help Understand the Trends? Molecules 2023, 28, 6447. https://doi.org/10.3390/molecules28186447
Ma C, Pietrucci F, Andreoni W. CO2 Capture and Release in Amine Solutions: To What Extent Can Molecular Simulations Help Understand the Trends? Molecules. 2023; 28(18):6447. https://doi.org/10.3390/molecules28186447
Chicago/Turabian StyleMa, Changru, Fabio Pietrucci, and Wanda Andreoni. 2023. "CO2 Capture and Release in Amine Solutions: To What Extent Can Molecular Simulations Help Understand the Trends?" Molecules 28, no. 18: 6447. https://doi.org/10.3390/molecules28186447
APA StyleMa, C., Pietrucci, F., & Andreoni, W. (2023). CO2 Capture and Release in Amine Solutions: To What Extent Can Molecular Simulations Help Understand the Trends? Molecules, 28(18), 6447. https://doi.org/10.3390/molecules28186447








